Abstract
For general metric theories of gravity, we compare the approach that describes/derives the field equations of gravity as a thermodynamic identity with the one which looks at them from entropy bounds. The comparison is made through the consideration of the matter entropy flux across (Rindler) horizons, studied by making use of the notion of a limiting thermodynamic scale of matter, previously introduced in the context of entropy bounds. In doing this: (i) a bound for the entropy of any lump of matter with a given energy-momentum tensor is considered, in terms of a quantity, which is independent of the theory of gravity that we use; this quantity is the variation of the Clausius entropy of a suitable horizon when the element of matter crosses it; (ii) by making use of the equations of motion of the theory, the same quantity is then expressed as the variation of Wald’s entropy of that horizon (and this leads to a generalized form of the generalized covariant entropy bound, applicable to general diffeomorphism-invariant theories of gravity); and (iii) a notion of for horizons, as well as an expression for it, is given.
PACS Classifications:
04.20.Cv; 04.50.-h; 04.60.-m; 04.70.Dy
1. Motivation
The thermodynamic description of the field equations of gravity was first performed by Jacobson in [1], where these equations were shown to be equivalent to a thermodynamic identity. In [2,3], Padmanabhan has shown that this identity was obtainable from the extremization of a suitable entropy functional (see also [4,5] for a general account of this). In these approaches, arbitrary accelerating observers at a generic point of spacetime are considered. The equations of motion are obtained through the proper consideration of a key quantity, (the energy flux of matter crossing the horizon over horizon temperature), or the variation of the Clausius entropy of the horizon, associated with the crossing of matter through local Rindler horizons. It represents the change of entropy of the “system beyond the horizon” or, in brief, of the horizon (concerning the general issue of whether patches of accelerating (or general) horizons, i.e., not only of black hole horizons, can consistently be associated with an entropy; cf. [6]).
Our aim here, is to contrast this approach with the one that obtains the equations of motion from entropy bounds. Crucial to these is the entropy of matter. In entropy bounds (in their generalized formulation [7], which can be thought of as subsuming many other formulations (including the first entropy bound ever formulated, the Bekenstein bound for the entropy-to-energy ratio [8]) and can be considered as a general statement of holography), the entropy of matter, which goes through a null hypersurface, is bounded by a quarter of the change of the area of the spatial cross-section of the hypersurface. The existence of such a bound is seen as remounting at the end to the existence of a lower limit to the “amount of space” to be assigned to the single bit of information, a limit of the order of the Planck length.
If one further postulates that this latter feature of information is intrinsic, that is unrelated to gravity, it is then possible to derive the equations of motion of gravity from it. That is, from the mere existence of this fundamental discretisation of space associated with information, one can derive that matter curves spacetime and the way that it does (independent explicit implementations of this idea are [9,10]; see also [11,12]; it can however be seen that it was already contained in [1]; in [13,14] and [5], a gravitational acceleration of entropic origin is also considered, but apparently, with no intention of considering this as a derivation of gravity from horizon entropy). If, on the contrary, on defining the limiting “amount of space” above, gravity itself intervenes, the derivation would turn into a description of gravity in terms of entropy bounds. Gravity would be one among the basic players and would no longer be reducible, at a fundamental level, to the pure thermodynamics of something else (while maintaining its emergent thermodynamic nature in the long wavelength limit).
What is behind the formulation of the entropy bounds in terms of the area/4 of suitable surfaces, is that, in case these surfaces act as (spatial cross-sections of) horizons, the area/4 does coincide with horizon entropy, and this implies Einstein gravity. The approach to the equations of motion as a thermodynamic identity is independent, instead, of being the horizon entropy given by area times , or by area times any other constant, or also, given by general expressions involving, say, a dependence on curvature at each point (we are insisting, pedantically perhaps, on the expression “area times a constant” in place of “proportional to area” because the latter expression can include entropies still locally proportional to area, but not given by area times a constant, due to a dependence on the point). The results in [1] have been obtained, indeed, on assuming horizon entropy as area times a constant; but extensions of these results to more general expressions for horizon entropy have been suggested in [1] itself and explicitly worked out in [15] for Gauss–Bonnet and general Lanczos–Lovelock models [16,17,18] (in a cosmological setting), in [19] (for theories) and (to include any diff-invariant theory) in [4,5,20], through the use of Wald’s entropy [21,22,23] as horizon entropy. The mentioned derivation in [2,3] of the equations of motion from extremization of a suitable entropy functional lives moreover in a context far more general than Einstein gravity (Lanczos–Lovelock models).
In our bridging of the two approaches, there is thus a need to disentangle in the entropy bounds what is gravitational dynamics dependent and what can act as a bound to matter entropy in the form of a quantity, which is irrespective of the gravitational theory in which we are. This is what we try to do in what follows.
The framework in which we move is arbitrary diffeomorphism-invariant theories of gravity with gravitational Lagrangians depending on the metric, on the Riemann tensor and on the derivatives of the latter of whichever order and nothing else and with minimal coupling between matter and gravity.
2. Bound to the Entropy of an Element of Matter as Variation of the Clausius Entropy of the Hottest Horizon that is Going to Swallow It
In the calculation of matter fluxes through the horizon, approaches differ in the assumptions they make concerning the local Rindler horizon that they are considering (for instance, Jacobson [1] and Padmanabhan [2,3,4,5]). In particular, the expansion of the null congruence, which generates the horizon, is assumed to be vanishing at the point under consideration in [1], while it is arbitrary in [2,3,4,5]. This difference in the assumptions has remarkable consequences concerning the definition/interpretation of some thermodynamic potentials associated with matter fluxes through horizons, as pointed out and discussed in [24]. However, it does not appear to affect the variation of Clausius entropy of the horizon, provided that a notion of Clausius entropy for arbitrary bifurcate null surfaces is introduced [25].
These topics are strictly connected to the present discussion. Here, however, we wish to elaborate on Clausius entropy of the horizon in its ability to bound the entropy of matter dropped through the horizon and in its independence of the gravity theory we are in, regardless of any given horizon expansion. We choose thus to consider the simplest possible case, namely the case of a patch of the Rindler horizon with vanishing expansion θ. The results we shall find are applicable to any horizon locally approximable by Rindler (as bifurcate Killing horizons are).
The Wald entropy associated with any patch of horizon, in particular to Rindler horizons with , does depend, of course, on the gravity theory in which we are. The emphasis in this section is that the variation of Clausius entropy of the horizon associated with the passage of a lump of matter through it is instead a (gravitational) dynamics-independent quantity. The reason for this emphasis is that, given any element of matter characterized by its energy-momentum tensor , besides its size, our aim is to construct a bound to its entropy in terms of the variation of the Clausius entropy of (a certain) horizon; a bound that thus turns out to be independent of gravitational dynamics. We do this by making use of the concept, introduced earlier [26,27].
We consider some smooth distribution of matter. We associate with it its energy-momentum tensor field defined in a D-dimensional (gauge [28]) spacetime () with metric , the geometry of this spacetime being determined, through some field equations, by that matter and all other matter in the Universe. At a generic point P in this spacetime, let be a null vector, directed to the future of P. We then consider a local inertial frame around P, with coordinates , such that P is at , and chosen in such a way as to have given by (1,1) in the plane . The null curve has affine parameter X and tangent . We consider a small piece of matter around P. The element of matter has a generic velocity in the local inertial frame. Its flow across any patch of surface is determined by the velocity vector, which has an intrinsic meaning independent of the gravity theory, which determined a given spacetime as a solution (and back-reaction effects, due to shrinking of the area while the element of matter goes through, are second order effects with respect to this in the flow).
Let us next consider the local Rindler frame [1,4] associated with an observer accelerating along X with acceleration κ, which is at rest with respect to the local inertial frame at Rindler time . We know that the metric can be written as with obvious notation, with Rindler coordinates and the Euclidean metric in the -plane. In these coordinates, the accelerating observer 𝒜 is, at , at .
The Killing vector corresponding to time translation invariance, null on the horizon and orthogonal to it, is what is needed to express the mass M of the horizon (of the “system beyond the horizon”), attributed to it by the accelerating observer. The condition that is , or , gives the location of the horizon. To this, the accelerating observer, which sees herself in a thermal bath, assigns a temperature . For the entire construction to be consistent, the size associated with the Rindler description must be much smaller than the size on which the local inertial frame approximation works, that is , where is the magnitude of a typical component of the curvature tensor. We assume to have chosen κ large enough such that this is the case.
Let us first review how it goes in the standard approach, that the variation of the Clausius entropy of the horizon associated with the passage of an element of matter is independent of the gravitational dynamics. For this, we have to obtain the energy flux entering in the expression . It coincides (since the horizon is orthogonal to ) with the increment in mass of the horizon. Standard calculation gives:
where A is the area of the cross-section of the element of matter in the -plane, and its size in the X-coordinate. This quantity depends on the characteristics of the lump of matter (, A, ) and on the geometric characteristics of the horizon (, ); in no way can it depend on the equations of motion of gravity, whatever they are, having as a solution associated with the assigned distribution of matter. The same can be said of the associated Clausius entropy variation of the horizon, since:
and is given with the field . Thus, the expression of the amount of Clausius entropy of the horizon associated with the passage of a lump of matter through it displays in an obvious way the independence of this quantity with respect to gravitational dynamics.
Let us now stay with the element of matter and consider any possible local Rindler horizon with any direction and any temperature, i.e., the horizon perceived by any possible accelerating observer sitting instantaneously where matter is and about to absorb it. We ask about the relation between the entropy of the lump of matter and the variation of the Clausius entropy of any of these horizons. This corresponds to considering the situation depicted in Figure 1, with now being the local frame of matter and the element of matter located at at and asking about the relation between and .
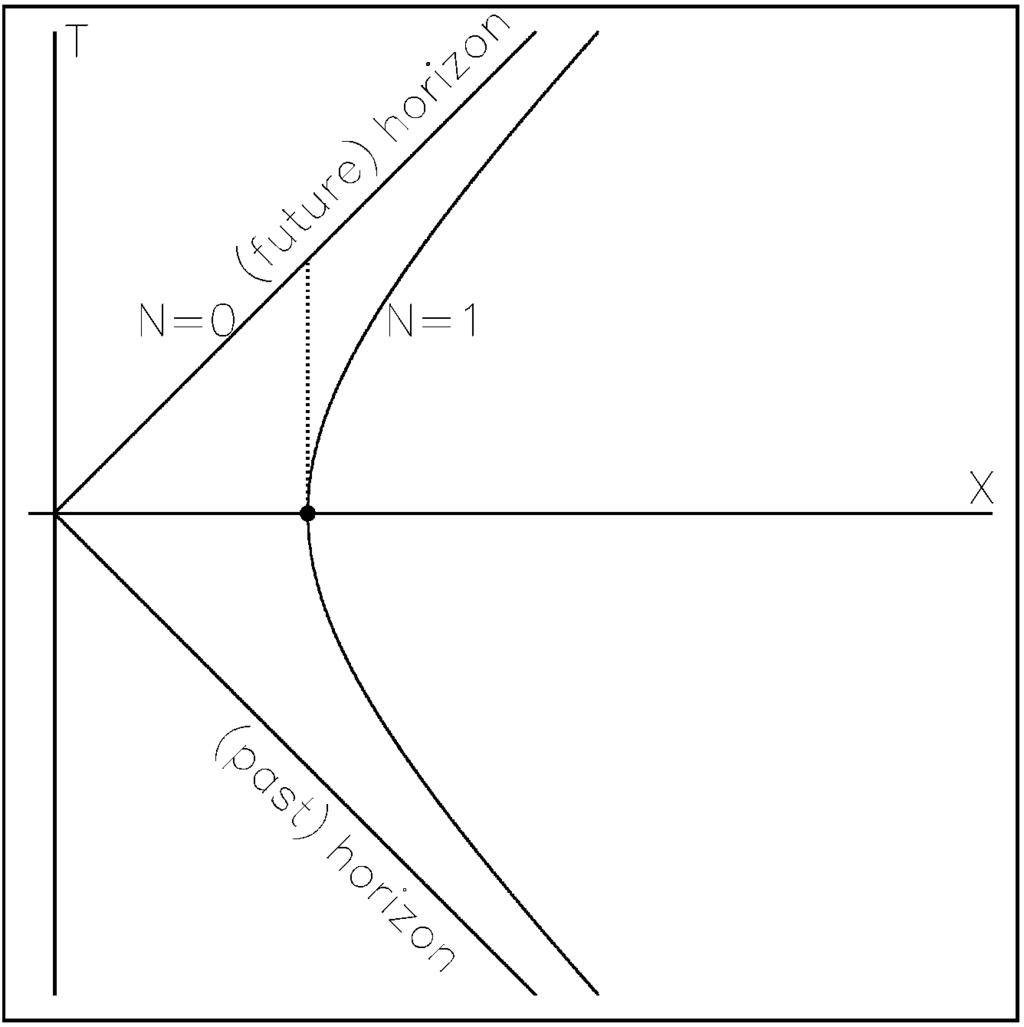
Figure 1.
(Piece of) the world line of an element of volume at , at rest in the inertial frame (see the text).
We evaluate from the Gibbs–Duhem relation (for a one-component thermodynamic system), in its local form:
a relation that merely expresses the first law of thermodynamics joined to the request of the (local) extensivity of pertinent thermodynamic potentials (cf. [29]). Here, ρ, s, θ, P, μ and n are respectively local energy density, entropy, temperature, pressure, chemical potential and the number density of the element of matter. As we are concerned with gravity, the rest-mass energy is thought here to be included in ρ; we know this means that this same energy must be thought of as also included in μ (cf., for example, [30] (p. 155)). We have:
where is the proper volume of the element of matter.
In the calculation of , we explicitly choose ( is the velocity vector of the element of matter), that is we choose the stress-energy tensor of an ideal fluid, in the assumption that this case is general enough to show what is happening here concerning the relation between and , without, unnecessary at this stage, further complications. In Equation (2), all we need to know is on any given horizon. From on the horizon (cf., for instance, [4]), we get:
and thus:
Comparing with , we see amounts to compare with . In this regard, we notice that what we are talking about is an element of matter of some proper size l, with temperature and other thermodynamic potentials assigned, which, initially, i.e., at and at a proper distance from the horizon, is assumed to be entirely ahead of the horizon. This means .
The circumstances can be conveniently described in terms of the length mentioned above, characteristic of the given local thermodynamic conditions. The meaning of is that, for whatever thermodynamic system with given (local) thermodynamic conditions, its size Δ cannot be smaller than the for these conditions. More precisely,
where the last equality follows from the Gibbs–Duhem relation. In practice, this means that, if we insist on saying that a system has certain given values of ρ, s and P, we have to realize that that system cannot have a size smaller than , as given in Equation (7).
Inequality (7) is not universally proven; it is a conjecture. It is however likely to be obeyed by any matter system, as an expression of the unavoidable quantum indeterminacy of the constituent particles, i.e., its reason rests on that it seems to be simply a manifestation, or reformulation, of the uncertainty principle. As such, it can be considered as a universal feature of any thermodynamic system, and it is moreover a basic expression of quantum mechanics alone (i.e., without reference to gravity, meaning with reference to the Minkowski limit only). In [26,27], an analysis is made on how the inequality (7) arises in some relevant and calculable systems.
Applying this here, we get:
and so:
where the equality is reached when and .
The possibility of fulfilling the condition is tied to the nature of the matter under consideration. For certain material media, the equality can indeed in principle be reached; for example, this happens for ultrarelativistic systems with , e.g., a blackbody photon gas, when the size l of the system is made very small, up to the limit of compatibility, in view of quantum uncertainty, with the assigned values of thermodynamic potentials [27]. In general media, even when this quantum limit is reached, l is still much larger than . For generic choices of the size of the element of matter, we will have , even for photon gases.
The condition deals with the location of the horizon that absorbs the element of matter. When , the horizon just starts to absorb, that is the element of matter is just ahead of the horizon, at the limit of the beginning of the absorption; and it is otherwise, i.e., when there is still some path before absorption begins. The eventuality is not allowed, since it is incompatible with the assumption that the system is entirely ahead of the horizon at the start; a system with , where is the temperature of the horizon about to absorb it, has necessarily a part of itself beyond the reach of the Rindler coordinates of the accelerating observer located where matter is and instantaneously at rest with respect to it, who perceives that horizon, so that this part of the system results already absorbed by the horizon.
We have thus shown the following.
Proposition Given an element of matter of size l and energy-momentum tensor , its entropy is bounded from above by the quantity , given by Equation (5), of a Rindler horizon at temperature as perceived by an accelerating observer sitting instantaneously where matter is, with the tangent vector to the generators of the horizon, i.e., by the variation of Clausius entropy of a Rindler horizon at the perceived temperature , which engulfs the element of matter.
The limiting value can in principle be reached: this happens for ultrarelativistic systems with , of a very small size, pushed to the (quantum) limit of compatibility with the assigned thermodynamic conditions for the element of matter. The bound can thus also be considered as the supremum among the for all possible material media, for given and l. Thus considered, it is manifest that the bound is a quantity inherent to matter, and is irrespective of the gravity theory, in agreement with what we already know since, as seen, the quantity is independent of the gravity theory.
3. The Generalized Covariant Entropy Bound Extended to General Theories of Gravity
In the descriptions/derivations of the equations of motion as a thermodynamic identity, the equality:
between the Clausius entropy variation of the horizon to the left, and the Wald entropy variation of horizon to the right (coinciding with the Bekenstein–Hawking entropy variation in Einstein theory) associated with the crossing of the horizon by some element of matter is stressed as entailing the equations of motion for the gravitational field, i.e., how matter curves geometry. Indeed, Wald’s entropy is a prescription, which, upon using the equations of motion, gives the amount of entropy associated with a patch of horizon of some -dimensional cross-sectional area A, the amount of entropy being different for different gravity theories. The l.h.s. is clearly independent of the gravity theory, as can be seen, for example, on noting that any bifurcate horizon can be approximated at a point by a Rindler horizon and applying the discussion of the previous section. The r.h.s. must also be independent of the gravity theory. Equality (10) then gives how much the area A must shrink, due to some passage of matter, this depending on the expression of . For each expression of , this gives the equations of motion for the theory, which has that expression as its Wald’s entropy of the horizon.
Using this, the bound discussed in the previous section becomes, in each specific theory of gravity, a bound in terms of the Wald entropy of that theory. From Equations (9) and (10), in fact, we get:
According to the previous section, we are considering this relation in terms of a patch of the Rindler horizon at P with tangent to the generators and temperature . We can however think of as referring to a generic bifurcate Killing horizon H at P with normal , tangent to the generators and surface gravity , on calculating it through the approximating Rindler patch at P with , and .
In dimensional Einstein gravity coincides with , and Equation (11) becomes:
However, this is the generalized covariant entropy bound [7] (GCEB), as applied to the patch of the-hypersurface of area A coinciding with the -section of a patch of a horizon and having as the null field orthogonal to it. Inequality (11) thus generalizes the GCEB to a form that applies in any metric theory of gravity, with the generalization being in that , with A the -area of a patch B of -hypersurface with an orthogonal null field , is replaced by , thought to be the Wald entropy of the patch of the sheet of the null hypersurface generated by null geodesics, which start at B with tangent .
4. for Horizons
The scale has been considered in the past for conventional matter only [26,27]. The discussion of Section 2 gives the opportunity of defining a value for it for horizons. The definition of given in Equation (7) can evidently be put also in the form:
This is the of the matter that is going to be swallowed by a horizon. The matter has an entropy content in some proper volume and gives an energy contribution to the horizon, which has a given temperature . Now, if we use matter for which the limit can be reached, and we choose , and if we furthermore assume that our choice of the thermodynamic parameters of matter is such that is the maximum value allowed for the matter to be absorbed in one bite by the given horizon, i.e., , we know that in Equation (9), the equality holds, and we are thus allowed to write for in Equation (13). However, the member to the right in Equation (13) is now given in terms of quantities, which refer to the horizon alone. This suggests:
where the subscript reminds us that the term in the round brackets must be evaluated for material media for which the choice is allowed. We said above that a blackbody photon gas, for which (cf. Equation (7)), does the job in that it allows for , and we get , provided the temperature of the gas equals the horizon temperature, . is thus the order of the wavelength of blackbody photons at the temperature of the thermal bath perceived by the accelerating observer. This quantity is supposed to conveniently characterize the behavior of a horizon from a pure quantum mechanical point of view, meaning in the Minkowski limit (and we know horizons do not imply we leave this limit). As such, it does not contain any information on gravity and is well defined also in a context for which, spacetime is purely Minkowskian (cf. [27]). It is therefore a concept clearly distinct from the Planck scale (and, in general, is enormously larger than the latter).
For a generic bifurcate Killing horizon, its can be defined in an obvious way through the Rindler horizon approximating it at a point. For systems collapsing to form black holes in Einstein gravity with temperature in asymptotically-flat spacetimes, for example, the photon gas (or ultrarelativistic matter) above, which gives , is a blackbody and must have temperature , as measured by distant observers (as can be verified from locally Rindler approximating the horizon); i.e., it turns out it is just their Hawking radiation. For the Schwarzschild black hole, we get:
where M and R are black hole mass and radius.
5. Concluding Remarks
We have seen that the limiting thermodynamical scale of matter can be used to show that the entropy of any element of matter is bounded by the variation of Clausius entropy of a suitable Rindler horizon absorbing it. From this, a form of the GCEB, valid for general metric theories of gravity, has been introduced, and the for horizons has been defined.
Using the perspective according to which the entropy of any patch of horizon is always (i.e., for any diff-invariant theory of gravity) given by a quarter of area in units of effective coupling [31], from Equation (11), we get:
where the effective coupling , defined as in [31], is explicitly reported, and, again, A is the area of a patch of the boundary surface. depends in general on the point in spacetime, and equals Newton’s constant, constant , for Einstein gravity. Formula (16) is a further (local) expression of the GCEB generalized to general theories of gravity. When we change the gravity theory, the quantity , and thus, remains unaffected. What changes are and individually. A gravity theory with a gravitational coupling, say, larger than that of Einstein’s theory (), will give a stronger focusing (a larger ), stronger by the amount exactly needed to leave invariant.
The fact that the black hole horizon has the same as its Hawking radiation can be interpreted as suggesting that in some respects it behaves like the Hawking radiation itself. This radiation is, after all, all that a distant observer can see of the black hole. This thermodynamic fact could provide some further understanding of the dynamic behavior of black holes. The dynamic relaxation times of perturbed black holes (for a review, see [32]), could be seen as an example of this kind. The argument for this goes as follows. A universal lower limit to the relaxation times τ of systems at temperature θ, has been introduced in [33] from thermodynamics and quantum information theory. As far as black holes can be considered thermodynamic objects, we would expect that could also limit the dynamic relaxation times of perturbed black holes with horizon temperature . Could this be inspected through the use of for horizons? Systems consisting of blackbody radiation at temperature θ actually obey this limit, and shaped as thin layers, they exhibit, when sufficiently thin, relaxation times τ approaching it, (in the limit , l being their thickness, a limit that, as mentioned above, for blackbody radiation can be reached) [34]. Now, the imprint on any radiation, of the variation of the properties of the black hole cannot have any evolution more rapid than that given by this limit with . That means that the distant observer cannot see variations of the black hole on a characteristic scale smaller than this, i.e., the relaxation times of black holes cannot be smaller than this limit: . This, namely that black holes comply with the bound, is precisely what is obtained by analytical and numerical evaluations [33]. In [33], it is found moreover that, when black holes are nearly extremal, i.e., in the limit, they saturate the bound. According to the perspective above, near-extremal black holes could thus be regarded as equivalent to a thickness of their own Hawking radiation, from a far observer point of view.
A last comment concerns the particular case of matter for which , i.e., matter mimicking the effects of a cosmological constant term in the equations of motion. For this matter, the Gibbs–Duhem relation (3) becomes:
where s, with its informational meaning, and θ and n should be regarded as intrinsically non-negative. We have two possibilities:
- (i)
- ; implying ;
- (ii)
- ; implying .
Looking at Equation (6), both cases give , and we do not get an increment of Clausius entropy of the horizon when such matter crosses it. In Case (i), this gives a violation of Equation (9) and, thus, of Equation (11). In terminology, the situation is characterized by in Equation (7), and thus, we see that we can never have for this matter for any l; that is, matter of this kind is incompatible with the assumption for it to be initially completely ahead of the horizon. The basic assumption itself that matter can be described in terms of local quantities (ρ, s, ...) in a volume , a pre-requisite for writing the local form of the Gibbs–Duhem relation (3), is put into question; the condition itself becomes of doubtful meaning in that s is found to be ill-defined. In view of this, we cannot claim that any matter of this kind would produce a violation of the entropy bound (11); what we could claim is that the bound could hold true even in the presence of this “matter”, since the real point is that, surely, our description of it in local terms is no longer adequate (this perhaps offers a different perspective on the issue of the effect of any cosmological constant term on entropy bounds as tackled in [35]). We could speculate that, if we believe in quantum mechanics as providing , the case would correspond to “cosmological matter”, which would intrinsically be completely delocalized (). If we think of constituents for it, they should be completely delocalized and maximally entangled.
Case (ii) gives , that is is undetermined without further input. Any finite value of would allow Inequality (9) to be satisfied irrespective of l, i.e., even when . This would suggest, for overall consistency, for Case (ii). It would correspond to matter completely localized, with no entanglement, with infinite energy and pressure (from quantum indeterminacy) and no entropy.
Acknowledgments
The author thanks Giovanni Venturi for the careful reading of the manuscript.
Conflicts of Interest
The author declares no conflict of interest.
References
- Jacobson, T. Thermodynamics of spacetime: The Einstein equation of state. Phys. Rev. Lett. 1995, 75, 1260–1263. [Google Scholar] [CrossRef] [PubMed]
- Padmanabhan, T.; Paranjape, A. Entropy of null surfaces and dynamics of spacetime. Phys. Rev. D 2007, 75, 064004. [Google Scholar] [CrossRef]
- Padmanabhan, T. Dark energy and gravity. Gen. Relativ. Gravit. 2008, 40, 529–564. [Google Scholar] [CrossRef]
- Padmanabhan, T. Gravitation: Foundations and Frontiers; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Padmanabhan, T. Thermodynamical aspects of gravity: New insights. Rep. Prog. Phys. 2010, 73, 046901. [Google Scholar] [CrossRef]
- Jacobson, T.; Parentani, R. Horizon entropy. Found. Phys. 2003, 33, 323–348. [Google Scholar] [CrossRef]
- Flanagan, É.É.; Marolf, D.; Wald, R.M. Proof of classical versions of the Bousso entropy bound and of the generalized second law. Phys. Rev. D 2000, 62, 084035. [Google Scholar]
- Bekenstein, J.D. Universal upper bound on the entropy-to-energy ratio for bounded systems. Phys. Rev. D 1981, 23, 287. [Google Scholar] [CrossRef]
- Jacobson, T. Gravitation and vacuum entanglement entropy. 2012; arXiv:1204.6349. [Google Scholar]
- Verlinde, E.P. On the origin of gravity and the laws of Newton. JHEP 2011, 1104, 029. [Google Scholar] [CrossRef]
- Pesci, A. Gravity from the entropy of light. Class. Quantum Gravity 2011, 28, 045001. [Google Scholar] [CrossRef]
- Pesci, A. The existence of a minimum wavelength for photons. 2011; arXiv:1108.5066. [Google Scholar]
- Padmanabhan, T. Entropy of static spacetimes and microscopic density of states. Class. Quantum Gravity 2004, 21, 4485–4494. [Google Scholar] [CrossRef]
- Padmanabhan, T. Equipartition of energy in the horizon degrees of freedom and the emergence of gravity. Mod. Phys. Lett. A 2010, 25, 1129–1136. [Google Scholar] [CrossRef]
- Cai, R.-G.; Kim, S.P. First law of thermodynamics and Friedmann equations of Friedmann-Robertson-Walker universe. JHEP 2005, 0502, 050. [Google Scholar] [CrossRef]
- Lanczos, C. Electricity as a natural property of Riemannian geometry. Rev. Mod. Phys. 1932, 39, 716. [Google Scholar] [CrossRef]
- Lanczos, C. A remarkable property of the Riemann-Christoffel tensor in four dimensions. Ann. Math. 1938, 39, 842–850. [Google Scholar] [CrossRef]
- Lovelock, D. The Einstein tensor and its generalizations. J. Math. Phys. 1971, 12, 498–501. [Google Scholar] [CrossRef]
- Elizalde, E.; Silva, P.J. F(R) gravity equation of state. Phys. Rev. D 2008, 78, 061501. [Google Scholar] [CrossRef]
- Brustein, R.; Hadad, M. The Einstein equations for generalized theories of gravity and the thermodynamic relation δQ = TδS are equivalent. Phys. Rev. Lett. 2009, 103, 101301, Erratum-ibid 2010, 105, 239902. [Google Scholar]
- Wald, R.M. Black hole entropy is Noether charge. Phys. Rev. D 1993, 48, 3427–3431. [Google Scholar] [CrossRef]
- Jacobson, T.; Kang, G.; Myers, R.C. On black hole entropy. Phys. Rev. D 1994, 49, 6587–6598. [Google Scholar] [CrossRef]
- Iyer, V.; Wald, R.M. A comparison of Noether charge and Euclidean methods for computing the entropy of stationary black holes. Phys. Rev. D 1995, 52, 4430–4439. [Google Scholar] [CrossRef]
- Kothawala, D. The thermodynamic structure of Einstein tensor. Phys. Rev. D 2011, 83, 024026. [Google Scholar] [CrossRef]
- Baccetti, V.; Visser, M. Clausius entropy for arbitrary bifurcate null surfaces. 2013; arXiv:1303.3185. [Google Scholar]
- Pesci, A. From Unruh temperature to the generalized Bousso bound. Class. Quantum Gravity 2007, 24, 6219–6226. [Google Scholar] [CrossRef]
- Pesci, A. On the statistical-mechanical meaning of the Bousso bound. Class. Quantum Gravity 2008, 25, 125005. [Google Scholar] [CrossRef]
- Rovelli, C. Quantum Gravity; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Oppenheim, J. Thermodynamics with long-range interactions: from Ising models to black-holes. Phys. Rev. E 2003, 68, 016108. [Google Scholar] [CrossRef]
- Huang, K. Statistical Mechanics; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Brustein, R.; Gorbonos, D.; Hadad, M. Wald’s entropy is equal to a quarter of the horizon area in units of the effective gravitational coupling. Phys. Rev. D 2009, 79, 044025. [Google Scholar] [CrossRef]
- Nollert, H.-P. Quasinormal modes: The characteristic ‘sound’ of black holes and neutron stars. Class. Quantum Gravity 1999, 16, R159. [Google Scholar] [CrossRef]
- Hod, S. Universal bound on dynamical relaxation times and black-hole quasinormal ringing. Phys. Rev. D 2007, 75, 064013. [Google Scholar] [CrossRef]
- Pesci, A. A note on the connection between the universal relaxation bound and the covariant entropy bound. Int. J. Mod. Phys. D 2009, 18, 831–835. [Google Scholar] [CrossRef]
- Lee, J.-W. Zero Cosmological Constant and Nonzero Dark Energy from Holographic Principle. J. Korean Phys. Soc. 2013, 63, 1088. [Google Scholar] [CrossRef]
© 2015 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).