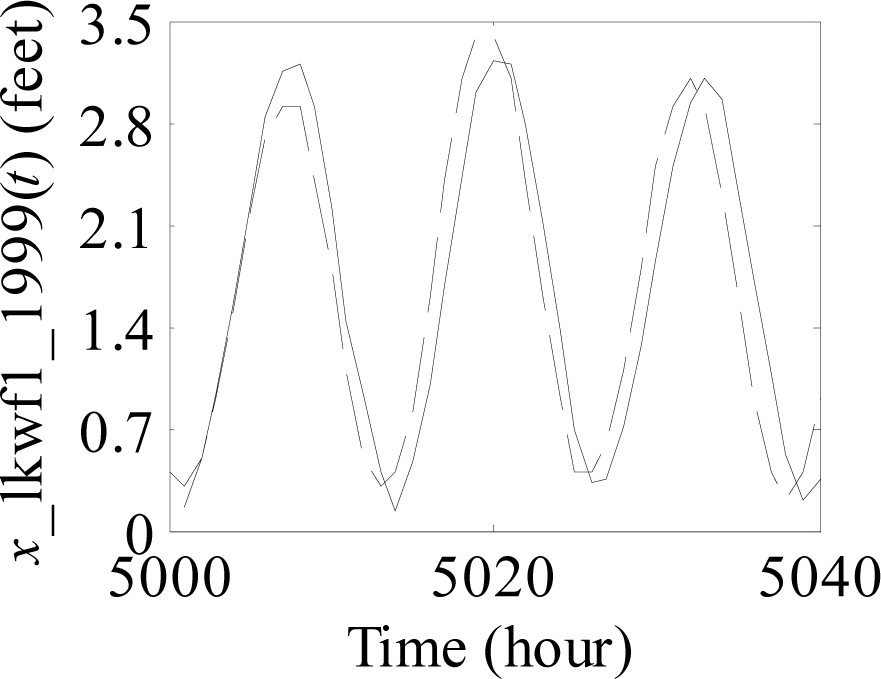
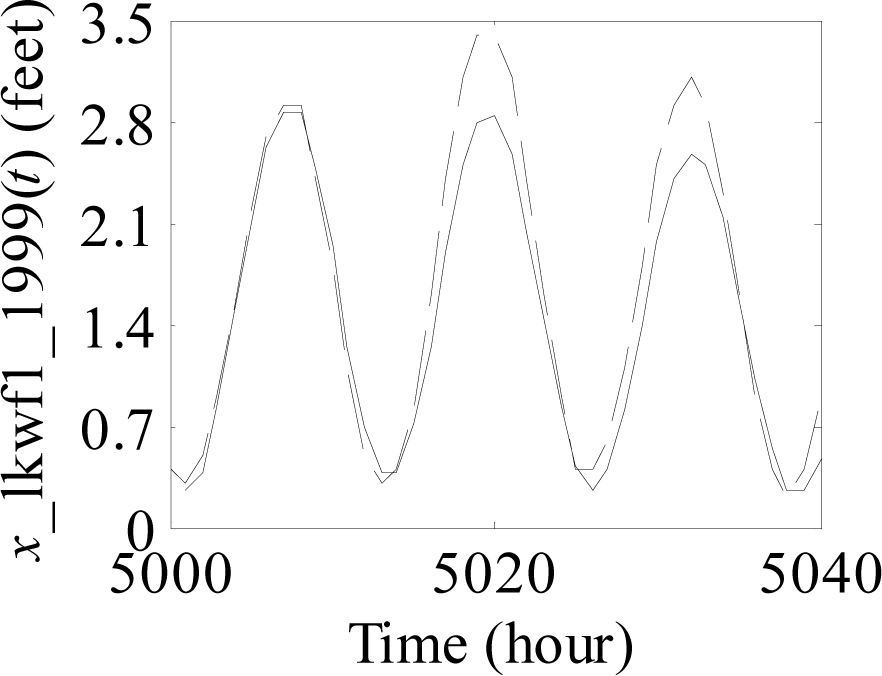
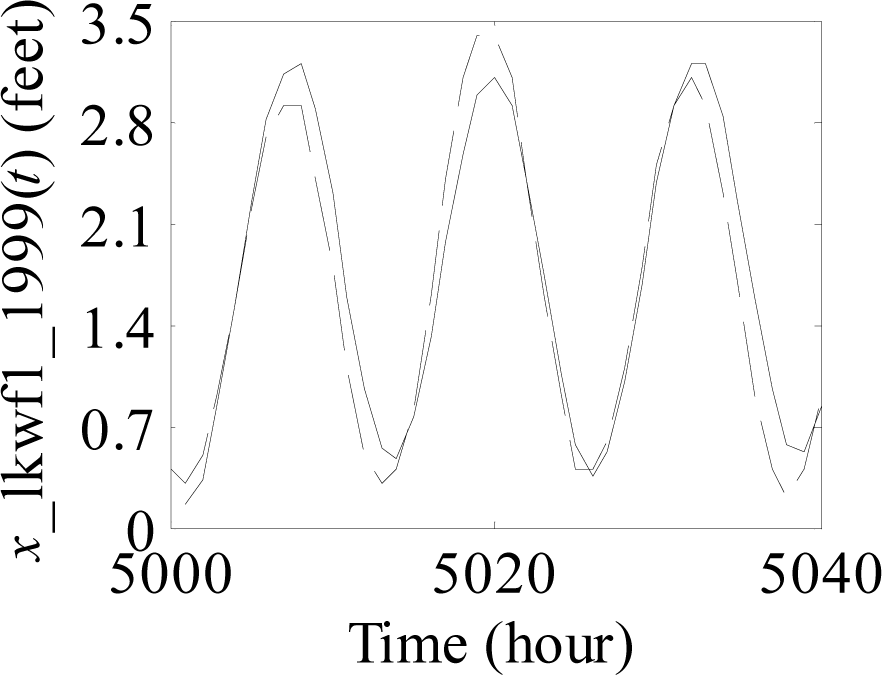
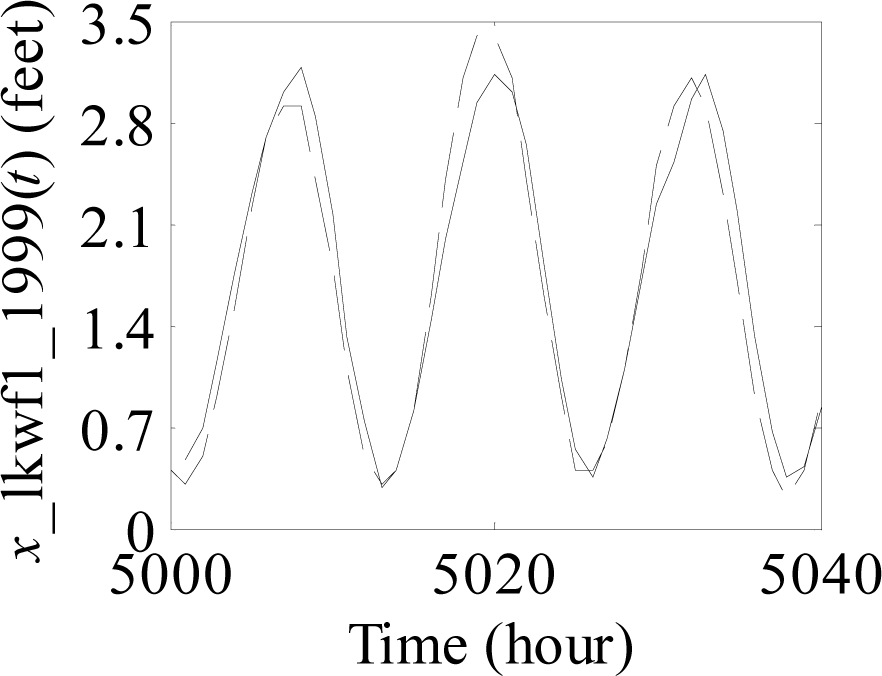
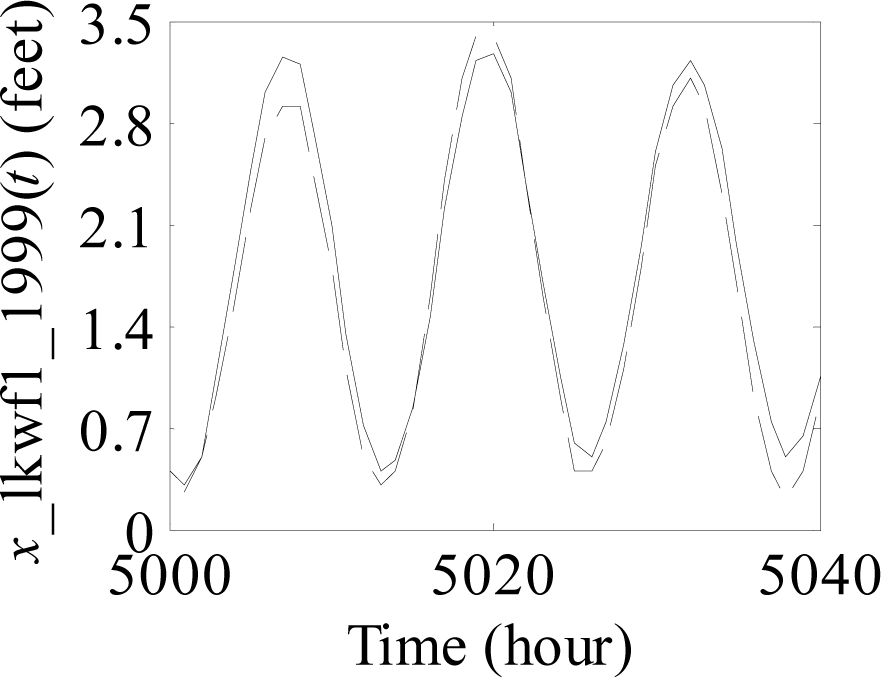
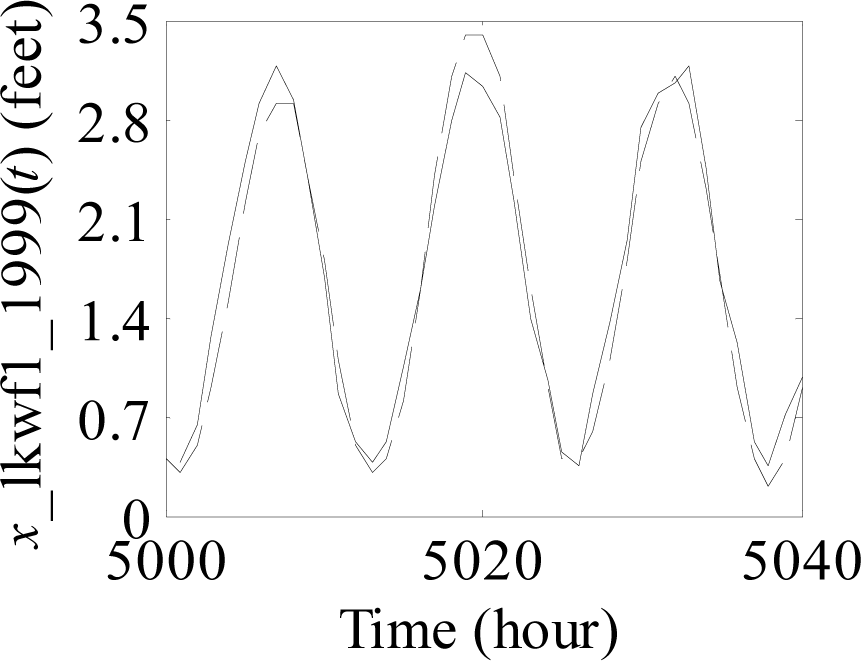
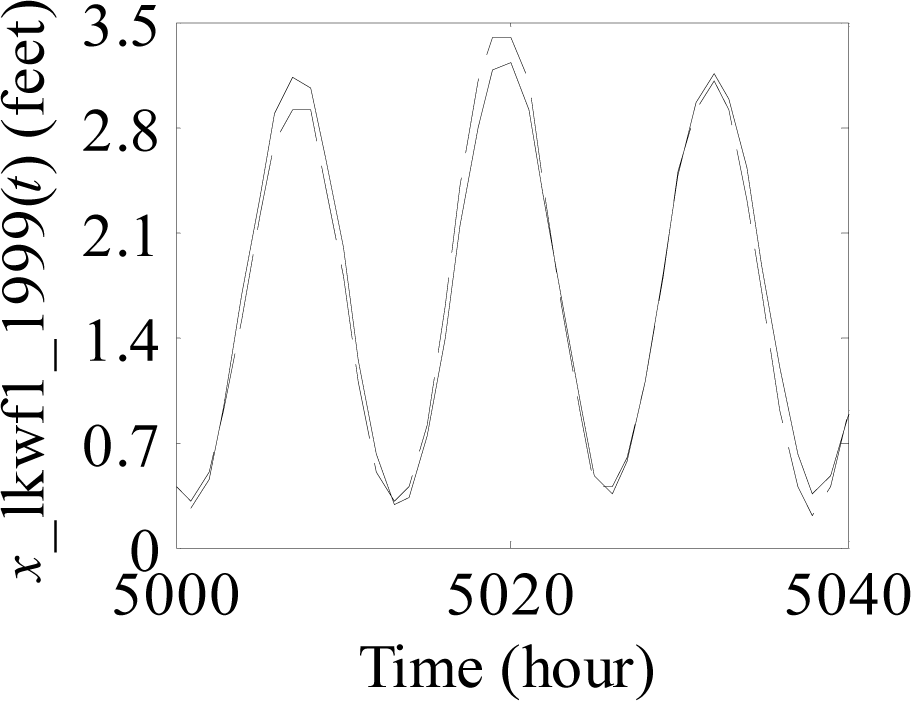
Figure 1.
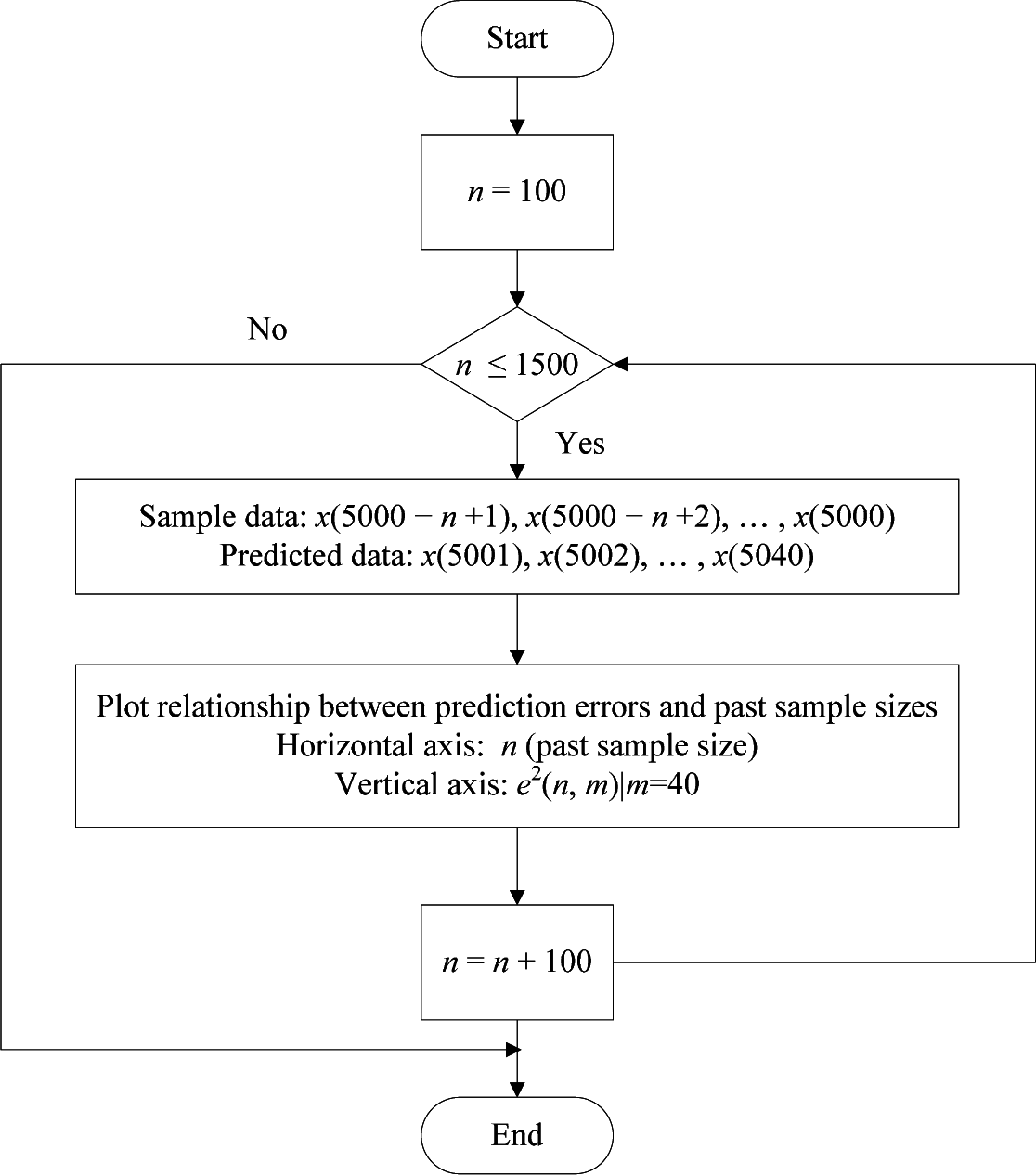
Process of predicting sea level time series from the 5001st value to the 5040th value.
Figure 1.
Process of predicting sea level time series from the 5001st value to the 5040th value.
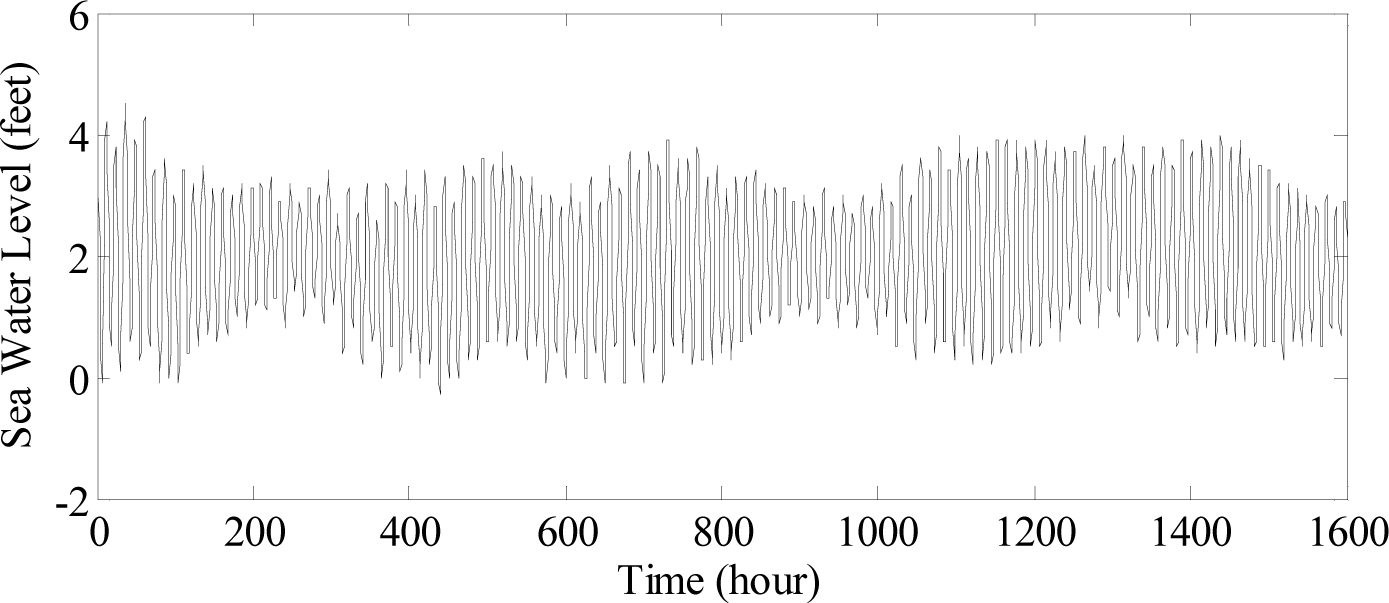
Figure 2.
Sea level series at the Station LKWF1 in 1999.
Figure 2.
Sea level series at the Station LKWF1 in 1999.
Figure 3.
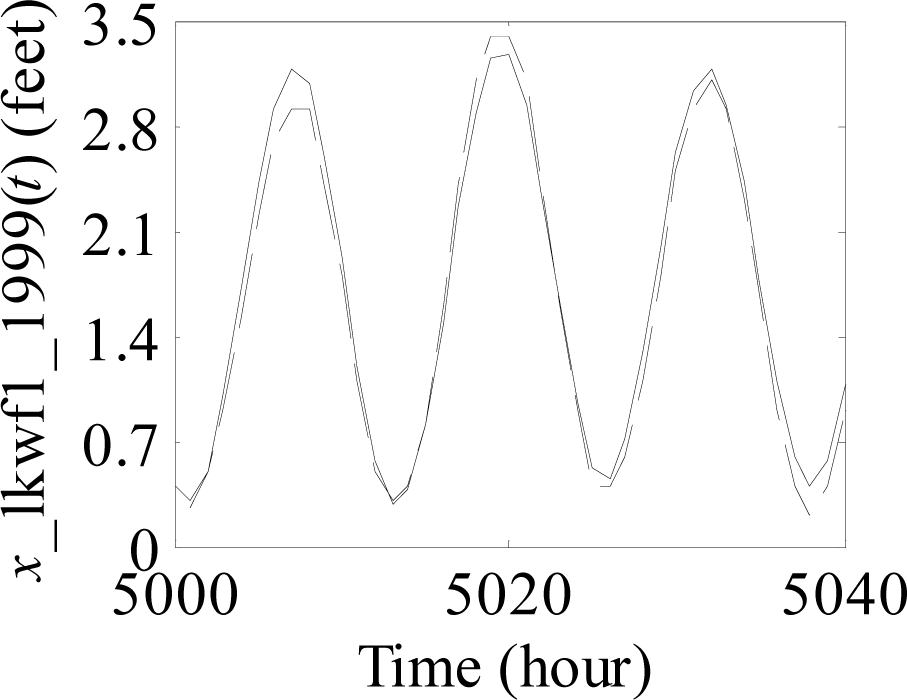
Prediction results with the sample size 100 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 3.
Prediction results with the sample size 100 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 4.
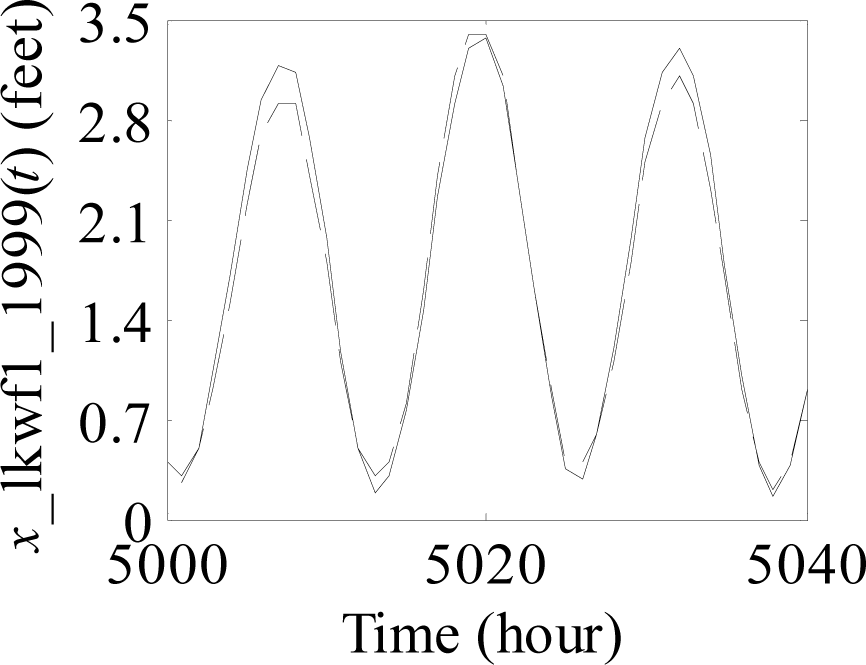
Prediction results with the sample size 200 at the Station LKWF1in 1999. Solid line: predicted values, dashed line: original values.
Figure 4.
Prediction results with the sample size 200 at the Station LKWF1in 1999. Solid line: predicted values, dashed line: original values.
Figure 5.
Prediction results with the sample size 300 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 5.
Prediction results with the sample size 300 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 6.
Prediction results with the sample size 400 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 6.
Prediction results with the sample size 400 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 7.
Prediction results with the sample size 500 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 7.
Prediction results with the sample size 500 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 8.
Prediction results with the sample size 600 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 8.
Prediction results with the sample size 600 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 9.
Prediction results with the sample size 700 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 9.
Prediction results with the sample size 700 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 10.
Prediction results with the sample size 800 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 10.
Prediction results with the sample size 800 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 11.
Prediction results with the sample size 900 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 11.
Prediction results with the sample size 900 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 12.
Prediction results with the sample size 1000 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 12.
Prediction results with the sample size 1000 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 13.
Prediction results with the sample size 1100 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 13.
Prediction results with the sample size 1100 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 14.
Prediction results with the sample size 1200 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 14.
Prediction results with the sample size 1200 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 15.
Prediction results with the sample size 1300 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 15.
Prediction results with the sample size 1300 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 16.
Prediction results with the sample size 1400 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 16.
Prediction results with the sample size 1400 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 17.
Prediction results with the sample size 1500 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
Figure 17.
Prediction results with the sample size 1500 at the Station LKWF1 in 1999. Solid line: predicted values, dashed line: original values.
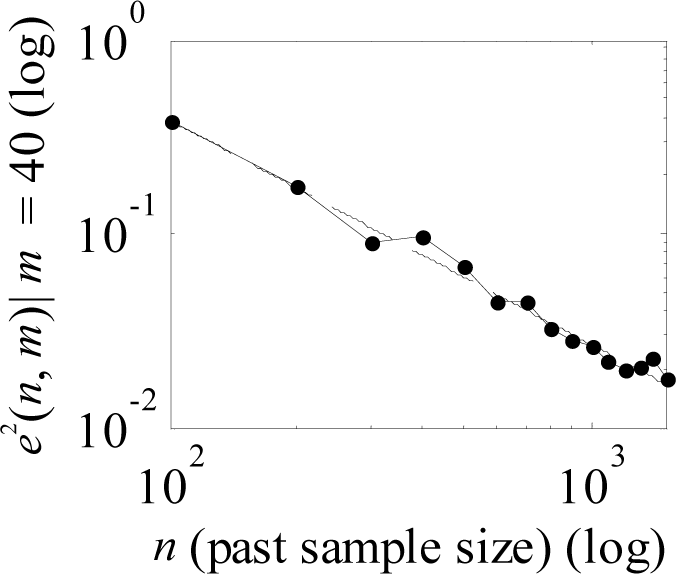
Figure 18.
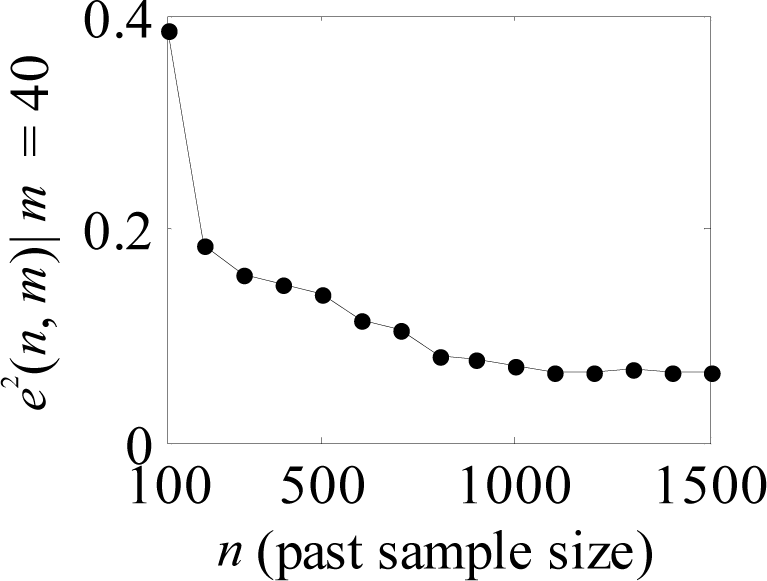
Relationship between the prediction error and the past sample size at the Station LKWF1 in 1999.
Figure 18.
Relationship between the prediction error and the past sample size at the Station LKWF1 in 1999.
Figure 19.
Generation process of relationship between prediction errors and past sample sizes.
Figure 19.
Generation process of relationship between prediction errors and past sample sizes.
Figure 20.
Relationship between the prediction error and the past sample size at the Station SMKF1 in 2003.
Figure 20.
Relationship between the prediction error and the past sample size at the Station SMKF1 in 2003.
Figure 21.
Relationship between the prediction error and the past sample size at the Station LONF1 in 2003.
Figure 21.
Relationship between the prediction error and the past sample size at the Station LONF1 in 2003.
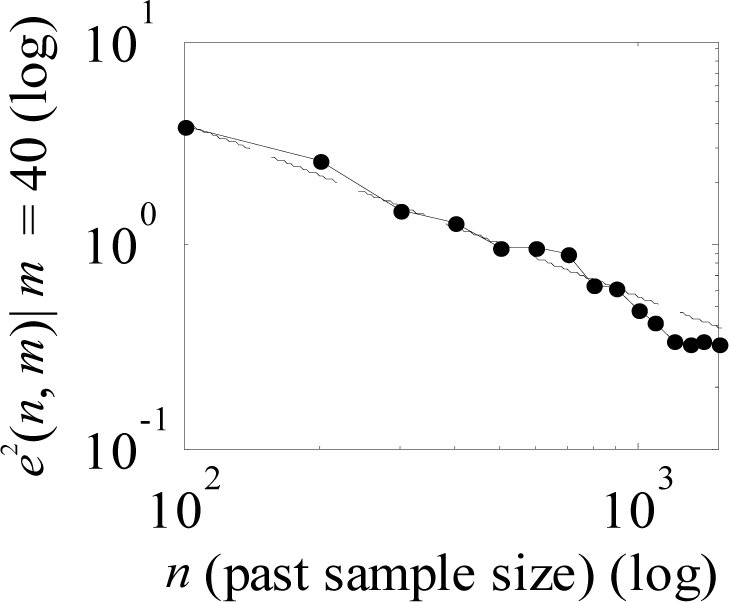
Figure 22.
Relationship between the prediction error and the past sample size at the Station SAUF1 in 2001.
Figure 22.
Relationship between the prediction error and the past sample size at the Station SAUF1 in 2001.
Figure 23.
Relationship between the prediction error and the past sample size at the Station SPGF1 in 1996.
Figure 23.
Relationship between the prediction error and the past sample size at the Station SPGF1 in 1996.
Figure 24.
Relationship between the prediction error and the past sample size at the Station VENF1 in 2003.
Figure 24.
Relationship between the prediction error and the past sample size at the Station VENF1 in 2003.
Figure 25.
Curve fitting of the Station LKWF1 in 1999. Solid line: original curve, dashed line: fitting curve.
Figure 25.
Curve fitting of the Station LKWF1 in 1999. Solid line: original curve, dashed line: fitting curve.
Figure 26.
Curve fitting of the Station SMKF1 in 2003. Solid line: original curve, dashed line: fitting curve.
Figure 26.
Curve fitting of the Station SMKF1 in 2003. Solid line: original curve, dashed line: fitting curve.
Figure 27.
Curve fitting of the Station LONF1 in 2003. Solid line: original curve, dashed line: fitting curve.
Figure 27.
Curve fitting of the Station LONF1 in 2003. Solid line: original curve, dashed line: fitting curve.
Figure 28.
Curve fitting of the Station SAUF1 in 2001. Solid line: original curve, dashed line: fitting curve.
Figure 28.
Curve fitting of the Station SAUF1 in 2001. Solid line: original curve, dashed line: fitting curve.
Figure 29.
Curve fitting of the Station SPGF1 in 1996. Solid line: original curve, dashed line: fitting curve.
Figure 29.
Curve fitting of the Station SPGF1 in 1996. Solid line: original curve, dashed line: fitting curve.
Figure 30.
Curve fitting of the Station VENF1 in 2003. Solid line: original curve, dashed line: fitting curve.
Figure 30.
Curve fitting of the Station VENF1 in 2003. Solid line: original curve, dashed line: fitting curve.
Table 1.
Measured data of six traces of sea level time series.
Table 1.
Measured data of six traces of sea level time series.
| Series Name | Record Date and Time | Data Size | Measurement Station |
|---|
| x_lkwf1_1999(t) | 0:00, 1 Jan.–23:00, 31 Dec. 1999 | 8760 | LKWF1 |
| x_smkf1_2003(t) | 0:00, 1 Jan.–23:00, 31 Dec. 2003 | 5851 | SMKF1 |
| x_lonf1_2003(t) | 0:00, 1 Jan.–23:00, 31 Dec. 2003 | 8697 | LONF1 |
| x_sauf1_2001(t) | 0:00, 1 Jan.–21:00, 31 Dec. 2001 | 8758 | SAUF1 |
| x_spgf1_1996(t) | 0:00, 1 Jan.–23:00, 15 Dec. 1996 | 8616 | SPGF1 |
| x_ven1_2003(t) | 0:00, 1 Jan.–23:00, 31 Dec. 2003 | 8760 | VENF1 |
Table 2.
Prediction errors investigated using x_lkwf1_1999(t) in the Station LKWF1.
Table 2.
Prediction errors investigated using x_lkwf1_1999(t) in the Station LKWF1.
| Past sample size: n | Number of data to be predicted: m | Past samples used | Predicted data | MSE: e2(n, m) |
|---|
| 100 | 40 | 4901st–5000th/4:00, 26 July–7:00, 30 July | 8:00, 30 Jul.–23:00, 31 Jul. | 0.38664 |
| 200 | 40 | 4801st–5000th/23:00, 21 Jul.–7:00, 30 Jul. | 8:00, 30 Jul.–23:00, 31 Jul. | 0.17422 |
| 300 | 40 | 4701st–5000th/19:00, 17 Jul.–7:00, 30 Jul. | 8:00, 30 Jul.–23:00, 31 Jul. | 0.09026 |
| 400 | 40 | 4601st–5000th/15:00, 13 Jul.–7:00, 30 Jul. | 8:00, 30 Jul.–23:00, 31 Jul. | 0.09519 |
| 500 | 40 | 4501st–5000th/10:00, 9 Jul.–7:00, 30 Jul. | 8:00, 30 Jul.–23:00, 31 Jul. | 0.06699 |
| 600 | 40 | 4401st–5000th/5:00, 5 Jul.–7:00, 30 Jul. | 8:00, 30 Jul.–23:00, 31 Jul. | 0.04418 |
| 700 | 40 | 4301st–5000th/1:00, 1 Jul.–7:00, 30 Jul. | 8:00, 30 Jul.–23:00, 31 Jul. | 0.04385 |
| 800 | 40 | 4201st–5000th/21:00, 26 Jun.–7:00, 30 Jul. | 8:00, 30 Jul.–23:00, 31 Jul. | 0.03291 |
| 900 | 40 | 4101st–5000th/17:00, 22 Jun.–7:00, 30 Jul. | 8:00, 30 Jul.–23:00, 31 Jul. | 0.02826 |
| 1000 | 40 | 4001st–5000th/13:00, 18 Jun.–7:00, 30 Jul. | 8:00, 30 Jul.–23:00, 31 Jul. | 0.02601 |
| 1100 | 40 | 3901st–5000th/9:00, 14 Jun.–7:00, 30 Jul. | 8:00, 30 Jul.–23:00, 31 Jul. | 0.02185 |
| 1200 | 40 | 3801st–5000th/5:00, 10 Jun.–7:00, 30 Jul. | 8:00, 30 Jul.–23:00, 31 Jul. | 0.02012 |
| 1300 | 40 | 3701st–5000th/20:00, 5 Jun.–7:00, 30 Jul. | 8:00, 30 Jul.–23:00, 31 Jul. | 0.02028 |
| 1400 | 40 | 3601st–5000th/16:00, 1 Jun.–7:00, 30 Jul. | 8:00, 30 Jul.–23:00, 31 Jul. | 0.02313 |
| 1500 | 40 | 3501st–5000th/12:00, 28 May–7:00, 30 Jul. | 8:00, 30 Jul.–23:00, 31 Jul. | 0.01762 |
Table 3.
Prediction errors investigated using x_smkf1_2003(t) in the Station SMKF1.
Table 3.
Prediction errors investigated using x_smkf1_2003(t) in the Station SMKF1.
| Past sample size: n | Number of data to be predicted: m | Past samples used | Predicted data | MSE: e2(n, m) |
|---|
| 100 | 40 | 4901st–5000th/13:00, 24 Jul.–16:00, 28 Jul. | 17:00, 28 Jul.–8:00, 30 Jul. | 0.37867 |
| 200 | 40 | 4801st–5000th/9:00, 20 Jul.–16:00, 28 Jul. | 17:00, 28 Jul.–8:00, 30 Jul. | 0.16937 |
| 300 | 40 | 4701st–5000th/5:00, 16 Jul.–16:00, 28 Jul. | 17:00, 28 Jul.–8:00, 30 Jul. | 0.11727 |
| 400 | 40 | 4601st–5000th/0:00, 12 Jul.–16:00, 28 Jul. | 17:00, 28 Jul.–8:00, 30 Jul. | 0.05214 |
| 500 | 40 | 4501st–5000th/20:00, 7 Jul.–16:00, 28 Jul. | 17:00, 28 Jul.–8:00, 30 Jul. | 0.02879 |
| 600 | 40 | 4401st–5000th/16:00, 3 Jul.–7:00, 30 Jul. | 17:00, 28 Jul.–8:00, 30 Jul. | 0.03622 |
| 700 | 40 | 4301st–5000th/12:00, 29 Jun.–16:00, 28 Jul. | 17:00, 28 Jul.–8:00, 30 Jul. | 0.02651 |
| 800 | 40 | 4201st–5000th/8:00, 25 Jun.–16:00, 28 Jul. | 17:00, 28 Jul.–8:00, 30 Jul. | 0.02235 |
| 900 | 40 | 4101st–5000th/4:00, 21 Jun.–16:00, 28 Jul. | 17:00, 28 Jul.–8:00, 30 Jul. | 0.02442 |
| 1000 | 40 | 4001st–5000th/0:00, 17 Jun.–16:00, 28 Jul. | 17:00, 28 Jul.–8:00, 30 Jul. | 0.02077 |
| 1100 | 40 | 3901st–5000th/20:00, 12 Jun.–16:00, 28 Jul. | 17:00, 28 Jul.–8:00, 30 Jul. | 0.02426 |
| 1200 | 40 | 3801st– 5000th/16:00, 8 Jun.–16:00, 28 Jul. | 17:00, 28 Jul.–8:00, 30 Jul. | 0.02265 |
| 1300 | 40 | 3701st–5000th/11:00, 4 Jun.–16:00, 28 Jul. | 17:00, 28 Jul.–8:00, 30 Jul. | 0.02037 |
| 1400 | 40 | 3601st–5000th/7:00, 31 May–16:00, 28 Jul. | 17:00, 28 Jul.–8:00, 30 Jul. | 0.02085 |
| 1500 | 40 | 3501st–5000th/3:00, 27 May–16:00, 28 Jul. | 17:00, 28 Jul.–8:00, 30 Jul. | 0.01981 |
Table 4.
Prediction errors investigated using x_lonf1_2003(t) in the Station LONF1.
Table 4.
Prediction errors investigated using x_lonf1_2003(t) in the Station LONF1.
| Past sample size: n | Number of data to be predicted: m | Past samples used | Predicted data | MSE: e2(n, m) |
|---|
| 100 | 40 | 4901st–5000th/18:00, 28 Jul.–21:00, 1 Aug. | 22:00, 1 Aug.–13:00, 3 Aug. | 0.15316 |
| 200 | 40 | 4801st–5000th/14:00, 24 Jul.–21:00, 1 Aug. | 22:00, 1 Aug.–13:00, 3 Aug. | 0.13100 |
| 300 | 40 | 4701st–5000th/10:00, 20 Jul.–21:00, 1 Aug. | 22:00, 1 Aug.–13:00, 3 Aug. | 0.12900 |
| 400 | 40 | 4601st–5000th/5:00, 16 Jul.–21:00, 1 Aug. | 22:00, 1 Aug.–13:00, 3 Aug. | 0.11930 |
| 500 | 40 | 4501st–5000th/1:00, 12 Jul.–21:00, 1 Aug. | 22:00, 1 Aug.–13:00, 3 Aug. | 0.10686 |
| 600 | 40 | 4401st–5000th/21:00, 7 Jul.–21:00, 1 Aug. | 22:00, 1 Aug.–13:00, 3 Aug. | 0.10962 |
| 700 | 40 | 4301st–5000th/17:00, 3 Jul.–21:00, 1 Aug. | 22:00, 1 Aug.–13:00, 3 Aug. | 0.10348 |
| 800 | 40 | 4201st–5000th/13:00, 29 Jun.–21:00, 1 Aug. | 22:00, 1 Aug.–13:00, 3 Aug. | 0.10434 |
| 900 | 40 | 4101st–5000th/4:00, 21 Jun.–21:00, 1 Aug. | 22:00, 1 Aug.–13:00, 3 Aug. | 0.10594 |
| 1000 | 40 | 4001st–5000th/9:00, 25 Jun.–21:00, 1 Aug. | 22:00, 1 Aug.–13:00, 3 Aug. | 0.10692 |
| 1100 | 40 | 3901st–5000th/23:00, 16 Jun.–21:00, 1 Aug. | 22:00, 1 Aug.–13:00, 3 Aug. | 0.10334 |
| 1200 | 40 | 3801st–5000th/19:00, 12 Jun.–21:00, 1 Aug. | 22:00, 1 Aug.–13:00, 3 Aug. | 0.09628 |
| 1300 | 40 | 3701st–5000th/15:00, 8 Jun.–21:00, 1 Aug. | 22:00, 1 Aug.–13:00, 3 Aug. | 0.09980 |
| 1400 | 40 | 3601st–5000th/11:00, 4 Jun.–21:00, 1 Aug. | 22:00, 1 Aug.–13:00, 3 Aug. | 0.10160 |
| 1500 | 40 | 3501st–5000th/16:00, 28 May–21:00, 1 Aug. | 22:00, 1 Aug.–13:00, 3 Aug. | 0.09752 |
Table 5.
Prediction errors investigated using x_sauf1_2001(t) in the Station SAUF1.
Table 5.
Prediction errors investigated using x_sauf1_2001(t) in the Station SAUF1.
| Past sample size: n | Number of data to be predicted: m | Past samples used | Predicted data | MSE: e2(n, m) |
|---|
| 100 | 40 | 4901st–5000th/21:00, 28 Jul.–8:00, 2 Aug. | 9:00, 2 Aug.–0:00, 4 Aug. | 3.80104 |
| 200 | 40 | 4801st–5000th/16:00, 24 Jul.–8:00, 2 Aug. | 9:00, 2 Aug.–0:00, 4 Aug. | 2.56308 |
| 300 | 40 | 4701st–5000th/12:00, 20 Jul.–8:00, 2 Aug. | 9:00, 2 Aug.–0:00, 4 Aug. | 1.45882 |
| 400 | 40 | 4601st–5000th/3:00, 16 Jul.–8:00, 2 Aug. | 9:00, 2 Aug.–0:00, 4 Aug. | 1.28306 |
| 500 | 40 | 4501st–5000th/21:00, 11 Jul.–8:00, 2 Aug. | 9:00, 2 Aug.–0:00, 4 Aug. | 0.96792 |
| 600 | 40 | 4401st–5000th/17:00, 7 Jul.–8:00, 2 Aug. | 9:00, 2 Aug.–0:00, 4 Aug. | 0.95034 |
| 700 | 40 | 4301st–5000th/11:00, 3 Jul.–8:00, 2 Aug. | 9:00, 2 Aug.–0:00, 4 Aug. | 0.89086 |
| 800 | 40 | 4201st–5000th/7:00, 29 Jun.–8:00, 2 Aug. | 9:00, 2 Aug.–0:00, 4 Aug. | 0.63288 |
| 900 | 40 | 4101st–5000th/3:00, 25 Jun.–8:00, 2 Aug. | 9:00, 2 Aug.–0:00, 4 Aug. | 0.61248 |
| 1000 | 40 | 4001st–5000th/21:00, 20 Jun.–8:00, 2 Aug. | 9:00, 2 Aug.–0:00, 4 Aug. | 0.48420 |
| 1100 | 40 | 3901st–5000th/16:00, 16 Jun.–8:00, 2 Aug. | 9:00, 2 Aug.–0:00, 4 Aug. | 0.41888 |
| 1200 | 40 | 3801st–5000th/12:00, 12 Jun.–8:00, 2 Aug. | 9:00, 2 Aug.–0:00, 4 Aug. | 0.33480 |
| 1300 | 40 | 3701st–5000th/7:00, 8 Jun.–8:00, 2 Aug. | 9:00, 2 Aug.–0:00, 4 Aug. | 0.33480 |
| 1400 | 40 | 3601st–5000th/3:00, 4 Jun.–8:00, 2 Aug. | 9:00, 2 Aug.–0:00, 4 Aug. | 0.33488 |
| 1500 | 40 | 3501st – 5000th/23:00, 30 May – 8:00, 2 Aug. | 9:00, 2 Aug.–0:00, 4 Aug. | 0.32614 |
Table 6.
Prediction errors investigated using x_spgf1_1996(t) in the Station SPGF1.
Table 6.
Prediction errors investigated using x_spgf1_1996(t) in the Station SPGF1.
| Past sample size: n | Number of data to be predicted: m | Past samples used | Predicted data | MSE: e2(n, m) |
|---|
| 100 | 40 | 4901st–5000th/3:00, 21 Jul.–7:00, 25 Jul. | 8:00, 25 Jul.–23:00, 26 Jul. | 0.38766 |
| 200 | 40 | 4801st–5000th/23:00, 16 Jul.–7:00, 25 Jul. | 8:00, 25 Jul.–23:00, 26 Jul. | 0.18390 |
| 300 | 40 | 4701st–5000th/14:00, 12 Jul.–7:00, 25 Jul. | 8:00, 25 Jul.–23:00, 26 Jul. | 0.15660 |
| 400 | 40 | 4601st–5000th/8:00, 8 Jul.–7:00, 25 Jul. | 8:00, 25 Jul.–23:00, 26 Jul. | 0.14834 |
| 500 | 40 | 4501st–5000th/2:00, 4 Jul.–7:00, 25 Jul. | 8:00, 25 Jul.–23:00, 26 Jul. | 0.13988 |
| 600 | 40 | 4401st–5000th/21:00, 4 Jul.–7:00, 25 Jul. | 8:00, 25 Jul.–23:00, 26 Jul. | 0.11374 |
| 700 | 40 | 4301st–5000th/14:00, 29 Jun.–7:00, 25 Jul. | 8:00, 25 Jul.–23:00, 26 Jul. | 0.10464 |
| 800 | 40 | 4201st–5000th/10:00, 25 Jun.–7:00, 25 Jul. | 8:00, 25 Jul.–23:00, 26 Jul. | 0.08100 |
| 900 | 40 | 4101st–5000th/6:00, 21 Jun.–7:00, 25 Jul. | 8:00, 25 Jul.–23:00, 26 Jul. | 0.07846 |
| 1000 | 40 | 4001st–5000th/1:00, 17 Jun.–7:00, 25 Jul. | 8:00, 25 Jul.–23:00, 26 Jul. | 0.07160 |
| 1100 | 40 | 3901st–5000th/20:00, 12 Jun.–7:00, 25 Jul. | 8:00, 25 Jul.–23:00, 26 Jul. | 0.06674 |
| 1200 | 40 | 3801st–5000th/16:00, 8 Jun.–7:00, 25 Jul. | 8:00, 25 Jul.–23:00, 26 Jul. | 0.06592 |
| 1300 | 40 | 3701st–5000th/11:00, 4 Jun.–7:00, 25 Jul. | 8:00, 25 Jul.–23:00, 26 Jul. | 0.06926 |
| 1400 | 40 | 3601st–5000th/7:00, 31 May–7:00, 25 Jul. | 8:00, 25 Jul.–23:00, 26 Jul. | 0.06532 |
| 1500 | 40 | 3501st–5000th/2:00, 27 May–7:00, 25 Jul. | 8:00, 25 Jul.–23:00, 26 Jul. | 0.06512 |
Table 7.
Prediction errors investigated using x_venf1_2003(t) in the Station VENF1.
Table 7.
Prediction errors investigated using x_venf1_2003(t) in the Station VENF1.
| Past sample size: n | Number of data to be predicted: m | Past samples used | Predicted data | MSE: e2(n, m) |
|---|
| 100 | 40 | 4901st–5000th/20:00, 24 Jul.–23:00 28 Jul. | 0:00, 29 Jul.–15:00, 30 Jul. | 0.44356 |
| 200 | 40 | 4801st–5000th/16:00, 20 Jul.–23:00, 28 Jul. | 0:00, 29 Jul.–15:00, 30 Jul. | 0.12978 |
| 300 | 40 | 4701st–5000th/12:00, 16 Jul.–23:00, 28 Jul. | 0:00, 29 Jul.–15:00, 30 Jul. | 0.08738 |
| 400 | 40 | 4601st–5000th/8:00, 12 Jul.–23:00, 28 Jul. | 0:00, 29 Jul.–15:00, 30 Jul. | 0.04698 |
| 500 | 40 | 4501st–5000th/23:00, 7 Jul.–23:00, 28 Jul. | 0:00, 29 Jul.–15:00, 30 Jul. | 0.03906 |
| 600 | 40 | 4401st–5000th/19:00, 3 Jul.–23:00, 28 Jul. | 0:00, 29 Jul.–15:00, 30 Jul. | 0.03502 |
| 700 | 40 | 4301st–5000th/15:00, 29 Jun.–23:00, 28 Jul. | 0:00, 29 Jul.–15:00, 30 Jul. | 0.02538 |
| 800 | 40 | 4201st–5000th/10:00, 25 Jun.–23:00, 28 Jul. | 0:00, 29 Jul.–15:00, 30 Jul. | 0.02060 |
| 900 | 40 | 4101st–5000th/6:00, 21 Jun.–23:00, 28 Jul. | 0:00, 29 Jul.–15:00, 30 Jul. | 0.01870 |
| 1000 | 40 | 4001st–5000th/2:00, 17 Jun.–23:00, 28 Jul. | 0:00, 29 Jul.–15:00, 30 Jul. | 0.01878 |
| 1100 | 40 | 3901st–5000th/22:00, 12 Jun.–23:00, 28 Jul. | 0:00, 29 Jul.–15:00, 30 Jul. | 0.01894 |
| 1200 | 40 | 3801st–5000th/18:00, 8 Jun.–23:00, 28 Jul. | 0:00, 29 Jul.–15:00, 30 Jul. | 0.01672 |
| 1300 | 40 | 3701st–5000th/14:00, 4 Jun.–23:00, 28 Jul. | 0:00, 29 Jul.–15:00, 30 Jul. | 0.01594 |
| 1400 | 40 | 3601st–5000th/10:00, 31 May–23:00, 28 Jul. | 0:00, 29 Jul.–15:00, 30 Jul. | 0.01716 |
| 1500 | 40 | 3501st–5000th/5:00, 27 May–23:00, 28 Jul. | 0:00, 29 Jul.–15:00, 30 Jul. | 0.01888 |
Table 8.
Curve fitting results of the six stations. f(n) = e2(n, m)|m = 40, n is the past sample size.
Table 8.
Curve fitting results of the six stations. f(n) = e2(n, m)|m = 40, n is the past sample size.
| Station name | Power functions |
|---|
| LKWF1 | |
| SMKF1 | |
| LONF1 | |
| SAUF1 | |
| SPGF1 | |
| VENF1 | |