Concurrence Measurement for the Two-Qubit Optical and Atomic States
Abstract
:1. Introduction
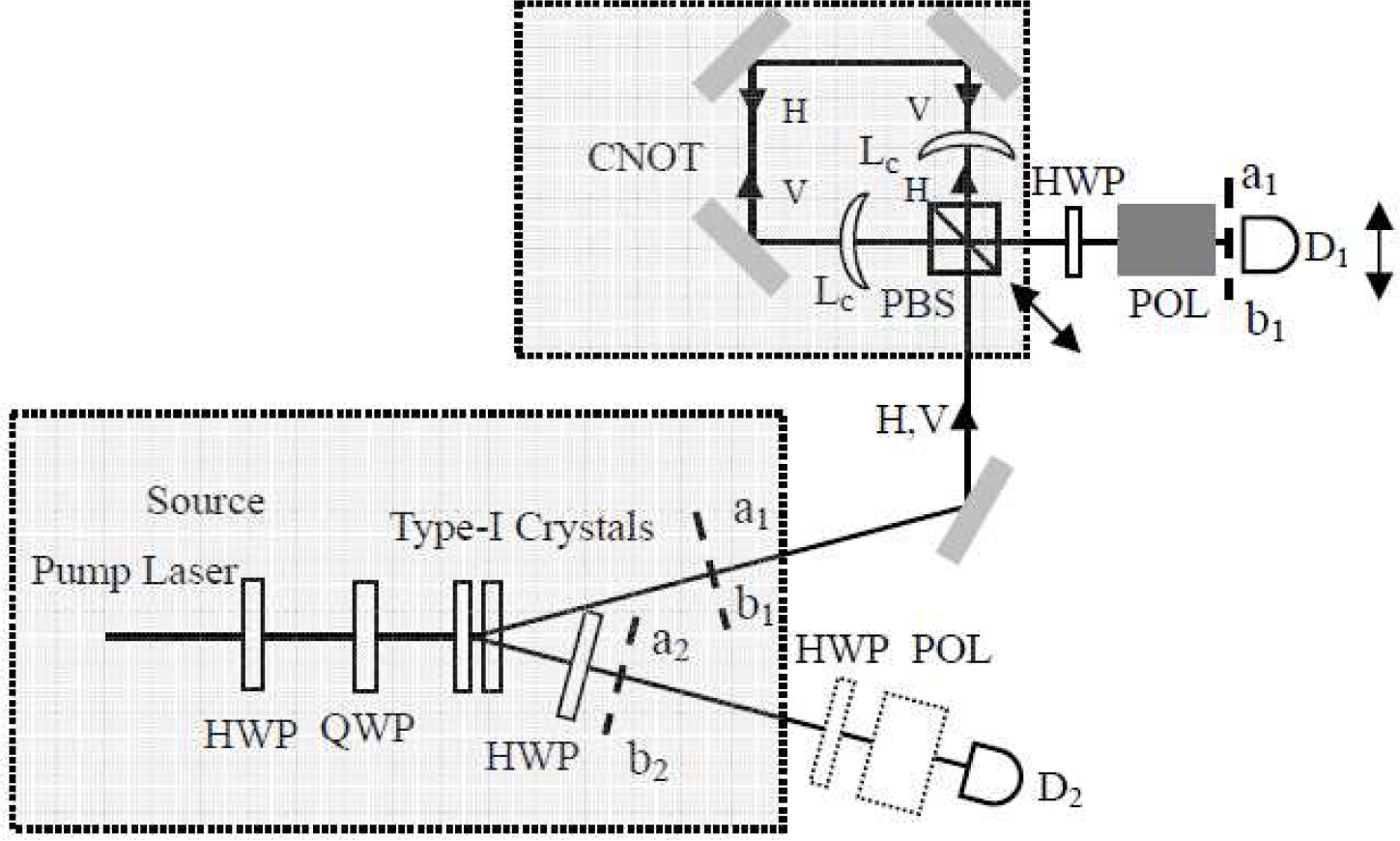
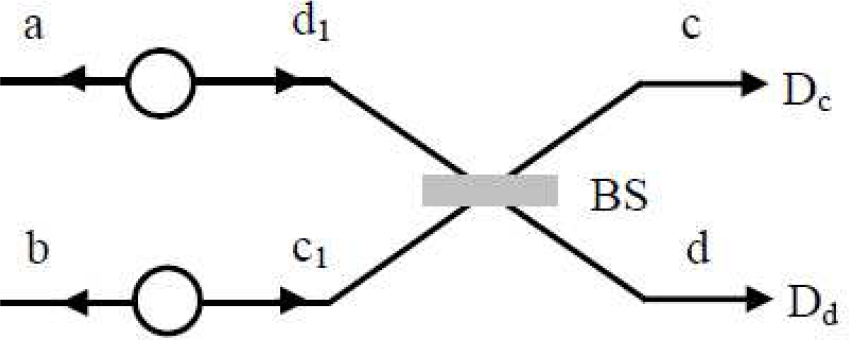
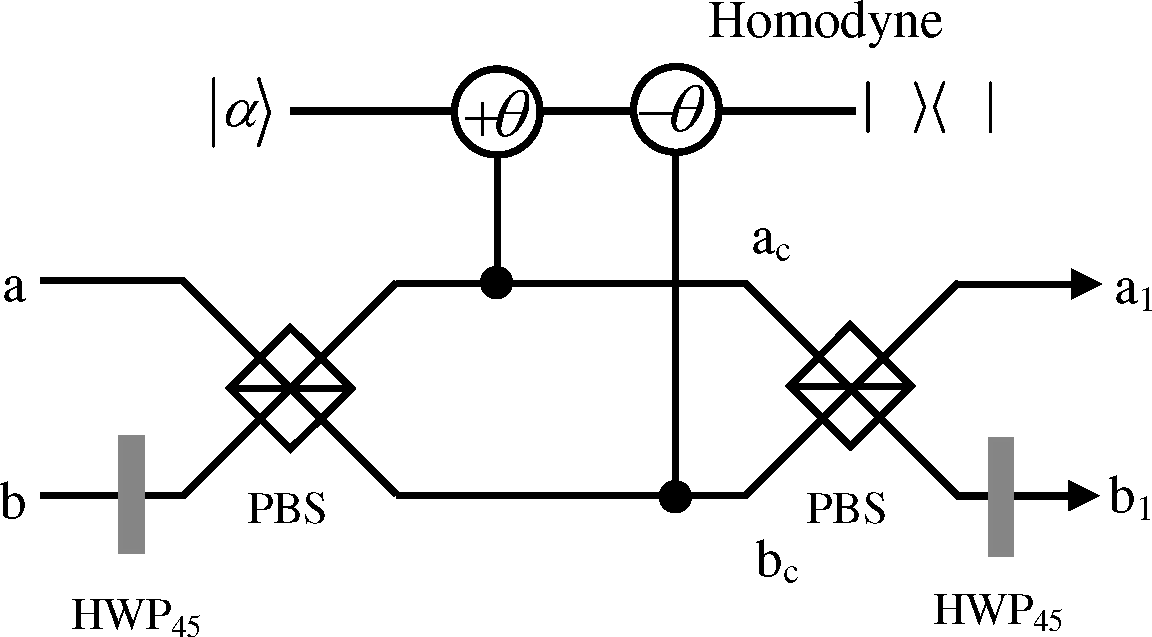
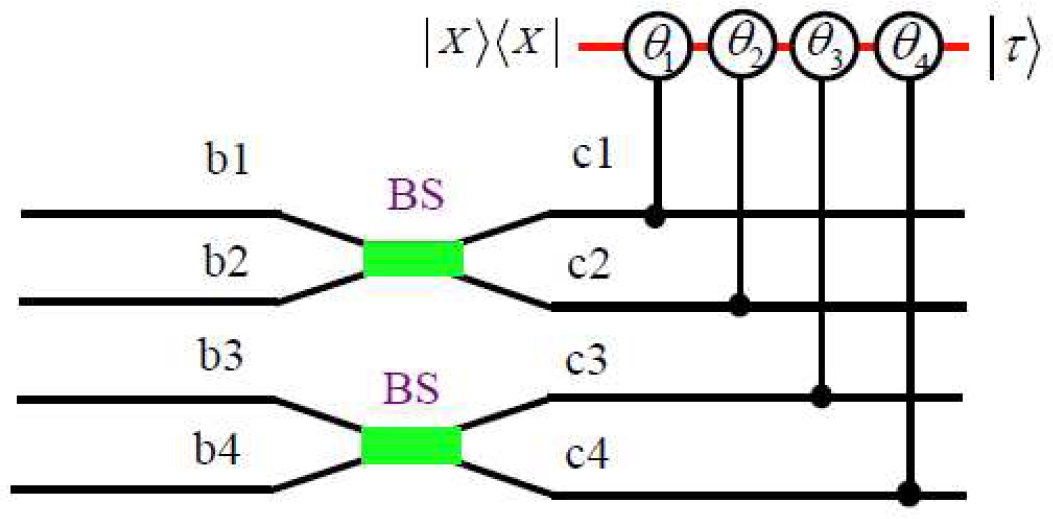
2. The Concurrence Measurement for the Optical States
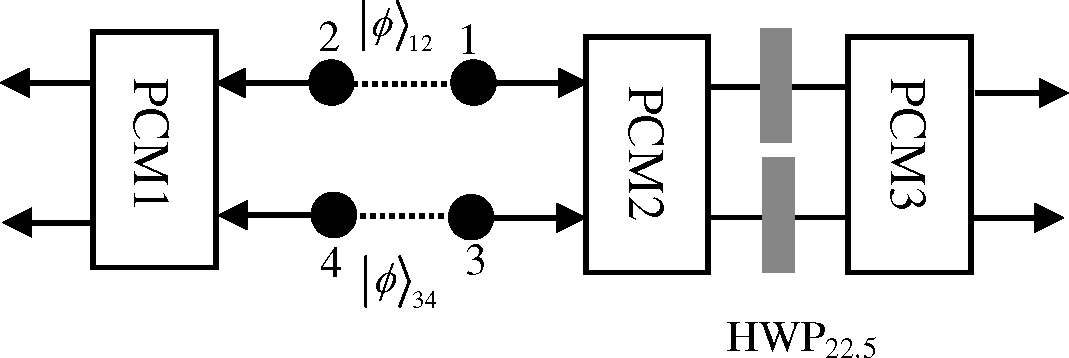
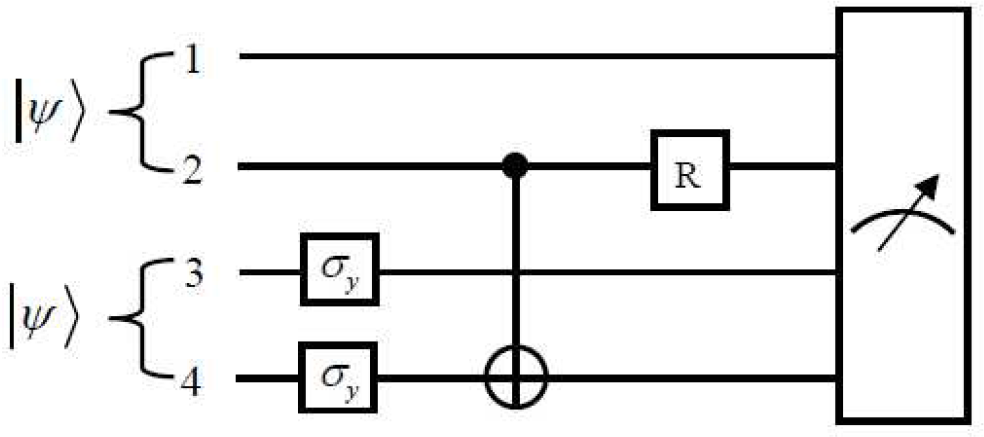
3. The Concurrence Measures for the Atomic State
4. Discussion and Conclusion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Einstein, A.; Podolsky, B.; Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935, 47, 777. [Google Scholar]
- Schrödinger, E. Die gegenwärtige situation in der quantenmechanik. Naturwissenschaften 1935, 23, 823–828. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bennett, C.H.; Brassard, G.; Crepeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein–Podolsky–Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar]
- Bouwmeester, D.; Pan, J.W.; Mattle, K.; Eibl, M.; Weinfurter, H.; Zeilinger, A. Experimental quantum teleportation. Nature 1997, 390, 575–579. [Google Scholar]
- Bennett, C.H.; DiVincenzo, D.P. Quantum information and computation. Nature 2000, 404, 247–255. [Google Scholar]
- Marzolino, U.; Buchleitner, A. Quantum teleportation with identical particles. Phys. Rev. A 2015, 91, 032316. [Google Scholar]
- Liu, X.S.; Long, G.L.; Tong, D.M.; Li, F. General scheme for superdense coding between multi-parties. Phys. Rev. A 2002, 65, 022304. [Google Scholar]
- Karlsson, A.; Bourennane, M. Superdense coding of quantum states. Phys. Rev. Lett. 2004, 92, 187901. [Google Scholar]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar]
- Zhang, C.M.; Song, X.T.; Treeviriyanupab, P.; Li, M.; Wang, C.; Li, H.W.; Yin, Z.Q.; Chen, W.; Han, Z.F. Delayed error verification in quantum key distribution. Chin. Sci. Bull. 2014, 59, 2825–2828. [Google Scholar]
- Su, X.L. Applying Gaussian quantum discord to quantum key distribution. Chin. Sci. Bull. 2014, 59, 1083–1090. [Google Scholar]
- Long, G.L.; Liu, X.S. Theoretically efficient high-capacity quantum-key-distribution scheme. Phys. Rev. A 2002, 65, 032302. [Google Scholar]
- Deng, F.G.; Long, G.L.; Liu, X.S. Two-step quantum direct communication protocol using the Einstein-Podolsky-Rosen pair block. Phys. Rev. A 2003, 68, 042317. [Google Scholar]
- Chang, Y.; Xu, C.X.; Zhang, S.B.; Yan, L. Quantum secure direct communication and authentication protocol with single photons. Chin. Sci. Bull. 2013, 58, 4571–4576. [Google Scholar]
- Wei, H.R.; Deng, F.G. Compact quantum gates on electron-spin qubits assisted by diamond nitrogen-vacancy centers inside cavities. Phys. Rev. A 2013, 88, 042323. [Google Scholar]
- Wei, H.R.; Deng, F.G. Universal quantum gates on electron-spin qubits with quantum dots inside single-side optical microcavities. Opt. Express 2014, 22, 593–607. [Google Scholar]
- Ren, B.C.; Deng, F.G. Hyper-parallel photonic quantum computation with coupled quantum dots. Sci. Rep. 2014, 4, 4623. [Google Scholar]
- Ren, B.C.; Wang, G.Y.; Deng, F.G. Universal hyperparallel hybrid photonic quantum gates with dipole-induced transparency in the weak-coupling regime. Phys. Rev. A 2015, 91, 032328. [Google Scholar]
- Liu, Y. Deleting a marked state in quantum database in a duality computing mode. Chin. Sci. Bull. 2013, 58, 2927–2931. [Google Scholar]
- Liu, Y.; Ou-Yang, X.P. A quantum algorithm that deletes marked states from an arbitrary database. Chin. Sci. Bull. 2013, 58, 2329–2333. [Google Scholar]
- Zheng, C.; Long, G.F. Quantum secure direct dialogue using Einstein–Podolsky–Rosen pairs. Sci. Chin. Phys. Mech. Astron. 2014, 57, 1238–1243. [Google Scholar]
- Su, X.L.; Jia, X.J.; Xie, C.D.; Peng, K.C. Preparation of multipartite entangled states used for quantum information networks. Sci. Chin. Phys. Mech. Astron. 2014, 57, 1210–1217. [Google Scholar]
- Leibfried, D.; Knill, E.; Seidelin, S.; Britton, J.; Blakestad, R.B.; Chiaverini, J.; Hume, D.B.; Itano, W.M.; Jost, J.D.; Langer, C.; et al. Creation of a six-atom ‘Schrödinger cat’ state. Nature 2005, 438, 639–642. [Google Scholar]
- Häffner, H.; Hänsel, W.; Roos, C.F.; Benhelm, J.; Chek-al-kar, D.; Chwalla, M.; Körber, T.; Rapol, U.D.; Riebe, M.; Schmidt, P.O.; Becher, C.; Gühne, O.; Dür, W.; Blatt, R. Scalable multiparticle entanglement of trapped ions. Nature 2005, 438, 643–646. [Google Scholar]
- Lu, C.Y.; Zhou, X.Q.; Gühne, O.; Gao, W.B.; Zhang, J.; Yuan, Z.S.; Goebel, A.; Yang, T.; Pan, J.W. Experimental entanglement of six photons in graph states. Nat. Phys. 2007, 3, 91–95. [Google Scholar]
- Gao, W.B.; Lu, C.Y.; Yao, X.C.; Xu, P.; Gühne, O.; Goebel, A.; Chen, Y.A.; Peng, C.Z.; Chen, Z.B.; Pan, J.W. Experimental demonstration of a hyper-entangled ten-qubit Schrödinger cat state. Nat. Phys. 2010, 6, 331–335. [Google Scholar]
- Hald, J.; Sörensen, J.L.; Schori, C.; Polzik, E.S. Spin squeezed atoms: A macroscopic entangled ensemble created by light. Phys. Rev. Lett. 1999, 83, 1319–1322. [Google Scholar]
- Mandel, O.; Greiner, M.; Widera, A.; Rom, T.; Hänsch, T.; Bloch, I. Controlled collisions for multi-particle entanglement of optically trapped atoms. Nature 2003, 425, 937–940. [Google Scholar]
- Huang, Y.F.; Liu, B.H.; Peng, L.; Li, Y.H.; Li, L.; Li, C.F.; Guo, G.C. Experimental generation of an eight-photon Greenberger–Horne–Zeilinger state. Nat. Commun. 2011, 2, 546. [Google Scholar]
- Yao, X.C.; Wang, T.X.; Xu, P.; Lu, H.; Pan, G.S.; Bao, X.H.; Peng, C.Z.; Lu, C.Y.; Chen, Y.A.; Pan, J.W. Observation of eight-photon entanglement. Nat. Photon. 2012, 6, 225–228. [Google Scholar]
- He, L.; Chen, L.K.; Liu, C.; Xu, P.; Yao, X.C.; Li, L.; Liu, N.L.; Zhao, B.; Chen, Y.A.; Pan, J.W. Experimental realization of a concatenated Greenberger-Horne-Zeilinger state for macroscopic quantum superpositions. Nat. Photon. 2014, 8, 364–368. [Google Scholar]
- Bell, J.S. On the Einstein–Podolsky–Rosen paradox. Physics 1964, 1, 195–200. [Google Scholar]
- Horodecki, M.; Horodecki, P.; Horodecki, R. Separability of mixed states: Necessary and sufficient conditions. Phys. Lett. A 1996, 223, 1–8. [Google Scholar]
- Bartkiewicz, K.; Beran, J.; Lemr, K.; Norek, M.; Miranowicz, A. Quantifying entanglement of a two-qubit system via measurable and invariant moments of its partially transposed density matrix. Phys. Rev. A 2015, 91, 022323. [Google Scholar]
- Bartkiewicz, K.; Horodecki, P.; Lemr, K.; Miranowicz, A.; Życzkowski, K. Method for universal detection of two-photon polarization entanglement. Phys. Rev. A 2015, 91, 032315. [Google Scholar]
- Gühne, O.; Tóth, G. Entanglement detection. Phys. Rep. 2009, 474, 1–75. [Google Scholar]
- James, D.F.V.; Kwiat, P.G.; Munro, W.J.; White, A.G. Measurement of qubits. Phys. Rev. A 2005, 64, 052312. [Google Scholar]
- Mohammadi, M.; Brańczyk, A.M.; James, D.F.V. Fourier-transform quantum state tomography. Phys. Rev. A 2013, 87, 012117. [Google Scholar]
- White, A.G.; James, D.F.V.; Eberhard, P.H.; Kwiat, P.G. Nonmaximally entangled states: Production, characterization, and utilization. Phys. Rev. Lett. 1999, 83, 3103–3107. [Google Scholar]
- Bennett, C.H.; Bernstein, H.J.; Popescu, S.; Schumacher, B. Concentrating partial entanglement by local operations. Phys. Rev. A 1996, 53, 2046–2052. [Google Scholar]
- Bennett, C.H.; Divincenze, D.P.; Smolin, J.A.; Wootters, W.K. Mixed-state entanglement and quantum error correction. Phys. Rev. A 1996, 54, 3824–3851. [Google Scholar]
- Wootters, W.K. Entanglement of formation and concurrence. Quantum Inf. Comput. 2001, 1, 27–44. [Google Scholar]
- Hill, S.; Wootters, W.K. Entanglement of a pair of quantum bits. Phys. Rev. Lett. 1997, 78, 5022–5025. [Google Scholar]
- Wootters, W.K. Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 1998, 80, 2245–2248. [Google Scholar]
- Mintert, F.; KuŚ, M.; Buchleitner, A. Concurrence of mixed multipartite quantum states. Phys. Rev. Lett. 2005, 95, 260502. [Google Scholar]
- Fei, S.M.; Zhao, M.J.; Chen, K.; Wang, Z.X. Experimental determination of entanglement for arbitrary pure states. Phys. Rev. A 2009, 80, 032320. [Google Scholar]
- Walborn, S.P.; Souto Ribeiro, P.H.; Davidovich, L.; Mintert, F.; Buchleitner, A. Experimental determination of entanglement with a single measurement. Nature 2006, 440, 1022–1024. [Google Scholar]
- Walborn, S.P.; Souto Ribeiro, P.H.; Davidovich, L.; Mintert, F.; Buchleitner, A. Experimental determination of entanglement by a projective measurement. Phys. Rev. A 2007, 75, 032338. [Google Scholar]
- Zhang, L.H.; Yang, Q.; Yang, M.; Song, W.; Cao, Z.L. Direct measurement of the concurrence of two-photon polarization-entangled states. Phys. Rev. A 2013, 88, 062342. [Google Scholar]
- Zhang, L.H.; Yang, M.; Cao, Z.L. Direct measurement of the concurrence for two-photon polarization entangled pure states by parity-check measurements. Phys. Lett. A 2013, 377, 1421–1424. [Google Scholar]
- Zhou, L. Measurement of arbitrary two-photon entanglement state with the photonic Faraday rotation 2014. arXiv: 1401.6719.
- Romero, G.; López, C.E.; Lastra, F.; Solano, E.; Retamal, J.C. Direct measurement of concurrence for atomic two-qubit pure states. Phys. Rev. A 2007, 75, 032303. [Google Scholar]
- Lee, S.M.; Ji, S.W.; Lee, H.W.; Zubairy, M.S. Proposal for direct measurement of concurrence via visibility in a cavity QED system. Phys. Rev. A 2008, 77, 040301(R). [Google Scholar]
- Zhou, L.; Sheng, Y.B. Detection of nonlocal atomic entanglement assisted by single photons. Phys. Rev. A 2014, 90, 024301. [Google Scholar]
- Liu, J.; Zhou, L.; Sheng, Y.B. Direct measurement of the concurrence for two-qubit electron spin entangled pure state base on charge detection. Chin. Phys. B 2015, 24, 070309. [Google Scholar]
- Sheng, Y.B.; Guo, R.; Pan, J.; Zhou, L.; Wang, X.F. Two-step measurement of the concurrence for hyperentangled state. Quantum Inf. Process. 2015, 14, 963–978. [Google Scholar]
- Kwiat, P.G. Hyper entangled states. J. Mod. Opt. 1997, 44, 2173–2184. [Google Scholar]
- Barbieri, M.; Cinelli, C.; Mataloni, P.; Martini, F.D. Polarization-momentum hyperentangled states: Realization and characterization. Phys. Rev. A 2005, 72, 052110. [Google Scholar]
- Rarity, J.; Tapster, P. Experimental violation of Bell’s inequality based on phase and momentum. Phys. Rev. Lett. 1990, 64, 2495–2498. [Google Scholar]
- Kwiat, P.G.; Waks, E.; White, A.G.; Appelbaum, I.; Eberhard, P.H. Ultrabright source of polarization-entangled photons. Phys. Rev. A 1999, 60, R773–R776. [Google Scholar]
- Fiorentino, M.; Wong, F.N.C. Deterministic controlled-not gate for single photon two-qubit quantum logic. Phys. Rev. Lett. 2004, 93, 070502. [Google Scholar]
- Sheng, Y.B.; Zhou, L.; Zhao, S.M.; Zheng, B.Y. Efficient single-photon-assisted entanglement concentration for partially entangled photon pairs. Phys. Rev. A 2012, 85, 012307. [Google Scholar]
- Sheng, Y.B.; Zhou, L.; Zhao, S.M. Efficient two-step entanglement concentration for arbitrary W states. Phys. Rev. A 2012, 85, 042302. [Google Scholar]
- Sheng, Y.B.; Zhou, L. Deterministic entanglement distillation for secure double-server blind quantum computation. Sci. Rep. 2015, 5, 7815. [Google Scholar]
- Zhou, L.; Sheng, Y.B.; Cheng, W.W.; Gong, L.Y.; Zhao, S.M. Efficient entanglement concentration for arbitrary less-entangled NOON states. Quantum Inf. Process. 2013, 12, 1307–1320. [Google Scholar]
- Zhou, L.; Sheng, Y.B.; Cheng, W.W.; Gong, L.Y.; Zhao, S.M. Efficient entanglement concentration for arbitrary single-photon multimode W state. J. Opt. Soc. Am. B 2013, 30, 71–77. [Google Scholar]
- Zhou, L.; Sheng, Y.B. Efficient single-photon entanglement concentration for quantum communications. Opt. Commun. 2014, 313, 217–222. [Google Scholar]
- Zhou, L.; Sheng, Y.B. Recyclable amplification protocol for the single-photon entangled state. Laser Phys. Lett. 2015, 12, 045203. [Google Scholar]
- Song, W.; Yang, M.; Cao, Z.L. Purifying entanglement of noisy two-qubit states via entanglement swapping. Phys. Rev. A 2014, 89, 014303. [Google Scholar]
- Guo, Q.; Bai, J.; Cheng, L.Y.; Shao, X.Q.; Wang, H.F.; Zhang, S. Simplified optical quantum-information processing via weak cross-Kerr nonlinearities. Phys. Rev. A 2011, 83, 054303. [Google Scholar]
- Nemoto, K.; Munro, W.J. Nearly deterministic linear optical controlled-not gate. Phys. Rev. Lett. 2004, 93, 250502. [Google Scholar]
- Wei, T.C.; Altepeter, J.B.; Branning, D.; Goldbart, P.M.; James, D.F.V.; Jeffrey, E.; Kwiat, P.G.; Mukhopadhyay, S.; Peters, N.A. Synthesizing arbitrary two-photon polarization mixed states. Phys. Rev. A 2005, 71, 032329. [Google Scholar]
- Collins, D.; Gisin, N. A relevant two qubit Bell inequality inequivalent to the CHSH inequality. J. Phys. A 2004, 37, 1775–1787. [Google Scholar]
- An, J.H.; Feng, M.; Oh, C.H. Fidelity in topological quantum phases of matter. Phys. Rev. A 2009, 79, 032303. [Google Scholar]
- Chen, J.J.; An, J.H.; Feng, M.; Liu, G. Teleportation of an arbitrary multipartite state via photonic Faraday rotation. J. Phys. B 2010, 43, 095505. [Google Scholar]
- Bastos, W.P.; Cardoso, W.B.; Avelar, A.T.; de Almeida, N.G.; Baseia, B. Controlled teleportation via photonic Faraday rotations in low-Q cavities. Quantum Inf. Process. 2012, 11, 1867–1881. [Google Scholar]
- Julsgaard, B.; Kozhekin, A.; Polzik, E.S. Experimental long-lived entanglement of two macroscopic objects. Nature 2001, 413, 400–403. [Google Scholar]
- Peng, Z.H.; Zou, J.; Liu, X.J.; Xiao, Y.J.; Kuang, L.M. Atomic and photonic entanglement concentration via photonic Faraday rotation. Phys. Rev. A 2012, 86, 034305. [Google Scholar]
- Zhou, L.; Sheng, Y.B. Arbitrary atomic cluster state concentration for one-way quantum computation. J. Opt. Soc. Am. B 2014, 31, 1–10. [Google Scholar]
- Zhou, L.; Wang, X.F.; Sheng, Y.B. Efficient entanglement concentration for arbitrary less-entangled N-atom GHZ state. Int. J. Theor. Phys. 2014, 53, 1752–1766. [Google Scholar]
- Vallone, G.; Ceccarelli, R.; De Martini, F.; Mataloni, P. Hyperentanglement of two photons in three degrees of freedom. Phys. Rev. A 2009, 79, 030301(R). [Google Scholar]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865–942. [Google Scholar]
- Osnaghi, S.; Bertet, P.; Auffeves, A.; Maioli, P.; Brune, M.; Raimond, J.M.; Haroche, S. Coherent control of an atomic collision in a cavity. Phys. Rev. Lett. 2001, 87, 037902. [Google Scholar]
- Zheng, S.B.; Guo, G.C. Efficient scheme for two-atom entanglement and quantum information processing in cavity QED. Phys. Rev. Lett. 2000, 85, 2392–2395. [Google Scholar]
- Rauschenbeutel, A.; Nogues, G.; Osnaghi, S.; Bertet, P.; Brune, M.; Raimond, J.M.; Haroche, S. Coherent operation of a tunable quantum phase gate in cavity QED. Phys. Rev. Lett. 2000, 83, 5166–5169. [Google Scholar]
- Jaeger, G.; Horne, M.A.; Shimony, A. Complementarity of one-particle and two-particle interference. Phys. Rev. A 1993, 48, 1023–1027. [Google Scholar]
- Jaeger, G.; Shimony, A.; Vaidman, L. Two interferometric complementarities. Phys. Rev. A 1995, 51, 54–67. [Google Scholar]
- Horne, M.A.; Shimony, A.; Zeilinger, A. Two-particle interferometry. Phys. Rev. Lett. 1989, 62, 2209–2212. [Google Scholar]
- Abouraddy, A.F.; Saleh, B.E.A.; Sergienko, A.V.; Teich, M.C. Degree of entanglement for two qubits. Phys. Rev. A 2001, 64, 050101(R). [Google Scholar]
- Kaszlikowski, D.; Kwek, L.C.; Zukowski, M.; Englert, B.G. Information-theoretic approach to single-particle and two-particle interference in multipath interferometers. Phys. Rev. Lett. 2003, 91, 037901. [Google Scholar]
- Jakob, M.; Bergou, J. Quantitative conditional quantum erasure in two-atom resonance fluorescence. Phys. Rev. A 2002, 66, 062107. [Google Scholar]
- Jakob, M.; Bergou, J.A. Generalized complementarity relations in composite quantum systems of arbitrary dimensions. Int. J. Mod. Phys. B 2006, 20, 1371–1381. [Google Scholar]
- de Melo, F.; Walborn, S.P.; Bergou, J.A.; Davidovich, L. Quantum nondemolition circuit for testing bipartite complementarity. Phys. Rev. Lett. 2007, 98, 250501. [Google Scholar]
- Zubairy, M.S.; Agarwal, G.S.; Scully, M.O. Quantum disentanglement eraser: A cavity QED implementation. Phys. Rev. A 2004, 70, 012316. [Google Scholar]
- Rauschenbeutel, A.; Nogues, G.; Osnaghi, S.; Bertet, P.; Brune, M.; Raimond, J.M.; Haroche, S. Coherent operation of a tunable quantum phase gate in cavity QED. Phys. Rev. Lett. 1999, 83, 5166–5169. [Google Scholar]
- Bertet, P.; Osnaghi, S.; Rauschenbeutel, A.; Nogues, G.; Auffeves, A.; Brune, M.; Raimond, J.M.; Haroche, S. A complementarity experiment with an interferometer at the quantum classical boundary. Nature 2001, 411, 166–170. [Google Scholar]
- Di, T.; Zubairy, M.S. Generation of arbitrary two-qubit entangled states in cavity QED. J. Mod. Opt. 2004, 51, 2387–2393. [Google Scholar]
- Barrett, S.D.; Kok, P.; Nemoto, K.; Beausoleil, R.G.; Munro, W.J.; Spiller, T.P. Symmetry analyzer for nondestructive Bell-state detection using weak nonlinearities. Phys. Rev. A 2005, 71, 060302(R). [Google Scholar]
- He, B.; Lin, Q.; Simon, C. Cross-Kerr nonlinearity between continuous-mode coherent states and single photons. Phys. Rev. A 2011, 83, 053826. [Google Scholar]
- He, B.; Scherer, A. Continuous-mode effects and photon-photon phase gate performance. Phys. Rev. A 2012, 85, 033814. [Google Scholar]
- He, B.; Ren, Y.; Bergou, J.A. Creation of high-quality long-distance entanglement with flexible resources. Phys. Rev. A 2009, 79, 052323. [Google Scholar]
- Lin, Q.; Li, J. Quantum control gates with weak cross-Kerr nonlinearity. Phys. Rev. A 2009, 79, 022301. [Google Scholar]
- Lin, Q.; He, B. Single-photon logic gates using minimal resources. Phys. Rev. A 2009, 80, 042310. [Google Scholar]
- Gea-Banacloche, J. Impossibility of large phase shifts via the giant Kerr effect with single-photon wave packets. Phys. Rev. A 2010, 81, 043823. [Google Scholar]
- Shapiro, J.H. Single-photon Kerr nonlinearities do not help quantum computation. Phys. Rev. A 2006, 73, 062305. [Google Scholar]
- Shapiro, J.H.; Razavi, M. Continuous-time cross-phase modulation and quantum computation. New J. Phys. 2007, 9, 16. [Google Scholar]
- Jeong, H. Quantum computation using weak nonlinearities: Robustness against decoherence. Phys. Rev. A 2006, 73, 052320. [Google Scholar]
- Barrett, S.D.; Milburn, G.J. Quantum-information processing via a lossy bus. Phys. Rev. A 2006, 74, 060302(R). [Google Scholar]
- Jeong, H.; Kim, M.S.; Ralph, T.C.; Ham, B.S. Generation of macroscopic superposition states with small nonlinearity. Phys. Rev. A 2004, 70, 061801(R). [Google Scholar]
- Jeong, H. Using weak nonlinearity under decoherence for macroscopic entanglement generation and quantum computation. Phys. Rev. A 2005, 72, 034305. [Google Scholar]
- Jeong, H.; An, N.B. Greenberger–Horne–Zeilinger-type and W-type entangled coherent states: Generation and Bell-type inequality tests without photon counting. Phys. Rev. A 2006, 74, 022104. [Google Scholar]
- Kok, P.; Munro, W.J.; Nemoto, K.; Ralph, T.C.; Dowling, J.P.; Milburn, G.J. Linear optical quantum computing with photonic qubits. Rev. Mod. Phys. 2007, 79, 135–174. [Google Scholar]
- Kok, P.; Lee, H.; Dowling, J.P. Single-photon quantum-nondemolition detectors constructed with linear optics and projective measurements. Phys. Rev. A 2002, 66, 063814. [Google Scholar]
- Feizpour, A.; Xing, X.; Steinberg, A.M. Amplifying single-photon nonlinearity using weak measurements. Phys. Rev. Lett. 2011, 107, 133603. [Google Scholar]
- Hofmann, H.F.; Kojima, K.; Takeuchi, S.; Sasaki, K. Optimized phase switching using a single-atom nonlinearity. J. Opt. B 2003, 5, 218–221. [Google Scholar]
- Zhu, C.; Huang, G. Giant Kerr nonlinearity, controlled entangled photons and polarization phase gates in coupled quantum-well structures. Opt. Express 2011, 19, 23364–23376. [Google Scholar]
- Hoi, I.C.; Kockum, A.F.; Palomaki, T.; Stace, T.M.; Fan, B.; Tornberg, L.; Sathyamoorthy, S.R.; Johansson, G.; Delsing, P.; Wilson, C.M. Giant cross-Kerr effect for propagating microwaves induced by an artificial atom. Phys. Rev. Lett. 2013, 111, 053601. [Google Scholar]
- He, B.; Sharypov, A.V.; Sheng, J.; Simon, C.; Xiao, M. Two-photon dynamics in coherent Rydberg atomic ensemble. Phys. Rev. Lett. 2014, 112, 133606. [Google Scholar]
- Stoler, D.; Saleh, B.E.A.; Teich, M.C. Binomial states of the quantized radiation field. Optica Acta 1985, 32, 345–355. [Google Scholar]
- Vidiella-Barranco, A.; Roversi, J.A. Statistical and phase properties of the binomial states of the electromagnetic field. Phys. Rev. A 1994, 50, 5233–5241. [Google Scholar]
- Lo Franco, R.; Compagno, G.; Messina, A.; Napoli, A. Generating and revealing a quantum superposition of electromagnetic-field binomial states in a cavity. Phys. Rev. A 2007, 76, 011804(R). [Google Scholar]
- Lo Franco, R.; Compagno, G.; Messina, A.; Napoli, A. Generation of entangled two-photon binomial states in two spatially separate cavities. Open Syst. Inf. Dyn. 2006, 13, 463–470. [Google Scholar]
- Lo Franco, R.; Compagno, G.; Messina, A.; Napoli, A. Single-shot generation and detection of a two-photon generalized binomial state in a cavity. Phys. Rev. A 2006, 74, 045803. [Google Scholar]
- Lo Franco, R.; Compagno, G.; Messina, A.; Napoli, A. Bell’s inequality violation for entangled generalized Bernoulli states in two spatially separate cavities. Phys. Rev. A 2005, 72, 053806. [Google Scholar]
- Nuβann, S.; Hijlkema, M.; Weber, B.; Rohde, F.; Rempe, G.; Kuhn, A. Submicron positioning of single atoms in a microcavity. Phys. Rev. Lett. 2005, 95, 173602. [Google Scholar]
- Fortier, K.M.; Kim, S.Y.; Gibbons, M.J.; Ahmadi, P.; Chapman, M.S. Deterministic loading of individual atoms to a high-finesse optical cavity. Phys. Rev. Lett. 2007, 98, 233601. [Google Scholar]
- Colombe, Y.; Steinmetz, T.; Dubois, G.; Linke, F.; Hunger, D.; Reichel, J. Strong atom-field coupling for Bose-Einstein condensates in an optical cavity on a chip. Nature 2007, 450, 272–276. [Google Scholar]







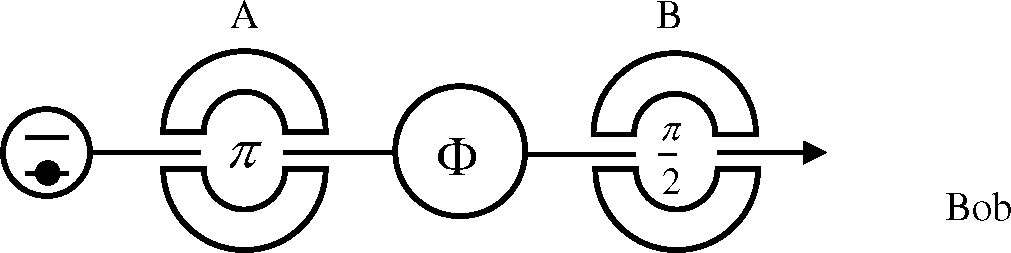


© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, L.; Sheng, Y.-B. Concurrence Measurement for the Two-Qubit Optical and Atomic States. Entropy 2015, 17, 4293-4322. https://doi.org/10.3390/e17064293
Zhou L, Sheng Y-B. Concurrence Measurement for the Two-Qubit Optical and Atomic States. Entropy. 2015; 17(6):4293-4322. https://doi.org/10.3390/e17064293
Chicago/Turabian StyleZhou, Lan, and Yu-Bo Sheng. 2015. "Concurrence Measurement for the Two-Qubit Optical and Atomic States" Entropy 17, no. 6: 4293-4322. https://doi.org/10.3390/e17064293
APA StyleZhou, L., & Sheng, Y.-B. (2015). Concurrence Measurement for the Two-Qubit Optical and Atomic States. Entropy, 17(6), 4293-4322. https://doi.org/10.3390/e17064293




