1. Introduction
Information geometry (IG) has been essentially developed by S.-I. Amari, see the monograph by Amari and Nagaoka [
1]. In his work, all previous geometric—essentially metric—descriptions of probabilistic and statistics concepts are extended in the direction of affine differential geometry, including the fundamental treatment of connections. A corresponding concept for abstract manifold, called statistical manifold, has been worked out by Lauritzen in [
2]. Amari’s framework is today considered a case of Hessian geometry as it is described in the monograph by Shima [
3].
Other versions of IG have been studied to deal with a non-parametric settings such as the Boltzmann equation as it is described in [
4,
5]. A very general set-up for information geometry is the following. Consider a one-dimensional family of positive densities with respect to a measure
µ,
θ ↦
pθ, and a random variable
U. A classical statistical computation, possibly due to Ronald Fisher, is
The previous computation suggests the following geometric construction which is rigorous if the sample space is finite and can be forced to work in general under suitable assumptions. We use the differential geometry language, e.g., [
6]. If Δ is the
probability simplex on a given sample space (Ω,
), we define the
statistical bundle of Δ to be
Given a one dimensional curve in Δ,
θ ↦ π
θ we can define its
velocity to be the curve be the curve
where we define
Each fiber
has a scalar product and we have a parallel transport
This structure provides an interesting framework to interpret the Fisher computation cited above. The basic case of a finite state space has been extended by Amari and coworkers to the case of a parametric set of strictly positive probability densities on a generic sample space. Following a suggestion by Dawid in [
7,
8], a particular nonparametric version of that theory was developed in a series of papers [
9–
19], where the set
P> of all strictly positive probability densities of a measure space is shown to be a Banach manifold (as it is defined in [
20–
22]) modeled on an Orlicz Banach space, see, e.g., [23, Chapter II].
In the present paper, Section 2 recalls the theory and our notation about the model Orlicz spaces. This material is included for convenience only and this part should be skipped by any reader aware of any of the papers [
9–
19] quoted above. The following Section 3 is mostly based on the same references and it is intended to introduce that manifold structure and to give a first example of application to the study of Kullback-Liebler divergence. The special features of statistical manifolds that contain the Maxwell density are discussed in Section 4. In this case we can define the Boltzmann–Gibbs entropy and study its gradient flow. The setting for the Boltzmann equation is discussed in Section 5 where we show that the equation can be derived from probabilistic operations performed on the statistical manifold. Our application to the study of the Kullback-Liebler divergence is generalized in Section 6 to the more delicate case of the Hyvarïnen divergence. This requires in particular a generalization of the manifold structure to include differential operators and leads naturally to the introduction of Orlicz-Sobolev spaces.
We are aware that there are other approaches to non-parametric information geometry that are not based on the notion of the exponential family and that we do not consider here. We mention in particular [
24] and [
25].
2. Model Spaces
Given a σ-finite measure space, (Ω, , µ), we denote by P> the set of all densities that are positive µ-a.s, by P≥ the set of all densities, by P1 the set of measurable functions f with ∫ f dµ = 1.
We introduce here the Orlicz spaces we shall mainly investigate in the sequel. We refer to [
10] and [23, Chapter 2] for more details on the matter. We consider the Young function
and, for any
p ∈
P>, the Orlicz space
LΦ(
p) =
Lcosh−1 (
p) is defined as follows: a real random variable
U belongs to
LΦ(
p) if
The Orlicz space
LΦ(
p) is a Banach space when endowed with the Luxemburg norm defined as
The conjugate function of Φ = cosh −1 is
which satisfies the so-called Δ
2-condition as
Since Φ
∗ is a Young function, for any
p ∈
P>, one can define as above the associated Orlicz space
LΦ∗(
p) =
L(cosh−1)∗ (
p) and its corresponding Luxemburg norm
Because the functions Φ and Φ
∗ form a Young pair, for each
U ∈
cosh −1(
p) and
V ∈
L(cosh−1)∗(
p) we can deduce from Young’s inequality
that the following Holder’s inequality holds:
Moreover, it is a classical result that the space
L(cosh−1)∗(
p) is separable and its dual space is
Lcosh−1(
p), the duality pairing being
We recall the following continuous embedding result that we shall use repeatedly in the paper:
Theorem 1. Given p ∈
P>, for any 1
< r < ∞, the following embeddingsare continuous. From this result, we deduce easily the following useful Lemma
Lemma 1. Given p ∈
P> and k ≥ 1.
For any u1,
…, uk ∈
Lcosh−1 (
p)
one has Proof. According to Theorem 1, ui ∈ Lr(p) for any 1 < r < ∞ and any i = 1,…, k. The proof follows then simply from the repeated use of Holder inequality. □
From now on we also define, for any
p ∈
P>In the same way, we set
.
2.1. Cumulant Generating Functional
Let p ∈ P> be given. With the above notations one can define:
Definition 1. The cumulant generating functional
is the mapping The following result [
9,
10] shows the properties of the exponential function as a superposition mapping [
26].
Proposition 1. Let a ≥ 1 and p ∈ P> be given.
For any n = 0, 1,
… and u ∈
LΦ(
p):
is a continuous, symmetric, n-multi-linear map from.
is a power series from LΦ(p) to La(p), with radius of convergence larger than 1.
The superposition mapping, v ↦ ev/a, is an analytic function from the open unit ball of LΦ(p) to La(p).
The cumulant generating functional enjoys the following properties (see [
9,
10,
14]):
Proposition 2.
Kp(0) = 0; otherwise, for each u ≠ 0, Kp(u) > 0.
Kp is convex and lower semi-continuous, and its proper domainis a convex set that contains the open unit ball of Bp. Kp is infinitely Gâteaux-differentiable in the interior of its proper domain.
Kp is bounded, infinitely Fréchet-differentiable and analytic on the open unit ball of Bp.
Remark 1. One sees from the above property 2 that the interior of the proper domain of Kp is a non-empty open convex set. From now on we shall adopt the notation Other properties of the functional Kp are described below, as they relate directly to the exponential manifold.
3. Exponential Manifold
The set of positive densities, P>, locally around a given p ∈ P>, is modeled by the subspace of centered random variables in the Orlicz space, Lcosh−1(p). Hence, it is crucial to discuss the isomorphism of the model spaces for different p’s in order to show the existence of an atlas defining a Banach manifold.
Definition 2 (Statistical exponential manifold [10, Definition 20]).
For p ∈
P>, the statistical exponential manifold
at p is We also need the following definition of connection
Definition 3 (Connected densities). Densities p, q ∈
P> are connected by an open exponential arc if there exists an open exponential family containing both, i.e.,
if for a neighborhood I of [0, 1]
In such a case, one simply writes p ⌣ q.
Theorem 2 (Portmanteau theorem, see [10, Theorems 19 and 21] and [27, Theorem 4.7] ).
Let p, q ∈
P>. The following statements are equivalent:p ⌣ q, ( i.e., p and q are connected by an open exponential arc);
;
;
;
LΦ(p) = LΦ(q), (i.e., they both coincide as vector spaces and their norms are equivalent);
There exists ε > 0
such that
We can now define the charts and atlas of the exponential manifold as follows:
Definition 4 (Exponential manifold [
9,
10,
14,
15]).
For each p ∈
P>, define the charts at
p as:with inverse The atlas,
is affine and defines the exponential (statistical) manifold
.
We collect here various results from [
9,
10,
14,
15] about additional properties of
Kp.
Proposition 3. Let with.
On the basis of the above result, it appears natural to define the following
parallel transports:
Definition 5.
The exponential transport
is computed as The mixture transport
is computed asOne has the following properties
Proposition 4. Let p,
be given. Then We reproduce here a scheme of how the affine manifold works. The domains of the charts centered at
p and
q respectively are either disjoint or equal if
p ⌣
q:
Our discussion of the tangent bundle of the exponential manifold is based on the concept of the velocity of a curve as in [20, Section 3.3] and it is mainly intended to underline its statistical interpretation, which is obtained by identifying curves with one-parameter statistical models. For a statistical model
p(
t),
t ∈
I, the random variable,
(which corresponds to the
Fisher score), has zero expectation with respect to
p(
t), and its meaning in the exponential manifold is velocity; see [
28] on exponential families. More precisely, let
,
I the open real interval containing zero. In the chart centered at
p, the curve is
u(
·):
I → Bp, where
.
Definition 6 (Velocity field of a curve and tangent bundle).
Assume is differentiable with derivative.
Define:Note that Dp does not depend on the chart sp and that the derivative of t ↦
p(
t)
in the last term of the equation is computed in LΦ∗(
p).
The curve is the velocity field
of the curve. On the set,
the charts:define the tangent bundle,
.
Remark 2. Let be a C1 function. Then,
is differentiable and: 3.1. Pretangent Bundle
Let M be a density and
its associated exponential manifold. Here M is generic, later it will be the Maxwell distribution. All densities are assumed to be in
.
Definition 7 (Pretangent bundle
.
The settogether with the charts:is the pretangent bundle,
.
Let
F be a vector field of the pretangent bundle,
. In the chart centered at
p, the vector field is expressed by
If
Fp is of class
C1 with derivative
dFp(
u) ∈
L(
Bp, ∗Bp), for each differentiable curve
.
p we have
and also
Definition 8 (Covariant derivative in
.
Let F be a vector field of class C1 of the pretangent bundle,
and let G be a continuous vector field in the tangent bundle.
The covariant derivative
is the vector field DGF of defined at each by In the definition above the covariant derivative is computed in the mobile frame because its value at
q is computed using the expression in the chart centered at
q. In a fixed frame centered at
p we write
sp(
q) =
w so that
, and compare the two expressions of
F as follows.
Derivation in the direction
v ∈
Bq gives
hence
and at
u = 0, we have
. It follows that the covariant derivative in the fixed frame at
p is
The tangent and pretangent bundle can be coupled to produce the vector bundle of order 2 defined by
with charts
and the duality coupling:
Proposition 5 (Covariant derivative of the duality coupling).
Let F be a vector field of,
and let G, X be vector fields of,
F, G of class C1 and X continuous. Proof. Consider the real function
in the chart centered at any
:
and compute its derivative at 0 in the direction
X(
p). □
We refer to [
18,
19] for further details on the geometric structure, namely the Hilbert bundle, the tangent mapping of an homeomorphism, the Riemannian Hessian. We now turn to a basic example.
3.2. Kullback-Leibler Divergence
The Kullback-Leibler divergence [
29] on the exponential manifold
is the mapping
Notice that, if
,
, then
is the expression in the chart centered at
q1 of the marginal Kullback-Leibler divergence
. Therefore, the Kullback-Leibler divergence is non-negative valued and zero if and only if
q2 =
q1 because of Item
(4) in Theorem 2. Its expression in the chart centered at a generic
is
which is the Bregman divergence [
30] of the convex function
.
It follows from Item
(4) in Proposition 2 that it is
C∞ jointly in both variables and, moreover, analytic with
This regularity result is to be compared with what is available when the restriction, q1 ⌣ q2, is removed, i.e., the semi-continuity [31, Section 9.4].
The partial derivative of
Dp in the first variable, that is the derivative of
, in the direction
v ∈
Bp is
with
. If
, we have
, so that we can compute both the covariant derivative of the partial functional
and its gradient as
The negative gradient flow is
As
, for each
t the random variable
is constant, so that
. It is the exponential arc of
q(0) ⌣
q2 in an exponential time scale.
The partial derivative of
Dp in the second variable, that is the derivative of
, in the direction
v ∈
Bp is
with
qi = e
p(
ui),
i = 1, 2. If
, we have
, so that we can compute both the covariant derivative of the partial functional
q ↦
D (
q1 ||
q) and its gradient as
The negative gradient flow is
whose solution starting at
q0 is
q(
t) =
q1+(
q0−q1)e
−t. It is a mixture model in an exponential time scale.
4. Gaussian Space
In this Section the sample space is ℝ
n,
M denotes the standard
n-dimensional Gaussian density (we denoted it
M because of James Clerk Maxwell (1831–1879))
and
is the exponential manifold containing
M. We recall that the Orlicz space
Lcosh−1 (
M) is defined with the Young function Φ :=
x ↦ cosh
x − 1. The following propositions depend on the specific properties of the Gaussian density
M. They do not hold in general.
Proposition 6.
Proof. 1. If
f is a polynomial of degree
d ≤ 2 then
and the latter is finite for all
α such that
α Hess
f − I is negative definite.
2. The result comes from the fact that all polynomials belong to L2(M) and one has L2(M) ⊂ L(cosh−1)∗ (M). □
4.1. Boltzmann–Gibbs Entropy
While the Kullback-Leibler divergence D (
q1 ||
q2) of Section 3.2 is defined and finite if the densities
q1 and
q2 belong to the same exponential manifold, the
Boltzmann–Gibbs entropy (BG-entropy in the sequel)
could be either non defined or infinite, precisely
−∞, everywhere on some exponential manifolds, or finite everywhere on other exponential manifolds.
Proposition 7. Assume p ⌣
q, Then:For each a ≥ 1, log p ∈ La(p) if, and only if, log q ∈ La(q).
log p ∈ Lcosh−1 (p) if, and only if, log q ∈ Lcosh−1 (q).
Proof. If
p, q belong to the same exponential manifold, we can write
q = e
u−Kp(u) ·p and, from Item
(4) in Theorem 2, we obtain log
q − log
p =
u − Kp(
u) ∈
Lcosh−1 (
p) =
Lcosh−1 (
q), so that log
q ∈
La(
q) if, and only if, log
p ∈
La(
p),
a ≥ 1, and log
q ∈
Lcosh−1 (
q) if, and only if, log
p ∈
Lcosh−1 (
p). □
In order to obtain a smooth function, we study the BG-entropy
H(
q) on all manifolds
, such that for at least one, and, hence for all,
, it holds log (
p) ∈
Lcosh−1 (
p). In such an exponential manifold we can write
so that
.
For example, it is the case when the reference measure is finite and p is constant. Another notable example is the Gaussian case, where the sample space is ℝn endowed with the Lebesgue measure and
. In such case ∫ cosh(α|x|2) exp (−|x|2/2) dx <∞ if 0< α<1/2.
We investigate here the main properties of the BG-entropy in this context. First, one has
Proposition 8. The BG-entropy is a smooth real function on the exponential manifold.
Namely, if thenis a C∞ real function. Moreover, its derivative in the direction v equalswhere q = ep(u). Proof. As − log
q =
−u +
Kp(
u) − log
p = −(
u + log
p +
H(
p)) +
Kp(
u) +
H(
p) ∈
Lcosh−1 (
p), with −(
u + log
p +
H(
p)) ∈
Bp, the representation of the BG-entropy in the chart centered at
p is
hence,
u ↦
Hp(
u) is a
C∞ real function. Notice that
Kp(
u)
− duKp(
u) ≤ 0, hence
, as we already know. The derivative of
Hp in the direction
v equals
□
Notice that, for
u = 0 and
q =
ep(
u), we have
, hence
Proposition 9. The gradient field ∇H over E can be identified, at each p, with random variable ∇H(
p) ∈
Bp ⊂
∗Bq,
Proof. The covariant derivative
DGH at
with respect to the vector field
G defined on
with
G(
p) ∈
Bp and
is
The gradient field ∇H over
, is then defined by
. This justifies the identification with the random variable ∇H(p) = −(log (p) + H(p)) ∈ Bp ⊂ ∗Bq. □
Remark 3. The equation ∇H(p) = 0 implies log p = −H(p), hence p has to be constant and this requires it is the finite reference measure µ.
We refer to [
19] for more details on the BG-entropy and in particular on the evolution of
H on
C1 curve in
of the type
I 3 t ↦
ft.
5. Boltzmann Equation
We consider a space-homogeneous Boltzmann operator as it is defined, for example, in [
5] and [
32]. We retell the basic story in order to introduce our notations and the IG background. Orlicz spaces as a setting for Boltzmann’s equation have been recently proposed by [
33], while the use of exponential statistical manifolds has been suggested in [18, Example 11] and sketched in [19, Section 4.4]. We start with an improvement of the latter, a few repetitions being justified by consistency between this presentation and [32, Sections 1.3, 4.5–6], compare also Proposition 10 below.
5.1. Collision Kinematics
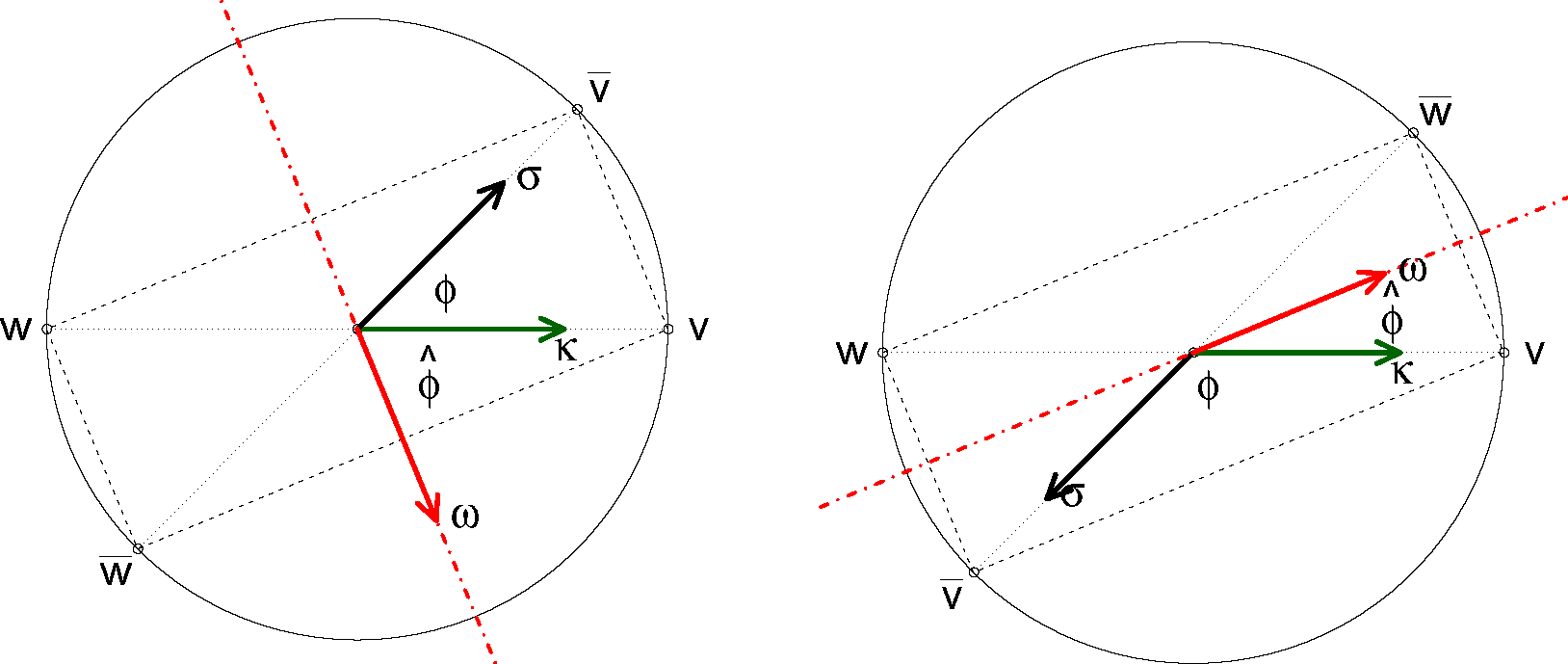
We review our notations, see our
Figure 1,
cf. [32,
Figure 1]. We denote by
v, w ∈ ℝ
3 the velocities before collision, while the velocities after collision are denoted by
. The quadruple
, is assumed to satisfy the
conservation lawswhich define an algebraic variety
that we expect to have dimension 12 − (3 + 1) = 8. The Jacobian matrix of the four defining
Equations (4) and
(5) is
The Jacobian matrix in
Equation (6) has in general position full rank, and rank 3 if
. We denote by
* the 8 dimensional manifold
. In the sequel, for
v ≠
w, we set
From
(4) and
(5) it follows the conservation of both the scalar product,
and of the norm of the difference,
, so that all the vectors of the quadruple lie on a circle with center
and are the four vertexes of a rectangle. If
v =
w then
, and also
as the circle collapse to one point, hence we have
.
There are various explicit and interesting parametrizations of * available.
An elementary parametrization consists of any algebraic solution of
Equations (4) and
(5) with respect to any of the free 8 coordinates. Other parametrizations are used in the literature, see classical references on the Boltzmann equation, e.g., [
5].
A
first parametrization is
where
and the
collision transformation Âσ : (
v, w) ↦ (
v, w) = (
vσ, wσ) is:
Viceversa, on
∗ the collision transformation depends on the unit vector
, while the other terms depend on the collision invariants, as |
v − w|
2 = 2(|
v|
2 + |
w|
2)
− |v +
w|
2. In conclusion, the transformation in
Equation (7) is 1-to-1 from
to
∗, where
.
A
second parametrization of
∗ is obtained using the common space of two parallel sides of the velocity’s rectangle,
, so that
, where ∏ is the orthogonal projection on the subspace. Vice versa, given any Π in the set ∏(1) of projections of rank 1, the mapping
The components in the direction of the image of Π are exchanged, Π
vΠ = Π
w and Π
wΠ = Π
v, while the orthogonal components are conserved. If
ω is any of the two unit vectors such that Π =
ω⊗ω′, the matrix
AΠ =
Aω⊗ω′ does not depend on the direction of
. Notice that
and
, that is
AΠ is an orthogonal symmetric matrix. This parametrization uses the set ∏(1) of projection matrices of rank 1,
The
σ-parametrization
(7) and the ∏-parametrization
(10) are related as follows. Given the unit vector
, the parameters ∏ and
σ in
Equations (9) and
(8) are in 1-to-1 relation as
The transition map from the parametrization
(7) to the parametrization
(10) is
while the inverse transition is
5.3. Conditioning on the Collision Invariants
Given a function
g : ℝ
3 × ℝ
3,
Equation (8) shows that the function
depends on the collision invariants only. This, in turn, implies that
ĝ is the conditional expectation of
g with respect of the collision invariants under any probability distribution on ℝ
3 × ℝ
3 such that the collision invariants and the unit vector of
σ are independent, the unit vector
σ being uniformly distributed. See below a more precise statement in the case of the Gaussian distribution.
On the sample space (ℝ
3,
dv), let
M be the standard normal density defined in
(3) (the Maxwell density). As, for all Π ∈ Π(1),
, in particular |det
AΠ| = 1, we have for each (
V, W ) ∼
M ⊗
M, (
i.e.,
V, W are i.i.d. with distribution
M) that
Under the same distributions, the random variables
,
,
, are independent, with distributions given by
respectively. Hence, given any
S ~
μ such that
,
,
S, are independent, we get
This equality of distribution generalizes the equality of random variables
. We state the results obtained above as follows.
The image distribution of
M ⊗
M ⊗
U induced on (ℝ
3)
4 by the parametrization in
Equation (7) is supported by the manifold
. Such a distribution has the property that the projections on both the first two and the last two components are
M ⊗
M. The joint distribution is not Gaussian; in fact the support
is not a linear subspace. We will call this distribution the
normal collision distribution.
The second parametrization in
Equation (9) shows that the variety
contains the bundle of linear spaces
The distribution of
under the normal collision distribution is obtained from
Equation (11). In fact Π is the projector on the subspace generated by
κ −
σ where
is uniformly distributed and independent from
σ. Hence,
Equation (18) shows that
is uniformly distributed on
so that the distribution in
Equation (24) is the
ν measure defined in
Equation (13). Conditionally to Π, the normal collision distribution is Gaussian with covariance
We can give the previous remarks a more probabilistic form as follows.
Proposition 10 (Conditioning). Let M be the density of the standard normal N(03, I3) and g : ℝ3×ℝ3 → ℝ be an integrable function. It holds the following
If (
V, W) ∼
M ⊗
M and Π ∈ Π(1),
then Assume (
V, W) ∼
F,
,
with F (
v, w) =
f(
v, w)
M(
v)
M(
w).
Thenand
Proof.
We use
V +
W =
VΠ +
WΠ, |
V|
2 + |
W|
2 = |
VΠ|
2 + |
WΠ|
2, (
V, W) ∼ (
VΠ,
WΠ). For all bounded
h1 : ℝ
3 → ℝ and
h2 : ℝ → ℝ, we have
For a generic integrable
h: ℝ
3 × ℝ
3 → ℝ we have
because
, and (
V +
W), |
V − W |,
are independent.
The random variable
is a function of the collision invariants,
i.e., it is of the form
. For all bounded
h1 : ℝ
3 → ℝ and
h2 : ℝ → ℝ, we apply the previous computation to
h =
gh1h2 to get
We use Item 2 and the equality
when
and
to write
where, for given vectors
u, v ∈ ℝ
3,
u, v ≠ 0 we simply denote
. From
Equation (17), the left-end-side can be rewritten as an integral with respect to
,
If Π =
ω ⊗
ω, then |
κ · ω| = |
ω ⊗
ωκ| = |Π
κ|. Using that together with the definition of the measure
ν on Π(1) in
Equation (13), we have the result:
We use 2. If
F ∈
ℇ (
M ⊗
M), then
and there exists a neighborhood
I of [0, 1], where the one dimensional exponential family
exists. The random variable
is a positive probability density with respect to
M ⊗
M because it is the conditional expectation in
M ⊗
M of the positive density
f.
In order to show that
for
t ∈
I, it is enough to consider the convex cases,
t < 0 and
t > 1, because otherwise
. We have
so that in the convex cases:
To conclude, use Bayes’ formula for conditional expectation,
to the expressions of conditional expectation in Item 2 and Item 3 above. □
Remark 4. In the last Item, we compute a conditional expectation of a density f, that is The random variable is the density of the image of F dvdw with respect to the image of M(v)M(w) dvdw.
5.4. Interactions
We introduce here the crucial role played by microscopic interaction in the definition of the Boltzmann collision operator. In the physics literature, such interaction are referred to as the kinetic collision kernel and takes into account the intermolecular forces suffered by particles during a collision [
5]. Before defining formally what we mean by interaction, we first observe that, if
M is the Maxwell density on ℝ
3 and
f, g⌣
M then
where
M ⊗
M is the standard normal density on ℝ
6 and
f ⊗
g is a density on ℝ
6. Indeed, one has
It follows that the product density has the form
which implies
f ⊗
g ⌣
M ⊗
M, with
KM⊗M(
U ⊕
V ) =
KM(
U) +
KM(
V).
Definition 9. With the previous notations, we say that b: ℝ
3 × ℝ
3 → ℝ
+ is an interaction
on ℇ (
M) ⊗
ℇ (
M),
if,
so thatis a density. Sometimes, we make the abuse of notation by writing E
b·f⊗g [
·], where the obvious normalization is not written down. As can been seen, here interactions indicate only a class of suitable weight functions
b for which
b(
v, w)
f(
v)
g(
w) is still (up to normalization) a density. This is in accordance with the usual role played by the kinetic collision kernel (see [
5]).
According to the Portmanteau Theorem 2, it holds
if and only if
, which, in turn, is equivalent to
for some >0.
Proposition 11. Let b: ℝ
3 × ℝ
3 → ℝ
+ be such that for some real A ∈ ℝ
and positive B, C, λ ∈ ℝ
>,
it holds Then the b is an interaction on ℇ (M) × ℇ (M) and for all f, g ⌣ M the following holds.
Proof. 1. We can assume
. As
b(
u, v) ⩽
A +
B |u −
v|
2 ⩽
A + 2
B |(
u, v)|
2, we have
b ∈
LΦ (
M ⊗
M) =
LΦ(
f ⊗
g), and hence
b ∈
L1+ϵ (
f ⊗
g) for
all ϵ > 0. For the second inequality we use the Hardy-Littlewood-Sobolev inequality [34, Theorem 4.3]. We have
If
, by the H-L-S inequality the last integral is bounded by a constant times ||f||α ||g||β. From f, g ⌣ M we get that ||f||α ||g||β is finite for α, β in a right neighborhood of 1. There exists
satisfying all conditions.
2. It is a special case of the Conditioning Theorem 10. □
Let us discuss the differentiability of the operations we have just introduced.
Proposition 12.
The product mapping ℇ (
M) ∋
f ↦
f ⊗
f is a differentiable map into ℇ (
M ⊗
M)
with tangent mapping given for any vector field X ∈
T ℇ (
M)
by Let b be an interaction on ℇ (
M) ⊗
ℇ (
M).
If the mappingis defined on ℇ (
M)
with values in ℇ (
M ⊗
M),
then it is differentiable with tangent mapping given for all vector field X ∈
Tℇ (
M)
by
Proof. 1. We have already proved that
f ⌣
M implies
f ⊗
f ⌣
M ⊗
M and that the mapping in the charts centered at
M and
M ⊗
M respectively is represented as
. The differential of the linear map is again
TM ℇ (
M) ∋
V ↦
V ⊕
V ∈
TM⊗ME (
M ⊗
M). The transport commutes with the ⊕ operation,
and the result follows.
2. Let
U be the coordinate of
f at
M. By assumption, we have
and
so that the coordinate of
in chart centered at
is
The expression if linear and so is the expression of the tangent map
In conclusion, for each vector field X of Tℇ (M), at f we have
and
, hence the action on Tfℇ (M)is as stated. □
Assume
f ⌣
M and let
b be an interaction on
f ⊗
f which depends on the invariants only and such that
b · f ⊗
f ⌣
M ⊗
M. For each random variable
g ∈
Lcosh−1(
M) =
Lcosh−1(
f), define
, which belongs to
Lcosh−1(
M ⊗ M) =
Lcosh−1(
f ⊗
f). Define the operator
by
As constant random variables are in the kernel of the operator A, we assume
.
5.5. Maxwell-Boltzmann and Boltzmann Operator
As explained by C. Villani [5, Section I.2.3], Maxwell obtained a weak form of Boltzmann operator before Boltzmann himself. We rephrase in geometric-probabilistic language such a Maxwell’s weak form by expanding and rigorously proving what was hinted to in [
19].
Let b: ℝ3 × ℝ3 → ℝ+ be an interaction on ℇ (M) × ℇ (M) which depends on the invariants only and such that b · f ⊗ f ⌣ M ⊗ M if f ⌣ M, cf. Proposition 11. We shall call such a b a proper interaction.
For each random variable
g ∈
Lcosh−1(
M) =
Lcosh−1(
f), define
by
which it is easily shown to belong to
Lcosh−1(
M ⊗
M) =
Lcosh−1(
f ⊗
f). The mapping
is a version of the conditional expectation
, where
is the
σ-algebra generated by symmetric random variables.
We define the operator
by
which is a version of
where
is the
σ-algebra generated by the
collision invariants (
v, w) ↦ (
v +
w, |
v|
2 + |
w|
2).
As constant random variables are in the kernel of the operator A, we assume
. Analogously, as the kernel of the operator contains all symmetric random variables, we could always assume that g is anti-symmetric.
The nonlinear operator
is the Maxwell’s weak form of the Boltzmann operator, g being a test function.
Proposition 13. Given a proper interaction b and a density f ∈ ε (
M),
the linear mapis continuous.It can be represented in the duality L(cosh−1)∗(
f)
× Lcosh−1(
f)
bywhere Q is the Boltzmann operator
with interaction b,
Especially, if and we take,
then
Proof. The continuity follows from the Portmanteau theorem and the continuity of the conditional expectation. Item 1 follows from the projection properties of the conditional expectation and from general properties of Orlicz spaces. Item 2 is a special case of the previous one. □
It follows from the previous theorem and from the discussion in [19, Proposition 10] that
f ↦
Q(
f)
/f is a vector field in the cotangent bundle
∗Tε (
M) and its flow
is equivalent to the standard Boltzmann equation
. We do not discuss in this paper the implications of that presentation of the Boltzmann equation to the existence properties. We turn our attention to the comparison of the Boltzmann field to the gradient field of the entropy.
5.6. Entropy Generation
If t ↦
p(
t) is a curve in ε (
M), the entropy of
p(
t) is defined for all
t and the variation of the entropy along the curve is computed as
In our setup, the computation takes the following form. Let
t ↦
pt be a differentiable curve in
ε (
M) with velocity
As the gradient
∇H is given at
p by (∇
H)(
p) = −(log
p +
H(
p)) ∈
Bp, we have
In particular, if
we recover the previous computation:
Assume now that (
p, t) ↦ γ(
t;
p) is the flow of a vector field
F:
ε (
M) →
*Tε (
M). Then
that is, for each
p ∈ ε (
M), the
entropy production at p along the vector field F isIn particular, if the vector field
F is the Boltzmann vector field,
F(
f) =
Q(
f)/
f, we have that for each
f ∈
ε (
M) the Boltzmann’s entropy production is
where
We recover a well-known formula for the entropy production of the Boltzmann operator [
5]. We now proceed to compute the covariant derivative of the entropy production.
Proposition 14.
Let X be a vector field of Tε (
M)
and let F be a vector field of ∗Tε (
M).
The Hessian of the entropy (in the exponential connection) is The covariant derivative of the entropy production along F is
Proof. We note that the entropy production along a vector field
, is a function of the duality coupling of
Tε (
M)
× ∗Tε (
M), so that we can apply Proposition 5 to compute its covariant derivative along
X as
Let us compute
DX∇
H(
p), which is the Hessian of the entropy in the exponential connection. First, we compute the expression of
∇H(
q) = − (log
q +
H(
q))
∈ Bq,
q ∈ ε (
M) in the chart centered at
p. We have
and
so that
and, finally, the expression of
∇H in the chart centered at
p is
Note that this function is affine, and its derivative in the direction X(p) is d(∇H)p(U)[X(p)] = −X(p). It follows that DX∇H = −X.
The application of this computation to the Boltzmann field, i.e., F (f) = Q(f)/f requires the existence of the covariant derivative of the Boltzmann operator. We leave this discussion as a research plan.
6. Weighted Orlicz–Sobolev Model Space
We show in this section that the Information Geometry formalism described in Sections 2 and 3 is robust enough to allow to take into account differential operators (e.g., the classical Laplacian). This yields naturally to the introduction of weighted Orlicz–Sobolev spaces. While the case “without derivative” studied in Section 3 was well-suited for the study of the fine properties of the Kullback-Leibler divergence, we illustrate in Section 6.3 our use of Orlicz–Sobolev spaces with the fine study of the Hyvärinen divergence. This is a special type of divergence between densities that involves an
L2-distance between gradients of densities [
35] which has multiple applications. In particular, it is related with the so called Fisher information as it is defined for example in [
32] (p. 49), which has deep connections with Boltzmann equation, see [
36]. However the name Fisher information should not be used in a statistics context where it rather refers to the expression in coordinates of the metric of statistical models considered as pseudo-Riemannian manifolds, e.g., [
1].
We introduce the Orlicz–Sobolev spaces with weight
M, Maxwell density on ℝ
n,
where
∂j is the derivative in the sense of distributions. They are both Banach spaces, see [23, Section 10]. (The classical Adams’s treatise [37, Chapter 8] has Orlicz–Sobolev spaces, but does not consider the case of a weight. The product functions (
u, x) → (cosh − 1)
*(
u)
M(
x) and (
u, x) →(cosh − 1)
∗(
u)
M(
x) are
ϕ -functions according the Musielak’s definition.) The norm on
is
and similarly for
. One begins with a first technical result in order to relate such spaces with statistical exponential families:
Proposition 15.
Given and,
one has Proof. For simplicity, set
. One knows from the Portmanteau Theorem 2 that
G M ∈ ℇ (
M) and therefore, there exists
ℇ > 0 such that
G ∈ L1+ℇ (
M). Let us prove that
f G ∈ L(cosh−1)∗(
M). First of all, since
L1+ℇ (
M)
⊂ L(cosh−1)∗(
M) and
f ∈ Lcosh−1 (
M) one has
f G ∈ L1(
M). Moreover, for any
x ∈ ℝ
n, according to classical Young’s inequality
Since Φ
∗ is increasing and convex
Now, since
f ∈ LΦ(
M), one has |
f|p ∈ L(cosh−1)∗(
M) for all
p > 1,
i.e., Φ
∗(|
f|p) ∈
L1(
M) for all
p > 1. Choosing then 1
< q < 1+
ε one has
so that Φ
∗(
Gq)
∈ L1(
M). This proves that Φ
∗(
fG)
∈ L1(
M),
i.e.,
In the same way, since
one also has
Moreover,
so that, for any
j = 1, …,
n,
for any
r > 1 and therefore Φ
∗(|
G∂ju|p)
∈ L1(
M) for any
p > 1. Repeating the above argument we get therefore
Since ∂j(fG) = G∂jf + Gf∂ju a.e., one gets ∂j(fG) ∈ L(cosh−1)∗ (M) for any j = 1, …, n which proves the result.
Remark 5.
As a particular case of the above Proposition, if,
then The Orlicz–Sobolev spaces
and
, as defined in
Equations (26) and
(27) respectively, are instances of Gaussian spaces of random variables and they inherit from the corresponding Orlicz spaces a duality form. In this duality the adjoint of the partial derivative has a special form coming from the form of the weight
M see, e.g., [38, Chapter V]. We have the following:
Proposition 16.
Let and.
Thenwhere Xj is the mutliplication operator by the j-th coordinate xj. If then Xjf ϵ
L(cosh −1)∗ (
M).
More precisely, there exists C > 0
such that If and,
then (29) holds.
Proof. 1. As
, we have by definition of distributional derivative,
2. Let us observe first that, according to Holder’s inequality
i.e.,
Xjf ∈ L1(
M). Since Φ
∗ = (cosh −1)
∗ enjoys the so-called Δ
2-condition, to prove the stronger result
X f ∈ L(cosh−1)∗(
M), it is enough to show that E
M [Φ
∗(
Xjf)]
< ∞. First of all, using the tensorization property of the Gaussian measure,
i.e., the fact that
M(
x) =
M1(
x1)
… M1(
xn) for any
x = (
x1,
…, xn)
∈ ℝ
n where
M1 stands for the one-dimensional standard Gaussian, we claim that it is enough to prove the result for
n = 1. Indeed, given
and
xj ∈ ℝ (
j = 1,
…, n), any
x = (
x1,
… xn)
∈ ℝ
n can be identified with
with
and
where
for any
,
. We also set
Then, for a.e.
,
with
and
where
F′ denotes the distributional derivative of
F =
F (
y). In particular, if there exists
C > 0 such that
we get the desired result.
Let us then prove
(31) and fix
. From
arsinh
u du together with the evenness of arsinh we obtain
Write for simplicity
one has
Now, the derivative of
G exists because of the assumption
(that is,
| and its derivative is given by the derivation of a composite function) and it is computed as
Using Young’s inequality with Φ = cosh −1 and Φ
∗ = (cosh −1)
∗ we get
All the terms in the right-hand side of the above inequality are integrable with respect to the measure
M1(
y)
dy over ℝ. Indeed the first term is bounded as
and
y 7↦
yF (
y)
∈ L1(ℝ,
M1(
y)
dy). The second term is integrable by assumption. The only concern is then the last term. For any
r > 0,
while,
Now, splitting the integral into the two integrals
and
, one can use the one-dimensional Hardy inequality in Orlicz–Sobolev space [
39] to get that there exists
C > 0 such that
This achieves to prove
(31).
3. Recall that
(29) holds for any
and any
g ∈
Lcosh−1 (
M). Since Φ
∗ = (cosh −1)
∗ enjoys the Δ
2-condition, it is a well-known fact that
is dense in
(for the norm
). Therefore, approximating any
by a sequence of
functions we deduce the result from point 1. □
Remark 6. In the second Item of the above Proposition, notice that a priori
Xjf belongs to but not to W 1(cosh 1) (
M),
j = 1,…,
n. For this to be true, one would require that for any k = 1,…,
n. 6.1. Stein and Laplace Operators
Following the language of [38, Chapter V], Item 3 of the above Proposition 16 can be reformulated saying that
where
This allows to define the
Stein operator δ on
L(cosh−1)∗ (
M) as
where the the domain Dom(
δ) of
δ is exactly
according to point 2. of the avobe Proposition. Notice that, since Φ
∗ enjoys the Δ
2-condition, Dom(
δ) is dense in
L(cosh−1)∗ (
M). One deduces then easily that
δ is a closed and densely defined operator in
L(cosh−1)∗ (
M).
One sees that
where
is the divergence of g. This allows to define the adjoint operator
δ∗ as follows, see [
40]
with
and
One sees from
(32) that
and one sees that there exists
C > 0 such that, for any
j = 1,…,
n and any
, it holds
Remark 7. Notice that, since Φ = cosh −1 does not satisfies the Δ2-condition, it is not clear whether Dom(δ∗) is dense in (Lcosh−1 (M))n or not. However, from the general theory of adjoint operators and since δ is a closed densely defined operator in L(cosh−1)∗ (M), the domain Dom(δ∗) is dense in (Lcosh−1 (M))n endowed with the weak-⋆ topology. Moreover, δ∗ is a closed operator from (Lcosh−1 (M))n to Lcosh−1 (M) (see [40, Chapter 2] for details).
We also define the gradient operator
by
One sees that, if
f ∈ Dom(∇
2),
i.e., if
is such that
, then ∇
f ∈ Dom(
δ∗) and
corresponds to the Laplace operator.
From now, set
as the dual space of
:
i.e., the set of all continuous linear forms continuous
and let 〈·,·〉 denotes the duality pairing:
One easily checks that
Lf is continuous and defines therefore an element of
. Clearly, the operator
is also linear. Using the identification Δ =
δ∗∇, we denote it by
defined as
Notice that, with this definition, Δ
f is an element of
whereas, from the above observation, Δ
f ∈
Lcosh−1 (
M). Also the domains of both operators are different. Of course, if
f ∈ Dom(∇
2) then Δ
f is actually an element of
Lcosh−1 (
M) and it coincides with Δ
f, namely, in such a case
Remark 8.
Given and u one hasbut, since (
M),
one can use (29) again to get One readily computes, for any,
so that Remark 9. Since the constant function (
M)
one checks easily thatwhere we notice that X·∇
f ∈
L1(
M)
for any.
Actually, since one can use (29) again to get,
i.e.,
Of course, if and one actually gets Δ
f = Δ
f ∈ Lcosh−1 (
M)
and For technical purposes, we finally state the following Lemma
Lemma 2. Given w1,
,
and g = e
M(
v)
one has Proof. For simplicity, set
. One knows from Proposition 15 that
so that, by definition
Moreover, one checks easily that
so that
which gives the result. □
6.2. Exponential Family Based on Orlicz–Sobolev Spaces with Gaussian Weights
If we restrict the exponential family ℇ (
M) to
M-centered random variable
, that is in
we obtain the following non parametric exponential family
Because of the continuous embedding
the set
is open in WM and the cumulant functional
is convex and differentiable.
In a similar way, we can define
so that for each
f ∈ ℇ1 (M) we have
, see Remark 5.
Every feature of the exponential manifold carries over to this case. In particular, we can define the spaces
to be models for the tangent spaces of
ℇ1 (
M). Note that the transport acts on these spaces
so that we can define the tangent bundle to be
and take as charts the restrictions of the charts defined on
T ℇ (
M).
As a first example of application, note that the gradient of the BG-entropy
is a vector field on
ℇ1 (
M), which implies the solvability in
ℇ1 (
M) of the gradient flow equation. Our concern here is to set up a framework for the study of evolution equation in
ℇ1 (
M). Following sections are devoted to discuss a special functional and its gradient.
6.3. Hyvärinen Divergence
We begin with the following general properties of
Proposition 17. Let f, g ∈ ℇ1 (
M),
with f = e
M(
u),
g = e
M(
v),
u,
.
The following hold.
.
.
.
Proof. In all the sequel, we set
and
. Recall from Proposition 15 that F,
.
Remark 10.
The equations in Proposition 17 could be written without reference to the score (chart) mapping sM :
f ↦
u by writing to get.
.
.
.
However, we feel that explicit reference to the chart clarifies the geometric picture.
The mapping f ↦∇ log
f is a vector field in Tℇ1 (
M)
with flow given by the translations: The KL-divergence (f, g) ↦D (f ||g) has expression (u, v) ↦dKM(v)[u−v]−KM(u)+KM(v) in the chart centered at M, with partial derivative with respect to v in the direction w given by Covg (u − v, w). If the direction is w = X − ∇v = −∇ log g, we have that is the derivative of the KL-divergence along the vector field of translations.
We introduce here the Hyvärinen divergence between two elements of ℇ1 (M):
Definition 10 (Hyvärinen divergence).
For each f, g ∈
ℇ1 (
M)
the Hyvärinen divergence
is the quantity The expression in the chart centered at M iswhere f = e
M(
u),
g = e
M(
v).
Remark 11.
The mapping is, in statistical terms, an estimating function
or a pivot,
because,
f ∈
ℇ1 (
M).
This means, it is a random variable whose value is zero in the mean if f is correct. If g is correct, then the expected value is.
The second moment of was used by Hyvärinen as a measure of deviation from f to g [
35].
Hyvärinen work has been used to discuss proper scoring rules
in [
41].
The same notion is known in Physics under the name of relative Fisher information,
e.g., see [
32].
In the following we denote the gradient of a function defined on the exponential manifold ℇ1 (M), which is a random variable, by ∂.
Proposition 18.
The Hyvärinen divergence is finite and infinitely differentiable everywhere in both variables.
.
Proof. 1. For each
w ∈
V the gradient ∇
w is in (
LΦ(
g))
n = (
LΦ(
M))
n for all
g ∈
ℇ1 (
M), hence it is
g-square integrable for all
g ∈
ℇ1 (
M). Moreover, the squared norm function
is ∞-differentiable because it is the moment functional,
We can compose this function with the linear function
2. Let
g = e
M(
v),
f = e
M(
u),
u,
be given. For any
w ∈
V, we compute first the directional derivative:
where we notice that all the terms are well defined whenever
u,
,
w ∈
V. Using now
(33) with
w2 =
u − v and
w1 =
w we get that
Since this is true for any
w ∈
V we get
where of course, Δ(
u − v) is meant in
(notice that
. The formula for the partial gradient in absolute variables follows from
for, with a slight abuse of notations, we identify
to Δ(
u − v).
3. As above, let
g = e
M(
v),
f = e
M(
u),
u,
be given. For any
w ∈
V, we compute first the directional derivative. One gets now
One recognizes in the first term
−d (
u ↦ DH
M(
v||
u)) [
w] while the second term is given by
As in the previous item, this gives the result. □
As well-documented, the Hyvarïnen divergence is a powerful tool for the study of general diffusion processes. We have just shown that the Information Geometry formalism and the exponential manifold approach are robust enough to allow for a generalization in Orlicz–Sobolev spaces. We believe then that, as Boltzmann equation can be studied through the exponential manifold formalism in Lcosh−1 (M), general diffusion processes can be investigated in
with the formalism discussed in the present section. This is a plan for future work.