A Hybrid Physical and Maximum-Entropy Landslide Susceptibility Model
Abstract
:1. Introduction
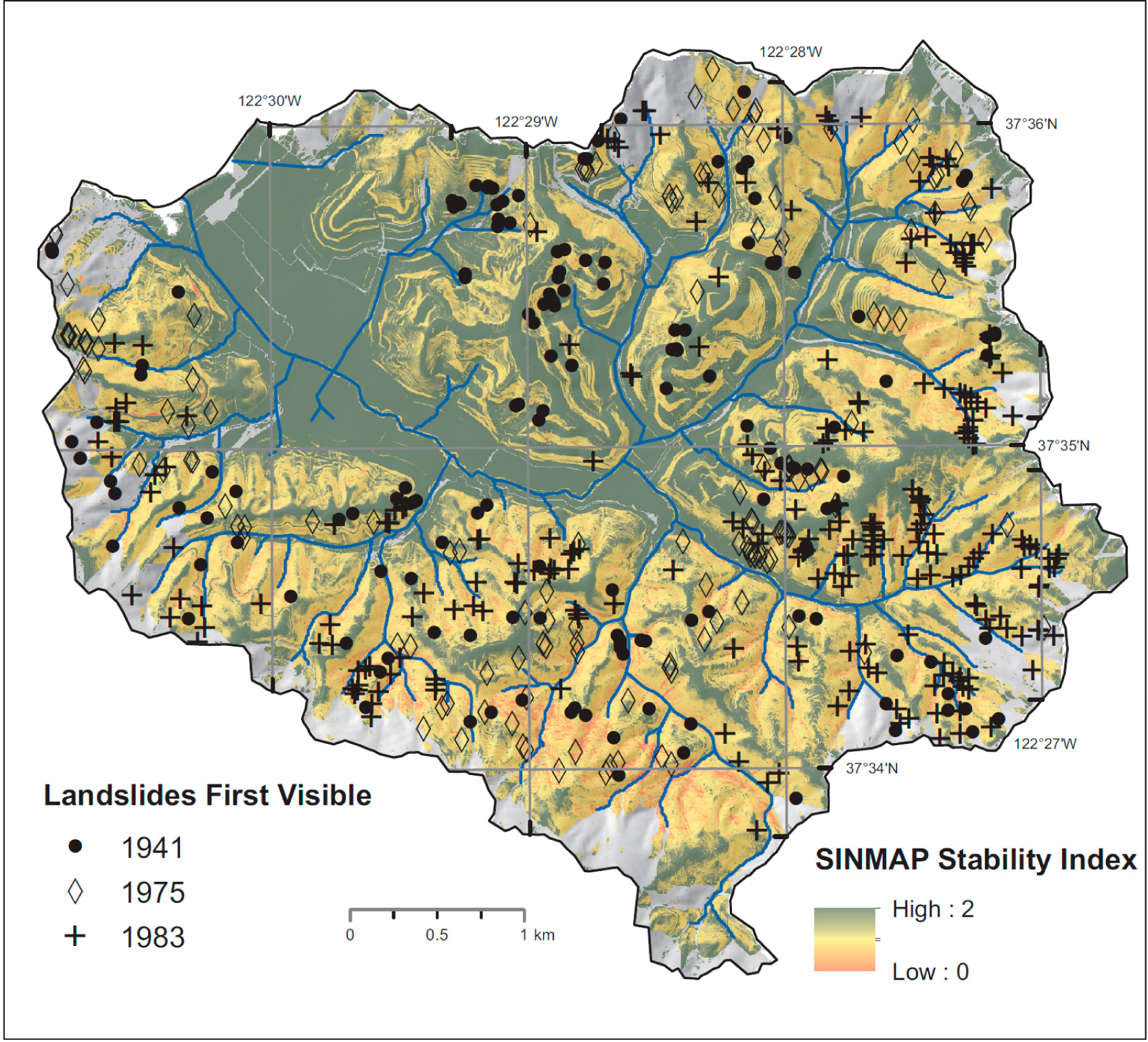
2. Study Area
3. Methodology
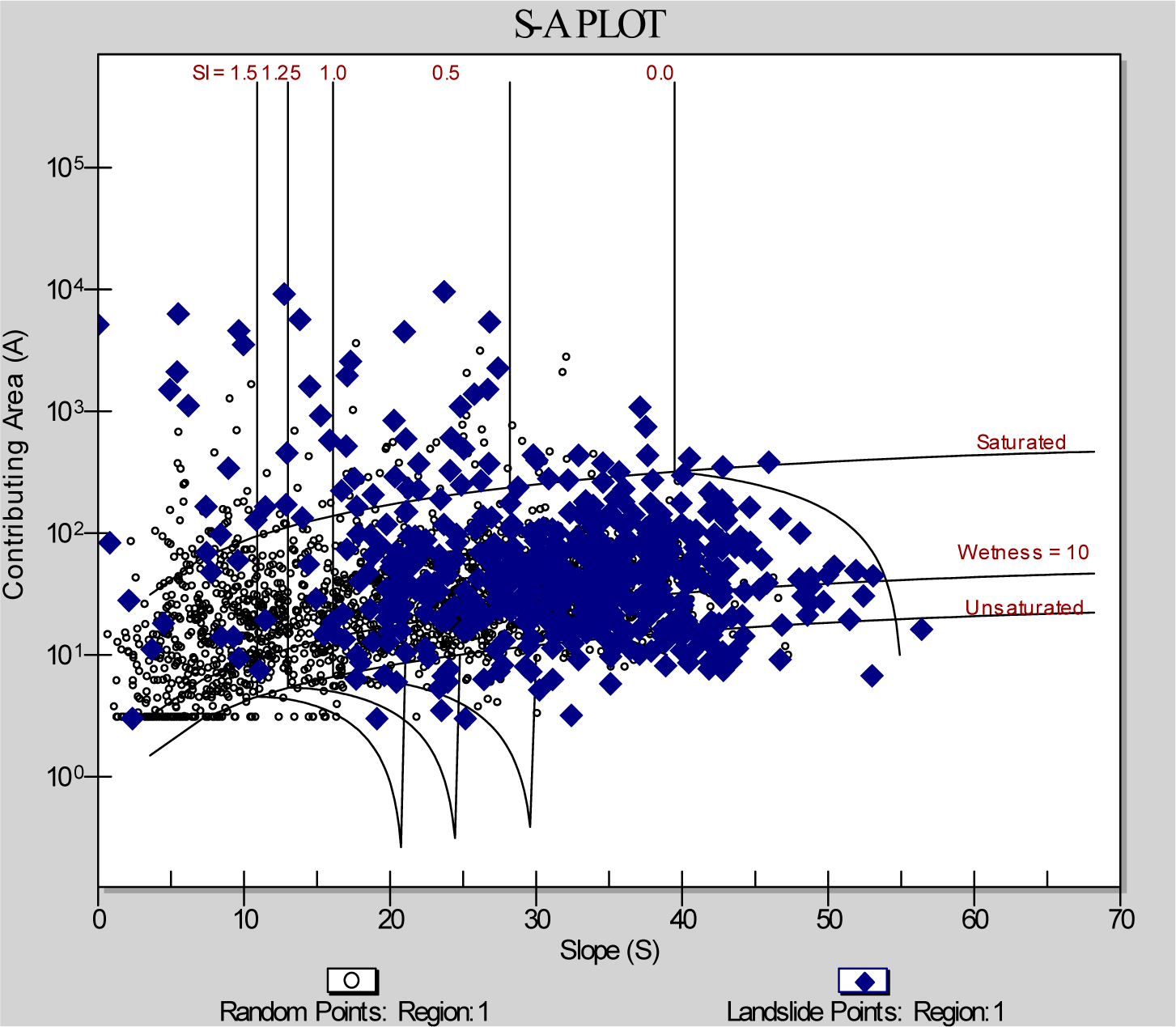
3.1. Physically-Based Model
3.2. Maximum Entropy Model
3.3. Hybrid Model
3.4. Landslide Scar Data and Causal Factors
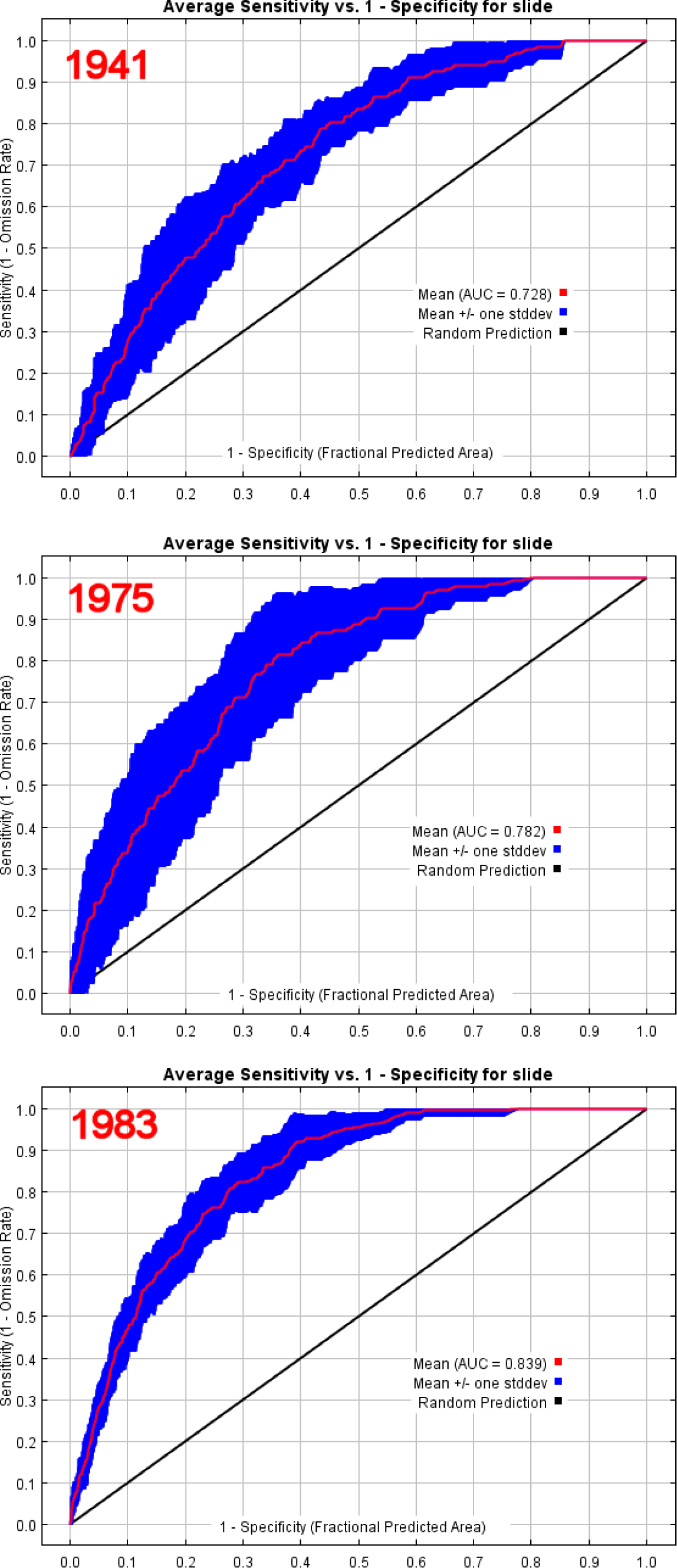
4. Results
5. Discussion and Conclusions
Author Contributions
Conflicts of Interest
References
- Varnes, D.J. Slope movement types and processes. In Landslides: Analysis and Control; Schuster, R.L., Krizek, R.J., Eds.; Volume Special Report 176; National Academy of Science Transportation Research Board: Washington, DC, USA, 1978; pp. 11–33. [Google Scholar]
- Schumm, S.A. Geomorphic thresholds: The concept and its applications. Trans. Inst. Br. Geogr. 1979, 4, 485–515. [Google Scholar]
- Uchida, T.; Kosugi, K.; Mizuyama, T. Effects of pipeflow on hydrological process and its relation to landslide: A review of pipeflow studies in forested headwater catchments. Hydrol. Process. 2001, 15, 2151–2174. [Google Scholar]
- Montgomery, D.R. Road surface drainage, channel initiation, and slope instability. Water Resour. Res. 1994, 30, 1925–1932. [Google Scholar]
- Iverson, R.M.; George, D.L.; Allstadt, K.; Reid, M.E.; Collins, B.D.; Vallance, J.W.; Schilling, S.P.; Godt, J.W.; Cannon, C.M.; Magirl, C.S. Landslide mobility and hazards: Implications of the 2014 Oso disaster. Earth Planet. Sci. Lett. 2015, 412, 197–208. [Google Scholar]
- Leshchinsky, B.A.; Olsen, M.J.; Tanyu, B.F. Contour Connection Method for automated identification and classification of landslide deposits. Comput. Geosci. 2015, 74, 27–38. [Google Scholar]
- Butt, M.; Umar, M.; Qamar, R. Landslide dam and subsequent dam-break flood estimation using HEC-RAS model in Northern Pakistan. Nat. Hazards 2013, 65, 241–254. [Google Scholar]
- Wills, C.J.; McCrink, T.P. Comparing landslide inventories: The map depends on the method. Environ. Eng. Geosci. 2002, VIII, 279–293. [Google Scholar]
- Van Westen, C.J.; Castellanos, E.; Kuriakose, S.L. Spatial data for landslide susceptibility, hazard, and vulnerability assessment: An overview. Eng. Geol. 2008, 102, 112–131. [Google Scholar]
- Martha, T.R.; Kerle, N.; Jetten, V.; van Westen, C.J.; Kumar, K.V. Characterising spectral, spatial and morphometric properties of landslides for semi-automatic detection using object-oriented methods. Geomorphology 2010, 116, 24–36. [Google Scholar]
- Parker, O.; Blesius, L. Object-Based Segmentation of Multi-Temporal Quickbird Imagery for Landslide Detection. Proceedings of XII International Symposium on Environmental Geotechnology, Energy and Global Sustainable Development, Los Angeles, CA, USA, 27–29 June 2012; Menezes, G.B., Moo-Young, H.K., Khachikian, C., de Brito Galvao, T.C., Eds.; Environmental Geotechnology: Los Angeles, CA, USA, 2012; pp. 291–299. [Google Scholar]
- Cascini, L. Applicability of landslide susceptibility and hazard zoning at different scales. Eng. Geol. 2008, 102, 164–177. [Google Scholar]
- Blesius, L.; Weirich, F. Shallow Landslide susceptibility mapping using stereo air photos and thematic maps. Cartogr. Geogr. Inf. Sci. 2010, 37, 105–118. [Google Scholar]
- Kavzoglu, T.; Sahin, E.K.; Colkesen, I. Landslide susceptibility mapping using GIS-based multi-criteria decision analysis, support vector machines and logistic regression. Landslides 2014, 11, 425–439. [Google Scholar]
- Dhakal, A.; Amada, T.; Aniya, M. Landslide hazard mapping and the application of GIS in the Kulekhani Watershed, Nepal. Mt. Res. Dev. 1999, 19, 3–16. [Google Scholar]
- Tosi, M. Root tensile strength relationships and their slope stability implications of three shrub species in the Northern Apennines (Italy). Geomorphology 2007, 87, 268–283. [Google Scholar]
- Rice, R.M.; Foggin, G.T. Effect of high intensity storms on soil slippage on mountainous watersheds in southern California. Water Resour. Res. 1971, 7, 1485–1496. [Google Scholar]
- Blesius, L.; Weirich, F. The use of high-resolution satellite imagery for deriving geotechnical parameters applied to landslide susceptibility. Proceedings of the ISPRS Hannover Workshop 2009 on High-resolution Earth Imaging for Geospatial Information, Hannover, Germany, 2–5 June 2009; Heipke, C., Jacobsen, K., Müller, S., Sörgel, U., Eds.; International Society for Photogrammetry and Remote Sensing: Hannover, Germany, 2009. [Google Scholar]
- Band, L.E.; Hwang, T.; Hales, T.C.; Vose, J.; Ford, C. Ecosystem processes at the watershed scale: Mapping and modeling ecohydrological controls of landslides. Geomorphology 2012, 137, 159–167. [Google Scholar]
- Cervi, F.; Berti, M.; Borgatti, L.; Ronchetti, F.; Manenti, F.; Corsini, A. Comparing predictive capability of statistical and deterministic methods for landslide susceptibility mapping: A case study in the northern Apennines (Reggio Emilia Province, Italy). Landslides 2010, 7, 433–444. [Google Scholar]
- Althuwaynee, O.F.; Pradhan, B.; Park, H.-J.; Lee, J.H. A novel ensemble decision tree-based CHi-squared Automatic Interaction Detection (CHAID) and multivariate logistic regression models in landslide susceptibility mapping. Landslides 2014, 11, 1063–1078. [Google Scholar]
- Tien Bui, D.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2015. [Google Scholar] [CrossRef]
- Tien Bui, D.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, O.B. Spatial prediction of landslide hazards in Hoa Binh province (Vietnam): A comparative assessment of the efficacy of evidential belief functions and fuzzy logic models. Catena 2012, 96, 28–40. [Google Scholar]
- Haigh, M.J. Dynamic systems approaches in landslide hazard risk. Z. Fuer Geomorphol. 1988, 67, 79–91. [Google Scholar]
- Phillips, S.; Anderson, R.; Schapire, R. Maximum entropy modeling of species geographic distributions. Ecol. Model. 2006, 190, 231–259. [Google Scholar]
- Convertino, M.; Troccoli, A.; Catani, F. Detecting fingerprints of landslide drivers: A MaxEnt model. J. Geophys. Res. Earth Surf. 2013, 118, 1367–1386. [Google Scholar]
- Brabb, E.E.; Pampeyan, E.H.; Bonilla, M.G. Landslide susceptibility in San Mateo County California scale 1:62500. In Miscellaneous Field Studies Map MF-360; US Geological Survey: Reston, VA, USA, 1972. [Google Scholar]
- Kashiwagi, J.H.; Hokholt, L.A. Soil Survey of San Mateo County, Eastern part, and San Francisco County, California; U.S. Department of Agriculture, Soil Conservation Service: Washington, DC, USA, 1991. [Google Scholar]
- Soil Survey Staff. Soil Taxonomy, A Basic System of Soil Classification for Making and Interpreting Soil Surveys, 2nd ed; US Department of Agriculture, Natural Resources Conservation Service: Washington DC, USA, 1999; Volume Agriculture Handbook #436; p. 869. [Google Scholar]
- Pampeyan, E.H. Geologic Map of the Montara Mountain and San Mateo 7–1/2′ Quadrangles, San Mateo County, California, Scale 1:24,000; US Geological Survey: Reston, VA, USA, 1994. [Google Scholar]
- Brabb, E.E.; Pampeyen, E.H. Preliminary map of landslide deposits in San Mateo County, California, scale 1:62,500. In Miscellaneous Field Studies Map MF-344; U.S. Geological Survey: Reston, VA, USA, 1972. [Google Scholar]
- Sims, S. Hillslope sediment source assessment of San Pedro Creek Watershed, California. Master’s Thesis, The San Francisco State University, San Francisco, CA, USA, 2004. [Google Scholar]
- United States Army Corps of Engineers, San Francisco District. San Pedro Creek Section 205 Flood Control Study; Engineers, U.S. Army Corps of Engineers: San Francisco, 1998. [Google Scholar]
- Pack, R.; Tarboton, D.; Goodwin, C.; Prasad, A. A Stability Index Approach to Terrain Stability Hazard Mapping 2005, User’s Manual; CEE Faculty Publications: Logan, UT, USA, 2005. Avaliable online: http://hydrology.usu.edu/sinmap2/ accessed on 8 May 2013.
- Dyke, J.; Kleidon, A. The maximum entropy production principle: Its theoretical foundations and applications to the earth system. Entropy 2010, 12, 613–630. [Google Scholar]
- Phillips, J.D. Divergence, convergence, and self-organization in landscapes. Ann. Assoc. Am. Geogr. 1999, 89, 466–488. [Google Scholar]
- Elith, J.; Phillips, S.; Hastie, T.; Dudík, M.; Chee, Y.; Yates, C. A statistical explanation of MaxEnt for ecologists. Divers. Distrib. 2011, 17, 43–57. [Google Scholar]
- Ruddell, B.L.; Brunsell, N.A.; Stoy, P. Applying information theory in the geosciences to quantify process uncertainty, feedback, scale. Eos Trans. Am. Geophys. Union 2013, 94, 56. [Google Scholar]
- Felicísimo, Á.; Cuartero, A.; Remondo, J.; Quirós, E. Mapping landslide susceptibility with logistic regression, multiple adaptive regression splines, classification and regression trees, and maximum entropy methods: A comparative study. Landslides 2013, 10, 175–189. [Google Scholar]
- Phillips, S.; Dudík, M. Modeling of species distributions with Maxent: New extensions and a comprehensive evaluation. Ecography 2008, 31, 161–175. [Google Scholar]
- Ghestem, M.; Sidle, R.; Stokes, A. The influence of plant root systems on subsurface flow: Implications for slope stability. BioScience 2011, 61, 869–879. [Google Scholar]
- Reneau, S.L.; Dietrich, W.E.; Donahue, D.J.; Jull, A.J.T.; Rubin, M. Late Quaternary history of colluvial deposition and erosion in hollows, central California Coast Ranges. Geol. Soc. Am. Bull. 1990, 102, 969–982. [Google Scholar]
- Rib, H.T.; Liang, T. Landslides: Analysis and control. In Recognition and Identification; Schuster, R.L., Krizek, R.J., Eds.; Volume Special Report 176; National Academy of Sciences: Washington, DC, USA, 1978; pp. 34–80. [Google Scholar]
- Collins, L.; Amato, P.; Morton, D. San Pedro Creek geomorphic analysis. In San Pedro Creek Watershed Assessment and Enhancement Plan; San Pedro Creek Watershed Coalition: Pacifica, CA, USA, 2001; pp. 631–646. [Google Scholar]
- Howard, T.R.; Baldwin, J.E.; Donley, H.F. Landslides in Pacifica California caused by the storm. In Landslides Floods and Marine Effects of the Storm of January 3–5, 1982 in the San Francisco Bay Region California; Volume US Geological Survey Professional Paper 1434; US Geological Survey: Reston, VA, USA, 1988; pp. 3–5. [Google Scholar]
- Cannon, S.H.; Ellen, S.D. Rainfall that resulted in abundant debris-flow activity during the storm. In Landslides, Floods, and Marine Effects of the Storm of January 3–5 1982 in the San Francisco Bay Region, California; Volume US Geological Survey Professional Paper 1434; U.S. Geological Survey: Reston, VA, USA, 1988; pp. 3–5. [Google Scholar]
- Davis, J.D.; Sims, S.M. Physical and maximum entropy models applied to inventories of hillslope sediment sources. J. Soils Sediments 2013, 13, 1784–1801. [Google Scholar]
- Wieslander, A.E. A vegetation type map of California. Madroño 1935, 3, 140–144. [Google Scholar]
- Davis, J.D.; Matuk, V.; Wilkinson, N.L.; Chan, C. San Pedro Creek Watershed Assessment and Enhancement Plan; San Pedro Creek Watershed Coalition: Pacifica, CA, USA, 2002. [Google Scholar]
- Davis, J.D.; Davis, A.W.; Harvey, B.J. Pedro Point Headlands 1941 to 2010: A Preliminary Study Using Historical Remote Sensing and Dendrochronology; Pacifica Land Trust: Pacifica, CA, USA, 2010. [Google Scholar]
- Wieczorek, G.F.; Harp, E.L.; Mark, R.K.; Bhattacharyya, A.K. Debris flows and other landslides in San Contra Costa, Alameda, Napa, Solano, Sonoma, Lake, and Yolo Counties, and other factors influencing debris-flow distribution. In Landslides, Floods, and Marine Effects of the Storm of January 3–5, 1982 in the San Francisco Bay Region, California; Volume US Geological Survey Professional Paper 1434; U.S. Geological Survey: Reston, VA, USA, 1988; pp. 3–5. [Google Scholar]
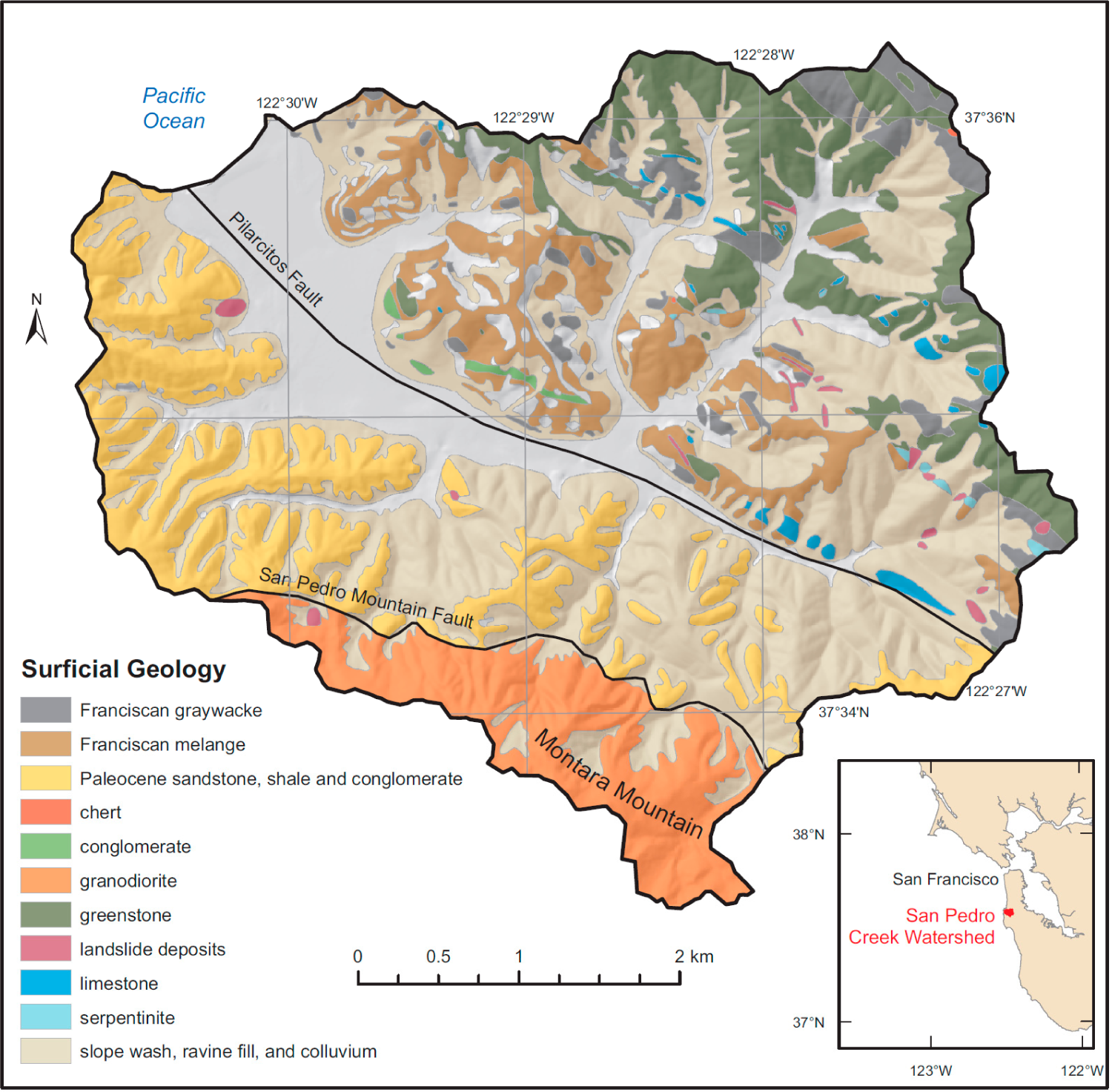
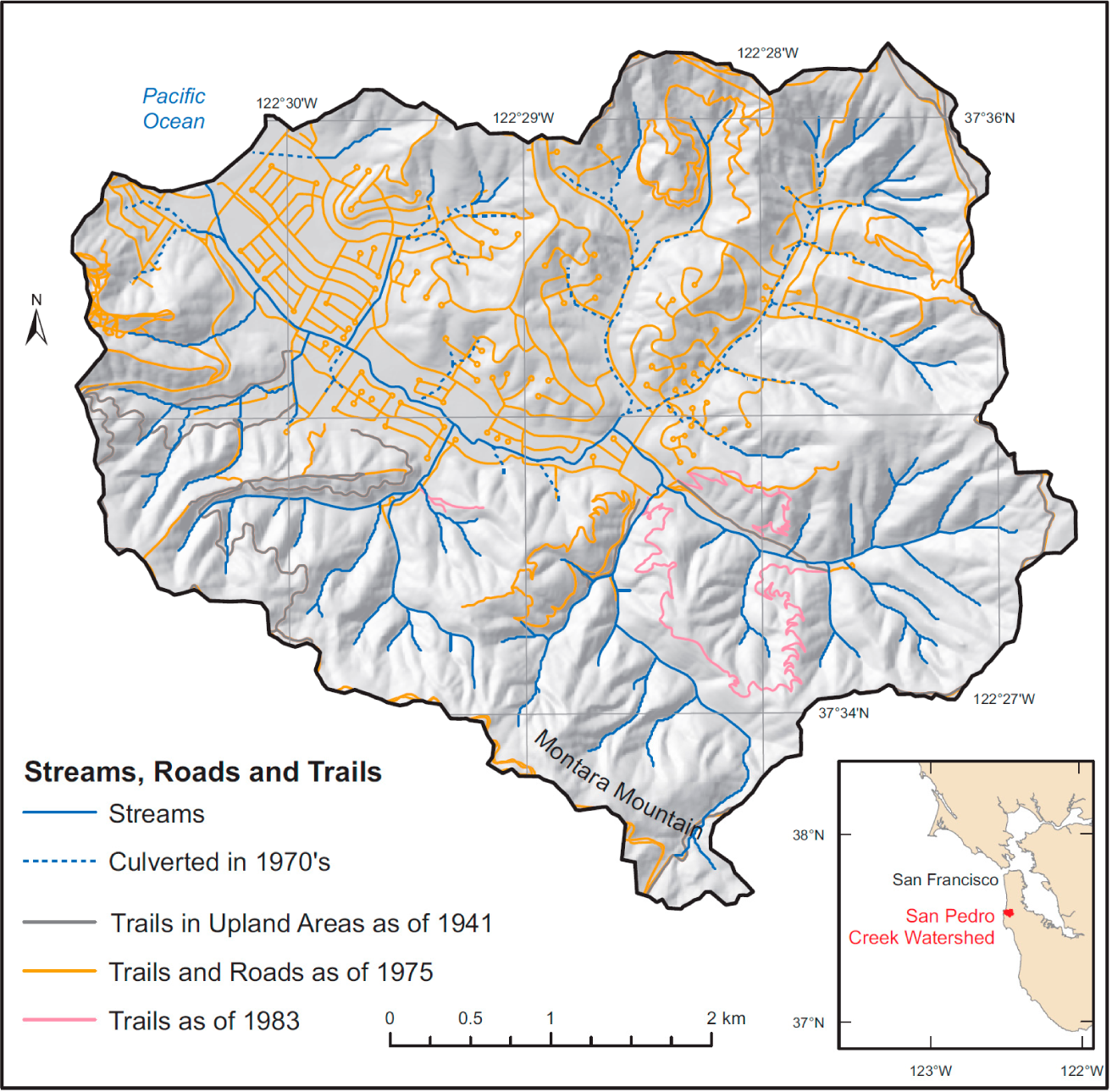
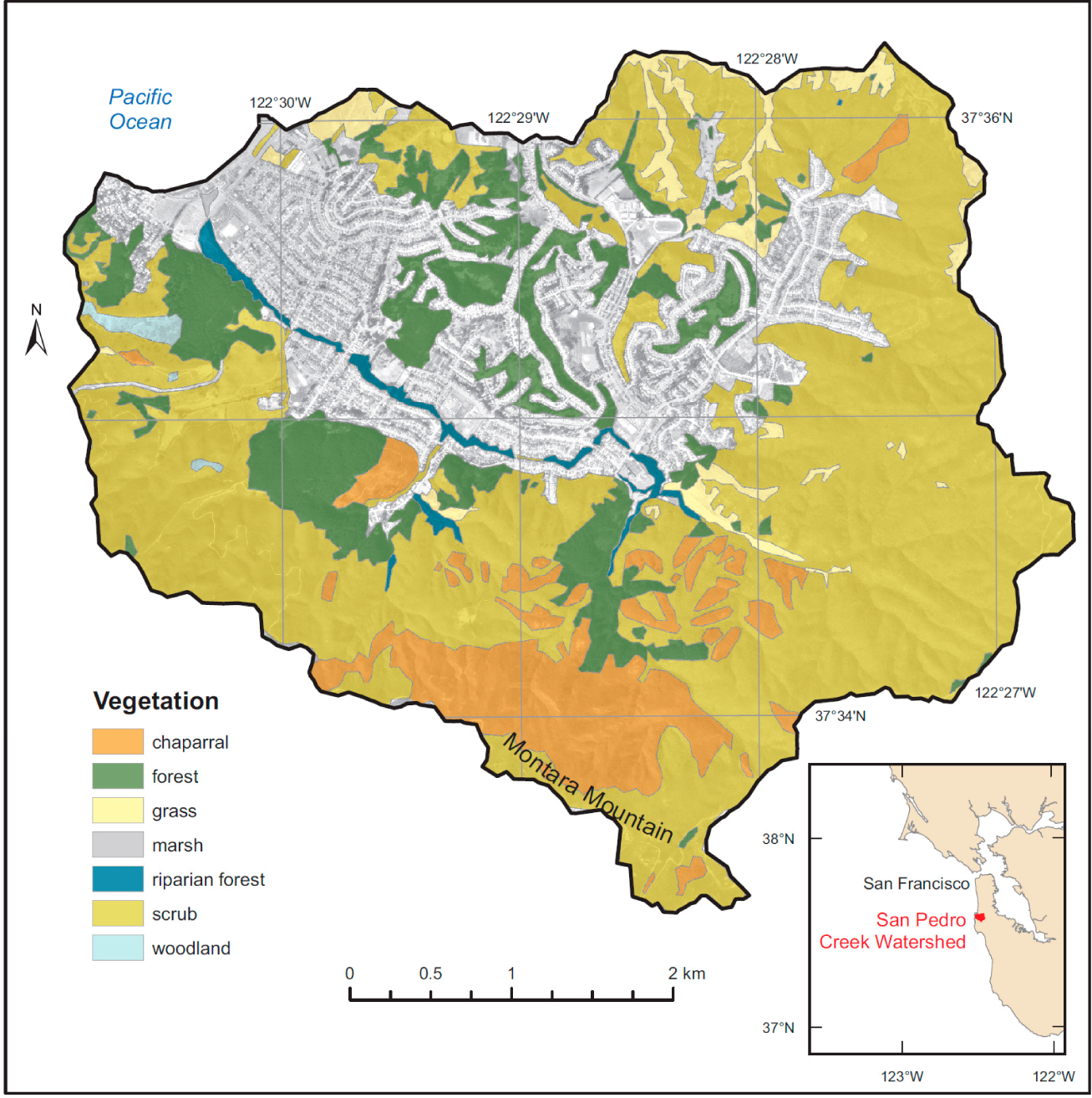




| Parent material | Soil depth (m) | Hydraulic conductivity (m h−1) | T (m2 h−1) | R (m h−1) | T/R (m) | C | Φ (°) | Ρ (kg m−3) |
|---|---|---|---|---|---|---|---|---|
| granitic | 1 | 0.10 | 0.1 | 0.0002–0.0042 | 24–500 | 0–0.25 | 30–45 | 2000 |
| colluvium | 3 | 0.03 | 0.1 | 0.0002–0.0042 | 24–500 | 0–0.25 | 30–45 | 2000 |
| Imagery Year | 1941 | 1955 | 1975 | 1983 | 1997 |
|---|---|---|---|---|---|
| n scars | 154 | 39 | 142 | 253 | 10 |
| n SI < 1.0 | 91 | 24 | 91 | 197 | 6 |
| % | 59% | 62% | 64% | 78% | 60% |
| 1941 | 1975 | 1983 | |||||
|---|---|---|---|---|---|---|---|
| using: | SI | slope | SI | slope | SI | slope | |
| n | 132 | 154 | 132 | 141 | 226 | 252 | |
| AUC (using all data) | 0.795 | 0.796 | 0.822 | 0.814 | 0.859 | 0.857 | |
| AUC subsequent-year test data | 0.778 | 0.795 | 0.749 | 0.742 | 0.853 | 0.842 | |
| subsequent test year | 1955 | 1983 | 1997 | ||||
| n slides in test year | 31 | 39 | 226 | 253 | 9 | 10 | |
| 10-fold replicates: | |||||||
| AUC with 10-fold replicates | 0.728 | 0.743 | 0.782 | 0.772 | 0.839 | 0.836 | |
| AUC standard deviation | 0.044 | 0.041 | 0.058 | 0.040 | 0.026 | 0.024 | |
| p: maximum test sensitivity + specificity | 0.004 | 0.041 | 0.001 | 0.000 | 0.000 | 0.000 | |
| SINMAP stability index | %C | 48.1 | 35.3 | 48 | |||
| PI | 50.2 | 49.7 | 57.4 | ||||
| Slope (°) | %C | 59.1 | 41 | 37.5 | |||
| PI | 59.3 | 49.2 | 46.4 | ||||
| Plan curvature | %C | 9.6 | 13.4 | 6.4 | 7.4 | 15.3 | 19.6 |
| PI | 9.4 | 15 | 3.9 | 6.6 | 13.9 | 18.8 | |
| Profile curvature | %C | 6.7 | 2.3 | 1.5 | 1.1 | 2.2 | 1.7 |
| PI | 10.1 | 4.8 | 4.2 | 3.1 | 5 | 2.7 | |
| 50-m trail buffer | %C | 0 | 0.3 | 22.5 | 16.8 | 0.1 | 0 |
| PI | 0 | 0.2 | 14.9 | 16.4 | 0.1 | 0 | |
| Vegetation | %C | 35 | 23.7 | 32.2 | 33.2 | 24.6 | 27 |
| PI | 29.9 | 20 | 24.9 | 23.6 | 15.5 | 20.3 | |
| 0. Farmed (1941), Developed (1975 & 1983) λ | 0.0 | 0.00 | −1.93 | −2.14 | −0.02 | −0.42 | |
| 1. Grassland λ | 1.76 | 1.17 | 1.06 | 1.25 | |||
| 2. Scrublands λ | 0.54 | 1.43 | 1.39 | ||||
| 3. Forest λ | −0.01 | −0.56 | −0.34 | ||||
| Geology | %C | 0.5 | 1.1 | 2.1 | 0.6 | 9.8 | 13.4 |
| PI | 0.1 | 0.7 | 2.2 | 1.2 | 7.9 | 11.4 | |
| 1. Granitic λ | −0.22 | −0.40 | 0.0 | 0.0 | −1.10 | −1.03 | |
| 2. Sandstone λ | 0.03 | 0.15 | |||||
| 3. Colluvium λ | 0.03 | −0.33 | −0.02 | 0.54 | 0.58 | ||
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Davis, J.; Blesius, L. A Hybrid Physical and Maximum-Entropy Landslide Susceptibility Model. Entropy 2015, 17, 4271-4292. https://doi.org/10.3390/e17064271
Davis J, Blesius L. A Hybrid Physical and Maximum-Entropy Landslide Susceptibility Model. Entropy. 2015; 17(6):4271-4292. https://doi.org/10.3390/e17064271
Chicago/Turabian StyleDavis, Jerry, and Leonhard Blesius. 2015. "A Hybrid Physical and Maximum-Entropy Landslide Susceptibility Model" Entropy 17, no. 6: 4271-4292. https://doi.org/10.3390/e17064271
APA StyleDavis, J., & Blesius, L. (2015). A Hybrid Physical and Maximum-Entropy Landslide Susceptibility Model. Entropy, 17(6), 4271-4292. https://doi.org/10.3390/e17064271






