New Hyperbolic Function Solutions for Some Nonlinear Partial Differential Equation Arising in Mathematical Physics
Abstract
:1. Introduction
2. General Structure of the Method
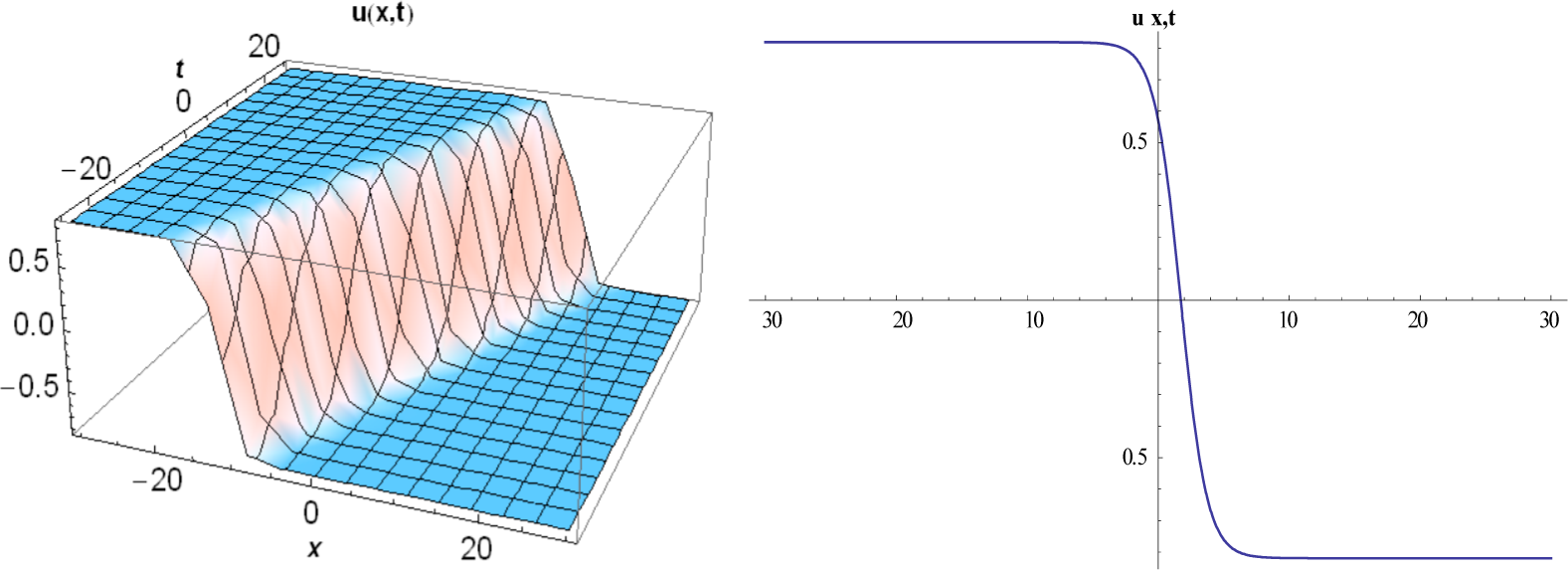
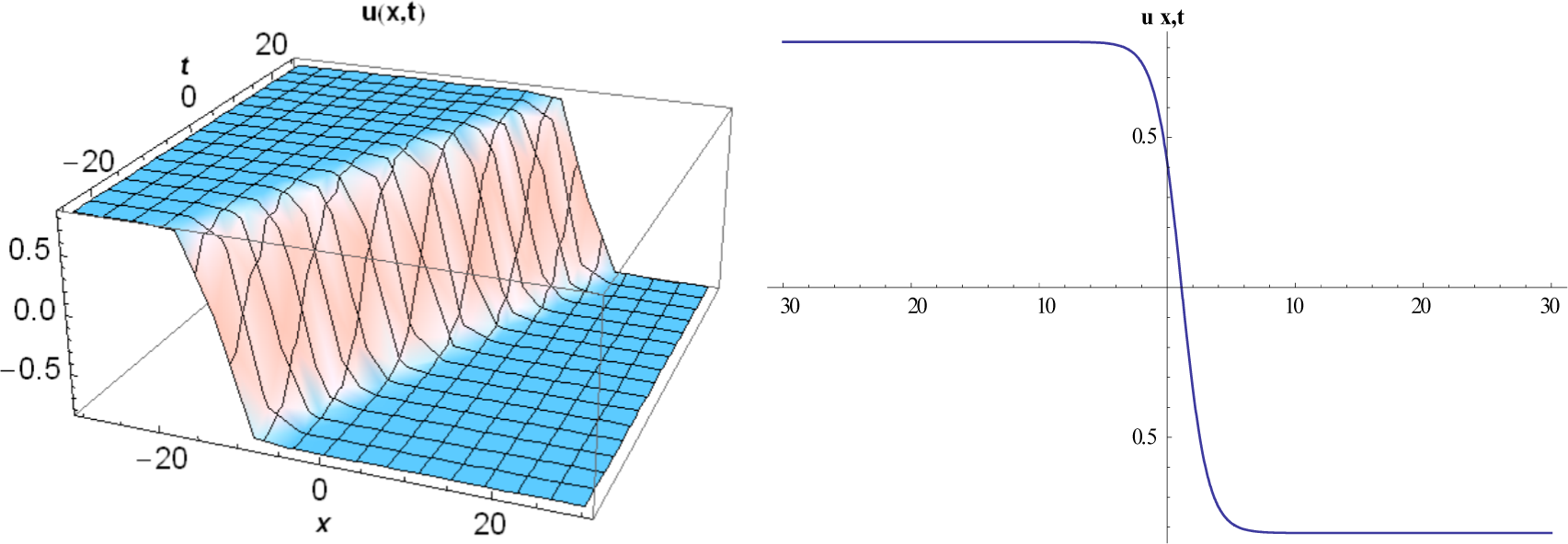
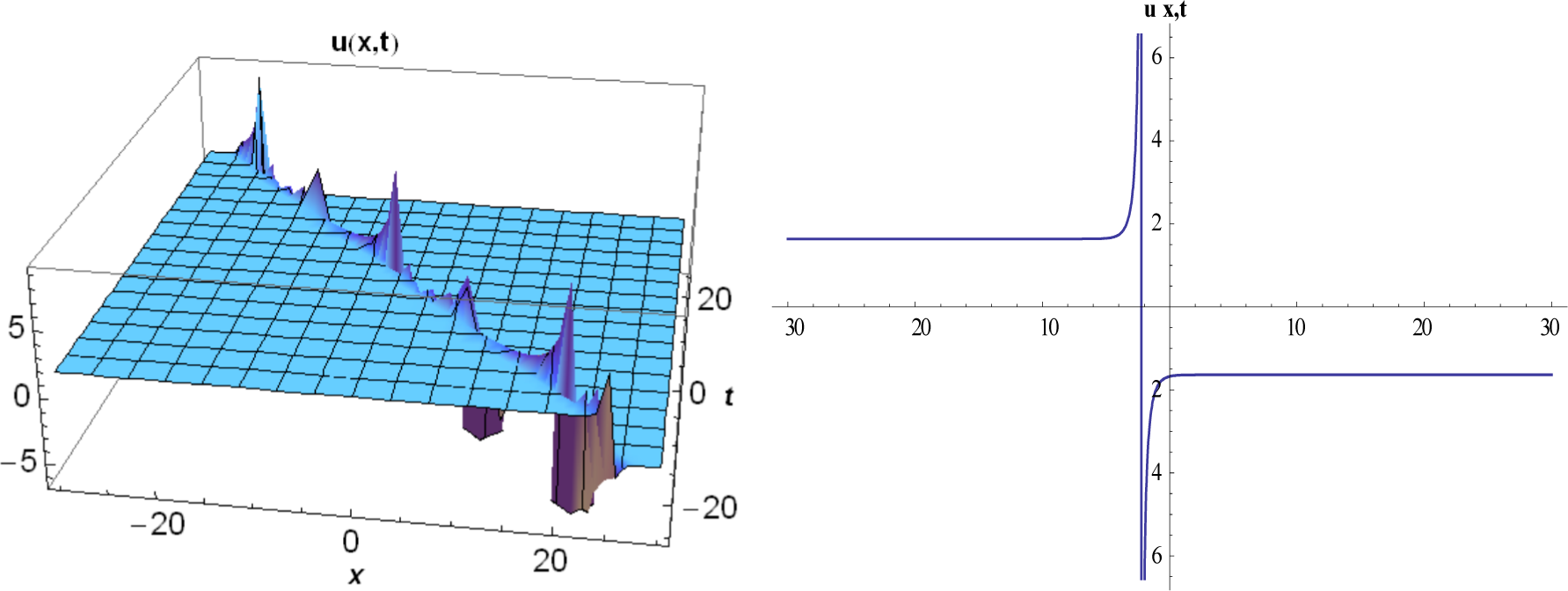
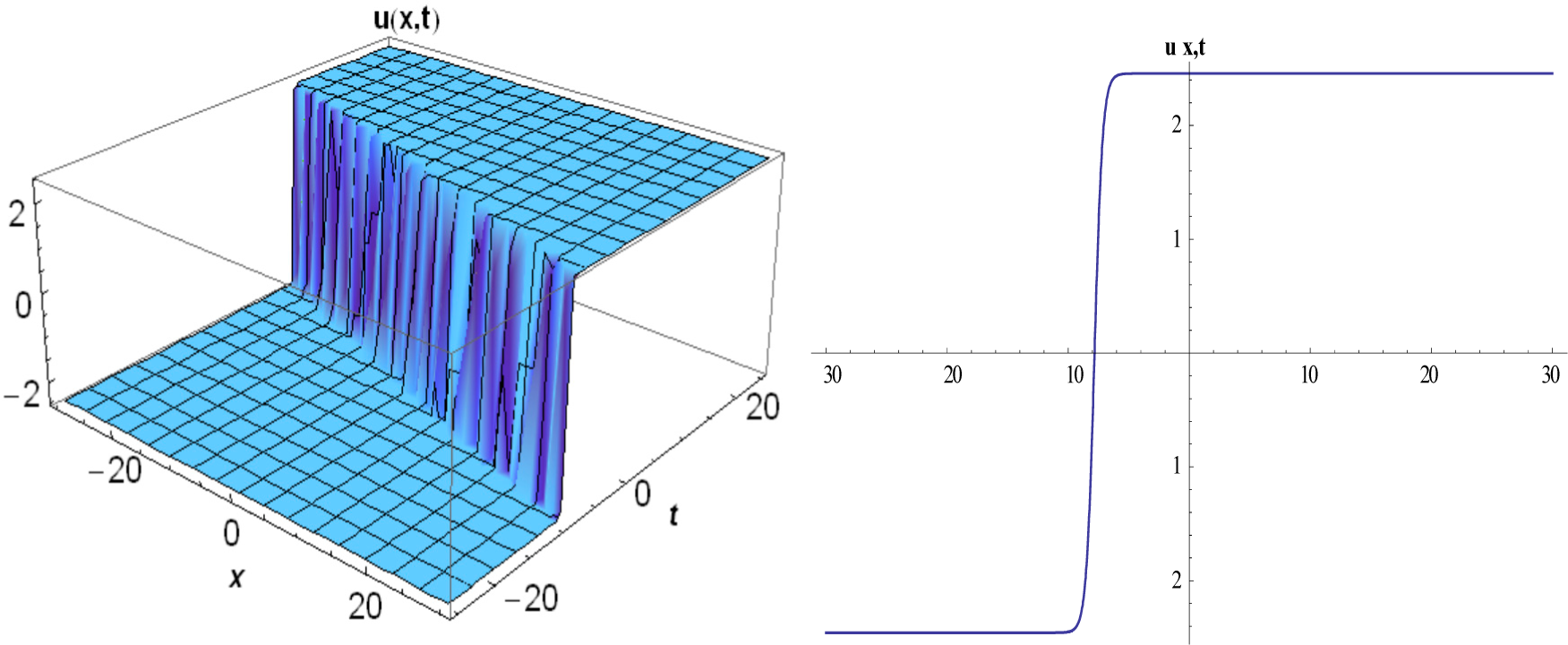
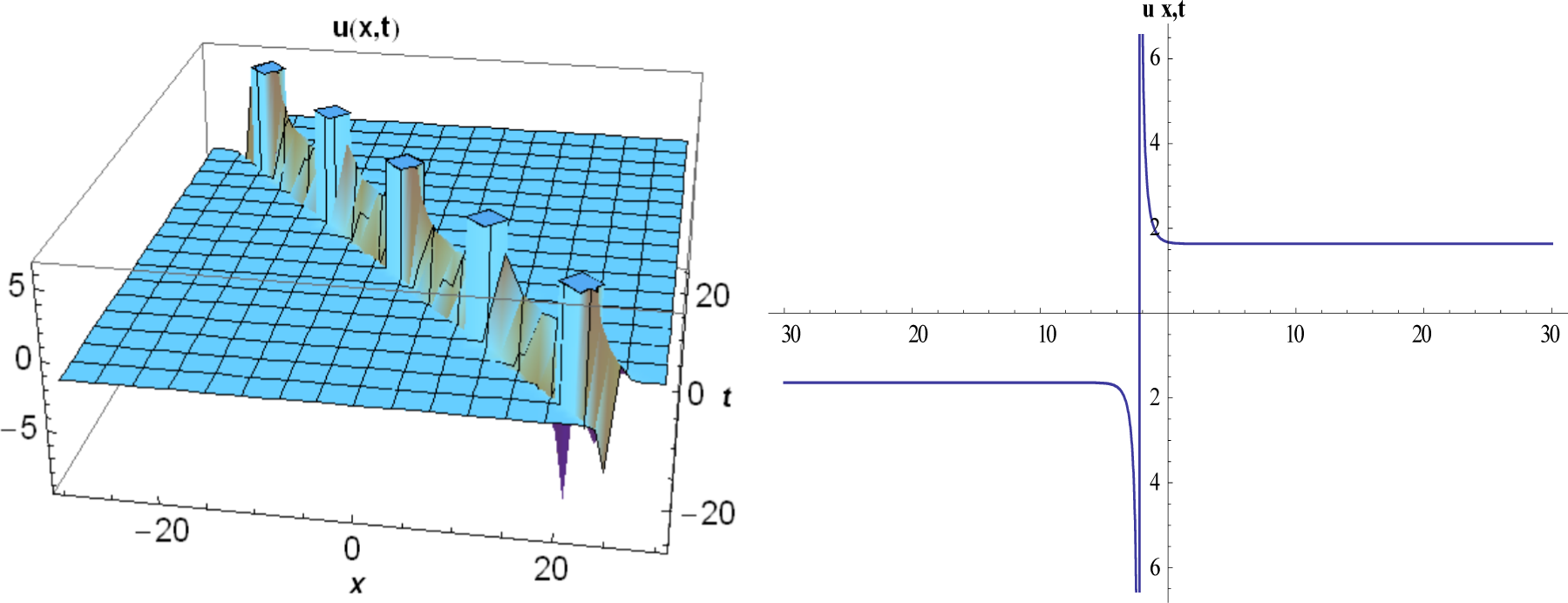
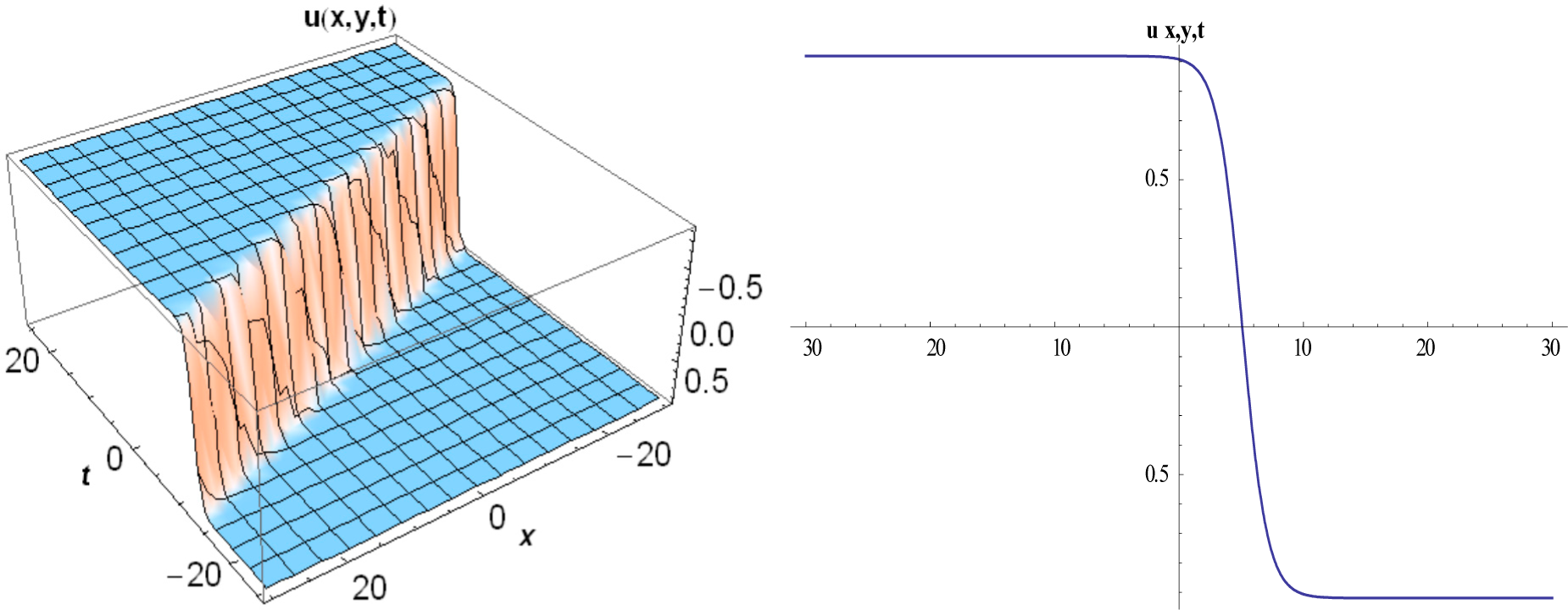
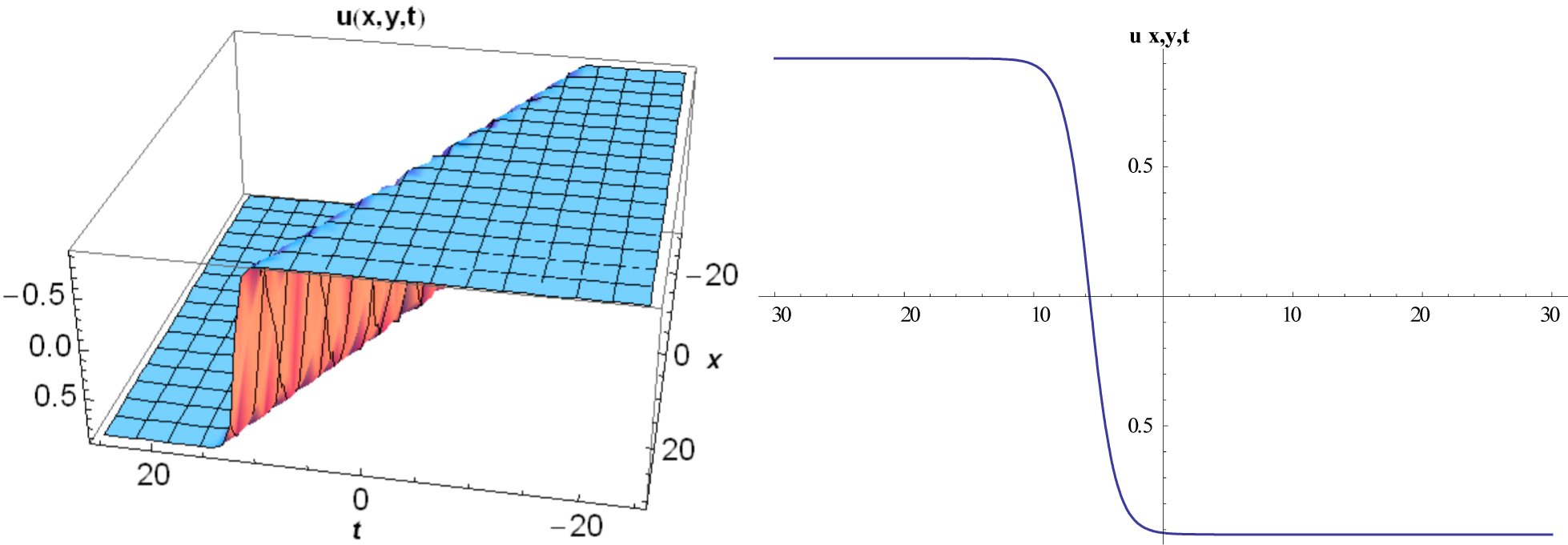
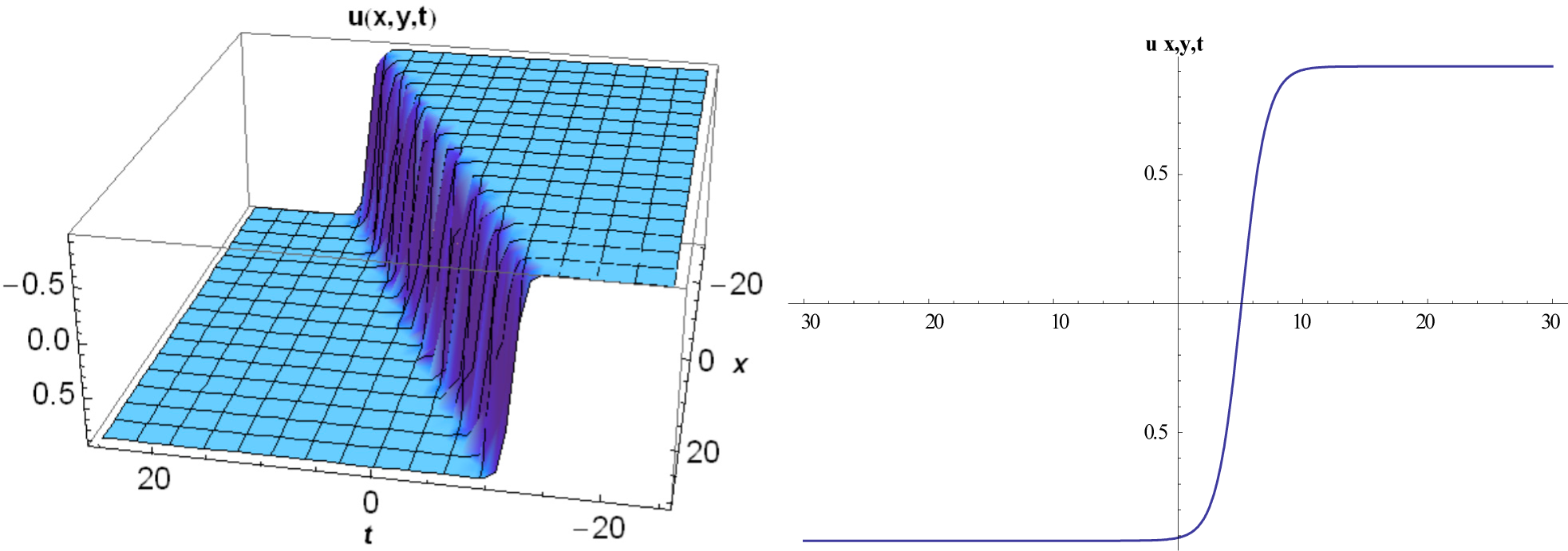
3. Implementation of Method Proposed
4. Conclusions
5. Discussions and Comparisons
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liu, C.S. Trial Equation Method and its Applications to Nonlinear Evolution Equations. Acta Phys. Sin. 2005, 54, 2505–2509. [Google Scholar]
- Liu, C.S. A New Trial Equation Method its Applications, Communications in Theoretical Physics. Commun. Theor. Phys. 2006, 45, 395–397. [Google Scholar]
- Liu, C.S. Trial Equation Method for Nonlinear Evolution Equations with Rank Inhomogeneous: Mathematical Discussions and Applications. Commun. Theor. Phys. 2006, 45, 219–223. [Google Scholar]
- Bulut, H.; Baskonus, H.M.; Pandir, Y. The Modified Trial Equation Method for Fractional Wave Equation and Time-Fractional Generalized Burgers Equation. Abstr. Appl. Anal. 2013, 2013, 636802. [Google Scholar]
- Zayed, E.M.E.; Abdelaziz, M.A.M. Exact Solutions for the Nonlinear Schrödinger Equation with Variable Coefficients Using the Generalized Extended Tanh-Function, the Sine-Cosine and the Exp-function Methods. Appl. Math. Comput. 2011, 218, 2259–2268. [Google Scholar]
- Wazwaz, A. M. The Tanh Method: Solitons and Periodic Solutions for Dodd–Bullough–Mikhailov and Tzitzeica–Dodd–Bullough Equations. Chaos Solitons Fractals 2005, 25, 55–56. [Google Scholar]
- Khan, K.; Ali Akbar, M. Traveling Wave Solutions of the (2 + 1)-Dimensional Zoomeron Equation and the Burgers Equations via the MSE Method and the Exp-function Method. Ain Shams Eng. J. 2014, 5, 247–256. [Google Scholar]
- Ma, W.X.; Lee, J.H. A Transformed Rational Function Method and Exact Solutions to the 3 + 1 Dimensional Jimbo–Miwa Equation. Chaos Solitons Fractals 2009, 42, 1356–1363. [Google Scholar]
- Ma, W.X.; Huang, T.W.; Zhang, Y. A Multiple Exp-function Method for Nonlinear Differential Equations and its Application. Phys. Scr. 2010, 82, 065003. [Google Scholar]
- Ma, W.X.; Zhu, Z.N. Solving the (3+1)-Dimensional Generalized KP and BKP Equations by the Multiple Exp-function Algorithm. Appl. Math. Comput. 2012, 218, 11871–11879. [Google Scholar]
- Ma, W.X. Generalized Bilinear Differential Equations. Stud. Nonlinear Sci. 2011, 2, 140–144. [Google Scholar]
- Ma, W.X.; Fuchssteiner, B. Explicit and Exact Solutions to a Kolmogorov–Petrovskii–Piskunov Equation. Int. J. Nonlinear Mech. 1996, 31, 329–338. [Google Scholar]
- Ma, W.X.; Wu, H.Y.; He, J.S. Partial Differential Equations Possessing Frobenius Integrable Decompositions. Phys. Lett. A 2007, 364, 29–32. [Google Scholar]
- Khan, K.; Ali Akbar, M.; Rayhanul Islam,, S.M. Exact Solutions for (1 + 1)-Dimensional Nonlinear Dispersive Modified Benjamin–Bona–Mahony Equation and Coupled Klein–Gordon Equations. SpringerPlus 2014, 3. [Google Scholar] [CrossRef]
- Khan, K.; Ali Akbar, M. Exact Solutions of the (2+1)-Dimensional Cubic Klein–Gordon Equation and the (3+1)-Dimensional Zakharov–Kuznetsov Equation Using the Modified Simple Equation Method. J. Assn. Arab Univ. Basic Appl. Sci. 2014, 15, 74–81. [Google Scholar]
- Benjamin–Bona–Mahony Equation. Available online: http://en.wikipedia.org/wiki/Benjamin%E2%80%93Bona%E2%80%93Mahony_equation accessed on 1 February 2015.
- Yusufoglu, E. New Solitary Solutions for the MBBM Equations Using Exp-function Method. Phys. Lett. 2008, 372, 442–446. [Google Scholar]
- Eme, Z.; Al-Joudi, S. Applications of an Extended (G’/G)-Expansion Method to Find Exact Solutions of Nonlinear PDEs in Mathematical Physics. Math. Probl. Eng. 2010, 2010, 768573. [Google Scholar]
- Klein–Gordon Equation. Available online: https://en.wikipedia.org/wiki/Klein%E2%80%93Gordon_equation accessed on 1 February 2015.
- Evans, L.C. Entropy and Partial Differential Equations. 2004. Available online: https://math.berkeley.edu/~evans/entropy.and.PDE.pdf accessed on 19 June 2015.
- Jüngel, A. Entropy Dissipation Methods for Nonlınear Partial Differentıal Equations; Lecture Notes; Spring School: Bielefeld, March 2012. Available online: http://www.asc.tuwien.ac.at/~juengel/scripts/Bielefeld1203.pdf accessed on 19 June 2015.
- Parsani, M.; Carpenter, M.H.; Nielsen, E.J. Entropy Stable Wall Boundary Conditions for the Three-Dimensional Compressible Navier–Stokes Equations. J. Comput. Phys. 2015, 292, 88–113. [Google Scholar]
- Zhao, Y.; Yuan, M.; Su, G.; Chen, T. Crowd Macro State Detection Using Entropy Model. Physica A 2015, 431, 84–93. [Google Scholar]
- Elling, V. Relative Entropy and Compressible Potential Flow. Acta. Math. Sci. 2015, 35, 763–776. [Google Scholar]
- Chen, S.; Yang, B.; Xiao, X.; Zheng, C. Analysis of Entropy Generation in Double-Diffusive Natural Convection of Nano fluid. Int. J. Heat Mass Tran. 2015, 87, 447–463. [Google Scholar]
- Lv, Y.; Ihme, M. Entropy-Bounded Discontinuous Galerkin Scheme for Euler Equations. J. Comput. Phys. 2015, 295, 715–739. [Google Scholar]
- Broadbridge, P. Entropy Diagnostics for Fourth Order Partial Differential Equations in Conservation Form. Entropy 2008, 10, 365–379. [Google Scholar]
- Kudryashov, N.A. One Method for Finding Exact Solutions of Nonlinear Differential Equations. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 2248–2253. [Google Scholar]
- Lee, J.; Sakthivel, R. Exact Travelling Wave Solutions for some Important Nonlinear Physical Models. Pramana 2013, 80, 757–769. [Google Scholar]
- Ryabov, P.N.; Sinelshchikov, D.I.; Kochanov, M.B. Application of the Kudryashov Method for Finding Exact Solutions of the High Order Nonlinear Evolution Equations. Appl. Math. Comput. 2011, 218, 3965–3972. [Google Scholar]
- Demiray, S.T.; Pandir, Y.; Bulut, H. Generalized Kudryashov Method for Time-Fractional Differential Equations. Abstr. Appl. Anal. 2014, 2014, 901540. [Google Scholar]
- Çimen, T. On the Existence of Solutions Characterized by Riccati Equations to Infinite-Time Horizon Nonlinear Optimal Control Problems. Proceeding of The 18th IFAC World Congress, Milano, Italy, 28 August–2 September 2011; pp. 9616–9626.
- Baxley, J.V. Existence Theorems for Nonlinear Second Order Boundary Value Problems. J. Differ. Equ. 1990, 85, 125–150. [Google Scholar]
- Olver, P.J. Euler Operators Conservation Laws of the BBM Equation. Math. Proc. Camb. Phil. Soc. 1979, 85, 143–160. [Google Scholar]
- Johnson, M.A. On the Stability of Periodic Solutions of the Generalized Benjamin–Bona–Mahony Equation. Physica D 2010, 239, 1892–1908. [Google Scholar]
- Zeng, L. Existence and Stability of Solitary-Wave Solutions of Equations of Benjamin–Bona–Mahony Type. J. Differ. Equ. 2003, 188, 1–32. [Google Scholar]
- Medeiros, L.A.; Perla Menzala, G. Existence and Uniqueness for Periodic Solutions of the Benjamin–Bona–Mahony Equation. SIAM J. Math. Anal. 1977, 8, 792–799. [Google Scholar]
- Moriyama, K. Normal Forms and Global Existence of Solutions to a Class of Cubic Nonlinear Klein–Gordon Equations in one Space Dimension. Differ. Integr. Equ. 1997, 10, 499–520. [Google Scholar]
- Selberg, S.; Tesfahun, A. Unconditional Uniqueness in the Charge Class for the Dirac–Klein–Gordon Equations in two Space Dimensions. Nonlinear Differ. Equ. Appl. 2013, 20, 1055–1063. [Google Scholar]

© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baskonus, H.M.; Bulut, H. New Hyperbolic Function Solutions for Some Nonlinear Partial Differential Equation Arising in Mathematical Physics. Entropy 2015, 17, 4255-4270. https://doi.org/10.3390/e17064255
Baskonus HM, Bulut H. New Hyperbolic Function Solutions for Some Nonlinear Partial Differential Equation Arising in Mathematical Physics. Entropy. 2015; 17(6):4255-4270. https://doi.org/10.3390/e17064255
Chicago/Turabian StyleBaskonus, Haci Mehmet, and Hasan Bulut. 2015. "New Hyperbolic Function Solutions for Some Nonlinear Partial Differential Equation Arising in Mathematical Physics" Entropy 17, no. 6: 4255-4270. https://doi.org/10.3390/e17064255
APA StyleBaskonus, H. M., & Bulut, H. (2015). New Hyperbolic Function Solutions for Some Nonlinear Partial Differential Equation Arising in Mathematical Physics. Entropy, 17(6), 4255-4270. https://doi.org/10.3390/e17064255




