Skip to Content
MDPIMDPI

Advanced

EntropyEntropy
PDF
  • Article
  • Open Access

9 June 2015

21 Pages

A Colour Image Encryption Scheme Using Permutation-Substitution Based on Chaos

,
and
1
Faculty of Electronic Information and Electrical Engineering, Dalian University of Technology, Dalian 116024, China
2
City Institute, Dalian University of Technology, Dalian 116600, China
*
Authors to whom correspondence should be addressed.
Entropy2015, 17(6), 3877-3897;https://doi.org/10.3390/e17063877
This article belongs to the Special Issue Recent Advances in Chaos Theory and Complex Networks
Version Notes
Order Reprints

Abstract

An encryption scheme for colour images using a spatiotemporal chaotic system is proposed. Initially, we use the R, G and B components of a colour plain-image to form a matrix. Then the matrix is permutated by using zigzag path scrambling. The resultant matrix is then passed through a substitution process. Finally, the ciphered colour image is obtained from the confused matrix. Theoretical analysis and experimental results indicate that the proposed scheme is both secure and practical, which make it suitable for encrypting colour images of any size.

1. Introduction

Nowadays the number of colour images which are transmitted over the Internet keeps increasing. Therefore, the security of transmitted colour images has attracted the interest of scholars in both science and engineering [1]. The encryption of images is different from text encryption due to some inherent features of images such as the bulk data capacity and the high correlation among pixels. Therefore, traditional encryption schemes such as Data Encryption Algorithm (DEA) and Rivest Shamir Adleman (RSA) are not suitable for encryption of images. Chaos contains some superior features, such as sensitivity to initial conditions, ergodicity and random series [2]. For the design of encryption schemes for images, such features are of great importance for developing good diffusions and confusions.
Recently, many encryption schemes based on chaos have been proposed [3–36], including schemes for grey-level images [3–7,27] and the schemes for colour images [8–14,20,26,34–36]. Inevitably, most of them have proven to be insecure because the trajectories in low dimension chaotic systems are periodic for finite precisions in digital computers [15,17,18,21,28,33]. To overcome this flaw, the Coupled Map Lattices (CML) system, which is a spatiotemporal chaos [16,37], has been widely employed in cryptography [17–23,32]. The CML system contains multiple positive Lyapunov exponents, which indicates that its trajectories have longer periodicity in digitalization of finite precision computations. Furthermore, the CML system has more parameters for a larger key space when the CML system is applied for cryptography.
As for colour images, each pixel’s value of a colour image consists of R, G and B colour components, and each colour component directly determines the intensity of the red, green or blue colour. Because the colour images provide more information than grey-level images, they have attracted more and more attention [12–14], but most of the previous algorithms for colour images used the same method to encrypt their R, G and B components, which is to encrypt the image three times independently. This neglects the correlations between R, G and B components and is more vulnerable to attacks [8–14]. To overcome this problem, this paper proposes a novel colour image encryption algorithm based on chaos. We use CML to encrypt the colour image and make the three components affect each other. The permutation and substitution stages effectively reduce the correlations between R, G and B components and enhance the encryption performance.
The remainder of the paper is organized as follows: in Section 2, CML and the permutation method used in the proposed algorithm are introduced. In Section 3, the encryption algorithm is described. Section 4 provides simulation results. Security analysis is given in Section 5. Finally, this paper is concluded in Section 6.

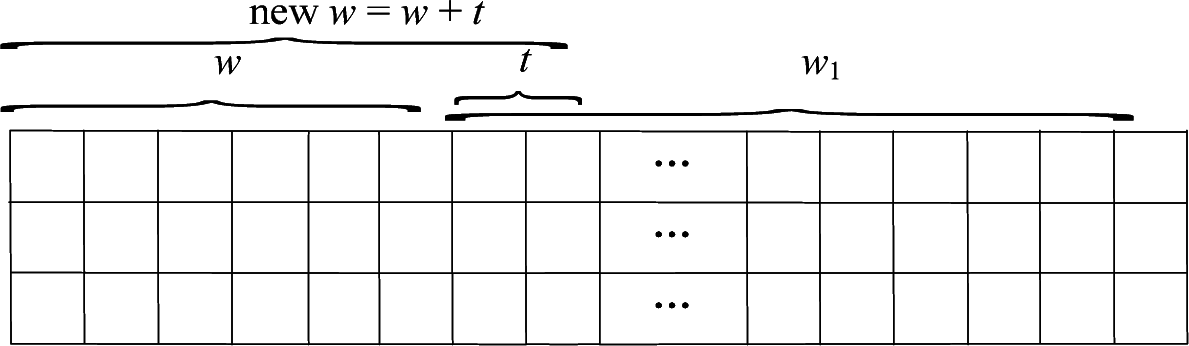
3. Colour Image Encryption Algorithm Based on Chaos

Without loss of generality, we assume that the size of the colour plain-image F is M × N. Convert F into its R, G and B components F r, F g, F b; the size of each colour’s (R, G or B) matrix is M × N, and the pixels’ values range from 0 to 255. F k r ( k ∈ [ 0 , M × N − 1 ] ) denotes the k-th pixel of F k g ( k ∈ [ 0 , M × N − 1 ] ) denotes the k-th pixel of F g; F k b ( k ∈ [ 0 , M × N − 1 ] ) denotes the kth pixel of F b.
ε in Equation (1) is decided by the colour plain-image F:
ε = ( ∑ k ∈ [ 0 , M × N − 1 ] F k r + ∑ k ∈ [ 0 , M × N − 1 ] F k g + ∑ k ∈ [ 0 , M × N − 1 ] F k b ) / ( 3 × M × N × 255 )
For different colour plain-image, our scheme has different secret key ε, so it could resist plaintext attack effectively. In more details, the encryption process may be summarized in the following steps:
Step 1: Use the R, G and B components F r, F g, F b to form a matrix B with size of 3 × ( M × N ):
F 0 r F 1 r … … F M × N − 2 r F M × N − 1 r
F ( M × N ) / 2 + 1 g F ( M × N ) / 2 + 2 g … … F M × N − 1 g F 0 g F 1 g … … F ( M × N ) / 2 − 1 g F ( M × N ) / 2 g
F M × N − 1 b F M × N − 2 b … … F 1 b F 0 b
The first row of B is composed of pixels of F r by arranging them from the first one to the last; the second is composed of pixels of F g by swapping the first half and the latter part; the third is composed of pixels of F b by arranging them from the last one to the first.
Step 2: Iterate the CML using, x0(1), x0(2), x0(3), x0(4), x0(5), x0(6), x0(7) μ, ε to get x i ( j ) ( j = 1 , 2 , ... , 7 ). i is set to 1 initially.
Step 3: Using x i ( 1 ), x i ( 2 ), x i ( 3 ), x i ( 4 ), x i ( 5 ), x i ( 6 ) to obtain t 1, t 2, t 3, m 1, m 2, m 3:
t 1 = mod ( ( x i ( 1 ) − ⌊ x i ( 1 ) ⌋ ) × 10 15 , 10 ) ,
t 2 = mod ( ( x i ( 2 ) − ⌊ x i ( 2 ) ⌋ ) × 10 15 , 10 ) ,
t 3 = mod ( ( x i ( 3 ) − ⌊ x i ( 3 ) ⌋ ) × 10 15 , 10 ) ,
m 1 = mod ( ( x i ( 4 ) − ⌊ x i ( 4 ) ⌋ ) × 10 15 , 256 ) ,
m 2 = mod ( ( x i ( 5 ) − ⌊ x i ( 5 ) ⌋ ) × 10 15 , 256 ) ,
m 3 = mod ( ( x i ( 6 ) − ⌊ x i ( 6 ) ⌋ ) × 10 15 , 256 ) .
t 1, t 2, t 3 are used in the permutation process and m 1, m 2, m 3 are used in the substitution process.
Step 4: Initially, randomly select three integers, assigned as r, g and b, serving as secret keys. Compare the value of r, g and b: if r is the maximum, set t = t1 + 1; if g is the maximum, set t = t2 + 1; if b is the maximum, set t = t3 + 1.
Step 5: We assume w represents the width of B processed; w1 represents the width of B not processed.
Case 1: w1 ≥ t. Select t columns from B after the w-th column, as shown in Figure 2.
Figure 2. The case of w1 ≥ t.
Set:
r = mod ( ( x i ( 7 ) − ⌊ x i ( 7 ) ⌋ ) × 10 15 , ⌊ 1.5 × t ⌋ )
  • Permute the selected block of width t for r times using the zigzag path scrambling.
  • Confuse the permutated block: implement exclusive OR operation bit-by-bit on the first row of the permutated block using m 1; implement exclusive OR operation bit-by-bit on the second row of the permutated block using m 2; implement exclusive OR operation bit-by-bit on the third row of the permutated block using m 3. Then set:
    r = B 0 , t + w − 1 ,
    g = B 1 , t + w − 1 ,
    b = B 2 , t + w − 1 ,
    w = w + t .
If w = M × N, encryption algorithm finishes. Finally, obtain the ciphered colour image from the resultant matrix B.
Case 2: w1 < t, select w1 columns from B after the w-th column, as shown in Figure 3.
Figure 3. The case of w1 < t.
Set:
r = mod ( ( x i ( 7 ) − ⌊ x i ( 7 ) ⌋ ) × 10 15 , ⌊ 1.5 × w 1 ⌋ ) .
  • Permute the selected block of width w1 for r times using the zigzag path scrambling.
  • Confuse the permutated block: implement exclusive OR operation bit-by-bit on the first row of the permutated block using m 1; implement exclusive OR operation bit-by-bit on the second row of the permutated block using m 2; implement exclusive OR operation bit-by-bit on the third row of the permutated block using m 3.
Encryption algorithm finishes. Finally, obtain the ciphered colour image from the resultant matrix B.
Step 6: Set i=i+1 and then go to Step 2.

4. Experimental Simulations

We have used MATLAB 7.6.0 to run programs that realize the proposed algorithm in a personal computer with an AMD Athlon (tm) 64 Processor 3000+ 2.00 GHz, 992 MB memory and 60 GB hard-disk capacity. The operating system is Microsoft Windows XP. Our simulation results are shown in Figures 4 and 5. The colour image “Lena” (Figure 4a) is used as the plain image. Figure 4b–d show its R, G and B components, respectively. The secret keys are set as follows: x 0 ( 1 ) = 0.45, x 0 ( 2 ) = 0.89, x 0 ( 3 ) = 0.56, x 0 ( 4 ) = 0.77, x 0 ( 5 ) = 0.22, x 0 ( 6 ) = 0.89, x 0 ( 7 ) = 0.45, μ = 4.0, r = 45, g = 133, b = 91.
Figure 4. Colour plain-image “Lena” and its R, G and B components. (a) Colour plain-image “Lena”; (b) R component; (c) G component; (d) B component.
Figure 5. Ciphered colour image of “Lena” and its R, G and B components. (a) Ciphered colour image of “Lena”; (b) R component; (c) G component; (d) B component.
The ciphered colour image is shown in Figure 5a, which becomes an unintelligible colour image. Figure 5b–d show the R, G and B components of the ciphered colour image, respectively.

5. Performance Analysis

A good encryption scheme should resist against all kinds of attacks. Security analyses are performed on the proposed algorithm in this section.

5.1. Key Space

A good encryption scheme should have a large key space size to resist against any kind of brute-force attack. In our algorithm, x 0 ( 1 ), x 0 ( 2 ), x 0 ( 3 ), x 0 ( 4 ), x 0 ( 5 ), x 0 ( 6 ), x 0 ( 7 ), μ, ε, r, g and b are used as the secret keys. The complexity of brute-force is great, so the key space is large enough for common applications to resist brute-force attacks.

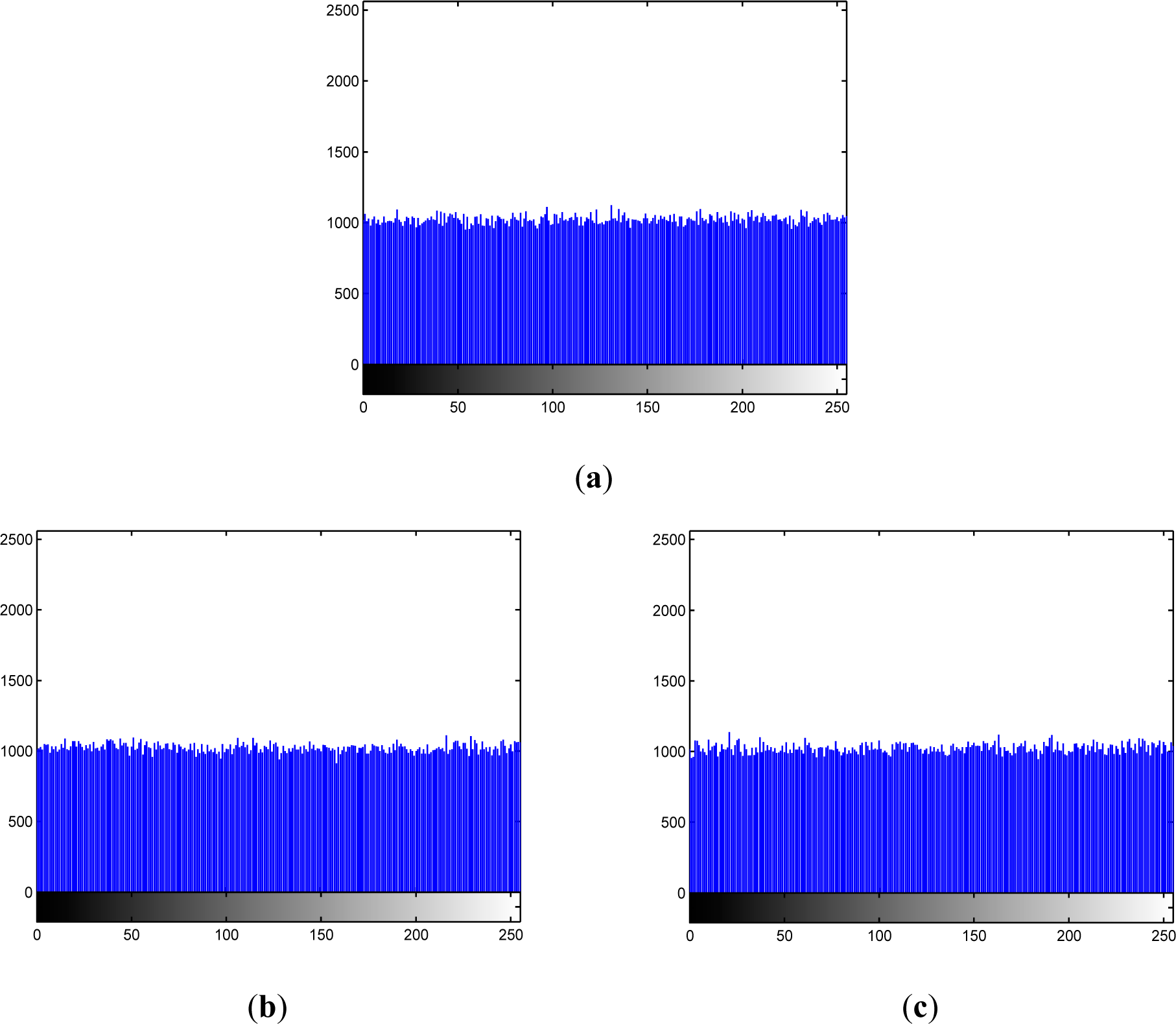
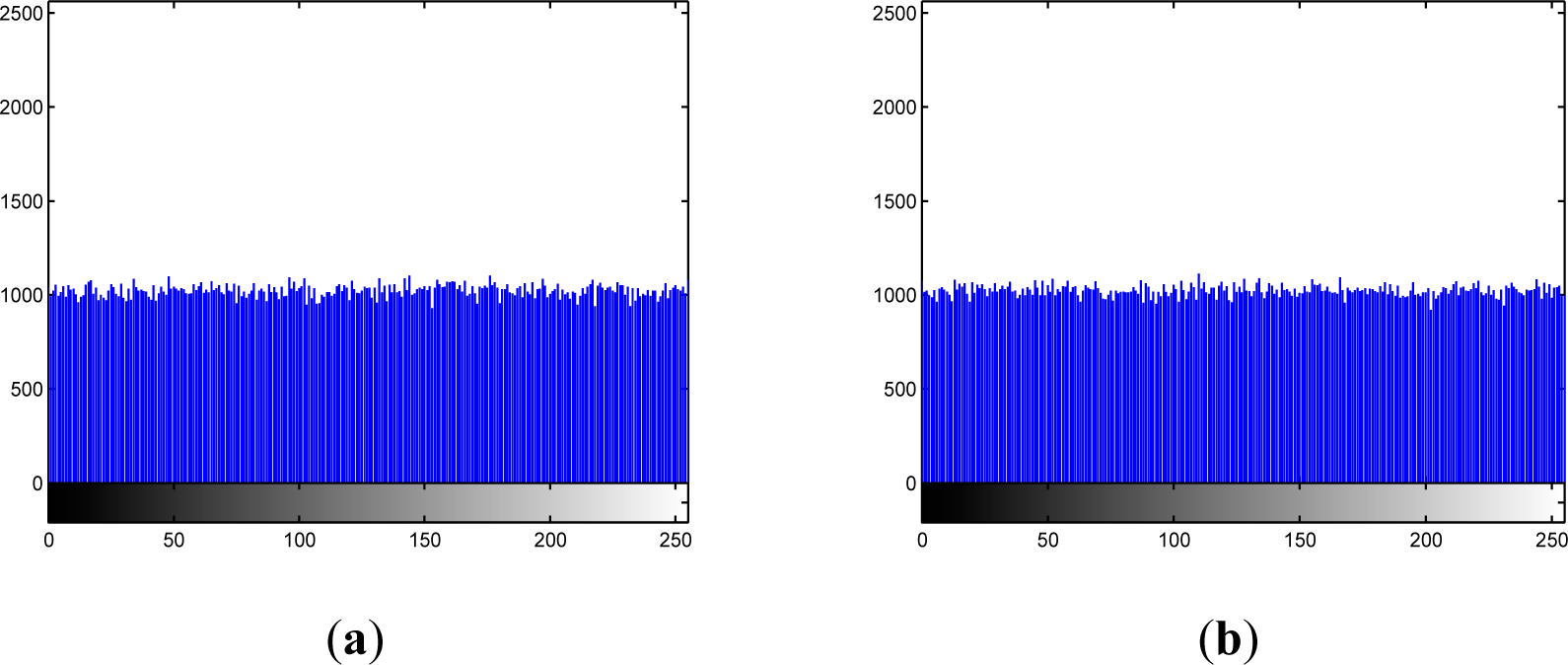
5.2. Histogram Analysis

The distribution of the ciphered image should be uniform. A histogram as a graph used for showing the distribution of pixel values of an image. An adversary can recover the corresponding information from the characteristics of the histogram of an image, when the histogram of the image is not flat enough. However, the adversary will be unable to do so when the histogram of a ciphered image is uniform. A flat distribution is important in cryptography.
Figure 6 illustrates the histograms of the colour plain-image “Lena”. Figure 6a shows the histogram of the R component; Figure 6b shows the histogram of the G component; Figure 6c shows the histogram of the B component. From Figure 6, the histograms of the plain-image are not flat.
Figure 6. Histograms of the R, G and B components of the colour plain-image “Lena”. (a) Histogram of the R component; (b) histogram of the G component; (c) histogram of the B component.
Figure 7 illustrates the histograms of the ciphered colour image of “Lena”. Figure 7a shows the histogram of the R component; Figure 7b shows the histogram of the G component; Figure 7c shows the histogram of the B component. It is clear from Figure 7 that the proposed algorithm results in very flat distributions and that statistical attacks on our algorithm are not effective.
Figure 7. Histograms of the R, G and B components of the ciphered colour image of “Lena”. (a) Histogram of the R component; (b) histogram of the G component; (c) histogram of the B component.
Without loss of generality, the plaintext images in USC-SIPI [38] database such as Girl, House, Mandrill and Peppers are included for encryption tests. The results are shown in Figure 8.
Figure 8. Histograms of the R, G and B components of the ciphered colour images. (a) R component in ciphered Girl; (b) G component in ciphered Girl; (c) B component in ciphered Girl; (d) R component in ciphered House; (e) G component in ciphered House; (f) B component in ciphered House; (g) R component in ciphered Mandrill; (h) G component in ciphered Mandrill; (i) B component in ciphered Mandrill; (j) R component in ciphered Peppers; (k) G component in ciphered Peppers; (l) B component in ciphered Peppers.
The χ 2 align tests are employed for quantity analysis of the uniformity in ciphered images. The value of the χ 2 tests for a ciphered colour image of dimension M × N is given by the following formula:
χ 2 = ∑ i = 0 255 ( ( v i r − v 0 ) 2 v 0 + ( v i g − v 0 ) 2 v 0 + ( v i b − v 0 ) 2 v 0 )
where v i r, v i g and v i b are the corresponding R, G and B components of the observed frequency of a pixel value i ( 0 ≤ i ≤ 255 ). The is the expected frequency of a pixel value i, so ν0 = (M × N)/256. The results obtained by applying the χ 2 tests on 100 encrypted images can be summarized as it follows: in 98% of the tests, the values obtained were lower than the critical value χ 767 , 0.05 2 = 832.54 and only in 2% of tests; the obtained values were lying in the interval [834.632, 861.045], which is close to the critical value χ 767 , 0.05 2 = 832.54. Table 1 shows the results of χ 2 tests of the five pairs of plaintext/ciphered images.
Table 1. Results of χ2 tests.

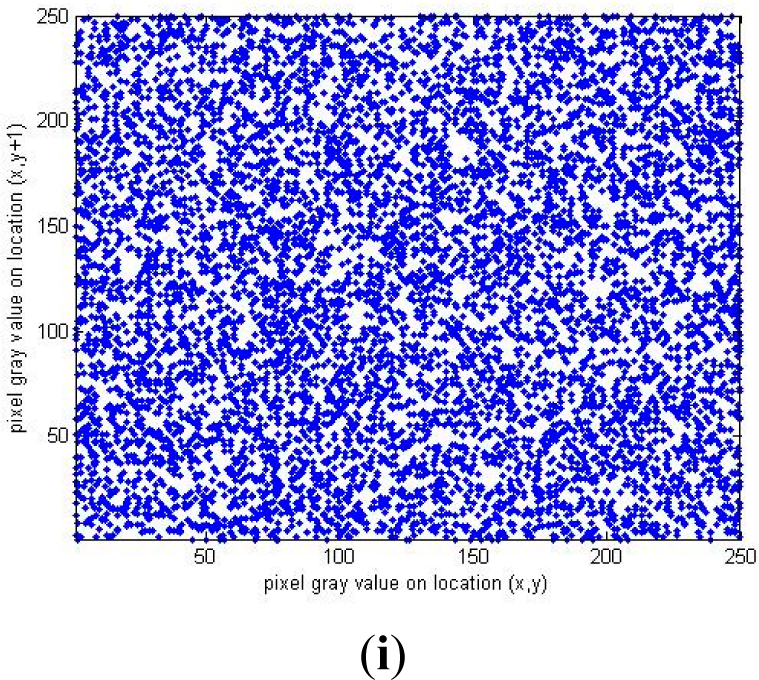
5.3. Information Entropy Analysis

Information entropy can indicate the feature of randomness. The global information entropy can be calculated as follows:
H ( m ) = ∑ i = 0 2 n − 1 p ( m i ) log 2 1 p ( m i )
where m is the information source and p ( m i ) represents the probability of symbol m i. When there are 2 8 states of the information source, the same probability appears. For Equation (5), we obtain H ( m ) = 8, which indicates the completely randomness of the information. Therefore, the information entropy of a ciphered image must be close to 8. The closer it is to 8, the less possible it is for the scheme to divulge information. Information entropies of the R, G and B components of the ciphered colour images of Lena, Girl, House, Mandrill and Peppers are displayed in Table 2. From the table, test results based on the proposed algorithm are closer to the ideal value of 8.
Table 2. Global information entropies of the ciphered colour images.
The local Shannon entropy [39] over image blocks is as follows:
H ( k , T B ) ( S ) = ∑ i = 1 k H ( S i ) k
where S 1 , S 2 , ... , S k are randomly selected non-overlapping blocks image with T B pixels within a test image S of L intensity scales and H ( S i ) are computed using Shannon entropy. The local Shannon entropy measure is evaluated for the five ciphered images. Non-overlapping image blocks with T B = 1936 pixels and k = 30 are selected randomly from the ciphered images. The observed value of local Shannon entropy [39] should lie in the confidence interval [7.9019, 7.9030], with respect to the α-level confidence equal to 0.05. Table 3 shows the results of five ciphered images lie in this confidence interval. We can conclude that the ciphered images obtained by the proposed algorithm could hardly divulge information.
Table 3. Local information entropies of the ciphered colour images.

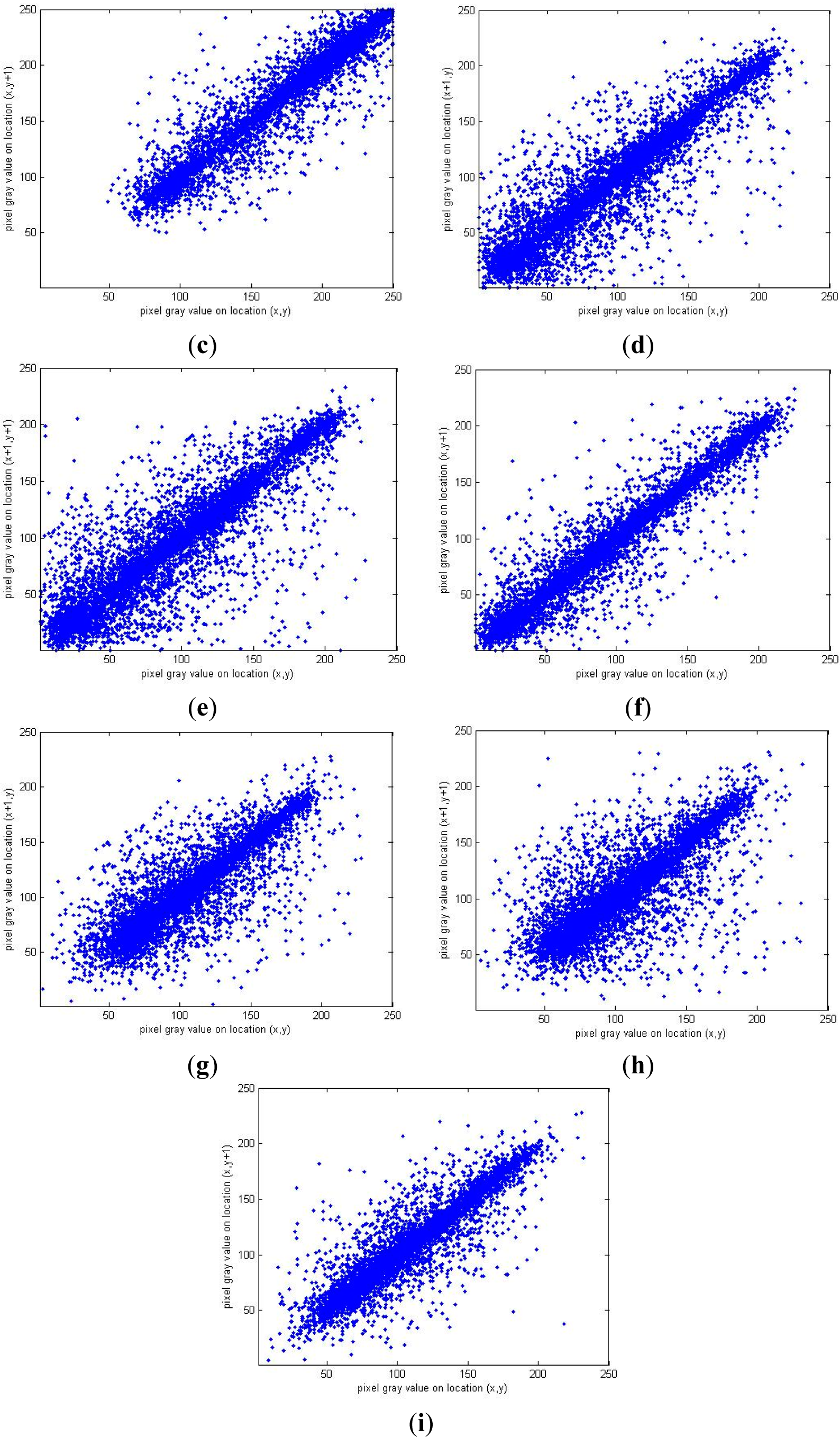
5.4. Correlation Analysis

Correlation between two random series indicates the strength and direction of their linear relationship. Therefore, correlation between two adjacent pixels of images is usually applied in image processing. The correlation of a recognizable image is usually high because plaintext images are information redundant. In cryptography, the correlation of two adjacent pixels should have a low value to ensure the security of the ciphered images.
For evaluation of the correlations, vertically adjacent pixels, diagonally adjacent pixels and horizontally adjacent pixels are tested, respectively. Equation (7) calculates the correlation of two adjacent pixels:
r x y = cov ( x , y ) D ( x ) D ( y )
where:
cov ( x , y ) = 1 N ∑ i = 1 N ( x i − E ( x ) ) ( y i − E ( y ) ) , E ( x ) = 1 N ∑ i = 1 N x i , D ( x ) = 1 N ∑ i = 1 N ( x i − E ( x ) ) 2 .
We choose 1.000 pairs of adjacent pixels randomly in each direction from the R, G and B components of the ciphered colour image. Without loss of generality, we plot the correlation distributions of the R, G and B components of “Lena” and its ciphered colour image in each direction, as illustrated in Figures 9 and 10. Figure 9a–c show the correlation distributions of the R component of “Lena” in each direction; Figure 9d–f show the correlation distributions of the G component of “Lena” in each direction; Figure 9g–i show the correlation distributions of the B component of “Lena” in each direction; Figure 10a–c show the correlation distributions of the R component of the ciphered colour image in each direction; Figures 10d–f show the correlation distributions of the G component of the ciphered colour image in each direction; Figure 10g–i show the correlation distributions of the B component of the ciphered colour image in each direction. The strong correlation between adjacent pixels of the plain image is evident as all the dots are congregated along the diagonal in Figure 9a–i. However, in Figure 10a–i, the dots are scattered over the entire plane, which indicates that the correlation is greatly reduced in the ciphered image. The corresponding correlation coefficients are calculated for ciphered Lena, Girl, House, Mandrill and Peppers and are listed in Table 4.
Figure 9. Correlation distributions. (a–c) Correlation distributions of the R component of “Lena” in each direction; (d–f) correlation distributions of the G component of “Lena” in each direction; (g–i) correlation distributions of the B component of “Lena” in each direction.
Figure 10. Correlation distributions. (a–c) Correlation distributions of the R component of the ciphered colour image in each direction; (d–f) correlation distributions of the G component of the ciphered colour image in each direction; (g–i) correlation distributions of the B component of the ciphered colour image in each direction.
Table 4. Correlation coefficients of the R, G and B components of the ciphered images.
From Table 4, in the R, G and B components of the ciphered colour image, correlation coefficients are all smaller than 0.01, indicating a negligible correlation between adjacent pixels.

5.5. Differential Attacks

Number of Pixels Change Rate (NPCR) shows the number of changed pixels when the value of a pixel in the plain image is changed. The NPCR indicates the sensitivity of the scheme to similar plain images with a tiny difference; therefore, the NPCR can evaluate the ability of a scheme against chosen plaintext attacks. Unified Average Changing Intensity (UACI) shows the average intensity of differences between the plain image and the corresponding ciphered image. Therefore, the UACI can evaluate the ability of a scheme for resistance to differential attacks. The NPCR and UACI are as follows:
NPCR = ∑ i j D ( i , j ) W × H × 100 %
UACI = 1 W × H [ ∑ i , j | C 1 ( i , j ) − C 2 ( i , j ) | 255 ] × 100 %
where W and H are the width and height of the image, respectively; C 1 is the ciphered image for the original image; C 2 are the ciphered image that one pixel changed in its plain image. For the pixel where its position is ( i , j ), if C 1 ( i , j ) ≠ C 2 ( i , j ), let D ( i , j ) = 1 ; else let D ( i , j ) = 0. NPCR and UACI of R, G and B components of Lena, Girl, House, Mandrill and Peppers are listed in Table 5. The idea values of UACI and NPCR must approach 99.609375% and 33.463541% respectively [33,40]. The results show that the proposed algorithm displays good NPCR and UACI performance against plaintext attacks and differential attacks.
Table 5. NPCR and UACI of R, G and B components of ciphered images.

5.6. Key Sensitivity

A good encryption scheme should be sensitive to the secret keys and the plaintext. Taking secret key x 0 ( 1 ) for instance, a sensitivity test on the R component of “Lena” is performed. Figure 11a shows the differences between two ciphered R components when x 0 ( 1 ) is changed from 0.45 to 0.45000000001 while the other keys remain the same. Figure 11b shows the differences between two ciphered R components when 1 bit of the pixel data of the R component of “Lena” is changed. Without loss of generality, the Girl and Mandrill images are also tested in the same manner. The results are shown in Figure 12.
Figure 11. Sensitivity tests. (a) Differences between two ciphered R components when x0(1) is changed from 0.45 to 0.45000000001; (b) Differences between two ciphered R components when 1 bit of the pixel data of the R component of “Lena” is changed.
Figure 12. Sensitivity tests result of Girl and Mandrill. (a) R components when x0(1) is changed in Girl; (b) R components when 1 bit is changed in Girl; (c) R components when x0(1) is changed in Mandrill; (d) R components when 1 bit is changed in Mandrill.
The experimental results indicate that the proposed scheme is sensitive to the plaintext. A tiny change in the plaintext image leads to entirely different changes in the ciphered image. The high sensitivity to plaintext ensures the scheme can resist plaintext attacks.

5.7. Speed Performance

To evaluate the running speed, all the tests are implemented in Visual C++ 6.0 under the Windows XP Professional operating system, and the computer is an Intel Core 2.4 GHz CPU, 2GB RAM and 500 GB hard disk. The colour images of Lena, Grill, House, Mandrill and peppers are encrypted by each algorithm ten times. The average execution time is 267.5 ms for one round. Therefore, the mean speed of encryption of the proposed scheme is 2.87 MB/s.

5.8. Performance Comparison with Other Colour Image Encryption Schemes

Some recent excellent image encryption schemes [25,29,35,36] are employed for comparison with the proposed scheme. Table 6 lists the mean values obtained for the correlation coefficient of adjacent pixels, NPCR, UACI and speed. The results indicate that the performance of the proposed scheme is similar or better than the previous excellent schemes.
Table 6. Comparison with previous excellent encryption schemes.

6. Conclusions

In this paper, we propose a colour image encryption algorithm based on the CML system. Initially, we form a matrix using the R, G and B components of a colour plain-image. The simplicity of the proposed scheme leads to an easy software implementation. Both experimental results and theoretical analysis indicate that the scheme is secure. For future work, we will design a parallel implementation of the scheme in order to reduce the execution time.

Acknowledgments

This research is supported by the National Natural Science Foundation of China (Nos: 61370145, 61173183, and 60973152), the Doctoral Program Foundation of Institution of Higher Education of China (No: 20070141014), Program for Liaoning Excellent Talents in University (No: LR2012003), the National Natural Science Foundation of Liaoning province (No: 20082165) and the Fundamental Research Funds for the Central Universities (No: DUT12JB06).

Author Contributions

Xing-Yuan Wang contributed the literature research, study concepts, experimental data proof and manuscript editing/review/final approval. Ying-Qian Zhang contributed the experimental studies, data analysis/interpretation, manuscript revision editing. Xue-Mei Bao contributed the study design, manuscript preparation editing and data acquisition/statistical analysis. All authors have read and approved the final manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Uhl, A.; Pommer, A. Image and Video Encryption: From Digital Rights Management to Secured Personal Communication; Springer: New York, NY, USA; 2004. [Google Scholar]
  2. Liu, B.; Peng, J. Nonlinear Dynamics; High Education Press: Beijing, China; 2004; in Chinese. [Google Scholar]
  3. Wang, X.Y.; Teng, L. An image blocks encryption algorithm based on spatiotemporal chaos. Nonlinear Dyn 2012, 67, 365–371. [Google Scholar]
  4. Bigdeli, N.; Farid, Y.; Afshar, K. A novel image encryption/decryption scheme based on chaotic neural networks. Eng. Appl. Artif. Intell 2012, 25, 753–765. [Google Scholar]
  5. Liao, X.F.; Lai, S.Y.; Zhou, Q. A novel image encryption algorithm based on self-adaptive wave transmission. Signal Proc 2010, 90, 2714–2722. [Google Scholar]
  6. Ren, X.; Liao, X.; Xiong, Y.; Jisuanji, Y. New image encryption algorithm based on cellular neural network. J. Comput. Appl 2011, 31, 1528–1530. [Google Scholar]
  7. Wang, X.Y.; Yang, L.; Liu, R.; Kadir, A. A chaotic image encryption algorithm based on perceptron model. Nonlinear Dyn 2010, 62, 615–621. [Google Scholar]
  8. Rhouma, R.; Soumaya, M.; Safya, B. CML-based colour image encryption. Chaos Solitons Fractals 2009, 40, 309–318. [Google Scholar]
  9. Sahar, M.; Amir, M.E. Colour image encryption based on coupled nonlinear chaotic map. Chaos Solitons Fractals 2009, 42, 1745–1754. [Google Scholar]
  10. Liu, H.J.; Wang, X.Y. Colour image encryption based on one-time keys and robust chaotic maps. Comput. Math. Appl 2010, 59, 3320–3327. [Google Scholar]
  11. Peng, Z.N.; Liu, W.B. Colour image authentication based on spatiotemporal chaos and SVD. Chaos Solitons Fractals 2008, 36, 946–952. [Google Scholar]
  12. Madhusudan, J.; Shakher, C.; Kehar, S. Colour image encryption and decryption for twin images in fractional Fourier domain. Opt. Commun 2008, 8, 5713–5720. [Google Scholar]
  13. Guo, Q.; Liu, Z.G.; Liu, S.T. Colour image encryption by using Arnold and discrete fractional random transforms in IHS space. Opt. Lasers Eng 2010, 48, 1174–1181. [Google Scholar]
  14. Tay, C.J.; Quan, C.; Chen, W.; Fu, Y. Colour image encryption based on interference and virtual optics. Opt. Laser Technol 2010, 42, 409–415. [Google Scholar]
  15. Wheeler, D.D. Problems with chaotic cryptosystems. Cryptologia 1991, 7, 243–250. [Google Scholar]
  16. Li, P.; Li, Z.; Halang, W.A.; Chen, G. A stream cipher based on a spatiotemporal chaotic system. Chaos Solitons Fractals 2007, 32, 1867–1876. [Google Scholar]
  17. Ziba, E.; Atieh, B. An improvement over an image encryption method based on total shuffling. Opt. Commun 2013, 286, 51–55. [Google Scholar]
  18. Fatih, O.; Bedri, O.A.; Sirma, Y. Cryptanalysis of a novel image encryption scheme based on improved hyperchaotic sequences. Opt. Commun 2012, 285, 4946–4948. [Google Scholar]
  19. Teng, L.; Wang, X. A bit-level image encryption algorithm based on spatiotemporal chaotic system and self-adaptive. Opt. Commun 2012, 285, 4048–4054. [Google Scholar]
  20. Liu, G.; Li, J.; Liu, H. Chaos-based color pathological image encryption scheme using one-time keys. Comput. Biol. Med 2014, 45, 111–117. [Google Scholar]
  21. Gonzalo, A.; Shujun, L.; Luis, H. Analysis of security problems in a medical image encryption system. Comput. Biol. Med 2007, 27, 424–427. [Google Scholar]
  22. Almasalha, F.; Hasimoto-Beltran, R.; Khokhar, A.A. Partial Encryption of Entropy-Coded Video Compression Using Coupled Chaotic Maps. Entropy 2014, 16, 5575–5600. [Google Scholar]
  23. Tong, X.; Liu, Y.; Zhang, M.; Xu, H.; Wang, Z. An Image Encryption Scheme Based on Hyperchaotic Rabinovich and Exponential Chaos Maps. Entropy 2015, 17, 181–196. [Google Scholar]
  24. Boriga, R.; Dăscălescu, A.C.; Diaconu, A.V. A New One-Dimensional Chaotic Map and its Use in a Novel Real Time Image Encryption Scheme. Adv. Multimed 2014, 2014. [Google Scholar] [CrossRef]
  25. Boriga, R.; Dăscălescu, A.C.; Diaconu, A.V. A New Fast Image Encryption Scheme Based on 2D Chaotic Maps. IAENG Int. J. Comput. Sci 2014, 41, 249–258. [Google Scholar]
  26. Huang, X.; Sun, T.; Li, Y.; Liang, J. A Color Image Encryption Algorithm Based on a Fractional-Order Hyperchaotic System. Entropy 2015, 17, 28–38. [Google Scholar]
  27. Huang, C.K.; Liao, C.W.; Hsu, S.L.; Jeng, Y.C. Implementation of gray image encryption with pixel shuffling and gray-level encryption by single chaotic system. Telecommun. Syst 2013, 52, 563–571. [Google Scholar]
  28. Diaconu, A.V.; Loukhaoukha, K. An Improved Secure Image Encryption Algorithm Based on Rubik’s Cube Principle and Digital Chaotic Cipher. Math. Probl. Eng 2013, 2013, 848392. [Google Scholar]
  29. Ghebleh, M.; Kanso, A.; Noura, H. An image encryption scheme based on irregularly decimated chaotic maps. Signal Proc. Image Commun 2014, 29, 618–627. [Google Scholar]
  30. El-Latif, A.A.; Li, L.; Wang, N.; Han, Q.; Niu, X. A new approach to chaotic image encryption based on quantum chaotic system, exploiting color spaces. Signal Proc. Image Commun 2013, 93, 2986–3000. [Google Scholar]
  31. Dăscălescu, A.C.; Boriga, R.; Mihăilescu, M.I. A Novel Chaos-Based Image Encryption Scheme. Ann. Univ. Craiova Math. Comput. Sci. Ser 2014, 41, 47–58. [Google Scholar]
  32. Ye, G.; Wong, K.W. An image encryption scheme based on time-delay and hyperchaotic system. Nonlinear Dyn 2013, 71, 259–267. [Google Scholar]
  33. Kwok, H.S.; Tang, W.K.S. A fast image encryption system based on chaotic maps with finite precision representation. Chaos Solitons Fractals 2007, 32, 1518–1529. [Google Scholar]
  34. Diaconu, A.V.; Costea, A.; Costea, M.A. Color image scrambling technique based on transposition of pixels between RBG channels using Knight’s moving rules and digital chaotic map. Math. Probl. Eng 2014, 2014. [Google Scholar] [CrossRef]
  35. Saraswathi, P.V.; Venkatesulu, M. A block cipher algorithm for multimedia content protection with random substitution using binary tree traversal. J. Comput. Sci 2012, 8, 1541–1546. [Google Scholar]
  36. Sivakumar, T.; Venkatesan, R. A novel approach for image encryption using dynamic SCAN pattern. IAENG Int. J. Comput. Sci 2014, 41, 91–101. [Google Scholar]
  37. Kaneko, K. Spatiotemporal intermittency in Coupled Map Lattices. Prog. Theor. Phys 1985, 74, 1033–1044. [Google Scholar]
  38. USC-SIPI Image Database. Available online: http://sipi.usc.edu/database/database.php accessed on 10 April 2015.
  39. Wu, Y.; Zhou, Y.; Saveriades, G.; Agaian, S.; Noonan, J.P.; Natarajan, P. Local Shannon entropy measure with statistical tests for image randomness. Inf. Sci 2013, 222, 323–342. [Google Scholar]
  40. Wu, Y.; Noonan, J.P.; Agaian, S. NPCR and UACI randomness tests for image encryption. J. Sel. Areas Telecommun 2011, 2, 31–38. [Google Scholar]

Article Metrics

Citations

Article Access Statistics

Journal Statistics
Multiple requests from the same IP address are counted as one view.
Radial Wavelet Neural Network with a Novel Self-Creating Disk-Cell-Splitting Algorithm for License Plate Character Recognition
Previous
General Hyperplane Prior Distributions Based on Geometric Invariances for Bayesian Multivariate Linear Regression
Next