1. Introduction
Nowadays automatic license plate recognition (ALPR) plays an important role in many automated transport systems such as road traffic monitoring, automatic payment of tolls on highways or bridges and parking lots access control. In general, four major steps are comprised in these recognition systems, namely locating of car plate regions, correction of slant plates, segmentation of characters from the plate regions and recognition of car plate characters. Many researchers have been making great efforts on ALPR systems. In [
1], a recognition system of China-style license plate is proposed, which adopt the color and vein characteristics locating plate, mathematical morphology and Radon transformation correcting the slant plate and BP neural network recognizing characters. In [
2], a distributed genetic algorithm is used to extract license plates from vehicle images. In [
3], a least-square-based skew detection method is proposed for skew correction and template matching combining with Bayes methods are used to get robust recognition rates in the recognition system. In [
4], the morphological method is used to detect the candidates of the Macao license plate region and a template matching combining a post-process is used to recognition characters. In [
5], the self-organizing map (SOM) algorithm is used to make the slant correction of plates and a hybrid algorithm cascading two steps of template matching is utilized to recognize Chinese characters segmented from the license plates, which is based on the connected region feature and standard deviation feature extracted from sample corresponding to each template. Some other methods can also been found in [
6–
10].
In this study, the character recognition step which belongs to the pattern recognition field is considered. As to the recognition of license plate character, there are two important aspects: feature extraction and classification method. There have been a lot of methods on the feature extraction of characters, which are based on the projections, strokes, counters, skeletons, pixels number in grids, Zernike moment and wavelet moment
etc. All these features can be used alone or associatively. The most commonly used classification methods are template matching [
3–
5,
9] and neural network [
1,
7,
8,
10]. The former is based on the difference between sample and template, and the latter is based on the generalization ability of the network.
Neural network approaches can be considered as “black-box” methods which possess the capability of learning from examples with both linear and nonlinear relationships between the input and output signals. After years of development, neural network has been a popular tool for time-series prediction [
11,
12], feature extraction [
13,
14], pattern recognition [
15,
16], and classification [
17,
18]. Due to the ability of wavelet transformation for revealing the property of function in localize region, different types of wavelet neural network (WNN) which combine wavelets with neural networks have been proposed [
19,
20]. In WNN, the wavelets were introduced as activation functions of the hidden neurons in traditional feedforward neural networks with a linear output neuron. As to the WNN with multidimensional input vectors, multidimensional wavelets must employed in the hidden neurons. There are two commonly used approaches for representing multidimensional wavelets [
21]. First one is to generate separable wavelets by the tensor product of several 1-D wavelet functions [
19]. Another popular scheme is to choose the wavelets to be some radial functions in which the Euclidian norms of the input variables are used as the inputs of single-dimensional wavelets [
21–
23]. In this paper, the radial wavelet neural network (RWNN) is used as the means for plate character data classification.
It is well-known that selecting an appropriate number of hidden neurons is crucial for good performance and meanwhile the first task determining the architecture of the feedforward neural networks. The same is true of radial wavelet neural network, which is based on the Euclidean distance. In this view, a novel self-creating and self-organizing algorithm is proposed to determine the number of hidden neurons. Based on the idea of SOM which can produce an ordered topology map of input dada in a low dimensional space, the proposed self-creating disk-cell-splitting algorithm can create neurons adaptively on a disk according to the distribution of input data and learning goals, which accordingly produces a RWNN with proper structure and parameters for the recognition task. In addition, the splitting method endows weights of new generated neurons through circle neighbor strategy and maintains the weights of non-splitting neurons which can ensure a faster convergence process.
The content of this paper is organized as follows. In Section 2, a brief introduction of radial wavelet neural network is given. Followed by a review of self-organizing map algorithm, the detailed self-creating disk-cell-splitting (SCDCS) algorithm combining the least square (LS) method which used for RWNN is described in Section 3. In Section 4, two simulation examples: recognition of English letters and recognition of numbers or English letters are implemented by SCDCS-LS based RWNN model as well as the classical K-means-LS based RBF model. The comparison results are presented to demonstrate the superior ability of our proposed model. Finally, some conclusions are drawn in the last section.
2. Radial Wavelet Neural Network (RWNN)
Wavelets in the following form:
are a family of functions generated from one single function
by the operation of dilation and translation.
is called a mother wavelet function that satisfies the admissibility condition:
where
is the Fourier transform of
[
24,
25].
Grossmann [
26] proved that any function
in
can be represented by
Equation (3):
where
given by
is the continuous wavelet transform of
f (
x).
Superior to conventional Fourier transform, the wavelet transform (WT) in its continuous form provides a flexible time-frequency window, which narrows when observing high frequency phenomena and widens when analyzing low frequency behavior. Thus, time resolution becomes arbitrarily good at high frequencies, while the frequency resolution becomes arbitrarily good at low frequencies. This kind of analysis is suitable for signals composed of high frequency components with short duration and low frequency components with long duration, which is often the case in practical situations.
Inspired by the wavelet decomposition of
in
Equation (3) and a single hidden layer network model, Zhang and Benveniste in [
19] had developed a new neural network model, namely, wavelet neural network (WNN) which adopts the wavelets called also wavelons as the activation functions. The simple mono-dimensional input structure is represented by the following expression (5).
The addition of the
value is to deal with function whose mean is nonzero. In a wavelet network, all parameters
(connecting parameter),
(bias term),
(dilation parameter),
(translation parameter) are adjustable, providing certainly more flexibility to derive different network structures.
To deal with multidimensional input vectors, the multidimensional wavelet activation functions must be adopted in the network. One of the typical alternative networks is the radial wavelet network (RWN) introduce by Zhang in [
22]. A wavelet function
is radial if it has the following form:
, where
and
is a mono-variable function. In this paper, translated and dilated version of the Mexican Hat wavelet function is used, which is given by the following equation:
where
is the translation parameter with dimension identical to input record
,
is the scalar dilation parameter. A 2-D radial Mexican Hat wavelet function is drawn in
Figure 1.
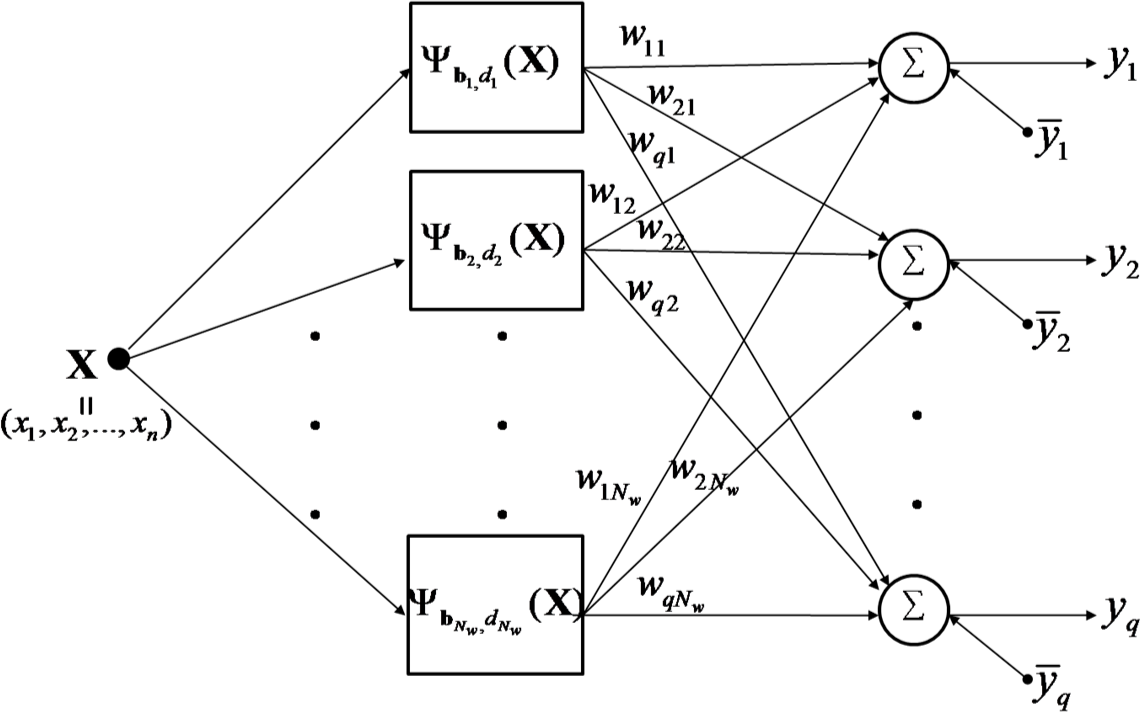
Figure 2 shows the architecture of a RWNN, whose output neurons produce linear combination of the outputs of hidden wavelons and bias terms by the following equation:
where
Nw and
q are the numbers of hidden and output neurons respectively.
3. Self-Creating Disk-Cell-Splitting (SCDCS) and Least Square (LS) Method Based RWNN
The parameters learning strategy of RWNN is different for the hidden layer and output layer as classical radial traditional radial-basis-function (RBF) network [
27]. For finding the weights between the hidden and output layer, a linear optimization strategy—LS method is used in RWNN. While for the translation parameters of radial wavelets as well as the number of neurons in the hidden layer, a novel self-organizing type SCDCS algorithm is employed. The SCDCS-LS algorithm is based on the competitive learning of SOM, but the map is organized on a disk instead of a rectangular, and the mapping scale is self-creating by the input data and learning goals other than pre-determined. In this section, a brief review of SOM is presented firstly. After that the SCDCS-LS algorithm is detailed described.
3.1. Self-Organizing Map
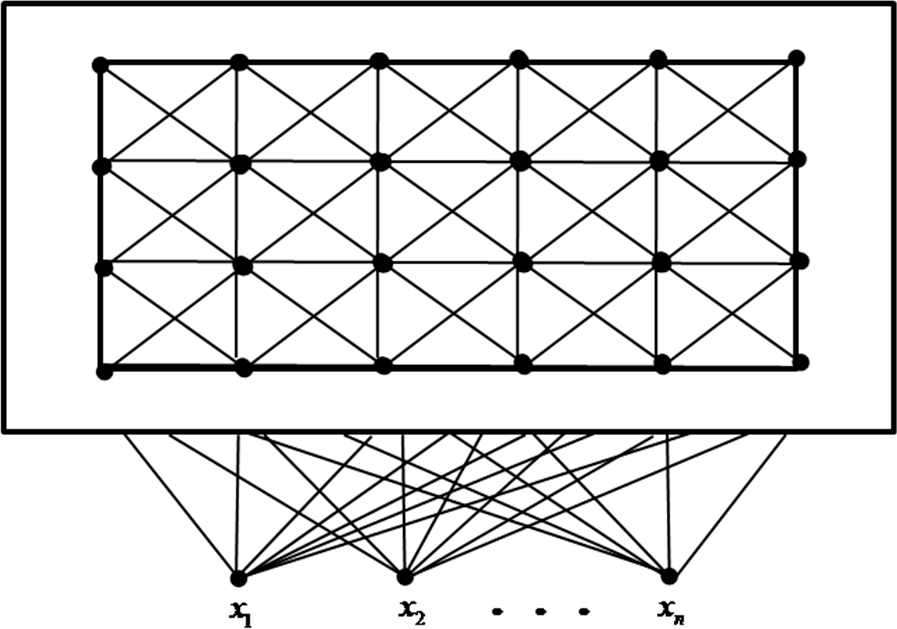
SOM is a type of artificial neural network that is trained using unsupervised learning to produce a low-dimensional (typically two-dimensional), discretized representation of the input space of the training samples, and called a map. The model was first described as an artificial neural network by Teuvo Kohonen [
28], and is sometimes called a Kohonen map.
Figure 3 shows a Kohonen network connected to the input layer representing a
n-dimensional vector.
The goal of learning in the self-organizing map is to cause different parts of the network to respond similarly to certain input patterns. This is partly motivated by how visual, auditory or other sensory information is handled in separate parts of the cerebral cortex in the human brain.
The training algorithm utilizes competitive learning. Detailed approach is as follows.
Randomize the map’s nodes’ weight vectors Wv s.
Grab an input vector X.
Traverse each node in the map.
(i) Use Euclidean distance formula to find similarity between the input vector and the map’s node’s weight vector.
(ii) Track the node that produces the smallest distance (this node is the best matching unit, BMU).
Update the nodes in the neighborhood of BMU by pulling them closer to the input vector as
Here
is a monotonically decreasing learning coefficient. The neighborhood function
, usually takes Gaussian function form, depends on the lattice distance between the BMU and neuron
v, and shrinks with time.
Increase t and repeat from Step 2 while
, where λ is the limit on time iteration.
3.2. SCDCS-LS Algorithm for RWNN
The main drawback of the conventional SOM is that one must predefine the map structure and the map size before commencement of the training process. This disadvantage is more obvious when the output neurons of one SOM are used as the hidden neurons of RWNN for clustering input data. Many trial tests may be required to find an appropriate number of hidden neurons, and re-clustering must be done when new neurons are added to the hidden layer. The proposed self-creating disk-cell-splitting algorithm is based on the competitive learning of SOM, but the map is organized on a disk instead of a rectangular, and the mapping scale is self-creating by the input data and learning goals. Moreover, the algorithm can effectively use the trained centers when new neurons are born, which makes the clustering process more efficiently.
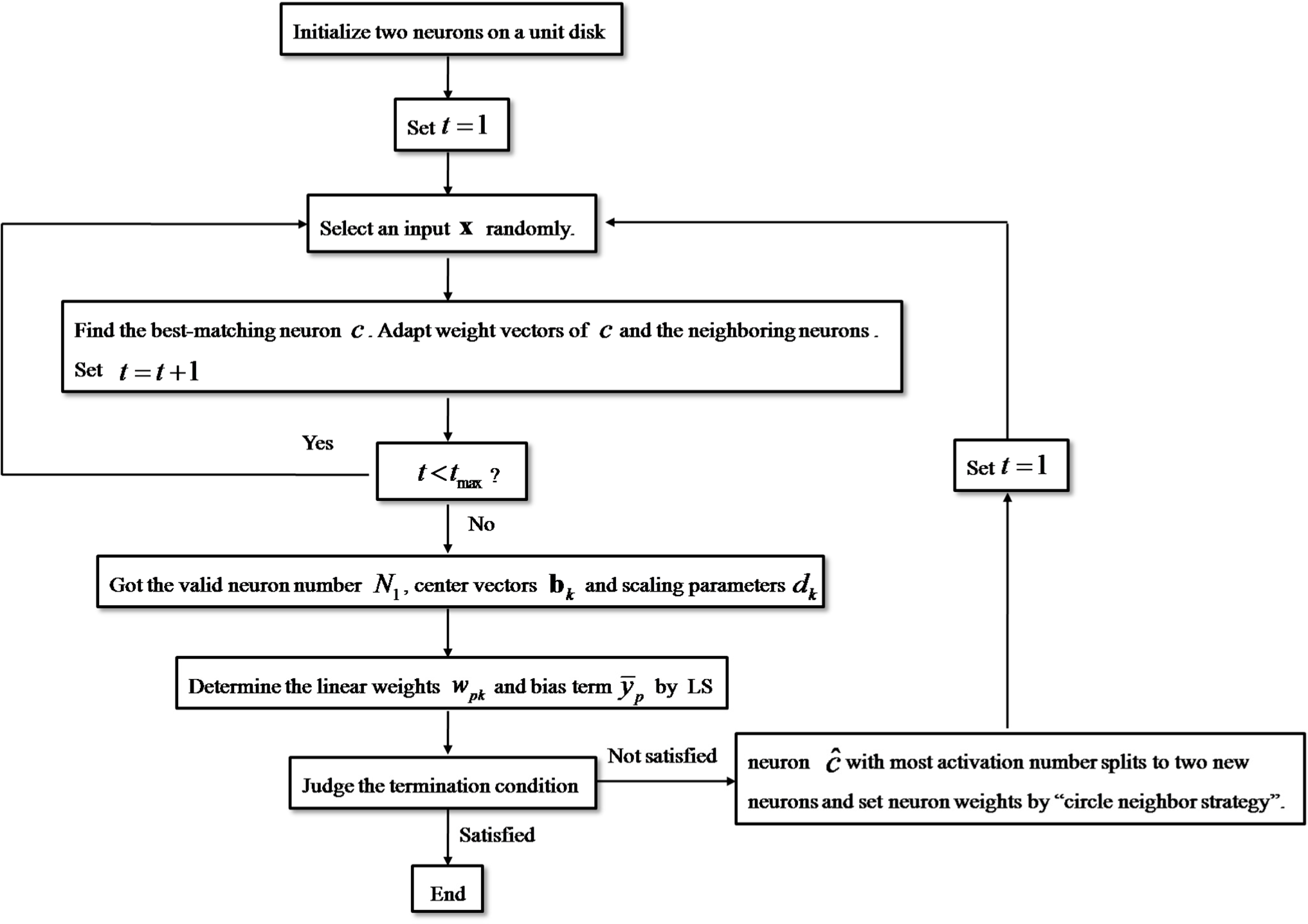
Figure 4 shows the flowchart of SCDCS-LS algorithm for RWNN. The executing steps can be divided into five modules expressed as follows.
♦ The second module: Competitive learning
1. Select an input x randomly from input samples and find the best-matching neuron c in neurons such that
,
. Increase the activation number of the winner neuron c by 1, i.e.,
.
2. Update weight vectors of the winner neuron
c and the neighboring neurons
bj of
c by
Equations (9) and
(10).
If the number of neurons N= 2, then the neighboring neuron is the not activated neuron, i.e., j = 1. If the number of neurons N = 2, then the neighboring neurons are the disk clockwise and counterclockwise adjacent neurons with respect to the winner neuron c, i.e., j = 2.
3. Set iterations
. If t is less than the pre-defined time value tmax, then go to Step 3.
Otherwise implement Step 6.
♦ The third module: Least square method
4. Cluster all input data by the generated neurons and their weight vectors which have been trained in the second module. Find all activated neurons
and their weights
,
.
is the number of “valid neurons”, which satisfies
. Determine the class radius rk by Euclidean distances between input data and centers (i.e., weights) of each class.
5. The center vectors
bk and scaling parameters
dk of hidden wavelet neurons in RWNN can be determined as follows:
σ is the window radius of wavelet function
,
is a relaxation parameter which satisfies
.
6. By means of the determined N1 wavelet neurons with their center vectors
and scaling parameters
, according to the input and output patterns
,
,
, the weights
and bias term
(
) between the hidden and output layer are straightforwardly solved by the linear optimization strategy—LS method. Here
is the number of training patterns,
is the number of output neurons.
♦ The fourth module: Judge the termination condition
♦ The fifth module: Disk cell splitting
8. The neuron
which has most activation number (
i.e., (13)) in competitive module splits to two new neurons,
As examples, a two-stage process of two neurons splitting to three neurons and then to four neurons are shown in
Figure 5a–c. The corresponding vector
A and
sita recording the number of splitting times that each neuron went through and the argument of each neuron label point are as follows:
9. Initialize the new weights of the new generated neurons through circle neighbor strategy (explained in the following “Remarks”) and maintain the weights of nonsplitting neurons. Set the activation number
for the ith neuron, where
, and the iterations
.
10. Perform Steps 3–9 to all
neurons with weights illustrated in Step 11.
Remarks:
A. In the competitive module,
and
(
) denote the leaning rate of the winner neuron and the neighboring neurons respectively. Fixed values or varied values monotonically decreasing with iterations are all acceptable. In the experiment of this paper, we choose the fixed values as
,
.
B. In order to create an ordered topology on the unit disk, the “circle neighbor strategy” is employed to initialize the weights of new neurons. Because the neuron label points are distributed on the unit circle, the circumferential distance between two points is only decided by the angle between corresponding two circle radiuses. For ensuring the close neurons with similar weights, the strategy can be executed as follows.
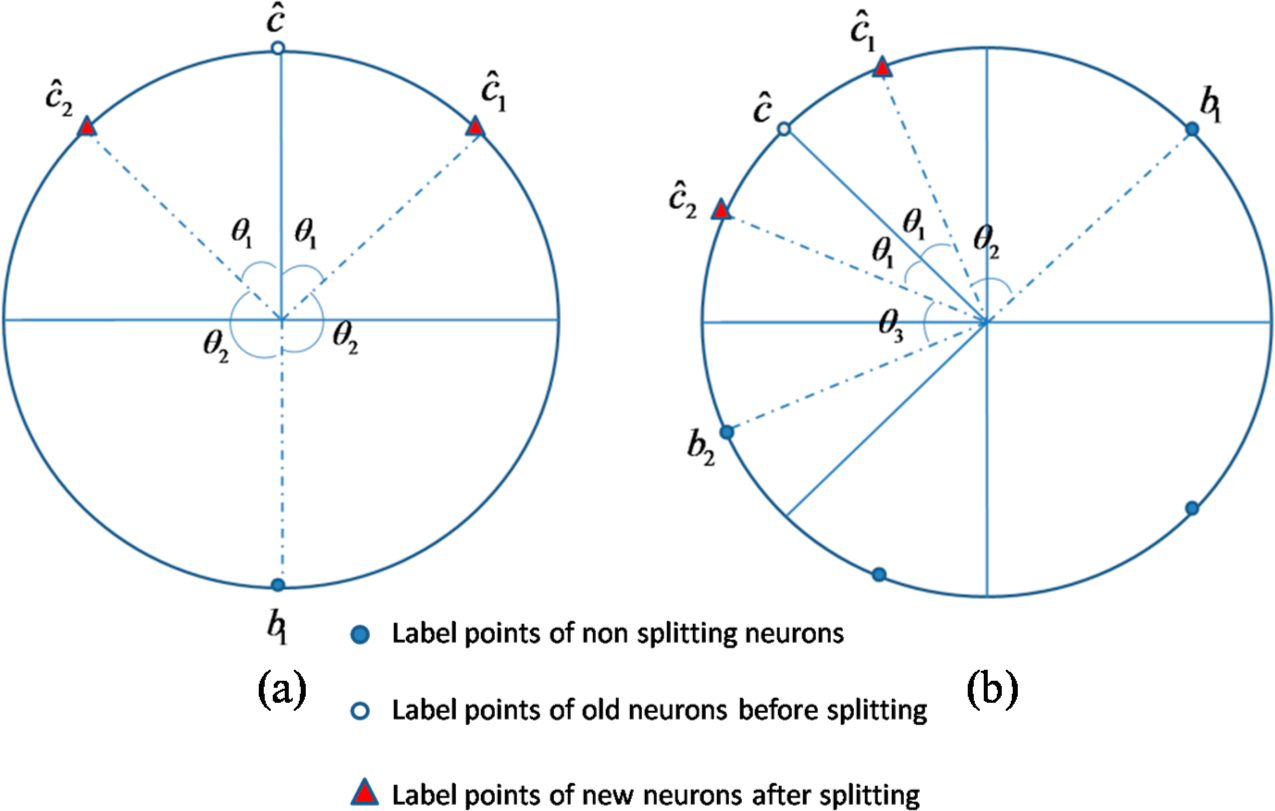
➢ Case 1: the neuron number is 2, i.e., 2 neurons splits to 3 neurons.
As illustrated in
Figure 6a, neuron
splits to two neurons
and
, and the nonsplitting neuron denotes as
. The angle between radiuses of
and
(same as that between
and
) is denoted by
; The angle between radiuses of
and
(same as that between
and
) is denoted by
. The initial weights of new neurons can be endowed as follows:
where
R is an random vector satisfying
.
As illustrated in
Figure 6b, the angle between radiuses of old neuron
and new neuron
(same as that between
and
) is denoted by
; The angle between radiuses of neighboring neuron
and neuron
is denoted by
; The angle between radiuses of neighboring neuron
and neuron
is denoted by
. The initial weights of new neurons can be endowed as follows:
The weight initialization with “circle neighbor strategy” ensures an ordered topology for newly created neurons and old neurons. Besides, all weights of new and nonsplitting neurons could be used in the next competitive learning algorithm which effectively avoids the retraining process.
4. License Plate Character Recognition and Results
In this section, we use the SCDCS-LS based RWNN for license plate character recognition. All character samples are extracted from pictures of Chinese license plates in our experiments. Chinese license plate is composed of seven characters in which the first one is a Chinese character, the second one is an English letter and the remaining ones are numbers or English letters. Two experiments are carried out here. The first one is recognition of English letters on the second position of plate which are the city code of vehicle license. The second one is recognition numbers or English letters on the three to seven positions of plate.
In order to avoid confusion, letters “I” and “O” are not employed in Chinese license plates. And because of the samples of letter “T” are few in number in our sample library, which cannot meet the training and testing requirement, the category of English letters are 23 letters except “I”, “O” and “T” in our experiments.
The character library in our experiments containing character samples extracted from plates which are located from images by algorithms proposed in [
1], slant corrected and segmented by algorithms proposed in [
5]. Due to the environment factors (for example the weather conditions and light effects
etc.) in the process of image acquisition and angle error in slant correction algorithm, some character images which are somewhat distorted are also contained in the library. Several sample examples are shown in
Figure 7.
4.1. Example 1: Recognition of English Letters
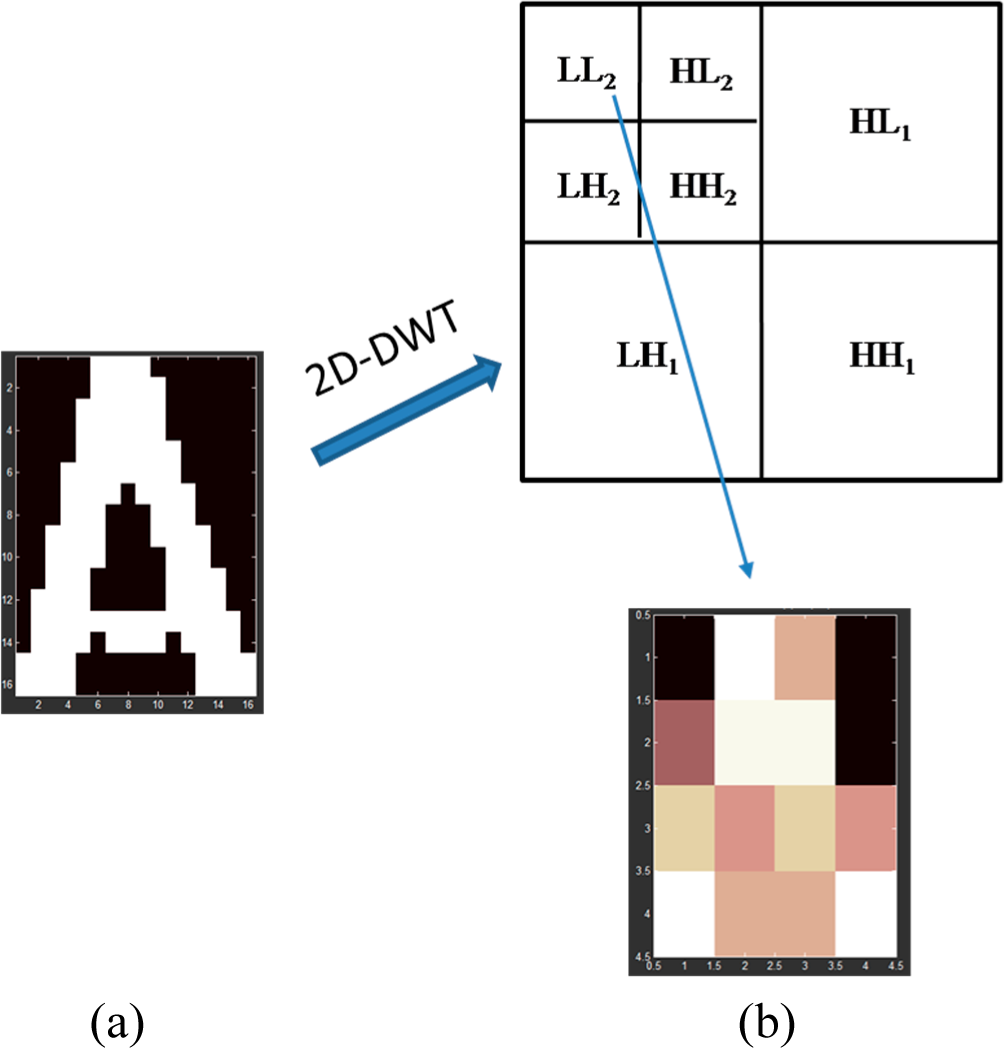
All samples resized as 16×16 pixels are randomly selected from our character library. 40 samples are chosen for training and 20 samples for testing for each type of character (except letters “M”, “N”, “P”, “U”, “V” and “Z” whose testing setshave 19, 16, 13, 12, 11 and 14 samples respectively). The approximation components of 2-level wavelet decomposition (see [
25]) are used as features for each character sample (
Figure 8), which compose the input vectors of RWNN in our experiment. That is to say, the number of input neurons is 16 in RWNN. The output vectors consist of 23 elements as the
ith element being 1 and others being 0 when the samples belonging to the
ith letter category.
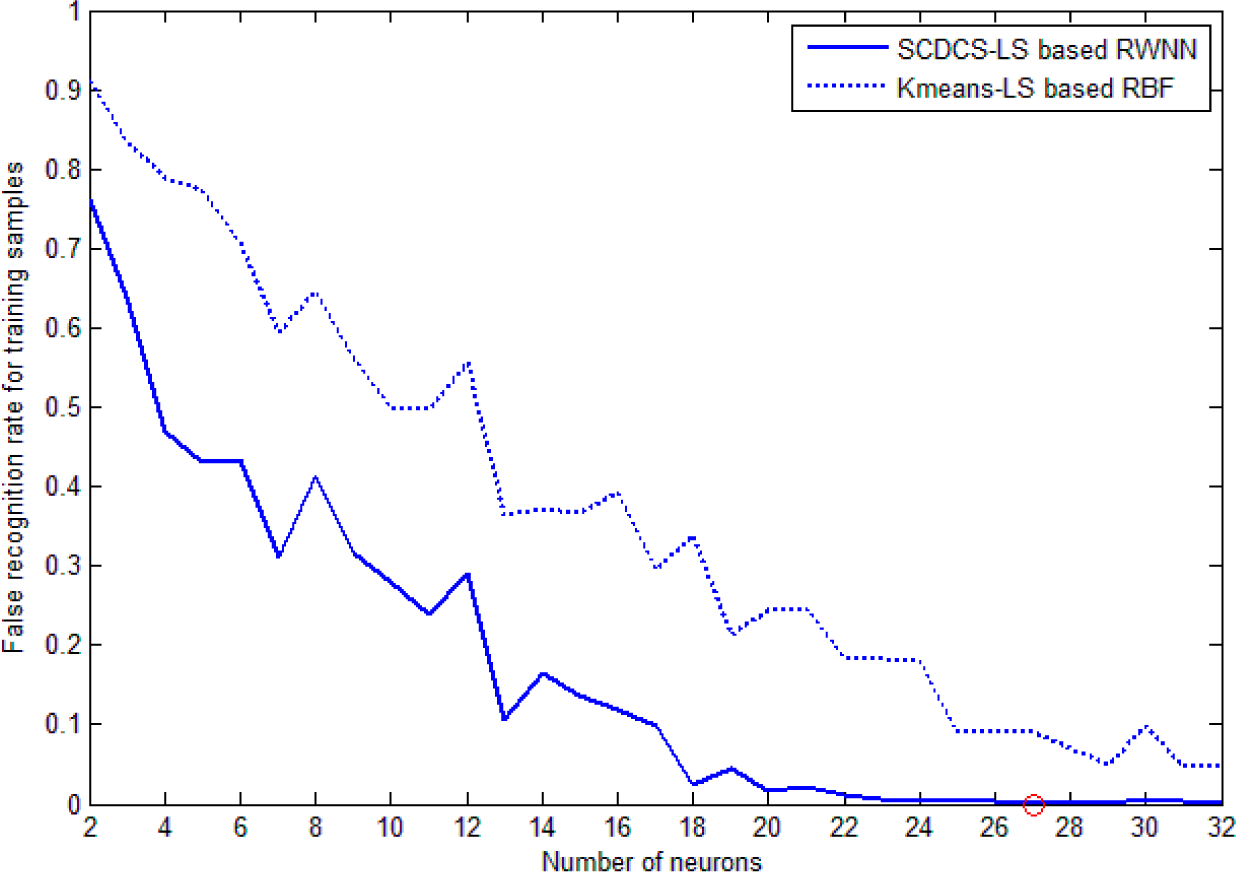
The training patterns’ false recognition rates during learning which correspond to the increasing number of neurons created by the SCDCS-LS algorithm are illustrated by the solid line in
Figure 9. In order to testify the effectiveness of the proposed model, the classical RBF network with K-means clustering and LS is used as the classifier to same training patterns. The curve of false recognition rate for K-means-LS based RBF is also drawn as dotted line in
Figure 9 for comparison. From
Figure 9, it can be seen that the SCDCS-LS based RWNN model has the better performance than the K-means-LS based RBF model. When the number of neurons in the splitting process increases to
N = 27 with the corresponding valid neurons number
N1 = 26, the total success recognition rate for training set and testing set of SCDCS-LS based RWNN reaches 99.89% and 99.76% respectively, and after that the false recognition rate will no longer be significantly decrease with newly added neurons. But when the neuron number of K-means-LS based RBF increases to
N = 32 as shown in
Figure 9, the total success recognition rate for training set and testing set are 95.34% and 96.71% respectively. The detailed recognition results for testing samples by two models are in
Table 1 and
Table 2, which adopt 26 and 32 hidden neurons respectively.
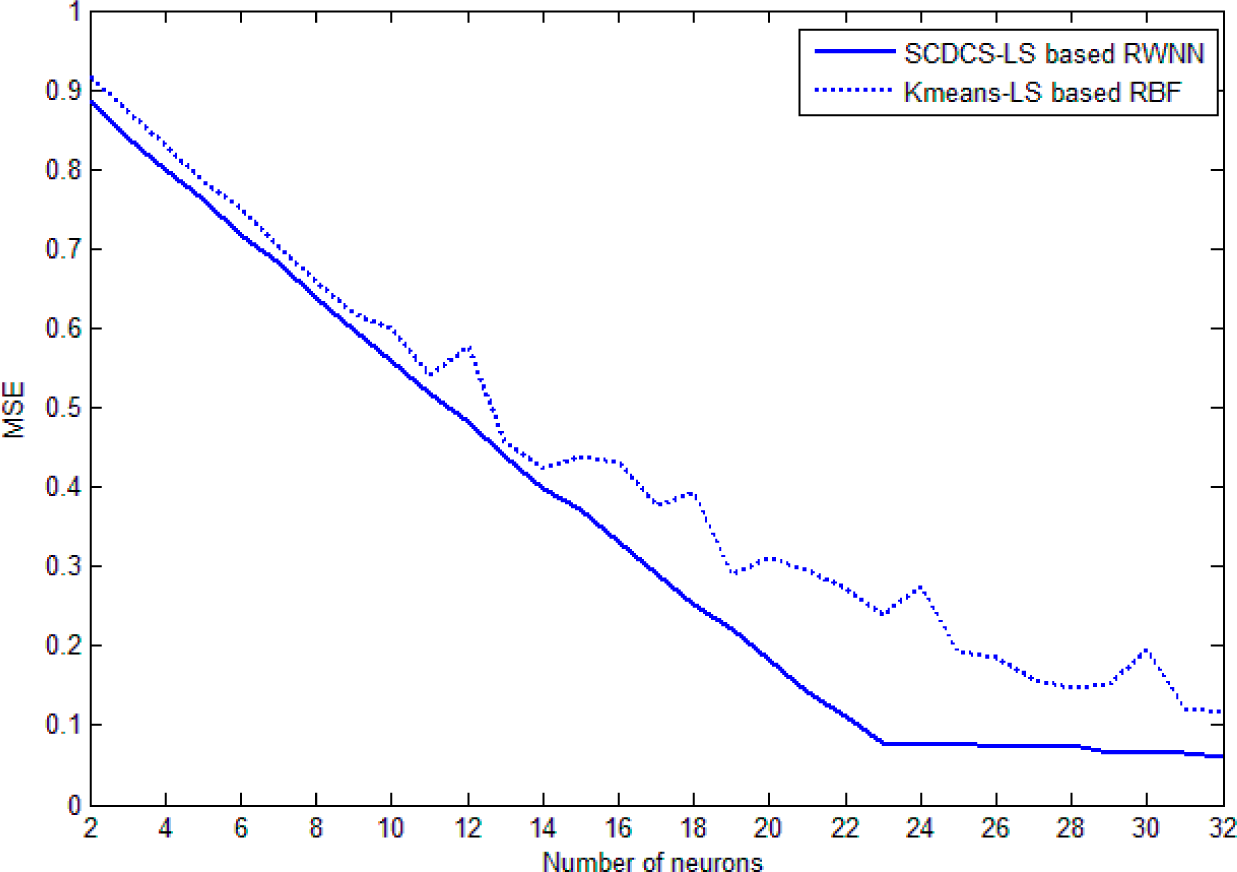
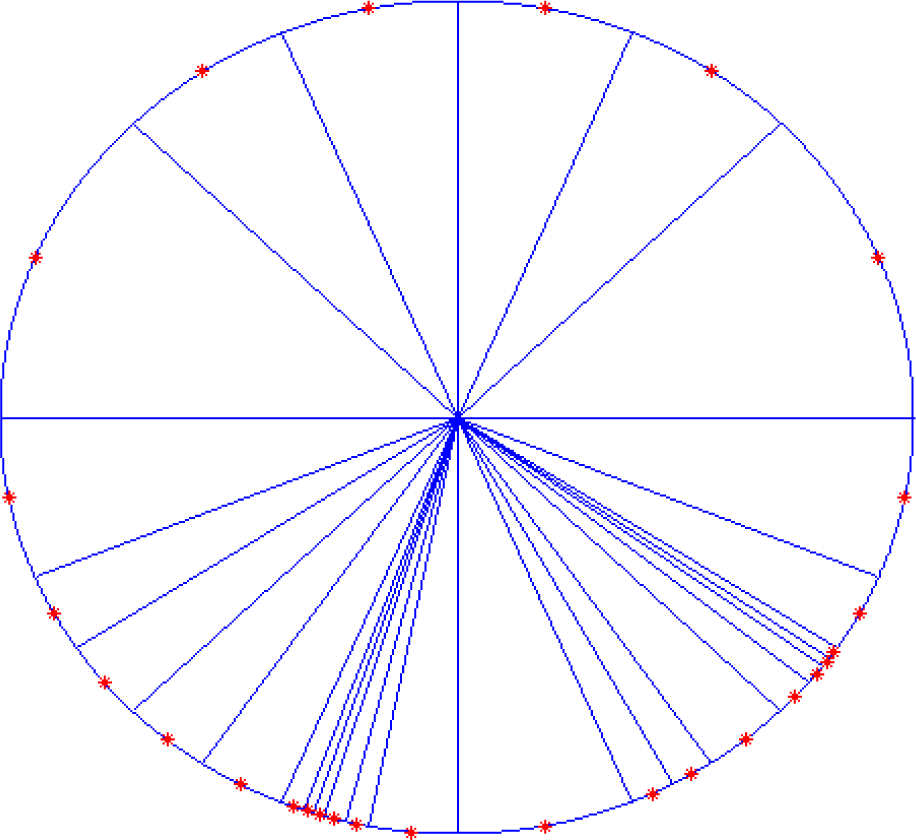
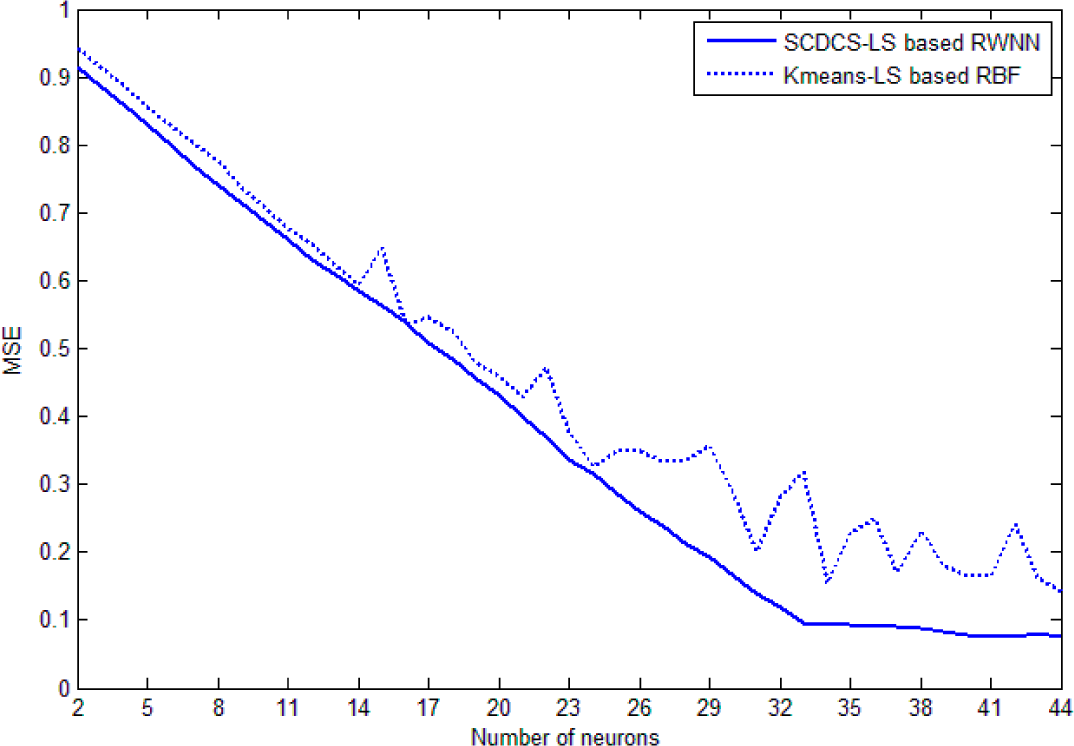
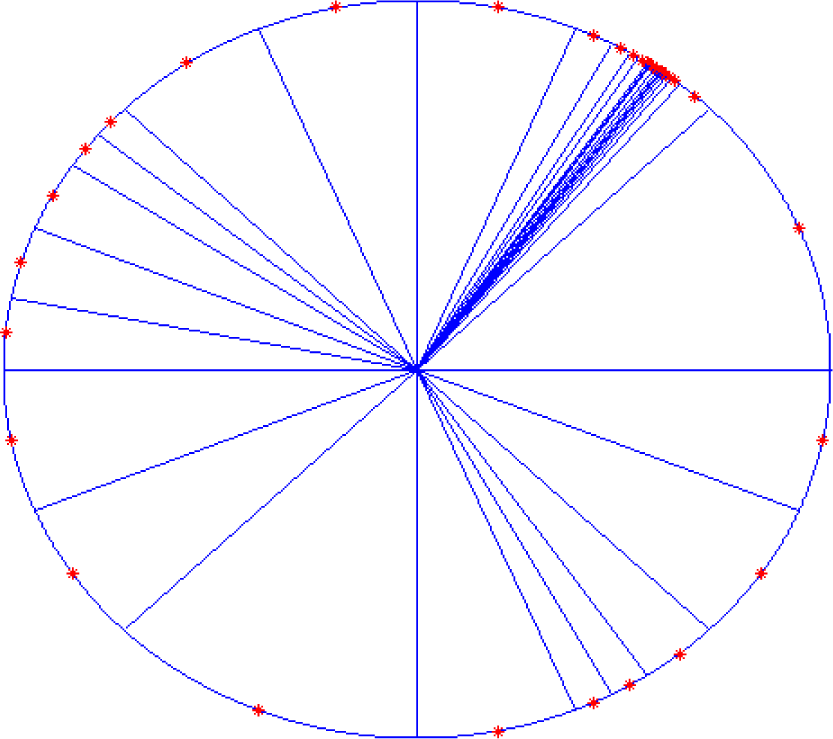
Figure 10 shows the comparative curves of mean square error (MSE) that varying with the increasing number of neurons for SCDCS-LS based RWNN and K-means-LS based RBF. The disk distribution map of 27 neurons got by SCDCS-LS algorithm is drawn in
Figure 11.
Table 3 illustrates the vector
A and
sita of these neurons which record the number of splitting times that each neuron went through and the argument of each neuron label point. The comparison results of different models are concluded in
Table 4. It can be seen that the SVM algorithm can make the highest recognition rate for training samples, but a lower recognition rate for testing samples. The proposed SCDCS-LS based RWNN can get higher recognition rates both for training and testing samples although fewer hidden neurons are employed.
4.2. Example 2: Recognition of Numbers or English Letters
Samples of numbers or English letters are chosen randomly from our character library like experiment 1. Equal numbers of samples in training set and testing set of each character category are employed as experiment 1 too. 16 input features for each sample consists of the approximation components of 2-level wavelet decomposition. 33 output neurons are needed for RWNN here for the 33 character categories corresponding to 23 English letters and 10 numbers.
In the experiment of recognition of numbers or English letters samples by SCDCS-LS based RWNN, when the number of neurons in the splitting process increases to
with the corresponding valid neurons number
, the total success recognition rate for training set reaches 99.54% and will no longer increase significantly during the splitting process as shown in
Figure 12 (the false recognition rate curve is drawn corresponding to neurons splitting from 2 to 44). Adopt the RWNN with
hidden neurons and parameters got by SCDCS-LS, the total success recognition rate for testing set reaches 99.20%. The detailed results are shown in
Table 5. For comparison, the curve of false recognition rate for K-means-LS based RBF is also drawn as dotted line in
Figure 12. When the neuron number of K-means-LS based RBF increases to
, the total success recognition rate for training set and testing set are 96.24% and 95.84% respectively with detailed recognition results for testing set in
Table 6. It can be seen that, the proposed SCDCS-LS based RWNN shows better performance than the K-means-LS based RBF in recognition of numbers or English letters even though fewer hidden neurons are employed.
Figure 13 shows the comparative curves of mean square error (MSE) that varying with the increasing number of neurons for SCDCS-LS based RWNN and K-means-LS based RBF for training samples of numbers or English letters. The disk distribution map of 34 neurons got by SCDCS-LS algorithm is drawn in
Figure 14.
Table 7 illustrates the vector
and
of these neurons which record the number of splitting times that each neuron went through and the argument of each neuron label point.
Table 8 gives the comparison results of recognition rates using different classifiers. It can be seen that the results are similar to that of example 1. Besides the slightly higher recognition rate for training samples by SVM, the proposed SCDCS-LS based RWNN can get both high recognition rates for training and testing samples.