Abstract
In applied investigations, the invariance of the Lyapunov dimension under a diffeomorphism is often used. However, in the case of irregular linearization, this fact was not strictly considered in the classical works. In the present work, the invariance of the Lyapunov dimension under diffeomorphism is demonstrated in the general case. This fact is used to obtain the analytic exact upper bound of the Lyapunov dimension of an attractor of the Shimizu–Morioka system.
1. Introduction
Two well-known definitions of Lyapunov exponents are the upper bounds of the exponential growth rate of the norms of linearized system solutions (LCEs) [] and the upper bounds of the exponential growth rate of the singular values of the fundamental matrix of a linearized system (LEs) []. These definitions usually give the same values (e.g., for a “typical” regular system that satisfies the conditions of the Oseledets theorem). For a particular system, the LCEs and LEs may be different. Lyapunov [] considered linearizations with bounded coefficients and introduced the class of regular linearizations: for regular linearization, the sum of LCEs equals the lower bound of the exponential growth rate of the normal fundamental matrix determinant (otherwise, the linearization is called irregular). Any regular linearization has exact LCEs (i.e., upper and lower bounds in the definition coincide), which are equal to LEs. In general, it can be shown that the ordered LEs are majorized by the ordered LCEs. More detailed discussions and examples can be found in [–]. Various characteristics of chaotic behavior are based on Lyapunov exponents. The sum of positive Lyapunov exponents is used [,] as the characteristic of the Kolmogorov–Sinai entropy rate [,]. Another measure of chaotic behavior is the Kaplan–Yorke or Lyapunov dimension, which is defined via the singular values or LEs [–].
It is well known that a homeomorphism can change dimensions based on the space metric []. Thus, the question arises whether the Lyapunov dimension is invariant under changes (see, e.g., [], “Is the Dimension of Chaotic Attractors Invariant under Coordinate Changes?”; and [–]). Since the singular values and LEs are defined via the linearization of a system, the smooth changes of variables are of interest.
In the applied investigations, the invariance of the Lyapunov dimension under diffeomorphism is often used. However, in the case of irregular linearization, this fact is not strictly considered (see, e.g., the surveys [,]). In the present work, it is demonstrated in the general case that while singular values may not be invariant under changes of coordinates, the Lyapunov dimension of an attractor is invariant under diffeomorphism. This fact is used to obtain the exact formula of the Lyapunov dimension of an attractor of the Shimizu–Morioka system.
2. Lyapunov Dimension
Consider a continuously-differentiable mapping F defined on an open set U ⊂ ℝn. Denote by TxF the Jacobian matrix of the mapping F at the point x. The continuous differentiability of F implies that:
By assumption, K ⊂ U is a bounded invariant set: F K = K.
Denote by αj(A) the singular numbers of (n×n)-matrix A, such that α1(A) ≥ α2(A) ≥ … ≥ αn(A). Consider the relation:
where d = j + s, s ∈ [0, 1], j ∈ ℕ, j ∈ [1, n].
We also write a well-known Horn inequality:
Definition 1. We say that a local Lyapunov dimension of the mapping F at the point x ∈ K is a number:
where j is the largest integer number from [0, n], such that:
and a number value s ∈ [0, 1) is as follows:
By definition, dimL(F, x) = 0 if α1(TxF) < 1, and dim L(F, x) = n if α1(TxF)α2(TxF) … αn(TxF) ≥ 1.
Definition 2. [,] The Lyapunov dimension of the mapping F on the set K is a number:
Definition 3. A local Lyapunov dimension of a one-parameter group of mappings Ft at the point x ∈ K is a number:
Definition 4. The Lyapunov dimension of mappings Ft on the set K is a number:
Consider a differential equation:
with a continuously-differentiable vector-function f(x). Suppose that for any initial value x0, there exists a solution of Equations (3)x(t, x0), defined on t ∈ [0, +∞). Here, x(0, x0) = x0.
Denote by Ft(x0) = x(t, x0) a shift operator along the solutions of Equations (3) and suppose that the set K ⊂ ℝn is bounded and invariant: FtK = K, ∀t ∈ ℝ1. TxFt is the Jacobian matrix of the mapping Ft at the point x.
Consider a differential equation:
with a continuously-differentiable vector function g(y). Suppose that for any initial value y0, there exists a solution of Equations (4)y(t, y0), defined on t ∈ [0, +∞). Here, y(0, y0) = y0.
Denote by
a shift operator along the solutions of Equations (4) and suppose that the set
is bounded and invariant:
, ∀t ∈ ℝ1.
is the Jacobian matrix of the mapping
at the point y.
Suppose that Q is a diffeomorphism between the set K and the set
, i.e., x ∈ K,
.
Hence, for a certain point y, there exists an inverse mapping Q−1 : y ↦ x that is continuously differentiable in the neighborhood of y.
Under the above assumptions, we state the following assertions.
Lemma 1. If for, then for the Lyapunov dimension of mapping Ft of the set K, the following estimate:
is satisfied. Here, j + s = d < d0,
, 0 < s ≤ 1, j is the largest integer: j ∈ [1; n]; µi = LEi(x), LEi(x) are Lyapunov exponents (LEs),
, µj+1 < 0.
Proof. Consider an arbitrary number
.
Recall that:
Here,
.
Using the well-known relation
, we obtain:
It follows that the inequality:
is satisfied for:
Thus, the assertion of the lemma
holds true.
From the definition of the Lyapunov dimension, we obtain that for all d < d0, Relation (5) is satisfied. □
Theorem 1. The Lyapunov dimension of the mapping Ft of the set K is invariant with respect to the diffeomorphism. Namely
Proof. For the mappings Ft and
, Relation (1) is satisfied.
Then, the continuous differentiability of
and the properties of diffeomorphism Q imply the following chain of relations:
where ỹ = y0 + hy,
, Q−1(y0) = x0,
,
The continuous differentiability of the inverse mapping Q−1 (property of diffeomorphism) implies the following relation:
Thus, for the nonsingular matrix
, Relation (10) is satisfied.
Denote
,
,
. Consider the following relations:
where
, k ∈ ℕ.
Applying Horn Inequality (2) to the last relation, we obtain the estimate:
This implies that:
In the last inequality, the following estimates
where m1, m2 ∈ ℝ +, are satisfied.
Repeating all of the above operations for the inverse transformation x = Q−1(y), we obtain relations similar to (10):
and (12):
where
,
, l1, l2 ∈ ℝ+. Suppose that M = max(m1, m2, l1, l2).
Then, Relations (12) and (13) take the form:
and:
respectively. Taking into account the assertion of the lemma, we obtain:
and:
as k → ∞.
Denote
,
.
Suppose that D1 < D2 and that d is an arbitrary number: D1 < d < D2. Consider the transformation Q. Then, from (14) and the definition of the Lyapunov dimension, it follows that D2 ≤ d, but this contradicts the initial assumption. Consequently, the inequality must be valid:
Suppose now that for inverse transformation Q−1, D2 < d < D1. Then, from (15), it follows that D1 ≤ d. This is in contrast with the above assumption. Consequently:
In addition, this implies that:
□
Thus, if Q is a diffeomorphism, then the change of coordinates of dynamical system y = Q(x) preserves the Lyapunov dimension of mapping Ft on compact sets.
3. Lyapunov Dimension of the Shimizu–Morioka System
Consider the Shimizu–Morioka system [] of the form:
where α, λ are the positive parameters.
Using the diffeomorphism:
System (18) can be reduced to the following system:
where α, λ are the positive parameters of System (18). We say that System (20) is a transformed Shimizu–Morioka system.
The following assertion is valid [–].
Theorem 2. Suppose that for the integers j ∈ [1, n] and s ∈ [0, 1], there exist a continuously differentiable function υ(x) and a nonsingular matrix S, such that:
Then, dimL K ≤ j + s.
Here,
, υ(x) is a Lyapunov function.
Further, for System (20), the following will be proven.
Theorem 3. Suppose that K is a bounded invariant set of System (20): (0, 0, 0) ∈ K and that the following relations:
are satisfied. Then:
Proof. Consider a nonsingular matrix:
where
.
The characteristic polynomial of the matrix:
takes the form:
Here, * denotes a transposition sign. This implies that the eigenvalues of Matrix (24) are the numbers:
where
. Obviously, λ1 ≥ λ2 ≥ λ3.
We choose the Lyapunov function to be of the form:
where:
Here, µ1, µ2, µ3, µ4 are running parameters, s ∈ [0, 1).
Inequality (21) takes the form:
where
.
Using the inequality:
we obtain the estimate:
We have:
where:
Condition:
is satisfied for all x, y, z, if and only if the following inequalities hold true:
We represent the second inequality from (27) in the form:
where
.
Inequality (29) is solvable with respect to µ2 if B1B3 ≥ 0. This implies that (27) is equivalent to the system of inequalities:
Inequality (32) is solvable with respect to µ4 if the discriminant of its left-hand side is nonnegative. This implies that:
Since C1 ≤ 0, for the last inequality to be valid, it is sufficient that:
is satisfied. The latter is equivalent to:
For the sake of convenience, we assume
,
. Then, from the first inequality in (28) and Inequalities (31) and (33), we obtain a system of linear inequalities with respect to
and
:
This implies two cases:
Then:
Then:
This means that (26) is valid if (38) and the inequality:
are satisfied. Thus, this implies that Inequality (26) is satisfied if and only if System (34)–(37) is solvable with respect to
and
, where
,
,
.
Thus, under Condition (22), we obtain the matrix S, the function υ(x, y, z) and a number s, satisfying (39), such that (25) is valid.
At the same time, considering the linearization of System (20) in a neighborhood of the points (0, 0, 0), we obtain:
For α = 0.375, λ = 0.81, classical Shimizu–Morioka System (18) possesses a strange self-excited local attractor of the Lorenz type (Figure 1a); for α = 0.191450, λ = 0.81, it changes to the self-excited local attractor of the Burke and Shaw type (Figure 2a). Transformed System (20) demonstrates similar types of local attractors under the same values of parameters α and λ (Figure 1b and Figure 2b). Here, numerical estimations of the Lyapunov dimension by the code from [] (2.0749, Figure 1b; 2.0059, Figure 2b) are consistent with the analytic exact upper bound for the Lyapunov dimension given by (40) (the corresponding values are 2.2014 and 2.3251, respectively).
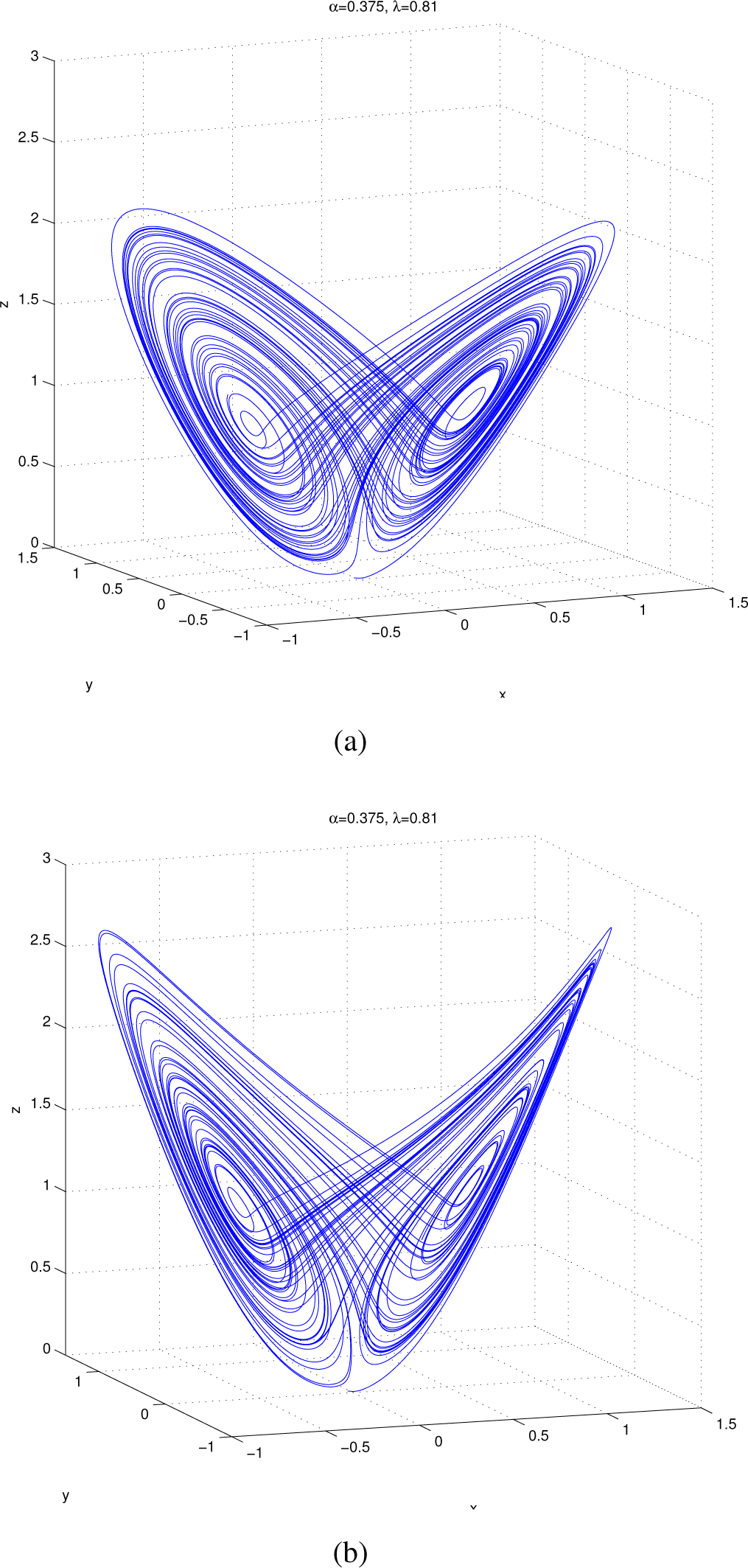
Figure 1.
Self-excited local attractors in: (a) System (18) for α = 0.375, λ = 0.81; (b) System (20) for α = 0.375, λ = 0.81.
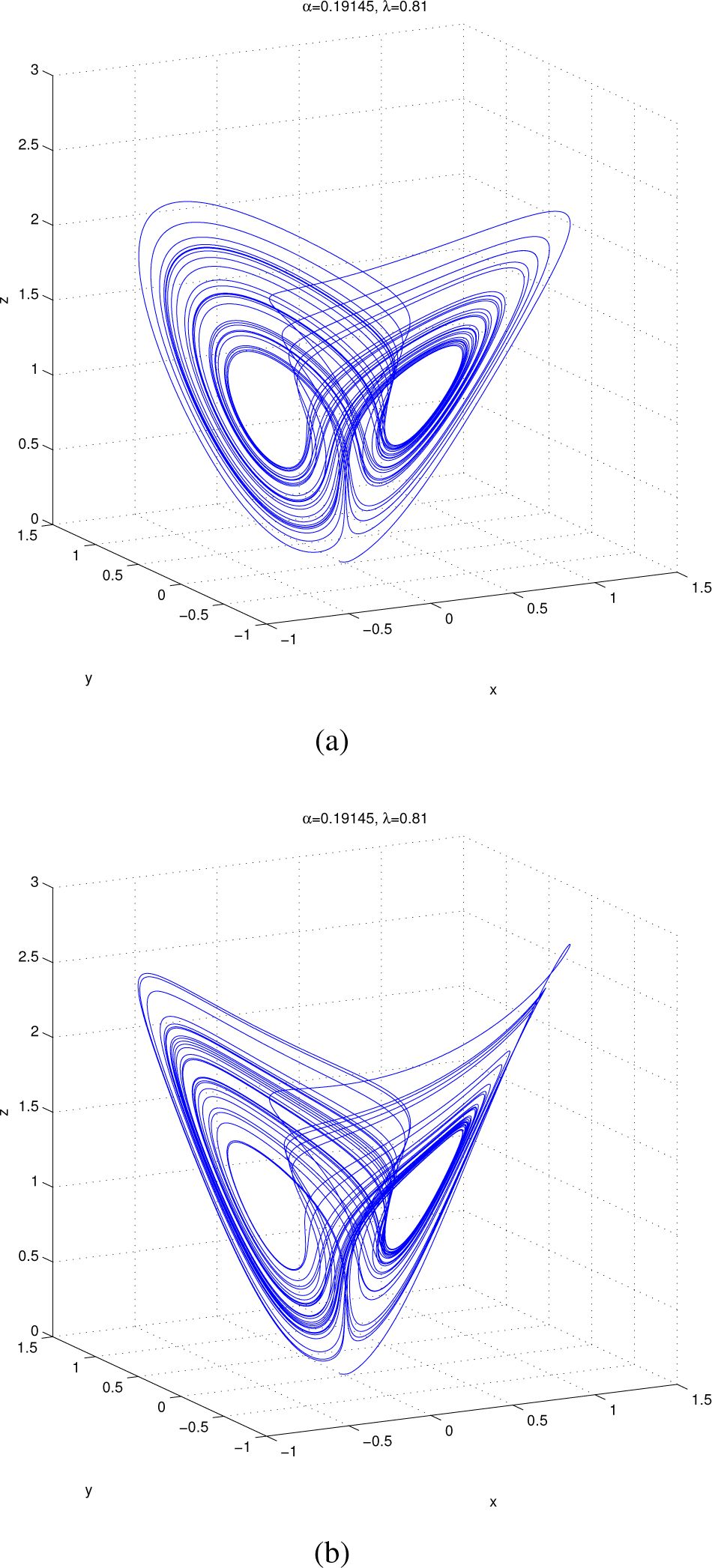
Figure 2.
Self-excited local attractors in: (a) System (18) for α = 0.191450, λ = 0.81, “Burke and Shaw-like”; (b) System (20) for α = 0.191450, λ = 0.81, “Burke and Shaw-like”.
Thus, using the diffeomorphism (19), which saves the Lyapunov dimension of an invariant bounded set K, it is possible to state that for classical Shimizu–Morioka System (18), the set K has the same Lyapunov dimension as System (20).
Remark 1. An oscillation can generally be easily numerically localized if the initial data from its open neighborhood in the phase space lead to a long-term behavior that approaches the oscillation. Therefore, from a computational perspective, it is natural to suggest the following classification of attractors [–], which is based on the simplicity of finding their basins of attraction in the phase space: an attractor is called a self-excited attractor if its basin of attraction intersects with any open neighborhood of an equilibrium; otherwise, it is called a hidden attractor. For a self-excited attractor, its basin of attraction is connected to an unstable equilibrium, and therefore (standard computational procedure), self-excited attractors can be localized numerically by the standard computational procedure: by constructing a solution using initial data from an unstable manifold in a neighborhood of an unstable equilibrium, observing how it is attracted and visualizing the oscillation. In contrast, the basin of attraction for a hidden attractor is not connected to any equilibrium. For example, hidden attractors are attractors in systems with no equilibria or with only one stable equilibrium (a special case of the multi-stability: the coexistence of attractors in multi-stable systems). Well-known examples of the hidden oscillations are nested limit cycles in the 16th Hilbert problem (see, e.g., [,]) and counterexamples to the Aizerman and Kalman conjectures on the absolute stability of nonlinear control systems [,–].
4. Conclusion
In the present work, the invariance of the Lyapunov dimension under diffeomorphism is strictly proven. For the attractor of the Shimizu–Morioka system, a smooth change of coordinates is suggested and a Lyapunov function constructed, which allow one to obtain the analytic exact upper bound for the Lyapunov dimension. Similar results for some other Lorenz-like systems can be found, e.g., in [,,].
Acknowledgments
This work was supported by the Russian Scientific Foundation (14-21-00041, Sections 1–2) and the Saint-Petersburg State University (6.38.505.2014, Section 3).
Author Contributions
Gennady Leonov, Tatyana Alexeeva and Nikolay Kuznetsov did the analytical estimates. Tatyana Alexeeva and Nikolay Kuznetsov made numerical experiments and wrote the paper. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of the data; in the writing of the manuscript; nor in the decision to publish the results
References
- Lyapunov, A.M. The General Problem of the Stability of Motion; CRC Press: Boca Raton, FL, USA, 1992. [Google Scholar]
- Oseledec, V.I. Multiplicative Ergodic Theorem: Characteristic Lyapunov Exponents of Dynamical Systems. Trans. Moscow Math. Soc. 1968, 19, 179–210. [Google Scholar]
- Leonov, G.A.; Kuznetsov, N.V. Time-Varying Linearization and the Perron Effects. Int. J. Bifurcat. Chaos. 2007, 17, 1079–1107. [Google Scholar]
- Kuznetsov, N.V.; Mokaev, T.N.; Vasilyev, P.A. Numerical Justification of Leonov Conjecture on Lyapunov Dimension of Rossler Attractor. Commun. Nonlinear Sci. Numer. Simulat. 2014, 19, 1027–1034. [Google Scholar]
- Kuznetsov, N.V.; Alexeeva, T.; Leonov, G.A. Invariance of Lyapunov Characteristic Exponents, Lyapunov Exponents, and Lyapunov Dimension for Regular and Non-regular Linearizations 2014. arXiv:1410.2016v2.
- Millionschikov, V.M. A Formula for the Entropy of Smooth Dynamical Systems. Differencial’nye Uravenija 1976, 12, 2188–2192. [Google Scholar]
- Pesin, Y. Characteristic Lyapunov Exponents and Smooth Ergodic Theory. Russ. Math. Surv. 1977, 32, 55–114. [Google Scholar]
- Kolmogorov, A. On Entropy per Unit Time as a Metric Invariant of Automorphisms. Dokl. Akad. Nauk SSSR 1959, 124, 754–755. [Google Scholar]
- Sinai, Y. On the Notion of Entropy of Dynamical Systems. Dokl. Akad. Nauk SSSR 1959, 124, 768–771. [Google Scholar]
- Kaplan, J.L.; Yorke, J.A. Chaotic Behavior of Multidimensional Difference Equations. In Functional Differential Equations and Approximations of Fixed Points; Springer: Berlin, Germany, 1979; pp. 204–227. [Google Scholar]
- Douady, A.; Oesterle, J. Dimension de Hausdorff des Attracteurs. CR Acad. Sci. Paris 1980, 290, 1135–1138. [Google Scholar]
- Ledrappier, F. Some Relations between Dimension and Lyapounov Exponents. Commun. Math. Phys. 1981, 81, 229–238. [Google Scholar]
- Pontrjagin, L.; Schnirelmann, L. Sur une Propriété Métrique de la Dimension. Ann. Math. 1932, 156–162. [Google Scholar]
- Ott, E.; Withers, W.; Yorke, J. Is the Dimension of Chaotic Attractors Invariant under Coordinate Changes? J. Stat. Phys. 1984, 36, 687–697. [Google Scholar]
- Dettmann, C.; Frankel, N.; Cornish, N. Chaos and Fractals around Black Holes. Fractals 1995, 3, 161–181. [Google Scholar]
- Hoover, W.; Hoover, C. Why Instantaneous Values of the “Covarian” Lyapunov Exponents Depend upon the Chosen State-Space Scale. Fractals 2014, 20, 5–8. [Google Scholar]
- Sprott, J.; Hoover, W.; Hoover, C. Heat Conduction, and the Lack Thereof, in Time-Reversible Dynamical Systems: Generalized Nosé-Hoover Oscillators with a Temperature Gradient. Phys. Rev. E 2014, 89, 042914. [Google Scholar]
- Gelfert, K.; Motter, A. (Non)Invariance of Dynamical Quantities for Orbit Equivalent Flows. Commun. Math. Phys. 2010, 300, 411–433. [Google Scholar]
- Barreira, L.; Gelfert, K. Dimension Estimates in Smooth Dynamics: A Survey of Recent Results. Ergod. Theor. Dyn. Syst. 2011, 31, 641–671. [Google Scholar]
- Temam, R. Infinite-Dimensional Dynamical Systems in Mechanics and Physics, 2nd ed; Springer: New York, NY, USA, 1997. [Google Scholar]
- Hunt, B. Maximum Local Lyapunov Dimension Bounds the Box Dimension of Chaotic Attractors. Nonlinearity 1996, 9, 845–853. [Google Scholar]
- Shimizu, T.; Morioka, N. On the Bifurcation of a Symmetric Limit Cycle to an Asymmetric One in a Simple Model. Phys. Lett. A 1980, 76, 201–204. [Google Scholar]
- Leonov, G.A. On Estimations of the Hausdorff Dimension of Attractors. Vestnik Leningradskogo Gos. Univ. Ser. 1991, 1, 41–44. [Google Scholar]
- Leonov, G.A.; Boichenko, V.A. Lyapunov’s Direct Method in the Estimation of the Hausdorff Dimension of Attractors. Acta Appl. Math. 1992, 26, 1–60. [Google Scholar]
- Boichenko, V.A.; Leonov, G.A.; Reitmann, V. Dimension Theory for Ordinary Differential Equations; Vieweg Teubner Verlag: Wiesbaden, Germany, 2005. [Google Scholar]
- Leonov, G.A. Strange Attractors and Classical Stability Theory. Nonlinear Dyn. Syst. Theor. 2008, 8, 49–96. [Google Scholar]
- Leonov, G.A. Lyapunov Functions in the Attractors Dimension Theory. J. Appl. Math. Mech. 2012, 76, 129–141. [Google Scholar]
- Leonov, G.; Kuznetsov, N.; Mokaev, T. Homoclinic Orbits, and Self-excited and Hidden Attractors in a Lorenz-Like System Describing Convective Fluid Motion. Eur. Phys. J. Special Topics. 2015, 224, 1421–1458. [Google Scholar]
- Kuznetsov, N.V.; Leonov, G.A.; Vagaitsev, V.I. Analytical-Numerical Method for Attractor Localization of Generalized Chua’s System. IFAC Proc. Vol. 2010, 4, 29–33. [Google Scholar]
- Leonov, G.A.; Kuznetsov, N.V.; Vagaitsev, V.I. Localization of Hidden Chua’s Attractors. Phys. Lett. A 2011, 375, 2230–2233. [Google Scholar]
- Leonov, G.A.; Kuznetsov, N.V.; Vagaitsev, V.I. Hidden Attractor in Smooth Chua Systems. Physica D 2012, 241, 1482–1486. [Google Scholar]
- Leonov, G.A.; Kuznetsov, N.V. Hidden Attractors in Dynamical Systems. From Hidden Oscillations in Hilbert-Kolmogorov, Aizerman, and Kalman Problems to Hidden Chaotic Attractors in Chua Circuits. Int. J. Bifurcat. Chaos. 2013, 23, 1330002. [Google Scholar]
- Kuznetsov, N.V.; Kuznetsova, O.A.; Leonov, G.A. Visualization of Four Normal Size Limit Cycles in Two-Dimensional Polynomial Quadratic System. Differ. Equ. Dyn. Syst. 2013, 21, 29–34. [Google Scholar]
- Leonov, G.A.; Bragin, V.O.; Kuznetsov, N.V. Algorithm for Constructing Counterexamples to the Kalman Problem. Dokl. Math. 2010, 82, 540–542. [Google Scholar]
- Leonov, G.A.; Kuznetsov, N.V. Algorithms for Searching for Hidden Oscillations in the Aizerman and Kalman Problems. Dokl. Math. 2011, 84, 475–481. [Google Scholar]
- Bragin, V.O.; Vagaitsev, V.I.; Kuznetsov, N.V.; Leonov, G.A. Algorithms for Finding Hidden Oscillations in Nonlinear Systems. The Aizerman and Kalman Conjectures and Chua’s Circuits. J. Comput. Syst. Sci. Int. 2011, 50, 511–543. [Google Scholar]
- Leonov, G.A.; Kuznetsov, N.V. On Differences and Similarities in the Analysis of Lorenz, Chen, and Lu Systems. Appl. Math. Comput. 2015, 256, 334–343. [Google Scholar]
- Leonov, G.; Kuznetsov, N.; Korzhemanova, N.; Kusakin, D. Estimation of Lyapunov Dimension for the Chen and Lu Systems 2015. arxiv:1504.04726.
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).