The Fisher Information as a Neural Guiding Principle for Independent Component Analysis
Abstract
:1. Introduction
1.1. Combining Objective Functions
1.2. Hebbian Learning in Neural Networks
1.3. Instantaneous Single Neuron
1.4. Information Theoretical Incentives for Synaptic Plasticity
2. Objective Functions for Synaptic Plasticity
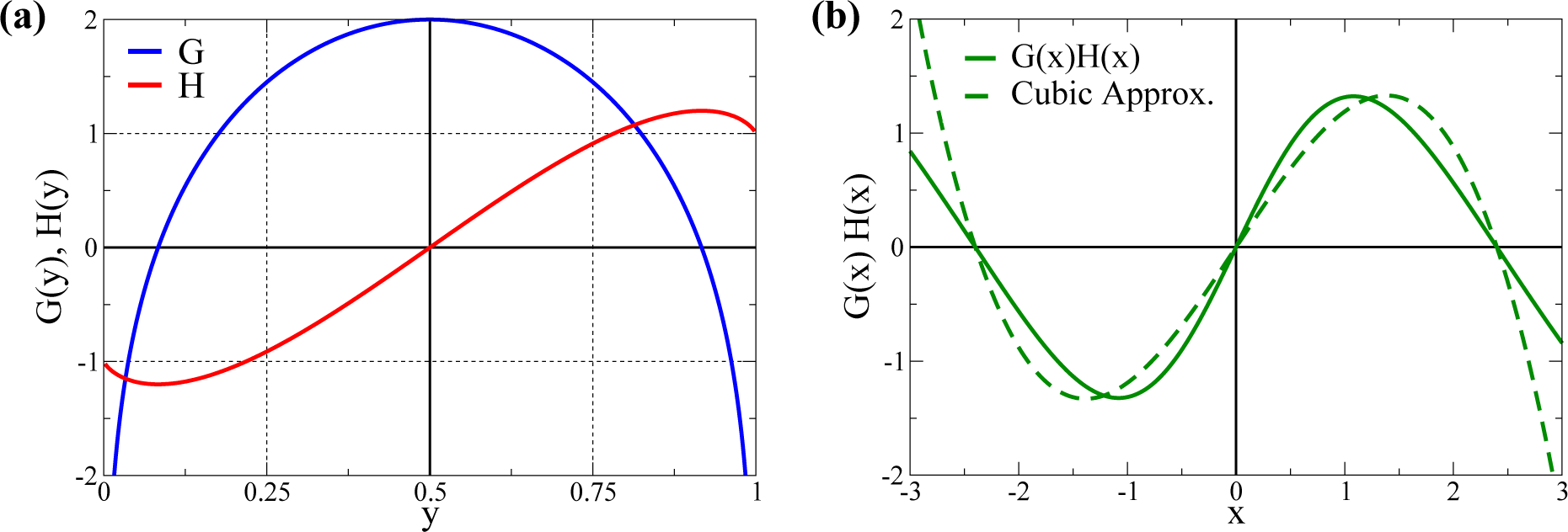
2.1. Cubic Approximation
2.1.1. Scaling of Dominant Components
2.1.2. Sensitivity to the Excess Kurtosis
- The trivial fixpoint (0; 0) is always unstable, with positive eigenvalues:
- For , one finds the eigenvalues:The first eigenvalue λ1 is hence always negative with the sign of the second eigenvalue λ2 depending exclusively on K1. The fixpoint is hence stable/unstable for negative/positive K1.
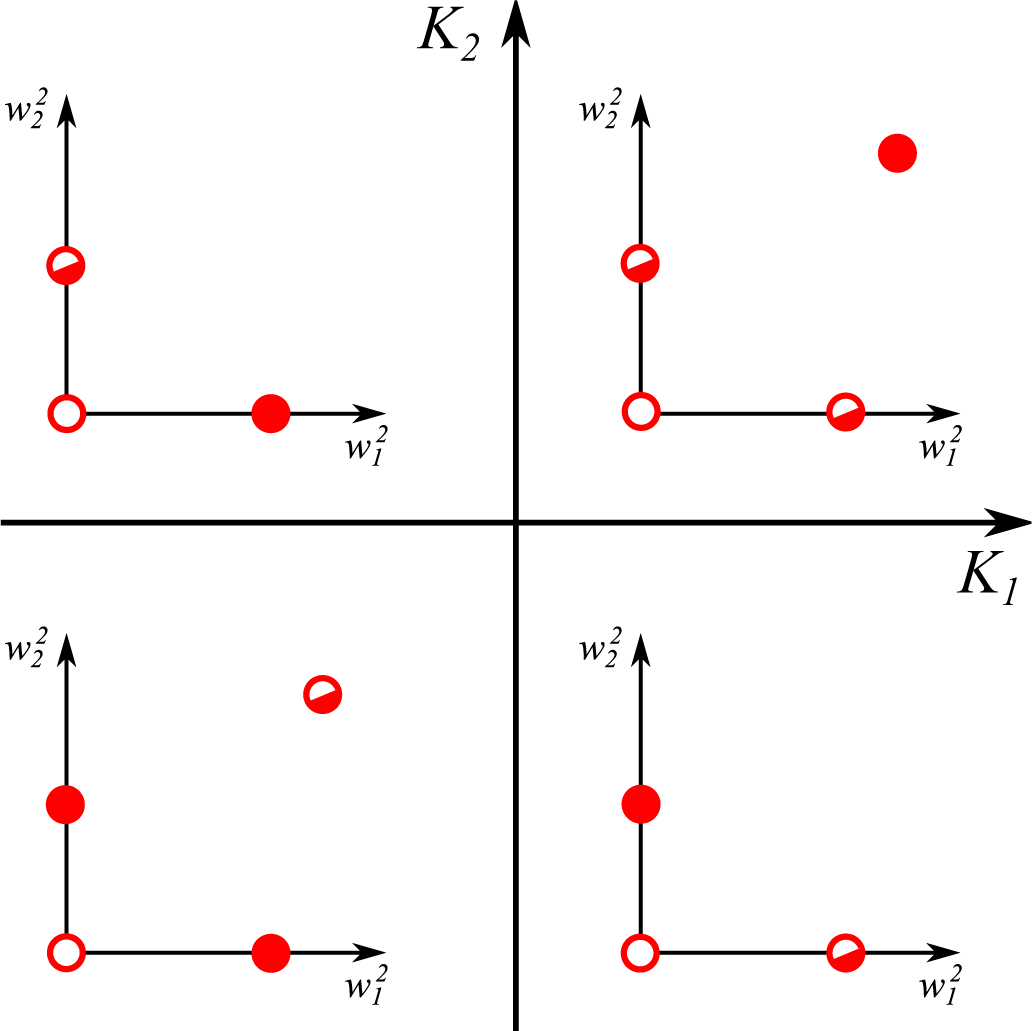
- The last term in Equation (12) is identical for all synapses. Two non-zero synaptic weights can hence only exist for identical signs of the respective excess kurtosis, K1K2 ≥ 0. It is easy to show that is unstable/stable whenever both K1,2 are negative/positive, in accordance with Equation (15).
2.1.3. Principal Component Analysis
2.2. Alternative Transfer Functions
2.3. The Stationarity Principle of Statistical Learning
2.3.1. The Fisher Information with Respect to the Synaptic Flux
- The operator w1∂/∂w1 corresponds to a dimensionless differential operator and, hence, to the log-derivative. The whole objective function is hence dimensionless.
- The average sensitivity is computed as an average over the probability distribution p(y1) of the presynaptic activity y1, since we are interested in minimizing the time average of the sensitivity of the postsynaptic activity with respect to synaptic weight changes in the context of a stationary presynaptic activity distribution p(y1).
- Minimizing , in accordance with the stationarity principle for statistical learning, leads to a synaptic weight vector w that is perpendicular to the gradient ∇w(log(p)), restricting consequently the overall growth of the modulus of w.
- In , there is no direct cross-talk between different synapses. Expression Equation (32) is hence adequate for deriving Hebbian-type learning rules in which every synapse has access only to locally-available information, together with the overall state of the postsynaptic neuron in terms of its firing activity y or its membrane potential x. We call Equation (32) the local synapse extension with respect to other formulations allowing for inter-synaptic cross-talk.
- It is straightforward to show [37] that Equation (31) reduces to Equation (5), when using the relations from Equation (3), viz. when we identify N → Nw. We have, however, opted to retain N generically as a free parameter in Equation (5), allowing us to shift appropriately the roots of G(x).
3. Results and Discussion
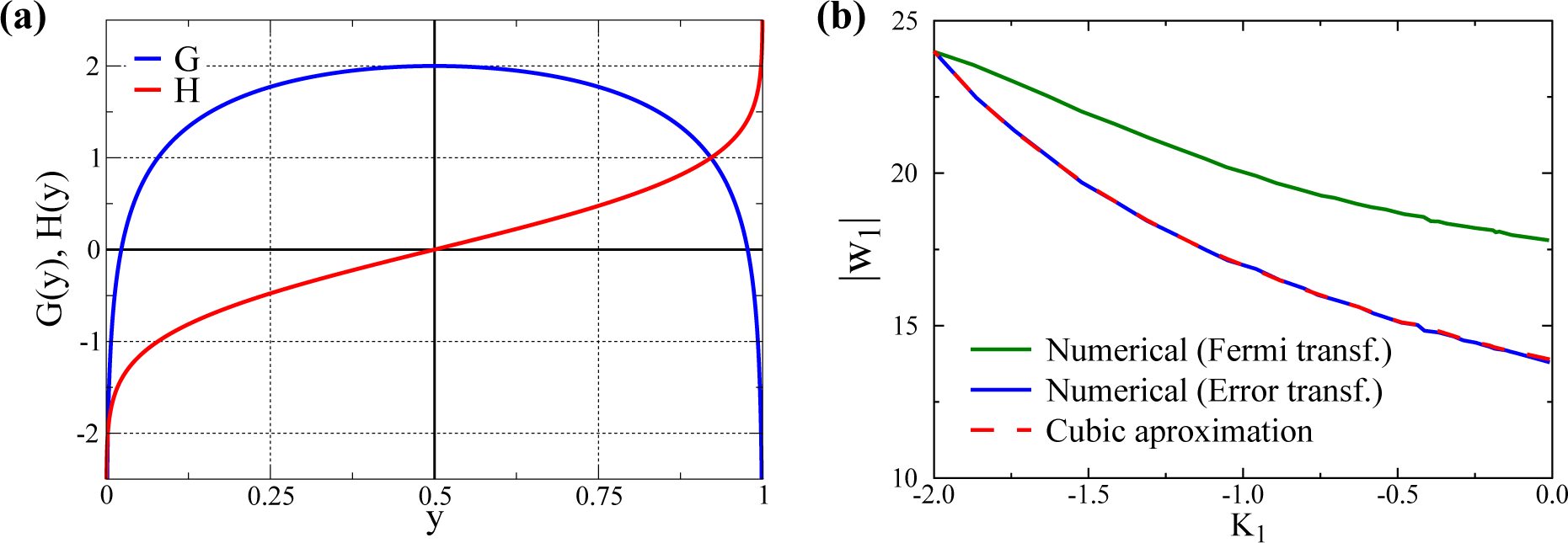
3.1. Quantitative Comparison of the Model and the Cubic Approximation
- σs is adjusted, changing d, such that the overall standard deviation σ1 remains constant. In this way, one can select with d different kurtosis levels, while retaining a constant standard deviation. For d = 0, one gets a bound (since y1 ∈ [0, 1]) normal distribution with K1 ≈ 0 (slightly negative, since the distributions are bound). In this way, we can evaluate the size of w1 after training for a varying K1 ∈ [−2, 0) for any given σ1.
- For the other Nw − 1 directions, we use bound normal distributions with standard deviations σi = σ1/2 as in [32].
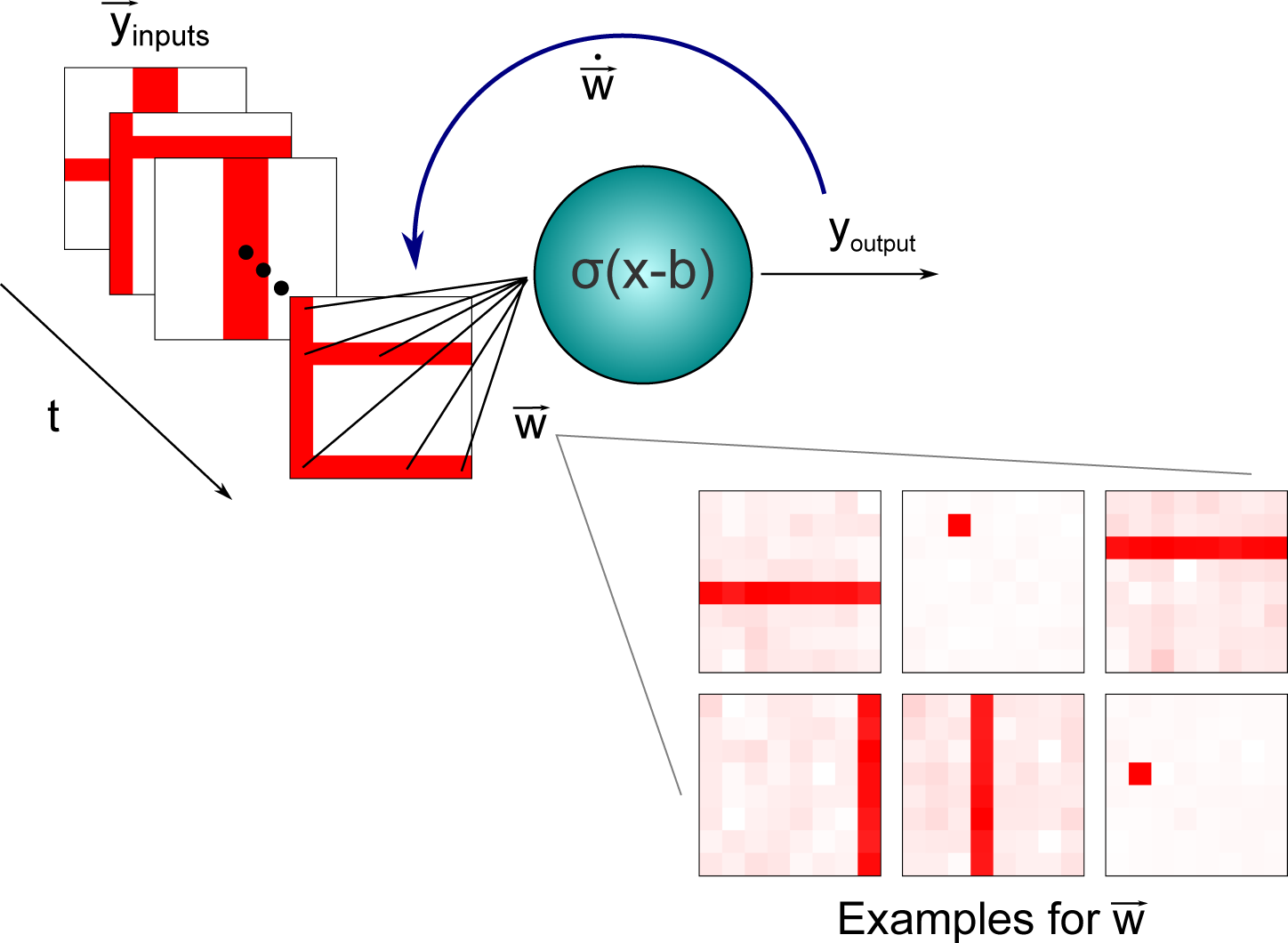
3.2. Independent Component Analysis: An Application to the Nonlinear Bars Problem
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Attwell, D.; Laughlin, S.B. An energy budget for signaling in the grey matter of the brain. J. Cereb. Blood Flow Metab. 2001, 21, 1133–1145. [Google Scholar]
- Mink, J.W.; Blumenschine, R.J.; Adams, D.B. Ratio of central nervous system to body metabolism in vertebrates: its constancy and functional basis. Am. J. Physiol.-Regul. Integr. Comp. Physiol. 1981, 241, R203–R212. [Google Scholar]
- Niven, J.E.; Laughlin, S.B. Energy limitation as a selective pressure on the evolution of sensory systems. J. Exp. Biol. 2008, 211, 1792–1804. [Google Scholar]
- Bullmore, E.; Sporns, O. The economy of brain network organization. Nat. Rev. Neurosci. 2012, 13, 336–349. [Google Scholar]
- Lee, H.; Battle, A.; Raina, R.; Ng, A.Y. Efficient sparse coding algorithms. In Advances in Neural Information Processing Systems: Proceedings of The First 12 Conferences; Jordan, M.I., LeCun, Y., Solla, S.A., Eds.; The MIT Press: Cambridge, MA, USA, 2001; pp. 801–808. [Google Scholar]
- Stemmler, M.; Koch, C. How voltage-dependent conductances can adapt to maximize the information encoded by neuronal firing rate. Nat. Neurosci. 1999, 2, 521–527. [Google Scholar]
- Gros, C. Generating functionals for guided self-organization. In Guided Self-Organization: Inception; Prokopenko, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 53–66. [Google Scholar]
- MacKay, D. Information-based objective functions for active data selection. Neural Comput. 1992, 4, 590–604. [Google Scholar]
- Marler, R.T.; Arora, J.S. Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar]
- Intrator, N.; Cooper, L.N. Objective function formulation of the BCM theory of visual cortical plasticity: Statistical connections, stability conditions. Neural Netw. 1992, 5, 3–17. [Google Scholar]
- Kay, J.W.; Phillips, W. Coherent infomax as a computational goal for neural systems. Bull. Math. Biol. 2011, 73, 344–372. [Google Scholar]
- Polani, D. Information: currency of life. HFSP J 2009, 3, 307–316. [Google Scholar]
- Zahedi, K.; Ay, N.; Der, R. Higher coordination with less control—A result of information maximization in the sensorimotor loop. Adapt. Behav. 2010, 18, 338–355. [Google Scholar]
- Polani, D.; Prokopenko, M.; Yaeger, L.S. Information and self-organization of behavior. Adv. Complex Syst. 2013, 16, 1303001. [Google Scholar]
- Prokopenko, M.; Gershenson, C. Entropy Methods in Guided Self-Organisation. Entropy 2014, 16, 5232–5241. [Google Scholar]
- Der, R.; Martius, G. The Playful Machine: Theoretical Foundation and Practical Realization of Self-Organizing Robots; Springer: Berlin, Heidelberg, Germany, 2012; Volume 15. [Google Scholar]
- Markovic, D.; Gros, C. Self-organized chaos through polyhomeostatic optimization. Phys. Rev. Lett. 2010, 105, 068702. [Google Scholar]
- Marković, D.; Gros, C. Intrinsic adaptation in autonomous recurrent neural networks. Neural Comput. 2012, 24, 523–540. [Google Scholar]
- Triesch, J. Synergies between intrinsic and synaptic plasticity mechanisms. Neural Comput. 2007, 19, 885–909. [Google Scholar]
- Linsker, R. Local synaptic learning rules suffice to maximize mutual information in a linear network. Neural Comput. 1992, 4, 691–702. [Google Scholar]
- Chechik, G. Spike-timing-dependent plasticity and relevant mutual information maximization. Neural Comput. 2003, 15, 1481–1510. [Google Scholar]
- Toyoizumi, T.; Pfister, J.P.; Aihara, K.; Gerstner, W. Generalized Bienenstock–Cooper–Munro rule for spiking neurons that maximizes information transmission. Proc. Natl. Acad. Sci. USA 2005, 102, 5239–5244. [Google Scholar]
- Friston, K. The free-energy principle: A unified brain theory. Nat. Rev. Neurosci. 2010, 11, 127–138. [Google Scholar]
- Mozzachiodi, R.; Byrne, J.H. More than synaptic plasticity: Role of nonsynaptic plasticity in learning and memory. Trends Neurosci. 2010, 33, 17–26. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology and Chemistry; Perseus Publishing: Boulder, CO, USA, 2001. [Google Scholar]
- Hebb, D.O. The Organization of Behavior: A Neuropsychological Theory; Psychology Press: Mahwah, NJ, USA, 2002. [Google Scholar]
- Oja, E. The nonlinear PCA learning rule in independent component analysis. Neurocomputing 1997, 17, 25–45. [Google Scholar]
- Bi, G.Q.; Poo, M.M. Synaptic modifications in cultured hippocampal neurons: Dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 1998, 18, 10464–10472. [Google Scholar]
- Froemke, R.C.; Dan, Y. Spike-timing-dependent synaptic modification induced by natural spike trains. Nature 2002, 416, 433–438. [Google Scholar]
- Izhikevich, E.M.; Desai, N.S. Relating stdp to bcm. Neural Comput. 2003, 15, 1511–1523. [Google Scholar]
- Echeveste, R.; Gros, C. Two-trace model for spike-timing-dependent synaptic plasticity. Neural Comput. 2015, 27, 672–698. [Google Scholar]
- Echeveste, R.; Gros, C. Generating functionals for computational intelligence: The Fisher information as an objective function for self-limiting Hebbian learning rules. Front. Robot. AI 2014, 1. [Google Scholar] [CrossRef]
- Bell, A.J.; Sejnowski, T.J. An information-maximization approach to blind separation and blind deconvolution. Neural Comput. 1995, 7, 1129–1159. [Google Scholar]
- Martius, G.; Der, R.; Ay, N. Information driven self-organization of complex robotic behaviors. PloS ONE 2013, 8, e63400. [Google Scholar]
- Földiak, P. Forming sparse representations by local anti-Hebbian learning. Biol. Cybern. 1990, 64, 165–170. [Google Scholar]
- Brunel, N.; Nadal, J.P. Mutual information, Fisher information, and population coding. Neural Comput. 1998, 10, 1731–1757. [Google Scholar]
- Echeveste, R.; Gros, C. An objective function for self-limiting neural plasticity rules. Proceedings of the 23th European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning (ESANN), Bruges, Belgium, 22–24 April 2015.
- Hyvärinen, A.; Karhunen, J.; Oja, E. Independent Component Analysis; Wiley: New York, NJ, USA, 2004; Volume 46. [Google Scholar]
- Bell, A.J.; Sejnowski, T.J. The “independent components” of natural scenes are edge filters. Vis. Res. 1997, 37, 3327–3338. [Google Scholar]
- Paradiso, M. A theory for the use of visual orientation information which exploits the columnar structure of striate cortex. Biol. Cybern. 1988, 58, 35–49. [Google Scholar]
- Seung, H.; Sompolinsky, H. Simple models for reading neuronal population codes. Proc. Natl. Acad. Sci. USA 1993, 90, 10749–10753. [Google Scholar]
- Gutnisky, D.A.; Dragoi, V. Adaptive coding of visual information in neural populations. Nature 2008, 452, 220–224. [Google Scholar]
- Bethge, M.; Rotermund, D.; Pawelzik, K. Optimal neural rate coding leads to bimodal firing rate distributions. Netw. Comput. Neural Syst. 2003, 14, 303–319. [Google Scholar]
- Lansky, P.; Greenwood, P.E. Optimal signal in sensory neurons under an extended rate coding concept. BioSystems 2007, 89, 10–15. [Google Scholar]
- Ecker, A.S.; Berens, P.; Tolias, A.S.; Bethge, M. The effect of noise correlations in populations of diversely tuned neurons. J. Neurosci. 2011, 31, 14272–14283. [Google Scholar]
- Reginatto, M. Derivation of the equations of nonrelativistic quantum mechanics using the principle of minimum Fisher information. Phys. Rev. A 1998, 58, 1775–1778. [Google Scholar]
- DeCarlo, L.T. On the meaning and use of kurtosis. Psychol. Methods. 1997, 2, 292. [Google Scholar]
- Comon, P. Independent component analysis, a new concept. Signal Process 1994, 36, 287–314. [Google Scholar]
- Hyvärinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar]
- Girolami, M.; Fyfe, C. Negentropy and Kurtosis as Projection Pursuit Indices Provide Generalised ICA Algorithms. Proceedings of NIPS 96 Workshop on Blind Signal Processing and Their Applications, Snowmaas, Aspen, CO, USA, 7 December 1996.
- Li, H.; Adali, T. A class of complex ICA algorithms based on the kurtosis cost function. IEEE Trans. Neural Netw. 2008, 19, 408–420. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Echeveste, R.; Eckmann, S.; Gros, C. The Fisher Information as a Neural Guiding Principle for Independent Component Analysis. Entropy 2015, 17, 3838-3856. https://doi.org/10.3390/e17063838
Echeveste R, Eckmann S, Gros C. The Fisher Information as a Neural Guiding Principle for Independent Component Analysis. Entropy. 2015; 17(6):3838-3856. https://doi.org/10.3390/e17063838
Chicago/Turabian StyleEcheveste, Rodrigo, Samuel Eckmann, and Claudius Gros. 2015. "The Fisher Information as a Neural Guiding Principle for Independent Component Analysis" Entropy 17, no. 6: 3838-3856. https://doi.org/10.3390/e17063838
APA StyleEcheveste, R., Eckmann, S., & Gros, C. (2015). The Fisher Information as a Neural Guiding Principle for Independent Component Analysis. Entropy, 17(6), 3838-3856. https://doi.org/10.3390/e17063838





