1. Introduction
Quantum cryptography is a mature and well established research field, at the core of which there is the fact, first noted about 30 years ago, that quantum physics allows for provably secure communication through an insecure communication channel [
1]. The most successful application of this core idea is quantum key distribution. In this protocol two honest parties, usually called Alice and Bob, wish to use a communication channel to generate a common bit-string, called a key, which must remain secret to an eavesdropper, usually called Eve, who could intercept the signal and tamper with the communication line (this secret key may be then used as a one-time pad). The security of the generated key is unconditional. That is, it is guaranteed by the laws of quantum physics and holds even if Eve possesses perfect technology and unlimited computational power (including a quantum computer). The price to pay for unconditional security is that the achievable rates of secret-key generation (measured in bits of secret key per use of the communication channel) are extremely low.
Consider for instance the recent results of [
2], which provide upper bounds on the secret-key generation rates of a communication channel. Suppose for example that the communication channel is a lossy single-mode optical fiber that attenuates the input signal by a factor
η. For linear loss,
η decreases exponentially with the length of the fiber. According to [
2], for small values of
η (
i.e., for long communication distances) the maximum secret-key generation rate through such a channel cannot be larger that about
η bits per mode, that is, the key rate decreases exponentially with the communication distance. This upper bound on the key generation rate can be compared with the rates of non-private communication. Unlike secret-key generation, one can in principle send non-private classical information through a lossy fiber at a constant rate across arbitrarily long distances, if sufficient input power is provided.
Here we ask the following question: Is it possible, by assuming a realistic constraint on Eve’s technological capabilities, to substantially improve the rate-loss tradeoff? We will show that, based on our previous results, a substantial improvement in the secret key can be achieved against an eavesdropper who, although endowed with unlimited computational power (including a quantum computer), can store quantum information only for a finite time. Indeed, any realistic quantum memory is subject to decoherence and can store quantum information only for a time of the order of its coherence time. Given that quantum information is sent at a certain rate, this condition is equivalent to saying that Eve can store only a limited number of qubits of quantum information, which is the assumption of the bounded storage model for quantum cryptography [
3]. We have indeed shown that this assumption on the ability of storing quantum information allows us to increase the rate of secret-key generation by a large amount. For quantum systems with finite dimensions, certain communication channels allow for a secret-key rate almost equal to the rate of non-private communication (less than 1 bit below it) [
4,
5]. Also, for optical lossy channels (as the optical fiber in the example above) it is in principle possible to achieve a constant secret-key rate of 1 bit per mode for arbitrarily long distances [
6], that is, the key rate does not decay with the communication distance. We remark that, although no specific restriction is imposed on Alice and Bob, they do not need a perfect quantum memory to run the communication protocol.
2. Security against an Eavesdropper with Time-Limited Storage
Suppose Alice wishes to use a memoryless quantum channel
to send private information to Bob. Upon
n uses of the channel, she encodes
M messages
x = 1,…,
M, each with probability
pX(
x), into the input states
ρA(
x)’s. Then Bob will receive the output states
. Let us recall that a quantum channel
can always be represented as the reduced dynamics induced by a unitary transformation on a larger space, that is,
where ω
E is a pure state for a quantum system associated with the environment of the channel, and
U is a unitary transformation coupling the system with its environment. In the worst-case scenario the eavesdropper Eve might collect all the information leaking into the channel environment, in which case the state obtained by Eve reads
, where
is the complementary channel, defined as
Let us consider the state
This state describes the correlations between the classical input
x and Eve’s quantum system. To quantify the security of the channel one usually considers the trace distance [
7]
where
,
are the reduced states of
σXE, and ∥ · ∥
1 = Tr| · |. If the trace distance is small, this implies that the state
σXE is close to the uncorrelated state
σX ⨂
σE. Recall that, from an operational point of view, the trace distance is the bias in distinguishing the states by a measurement. The trace norm is indeed the standard security quantifier used in quantum key distribution: if Δ ≤
ϵ, the communication protocol is secure up to a probability
ϵ [
7].
The trace norm is the proper security quantifier in a generic setting. However, under certain assumptions on the technological capabilities of the eavesdropper, we can adopt a weaker security criterion. If we know that the eavesdropper cannot store quantum information for longer than a given time
τ, then we know that she is forced to make a measurement within a time
τ after she received the quantum state. This leads us to consider a post-measurement security quantifier. A measurement Λ on Eve’s system defines a classical random variable
Y with conditional probability distribution
where {Λ
y} are POVM elements, satisfying Λ
y ≥ 0 and the completeness relation
. A post-measurement security criterion requires that the joint probability distribution
is close to the product of its marginals
, where
, for all measurements Λ. Here we consider the distance
(the meaning of the subscript “acc” will be clear in the next paragraph) where
is the total variation distance. The operational meaning of Δ
acc is the bias in distinguishing between the classical distributions
and
. In other words, Δ
acc is the bias in distinguishing between the states
σXE and σ
X ⨂ σ
E by a local measurement.
The accessible information is an entropic quantity naturally associated with the distance Δ
acc. Let us recall that the accessible information is defined as the maximum classical mutual information that Eve can obtain about the input variable by local measurements on her subsystem, that is,
where
I(
X;
Y) =
H(
X) +
H(
Y) −
H(
XY) is the classical mutual information of the variables
X and
Y. From Alicki-Fannes’ inequality [
8]:
where
η(·) = −(·) log (·). On the other hand, Pinsker’s inequality yields [
9]
These two inequalities imply the effective equivalence of Δacc and Iacc(X; E) as security quantifiers. If the accessible information is small, Pinsker’s inequality implies that the Δacc is also small. Viceversa, if Δacc is small, then the accessible information is small provided Δacc ≪ (log dn)−1 = n−1/log d.
3. Quantum Data Locking
In a quantum data locking protocol [
10,
11] the legitimate parties Alice and Bob initially share a secret key of log
K bits. They use the key to agree on a code to be used to send classical information through a quantum channel. If they publicly declare a list of
K codes, then they can use the shared key to secretly agree on one of them. On the other hand, if an eavesdropper, who does not know the secret key, intercepts and measures the quantum codewords, we require that her accessible information about the input messages must be negligibly small.
Let us first consider the case in which the channel from Alice to Bob is noiseless. In this case Alice can simply encode classical information using a set of orthogonal
n-qudit states belonging to a given basis. If Bob knows the basis chosen by Alice, he can reliably decode by measuring in the same basis. Suppose that Eve intercepts the whole set of
n qudits. To ensure the security of the quantum data locking protocol,
K must be chosen large enough to make Eve’s mutual information negligibly small. It was shown in [
12] (see also [
11,
13,
14]) that for
n large enough, there exist choices of log
K = 4 log 1/
ϵ +
O(log log 1/
ϵ) bases such that
Iacc(
X;
E) ≤
ϵ log
dn.
Notice that for any given (small)
ϵ and for
n large enough, this implies that a relatively small secret key is sufficient to
lock an arbitrarily long message. It is worth stressing that this result represents a strong violation of classical information theory in the quantum framework. Indeed, it is well known that in the classical framework the secure encryption of a message of
m bits requires at least
m bits of secret key (this result is at the basis of the security of the one-time pad). The results of [
12] imply that one can lock information through a noiseless qudit channel at a rate of log
d bits per channel use by consuming secret key at a rate (in bits per channel use) of
Such a secret-key consumption rate is asymptotically zero if ϵ is constant or decreases sub-exponentially in n.
While the phenomenon of quantum data locking has been known for more than 10 years, the problem of locking information through noisy channels has been considered only recently in [
15], where the notion of locking capacity of a noisy channel was introduced. The latter is defined as the maximum number of bits per channel use that can be reliably sent through a given channel, in such a way that the eavesdropper’s accessible information is negligibly small. Two notions of locking capacities have been defined. The
weak-locking capacity is defined by requiring security against an eavesdropper who measures the output of the complementary channel of the channel from Alice to Bob. The
strong-locking capacity instead requires security against an eavesdropper having direct access to the input states prepared by Alice. In an optical setting, a cipher based on the quantum data locking effect is dubbed a
quantum enigma machine [
16]. While the twentieth century’s Enigma machine relied on computational security (the presumed difficulty of inverting the complex pattern of electromechanical elements that was used to scramble the inputs of a typing machine), a quantum enigma machine would ensure provable information-theoretical security against an eavesdropper who cannot store quantum information for an arbitrarily long time.
Given a quantum channel, it is natural to compare the weak-locking capacity with the private capacity [
17,
18]. The latter is defined as the maximum rate of secret communication given that the security is defined in terms of the trace distance
(4). A private communication protocol allows for unconditional security and does not rely on any assumption on the technological capability of the eavesdropper. While it is easy to see that the weak-locking capacity is at least equal to the private capacity [
15], it is non-trivial to show that a (large) gap exist between these two capacities. The first examples of noisy channels with a weak-locking capacity much larger than the private capacity were provided in [
19].
Unlike the case of a noiseless channel, in a noisy setting Alice and Bob should use codes that allow for both data locking and error correction. In our recent works we have derived families of random codes that allow for error correction and data locking through noisy channels that have enough symmetry (These channels are covariant under the action of a symmetry group. We expect a lower data locking rate for channels that do not have such a symmetry). Examples include the erasure and depolarizing channels (in finite dimensions) [
4,
5] and the lossy bosonic channel (for continuous-variable systems) [
6]. The price to pay for being able to correct the errors and hence send information reliably through the noisy channel, is a higher rate of secret-key consumption. Assume that Alice encodes
M messages into
n uses of a memoryless qudit channel. In a strong-locking scenario, in order to guarantee
Iacc(
X;
E) ≤
ϵ log
dn we need an asymptotic secret-key consumption rate (in bits per channel use) of (assuming that
ϵ is either constant or decreases sub-exponentially in
n)
where χ = lim
n→∞ 1/
n log
M is the asymptotic communication rate, and
γ depends on the details of communication channel and of the codes employed.
3.1. Methods
Alice and Bob publicly agree on a set of
K codes
, where each code contains
M equi-probable codewords
, with
. In a strong-locking scenario Eve intercepts the input states |
ψk (
x)⟩’s. Since she does not know the code, the state
(3) reads:
Putting
and
, the accessible information of
σXE reads
where the maximum is over POVM’s Λ.
By convexity of mutual information, the maximum is achieved for a rank-one measurement with POVM elements of the form Λ
y =
μy|
ϕy〉 〈
ϕy| where the |
ϕy〉’s s are unit vectors and
μy >0. The condition
implies ∑
y|
μy/
dn = 1. Putting
Qx(
ϕy) = ⟨
ϕy|ρ(
x)|
ϕy⟩, we then obtain
where
H[
Q(
ϕy)] = − ∑
x Qx(
ϕy) log
Qx(
ϕy). Finally, we notice that the positive quantities
μy/
dn can be interpreted as probability weights. An upper bound on the accessible information is then obtained by the fact that the average cannot exceed the maximum, which yields
where the minimum is over all unit vectors
.
We now show that for certain choices of the codes
, the accessible information is smaller than
ϵ log
dn for
n and
K large enough. Consider the case of random codes, where the codewords in
are chosen i.i.d. from a certain ensemble of states. Then for any given
x and |
ϕ⟩ the quantity
is the sum of random variables which, for
K large enough, will converge to its average
. If the random codewords are chosen from an isotropic ensemble, that is, one satisfying
, then
. In turn, if
Qx(
ϕ) ~ (1 ±
ϵ)/
dn, then
H[
Q(
ϕ)] ≳ (1 −
ϵ)
M=dn log
dn, and
η[∑
x Qx(
ϕ)]
~ η[
M/
dn] = −
M/
dn log
M/
dn, which finally implies
Iacc(
X;
E) ≲
ϵ log
dn.
The minimum value of
K for which
Qx(
ϕ) is close enough to its average for all
x and |
ϕ⟩ can be obtained by applying suitable concentration inequalities [
20,
21]. For
n large enough and if
ϵ decreases sublinearly with
n, we have obtained the following condition on
K [
5]:
where
is the communication rate, and
Notice that the factor depends on the ensemble from which the random codewords are drawn.
If the codewords are drawn from the uniform distribution on the unit sphere in
, one obtains
, which yields
. If the channel from Alice to Bob is noiseless, we have χ = log
d and thus obtain an asymptotically vanishing secret-key consumption rate,
. This result corresponds to the findings of [
11,
12], which considered random codewords in a high-dimensional Hilbert space and obtained quantum data locking protocols with zero asymptotic secret-key consumption rate through a noiseless channel.
Suppose instead that the codewords are of the form
, where for any
j = 1,…,
n, the vectors |
ψk;j(
x)⟩’s are drawn i.i.d. from the uniform distribution on the unit sphere in ℂ
d. For these separable codewords we obtain
, which yields
This result corresponds to the quantum data locking protocols discussed in [
5]. Given a noisy channel allowing a classical communication rate χ, we obtain a secret-key consumption rate of
k = max {1 − log (1 + 1/
d), log
d – χ} bits per channel use.
We conclude this section by remarking that there is no reason to consider only random codewords generated by spherically symmetric distributions. First, since γ is only determined by the first and second moments of the distribution, quantum data locking protocols with the same performances can be obtained by choosing random codewords from a spherical 2-design. Second, non-uniform distributions can also be used and may lead to similar results (see [
4,
14]).
3.2. Applications
The results reviewed in the previous section can be applied to achieve secure communication against an eavesdropper with time-limited quantum storage. Suppose Alice and Bob initially share nk bits of secret key. They can use this secret key to lock n uses of the quantum channel. If the channel allows a classical communication rate of χ bits per channel use, they will be able to communicate about nχ bits of locked information.
After a waiting time sufficiently longer than the coherence time of Eve’s quantum memory, Alice and Bob can run a second quantum data locking protocol. If χ > k they can recycle nk bits of the previous message as a secret key for the new round of quantum data locking. By repeating this procedure many times, they will achieve a net rate of locked communication of r = χ − k bits per channel use.
A simple non-trivial example of noisy communication is the
d-dimensional erasure channel. Upon
n uses of the erasure channel, Alice prepares quantum data locking codewords of the form
, where |
ψk;j(
x)⟩ are random codewords drawn from the uniform distribution on the unit sphere in ℂ
d. Given that the channel from Alice to Bob is a memoryless qudit erasure channel with erasure probability
p, they can achieve a classical communication rate (in bits per channel use) of
The complementary channel from Alice to Eve is also a qudit erasure channel, with erasure probability (1 −
p). As discussed in the previous section, a secret-key consumption rate of
k = max {1 − log (1 + 1/
d), log
d – χ} bits is needed for quantum data locking. In our example, the erasure channel from Alice to Eve will erase all but a fraction
p of the qudits sent by Alice. This implies that the secret-key consumption rate will be also reduced by a factor
p, leading to
k = max {
p −
p log (1 + 1/
d),
p log
d – χ}.
Figure 1 shows, for an 8-bit channel (
d = 256), the net rate of weak locking for the erasure channel,
compared with its classical capacity
C = (1 −
p) log
d and the private capacity
P = (1 − 2
p) log
d. Similar results are obtained for other channels of the form
, where
ρ0 is a given density operator [
5].
We now apply quantum data locking to a continuous-variable quantum system. In [
6] we have considered the case of a lossy bosonic channel with transmissivity
η, where the input codewords are multimode coherent states drawn from a Gaussian distribution with
N mean photons per mode. Although the quantum system has infinite dimensions, it is sufficient to consider the typical subspace spanned by these random codewords. For
n-mode coherent states, such a typical subspace has dimension
dn ~ 2
ng(N), with
g(
N) = (
N + 1) log (
N + 1) −
N log
N. Here we consider a weak-locking scenario where Eve measures the complementary channel, which in this case is also a lossy bosonic channel with transmissivity (1 −
η). Inspired by [
22] we have introduced a reverse-reconciliation protocol for secret-key generation by quantum data locking. In this protocol Alice and Bob publicly agree on a collection of measurements Λ
k, for
k = 1,…,
K. Then Alice locally prepares a bipartite entangled state and sends one subsystems to Bob through the quantum channel. According to the value of the pre-shared secret key, Bob makes the measurement Λ
k. This induces a virtual backward quantum channel from Bob to Alice. As shown in [
6], this protocol may achieve an asymptotic classical communication rate of χ =
g(
N) −
g[(1 −
η)
N′] bits per mode, with
N′ =
N/(1 +
ηN). On the other hand, weak locking can be obtained with a secret-key consumption rate of
k = 2
g[(1 −
η)
N] −
g[(1 −
η)
N′] −
g[(1 −
η)
N″], with
N″ = (1 + 2
ηN)
N′. In this way we achieve a net weak-locking rate of
r = χ −
k bits per mode which, in the limit of
N → ∞ yields, for any
η > 0,
This yields a rate larger than 1 bit per mode for any non-zero transmissivity, i.e., a constant rate of secret-key generation across arbitrarily long communication distances.
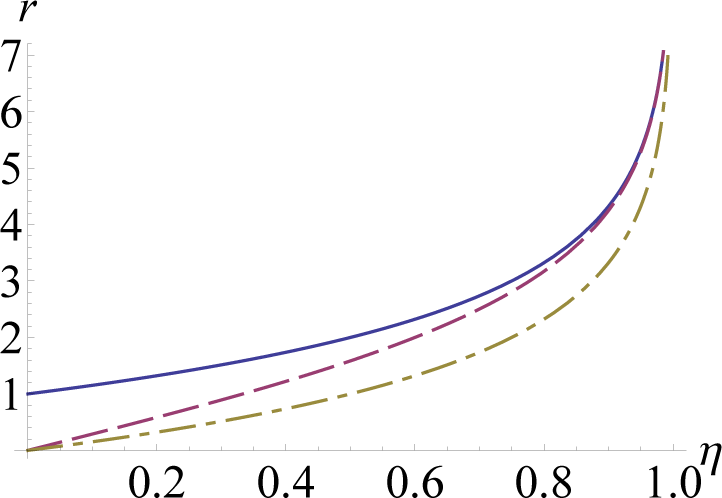
The obtained rate of weak-locking can be compared with the secret-key rate achievable assuming the standard security criterion quantified by the trace distance. For the lossy channel a lower and an upper bound on this rate are respectively given by
[
22] and
[
2].
Figure 2 shows a comparison between these three rates versus the channel transmissivity
η. Our result shows that secure communication against an eavesdropper with time-limited quantum storage not only allows for a quantitative enhancement in the private communication rate, but also yields striking qualitative changes in the rate-loss tradeoff.
4. Conclusions
We have reviewed recent results on quantum data locking, speculating on applications of this intriguing quantum phenomenon to secret communication and key distribution through an insecure quantum channel. As quantum data locking relies on a post-measurement security criterion, it protects against an eavesdropper who can store quantum information only for a finite time.
Since a quantum memory is always limited by its coherence time, our assumption may be justified in some cases. We have seen that under this assumption one obtains not only a quantitative enhancement in the secret-key generation rate, but also a qualitative improvement in the rate-loss tradeoff. In the most important case of a lossy channel, we have seen that this assumption allows us to achieve a constant secret-key generation rate at any distance. This result must be compared with the performance of standard quantum key distribution, which yields a rate that decays exponentially with the communication distance.
Finally, it is worth remarking that the assumption of limited quantum memory is also at the basis of the bounded storage model for quantum cryptography. We argue that our results can also be applied to obtain achievable secret-key rates within this model.