Passive Decoy-State Quantum Key Distribution with Coherent Light
Abstract
:1. Introduction
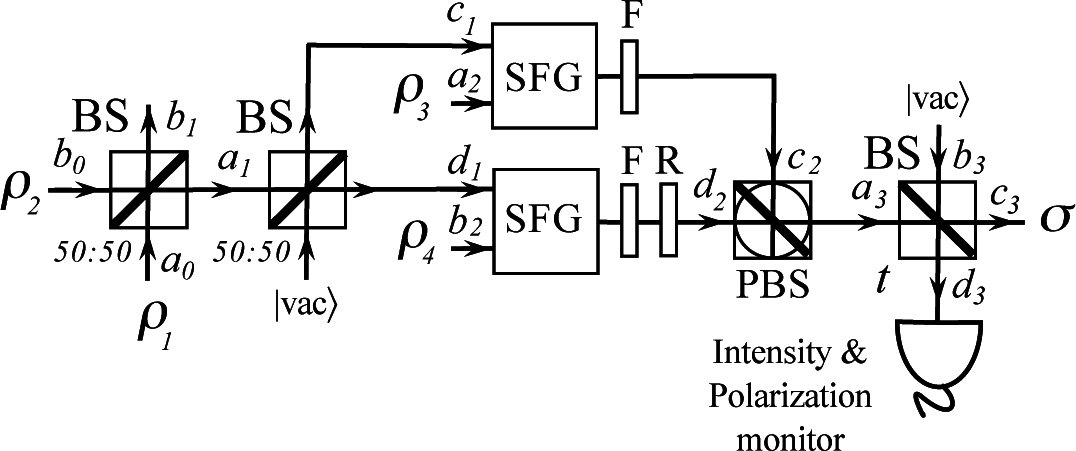
2. Passive Decoy-State BB84 Transmitter
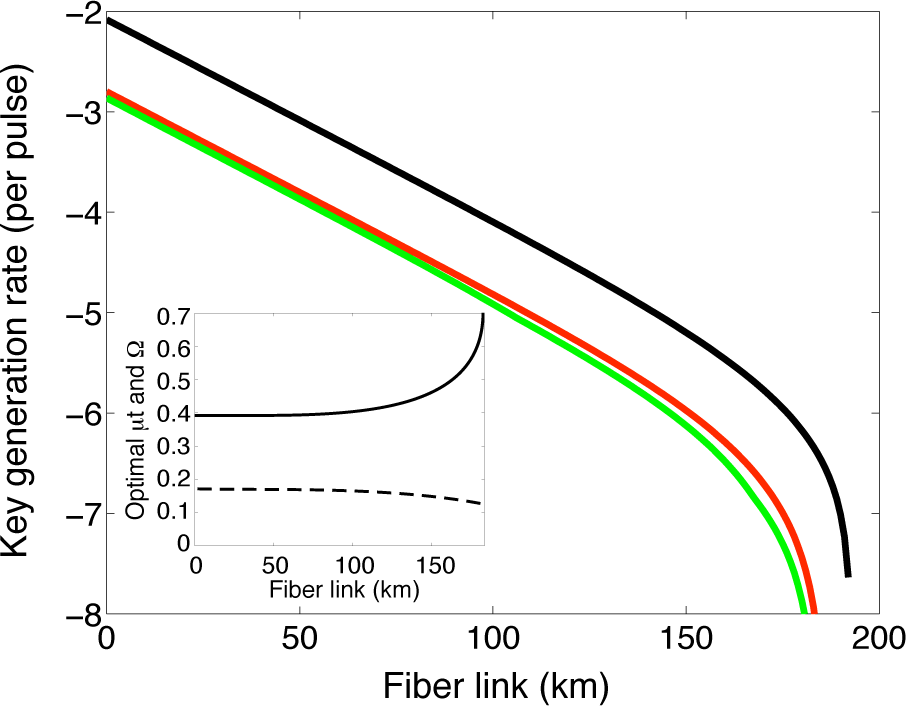
3. Lower Bound on the Secret Key Rate
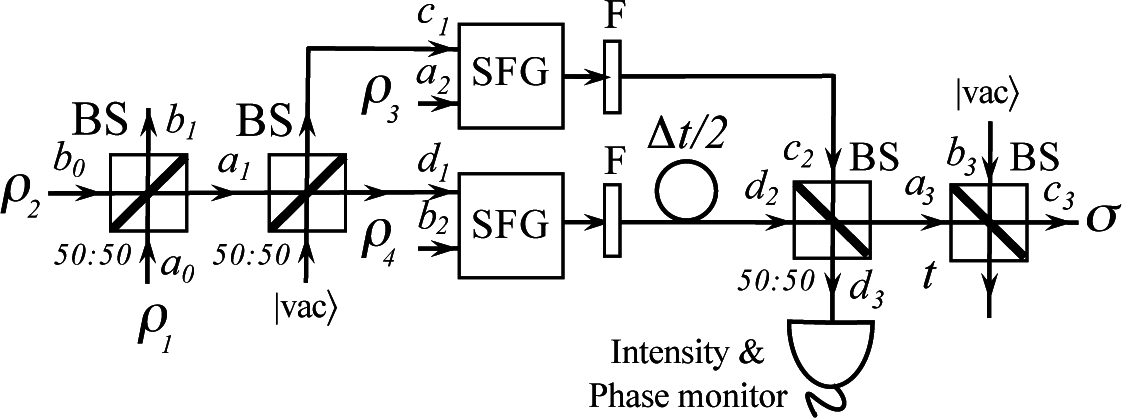
4. Phase Encoding
5. Conclusions
Acknowledgments
Appendix
A. Sum-Frequency Generation
B. Gain and QBER
C. Estimation procedure
D. Asymptotic Passive Decoy-State BB84 Transmitter
Author Contributions
Conflicts of Interest
References
- Scarani, V.; Bechmann-Pasquinucci, H.; Cerf, N.J.; Dušek, M.; Lütkenhaus, N.; Peev, M. The security of practical quantum key distribution. Rev. Mod. Phys. 2009, 81, 1301–1350. [Google Scholar]
- Lo, H.-K.; Curty, M.; Tamaki, K. Secure quantum key distribution. Nat. Photonics. 2014, 8, 595–604. [Google Scholar]
- Vernam, G.S. Cipher printing telegraph systems for secret wire and radio telegraphic communications. J. Am. Inst. Elect. Eng. 1926, 45, 109–115. [Google Scholar]
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Proceedings of the IEEE International Conference on Computers, Systems and Signal Processing, Bangalore, India, 10–12 December 1984; p. 175.
- Hwang, W.-Y. Quantum Key Distribution with High Loss: Toward Global Secure Communication. Phys. Rev. Lett. 2003, 91, 057901. [Google Scholar]
- Lo, H.-K.; Ma, X.; Chen, K. Decoy State Quantum Key Distribution. Phys. Rev. Lett. 2005, 94, 230504. [Google Scholar]
- Wang, X.-B. Beating the Photon-Number-Splitting Attack in Practical Quantum Cryptography. Phys. Rev. Lett. 2005, 94, 230503. [Google Scholar]
- Zhao, Y.; Qi, B.; Ma, X.; Lo, H.-K.; Qian, L. Experimental Quantum Key Distribution with Decoy States. Phys. Rev. Lett. 2006, 96, 070502. [Google Scholar]
- Rosenberg, D.; Harrington, J.W.; Rice, P.R.; Hiskett, P.A.; Peterson, C.G.; Hughes, R.J.; Lita, A.E.; Nam, S.W.; Nordholt, J.E. Long-Distance Decoy-State Quantum Key Distribution in Optical Fiber. Phys. Rev. Lett. 2007, 98, 010503. [Google Scholar]
- Peng, C.Z.; Zhang, J.; Yang, D.; Gao, W.B.; Ma, H.X.; Yin, H.; Zeng, H.P.; Yang, T.; Wang, X.B.; Pan, J.W. Experimental Long-Distance Decoy-State Quantum Key Distribution Based on Polarization Encoding. Phys. Rev. Lett. 2007, 98, 010505. [Google Scholar]
- Yuan, Z.L.; Sharpe, A.W.; Shields, A.J. Unconditionally secure one-way quantum key distribution using decoy pulses. Appl. Phys. Lett. 2007, 90, 011118. [Google Scholar]
- Dixon, A.R.; Yuan, Z.L.; Dynes, J.F.; Sharpe, A.W.; Shields, A.J. Gigahertz decoy quantum key distribution with 1 Mbit/s secure key rate. Opt. Express. 2008, 16, 18790–18979. [Google Scholar]
- Tanaka, A.; Fujiwara, M.; Nam, S.W.; Nambu, Y.; Takahashi, S.; Maeda, W.; Yoshino, K.; Miki, S.; Baek, B.; Wang, Z.; et al. Ultra fast quantum key distribution over a 97 km installed telecom fiber with wavelength division multiplexing clock synchronization. Opt. Express. 2008, 16, 11354–11360. [Google Scholar]
- Rosenberg, D.; Peterson, C.G.; Harrington, J.W.; Rice, P.R.; Dallmann, N.; Tyagi, K.T.; McCabe, K.P.; Nam, S.; Baek, B.; Hadfield, R.H.; et al. Practical long-distance quantum key distribution system using decoy levels. New J. Phys. 2009, 11, 045009. [Google Scholar]
- Dixon, A.R.; Yuan, Z.L.; Dynes, J.F.; Sharpe, A.W.; Shields, A.J. Continuous operation of high bit rate quantum key distribution. Appl. Phys. Lett. 2010, 96, 161102. [Google Scholar]
- Liu, Y.; Chen, T.-Y.; Wang, J.; Cai, W.-Q.; Wan, X.; Chen, L.-K.; Wang, J.-H.; Liu, S.-B.; Liang, H.; Yang, L.; et al. Decoy-State quantum key distribution with polarized photons over 200 km. Opt. Express. 2010, 18, 8587–8594. [Google Scholar]
- Sasaki, M.; Fujiwara, M.; Ishizuka, H.; Klaus, W.; Wakui, K.; Takeoka, M.; Miki, S.; Yamashita, T.; Wang, Z.; Tanaka, A.; et al. Field test of quantum key distribution in the Tokyo QKD Network. Opt. Express. 2011, 19, 10387–10409. [Google Scholar]
- Wang, J.-Y.; Yang, B.; Liao, S.-K.; Zhang, L.; Shen, Q.; Hu, X.-F.; Wu, J.-C.; Yang, S.-J.; Jiang, H.; Tang, Y.-L.; et al. Direct and full-scale experimental verifications towards ground-satellite quantum key distribution. Nat. Photonics. 2013, 7, 387–393. [Google Scholar]
- Pironio, S.; Acín, A.; Massar, S.; Boyer de la Giroday, A.; Matsukevich, D.N.; Maunz, P.; Olmschenk, S.; Hayes, D.; Luo, L.; Manning, T.A.; et al. Random numbers certified by Bell’s theorem. Nature 2010, 464, 1021–1024. [Google Scholar]
- Williams, C.R.S.; Salevan, J.C.; Li, X.; Roy, R.; Murphy, T.E. Fast physical random number generator using amplified spontaneous emission. Opt. Express. 2010, 18, 23584–23597. [Google Scholar]
- Jofre, M.; Curty, M.; Steinlechner, F.; Anzolin, G.; Torres, J.P.; Mitchell, M.W.; Pruneri, V. True random numbers from amplified quantum vacuum. Opt. Express. 2011, 19, 20665–20672. [Google Scholar]
- Abellán, C.; Amaya, W.; Jofre, M.; Curty, M.; Acín, A.; Capmany, J.; Pruneri, V.; Mitchell, M.W. Ultra-Fast quantum randomness generation by accelerated phase diffusion in a pulsed laser diode. Opt. Express. 2014, 22, 1645–1654. [Google Scholar]
- Qi, B.; Chi, Y.-M.; Lo, H.-K.; Qian, L. High-Speed quantum random number generation by measuring phase noise of a single-mode laser. Opt. Lett. 2010, 35, 312–314. [Google Scholar]
- Hughes, R.J.; Nordholt, J.E.; Derkacs, D.; Peterson, C.G. Practical free-space quantum key distribution over 10 km in daylight and at night. New J. Phys. 2002, 4. [Google Scholar] [CrossRef]
- Kurtsiefer, C.; Zarda, P.; Halder, M.; Weinfurter, H.; Gorman, P.M.; Tapster, P.R.; Rarity, J.G. Quantum cryptography: A step towards global key distribution. Nature 2002, 419. [Google Scholar] [CrossRef]
- Bennett, C.H.; Bessette, F.; Brassard, G.; Salvail, L.; Smolin, J. Experimental Quantum Cryptography. J. Cryptol. 1992, 5, 3–28. [Google Scholar]
- Muller, A.; Bréguet, J.; Gisin, N. Experimental Demonstration of Quantum Cryptography Using Polarized Photons in Optical Fibre over More than 1 km. Europhys. Lett. 1993, 23, 383–388. [Google Scholar]
- Muller, A.; Zbinden, H.; Gisin, N. Underwater quantum coding. Nature 1995, 378, 449. [Google Scholar] [CrossRef]
- Townsend, P.D. Experimental investigation of the performance limits for first telecommunications-window quantum cryptography systems. IEEE Photonics Tech. Lett. 1998, 10, 1048–1050. [Google Scholar]
- Xavier, G.B.; Walenta, N.; Vilela de Faria, G.; Temporão, G.P.; Gisin, N.; Zbinden, H.; von der Weid, J.P. Experimental polarization encoded quantum key distribution over optical fibres with real-time continuous birefringence compensation. New J. Phys. 2009, 11, 045015. [Google Scholar]
- Hayashi, M.; Nakayama, R. Security analysis of the decoy method with the Bennett–Brassard 1984 protocol for finite key lengths. New J. Phys. 2014, 16, 063009. [Google Scholar]
- Lim, C.C.W.; Curty, M.; Walenta, N.; Xu, F.; Zbinden, H. Concise security bounds for practical decoy-state quantum key distribution. Phys. Rev. A. 2014, 89, 022307. [Google Scholar]
- Rarity, J.G.; Owens, P.C.M.; Tapster, P.R. Quantum Random-number Generation and Key Sharing. J. Mod. Opt. 1994, 41, 2435–2444. [Google Scholar]
- Mauerer, W.; Silberhorn, C. Quantum key distribution with passive decoy state selection. Phys. Rev. A. 2007, 75, 050305(R). [Google Scholar]
- Adachi, Y.; Yamamoto, T.; Koashi, M.; Imoto, N. Simple and Efficient Quantum Key Distribution with Parametric Down-Conversion. Phys. Rev. Lett. 2007, 99, 180503. [Google Scholar]
- Ma, X.; Lo, H.-K. Quantum key distribution with triggering parametric down-conversion sources. New J. Phys. 2008, 10, 073018. [Google Scholar]
- Curty, M.; Moroder, T.; Ma, X.; Lütkenhaus, N. Non-Poissonian statistics from Poissonian light sources with application to passive decoy state quantum key distribution. Opt. Lett. 2009, 34, 3238–3240. [Google Scholar]
- Curty, M.; Ma, X.; Qi, B.; Moroder, T. Passive decoy-state quantum key distribution with practical light sources. Phys. Rev. A. 2010, 81, 022310. [Google Scholar]
- Adachi, Y.; Yamamoto, T.; Koashi, M.; Imoto, N. Boosting up quantum key distribution by learning statistics of practical single-photon sources. New J. Phys. 2009, 11, 113033. [Google Scholar]
- Ribordy, G.; Brendel, J.; Gauthier, J.-D.; Gisin, N.; Zbinden, H. Long-Distance entanglement-based quantum key distribution. Phys. Rev. A. 2000, 63, 012309. [Google Scholar]
- Tittel, W.; Brendel, J.; Zbinden, H.; Gisin, N. Quantum Cryptography Using Entangled Photons in Energy-Time Bell States. Phys. Rev. Lett. 2000, 84, 4737–4740. [Google Scholar]
- Curty, M.; Ma, X.; Lo, H.-K.; Lütkenhaus, N. Passive sources for the Bennett-Brassard 1984 quantum-key-distribution protocol with practical signals. Phys. Rev. A. 2010, 82, 052325. [Google Scholar]
- Boyd, R.W. Nonlinear Optics; Academic Press: Waltham, MA, USA, 2008. [Google Scholar]
- Shen, Y.R. The Principles of Nonlinear Optics; Wiley-Interscience: Hoboken, NJ, USA, 1984. [Google Scholar]
- Kumar, P. Quantum frequency conversion. Opt. Lett. 1990, 15, 1476–1478. [Google Scholar]
- Huang, J.; Kumar, P. Observation of quantum frequency conversion. Phys. Rev. Lett. 1992, 68, 2153–2156. [Google Scholar]
- Kim, Y.-H.; Kulik, S.P.; Shih, Y. Quantum Teleportation of a Polarization State with a Complete Bell State Measurement. Phys. Rev. Lett. 2001, 86, 1370–1373. [Google Scholar]
- Dayan, B.; Pe’er, A.; Friesem, A.A.; Silberberg, Y. Nonlinear Interactions with an Ultrahigh Flux of Broadband Entangled Photons. Phys. Rev. Lett. 2005, 94, 043602. [Google Scholar]
- Pe’er, A.; Dayan, B.; Friesem, A.A.; Silberberg, Y. Temporal Shaping of Entangled Photons. Phys. Rev. Lett. 2005, 94, 073601. [Google Scholar]
- Zäh, F.; Halder, M.; Feurer, T. Amplitude and phase modulation of time-energy entangled two-photon states. Opt. Express. 2008, 16, 16452–16458. [Google Scholar]
- Tanzilli, S.; Tittel, W.; Halder, M.; Alibart, O.; Baldi, P.; Gisin, N.; Zbinden, H. A photonic quantum information interface. Nature 2005, 437, 116–120. [Google Scholar]
- Thew, R.T.; Zbinden, H.; Gisin, N. Tunable upconversion photon detector. Appl. Phys. Lett. 2008, 93, 071104. [Google Scholar]
- Sangouard, N.; Sanguinetti, B.; Curtz, N.; Gisin, N.; Thew, R.; Zbinden, H. Faithful Entanglement Swapping Based on Sum-Frequency Generation. Phys. Rev. Lett. 2011, 106, 120403. [Google Scholar]
- Kok, P.; Munro, W.J.; Nemoto, K.; Ralph, T.C.; Dowling, J.P.; Milburn, G.J. Linear optical quantum computing with photonic qubits. Rev. Mod. Phys. 2007, 79, 135–174. [Google Scholar]
- Gottesman, D.; Lo, H.-K.; Lütkenhaus, N.; Preskill, J. Security of quantum key distribution with imperfect devices. Quantum Inf. Comput. 2004, 4, 325–360. [Google Scholar]
- Lo, H.-K. Getting something out of nothing. Quantum Inf. Comput. 2005, 5, 413–418. [Google Scholar]
- Lo, H.-K.; Chau, H.F.; Ardehali, M. Efficient Quantum Key Distribution Scheme and a Proof of Its Unconditional Security. J. Cryptol. 2005, 18, 133–165. [Google Scholar]
- Brassard, G.; Salvail, L. Secret-Key Reconciliation by Public Discussion. In Advances in Cryptology EUROCRYPT’93; Helleseth, T., Ed.; Springer: Berlin, Germany, 1994; pp. 410–423. [Google Scholar]
- Ma, X.; Qi, B.; Zhao, Y.; Lo, H.-K. Practical decoy state for quantum key distribution. Phys. Rev. A. 2005, 72, 012326. [Google Scholar]
- Bazaraa, M.S.; Jarvis, J.J.; Sherali, H.D. Linear Programming and Network Flows, 3rd ed; Wiley: New York, NY, USA, 2004. [Google Scholar]
- Arfken, G. Mathematical Methods for Physicists, 3rd ed; Academic Press: New York, NY, USA, 1985. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th ed; Dover: New York, NY, USA, 1972. [Google Scholar]
- Corcoran, B.; Monat, C.; Grillet, C.; Moss, D.J.; Eggleton, B.J.; White, T.P.; O’Faolain, L.; Krauss, T.F. Green light emission in silicon through slow-light enhanced third-harmonic generation in photonic-crystal waveguides. Nat. Photonics. 2009, 3, 206–210. [Google Scholar]
- Rivoire, K.; Lin, Z.; Hatami, F.; Vučković, J. Sum-frequency generation in doubly resonant GaP photonic crystal nanocavities. Appl. Phys. Lett. 2010, 97, 043103. [Google Scholar]
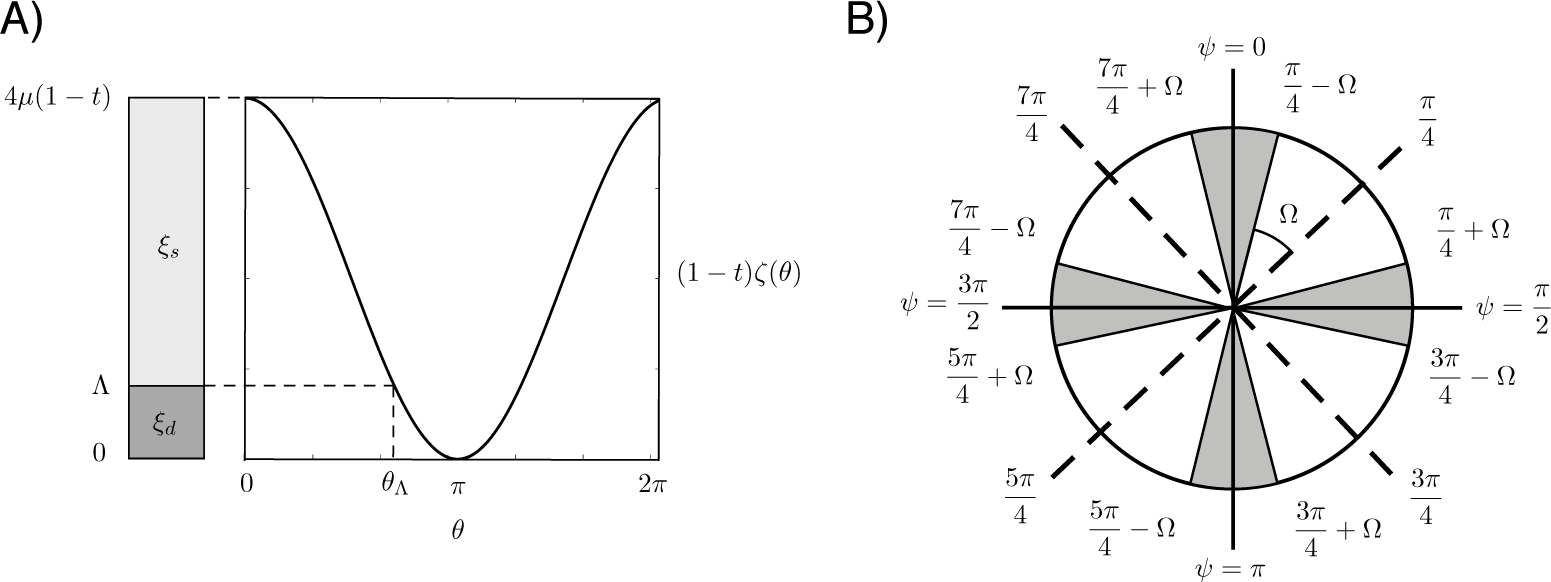
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Curty, M.; Jofre, M.; Pruneri, V.; Mitchell, M.W. Passive Decoy-State Quantum Key Distribution with Coherent Light. Entropy 2015, 17, 4064-4082. https://doi.org/10.3390/e17064064
Curty M, Jofre M, Pruneri V, Mitchell MW. Passive Decoy-State Quantum Key Distribution with Coherent Light. Entropy. 2015; 17(6):4064-4082. https://doi.org/10.3390/e17064064
Chicago/Turabian StyleCurty, Marcos, Marc Jofre, Valerio Pruneri, and Morgan W. Mitchell. 2015. "Passive Decoy-State Quantum Key Distribution with Coherent Light" Entropy 17, no. 6: 4064-4082. https://doi.org/10.3390/e17064064
APA StyleCurty, M., Jofre, M., Pruneri, V., & Mitchell, M. W. (2015). Passive Decoy-State Quantum Key Distribution with Coherent Light. Entropy, 17(6), 4064-4082. https://doi.org/10.3390/e17064064



