Dimensional Upgrade Approach for Spatial-Temporal Fusion of Trend Series in Subsidence Evaluation
Abstract
:1. Introduction
2. Study Background
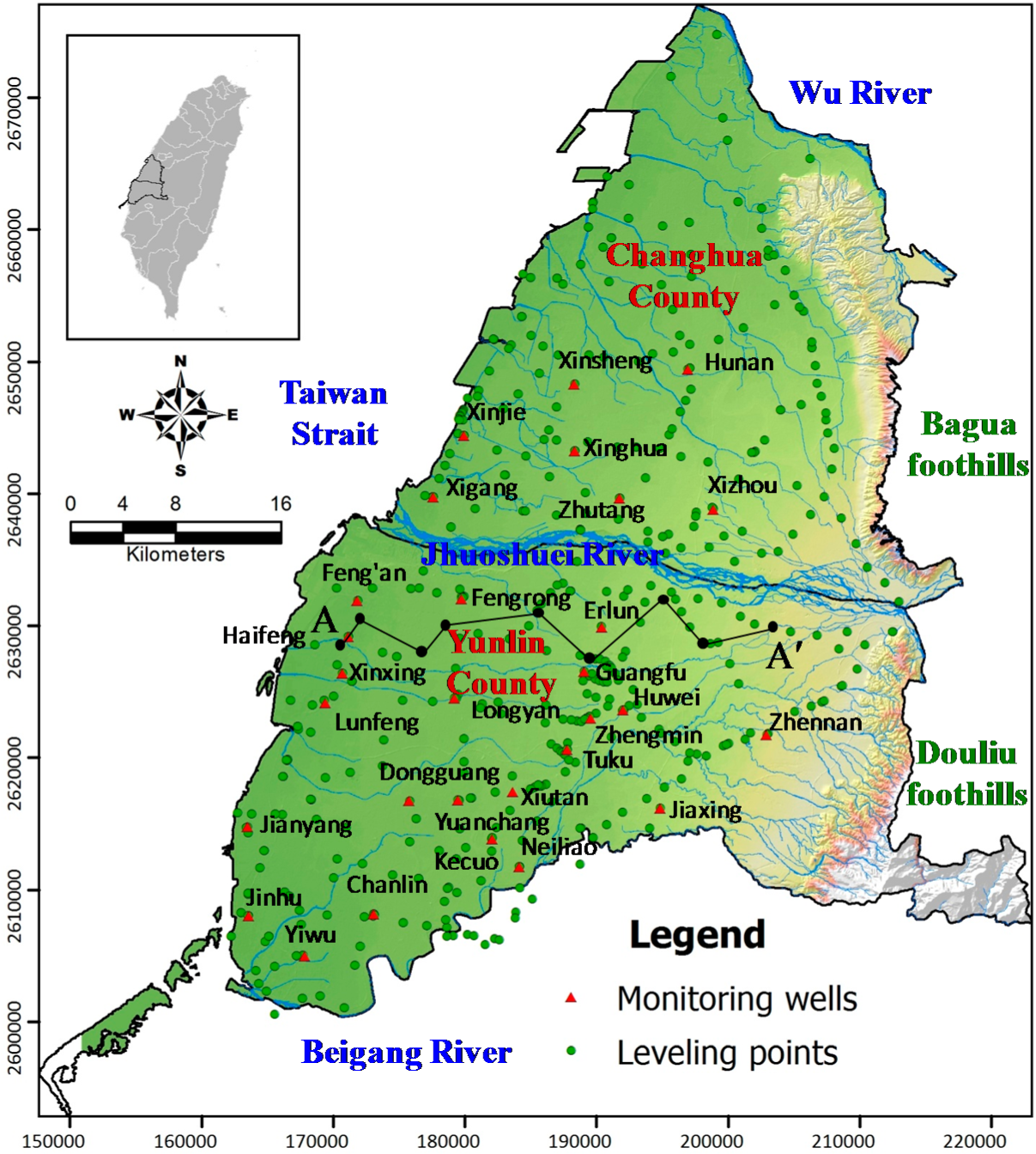
2.1. Study Area
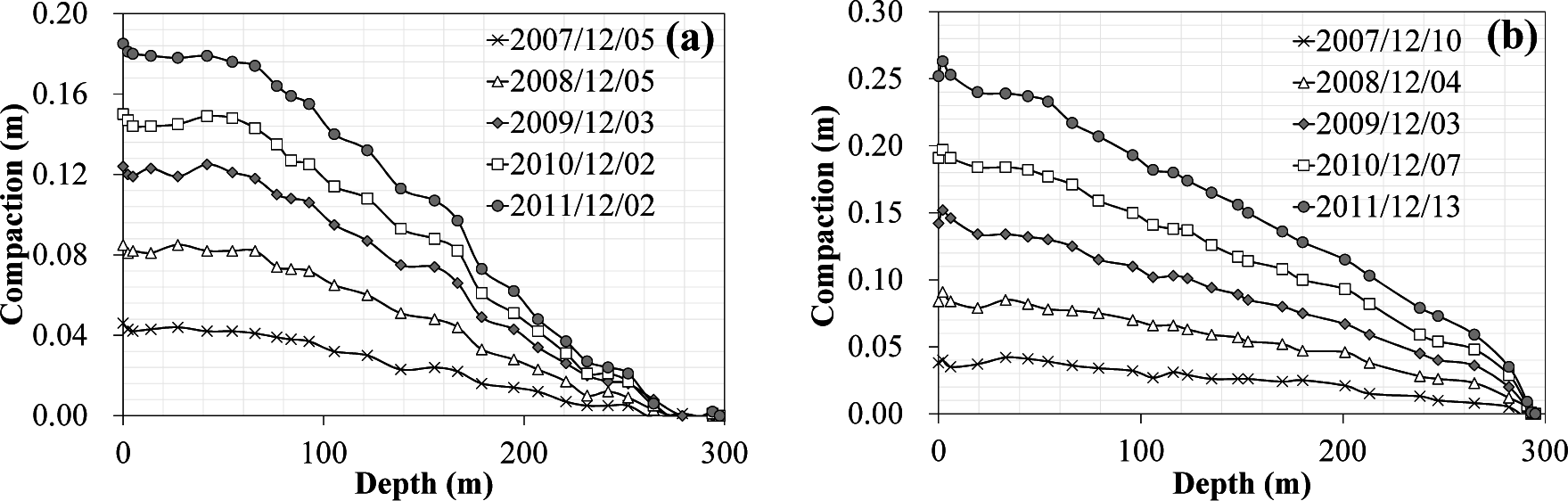
2.2. Subsidence Monitoring
3. Methodology
3.1. Nonlinear Poroelastic Model
3.2. Grey System Model
3.3. Model Settings
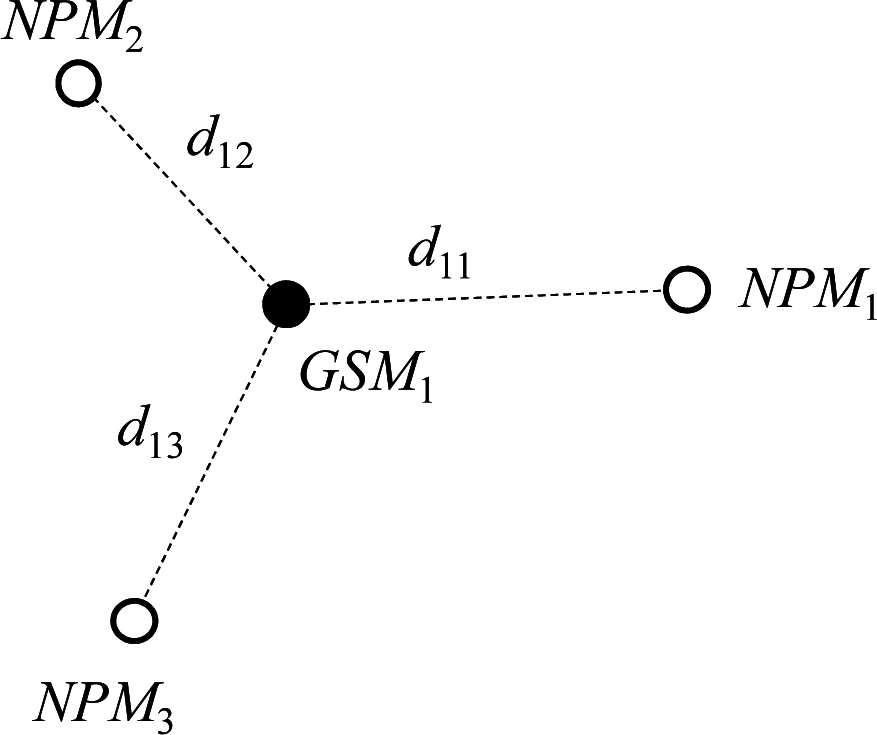
3.4. Fusion Method
4. Results and Discussion
4.1. Results for Nonlinear Poroelastic Model
4.2. Results for Grey System Model
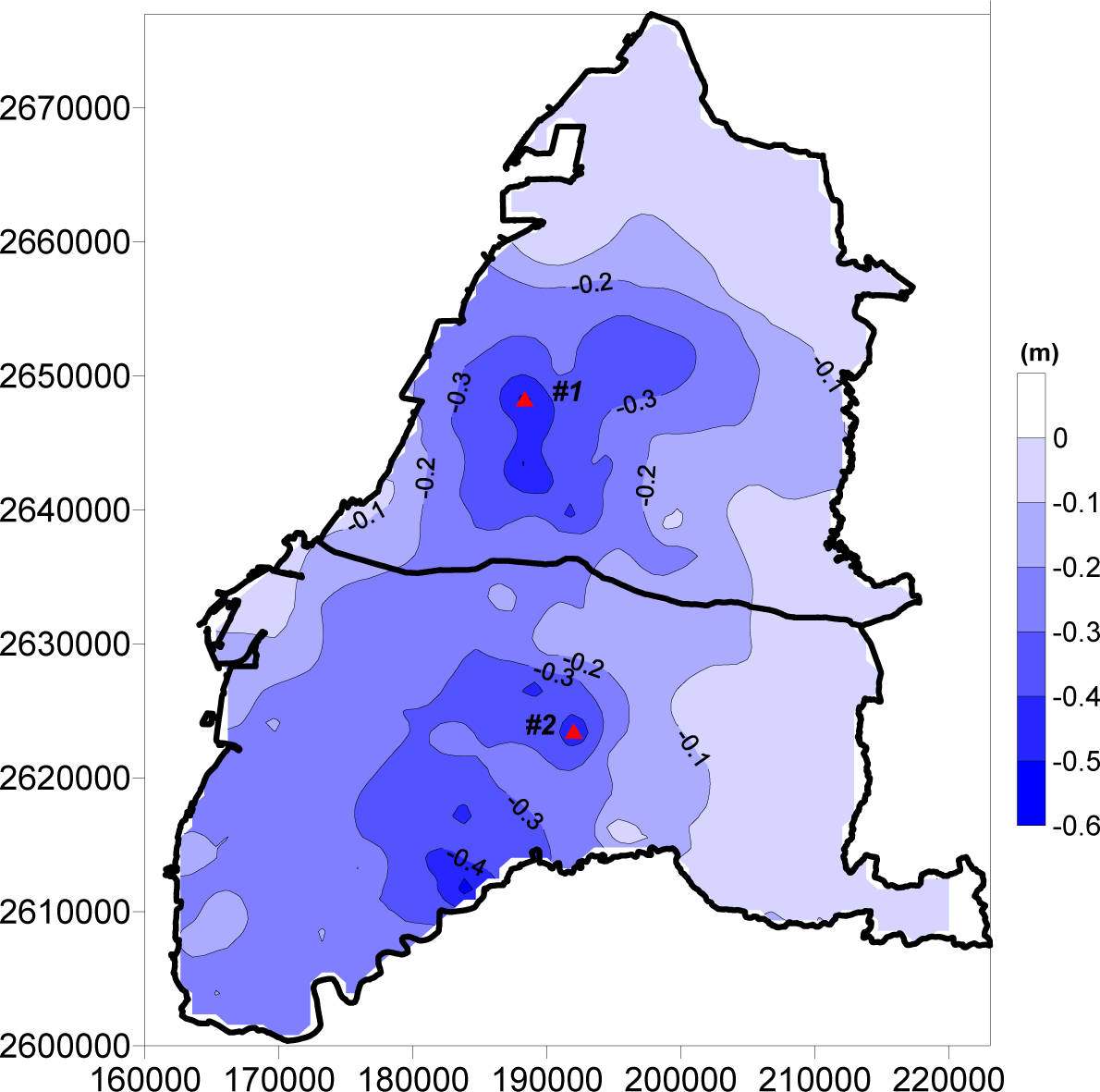
4.3. Subsidence Fusion Results
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Bell, F. Engineering Geology, 2nd ed; Butterworth-Heinemann: Oxford, UK, 2007. [Google Scholar]
- Chen, Z.; Rybczyk, J. Coastal Subsidence. In Encyclopedia of Coastal Science; Schwartz, M., Ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2005. [Google Scholar]
- Galloway, D.; Burbey, T. Review: Regional land subsidence accompanying groundwater extraction. Hydrogeol. J 2011, 19, 1459–1486. [Google Scholar]
- Galloway, D.L.; Jones, D.R.; Ingebritsen, S.E. Land Subsidence in the United States: US Geological Survey Circular 1182; U.S. Department of the Interior, U.S. Geological Survey: Washington, DC, USA, 1999. [Google Scholar]
- Bell, J.W.; Amelung, F.; Ramelli, A.R.; Blewitt, G. Land subsidence in Las Vegas, Nevada, 1935–2000: New geodetic data show evolution, revised spatial patterns, and reduced rates. Environ. Eng. Geosci 2002, 8, 155–174. [Google Scholar]
- Bock, Y.; Wdowinski, S.; Ferretti, A.; Novali, F.; Fumagalli, A. Recent subsidence of the Venice Lagoon from continuous GPS and Interferometric Synthetic Aperture Radar. Geochem. Geophys. Geosyst 2012, 13, 1–13. [Google Scholar]
- Galloway, D.; Jones, D.R.; Ingebritsen, S. Measuring Land Subsidence from Space; USGS Fact Sheet-051-00; US Department of the Interior, US Geological Survey: Washington, DC, USA, 2000. [Google Scholar]
- Hung, W.C.; Hwang, C.W.; Chang, C.P.; Yen, J.Y.; Liu, C.H.; Yang, W.H. Monitoring severe aquifer-system compaction and land subsidence in Taiwan using multiple sensors: Yunlin, the southern Choushui River Alluvial Fan. Environ. Earth Sci 2010, 59, 1535–1548. [Google Scholar]
- Jambrik, R. Analysis of water level and land subsidence data from thorez open-pit mine, Hungary. Mine Water Environ 1995, 14, 13–22. [Google Scholar]
- Liu, B.; Dai, W.; Peng, W.; Meng, X. Spatio-temporal analysis of the land subsidence in the UK using Independent Component Analysis. Proceedings of the 2014 3rd International Workshop on Earth Observation and Remote Sensing Applications, Changsha, China, 11–14 June 2014.
- Asadi, A.; Shahriar, K.; Goshtasbi, K.; Najm, K. Development of a new mathematical model for prediction of surface subsidence due to inclined coal-seam mining. J. S. Afr. Inst. Min. Metall 2005, 105, 15–20. [Google Scholar]
- Cui, X.; Miao, X.; Wang, J.; Yang, S.; Liu, H.; Hu, X. Improved prediction of differential subsidence caused by underground mining. Int. J. Rock Mech. Min. Sci 2000, 37, 615–627. [Google Scholar]
- Dai, H.; Wang, J.; Cai, M.; Wu, L.; Guo, Z. Seam dip angle based mining subsidence model and its application. Int. J. Rock Mech. Min. Sci 2002, 39, 115–123. [Google Scholar]
- Donnelly, L.J.; de la Cruz, H.; Asmar, I.; Zapata, O.; Perez, J.D. The monitoring and prediction of mining subsidence in the Amaga, Angelopolis, Venecia and Bolombolo Regions, Antioquia, Colombia. Eng. Geol 2001, 59, 103–114. [Google Scholar]
- Rodriguez, R.; Torano, J. Hypothesis of the multiple subsidence trough related to very steep and vertical coal seams and its prediction through profile function. Geotech. Geol. Eng 2000, 18, 289–311. [Google Scholar]
- Ferronato, M.; Gambolati, G.; Janna, C.; Teatini, P. Numerical modelling of regional faults in land subsidence prediction above gas/oil reservoirs. Int. J. Numer. Anal. Methods Geomech 2008, 32, 633–657. [Google Scholar]
- Ferronato, M.; Gambolati, G.; Teatini, P.; Bau, D. Stochastic poromechanical modeling of anthropogenic land subsidence. Int. J. Solids Struct 2006, 43, 3324–3336. [Google Scholar]
- Gambolati, G.; Ricceri, G.; Bertoni, W.; Brighenti, G.; Vuillermin, E. Mathematical simulation of the subsidence of Ravenna. Water Resour. Res 1991, 27, 2899–2918. [Google Scholar]
- Gambolati, G.; Teatini, P.; Bau, D.; Ferronato, M. Importance of poroelastic coupling in dynamically active aquifers of the Po river basin, Italy. Water Resour. Res 2000, 36, 2443–2459. [Google Scholar]
- Hoffmann, J.; Galloway, D.; Zebker, H. Inverse modeling of interbed storage parameters using land subsidence observations, Antelope Valley, California. Water Resour. Res 2003, 39. [Google Scholar] [CrossRef]
- Hung, W.C.; Hwang, C.W.; Liou, J.C.; Lin, Y.S.; Yang, H.L. Modeling aquifer-system compaction and predicting land subsidence in central Taiwan. Eng. Geol 2012, 147–148, 78–90. [Google Scholar]
- Teatini, P.; Ferronato, M.; Gambolati, G.; Gonella, M. Groundwater pumping and land subsidence in the Emilia-Romagna coastland, Italy: Modeling the past occurrence and the future trend. Water Resour. Res 2006, 42. [Google Scholar] [CrossRef]
- Teatini, P.; Ferronato, M.; Gambolati, G.; Baù, D.; Putti, M. Anthropogenic Venice uplift by seawater pumping into a heterogeneous aquifer system. Water Resour. Res 2010, 46. [Google Scholar] [CrossRef]
- Wang, S.J.; Lee, C.H.; Hsu, K.C. A Technique for quantifying groundwater pumping and land subsidence using a nonlinear stochastic poroelastic model. Environ. Earth Sci 2015. [Google Scholar] [CrossRef]
- Wang, S.J.; Lee, C.H.; Chen, J.W.; Hsu, K.C. Combining grey system and poroelastic models to investigate subsidence problem in Tainan, Taiwan. Environ. Earth Sci 2015. [Google Scholar] [CrossRef]
- Terzaghi, K. Erdbaumechanik auf Boenphysikalischer Grundlage; Deuticke: Vienna, Austria, 1925. [Google Scholar]
- Biot, M.A. General theory of three-dimensional consolidation. J. Appl. Phys 1941, 12, 155–164. [Google Scholar]
- Hoffmann, J.; Leake, S.A.; Galloway, D.L.; Wilson, A.M. MODFLOW-2000 Ground-Water Model-User Guide to the Subsidence and Aquifer-System Compaction (SUB) Package; Open-File Report 03—233; US Department of the Interior, US Geological Survey: Washington, DC, USA, 2003. [Google Scholar]
- Angulo, J.; Yu, H.L.; Langousis, A.; Madrid, A.E.; Christakos, G. Modeling of space-time infectious disease spread under conditions of uncertainty. Int. J. Geogr. Inf. Sci 2012, 26, 1751–1772. [Google Scholar]
- Azmani, M.; Reboul, S.; Benjelloun, M. Non-linear fusion of observations provided by two sensors. Entropy 2013, 15, 2698–2715. [Google Scholar]
- Buza, K.; Nanopoulos, A.; Schmidt-Thieme, L. Fusion of Similarity Measures for Time Series Classification. In Hybrid Artificial Intelligent Systems (HAIS) 2011; Goebel, R., Siekmann, J., Wahlster, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Part II, LNAI 6679; pp. 253–261. [Google Scholar]
- Lu, L.; Zhao, H. A novel convex combination of LMS adaptive filter for system identification. Proceedings of the 2014 12th International Conference on Signal Processing (ICSP), Hangzhou, China, 26–30 October 2014; pp. 225–229.
- Scarpiniti, M.; Comminiello, D.; Parisi, R.; Uncini, A. A collaborative approach to time-series prediction. Neural Nets WIRN11, Proceedings of the 21st Italian Workshop on Neural Nets, Salerno, Italy, 3–5 June 2011; pp. 178–185.
- Yan, W. Multiple model fusion for robust time-series forecasting. Proceedings of the Time-Series Forecasting Workshop of International Joint Conference on Neural Networks (IJCNN), Orlando, FL, USA, 12–17 August 2007.
- Yu, H.L.; Angulo, J.; Cheng, M.H.; Christakos, G. An online spatiotemporal prediction model for dengue fever epidemic in Kaohsuing (Taiwan). Biom. J 2014, 56, 428–440. [Google Scholar]
- Wang, S.J.; Hsu, K.C. Dynamic interactions of groundwater flow and soil deformation in randomly heterogeneous porous media. J. Hydrol 2013, 499, 50–60. [Google Scholar]
- Kim, J.M.; Parizek, R.R. A mathematical model for the hydraulic properties of deforming porous media. Ground Water 1999, 37, 546–554. [Google Scholar]
- Wang, S.J.; Hsu, K.C. Dynamics of deformation and water flow in heterogeneous porous media and its impact on soil properties. Hydrol. Processes 2009, 23, 3569–3582. [Google Scholar]
- Hsu, K.-C.; Wang, S.-J.; Wang, C.-L. Estimating Poromechanical Properties Using a Nonlinear Poroelastic Model. J. Geotech. Geoenviron. Eng 2013, 139, 1396–1401. [Google Scholar]
- Deng, J.L. Control problems of grey system. Syst. Control Lett 1982, 1, 288–294. [Google Scholar]
- Hydrotech Research Institute, National Taiwan University, The Execution Performance, Development and Planning of Groundwater Monitoring Networks (1/2); Taiwan Water Resources Agency, Ministry of Economic Affairs; Taipei, Taiwan, 2007; In Chinese.
- Green Environmental Engineering Consultant, Application of Multi-Sensor and Integrated Technologies to the Monitoring of Subsidence in Taipei, Changhua and Yunlin Area in 2014; Taiwan Water Resources Agency, Ministry of Economic Affairs: Taipei, Taiwan, 2014; In Chinese.
- Hwang, C.; Hung, W.C.; Liu, C.H. Results of geodetic and geotechnical monitoring of subsidence for Taiwan High Speed Rail operation. Nat. Hazards 2008, 47, 1–16. [Google Scholar]
- Wang, S.J.; Hsu, K.C. The application of the first-order second-moment method to analyze poroelastic problems in heterogeneous porous media. J. Hydrol 2009, 369, 209–221. [Google Scholar]
- Deng, J.L. Introduction to Grey System Theory. J. Grey Syst 1989, 1, 1–24. [Google Scholar]
- Hung, Y.F.; Wen, K.L.; Wang, L.K. GM(1,1), version 1.0; Grey System and Information Security Lab (GSISL) & Grey System Research Center (GSRC): Taichung, Taiwan, 2003. [Google Scholar]
- Das, B.M. Principles of Geotechnical Engineering, 4th ed; PWS Publishing Company: Boston, MA, USA, 1998. [Google Scholar]
- Institute for Physical Planning and Information, The Project of Territory Plan in 2006: 7-4-3 the Divisions of the National Disaster Prevention, to Review the Existing Disaster Prevention and the Network Planning of the Space System; Construction and Planning Agency, Ministry of the Interior: Taipei, Taiwan, 2007; In Chinese.




| County | MCMWName | Monitoring Depth (m) | Install Time (month-year) | E (TWD97) | N (TWD97) |
|---|---|---|---|---|---|
| Changhua | Xinjie | 300 | May-98 | 179967 | 2644391 |
| Xigang | 300 | May-97 | 177633 | 2639733 | |
| Xinghua | 300 | October-03 | 188363 | 2643201 | |
| Xinsheng | 300 | April-08 | 188341 | 2648279 | |
| Hunan | 300 | September-05 | 196984 | 2649404 | |
| Xizhou | 300 | October-07 | 198873 | 2638772 | |
| Zhutang | 300 | October-07 | 191773 | 2639649 | |
| Yunlin | Feng’an | 300 | July-96 | 171858 | 2631893 |
| Haifeng | 200 | December-94 | 171149 | 2629139 | |
| Xinxing | 300 | July-96 | 170720 | 2626355 | |
| Lunfeng | 200 | December-94 | 169441 | 2624157 | |
| Jianyang | 200 | December-94 | 163505 | 2614756 | |
| Dongguang* | 300 | August-09 | 175782 | 2616754 | |
| Jinhu | 200 | December-94 | 163597 | 2608018 | |
| Yiwu* | 300 | August-09 | 167840 | 2604973 | |
| Chanlin | 300 | April-08 | 173087 | 2608156 | |
| Erlun | 300 | April-08 | 190428 | 2629865 | |
| Fengrong | 300 | April-08 | 179784 | 2632015 | |
| Yuanchang | 300 | January-03 | 179484 | 2616803 | |
| Kecuo | 300 | October-03 | 182074 | 2613831 | |
| Neiliao | 300 | October-07 | 184141 | 2611722 | |
| Tuku | 300 | September-03 | 187771 | 2620610 | |
| Xiutan | 300 | August-06 | 183651 | 2617396 | |
| Huwei | 300 | March-06 | 192040 | 2623605 | |
| Guangfu | 300 | October-07 | 189083 | 2626507 | |
| Zhengmin* | 330 | August-09 | 189570 | 2622974 | |
| Longyan | 300 | March-06 | 179249 | 2624490 | |
| Zhennan | 300 | October-07 | 202938 | 2621719 | |
| Jiaxing | 300 | April-08 | 194874 | 2616145 | |
| MCMW Name | Hydraulic Conductivity (m/s)a | Porositya | Young’s Modulus (N/m2)b | Poisson’s Ratio b |
|---|---|---|---|---|
| Xinjie | 8.17 × 10−8 | 0.449 | 1.00 × 107 | 0.3 |
| Xigang | 8.17 × 10−8 | 0.449 | 1.00 × 107 | 0.3 |
| Xinghua | 5.39 × 10−8 | 0.421 | 1.00 × 107 | 0.3 |
| Xinsheng | 8.17 × 10−8 | 0.449 | 1.00 × 107 | 0.3 |
| Hunan | 8.17 × 10−8 | 0.449 | 1.00 × 107 | 0.3 |
| Xizhou | 8.54 × 10−7 | 0.469 | 1.00 × 106 | 0.3 |
| Zhutang | 8.17 × 10−8 | 0.449 | 1.00 × 107 | 0.3 |
| Feng’an | 8.17 × 10−8 | 0.449 | 1.00 × 107 | 0.3 |
| Haifeng | 8.17 × 10−8 | 0.449 | 1.00 × 107 | 0.3 |
| Xinxing | 8.17 × 10−8 | 0.449 | 1.00 × 107 | 0.3 |
| Lunfeng | 8.17 × 10−8 | 0.449 | 1.00 × 107 | 0.3 |
| Jianyang | 8.17 × 10−8 | 0.449 | 1.00 × 107 | 0.3 |
| Dongguang | 5.34 × 10−8 | 0.452 | 1.00 × 107 | 0.3 |
| Jinhu | 8.17 × 10−8 | 0.449 | 1.00 × 107 | 0.3 |
| Yiwu | 4.05 × 10−9 | 0.474 | 1.00 × 107 | 0.3 |
| Chanlin | 8.17 × 10−8 | 0.449 | 1.00 × 107 | 0.3 |
| Erlun | 8.17 × 10−8 | 0.449 | 1.00 × 107 | 0.3 |
| Fengrong | 8.17 × 10−8 | 0.449 | 1.00 × 107 | 0.3 |
| Yuanchang | 1.66 × 10−8 | 0.431 | 1.00 × 107 | 0.3 |
| Kecuo | 8.17 × 10−8 | 0.449 | 1.00 × 107 | 0.3 |
| Neiliao | 8.17 × 10−8 | 0.449 | 1.00 × 107 | 0.3 |
| Tuku | 4.48 × 10−6 | 0.447 | 1.00 × 106 | 0.3 |
| Xiutan | 8.17 × 10−8 | 0.449 | 1.00 × 107 | 0.3 |
| Huwei | 3.88 × 10−8 | 0.453 | 1.00 × 107 | 0.3 |
| Guangfu | 5.43 × 10−8 | 0.461 | 1.00 × 107 | 0.3 |
| Zhengmin | 5.27 × 10−8 | 0.467 | 1.00 × 107 | 0.3 |
| Longyan | 1.36 × 10−7 | 0.411 | 1.00 × 107 | 0.3 |
| Zhennan | 6.62 × 10−8 | 0.443 | 1.00 × 107 | 0.3 |
| Jiaxing | 8.17 × 10−8 | 0.449 | 1.00 × 107 | 0.3 |
| County | Station | Loading (N/m2) | Discharge (m/s) | R2 |
|---|---|---|---|---|
| Changhua | Xinjie | 1.07 × 104 | 0 | 0.945 |
| Xigang | 6.64 × 103 | 0 | 0.710 | |
| Xinghua | 5.02 × 103 | 9.25 × 10−10 | 0.990 | |
| Xinsheng | 0 | 1.44 × 10−9 | 0.991 | |
| Hunan | 0 | 1.21 × 10−9 | 0.990 | |
| Xizhou | 0 | 4.46 × 10−10 | 0.980 | |
| Zhutang | 1.29 × 103 | 1.04 × 10−9 | 0.993 | |
| Yunlin | Feng’an | 0 | 4.43 × 10−9 | 0.917 |
| Haifeng | 0 | 2.52 × 10−10 | 0.795 | |
| Xinxing | 0 | 8.62 × 10−10 | 0.958 | |
| Lunfeng | 0 | 4.37 × 10−10 | 0.898 | |
| Jianyang | 7.77 × 101 | 3.03 × 10−10 | 0.887 | |
| Jinhu | 1.27 × 103 | 3.26 × 10−10 | 0.813 | |
| Chanlin | 0 | 4.45 × 10−10 | 0.505 | |
| Erlun | 1.38 × 103 | 3.14 × 10−10 | 0.962 | |
| Fengrong | 0 | 7.84 × 10−10 | 0.893 | |
| Yuanchang | 0 | 1.96 × 10−9 | 0.954 | |
| Kecuo | 3.53 × 101 | 1.37 × 10−9 | 0.972 | |
| Neiliao | 4.21 × 102 | 1.51 × 10−9 | 0.950 | |
| Tuku | 0 | 2.58 × 10−9 | 0.867 | |
| Xiutan | 0 | 1.29 × 10−9 | 0.948 | |
| Huwei | 4.22 × 103 | 7.87 × 10−10 | 0.985 | |
| Guangfu | 0 | 9.46 × 10−10 | 0.978 | |
| Longyan | 0 | 1.40 × 10−9 | 0.975 | |
| Zhennan | 1.95 × 103 | 7.78 × 10−11 | 0.639 | |
| Jiaxing | 0 | 6.80 × 10−11 | 0.101 | |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.-J. Dimensional Upgrade Approach for Spatial-Temporal Fusion of Trend Series in Subsidence Evaluation. Entropy 2015, 17, 3035-3052. https://doi.org/10.3390/e17053035
Wang S-J. Dimensional Upgrade Approach for Spatial-Temporal Fusion of Trend Series in Subsidence Evaluation. Entropy. 2015; 17(5):3035-3052. https://doi.org/10.3390/e17053035
Chicago/Turabian StyleWang, Shih-Jung. 2015. "Dimensional Upgrade Approach for Spatial-Temporal Fusion of Trend Series in Subsidence Evaluation" Entropy 17, no. 5: 3035-3052. https://doi.org/10.3390/e17053035
APA StyleWang, S.-J. (2015). Dimensional Upgrade Approach for Spatial-Temporal Fusion of Trend Series in Subsidence Evaluation. Entropy, 17(5), 3035-3052. https://doi.org/10.3390/e17053035







