Multifractal Dimensional Dependence Assessment Based on Tsallis Mutual Information
Abstract
:1. Introduction
2. Preliminaries
2.1. Entropy, Divergence and Mutual Information
2.1.1. Entropy
2.1.2. Divergence
2.1.3. Mutual Information
2.2. Scaling Behavior and Multifractality
2.2.1. Generalized Rényi Dimensions
- “Capacity” dimension, : This shows how the points of a multifractal pattern fill the domain under study. The larger the value of this dimension, the better the space is covered.
- “Entropy” dimension, : This is a measure of order-disorder of the points in the domain under study. Larger values indicate higher disorder.
- “Correlation” dimension, : This quantifies the degree of clustering/inhibition. Lower values correspond to a higher level of clustering.
- “Multifractal step”, : This indicates the degree of multifractality. Larger values correspond to a stronger multifractal behavior. The multifractal step is zero for monofractal behavior.
2.2.2. Generalized Tsallis Dimensions
3. Dependence Analysis
3.1. Generalized Dependence Coefficients
3.1.1. A Formal Justification and Discussion
- (i)
- ,
- (ii)
- ,
- (iii)
- if and only if X and Y are independent and ,
- (iv)
- if and only if .
3.2. Generalized Dependence Coefficients in the Multifractal Domain
4. Application to a Real Seismic Series
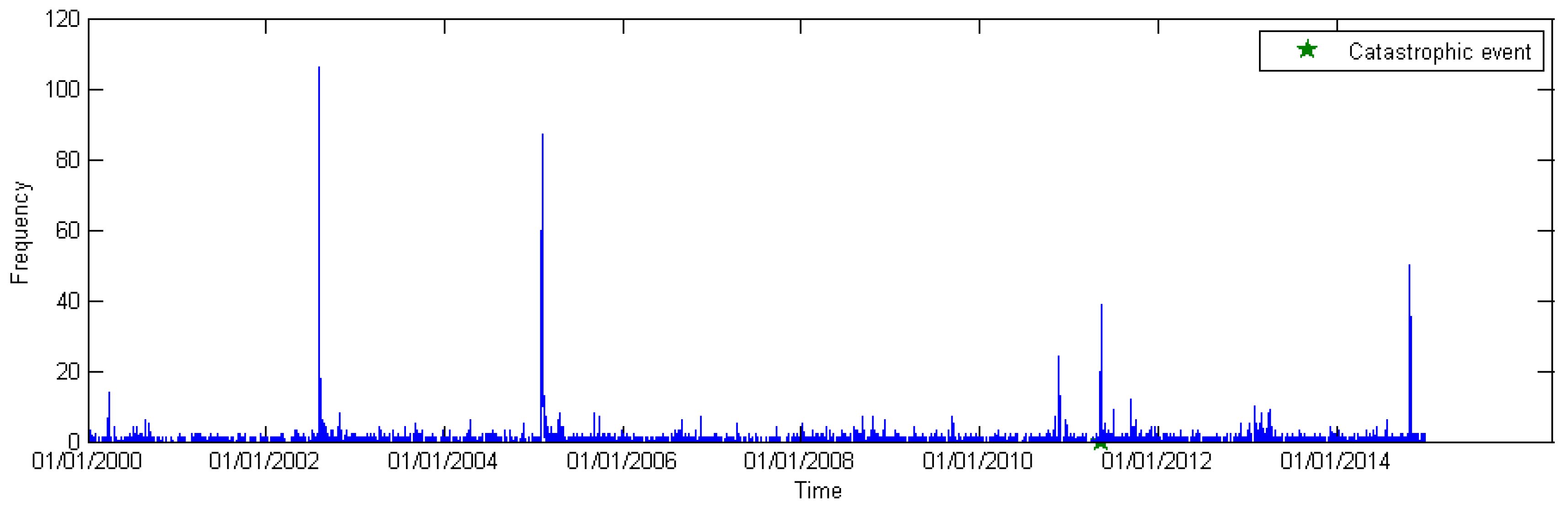
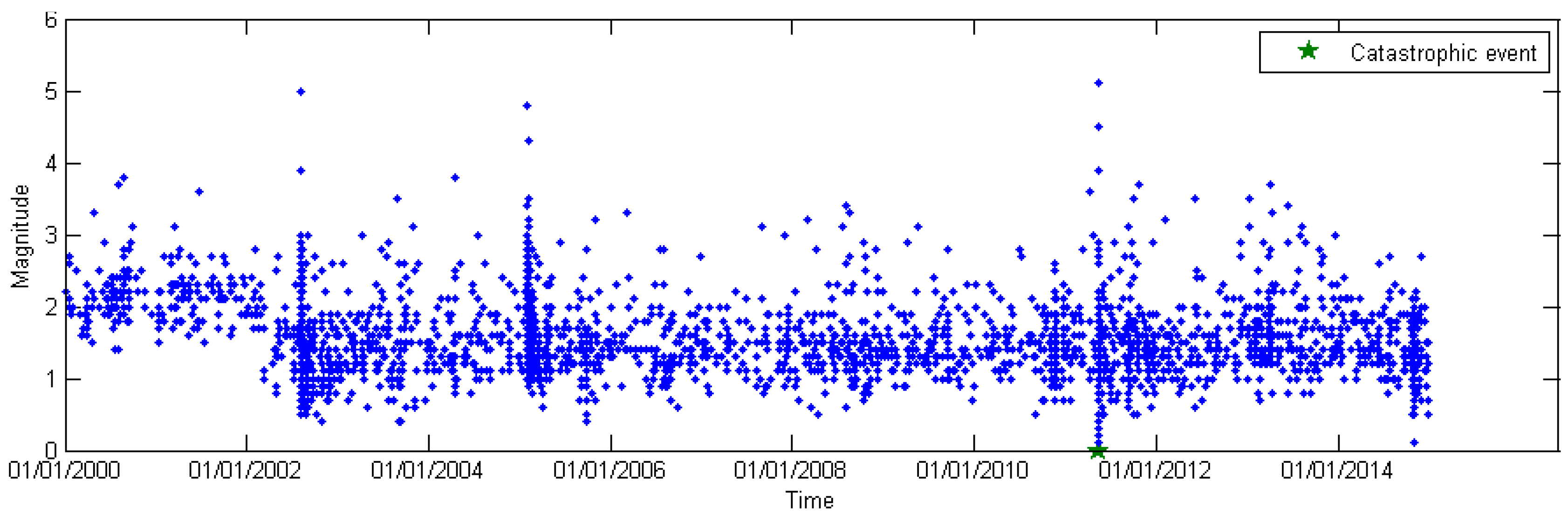
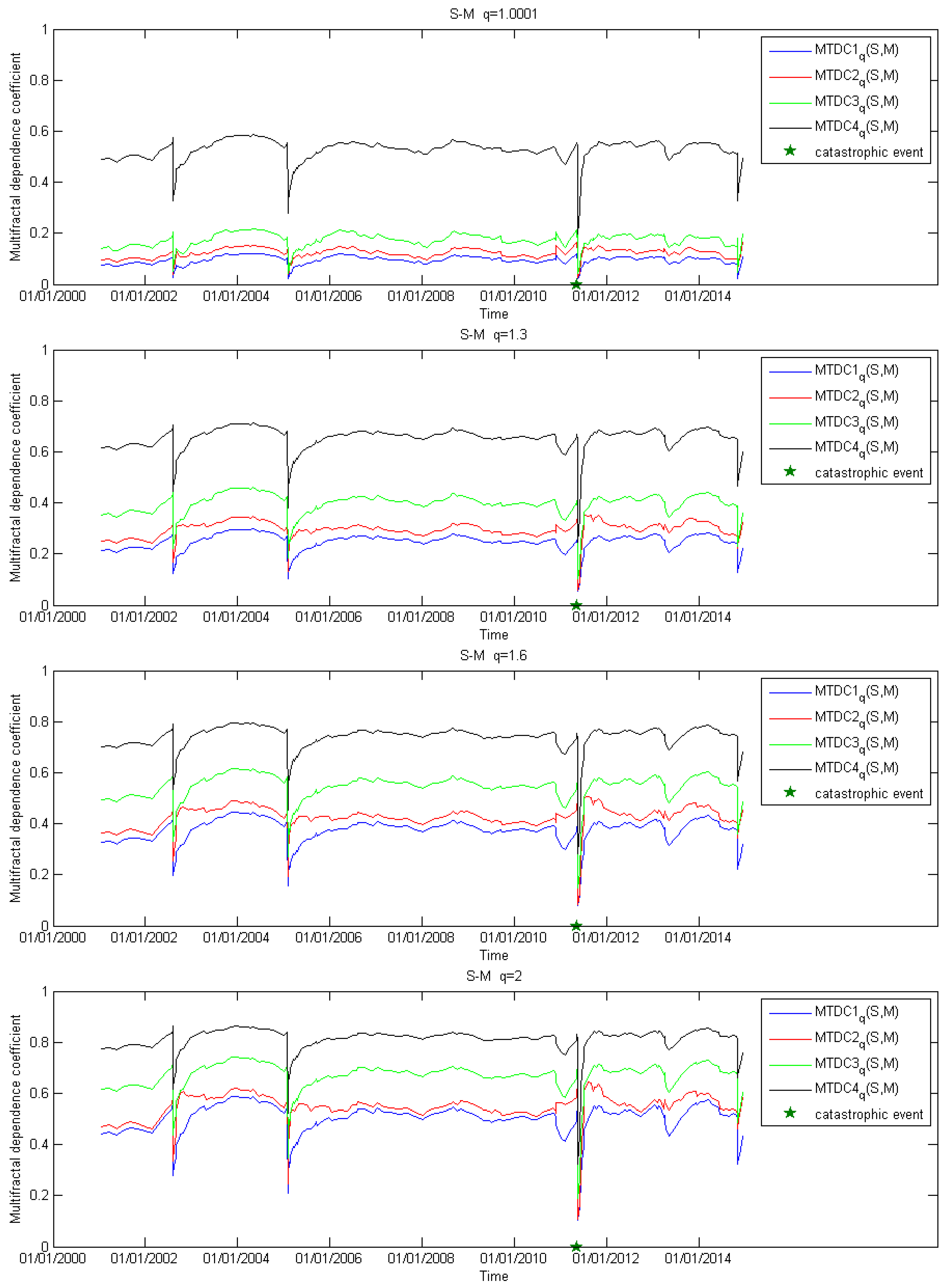

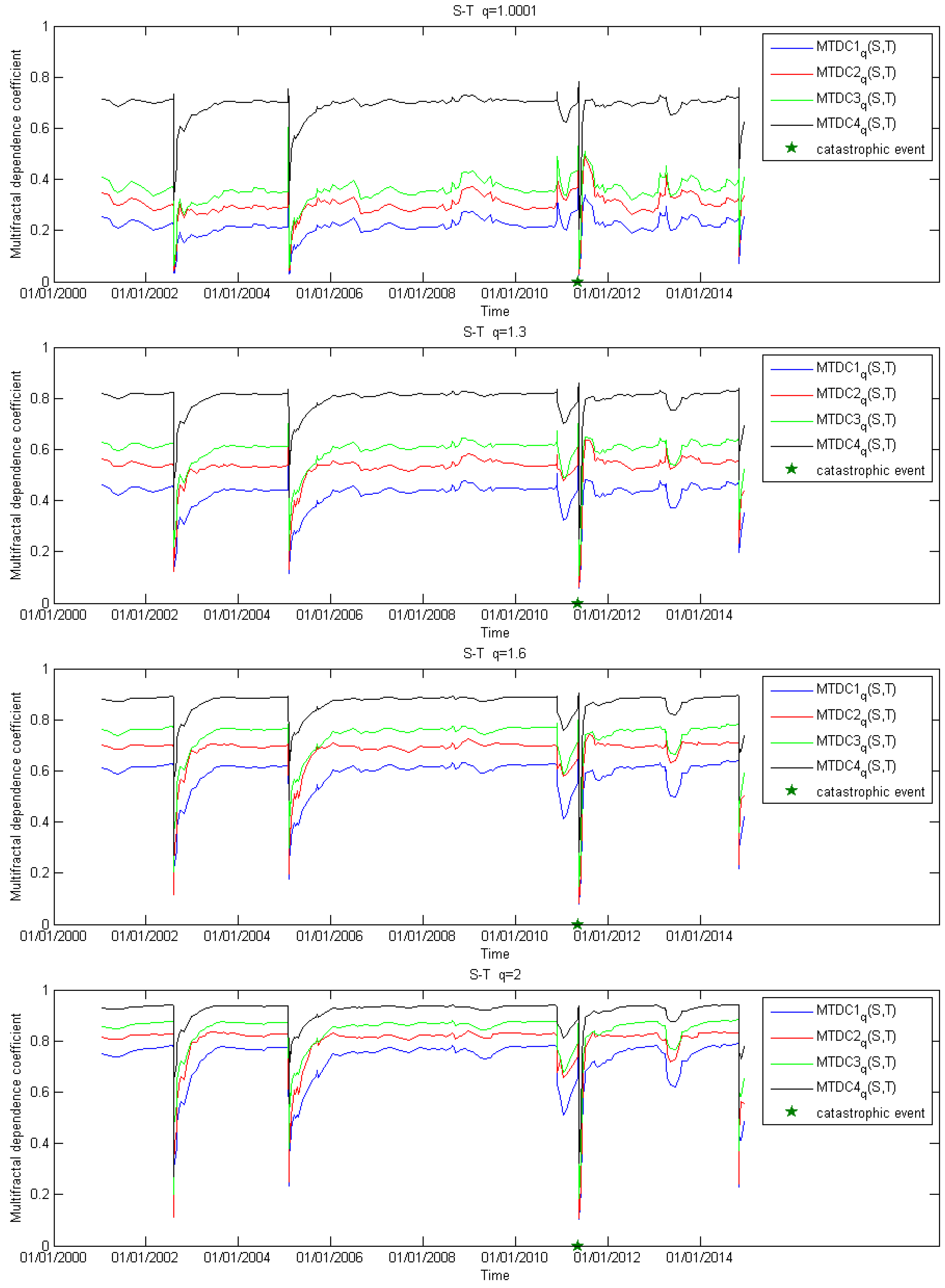
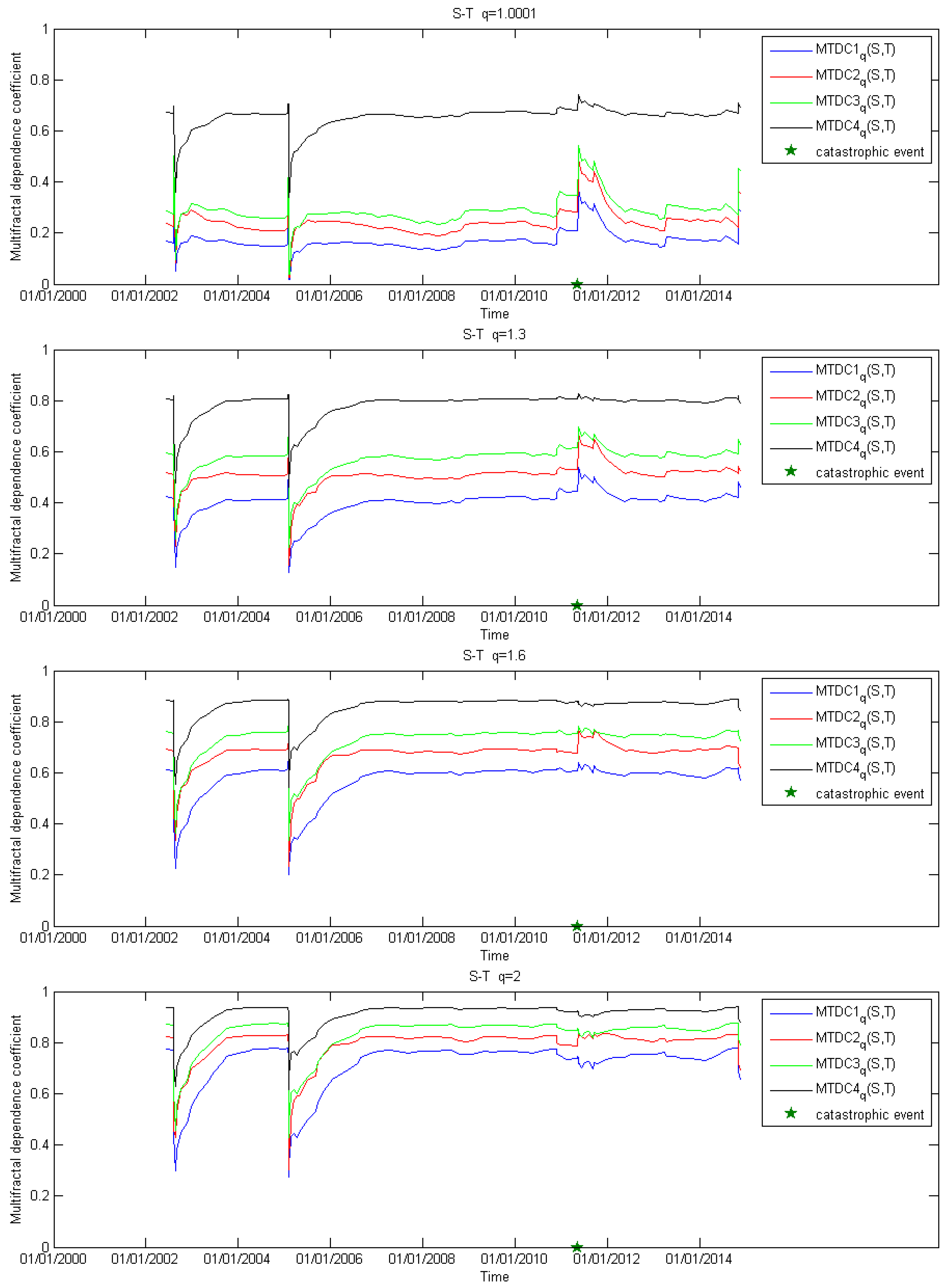
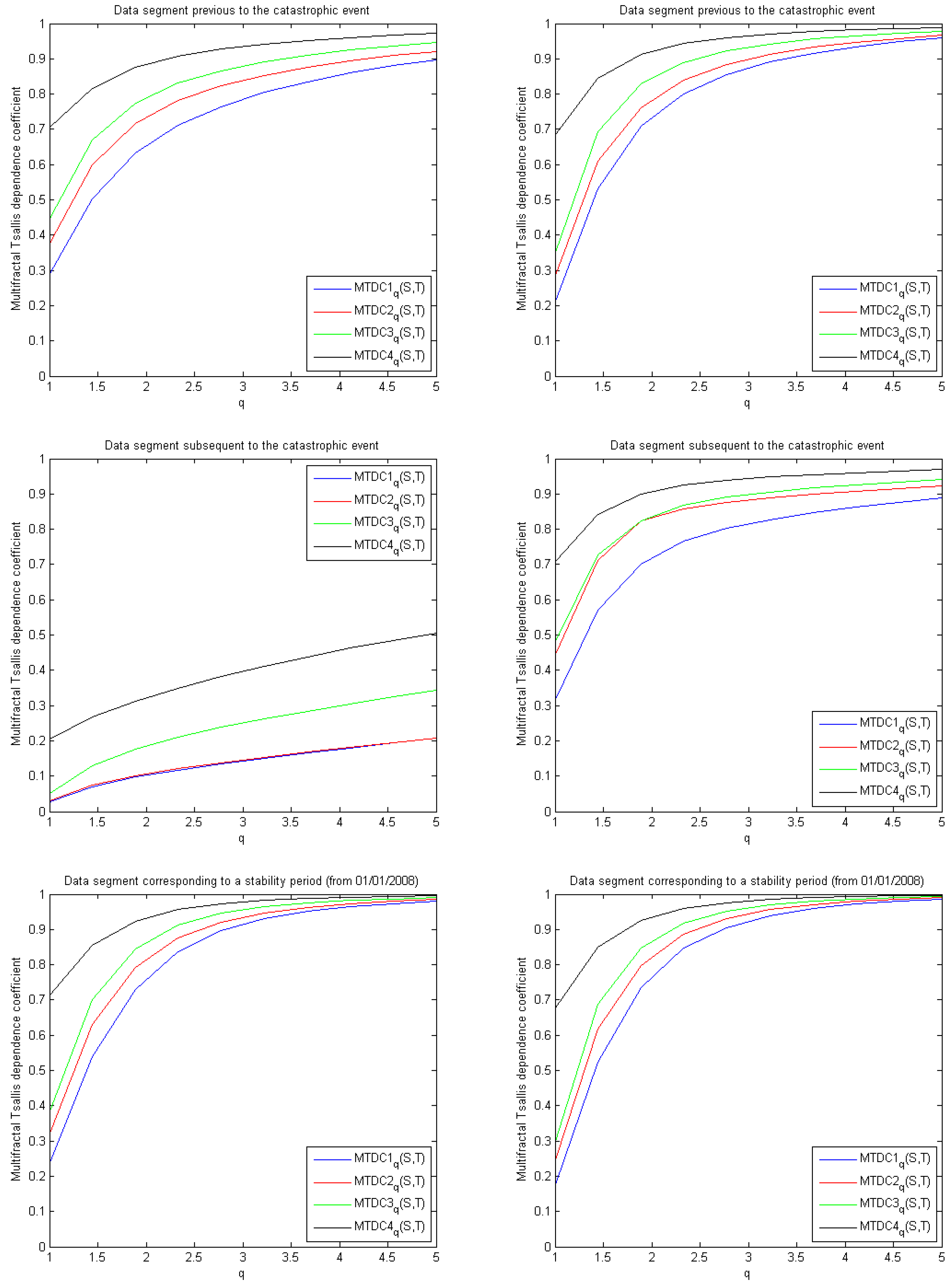
5. Conclusion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Beckerman, L.P. Application of Complex Systems Science to Systems Engineering. Syst. Eng. 2000, 3, 96–102. [Google Scholar] [CrossRef]
- Newth, D.; Finnigan, J. Emergence and Self-organization in Chemistry and Biology. Aust. J. Chem. 2007, 59, 841–848. [Google Scholar] [CrossRef]
- Prokopenko, M.; Boschetti, F.; Ryan, A.J. An Information-Theoretic Primer on Complexity, Self-organization, and Emergence. Complexity 2009, 15, 11–28. [Google Scholar] [CrossRef]
- Baranger, M. Chaos, Complexity, and Entropy. Available online: http://necsi.edu/projects/baranger/cce.pdf (accessed on 21 July 2015).
- Samet, R.H. Long-Range Futures Research: An Application of Complexity Science; Book Surge Publishing: North Charleston, SC, USA, 2009. [Google Scholar]
- Biswas, A.; Zeleke, T.B.; Si, B.C. Multifractal Detrended Fluctuation Analysis in Examining Scaling Properties of the Spatial Patterns of Soil Water Storage. Nonlin. Proc. Geophys. 2012, 19, 227–238. [Google Scholar] [CrossRef]
- Harte, D. Multifractals: Theory and Applications; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal Detrended Fluctuation Analysis of Nonstationary Time Series. Physica A 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Lin, A.; Ma, H.; Shang, P. The Scaling Properties of Stock Markets Based on Modified Multiscale Multifractal Detrended Fluctuation Analysis. Physica A 2015, 436, 525–537. [Google Scholar] [CrossRef]
- Stanley, H.E.; Meakin, P. Multifractal Phenomena in Physics and Chemistry. Nature 1988, 335, 405–409. [Google Scholar]
- Bouchet, F.; Gupta, S.; Mukamel, D. Thermodynamics and Dynamics of Systems with Long-Range Interactions. Physica A 2010, 389, 4389–4405. [Google Scholar] [CrossRef]
- Michas, G.; Vallianatos, F.; Sammonds, P. Non-extensivity and Long-Range Correlations in the Earthquake Activity at the West Corinth Rift (Greece). Nonlinear Proc. Geoph. 2013, 20, 713–724. [Google Scholar] [CrossRef]
- Prehl, J.; Essex, C.; Hoffmann, K.H. Tsallis Relative Entropy and Anomalous Diffusion. Entropy 2012, 14, 701–716. [Google Scholar] [CrossRef]
- Tsallis, C. Possible Generalization of Boltzmann-Gibbs Statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Yamano, T. Information Theory Based on Non-additive Information Content. Phys. Rev. E 2001, 63, 046105. [Google Scholar] [CrossRef]
- Yamano, T. A Possible Extension of Shannon's Information Theory. Entropy 2001, 3, 280–292. [Google Scholar] [CrossRef]
- Furuichi, S. Information Theoretical Properties of Tsallis Entropies. J. Math. Phys. 2006, 47, 023302. [Google Scholar] [CrossRef]
- Angulo, J.M.; Esquivel, F.J. Structural Complexity in Space-Time Seismic Event Data. Stoch. Env. Res. Risk. A 2014, 28, 1187–1206. [Google Scholar] [CrossRef]
- Esquivel, F.J.; Angulo, J.M. Non-extensive Analysis of the Seismic Activity Involving the 2011 Volcanic Eruption in El Hierro. Spat. Stat. 2015. (accepted). [Google Scholar]
- Bak, P.; Christensen, K.; Danon, L.; Scanlon, T. Unified Scaling Law for Earthquakes. Phys. Rev. Lett. 2002, 88, 178501. [Google Scholar] [CrossRef]
- Lennartz, S.; Bunde, A.; Turcotte, D.L. Modelling Seismic Catalogues by Cascade Models: Do We Need Long-Term Magnitude Correlations? Geophys. J. Int. 2011, 184, 1214–1222. [Google Scholar] [CrossRef]
- Main, I. Statistical Physics, Seismogenesis, and Seismic Hazard. Rev. Geophys. 1996, 34, 433–462. [Google Scholar] [CrossRef]
- Rundle, J.B.; Turcotte, D.L.; Shcherbakov, R.; Klein, W.; Sammis, C. Statistical Physics Approach to Understanding the Multiscale Dynamics of Earthquake Fault Systems. Rev. Geophys. 2003, 41, 1019. [Google Scholar]
- Saleur, H.; Sammis, C.G.; Sornette, D. Discrete Scale Invariance, Complex Fractal Dimensions and Log-Periodic Fluctuations in Seismicity. J. Geophys. Res. 1996, 101, 17661–17677. [Google Scholar] [CrossRef]
- Turcotte, D.L. Fractals and Chaos in Geology and Geophysics, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Varotsos, P.A.; Sarlis, N.V.; Tanaka, H.K.; Skordas, E.S. Similarity of Fluctuations in Correlated Systems: The Case of Seismicity. Phys. Rev. E 2005, 72, 041103. [Google Scholar] [CrossRef]
- Vere-Jones, D. Seismology—A Statistical Vignette. J. Am. Stat. Assoc. 2000, 95, 975–978. [Google Scholar]
- Vere-Jones, D. The Marriage of Statistics and Seismology. J. Appl. Probab. 2001, 38, 1–5. [Google Scholar] [CrossRef]
- Vere-Jones, D. Foundations of Statistical Seismology. Pure Appl. Geophys. 2010, 167, 645–653. [Google Scholar] [CrossRef]
- Sotolongo-Costa, O.; Rodriguez, A.H.; Rodgers, G.J. Tsallis Entropy and the Transition to Scaling in Fragmentation. Entropy 2000, 2, 172–177. [Google Scholar] [CrossRef]
- Telesca, L. A Non-extensive Approach in Investigating the Seismicity of L'Aquila Area (Central Italy), Struck by the 6 April 2009 Earthquake (ML = 5.8). Terra Nova 2010, 22, 87–93. [Google Scholar] [CrossRef]
- Telesca, L. Analysis of Italian Seismicity by Using a Nonextensive Approach. Tectonophysics 2010, 494, 155–162. [Google Scholar] [CrossRef]
- Telesca, L. Tsallis-Based Nonextensive Analysis of the Southern California Seismicity. Entropy 2011, 13, 1267–1280. [Google Scholar] [CrossRef]
- Telesca, L. Maximum Likelihood Estimation of the Nonextensive Parameters of the Earthquake Cumulative Magnitude Distribution. Bull. Seismol. Soc. Am. 2012, 102, 886–891. [Google Scholar] [CrossRef]
- Vallianatos, F.; Michas, G.; Papadakis, G.; Tzanis, A. Evidence of Non-extensivity in the Seismicity Observed during the 2011–2012 Unrest at the Santorini Volcanic Complex, Greece. Nat. Hazards Earth Syst. Sci. 2013, 13, 177–185. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Rényi, A. On Measures of Entropy and Information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, June 20–July 30 1960; Neyman, J., Ed.; University of California Press: Berkeley, CA, USA, 1961; Volume 1, pp. 547–561. [Google Scholar]
- Hanel, R.; Thurner, S. Generalized (c,d)-Entropy and Aging Random Walks. Entropy 2013, 15, 5324–5337. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Tsallis, C. Generalized Entropy-Based Criterion for Consistent Testing. Phys. Rev. E 1998, 58, 1442–1445. [Google Scholar] [CrossRef]
- Swingle, B. Rényi Entropy, Mutual Information, and Fluctuation Properties of Fermi Liquids. Phys. Rev. B 2012, 86, 045109. [Google Scholar] [CrossRef]
- Cvejic, N.; Canagarajah, C.N.; Bull, D.R. Image Fusion Metric Based on Mutual Information and Tsallis Entropy. Electron. Lett. 2006, 42, 626–627. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, L.; Guo, C.P. Medical Image Registration by Minimizing Divergence Measure Based on Tsallis Entropy. Int. J. Biol. Sci. 2008, 13, 809–814. [Google Scholar]
- Vila, M.; Bardera, A.; Feixas, M.; Sbert, M. Tsallis Mutual Information for Document Classification. Entropy 2011, 13, 1694–1707. [Google Scholar] [CrossRef]
- Halsey, T.C.; Jensen, M.H.; Kadanoff, L.P.; Procaccia, I.; Shraiman, B.I. Fractal Measures and Their Singularities: The Characterization of Strange Sets. Nucl. Phys. B 1986, 33, 1141–1151. [Google Scholar] [CrossRef]
- Hentschel, H.; Procaccia, I. The Infinite Number of Generalized Dimensions of Fractals and Strange Attractors. Physica D 1983, 8, 435–444. [Google Scholar] [CrossRef]
- Morales, J.; Cantavella, J.V.; Mancilla, F.; Lozano, L.; Stich, D.; Herraiz, E.; Matín, J.B.; Lopez-Comino, J.A.; Martinez-Solares, J.M. The 2011 Lorca Seismic Series: Temporal Evolution, Faulting Parameters and Hypocentral Relocation. Bull. Earthquake Eng. 2014, 12, 1871–1888. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Angulo, J.M.; Esquivel, F.J. Multifractal Dimensional Dependence Assessment Based on Tsallis Mutual Information. Entropy 2015, 17, 5382-5401. https://doi.org/10.3390/e17085382
Angulo JM, Esquivel FJ. Multifractal Dimensional Dependence Assessment Based on Tsallis Mutual Information. Entropy. 2015; 17(8):5382-5401. https://doi.org/10.3390/e17085382
Chicago/Turabian StyleAngulo, José M., and Francisco J. Esquivel. 2015. "Multifractal Dimensional Dependence Assessment Based on Tsallis Mutual Information" Entropy 17, no. 8: 5382-5401. https://doi.org/10.3390/e17085382
APA StyleAngulo, J. M., & Esquivel, F. J. (2015). Multifractal Dimensional Dependence Assessment Based on Tsallis Mutual Information. Entropy, 17(8), 5382-5401. https://doi.org/10.3390/e17085382




