1. Introduction
A critical factor in determining whether a surgical operation will succeed or not, lies in the regulation of depth of anaesthesia (DoA). Monitoring the DoA is an important task during any invasive surgical procedures which requires the patient to be unconscious [
1]. Most DoA monitoring methods to evaluate the degree of awareness of the patient during surgery are based on heart rate, blood pressure, electrocardiography (ECG) or electroencephalography (EEG). Among these, EEG can be used to clearly express the patient’s degree of consciousness as it has been shown that there is a significant difference between EEG signals acquired during conscious and unconscious states [
2–
4].
The whole operation process can be divided into three stages: before, maintenance and recovery, which are based on the time of induction, excision and the end of the operation. The before stage is defined from the moment the patient enters the operating room to them being intubated. At this stage, the patient can move his/her body or eyes, so the EEG signals tend to be very noisy and confused. The maintenance stage occurs between intubation and the end of operation during which the patient is under a deeply anaesthetized state. Consequently, the EEG signals at this maintenance stage are relatively more orderly than in other stages. After the surgery ends, the patient gradually regains consciousness during the recovery stage and the EEG signals will tend to be more complex during this stage. In order to accurately evaluate the DoA from the EEG signal, instantaneous frequency provides a convenient way of decomposing the different frequencies of the EEG signal, which can help the anaesthetist to better understand the different signal characteristics associated with the degree of consciousness of a patient [
5]. This can then be used to distinguish the different stages during a surgical procedure and as a consequence improve the monitoring of DoA though better managing the patients’ responses to the amount of anaesthetic administered. Empirical mode decomposition (EMD) is a method for analyzing non-stationary and nonlinear data such as analog as well as digitized signals, representing time-varying or spatially varying physical quantities [
6–
9]. The process involves decomposing these signals into several intrinsic mode functions (IMF), which are simple oscillatory functions with varying amplitude and frequency. IMFs provide a useful means for analysis in both the time and frequency domain simultaneously. Fast Fourier Transform (FFT) can then be used to convert these IMF back into a frequency domain, so that noise can be filtered out according to a desired frequency range of each IMF.
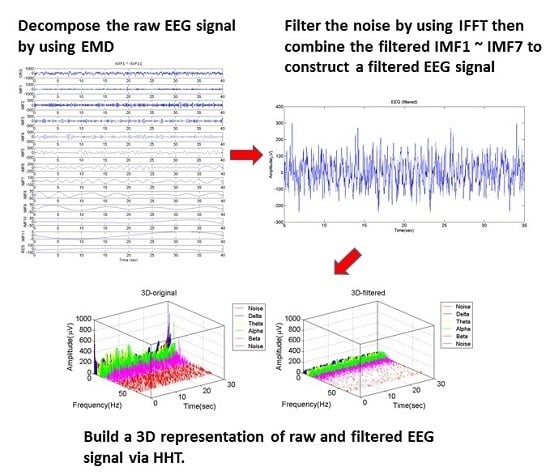
EMD can be used to initially filter out noise-related frequencies from the raw EEG signal and combine selected IMFs to represent a filtered EEG signal [
10]. The Hilbert–Huang transform (HHT) [
6] is then used to get the instantaneous frequency and instantaneous amplitude of the filtered EEG signal, which is suitable for analyzing non-stationary and nonlinear data, such as physiological signals [
6,
7]. The instantaneous frequency, instantaneous amplitude and time elements of the filtered EEG signal can then be recombined to build a real-time 3D representation of the EEG signal which can simultaneously express the amplitude and brain wave frequencies of the EEG signal and their variation with time. This can be achieved more accurately than traditional approaches, such as direct EEG monitoring or the FFT method, which cannot simultaneously display the instantaneous amplitude, frequency and time of an EEG signal. The 3D instantaneous frequency based model of the EEG signal can be used to differentiate the frequency band characteristics associated with the degrees of consciousness of the patient over the different surgical stages.
In this paper, we propose an approach towards the development of a 3D real-time visualization which can show the instantaneous frequency and instantaneous amplitude of EEG simultaneously by using EMD and HHT. Compared with the traditional physiological monitors, which are based on a 2D representation, this new representation can be used to enable the anaesthetist to more accurately monitor and evaluate the DoA of the patient during surgery and reduce risks to the patient during and from post-operative complications after surgery. The anaesthetist can also use the approach to visualize and assess the effects of different surgical procedures and patient’s pre-operative conditions by observing the 3D real-time representation.
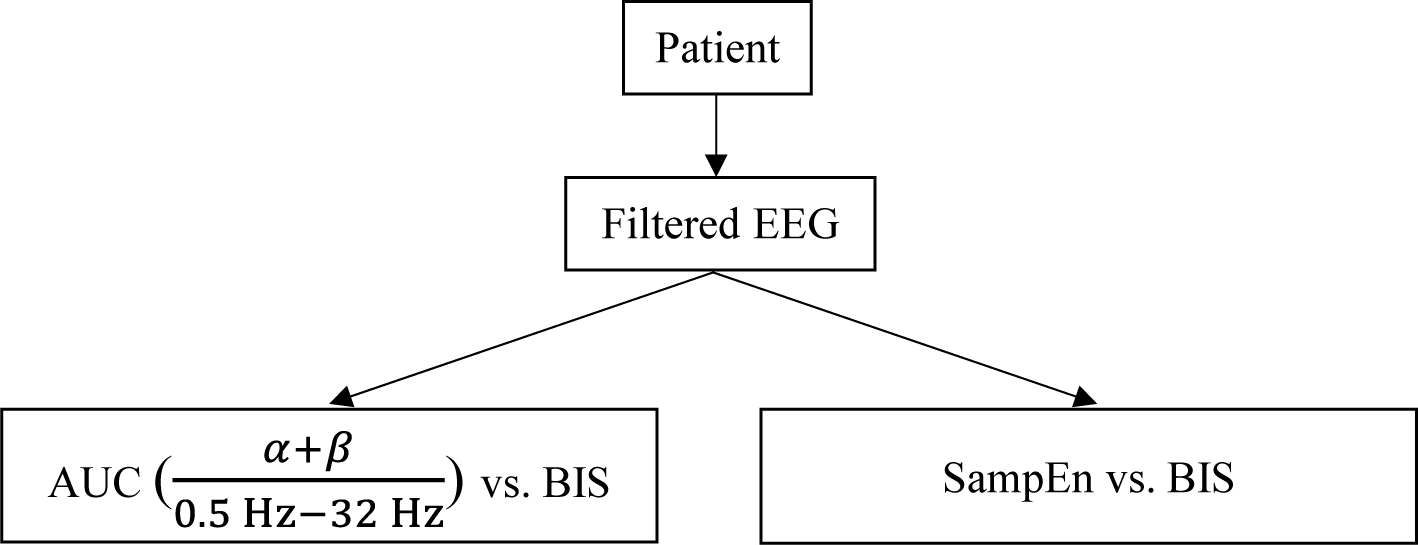
Our approach is evaluated based on its ability to differentiate between each of the three surgical stages (before, maintenance and recovery) using EEG data acquired during surgical procedures performed on thirty patients. Two indexes are applied at the end of the filtering process to distinguish the different operational stages, specifically the area ratio of α + β waves (8–32 Hz) under FFT curve (AUC) and sample entropy (SampEn) [
11–
13]. The bispectral index (BIS) is a non-invasive technology used to monitor DoA. It has been shown to be a quantifiable measure of the effect of anaesthetics on the central nervous system [
14,
15] and can be regarded as a measure of the actual degree of awareness of the patient. The BIS ranges from 0 to 100, where a higher score corresponds to a higher state of consciousness. BIS was used to compare and validate the results of calculating the AUC ratio of α + β waves and SampEn methods used in this study to judge whether these approaches can be suitably applied for monitoring DoA. The result shows that the SampEn approach is able to distinguish between key operational stages related to DoA, which is consistent with the clinically based observations.
The rest of this paper is organized as follows: Section 2 describes the analysis methodology that includes the steps of our proposed signal filtering approach to produce the 3D instantaneous frequency and instantaneous amplitude representation of the EEG. In Section 3 we describe the experiments and results of evaluating the proposed approach based on DoA data obtained from real patients. Finally Sections 4 and 5 provide the discussion and conclusions, respectively.
2. Analysis Methodology
2.1. Proposed Signal Filtering Approach Used to Generate 3D Representation of EEG
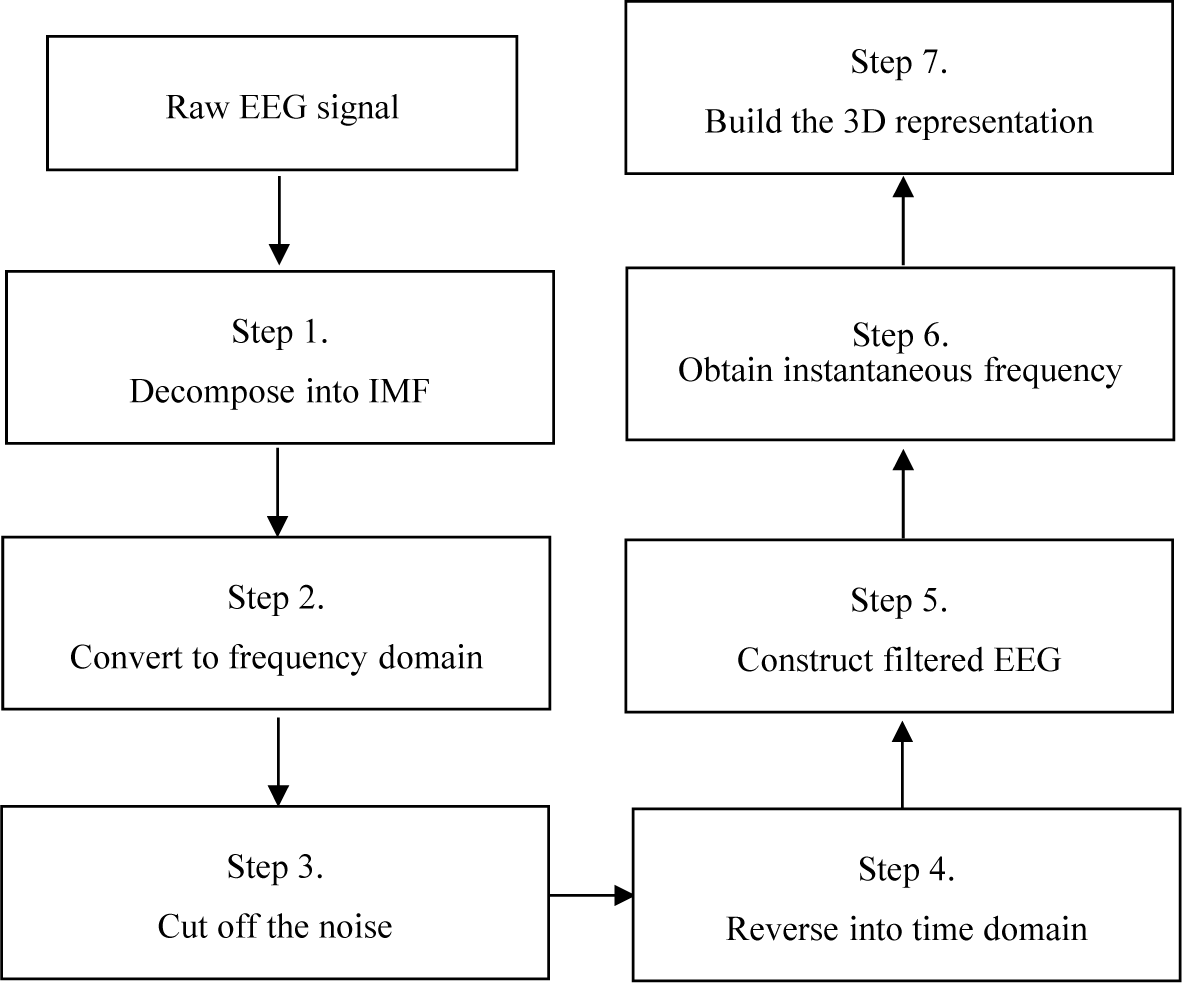
To illustrate the proposed signal filtering approach, EEG sample data acquired from the maintenance stage of a nasal tumor excision procedure that was performed on a 44-year-old patient using a harmonic scalpel will be used. The flow chart of the processing steps in the proposed approach is shown in
Figure 1, and the details of each step are described in the following paragraphs.
Step 1. Decompose the EEG signal into several IMF
EMD is used to decompose the EEG signal into a finite number of IMFs [
6,
16], which can be expressed as follows:
where
x(
t) is the original signal in time domain,
ci(
t) is
ith IMF, and
rn(
t) is residue. The IMFs are simple oscillatory functions with varying amplitude and frequency. Therefore, they are suitable for analysis in both the time and frequency domains simultaneously. The original signal is decomposed repeatedly until its residue becomes a monotonic function. Hence, we can choose different suitably selected IMF combinations to reduce the noise in the signal and then re-construct the signal [
5,
16]. To illustrate this using the sample EEG data
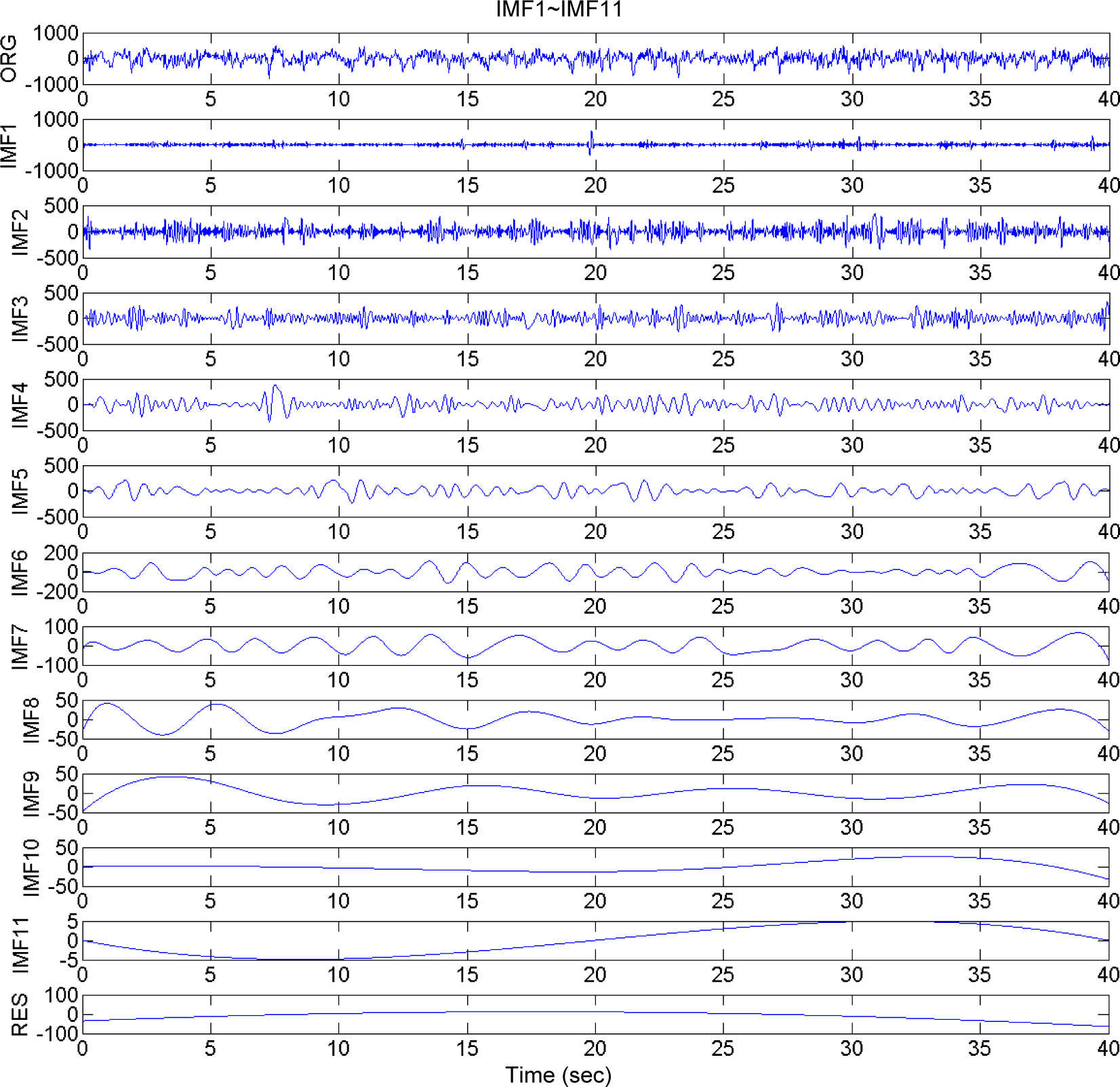
Figure 2 shows the decomposed IMFs of a 40 s segment of the EEG signals that were acquired.
Step 2. Convert the IMFs to frequency domain
The IMFs are converted from the time domain to the frequency domain using a FFT which has been shown to improve the efficiency of the Hilbert transform (HT) by more accurately capturing the frequency ranges present in the signal and also helps reduce errors derived from the estimation of time period from the time-domain based signal [
17]. Thus, we can filter the noise according to the frequency from each IMF.
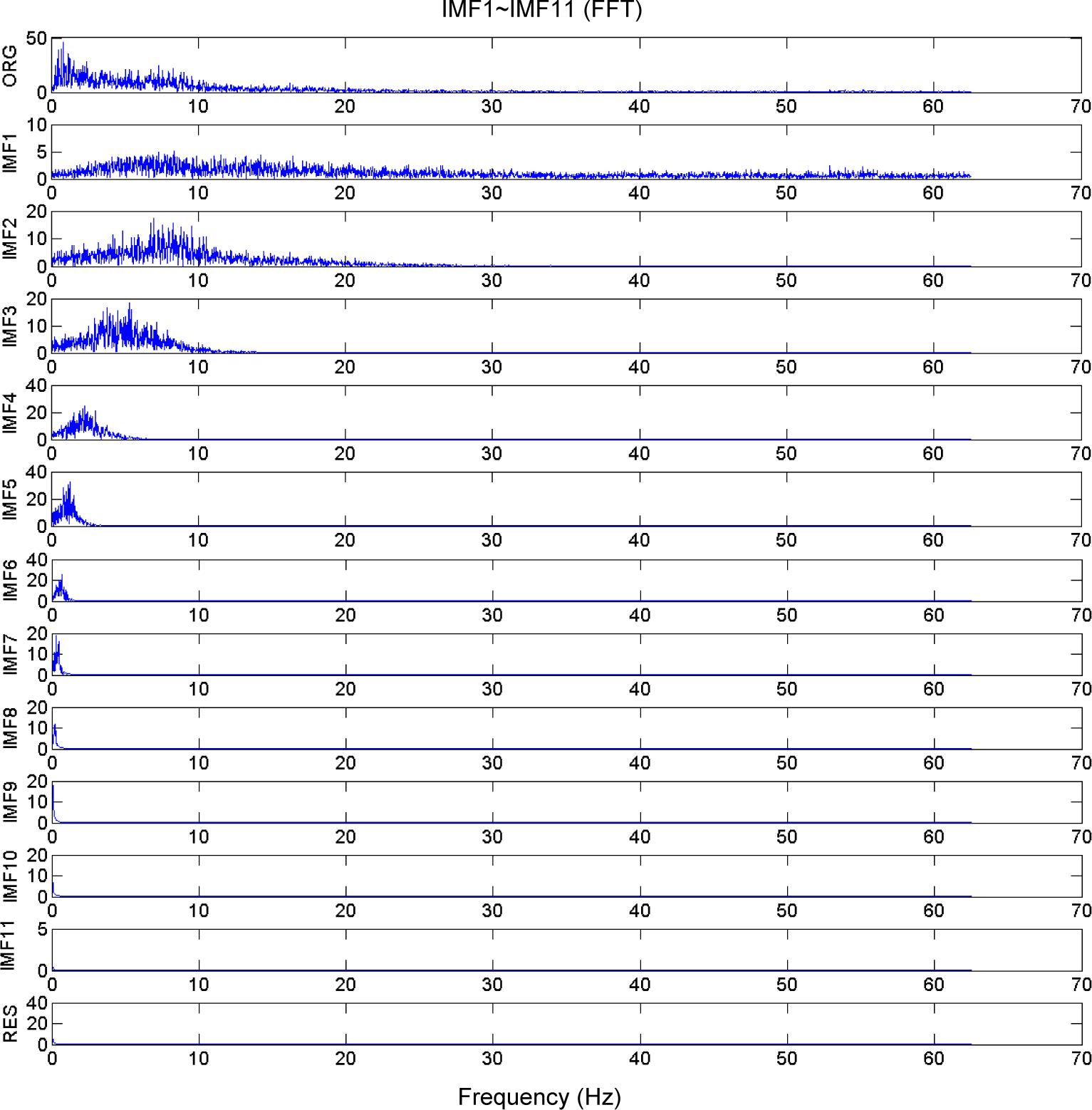
Figure 3 shows the IMFs after using FFT.
Step 3. Cut off the Noise of Each IMF
The normal frequency of EEG signals generated by the human brain is between 0.5 Hz and 32 Hz, and they contain δ, θ, α and β waves, arranged from low frequency to high frequency, respectively. Frequencies outside this range can be regarded as noise. EEG signals are easily interfered by noise from equipment used during surgery (e.g., from electromyography (EMG), electrooculography (EOG) and electrosurgical units (ESUs)) [
9,
18]. These will affect the accuracy when the anaesthetist evaluates the DoA of the patient. Hence filtering out this noise is a necessary task and the goal of this step is to cut off the noise whose frequency is less than 0.5 Hz and greater than 32 Hz, from each IMF.
Step 4. Reverse the filtered IMF into time domain
Inverse fast Fourier transform (IFFT) is then used to convert the signal from a frequency domain back into a time domain. The time segment used in this approach is 40 s with an overlap 10 s. Having a shifting window of 30 s was selected based on trial and error to sample the signal when monitoring DoA, which is explained in the next step.
Step 5. Construct the IMF of filtered EEG signal
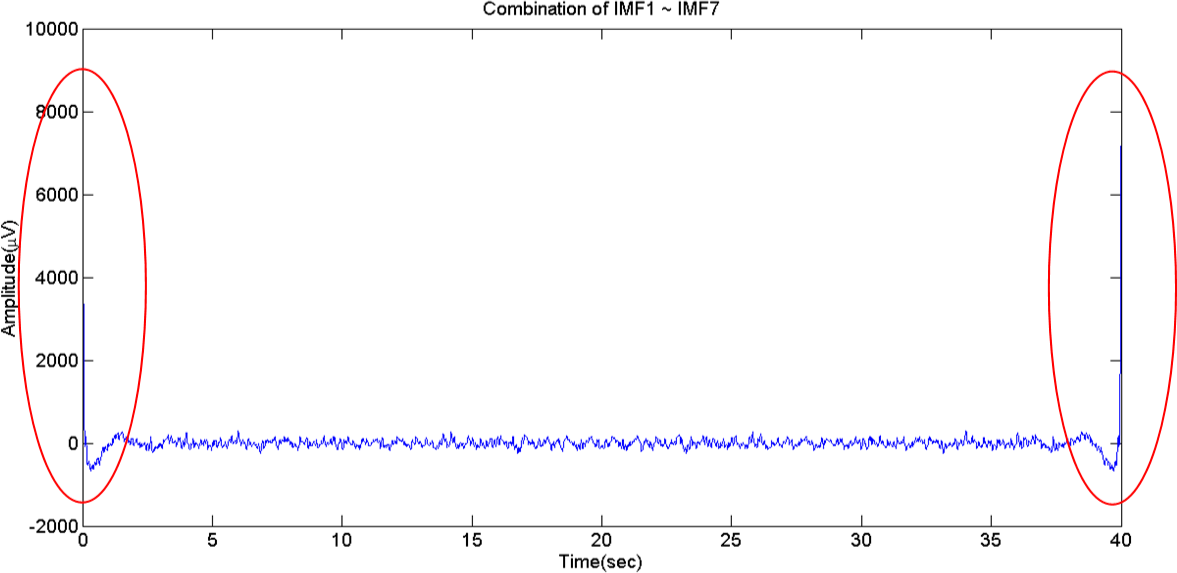
From observing the IMFs in the frequency domain, we found that the frequencies of the decomposed signal beyond IMF7 are small enough to be ignored. Hence, we choose to combine IMF1 to IMF7 produced from the previous step, to obtain a new EEG signal, as shown in
Figure 4. Using IFFT brings out an edge effect which causes the amplitudes of the EEG signal to be unusually high during the first 5 and last 5 s, as shown in the red parts of
Figure 4. This will lead to inaccurate analysis results. We therefore cut off the first and the final 5 s segments, and the result is represented as the filtered 30 s EEG signal segment, as shown in
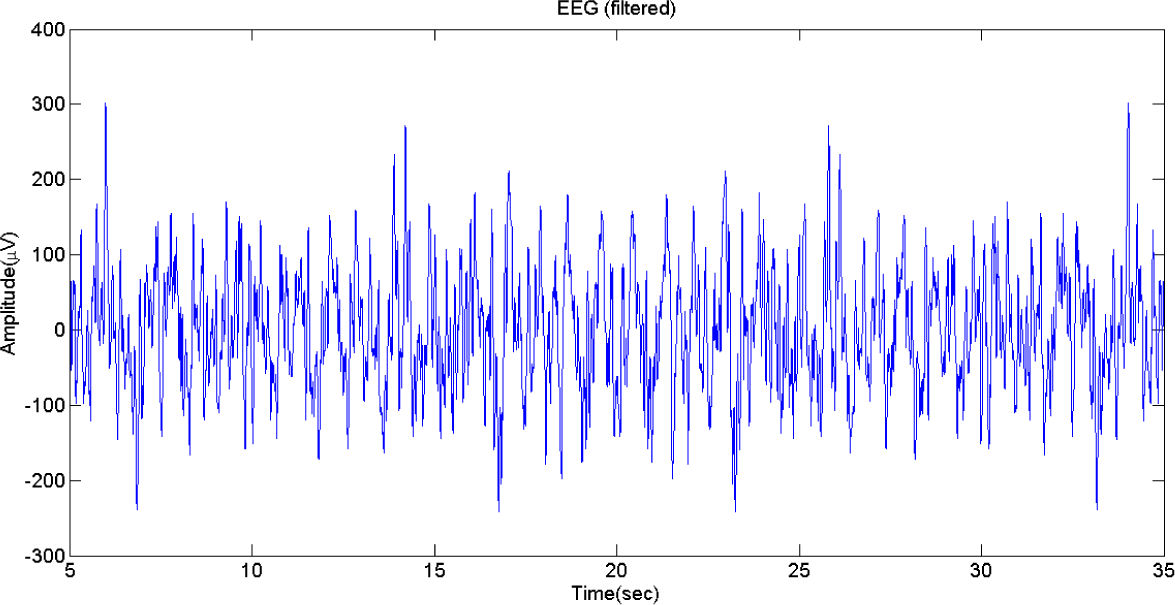
Figure 5.
Step 6. Obtain the instantaneous frequency via HHT
From the previous step, we obtain the filtered EEG signal. We then obtain the instantaneous frequency and instantaneous amplitude of the filtered EEG signal by applying the HHT, which is suitable for analysing non-stationary and nonlinear data [
6]. The main purpose of using the HHT approach [
6,
7] is to get an accurate instantaneous frequency-based representational decomposition of the complex EEG signal. This enables the EEG signal to be separated into its constituent frequencies providing a convenient way for the anaesthetist to read the signal information and associate it to different consciousness states of a patient.
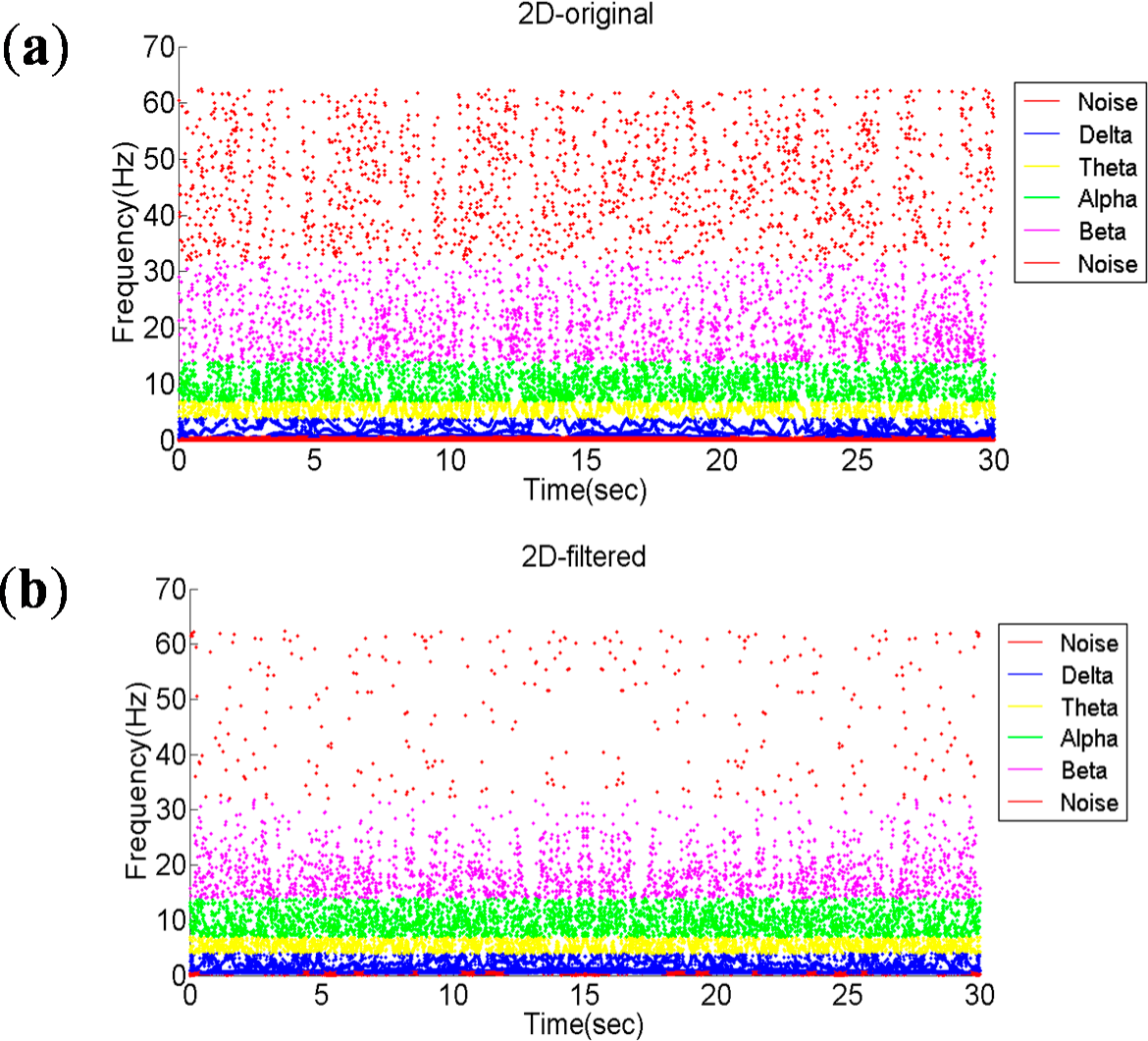
Figure 6 shows the frequency distribution varying with time (before and after filtering), for the maintenance stage of the previously described nasal tumor excision surgery. The x-axis is time and the y-axis shows the instantaneous frequency. The normal EEG signal for a human can be classified into four frequency ranges: δ (0.5–4 Hz), θ (4–8 Hz), α (8–16 Hz) and β (16–32 Hz), represented in
Figure 6 by blue, yellow, green and pink, respectively. The red parts of the signal represent noise, which lie in the range greater than 32 Hz and less than 0.5 Hz. Hence the filtered EEG signal can be shown to have a reduced proportion of noise present in the signal.
Step 7. Build the three-dimensional signal representation
By using the data obtained from Step 6, we build the 3D real-time representation of a patient’s EEG signal output, where the x-axis shows the instantaneous frequency, the y-axis is time and the z-axis is the instantaneous amplitude.
2.2. Evaluation Approaches for Quantifying Filtered Signal Efficiency in Identifying Patient Conscious States Associated to Surgical Stages
Previous studies have shown that the different frequencies of an observed EEG can indicate the different states of consciousness of a patient during surgery, which can be used by the anaesthetist to evaluate the patient’s degree of consciousness [
3]. Therefore, calculating the ratio of high frequency and the complexity of EEG signal can be used as indexes for evaluating the DoA of patients. In this study, two quantitative approaches are used to distinguish the different surgical stages, as shown in
Figure 7.
The first approach is a well-known technique for calculating the area ratio of α + β waves (8–32 Hz) in the EEG frequency for normal human and (0.5–32 Hz) under the FFT curve. The second approach is based on computing the sample entropy (SampEn) value of the signal. SampEn is an improvement of approximate entropy (ApEn) [
11], which is a method for quantifying the amount of regularity in data [
12,
19]. SampEn is more consistent with previous research results compared to the ApEn approach [
11]. This is because the ApEn method lacks two important properties: firstly, ApEn is heavily dependent on the record length and is uniformly lower than expected for short records, secondly, ApEn lacks relative consistency [
20]. BIS has been shown to be a quantifiable measure of the anaesthetic effect on the central nervous system [
14,
15]. We use BIS collected from patients in the operation room during surgery as a means of evaluating the consistency of the results produced from the two quantitative approaches with the clinical observation. The results will compare both approaches to determine which one is better in assessing DoA.
3. Experiments and Results
In this study, the EEG signals were collected from thirty patients, all male and whose ages ranged from 20 to 70. Fifteen of these patients were suffering from tumors, while the remaining 15 had hernias, gallbladder stone, common bile duct (CBD) stones, sleep apnea syndrome, neck mass, allergic rhinitis, nodular goiter, hyperthyroidism, cholecystitis, and open fractured finger and cellulitis. The equipment in the operating room included a physiological monitor (IntelliVue MP60, Philips, Amsterdam, The Netherlands) and a portable computer. This equipment displays the patient’s physiological signals, specifically: ECG, EEG, blood pressure (BP) and saturated percentage of oxygen (SpO2) in real time. This study is aimed at single channel EEG signal analysis, based on a sample frequency of 125 Hz, for interpretation of DoA using the BIS™ Sensor (Aspect Medical Systems AG, Feuerthalen, Switzerland). Since only consciousness is being measured during anaesthesia, data from only a single channel of the EEG signal was collected. This study was also approved by an institutional review board and written informed consent was obtained from all the patients. The EEG signals were analyzed and processed every 40 s using MATLAB (R2012a, MathWorks, Natick, MA, U.S.A.) based on the approach introduced in Section 2.
3.1. 3D Real-Time Representation of EEG at Each Stage
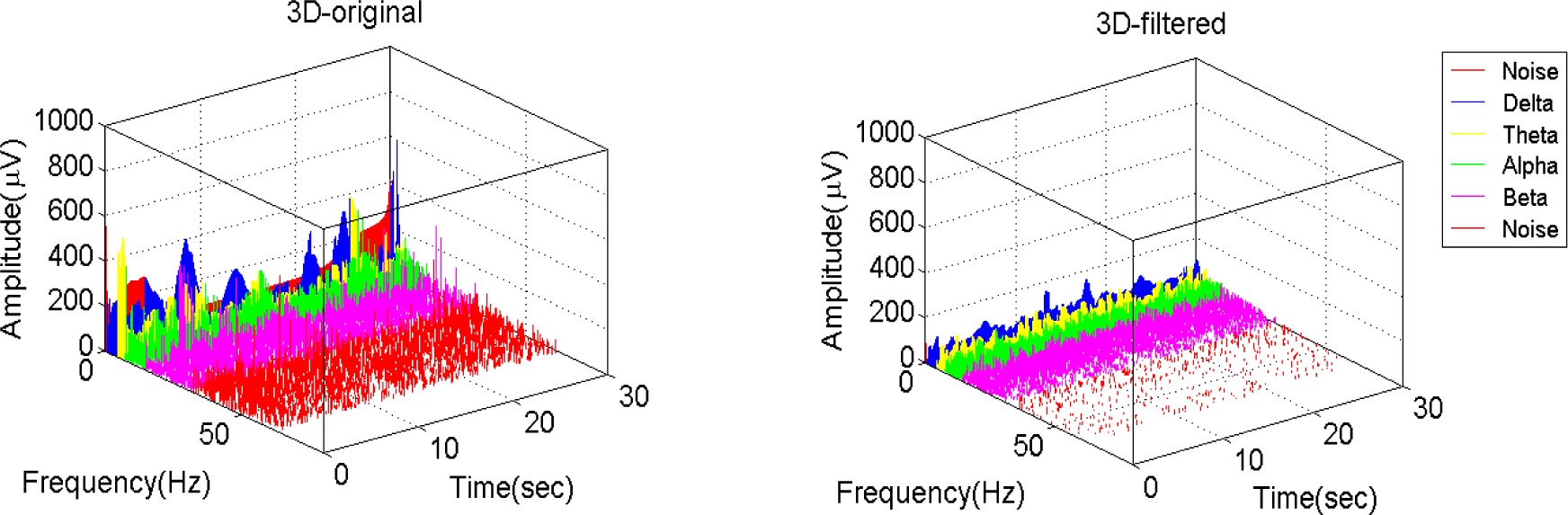
The following 3D real-time representations in
Figures 8 and
10 are from the EEG signal output produced during the same nasal tumor excision operation that was used to illustrate the proposed signal filtering approach in Section 2. The total operation time was approximately 67 min and the plots shown are based on a 30 s sample from each of the three surgical stages (before, maintenance, recovery).
Figures 8 and
10 show the 3D real-time representations of the EEG signals before and after filtering (based on using the proposed filtering method) at the before, maintenance and recovery stages respectively. Note that the amplitude of the EEG signal tends to be less after filtering irrespective of the operational stage. Both the filtered and non-filtered signals indicate that the high frequency (α and β waves) occurring at stage 1 and stage 3 were higher than at stage 2 which is similar to the clinical expectations of α and β waves recorded from awake patients.
3.2. Evaluations and Results of Using AUC, SampEn on Filtered and Non-Filtered Signal, Compared to Obtained BIS at Each Surgical Stage
As previously discussed the area ratio of α + β waves under the FFT curve and the SampEn approach were used to distinguish the different surgical stages based on the filtered EEG signals derived from using our proposed approach. To objectively evaluate the ability of the proposed EEG signal filtering approach in assessing DoA, it was also compared to a standard filtering approach comprising of the following steps: First the raw EEG signal is filtered by a band-pass (0.5~32 Hz) filter. Then EMD is used to obtain IMFs from the band-pass filtered signal. Following this a filtered signal is constructed from the combination of IMF1 to IMF7. The subsequent steps are the same as steps 6 to 7 of the proposed signal filtering approach as described in Section 2.1.
Figure 11 shows a part of filtered signals (by using the proposed and standard filtering approaches) in the frequency domain obtained via FFT again.
Figure 11(a) shows that noisy signal amplitudes over 32 Hz have been reduced considerably after using proposed approach. In comparison with the standard approach, the filtered signal contains more pronounced amplitudes (noise) in the frequencies greater than 32 Hz, as shown in
Figure 11(b).
Table 1 shows the area ratio of α + β waves in 0.5–32 Hz under the FFT curve (AUC) of the thirty patients before and after filtering (for the proposed and standard filtering approaches) at each operational stage.
The sample entropies from each of the thirty patients before and after filtering at each surgical stage are shown in
Table 2. Finally,
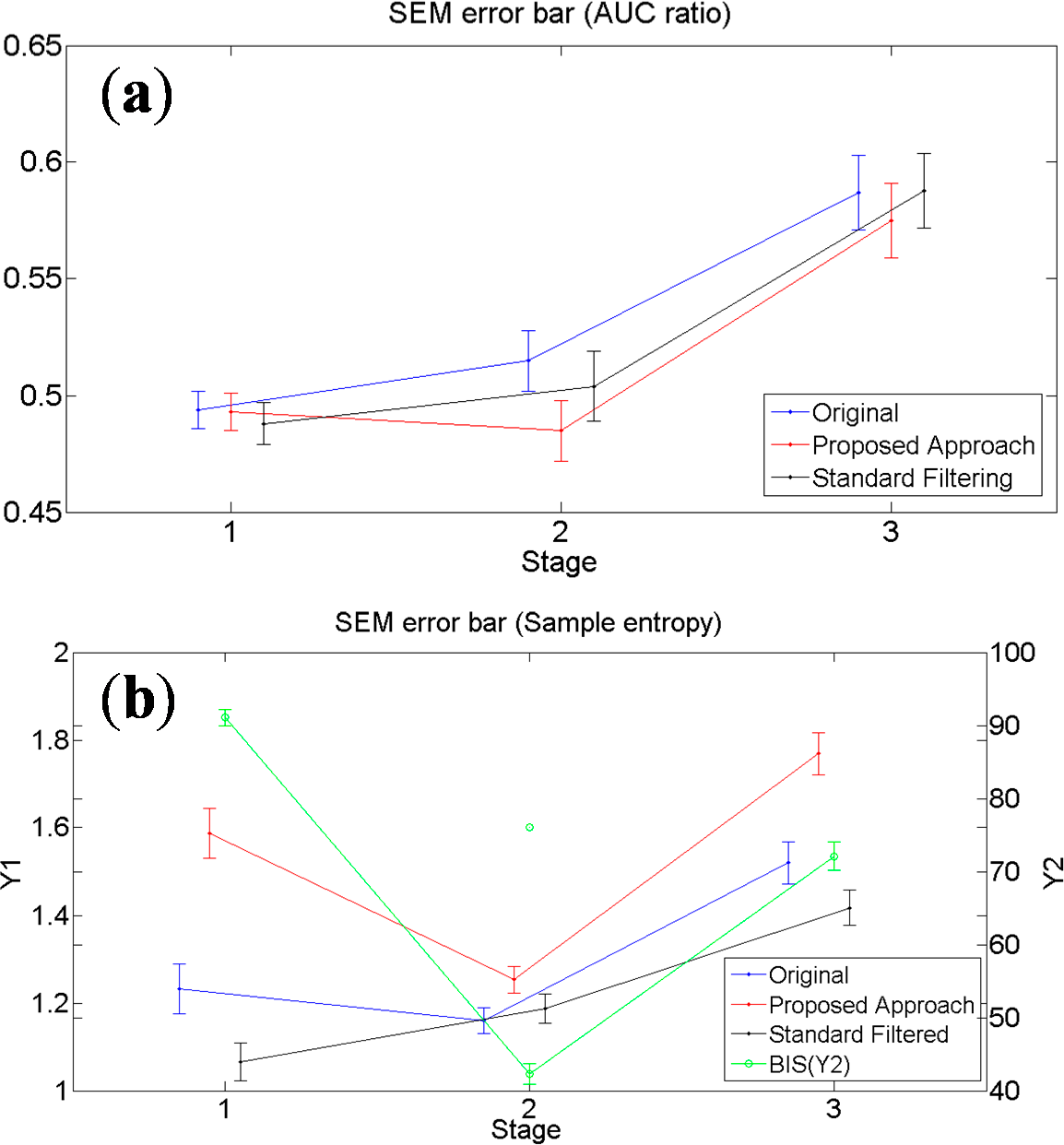
Table 3 shows the BISs of thirty patients at each surgical stage. These three indexes, indicate that the average value at stage 2 (maintenance) is less than at stage 1 (before) and stage 3 (recovery) with the exception of the standard filtering method. Moreover, the error bars of standard error of the mean (SEM) as shown in
Figures 12(a,b) indicate that this differentiation between the stages is more pronounced when employing the SampEn method on the filtered signal generated using the proposed approach. Here the obtained results are also closer to the clinical observations based on using BIS. Although BIS can have variable reliability issues when used in conjunction with certain administered anaesthetic drugs, it is still considered a popular benchmark for evaluating DoA.
3.3. Statistical Comparison of Differences between Each Operational Stage
The following analysis was conducted to determine the statistical significance of whether the results from using the original signal, proposed and standard filtering approaches were consistent with the clinical observation. A one-way analysis of variance using a one-way ANOVA [
21] was used to compute the
p-value between each operational stage, to examine whether there was a significant difference between each surgical stage. A Student–Newman–Keuls (SNK) test was then conducted for multiple comparisons when the null hypothesis was not applicable [
22]. If
p < 0.05, it indicated there was a significant difference between the two stages being compared. On the contrary,
p > 0.05 suggested the two compared stages were very similar.
The use of both indexes: AUC ratio of α + β and SampEn, show a significant difference between stage 2 and stage 3 after filtering, which is consistent with the BIS results as shown in
Table 4. Furthermore, the statistical analysis results of the SampEn method and BIS are identical, showing a significant difference between each of the three stages using both the standard and proposed filtering methods. The results however indicate that using the proposed filtering method is closer to the clinical observations as the mean value at stage 1 is lower than stage 2 when using the standard filtering method, which is inconsistent with the results of BIS as shown in
Table 4.
4. Discussions
In this study, SampEn was used as a quantitative method to distinguish the different surgical stages, where it has been previously shown to be a practical and efficient method to monitor the DoA during surgeries in real time [
5]. From the results in
Table 2, we can see that there have been three cases that violate the clinical observation, in which SampEn at stage 1 are still lower than at stage 2 after filtering (for proposed and standard filtering approaches) is applied. The main reason for this may be because of the extensive use in those interventions of an electrotome, which is a kind of electronic instrument that uses heat produced from high current density to achieve a cutting or hemostasis effect. This kind of instrument will produce high frequencies when used, which will interfere with the EEG signals and make the signals become noisy and complex. An example of this can be seen from the results of patient 8 (see
Table 2), where according to the surgical records an electrotome was used in stage 2 which accounted for half the operating time. This had the effect of causing the SampEn at stage 2 to be higher. Future work will look at removing the noise produced by the use of electrotomes and other high frequency cutting instruments during stage 2 over a longer time period to see if the results will be closer to what tends to be clinically observed.
The results of the statistical analysis show that the differences between each surgical stage for the standard filtered signal (computed by using SampEn) is consistent with the trend of difference between each stage based on BIS. However, the mean value of the standard filtered signal at stage 1 is lower than stage 2 (see
Table 2), which is not consistent with the BIS results. This inconsistency is mainly caused by the use of the band-pass filter, which will generate transition regions in the filtered signal as the noise in the original signal outside the 0.5 Hz to 32 Hz range cannot be effectively filtered out as shown in
Figure 11(b) for frequencies over 32 Hz. In comparison the proposed approach obtains a cleaner signal over the same range as shown in
Figure 11(a), and hence is more effective in filtering out signal noise resulting in more consistency between the BIS results and the clinical expectations. This is due to the additional step of performing FFT of the IMFs from EMD which has allowed us to considerably reduce noise (frequencies less than 0.5 Hz and over 32 Hz) in the EEG signals more easily in the frequency domain prior to applying the HHT process. Previous work has shown that performing FFT of the IMFs can improve the efficiency of HT by more accurately capturing the frequency ranges present in the signal, as compared to using the FFT alone which is less capable in analyzing the frequency content of the EEG signal [
17]. This is because the time resolution significantly affects the calculation of corresponding frequency content of the signal [
23]. The application of FFT on the IMFs has been applied in fault detection of bearing element [
17,
23] as well as power quality analysis [
24]. In our application, the IMFs of EEG signals derived from EMD are enhanced by applying FFT for separating out frequencies that lie within 0.5~32 Hz more accurately. The signals comprising of the selected IMFs can obtain the instantaneous frequency and amplitude after the Hilbert transform is applied. However, if the signals have been contaminated by noise, the HHT process would generate degraded and error prone signals. Therefore, through applying FFT which performs an integration of the signals (
i.e., similar to averaging the signals), the noise in the signals can be reduced.
The use of EEG signals for monitoring DoA has been extensively researched over the past two decades. The most popular and dominant method is the BIS algorithm [
25] which is based on a weighted sum of several EEG parameters, including time domain, frequency domain, and three spectral sub parameters (
i.e., relative beta-ratio, a parameter from the power spectrum; SyncFastSlow, a parameter derived from bispectral analysis quantifying the degree of phase coupling; and a suppression ratio, quantifying the percentage of suppression during burst suppression pattern [
26]). BIS is a statistically based and empirically derived complex parameter and has been effectively used for monitoring DoA compared to traditional Fourier transform algorithms that are ineffective in processing non-linear and non-stationary EEG signals. However BIS cannot tolerate persistent noise, such as substantial electrotome use, which can interfere and disrupt the BIS reading output [
27]. Another DoA monitoring approach is the Datex Ohmeda S/5 Entropy Module approach that is based on entropy to describe the irregularity, complexity, or unpredictability characteristics of a signal. This is an innovative monitoring modality that provides information on the electrical activity of the central nervous system (CNS) during general anaesthesia. The method uses spectral entropy based on information theory to acquire and process raw EEG and frontal EMG signals. However, the spectral entropy is still based on the Fourier transform and assumes the EEG signals can be processed based on the sine and cosine of linear signals [
28]. Hence, this approach also does not account for the non-linear and non-stationary nature of EEG signals. In this study, our approach has several advantages in comparison with these two popular commercially used DoA monitoring methods. Firstly, using EMD to decompose the complex EEG signals does not require processing the signals as the sine or cosine of linear signals, as the signal is decomposed directly from original signal. EMD allows the decomposition of the complex EEG signal from high to low frequencies of different IMFs from which a subset of IMFs can be selected to capture the required frequency ranges to be processed and represented. Secondly, our approach converts the IMFs from the time domain to the frequency domain using FFT, which has been shown to improve the efficiency of HT by more accurately capturing the frequency ranges present in the signals, while reducing errors from the estimation of the time period from the time-domain based signal [
17]. Therefore we can more effectively filter the noise according to the frequency from each IMF. In comparison the use of traditional band-pass filtering results in transition region problems which cannot be effectively removed from the signal. Finally, applying HHT has provided us with a mean to visualize instantaneous frequency and amplitude
versus time in a real-time representation of the signal. This would be impossible to see using FFT which can only obtain an average frequency and amplitude
versus time based representation.
5. Conclusions
Compared with the traditional physiological monitors, the real-time 3D signal representation method proposed in this paper provides a more convenient way for the anaesthetist to evaluate DoA from EEG output. The anaesthetist can read the complete information of EEG signal more clearly and instantaneously reducing the cognitive burden on him for determining the patients’ conscious state and their reaction to administered drug by analyzing the raw signal and other monitored parameters. This will potentially significantly reduce the surgical as well as post-operative risks to the patient.
A proposed filtering approach is used to filter the raw EEG signals based on EMD and HHT to obtain instantaneous frequency and instantaneous amplitude of EEG simultaneously. The approach has been shown to be more effective over the standard filtering method in filtering out signal noise. This has been due to the additional step of performing FFT of the IMFs from EMD to allow us to reduce signal noise (at frequencies that are less than 0.5 and greater than 32 Hz) more easily in the frequency domain prior to performing HHT.
SampEn is a nonlinear quantitative method which can be used to distinguish the different stages of surgery based on the degree of consciousness of the patient. In comparison with other linear approaches such as calculating the AUC ratio of α + β waves, which is based on FFT, SampEn is more accurate in identifying the difference between each of three operational stages (before, maintenance and recovery).
The results from statistical analysis show that the differences between each stage computed by using SampEn is consistent with the trend of difference between each stage based on BIS which has been shown to be a quantifiable measure of the effect of anaesthetics on the central nervous system [
14,
15]. These results are further improved when SampEn is used with the proposed filtering approach as compared with the standard filtering method. Therefore, SampEn can also be viewed as a useful index for evaluating the DoA of a patient. In conjunction with the proposed 3D EEG signal filtering and signal representation method, this new index can be used to develop a semi-automated DoA monitor which can both visually monitor EEG signals as well as more directly inform or alert surgical staff on the patients DoA in relation to any given point during the surgical procedure.
Future work will investigate the development of a deployable system which can be used in clinical settings in conjunction with an adaptive anaesthetic drug delivery system to help in the management of anaesthetic dosage based on patients’ physiological responses.
Acknowledgments
This research was supported by the Center for Dynamical Biomarkers and Translational Medicine, National Central University, Taiwan, which is sponsored by Ministry of Science and Technology (Grant Number: MOST103-2911-I-008-001). In addition, it was supported by National Chung-Shan Institute of Science & Technology in Taiwan (Grant Numbers: CSIST-095-V301 and CSIST-095-V302).
Author Contributions
Mu-Tzu Shih designed the study, analyzed and interpreted the data, and drafted the manuscript. Faiyaz Doctor interpreted the data, critically revised the entire article content, and reread the final version prior to its publication. Shou-Zen Fan took part in the diagnosis of subjects and the collection of data, and interpreted the results. Kuo-Kuang Jen took part in the collection of data, analyzed the data, and interpreted the results. Jiann-Shing Shieh designed the study, interpreted the data, critically revised the article for signal processing, and final approval of the version to be published. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kent, C.D.; Domino, K.B. Depth of anesthesia. Curr. Opin. Anaesthesiol. 2009, 22, 782–787. [Google Scholar]
- Bruhn, J.; Röpcke, H.; Hoeft, A. Approximate entropy as an electroencephalographic measure of anesthetic drug effect during anesthesia. Anaesthesiology 2000, 92, 715–726. [Google Scholar]
- Mashour, G.A. Monitoring consciousness: EEG-based measures of anesthetic depth. Semin. Anesth. Perioper. Med. Pain. 2006, 25, 187–238. [Google Scholar]
- Rutkowski, T.M.; Cichocki, A.; Ralescu, A.L.; Mandic, D.P. Emotional states estimation from multichannel EEG maps. In Advances in Cognitive Neurodynamics ICCN 2007; Wang, R., Gu, F., Shen, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Wei, Q.; Liu, Q.; Fan, S.Z.; Lu, C.W.; Lin, T.U.; Abbod, M.F.; Shieh, J.S. Analysis of EEG via multivariate empirical mode decomposition for depth of anesthesia based on sample entropy. Entropy 2013, 15, 3458–3470. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar]
- Wu, M.C.; Huang, N.E. The bimedical data processing using HHT: A review. In Advanced Biosignal Processing; Naït-Ali, A., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 335–352. [Google Scholar]
- Martis, R.J.; Acharya, U.R.; Tan, J.H.; Petznick, A.; Yanti, R.; Chua, C.K.; Ng, E.Y.; Tong, L. Application of empirical mode decomposition (EMD) for automated detection of epilepsy using EEG signals. Int. J. Neural Syst. 2012, 22. [Google Scholar] [CrossRef]
- Labate, D.; Foresta, F.L.; Occhiuto, G. Empirical mode decomposition vs. wavelet decomposition for the extraction of respiratory signal from single-channel ECG: A comparison. IEEE Sens. J. 2013, 13, 2666–2674. [Google Scholar]
- Looney, D.; Goverdovsky, V.; Kidmose, P.; Mandic, D.P. Subspace denoising of EEG artefacts via multivariate EMD. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Florence, Italy, 4–9 May 2014; pp. 4688–4692.
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar]
- Fan, S.Z.; Yeh, J.R.; Chen, B.C.; Shieh, J.S. Comparison of EEG approximate entropy and complexity measures of depth of anaesthesia during inhalational general anaesthesia. J. Med. Biol. Eng. 2011, 31, 359–366. [Google Scholar]
- Shalbaf, R.; Behnam, H.; Sleigh, J.; Voss, L. Measuring the effects of sevoflurane on electroencephalogram using sample entropy. Acta Anaesthesiol. Scand. 2012, 56, 880–889. [Google Scholar]
- Avidan, M.S.; Zhang, L.; Burnside, B.A.; Finkel, K.J.; Searleman, A.C.; Selvidge, J.A.; Saager, L.; Turner, M.S.; Rao, S.; Bottros, M.; et al. Anesthesia awareness and the bispectral index. New Engl. J. Med. 2008, 358, 1097–1108. [Google Scholar]
- Myles, P.S.; Leslie, K.; McNeil, J.; Forbes, A.; Chan, M.T. Bispectral index monitoring to prevent awareness during anaesthesia: The B-Aware randomized trial. Lancet 2004, 363, 1757–1763. [Google Scholar]
- Huang, J.R.; Fan, S.Z.; Abbod, M.F.; Jen, K.K.; Wu, J.F.; Shieh, J.S. Application of multivariate empirical mode decomposition and sample entropy in EEG signals via neutral networks for interpreting depth of anesthesia. Entropy 2013, 15, 3325–3339. [Google Scholar]
- Rai, V.K.; Mohanty, A.R. Bearing fault diagnosis using FFT of intrinsic mode functions in Hilbert–Huang transform. Mech. Syst. Signal Process. 2007, 21, 2607–2615. [Google Scholar]
- Safieddine, D.; Kachenoura, A.; Albera, L.; Birot, G.; Karfoul, A.; Pasnicu, A.; Biraben, A.; Wendling, F.; Senhadji, L.; Merlet, I. Removal of muscle artifact from EEG data: Comparison between stochastic (ICA and CCA) and deterministic (EMD and wavelet-based) approaches. EURASIP J. Adv. Signal Process. 2012, 127. [Google Scholar] [CrossRef]
- Xie, H.B.; He, W.X.; Liu, H. Measuring time series regularity using nonlinear similarity-based sample entropy. Phys. Lett. A 2008, 372, 7140–7146. [Google Scholar]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar]
- Howell, D.C. Statistical Methods for Psychology, 8th ed; Cengage Learning: Belmont, CA, USA, 2012; pp. 325–361. [Google Scholar]
- Glantz, S.A. Primer of Biostatistics, 4th ed; McGraw-Hill: Singapore, Singapore, 1997. [Google Scholar]
- Xu, L. Study on fault detection of rolling element bearing based on translation-invariant denoising and Hilbert–Huang transform. J. Comput. 2012, 7, 1142–1146. [Google Scholar]
- Senroy, N.; Suryanarayanan, S.; Ribeiro, P.F. An improved Hilbert–Huang method for analysis of time-varying waveforms in power quality. IEEE T. Power Syst. 2007, 22, 1843–1850. [Google Scholar]
- Schmidt, G.N.; Bischoff, P.; Standl, T.; Hellstern, A.; Teuber, O.; Schulte Esch, J. Comparative evaluation of the Datex-Ohmeda S/5 Entropy Module and the Bispectral Index monitor during propofol-remifentanil anesthesia. Anesthesiology 2004, 101, 1283–1290. [Google Scholar]
- Bruhn, J.; Bouillon, T.W.; Shafer, S.L. Bispectral index (BIS) and burst suppression: Revealing a part of the BIS algorithm. J. Clin. Monit. Comput. 2000, 16, 593–596. [Google Scholar]
- Nunes, R.R.; Chaves, I.M.; de Alencar, J.C.; Franco, S.B.; de Oliveira, Y.G.; de Menezes, D.G. Bispectral index and other processed parameters of electroencephalogram: An update. Rev. Bras. Anestesiol. 2012, 62, 105–117, In Portuguese. [Google Scholar]
- Viertiö-Oja, H.; Maja, V.; Särkelä, M.; Talja, P.; Tenkanen, N.; Tolvanen-Laakso, H.; Paloheimo, M.; Vakkuri, A.; Yli-Hankala, A.; Meriläinen, P. Description of the Entropy™ algorithm as applied in the Datex-Ohmeda S/5™ Entropy Module. Acta Anaesthesiol. Scand. 2004, 48, 154–161. [Google Scholar]
Figure 1.
Flow chart of Proposed EEG Signal Filtering Approach.
Figure 1.
Flow chart of Proposed EEG Signal Filtering Approach.
Figure 2.
IMFs for a 40 s segment of EEG signals acquired during the maintenance stage of a nasal tumor excision operation, showing the original EEG signal, decomposed IMFs from 1 to 11, and the residue signal in the time domain.
Figure 2.
IMFs for a 40 s segment of EEG signals acquired during the maintenance stage of a nasal tumor excision operation, showing the original EEG signal, decomposed IMFs from 1 to 11, and the residue signal in the time domain.
Figure 3.
IMFs for a 40 s segment EEG signal acquired during the maintenance stage of the nasal tumor excision operation, showing the original EEG signal, the IMFs 1 to 11, and the residue signal in the frequency domain.
Figure 3.
IMFs for a 40 s segment EEG signal acquired during the maintenance stage of the nasal tumor excision operation, showing the original EEG signal, the IMFs 1 to 11, and the residue signal in the frequency domain.
Figure 4.
The circled red parts of the signal in this figure are the edge effects caused from the use of IFFT.
Figure 4.
The circled red parts of the signal in this figure are the edge effects caused from the use of IFFT.
Figure 5.
EEG signal after filtering.
Figure 5.
EEG signal after filtering.
Figure 6.
The time and instantaneous frequency diagram at maintenance stage. (a) Before filtering; (b) After filtering.
Figure 6.
The time and instantaneous frequency diagram at maintenance stage. (a) Before filtering; (b) After filtering.
Figure 7.
Comparison of quantitative evaluation approaches.
Figure 7.
Comparison of quantitative evaluation approaches.
Figure 8.
The 3D real-time representation of EEG at before stage. (a) Before filtering; (b) After filtering.
Figure 8.
The 3D real-time representation of EEG at before stage. (a) Before filtering; (b) After filtering.
Figure 9.
The 3D real-time representation of EEG at maintenance stage. (a) Before filtering; (b) After filtering.
Figure 9.
The 3D real-time representation of EEG at maintenance stage. (a) Before filtering; (b) After filtering.
Figure 10.
The 3D real-time representation of EEG at recovery stage. (a) Before filtering; (b) After filtering.
Figure 10.
The 3D real-time representation of EEG at recovery stage. (a) Before filtering; (b) After filtering.
Figure 11.
A part of FFT curve. (a) Proposed approach; (b) Standard filtering.
Figure 11.
A part of FFT curve. (a) Proposed approach; (b) Standard filtering.
Figure 12.
SEM error bar before and after filtering. (a) By calculating AUC ratio of α + β waves; (b) By using SampEn and BIS. Red, blue and black lines are corresponding to Y1 axis which is the scale for EEG signal before and after filtering, and the green line is corresponding to Y2 axis which is the scale for BIS.
Figure 12.
SEM error bar before and after filtering. (a) By calculating AUC ratio of α + β waves; (b) By using SampEn and BIS. Red, blue and black lines are corresponding to Y1 axis which is the scale for EEG signal before and after filtering, and the green line is corresponding to Y2 axis which is the scale for BIS.
Table 1.
AUC ratio of α + β waves of thirty patients.
Table 1.
AUC ratio of α + β waves of thirty patients.
| Before | Maintenance | Recovery |
|---|
|
|
|---|
| Patients | Original | Standard Filtering | Proposed Approach | Original | Standard Filtering | Proposed Approach | Original | Standard Filtering | Proposed Approach |
|---|
| 1 | 0.524 | 0.519 | 0.531 | 0.474 | 0.470 | 0.454 | 0.547 | 0.541 | 0.555 |
| 2 | 0.444 | 0.438 | 0.437 | 0.554 | 0.552 | 0.503 | 0.661 | 0.657 | 0.634 |
| 3 | 0.369 | 0.366 | 0.377 | 0.552 | 0.550 | 0.503 | 0.559 | 0.558 | 0.535 |
| 4 | 0.587 | 0.582 | 0.567 | 0.362 | 0.359 | 0.352 | 0.441 | 0.438 | 0.432 |
| 5 | 0.527 | 0.519 | 0.541 | 0.571 | 0.568 | 0.533 | 0.496 | 0.490 | 0.497 |
| 6 | 0.531 | 0.528 | 0.510 | 0.445 | 0.443 | 0.428 | 0.570 | 0.568 | 0.539 |
| 7 | 0.513 | 0.509 | 0.506 | 0.556 | 0.555 | 0.521 | 0.542 | 0.540 | 0.531 |
| 8 | 0.428 | 0.424 | 0.428 | 0.635 | 0.634 | 0.584 | 0.553 | 0.550 | 0.550 |
| 9 | 0.480 | 0.476 | 0.484 | 0.586 | 0.584 | 0.553 | 0.536 | 0.532 | 0.523 |
| 10 | 0.474 | 0.471 | 0.474 | 0.623 | 0.621 | 0.561 | 0.486 | 0.483 | 0.495 |
| 11 | 0.423 | 0.419 | 0.420 | 0.595 | 0.593 | 0.546 | 0.692 | 0.689 | 0.661 |
| 12 | 0.533 | 0.529 | 0.521 | 0.513 | 0.511 | 0.468 | 0.601 | 0.598 | 0.591 |
| 13 | 0.489 | 0.483 | 0.481 | 0.452 | 0.450 | 0.425 | 0.484 | 0.482 | 0.468 |
| 14 | 0.477 | 0.473 | 0.483 | 0.480 | 0.478 | 0.447 | 0.586 | 0.582 | 0.566 |
| 15 | 0.477 | 0.471 | 0.493 | 0.465 | 0.463 | 0.442 | 0.454 | 0.455 | 0.479 |
| 16 | 0.482 | 0.426 | 0.484 | 0.390 | 0.383 | 0.377 | 0.680 | 0.672 | 0.647 |
| 17 | 0.453 | 0.449 | 0.446 | 0.485 | 0.484 | 0.462 | 0.651 | 0.646 | 0.653 |
| 18 | 0.450 | 0.445 | 0.453 | 0.389 | 0.386 | 0.375 | 0.524 | 0.520 | 0.529 |
| 19 | 0.568 | 0.562 | 0.554 | 0.455 | 0.453 | 0.439 | 0.733 | 0.728 | 0.711 |
| 20 | 0.486 | 0.483 | 0.473 | 0.581 | 0.579 | 0.534 | 0.619 | 0.614 | 0.617 |
| 21 | 0.487 | 0.483 | 0.488 | 0.603 | 0.602 | 0.563 | 0.660 | 0.652 | 0.625 |
| 22 | 0.546 | 0.538 | 0.562 | 0.628 | 0.626 | 0.576 | 0.593 | 0.590 | 0.579 |
| 23 | 0.478 | 0.474 | 0.481 | 0.574 | 0.573 | 0.523 | 0.754 | 0.752 | 0.713 |
| 24 | 0.494 | 0.489 | 0.510 | 0.528 | 0.527 | 0.487 | 0.603 | 0.602 | 0.562 |
| 25 | 0.488 | 0.483 | 0.497 | 0.484 | 0.482 | 0.458 | 0.730 | 0.728 | 0.706 |
| 26 | 0.500 | 0.496 | 0.485 | 0.453 | 0.451 | 0.435 | 0.704 | 0.696 | 0.660 |
| 27 | 0.538 | 0.534 | 0.538 | 0.538 | 0.489 | 0.538 | 0.538 | 0.629 | 0.610 |
| 28 | 0.532 | 0.529 | 0.532 | 0.532 | 0.378 | 0.532 | 0.532 | 0.452 | 0.434 |
| 29 | 0.498 | 0.493 | 0.498 | 0.498 | 0.424 | 0.498 | 0.498 | 0.615 | 0.604 |
| 30 | 0.547 | 0.541 | 0.535 | 0.447 | 0.444 | 0.433 | 0.589 | 0.586 | 0.553 |
| Mean ± SD | 0.494 ± 0.046 | 0.488 ± 0.047 | 0.493 ± 0.044 | 0.515 ± 0.074 | 0.504 ± 0.080 | 0.458 ± 0.063 | 0.587 ± 0.086 | 0.588 ± 0.086 | 0.575 ± 0.078 |
Table 2.
Sample entropies of thirty patients.
Table 2.
Sample entropies of thirty patients.
| Before | Maintenance | Recovery |
|---|
|
|
|---|
| Patients | Original | Standard Filtering | Proposed Approach | Original | Standard Filtering | Proposed Approach | Original | Standard Filtering | Proposed Approach |
|---|
| 1 | 1.233 | 1.069 | 1.811 | 0.995 | 0.917 | 1.394 | 1.917 | 1.475 | 2.091 |
| 2 | 1.248 | 0.959 | 1.379 | 1.180 | 1.251 | 1.281 | 1.655 | 1.577 | 1.910 |
| 3 | 0.930 | 0.886 | 0.985 | 1.243 | 1.290 | 1.360 | 1.253 | 1.308 | 1.463 |
| 4 | 1.803 | 1.567 | 2.006 | 0.932 | 0.899 | 1.004 | 1.234 | 1.097 | 1.280 |
| 5 | 1.838 | 1.380 | 1.947 | 1.266 | 1.293 | 1.464 | 1.409 | 1.166 | 1.534 |
| 6 | 1.303 | 1.222 | 1.532 | 0.965 | 1.075 | 1.226 | 1.362 | 1.335 | 1.506 |
| 7 | 1.088 | 1.012 | 1.637 | 1.263 | 1.313 | 1.297 | 1.119 | 1.130 | 1.500 |
| 8 | 0.995 | 0.827 | 1.133 | 1.410 | 1.456 | 1.430 | 1.473 | 1.376 | 1.864 |
| 9 | 1.193 | 0.970 | 1.565 | 1.345 | 1.385 | 1.489 | 1.331 | 1.199 | 1.688 |
| 10 | 0.648 | 0.697 | 1.352 | 1.402 | 1.453 | 1.310 | 1.020 | 0.966 | 1.517 |
| 11 | 1.069 | 0.838 | 1.224 | 1.323 | 1.382 | 1.328 | 1.667 | 1.662 | 1.972 |
| 12 | 1.668 | 1.459 | 1.821 | 1.186 | 1.228 | 1.168 | 1.585 | 1.510 | 1.865 |
| 13 | 1.267 | 0.996 | 1.600 | 1.000 | 1.040 | 1.230 | 1.288 | 1.229 | 1.310 |
| 14 | 1.114 | 0.971 | 1.441 | 1.095 | 1.144 | 1.140 | 1.597 | 1.397 | 1.917 |
| 15 | 1.472 | 1.179 | 1.664 | 0.877 | 0.927 | 1.219 | 1.685 | 1.341 | 1.657 |
| 16 | 1.106 | 0.797 | 1.503 | 0.886 | 0.941 | 1.021 | 1.801 | 1.615 | 1.867 |
| 17 | 0.739 | 0.727 | 1.346 | 1.119 | 1.155 | 1.243 | 1.858 | 1.676 | 2.287 |
| 18 | 1.420 | 1.070 | 1.448 | 0.972 | 0.974 | 0.995 | 1.522 | 1.336 | 1.736 |
| 19 | 1.827 | 1.465 | 1.972 | 1.088 | 1.101 | 1.234 | 2.195 | 1.889 | 2.241 |
| 20 | 1.189 | 1.049 | 1.414 | 1.361 | 1.393 | 1.394 | 1.769 | 1.637 | 2.243 |
| 21 | 0.942 | 0.819 | 1.479 | 1.363 | 1.434 | 1.471 | 1.389 | 1.470 | 2.031 |
| 22 | 1.789 | 1.539 | 2.154 | 1.385 | 1.464 | 1.455 | 1.226 | 1.237 | 1.876 |
| 23 | 0.835 | 0.874 | 1.523 | 1.333 | 1.381 | 1.243 | 1.637 | 1.697 | 1.786 |
| 24 | 1.105 | 0.948 | 1.709 | 1.138 | 1.267 | 1.174 | 1.360 | 1.370 | 1.414 |
| 25 | 1.123 | 0.939 | 1.647 | 1.153 | 1.160 | 1.251 | 1.628 | 1.686 | 1.911 |
| 26 | 1.259 | 1.089 | 1.574 | 1.107 | 1.117 | 1.224 | 1.671 | 1.646 | 1.766 |
| 27 | 0.945 | 1.087 | 1.731 | 1.199 | 1.169 | 1.231 | 1.624 | 1.477 | 1.831 |
| 28 | 1.196 | 1.170 | 1.541 | 0.938 | 0.951 | 1.003 | 1.152 | 1.115 | 1.231 |
| 29 | 1.303 | 1.115 | 1.653 | 1.044 | 0.999 | 1.064 | 1.744 | 1.452 | 2.166 |
| 30 | 1.302 | 1.252 | 1.854 | 1.218 | 1.063 | 1.261 | 1.422 | 1.422 | 1.605 |
| Mean ± SD | 1.232 ± 0.312 | 1.066 ± 0.235 | 1.588 ± 0.260 | 1.160 ± 0.165 | 1.187 ± 0.183 | 1.253 ± 0.143 | 1.520 ± 0.264 | 1.417 ± 0.218 | 1.769 ± 0.291 |
Table 3.
BISs of thirty patients.
Table 3.
BISs of thirty patients.
| Patients | Before | Maintenance | Recovery |
|---|
| 1 | 96.707 | 42.478 | 78.716 |
| 2 | 88.129 | 43.266 | 73.252 |
| 3 | 83.761 | 42.633 | 60.600 |
| 4 | 89.786 | 41.869 | 64.857 |
| 5 | 94.591 | 49.601 | 72.389 |
| 6 | 83.140 | 34.439 | 65.506 |
| 7 | 92.056 | 47.117 | 67.697 |
| 8 | 91.524 | 56.193 | 81.393 |
| 9 | 97.073 | 51.492 | 74.253 |
| 10 | 95.158 | 45.326 | 70.980 |
| 11 | 91.524 | 56.193 | 81.393 |
| 12 | 90.317 | 38.619 | 80.968 |
| 13 | 94.222 | 29.563 | 48.891 |
| 14 | 91.403 | 37.051 | 74.931 |
| 15 | 87.636 | 35.432 | 92.934 |
| 16 | 94.526 | 32.975 | 67.635 |
| 17 | 93.916 | 40.681 | 83.287 |
| 18 | 96.976 | 31.599 | 66.262 |
| 19 | 90.619 | 35.775 | 87.218 |
| 20 | 85.220 | 47.173 | 85.570 |
| 21 | 95.158 | 56.510 | 55.638 |
| 22 | 96.488 | 57.252 | 82.872 |
| 23 | 92.511 | 44.229 | 63.041 |
| 24 | 94.634 | 42.456 | 78.343 |
| 25 | 71.784 | 43.177 | 68.506 |
| 26 | 94.032 | 32.501 | 65.099 |
| 27 | 96.793 | 42.598 | 73.204 |
| 28 | 75.736 | 33.797 | 51.473 |
| 29 | 93.918 | 35.536 | 83.975 |
| 30 | 93.133 | 42.076 | 61.803 |
| Mean ± SD | 91.082 ± 6.042 | 42.320 ± 7.844 | 72.090 ± 10.770 |
Table 4.
p-Values between each stage before and after filtering.
Table 4.
p-Values between each stage before and after filtering.
| AUC Ratio of α + β | SampEn | BIS |
|---|
|
|
|---|
| Stages | Original | Standard Filtering | Proposed Approach | Original | Standard Filtering | Proposed Approach | Original |
|---|
| Stage 1 vs. Stage 3 | 0.494 ± 0.046* vs. 0.587 ± 0.086 | 0.488 ± 0.047* vs. 0.588 ± 0.086 | 0.493 ± 0.044* vs. 0.575 ± 0.078 | 1.232 ± 0.312* vs. 1.520 ± 0.264 | 1.066 ± 0.235* vs. 1.417 ± 0.218 | 1.588 ± 0.260* vs. 1.769 ± 0.291 | 91.082 ± 6.042* vs. 72.090 ± 10.770 |
| Stage 2 vs. Stage 3 | 0.515 ± 0.074* vs. 0.587 ± 0.086 | 0.504 ± 0.080* vs. 0.588 ± 0.086 | 0.458 ± 0.063* vs. 0.575 ± 0.078 | 1.160 ± 0.165* vs. 1.520 ± 0.264 | 1.187 ± 0.183* vs. 1.417 ± 0.218 | 1.253 ± 0.143* vs. 1.769 ± 0.291 | 42.320 ± 7.844* vs. 72.090 ± 10.770 |
| Stage 1 vs. Stage 2 | 0.494 ± 0.046 vs. 0.515 ± 0.074 | 0.488 ± 0.047 vs. 0.504 ± 0.080 | 0.493 ± 0.044 vs. 0.458 ± 0.063 | 1.232 ± 0.312 vs. 1.160 ± 0.165 | 1.066 ± 0.235* vs. 1.187 ± 0.183 | 1.588 ± 0.260* vs. 1.253 ± 0.143 | 91.082 ± 6.042* vs. 42.320 ± 7.844 |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).