Complexity Analysis and DSP Implementation of the Fractional-Order Lorenz Hyperchaotic System
Abstract
:1. Introduction
2. Numerical Solution of the Fractional-Order Lorenz Hyperchaotic System
2.1. Adomian Decomposition Method
2.2. Fractional-Order Lorenz Hyperchaotic System
3. Dynamics Analysis of the Fractional-Order Lorenz Hyperchaotic System
3.1. Bifurcation Analysis
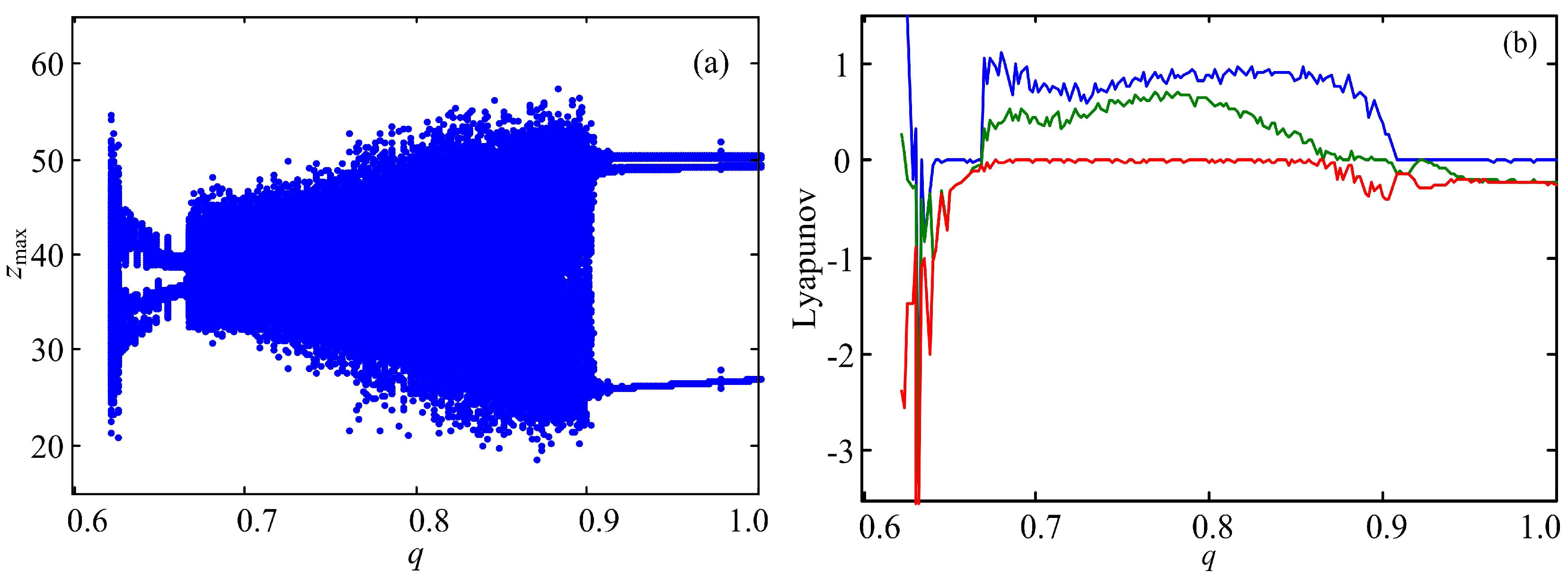
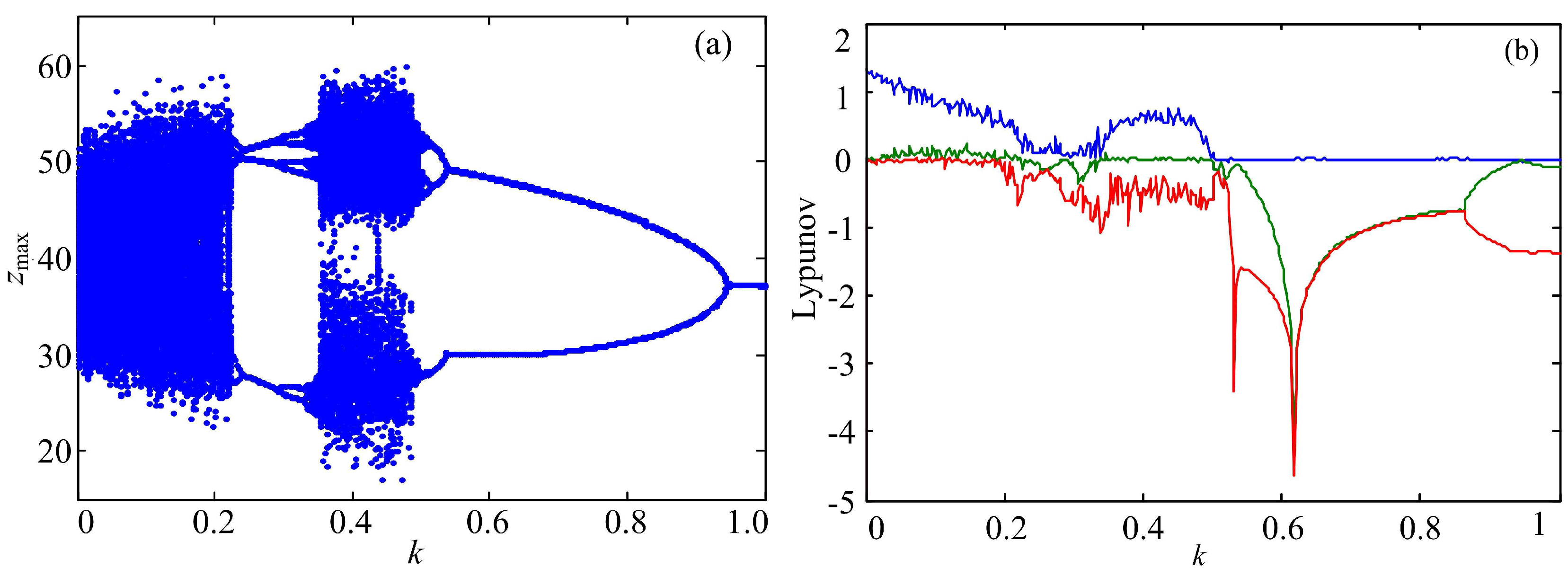
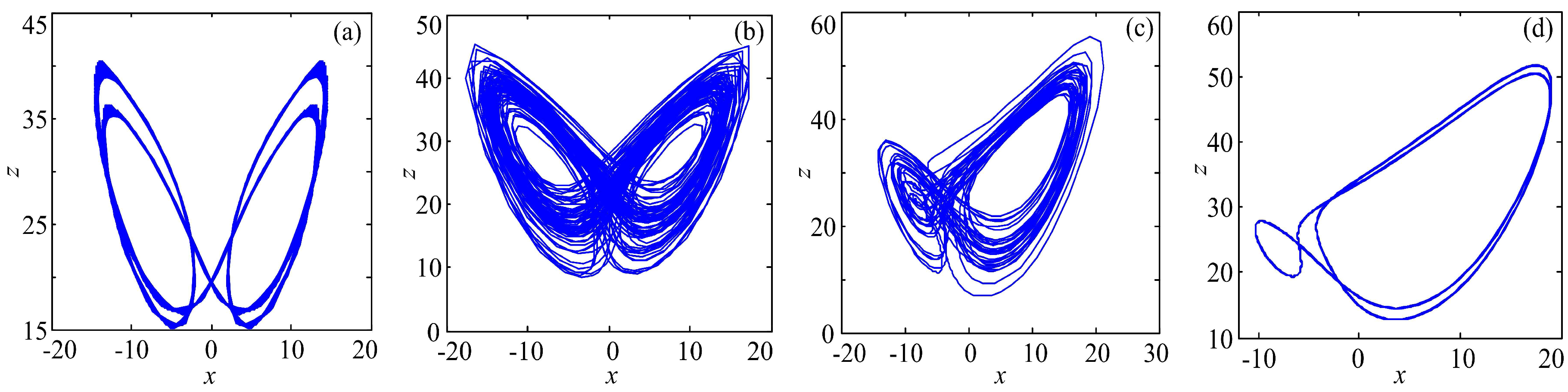
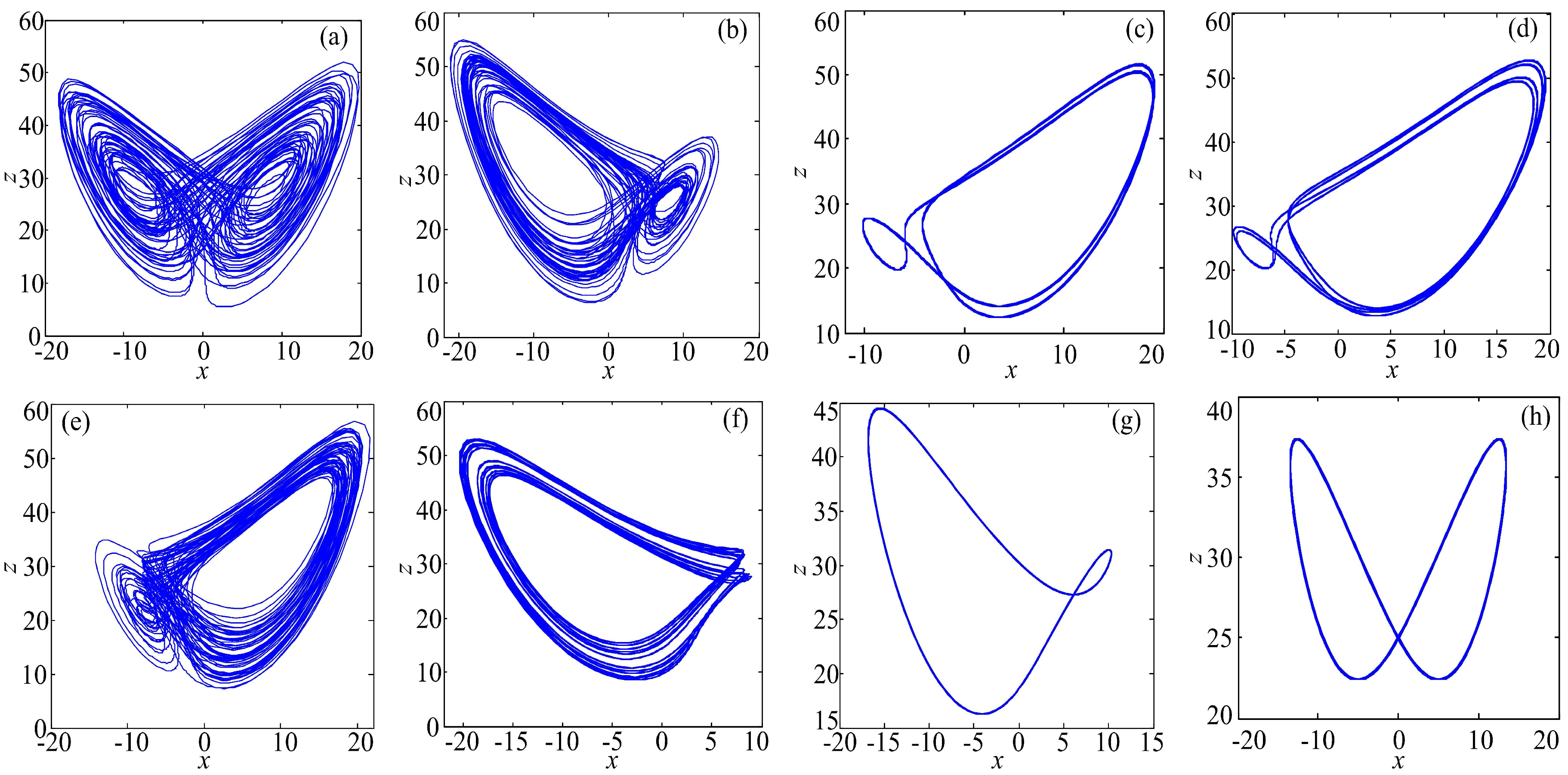
3.2. Observation of Chaotic Attractors
3.3. Spectral Entropy Complexity Analysis

3.4. C Complexity Analysis
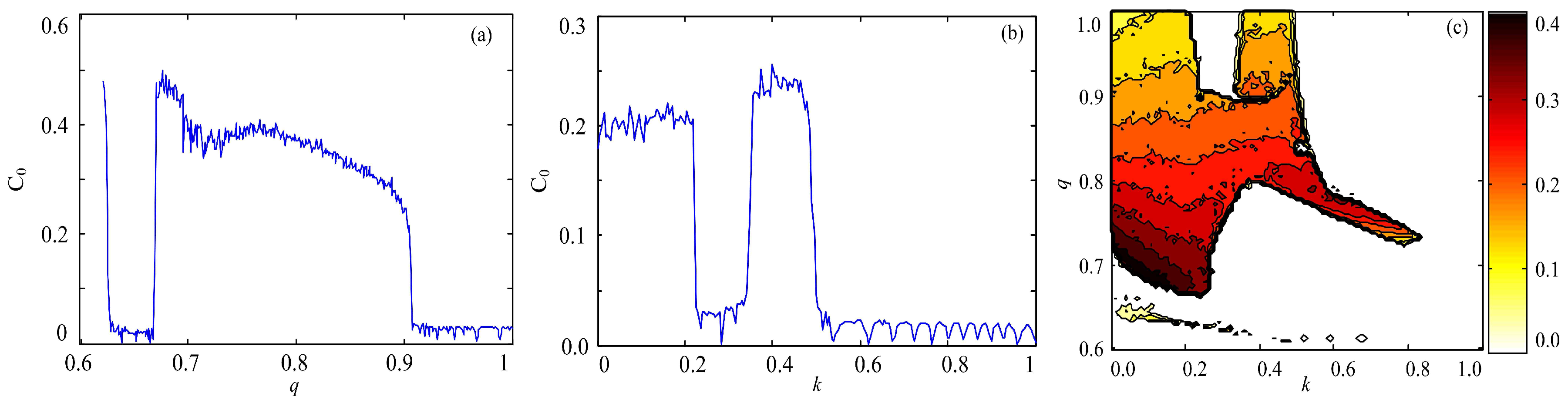
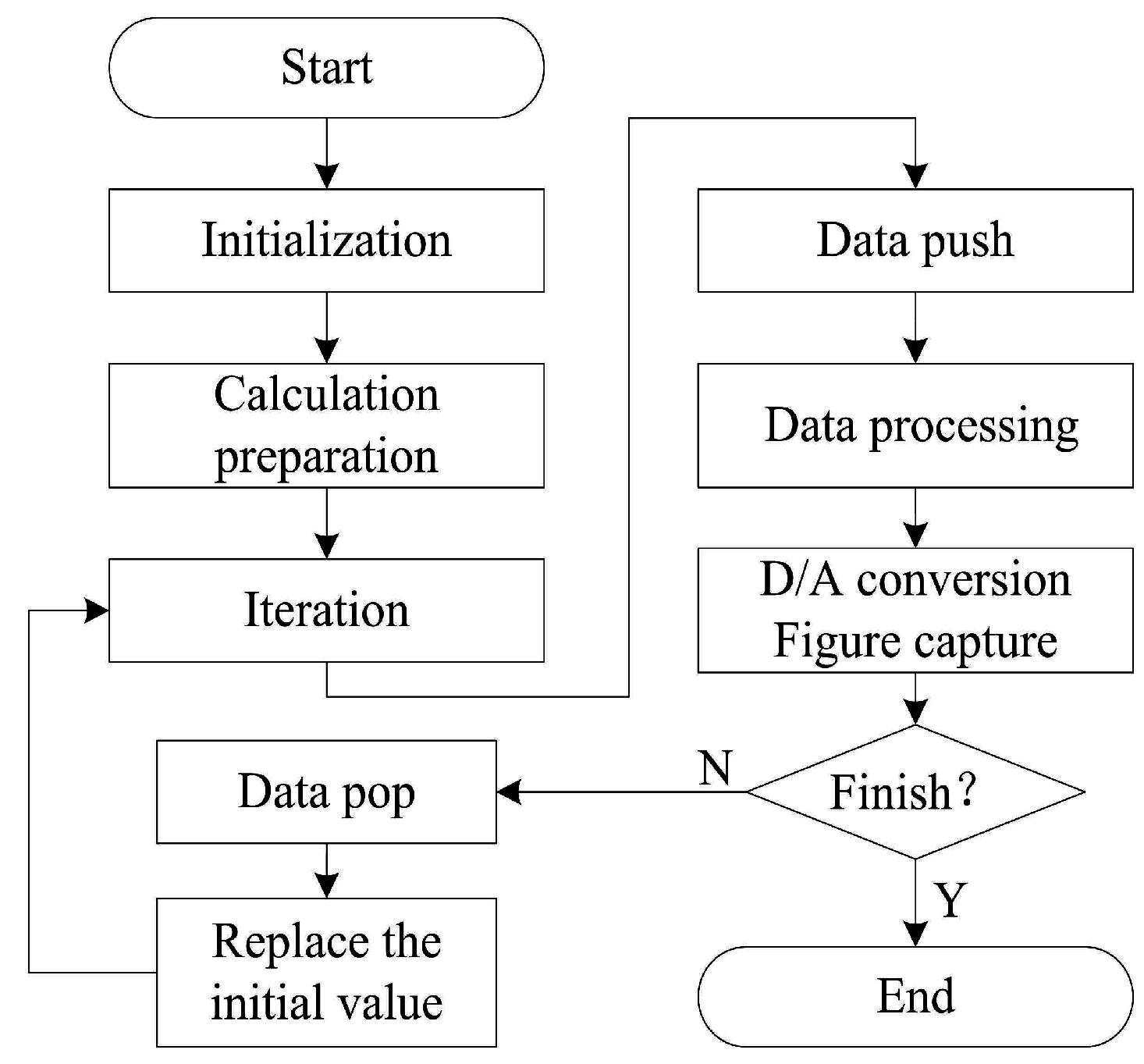
4. Digital Circuit Implementation
4.1. DSP Implementation


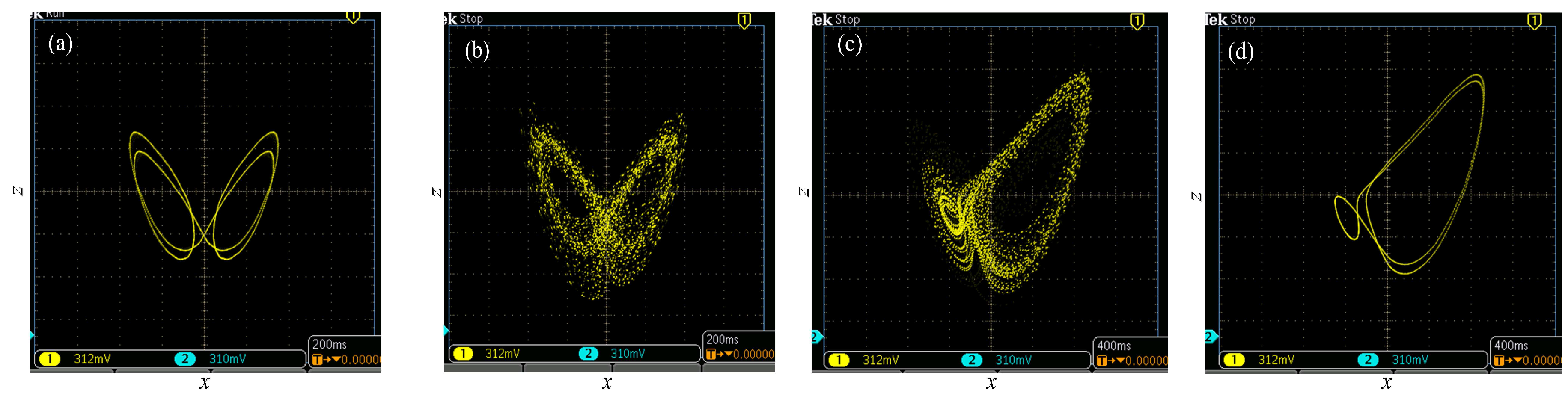
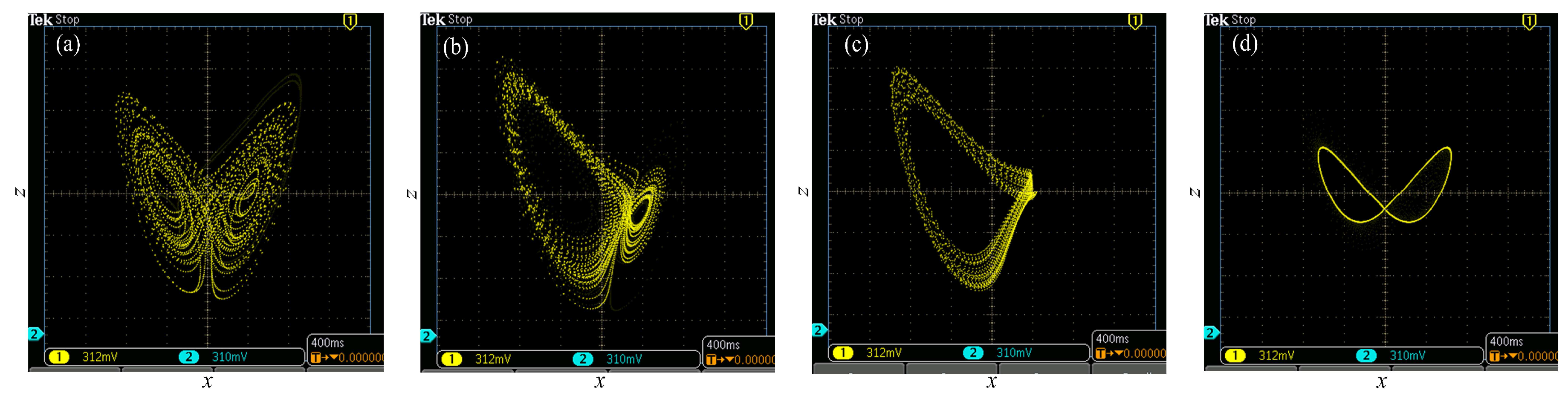
4.2. Pseudo-Random Sequence Generator
| p-Value | Proportion | Success | |
|---|---|---|---|
| Frequency | 0.366918 | 100% | √ |
| B. Frequency | 0.002559 | 99% | √ |
| C. Sums | 0.275709 | 99% | √ |
| Runs | 0.048716 | 98% | √ |
| Longest Run | 0.935716 | 99% | √ |
| Rank | 0.883171 | 99% | √ |
| FFT | 0.574903 | 100% | √ |
| N.O.Temp. | 0.002203 | 97% | √ |
| O.Temp. | 0.834308 | 100% | √ |
| Universal | 0.759756 | 99% | √ |
| App. Entropy | 0.759756 | 98% | √ |
| R.Excur. | 0.005166 | 96.7% | √ |
| R.Excur.V. | 0.105618 | 96.7% | √ |
| Serial | 0.075719 | 99% | √ |
| L. Complexity | 0.554420 | 99% | √ |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, Z.L.; Yang, D.S. Stability analysis for nonlinear fractional-order systems based on comparison principle. Nonlinear Dyn. 2014, 75, 387–402. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, K.H.; He, S.B.; Wang, H.H. Dynamics of fractional-order sinusoidally forced simplified Lorenz system and its synchronization. Eur. Phys. J. Special Top. 2014, 223, 1591–1600. [Google Scholar] [CrossRef]
- Daftardar, G.V.; Bhalekar, S. Chaos in fractional ordered Liu system. Comp. Math. Appl. 2010, 59, 1117–1127. [Google Scholar] [CrossRef]
- Chen, D.; Wu, C.; Herbert, H.C.I. Circuit simulation for synchronization of a fractional-order and integer-order chaotic system. Nonlinear Dyn. 2013, 73, 1671–1686. [Google Scholar] [CrossRef]
- Tian, X.M.; Fei, S.M. Robust control of a class of uncertain fractional-order chaotic systems with input nonlinearity via an adaptive sliding mode technique. Entropy 2014, 16, 729–746. [Google Scholar] [CrossRef]
- Zhang, L.G.; Yan, Y. Robust synchronization of two different uncertain fractional-order chaotic systems via adaptive sliding mode control. Nonlinear Dyn. 2014, 76, 1761–1767. [Google Scholar] [CrossRef]
- Charef, A.; Sun, H.H.; Tsao, Y.Y. Fractal system as represented by singularity function. IEEE Trans. Auto. Contr. 1992, 37, 1465–1470. [Google Scholar] [CrossRef]
- Adomian, G.A. Review of the decomposition method and some recent results for nonlinear equations. Math. Comp. Model. 1990, 13, 17–43. [Google Scholar] [CrossRef]
- Sun, H.H.; Abdelwahab, A.A.; Onaral, B. Linear approximation of transfer function with a pole of fractional power. IEEE Trans. Auto. Contr. 1984, 29, 441–444. [Google Scholar] [CrossRef]
- Tavazoei, M.S.; Haeri, M. Unreliability of frequency-domain approximation in recognizing chaos in fractional-order systems. IET Sign. Proc. 2007, 1, 171–181. [Google Scholar] [CrossRef]
- He, S.B.; Sun, K.H.; Wang, H.H. Solving of fractional-order chaotic system based on Adomian decomposition algorithm and its complexity analyses. Acta Phys. Sin. 2014, 63, 030502. [Google Scholar]
- Li, C.; Gong, Z.; Qian, D. On the bound of the Lyapunov exponents for the fractional differential systems. Chaos 2010, 20, 013127. [Google Scholar] [CrossRef] [PubMed]
- Wolf, A.; Swift, J.B.; Swinney, H.L. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Ellner, S.; Gallant, A.R.; McCaffrey, D. Convergence rates and data requirements for Jacobian-based estimates of Lyapunov exponents from data. Phys. Lett. A 1991, 153, 357–363. [Google Scholar] [CrossRef]
- Maus, A.; Sprott, J.C. Evaluating Lyapunov exponent spectra with neural networks. Chaos Solit. Fract. 2013, 51, 13–21. [Google Scholar] [CrossRef]
- Caponetto, R.; Fazzino, S. An application of Adomian decomposition for analysis of fractional-order chaotic systems. Int. J. Bifur. Chaos 2013, 23, 1350050. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Larrondo, H.A.; Gonzlez, C.M.; Martin, M.T. Intensive statistical complexity measure of pseudorandom number generators. Phys. A 2005, 356, 133–138. [Google Scholar] [CrossRef]
- Wei, Q.; Liu, Q.; Fan, S.Z. Analysis of EEG via multivariate empirical mode decomposition for depth of anesthesia based on sample entropy. Entropy 2013, 15, 3458–3470. [Google Scholar] [CrossRef]
- Chen, W.T.; Zhuang, J.; Yu, W.X. Measuring complexity using FuzzyEn, ApEn, and SampEn. Med. Eng. Phys. 2009, 31, 61–68. [Google Scholar] [CrossRef] [PubMed]
- Phillip, P.A.; Chiu, F.L.; Nick, S.J. Rapidly detecting disorder in rhythmic biological signals: A spectral entropy measure to identify cardiac arrhythmias. Phys. Rev. E 2009, 79, 011915. [Google Scholar]
- Shen, E.H.; Cai, Z.J.; Gu, F.J. Mathematical foundation of a new complexity measure. Appl. Math. Mech. 2005, 26, 1188–1196. [Google Scholar]
- He, S.B.; Sun, K.H.; Zhu, C.X. Complexity analyses of multi-wing chaotic systems. Chin. Phys. B 2013, 22, 050506. [Google Scholar] [CrossRef]
- Sun, K.H.; He, S.B.; He, Y. Complexity analysis of chaotic pseudo-random sequence based on spectral entropy algorithm. Acta Phys. Sin. 2013, 62, 010501. [Google Scholar]
- Cao, Y.; Cai, Z.J.; Shen, E.H. Quantitative analysis of brain optical images with 2D C0 complexity measure. J. Neurosci. Meth. 2007, 159, 181–186. [Google Scholar] [CrossRef] [PubMed]
- Cafagna, D.; Grassim, G. Bifurcation and chaos in the fractional-order Chen system via a time-domain approach. Int. J. Bifur. Chaos 2008, 18, 1845–1863. [Google Scholar] [CrossRef]
- Shawagfeh, N.T. Analytical approximate solutions for nonlinear fractional differential equations. Appl. Math. Comp. 2002, 131, 517–529. [Google Scholar] [CrossRef]
- Gao, T.G.; Chen, G.R.; Chen, Z.Q. The generation and circuit implementation of a new hyper-chaos based upon Lorenz system. Phys. Lett. A 2007, 361, 78–86. [Google Scholar] [CrossRef]
- NIST Computer Security Resource Center. Available online: http://csrc.nist.gov/groups/ST/toolkit/rng/documentation_software.html (accessed on 17 December 2015).
- Runkin, A.; Soto, J.; Nechvatal, J. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications. Available online: http://nvlpubs.nist.gov/nistpubs/Legacy/SP/nistspecialpublication800-22.pdf (accessed on 17 December 2015).
- Tlelo-Cuautle, E.; Carbajal-Gomez, V.H.; Obeso-Rodelo, P.J. FPGA realization of a chaotic communication system applied to image processing. Nonlinear Dyn. 2015, 82, 1879–1892. [Google Scholar] [CrossRef]
- Hidalgo, R.M.; Fernández, J.G.; Larrondo, H.A. Versatile DSP-based chaotic communication system. Electr. Lett. 2001, 37, 1204–1205. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, S.; Sun, K.; Wang, H. Complexity Analysis and DSP Implementation of the Fractional-Order Lorenz Hyperchaotic System. Entropy 2015, 17, 8299-8311. https://doi.org/10.3390/e17127882
He S, Sun K, Wang H. Complexity Analysis and DSP Implementation of the Fractional-Order Lorenz Hyperchaotic System. Entropy. 2015; 17(12):8299-8311. https://doi.org/10.3390/e17127882
Chicago/Turabian StyleHe, Shaobo, Kehui Sun, and Huihai Wang. 2015. "Complexity Analysis and DSP Implementation of the Fractional-Order Lorenz Hyperchaotic System" Entropy 17, no. 12: 8299-8311. https://doi.org/10.3390/e17127882
APA StyleHe, S., Sun, K., & Wang, H. (2015). Complexity Analysis and DSP Implementation of the Fractional-Order Lorenz Hyperchaotic System. Entropy, 17(12), 8299-8311. https://doi.org/10.3390/e17127882






