Abstract
Cloud computing (CC) capacities deliver high quality, connected with demand services and service-oriented construction. Nevertheless, a cloud service (CS) is normally derived from numerous stages of facilities and concert features, which determine the value of the cloud service. Therefore, it is problematic for the users to estimate these cloud services and select them to appropriate their requirements. In this study, a new algorithm is carried out for a multi-agent system (MAS) based on fractional power. The study depends on a fractional difference equation of type two point boundary value problem (BVP) based on the fractional entropy. We discuss the existence of solutions for the system as well as the stability, utilizing the Hadamard well-posed problem. Experimental results show that the proposed method demonstrates stability and performance.
1. Introduction
Recently, numerous huge groups such as Google, Amazon, etc., have capitalized on massive data centers (DC). These funds have still not achieved rising client supplies. Nevertheless, the process and conservation budget of such data centers is significant. Therefore, to reduce the DC overall budget, these groups have started moving to cloud computing (CC), as service benefactors.
The aim of CC is to optimize the tradition of software resources, physical, develops suppleness and mechanizes organization, which is consequently realized as a method to reduce costs and to increase income for cloud service sources. The achievement of CC will be contingent on how successfully it: drives skilled to instantiate and dynamically working computing platforms, is constructed out of cloud service (CS), and encompasses the arbitrarily varying service requirements of cloud costumers. Usually, these services will be described by the quality of CS requirements, such as capability, timeliness, high availability, security, trust, etc. Moreover, the assistance of CC comes from new experiments such as security, consistency, etc., that must be suitably addressed. Consequently, corresponding and defining the best cloud for a modified request is significant and often controls the achievement of the fundamental business of the cloud users.
Multi-agent system (MAS) are significant classification schemes because of their trade and armed requests. Saber et al. [1] introduced multi-agent systems, with a stress on the attractiveness of the fixed data flow, strength to variations in network topology due to link/node failures, performance guarantees and time-delays. Xie and Wang [2] imposed the consensus of second order discrete time MAS with fixed topology. Ma et al. [3] reflected the group consensus problem of second-order nonlinear multi-agent systems through leader-following approach and pinning control. Recently, Meng et al. [4] studied finite time multi-agent consensus problems under networks based on signed graphs whose edge weights can be not only positive but also negative. Chu et al. [5] investigated the agreement tracking problem for MAS with direct graph applying the Lyapunov function. The fractional integral system in the economy was suggested for the first time by Baillie [6]. Studies of the multi-agent systems focus fundamentally on integer calculus, whose dynamical equations are ordinary differential equations. However, various MAS cannot be deliberated with the integer cases in the complex physical situation, although they only are selected with fractional order (non-integer) differential equations. Recently, fractional economic systems have been investigated by Machado and Mata [7,8].
The distributed work is based on three factors; database, platform and service node. Moreover, cloud computing depends on a large number of users and in the normal structure the load is not equal. The changing of the load casues the usage of various classes of difference equations. In addition, this class provides a good comparison and improves the quality of the cloud service. The applications show the simplicity and validity of our system, which has perfect usability, reliability and stability. We shall consider a special type of fractional power operator. This operator allows us to make sure that there is a connection between the users in the cloud system. This connection can be controlled by employing a sufficient fractional power. Another reason to utilize the difference equation is that the database is distributed and shared between different computers. The database system involves one logical database, which is divided into various segments. Each segment is stored in one or more computers which are connected by a communication network.
In 1974, Diaz and Osler [9] carried out a discrete fractional difference operator founded by infinite power series. In 1988, Gray and Zhang [10] offered a group of fractional difference operators and presented the Leibniz formal. In 2009, Atici and Eloe [11] announced the approaches for composing fractional differences and sums. Mathematicians, physicists, and engineers have lately been employing fractional calculus to explain and model changes of applied problems in diverse areas. Recently, Ibrahim and Jalab [12,13] investigated a positive solution of discrete fractional boundary value problems for continuous Gâteaux differentiable functions. A generalized Gâteaux derivative is introduced by employing a fractional discrete operator.
In this study, a new algorithm is carried out for an entropy MAS based on fractional power. The study depends on a fractional difference equation of type two point boundary value problem (fractional boundary value problem (BVP)). We discuss the existence of solutions for the system as well as the stability, utilizing the Hadamard well-posed problem. Experimental outcomes show that the proposed method is furnished with stability and performance.
2. Formal Algorithm
The formal emphasis is upon the influence of the overall trend of choices of technology transition times. In this setting, a continuum of agents having non homogenous preferences, pay a cost to transfer from one point to another point in the state space. Assume that there are agents whose communication network is a directed graph. The agent has the cost function and representing what an agent pays to have the features (i.e., the level of cloud computing at time ) under the controller input and the density of the population for a given level of It has been shown that the integer linear system
is a distributed agreement algorithm [14] such that is the (agent can receive information from agent otherwise ) element of the adjacency matrix . The contract is asymptotically touched when the mutual conclusion is equivalent to the average of the initial state of all agents. A consensus algorithm with this specific invariance property is called an average-agreement algorithm and has wide implications on distributed computing in networks
In this study, we deal with a multi-agent system of fractional difference equations of type two points BVP, taking the formal
where are constants, and is defined by
It is clear that the extended binomial coefficients satisfies for all (see [14,15]).
Recently, fractional entropy has played an important role in improving many results in various applications in science engineering. In [16], Tsallis imposed a fractional entropy, which is a modification of Shannon entropy. In [17], Mathai and Haubold generalized the Tsallis formula. Machado recently considered a novel formula for entropy by applying fractional calculus [18]. Ibrahim and Jalab employed the fractional entropy in image processing and dynamical systems [19,20,21]. The arrangement of multiple managers on a particular physical machine increases various security concerns. Many of these concerns are associated with problems that multi-agent systems had to address when they went from the single agent to MAS. Of chief concern is keeping one user’s data, programs, activity and resources separate from all others. Usually, to avoid these weaknesses, a modified cloud entropy management system is considered and employed [22,23,24,25].
By employing the fractional Tsallis entropy, given by
or in a discreet form
and by using the coefficients we have the following modify entropy:
for a suitable and a large value of we suggest a new difference operator of the formal
where
Our aim is to study the multi-agent system of fractional difference equations of type two points BVP, taking the formal
Subjected to the following boundary condition (BC):
where is the cost function for all agents in the cloud system.
3. Findings
The mathematical concept well-posed problem (or Hadamard well-posed) is defined as the mathematical platforms of physical phenomena that should have properties such that:
- (i)
- A solution exists;
- (ii)
- The solution is unique;
- (iii)
- The solution’s behavior changes continuously with the initial conditions.
Otherwise, it is called ill-posed. It is well known that, if the problem is well-posed, then it can be viewed as a good algorithm of outcome on a computer employing a stable algorithm. Since the system Equation (1) is formulated for multi users, it is enough to show that Equation (1) has multi-solutions. In this case, we satisfy part (i) of the well-posed problem.
3.1. Uniqueness
The main result can be formulated as follows:
Theorem 3.1.
Let be continuous and
Suppose that there exist constants and a positive function If
and
where
and
Then the problem Equation (1) has a unique solution for each .
Proof.
Consider the complete metric space and for all
System (1) can be viewed as the following summation equation:
where
We aim to show that Equation (1) has a unique solution. Define the following operator:
So that
Evidently, is bounded
where is the zero element in .
We proceed to demonstrate that for a unique Since is well-defined on it implies that We display that is a contraction mapping on with respect , i.e., there is a constant such that
A calculation yields, for
Hence, yields
Consequently, we obtain
where Thus, is a contraction mapping on with respect to the metric and thus, all of the conditions of Banach’s fixed point theorem valid. Therefore, there exists a unique solution such that This completes the proof. ☐
Theorem 3.2.
Let the inequality Equation (2) be satisfied. If and such that
then the problem Equation (1) has a unique solution.
Proof.
Consider the metric space and for all
It is easy to show that is a complete metric space. By the assumption, we conclude that for all then operator Equation (4) implies that
Taking the we obtain
Thus, we conclude that
with
Hence, is a contraction mapping on with respect to the metric and so, all of the conditions of the Banach fixed point theorem archived. Therefore, there is a unique such that Λ χ = χ, implying the existence of a unique solution to the problem Equation (1). ☐
3.2. Exact Solution
The solution of system Equation (1) has the formal type
with
Thus, the group property of the solution Equation (6) can be read as
By applying the following substitution in Equation (7),
we have
which is the solution of Equation (1). We have the following result :
Theorem 3.3.
The system Equation (1) has an exact finite scheme solution taking the form Equation (8).
There are various well-known cloud computing service suppliers, such as, Google, Amazon, IBM and Microsoft, etc. How should one select the furthermost proper cloud service for owners from the suppliers? It has been shown that information-entropy is the best method for the selection of cloud computing services. We believe that system Equation (1) can be used for this purpose, because it calculates the entropy of the cost function of the multi-agent system. Consequently, affording the difference equation involving the entropy, and the evaluation values given by experts for each case, we may conclude that the cloud tends to be a more objective and reasonable one.
4. Applications
Wireless networks aim to offer an Internet connection over numerous technologies anywhere and anytime. The collection of an optimal technology of these obtainable technologies is necessary and critical in terms of assurance, customer flexibility and service permanency in a mixed wireless cloud environment. In this section, we prepare an application for the above algorithm (see Figure 1) and compare it with the model which is based on the integration of simple additive weighting (SAW) method (see [26]),
where denotes the connection between i and j, else is the utility of the agent i in the cloud service during time t. Moreover, the maximum utility of the cloud can be calculated by the following equation:
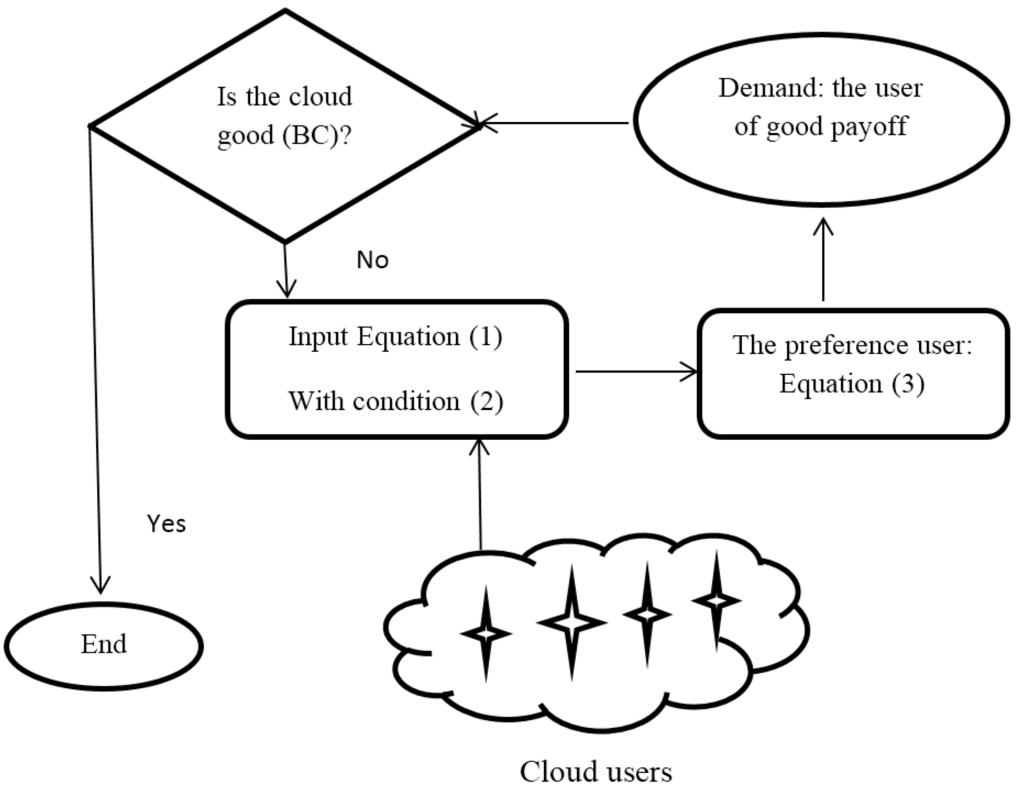
Figure 1.
The proposed algorithm.
The aim of the new algorithm is to select the greatest network of the various available networks.There are four agents and a supervisory agent (a leader). At the first stage, one service agent is started. An arrangement of each service agent is the same. The relation of demand, the number of agents and time of receipt of all agents (per seconds) is shown in Table 1. It can be seen that for and the system service load is 30 service demands; therefore, the cloud has one agent. In the second interval of time , the demand increased to 35, hence the number of agents in the system is 3. The highest value appeared at Demand = 42, thus, the system involves four agents in the third period of time. For the fractional power and the system converges to the normal case.

Table 1.
Fractional multi-agent system.
| α | Timeof Receiption | Demand (Service Load) | Number of Agents |
|---|---|---|---|
| 1 | 90.1 | 30 | 1 |
| 163.1 | 35 | 3 | |
| 285.4 | 42 | 4 | |
| 365.7 | 35 | 3 | |
| 467.7 | 30 | 2 | |
| 0.75 | 90.1 | 27.57 | 1 |
| 163.1 | 32.165 | 3 | |
| 285.4 | 38.6 | 4 | |
| 365.7 | 32.165 | 3 | |
| 467.7 | 27.57 | 2 | |
| 0.5 | 90.1 | 26.58 | 1 |
| 163.1 | 31.01 | 3 | |
| 285.4 | 37.212 | 4 | |
| 365.7 | 31.01 | 3 | |
| 467.7 | 26.58 | 2 |
In general, by utilizing the proposed algorithm, we receive less loading of the service request. For instance, for α = 0.5, we obtain Demand = 37.212, while when α = 1, Demand = U* = 42. Figure 2 shows the performance comparison of cloud service, multi-agent system algorithm with the proposed arrangement algorithm. The proposed method has a good performance. The cloud Sim tool is utilized in cloud computing. As an outcome of simulation tests, for a 4-agent system, we conclude that the maximal Demand = 42 appears for α = 1.0 and the minimum Demand = 37.2 for α = 0.5, i = 4.
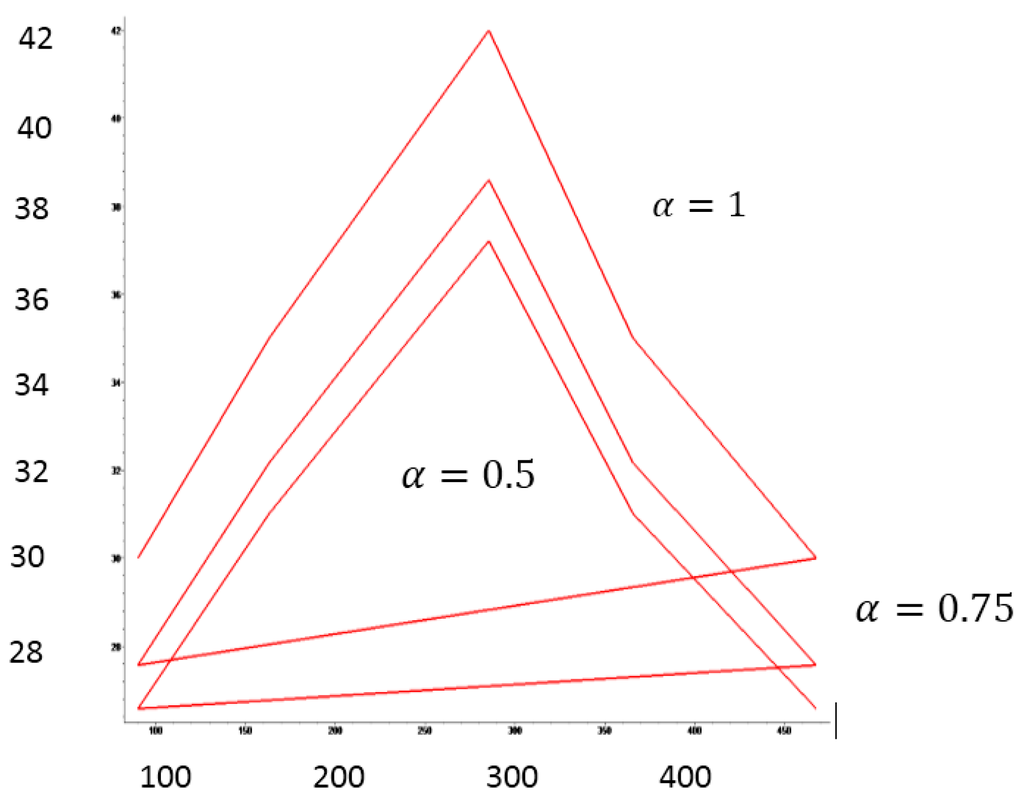
Figure 2.
Convergence of the algorithm: four-agent system: demand with respect to time.
5. Discussion
Recognized analysis of the performance of multi-agent systems that include additional categories of instrument is developed in this study. An equilibrium of the suggested system in (1) is read in the formal
It has been exposed to an associated network, and the equilibrium is globally exponentially stable (see [1]). For System Equation (1), we calculate the initial value
If we let
then Equation (4) implies the unique solution
Similarly, if we let
then the unique solution can be read as follows:
Hence, we obtain
Moreover, the combined dynamics of the assembly of agents ensuing formal (6) can be read as follows:
where is the Laplacian of the system, which always has a zero eigenvalue corresponding to normal vector Therefore, the system Equation (6) has the same equilibrium of the system Equation (2) namely Finally, we consider the usage of conjunction investigation approaches that employ the properties of Laplacian determination of the presentation, and the conjunction investigation of self-synchrony in oscillator systems [22].
6. Conclusions
Investigators in different areas such as computer science, communications, neural networks, dynamical systems, control systems, food processing, signal processing and economics focus on mathematical modeling because it naturally influences the nonlinear difference equation. This study delivered a hypothetical outline for the investigation of procedures for MAS of fractional order with a foczs on the character of concentrating data movement, toughness to modifications in complex system topology owing demands, time, and routine guarantees. A summary of straightforward concepts of information in approaches of convergence and performance investigation of the procedures is delivered. Our analytical framework is founded depending on the theory of fractional difference equations and control theory. We established direct connections between the graph Laplacian of the network and the proposed algorithm. Applications are presented that show the algorithms and cooperative control. Furthermore, we proved that the algorithm is asymptotic under some condition using the concept of the well-posed Hadamard. The applications showed the simplicity and validity of our system, which has perfect usability, reliability and stability. The comparison was established by using the (SAW) method, because this method is quite similar to Saber’s system [1].
Acknowledgments
The authors would like to thank the reviewers for their useful comments to improve the paper. This research is supported by Malaysian Ministry of Higher Education under the University Malaya High Impact Research Grant with reference: RG312-14AFR from the University of Malaya and UM.C/625/1/HIR/MOE/FCSIT/03.
Author Contributions
Rabha W. Ibrahim designed the mathematical model; Hamid A. Jalab performed the experiments; Abdullah Gani Wrote the paper; all the authors jointly worked on deriving the results. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Olfati-Saber, R.; Fax, A.; Murray, R.M. Consensus and cooperation in networked multi-agent systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef]
- Xie, D.; Wang, S. Consensus of second-order discrete-time multi-agent systems with fixed topology. J. Math. Anal. Appl. 2012, 387, 8–16. [Google Scholar] [CrossRef]
- Ma, Q.; Wang, Z.; Miao, G. Second-order group consensus for multi-agent systems via pinning leader-following approach. J. Frankl. Inst. 2014, 351, 1288–1300. [Google Scholar] [CrossRef]
- Meng, D.; Jia, Y.; Du, J. Nonlinear finite-time bipartite consensus protocol for multi-agent systems associated with signed graphs. Int. J. Control 2015, 88. [Google Scholar] [CrossRef]
- Chu, H.; Cai, Y.; Zhang, W. Consensus tracking for multi-agent systems with directed graph via distributed adaptive protocol. Neurocomputing 2015, 166, 8–13. [Google Scholar] [CrossRef]
- Baillie, R.T. Long memory processes and fractional integration in econometrics. J. Econ. 1996, 73, 5–59. [Google Scholar] [CrossRef]
- Machado, J.A.T.; Mata, M.E. Pseudo phase plane and fractional calculus modeling of western global economic downturn. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 396–406. [Google Scholar] [CrossRef]
- Machado, J.A.T.; Mata, M.E. A fractional perspective to the bond graph modelling of world economies. Nonlinear Dyn. 2014, 80, 1839–1852. [Google Scholar] [CrossRef]
- Diaz, J.B.; Osler, T.J. Differences of fractional order. Math. Comput. 1974, 28, 185–202. [Google Scholar] [CrossRef]
- Gray, H.L.; Zhang, N.F. On a new definition of the fractional difference. Math. Comput. 1988, 50, 513–529. [Google Scholar] [CrossRef]
- Atici, F.; Eloe, P. Initial value problems in discrete fractional calculus. Proc. Am. Math. Soc. 2009, 137, 981–989. [Google Scholar]
- Ibrahim, R.W.; Jalab, H.A. Discrete boundary value problem based on the fractional gâteaux derivative. Bound. Value Probl. 2015, 2015. [Google Scholar] [CrossRef]
- Ibrahim, R.W.; Jalab, H.A. Existence of a class of fractional difference equations with two point boundary value problem. Adv. Differ. Equ. 2015, 2015. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Murray, R.M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Mohan, J.J.; Deekshitulu, G.V.S.R. Fractional order difference equations. Int. J. Differ. Equ. 2012, 2012, 780619. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Mathai, A.M.; Haubold, H.J. On a generalized entropy measure leading to the pathway model with a preliminary application to solar neutrino data. Entropy 2013, 15, 4011–4025. [Google Scholar] [CrossRef]
- Machado, J.A.T. Fractional order generalized information. Entropy 2014, 16, 2350–2361. [Google Scholar] [CrossRef]
- Ibrahim, R.W.; Jalab, H.A. Existence of entropy solutions for nonsymmetric fractional systems. Entropy 2014, 16, 4911–4922. [Google Scholar] [CrossRef]
- Ibrahim, R.W.; Jalab, H.A. Existence of Ulam stability for iterative fractional differential equations based on fractional entropy. Entropy 2015, 17, 3172–3181. [Google Scholar] [CrossRef]
- Ibrahim, R.W.; Moghaddasi, Z.; Jalab, H.A.; Noor, R.M. Fractional differential texture descriptors based on the machado entropy for image splicing detection. Entropy 2015, 17, 4775–4785. [Google Scholar] [CrossRef]
- Kerrigan, B.; Chen, Y. A Study of Entropy Sources in Cloud Computers: Random Number Generation on Cloud Hosts; Springer: Berlin, Germany, 2012. [Google Scholar]
- Jiang, R.; Liao, H.; Yang, M.; Li, C. A decision-making method for selecting cloud computing service based on information entropy. Int. J. Grid Distrib. Comput. 2015, 8, 225–262. [Google Scholar] [CrossRef]
- Whaiduzzaman, M.; Sookhak, M.; Gani, A.; Buyya, R. A survey on vehicular cloud computing. J. Netw. Comput. Appl. 2014, 40, 325–344. [Google Scholar] [CrossRef]
- Preciado, V.M.; Verghese, G.C. Synchronization in Generalized Erd ö s-R é nyi Networks of Nonlinear Oscillators. In Proceedings of the 44th IEEE Conference on Decision and Control and European Control Conference (CDC-ECC ‘05), Seville, Spain, 12–15 December 2005; pp. 4628–4633.
- Salih, Y.K.; See, O.H.; Ibrahim, R.W.; Yussof, S.; Iqbal, A. A user-centric game selection model based on user preferences for the selection of the best heterogeneous wireless network. Ann. Telecommun. 2015, 70, 239–248. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).