From Lattice Boltzmann Method to Lattice Boltzmann Flux Solver
Abstract
:1. Introduction
2. Lattice Boltzmann Method
3. Chapman–Enskog Analysis
4. LBFS for Isothermal and Thermal Incompressible Flows
4.1. Finite Volume Discretization
4.2. Local Reconstruction of Fluxes at Each Interface
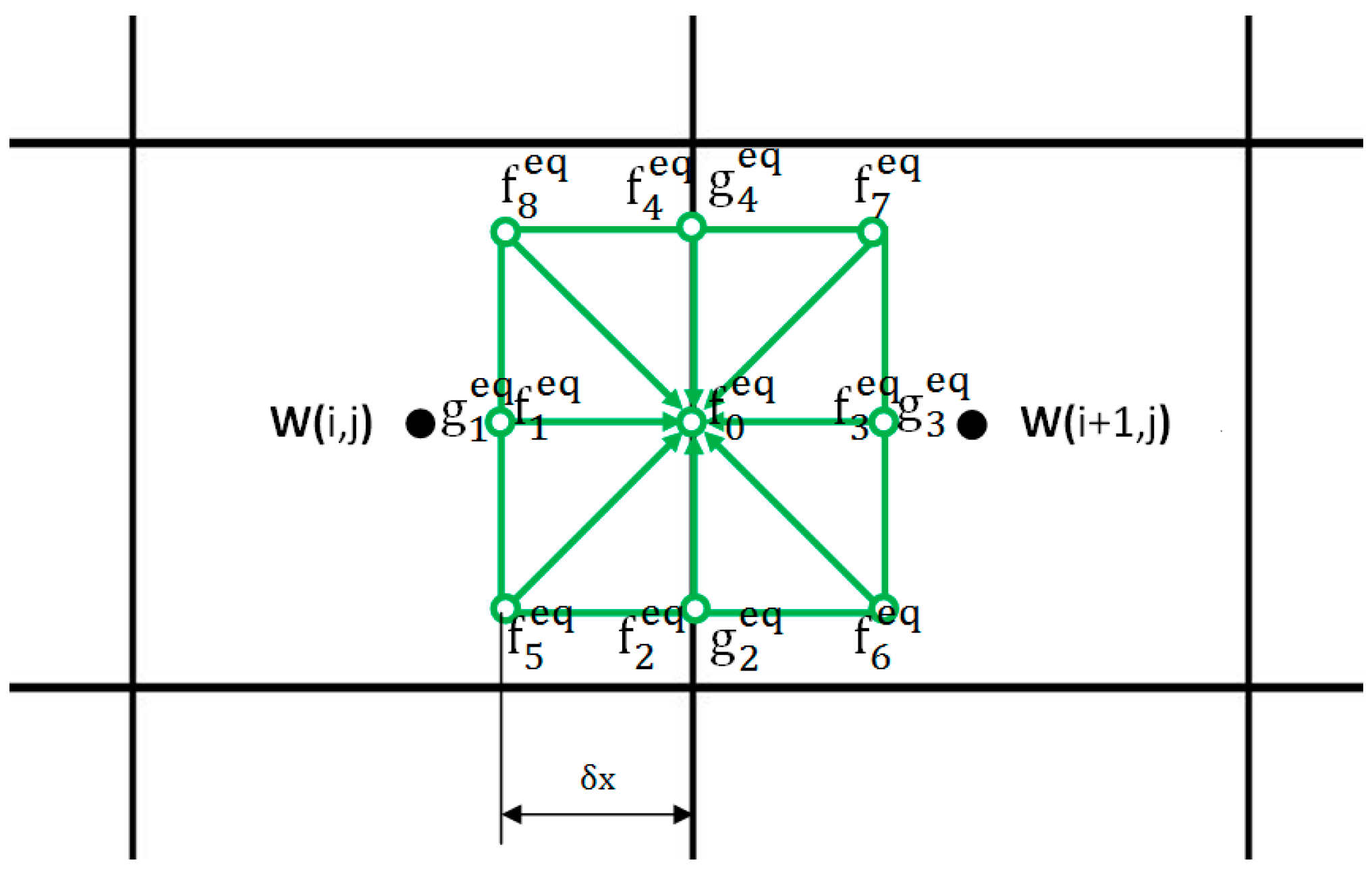
5. LBFS for Compressible Flows
5.1. Navier–Stokes Equations Discretized by FVM and Compressible Lattice Boltzmann Model

5.2. Evaluation of Inviscid Flux by LBFS
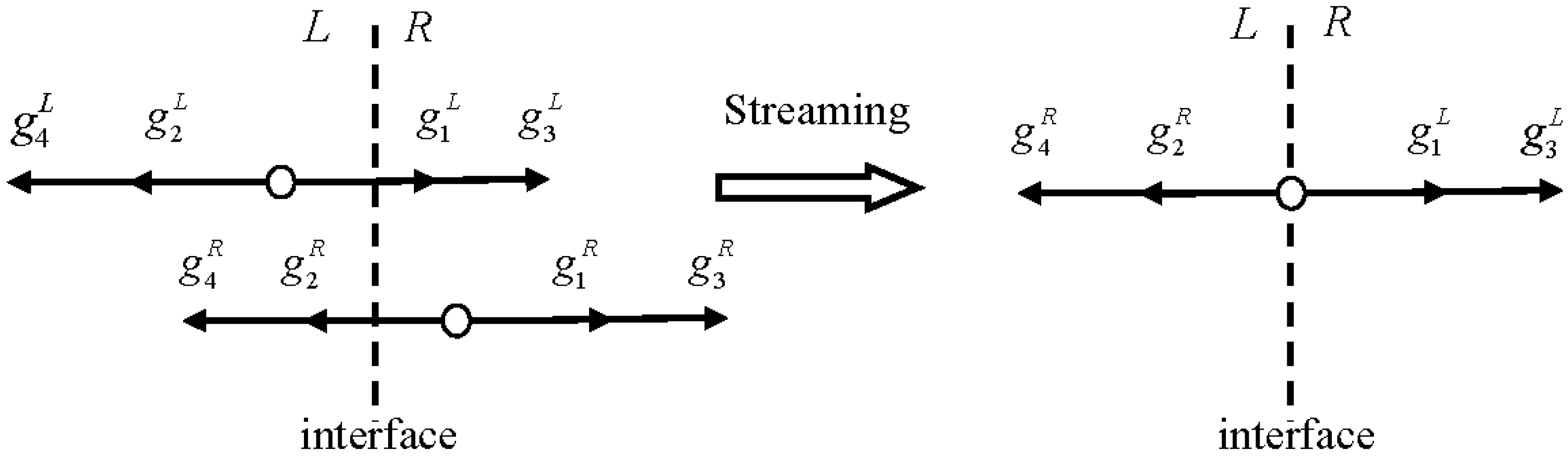
6. Numerical Examples and Discussion
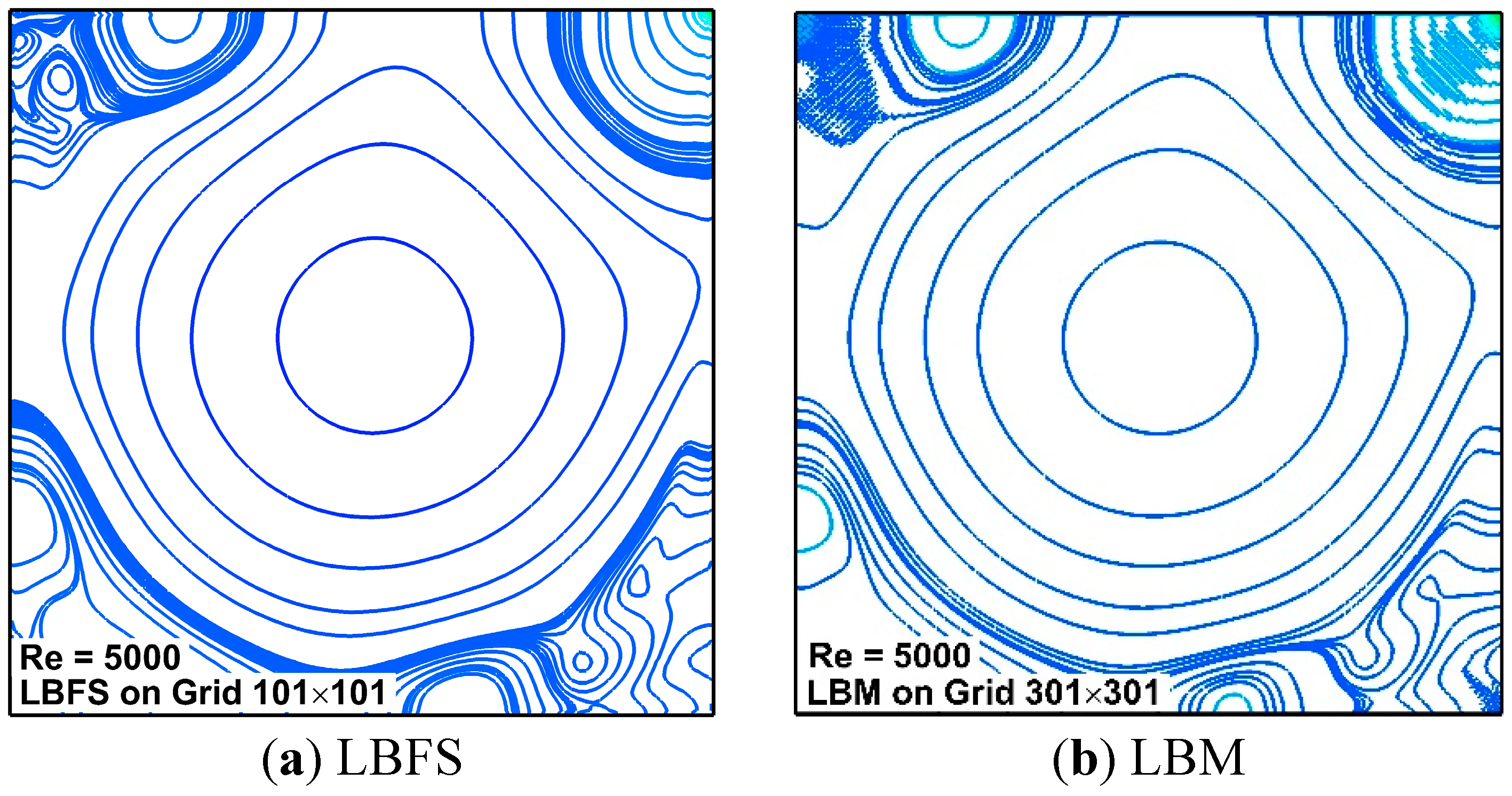
6.1. Lid-Driven Cavity Flows
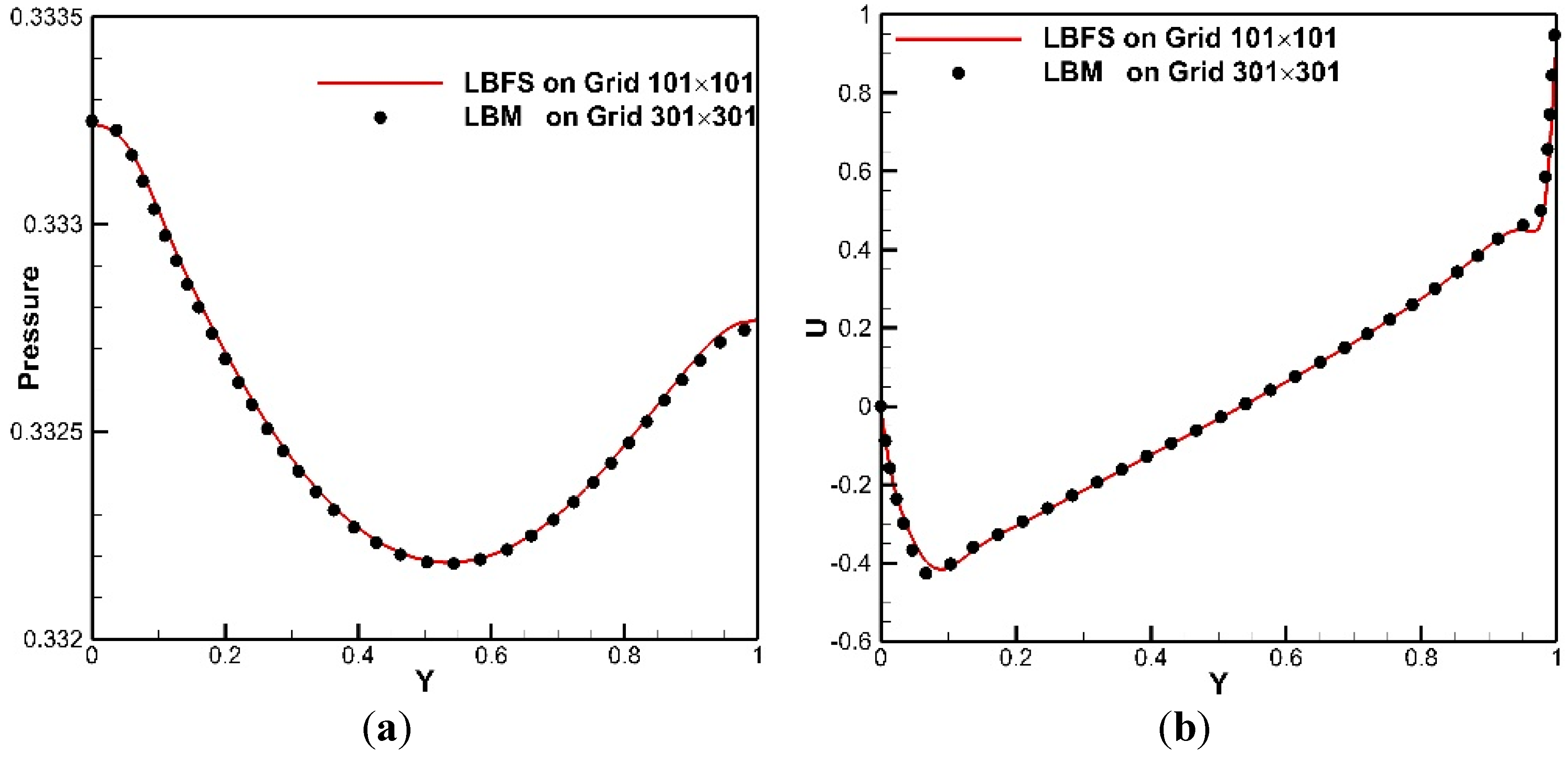
| Re | 100 | 1000 | 5000 | 7500 |
|---|---|---|---|---|
| LBGK | 5 × 5 | 39 × 39 | 219 × 219 | 341 × 341 |
| LBFS | 4 × 4 | 4 × 4 | 4 × 4 | 4 × 4 |
| Object Type | Method | Min. | Max. | Avg. | Std. Dev. |
|---|---|---|---|---|---|
| Facility | V2SFCA | 5 | 67 | 25.53 | 13.95 |
| EV2SFCA | 5 | 118 | 27.71 | 23.88 | |
| Population | V2SFCA | 5 | 63 | 23.20 | 15.08 |
| EV2SFCA | 5 | 70 | 25.49 | 17.54 |
6.2. Natural Convection in a Square Cavity at High Rayleigh Number
| Grid Size | Present | Contrino et al. [35] | Quere [43] | |||
|---|---|---|---|---|---|---|
| 2012 | 3012 | 3792 | 10192 | 15312 | ||
| 30.165 | 30.164 | 30.349 | 30.310 | 30.185 | 30.165 | |
| x | 0.0868 | 0.0857 | 0.0848 | 0.0856 | 0.0857 | 0.86 |
| y | 0.5545 | 0.5559 | 0.5578 | 0.5562 | 0.5559 | 0.556 |
| Nu1/2 | 16.550 | 16.543 | 16.526 | 16.523 | 16.523 | 16.52 |
| Umax | 148.17 | 148.84 | 148.48 | 148.57 | 148.58 | 148.59 |
| y | 0.8788 | 0.8789 | 0.8794 | 0.8793 | 0.8793 | 0.879 |
| Vmax | 699.19 | 699.91 | 699.11 | 699.27 | 699.31 | 699.18 |
| x | 0.0204 | 0.0216 | 0.0214 | 0.0213 | 0.0213 | 0.021 |
| Grid Size | Present | Contrino et al. [35] | Quere [43] | |||
|---|---|---|---|---|---|---|
| 301 | 4012 | 3792 | 10192 | 15312 | ||
| 53.955 | 53.893 | 54.870 | 54.106 | 53.953 | 53.85 | |
| x | 0.0482 | 0.4760 | 0.0469 | 0.0478 | 0.0480 | 0.048 |
| y | 0.5536 | 0.5528 | 0.5594 | 0.5545 | 0.5533 | 0.553 |
| Nu1/2 | 30.353 | 30.301 | 30.257 | 30.229 | 30.227 | 30.225 |
| Umax | 316.07 | 323.65 | 315.08 | 320.74 | 321.37 | 321.9 |
| x | 0.9267 | 0.9288 | 0.9239 | 0.9273 | 0.9276 | 0.928 |
| Vmax | 2221.1 | 2222.9 | 2221.4 | 2222.1 | 2222.3 | 2222 |
| y | 0.0118 | 0.1192 | 0.0121 | 0.0120 | 0.0120 | 0.012 |
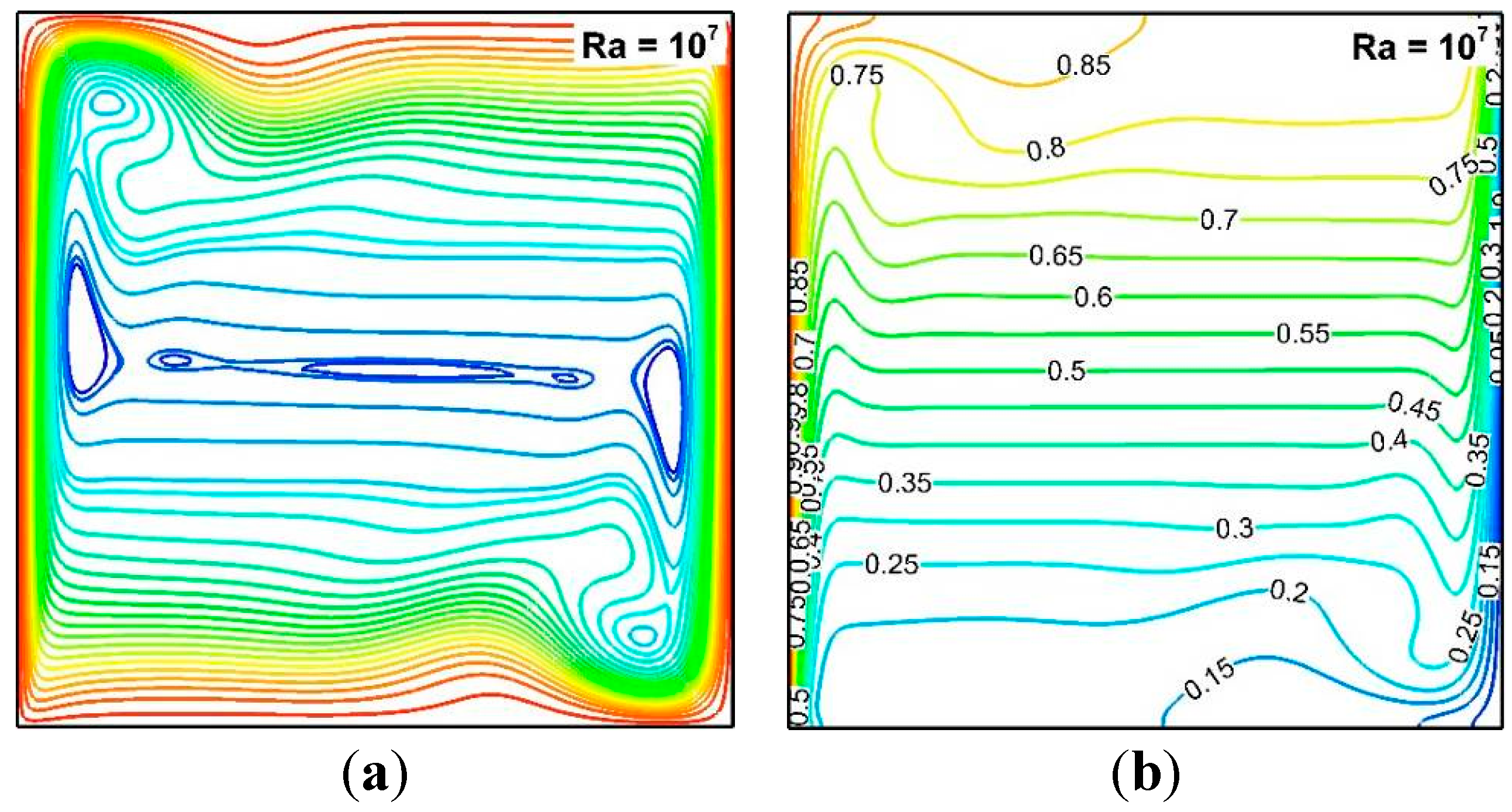
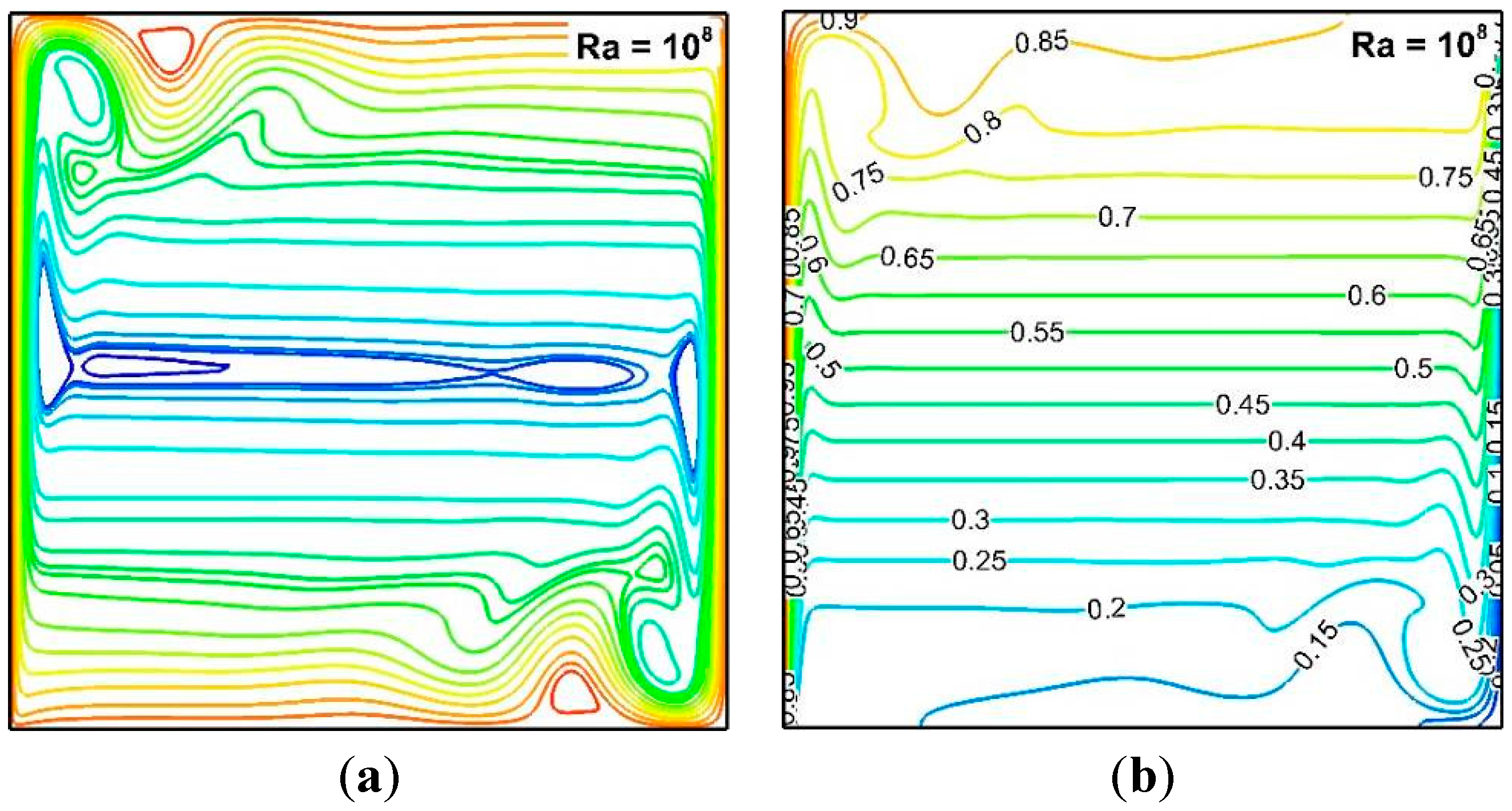
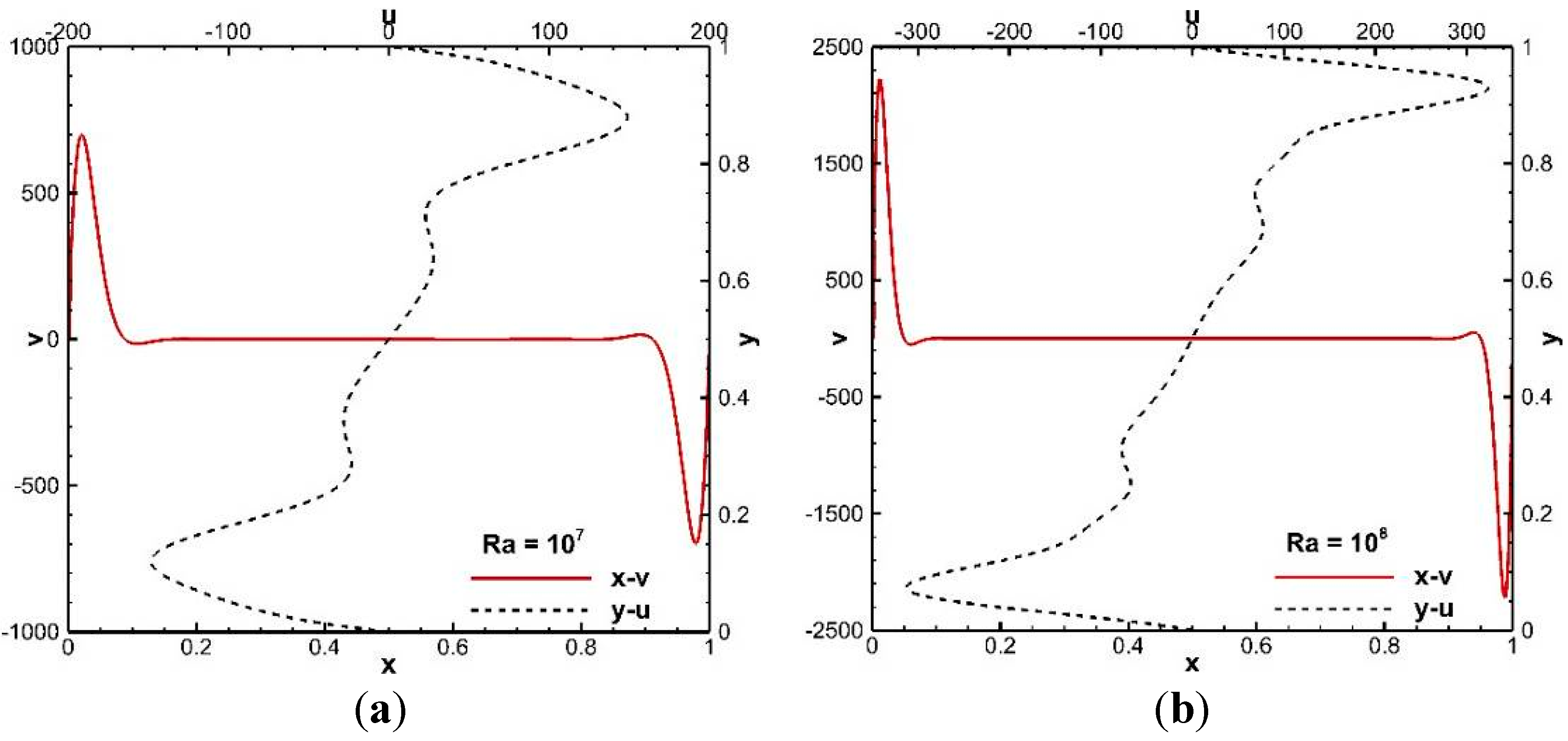
6.3. Inviscid and Viscous Transonic Flows Around a Staggered-Biplane Configuration
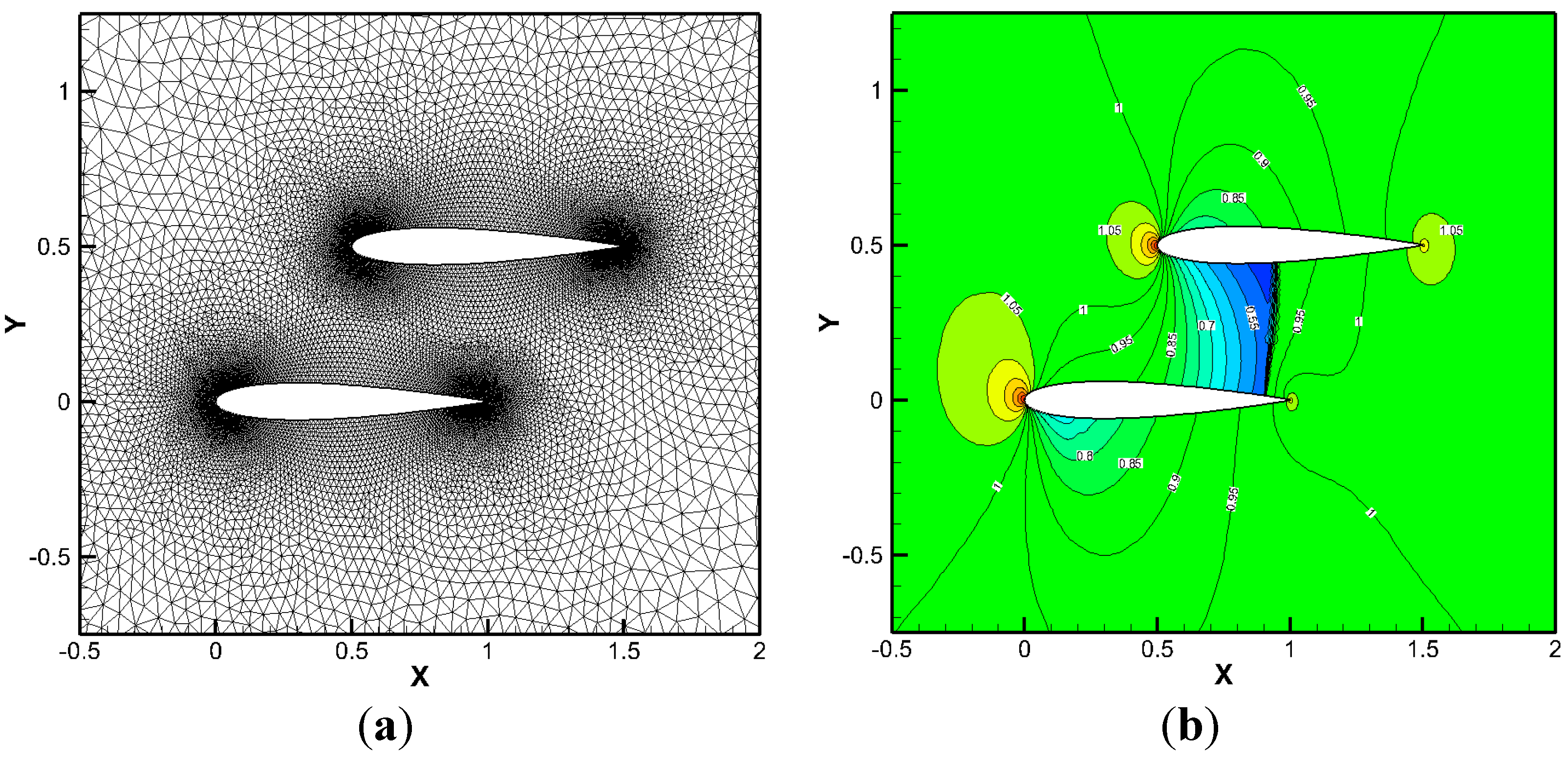
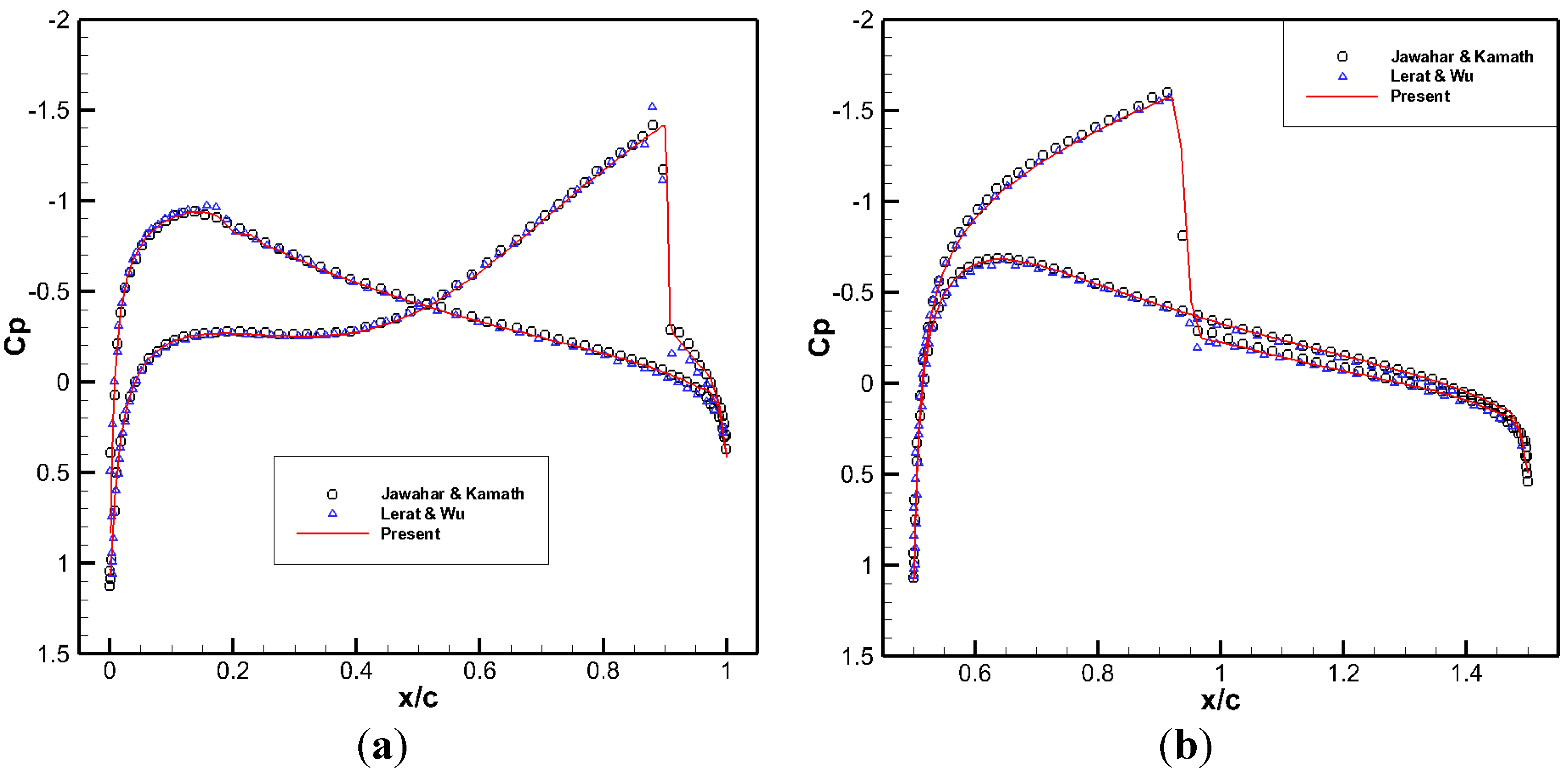

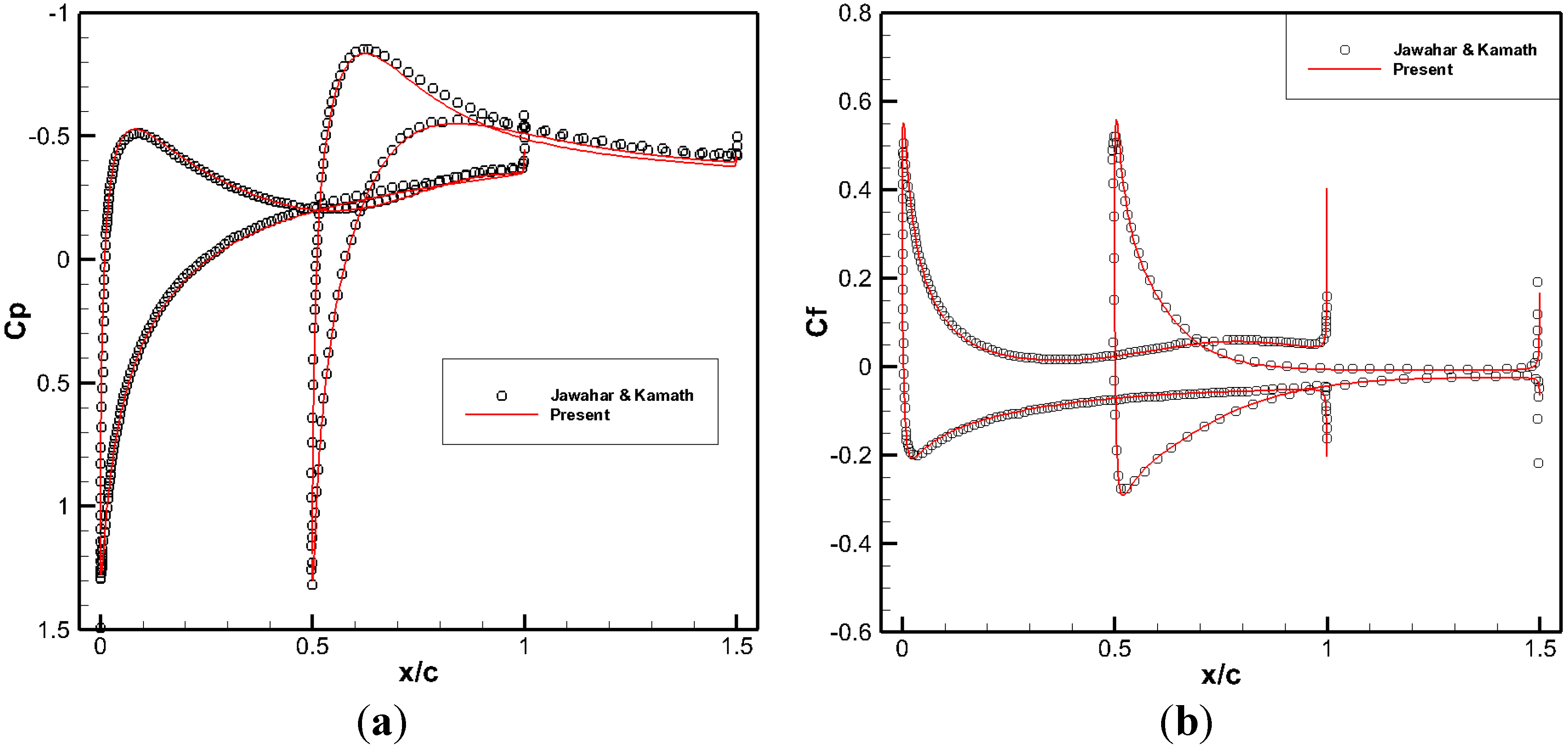
7. Conclusions
Author Contributions
Conflicts of Interest
References
- McNamara, G.R.; Zanetti, G. Use of the Boltzmann Equation to Simulate Lattice-Gas Automata. Phys. Rev. Lett. 1988, 61, 2332–2335. [Google Scholar] [CrossRef] [PubMed]
- Higuera, F.J.; Succi, S.; Benzi, R. Lattice gas-dynamics with enhanced collisions. Europhys. Lett. 1989, 9, 345–349. [Google Scholar] [CrossRef]
- Chen, S.Y.; Chen, H.D.; Martinez, D.; Matthaeus, W. Lattice Boltzmann model for simulation of magnetohydrodynamics. Phys. Rev. Lett. 1991, 67, 3776–3779. [Google Scholar] [CrossRef] [PubMed]
- Qian, Y.H.; D’Humières, D.; Lallemand, P. Lattice BGK models for Navier–Stokes equation. Europhys. Lett. 1992, 17, 479–484. [Google Scholar] [CrossRef]
- Mei, R.; Shyy, W. On the Finite Difference-Based Lattice Boltzmann Method in Curvilinear Coordinates. J. Comput. Phys. 1998, 143, 426–448. [Google Scholar] [CrossRef]
- Hejranfar, K.; Ezzatneshan, E. Implementation of a high-order compact finite-difference lattice Boltzmann method in generalized curvilinear coordinates. J. Comput. Phys. 2014, 267, 28–49. [Google Scholar] [CrossRef]
- Zarghami, A.; Ubertini, S.; Succi, S. Finite-volume lattice Boltzmann modeling of thermal transport in nanofluids. Comput. Fluids 2013, 77, 56–65. [Google Scholar] [CrossRef]
- Wang, Y.; Shu, C.; Huang, H.B.; Teo, C.J. Multiphase lattice Boltzmann flux solver for incompressible multiphase flows with large density ratio. J. Comput. Phys. 2015, 280, 404–423. [Google Scholar] [CrossRef]
- Wang, Y.; Shu, C.; Teo, C.J. Thermal lattice Boltzmann flux solver and its application for simulation of incompressible thermal flows. Comput. Fluids 2014, 94, 98–111. [Google Scholar] [CrossRef]
- Shu, C.; Wang, Y.; Teo, C.J.; Wu, J. Development of Lattice Boltzmann Flux Solver for Simulation of Incompressible Flows. Adv. Appl. Math. Mech. 2014, 6, 436–460. [Google Scholar]
- Yang, L.M.; Shu, C.; Wu, J. A moment conservation-based non-free parameter compressible lattice Boltzmann model and its application for flux evaluation at cell interface. Comput. Fluids 2013, 79, 190–199. [Google Scholar] [CrossRef]
- Guo, Z.; Shi, B.; Wang, N. Lattice BGK Model for Incompressible Navier–Stokes Equation. J. Comput. Phys. 2000, 165, 288–306. [Google Scholar] [CrossRef]
- Shan, X.; Chen, H. Lattice Boltzmann model for simulating flows with multiple phases and components. Phys. Rev. E 1993, 47, 1815–1819. [Google Scholar] [CrossRef]
- Lee, T.; Lin, C.-L. A stable discretization of the lattice Boltzmann equation for simulation of incompressible two-phase flows at high density ratio. J. Comput. Phys. 2005, 206, 16–47. [Google Scholar] [CrossRef]
- He, X.; Chen, S.; Zhang, R. A Lattice Boltzmann Scheme for Incompressible Multiphase Flow and Its Application in Simulation of Rayleigh–Taylor Instability. J. Comput. Phys. 1999, 152, 642–663. [Google Scholar] [CrossRef]
- Li, Q.; He, Y.L.; Wang, Y.; Tao, W.Q. Coupled double-distribution-function lattice Boltzmann method for the compressible Navier–Stokes equations. Phys. Rev. E 2007, 76, 056705. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Xu, A.; Zhang, G.; Li, Y.; Succi, S. Multiple-relaxation-time lattice Boltzmann approach to compressible flows with flexible specific-heat ratio and Prandtl number. Europhys. Lett. 2010, 90. [Google Scholar] [CrossRef]
- He, Y.-L.; Liu, Q.; Li, Q. Three-dimensional finite-difference lattice Boltzmann model and its application to inviscid compressible flows with shock waves. Physica A 2013, 392, 4884–4896. [Google Scholar] [CrossRef]
- Nie, X.; Doolen, G.D.; Chen, S. Lattice-Boltzmann Simulations of Fluid Flows in MEMS. J. Stat. Phys. 2002, 107, 279–289. [Google Scholar] [CrossRef]
- Lim, C.Y.; Shu, C.; Niu, X.D.; Chew, Y.T. Application of lattice Boltzmann method to simulate microchannel flows. Phys. Fluids 2002, 14, 2299–2308. [Google Scholar] [CrossRef]
- Meng, J.; Zhang, Y. Accuracy analysis of high-order lattice Boltzmann models for rarefied gas flows. J. Comput. Phys. 2011, 230, 835–849. [Google Scholar] [CrossRef] [Green Version]
- Lallemand, P.; Luo, L.-S. Theory of the lattice Boltzmann method: Dispersion, dissipation, isotropy, Galilean invariance, and stability. Phys. Rev. E 2000, 61, 6546–6562. [Google Scholar] [CrossRef]
- Niu, X.D.; Shu, C.; Chew, Y.T. A lattice Boltzmann BGK model for simulation of micro flows. Europhys. Lett. 2004, 67, 600–606. [Google Scholar] [CrossRef]
- Yuan, H.-Z.; Niu, X.-D.; Shu, S.; Li, M.; Yamaguchi, H. A momentum exchange-based immersed boundary-lattice Boltzmann method for simulating a flexible filament in an incompressible flow. Comput. Math. Appl. 2014, 67, 1039–1056. [Google Scholar] [CrossRef]
- Yuan, H.-Z.; Shu, S.; Niu, X.-D.; Li, M.; Hu, Y. A Numerical Study of Jet Propulsion of an Oblate Jelly fish Using a Momentum Exchange-Based Immersed Boundary-Lattice Boltzmann Method. Adv. Appl. Math. Mech. 2014, 6, 307–326. [Google Scholar]
- Ubertini, S.; Succi, S. Recent advances of Lattice Boltzmann techniques on unstructured grids. Prog. Comput. Fluid Dyn. Int. J. 2005, 5, 85–96. [Google Scholar] [CrossRef]
- Rossi, N.; Ubertini, S.; Bella, G.; Succi, S. Unstructured lattice Boltzmann method in three dimensions. Int. J. Numer. Methods Fluids 2005, 49, 619–633. [Google Scholar] [CrossRef]
- Patankar, S.V.; Spalding, D.B. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int. J. Heat Mass Transf. 1972, 15, 1787–1806. [Google Scholar] [CrossRef]
- Sun, D.L.; Qu, Z.G.; He, Y.L.; Tao, W.Q. An efficient segregated algorithm for incompressible fluid flow and heat transfer problems-IDEAL (Inner Doubly Iterative Efficient Algorithm for Linked Equations) Part I: Mathematical formulation and solution procedure. Numer. Heat Transf. B 2008, 53. [Google Scholar] [CrossRef]
- Bruneau, C.-H.; Saad, M. The 2D lid-driven cavity problem revisited. Comput. Fluids 2006, 35, 326–348. [Google Scholar] [CrossRef]
- Kalita, J.C.; Gupta, M.M. A streamfunction–velocity approach for 2D transient incompressible viscous flows. Int. J. Numer. Methods Fluids 2010, 62, 237–266. [Google Scholar] [CrossRef]
- Lin, L.-S.; Chang, H.-W.; Lin, C.-A. Multi relaxation time lattice Boltzmann simulations of transition in deep 2D lid driven cavity using GPU. Comput. Fluids 2013, 80, 381–387. [Google Scholar] [CrossRef]
- Zhuo, C.; Zhong, C.; Cao, J. Filter-matrix lattice Boltzmann simulation of lid-driven deep-cavity flows, Part I—Steady flows. Comput. Math. Appl. 2013, 65, 1863–1882. [Google Scholar] [CrossRef]
- Zhuo, C.; Zhong, C.; Cao, J. Filter-matrix lattice Boltzmann simulation of lid-driven deep-cavity flows, Part II—Flow bifurcation. Comput. Math. Appl. 2013, 65, 1883–1893. [Google Scholar] [CrossRef]
- Contrino, D.; Lallemand, P.; Asinari, P.; Luo, L.-S. Lattice-Boltzmann simulations of the thermally driven 2D square cavity at high Rayleigh numbers. J. Comput. Phys. 2014, 275, 257–272. [Google Scholar] [CrossRef]
- Luan, H.-B.; Xu, H.; Chen, L.; Sun, D.-L.; He, Y.-L.; Tao, W.-Q. Evaluation of the coupling scheme of FVM and LBM for fluid flows around complex geometries. Int. J. Heat Mass Transf. 2011, 54, 1975–1985. [Google Scholar] [CrossRef]
- Guo, Z.; Shi, B.; Zheng, C. A coupled lattice BGK model for the Boussinesq equations. Int. J. Numer. Methods Fluids 2002, 39, 325–342. [Google Scholar] [CrossRef]
- Chen, L.; He, Y.-L.; Kang, Q.; Tao, W.-Q. Coupled numerical approach combining finite volume and lattice Boltzmann methods for multi-scale multi-physicochemical processes. J. Comput. Phys. 2013, 255, 83–105. [Google Scholar] [CrossRef]
- Chen, L.; Luan, H.; Feng, Y.; Song, C.; He, Y.-L.; Tao, W.-Q. Coupling between finite volume method and lattice Boltzmann method and its application to fluid flow and mass transport in proton exchange membrane fuel cell. Int. J. Heat Mass Transf. 2012, 55, 3834–3848. [Google Scholar] [CrossRef]
- Yang, L.M.; Shu, C.; Wu, J.; Zhao, N.; Lu, Z.L. Circular function-based gas-kinetic scheme for simulation of inviscid compressible flows. J. Comput. Phys. 2013, 255, 540–557. [Google Scholar] [CrossRef]
- Yang, L.M.; Shu, C.; Wu, J. A three-dimensional explicit sphere function-based gas-kinetic flux solver for simulation of inviscid compressible flows. J. Comput. Phys. 2015, 295, 322–339. [Google Scholar] [CrossRef]
- Peng, Y.; Shu, C.; Chew, Y.T. Simplified thermal lattice Boltzmann model for incompressible thermal flows. Phys. Rev. E 2003, 68, 026701. [Google Scholar] [CrossRef] [PubMed]
- Le Quéré, P. Accurate solutions to the square thermally driven cavity at high Rayleigh number. Comput. Fluids 1991, 20, 29–41. [Google Scholar] [CrossRef]
- Jawahar, P.; Kamath, H. A High-Resolution Procedure for Euler and Navier–Stokes Computations on Unstructured Grids. J. Comput. Phys. 2000, 164, 165–203. [Google Scholar] [CrossRef]
- Lerat, A.; Wu, Z.N. Stable Conservative Multidomain Treatments for Implicit Euler Solvers. J. Comput. Phys. 1996, 123, 45–64. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Yang, L.; Shu, C. From Lattice Boltzmann Method to Lattice Boltzmann Flux Solver. Entropy 2015, 17, 7713-7735. https://doi.org/10.3390/e17117713
Wang Y, Yang L, Shu C. From Lattice Boltzmann Method to Lattice Boltzmann Flux Solver. Entropy. 2015; 17(11):7713-7735. https://doi.org/10.3390/e17117713
Chicago/Turabian StyleWang, Yan, Liming Yang, and Chang Shu. 2015. "From Lattice Boltzmann Method to Lattice Boltzmann Flux Solver" Entropy 17, no. 11: 7713-7735. https://doi.org/10.3390/e17117713
APA StyleWang, Y., Yang, L., & Shu, C. (2015). From Lattice Boltzmann Method to Lattice Boltzmann Flux Solver. Entropy, 17(11), 7713-7735. https://doi.org/10.3390/e17117713







