Analytical Solutions of the Black–Scholes Pricing Model for European Option Valuation via a Projected Differential Transformation Method
Abstract
:1. Introduction
2. The Differential Transformation Method (DTM) and Its Modification
2.1. Analysis of a Two-Dimensional DTM
2.2. The Overview of the PDTM
2.3. Some Fundamental Theorems and Properties of the PDTM
3. Applications and Illustrative Examples
4. Discussion of Results
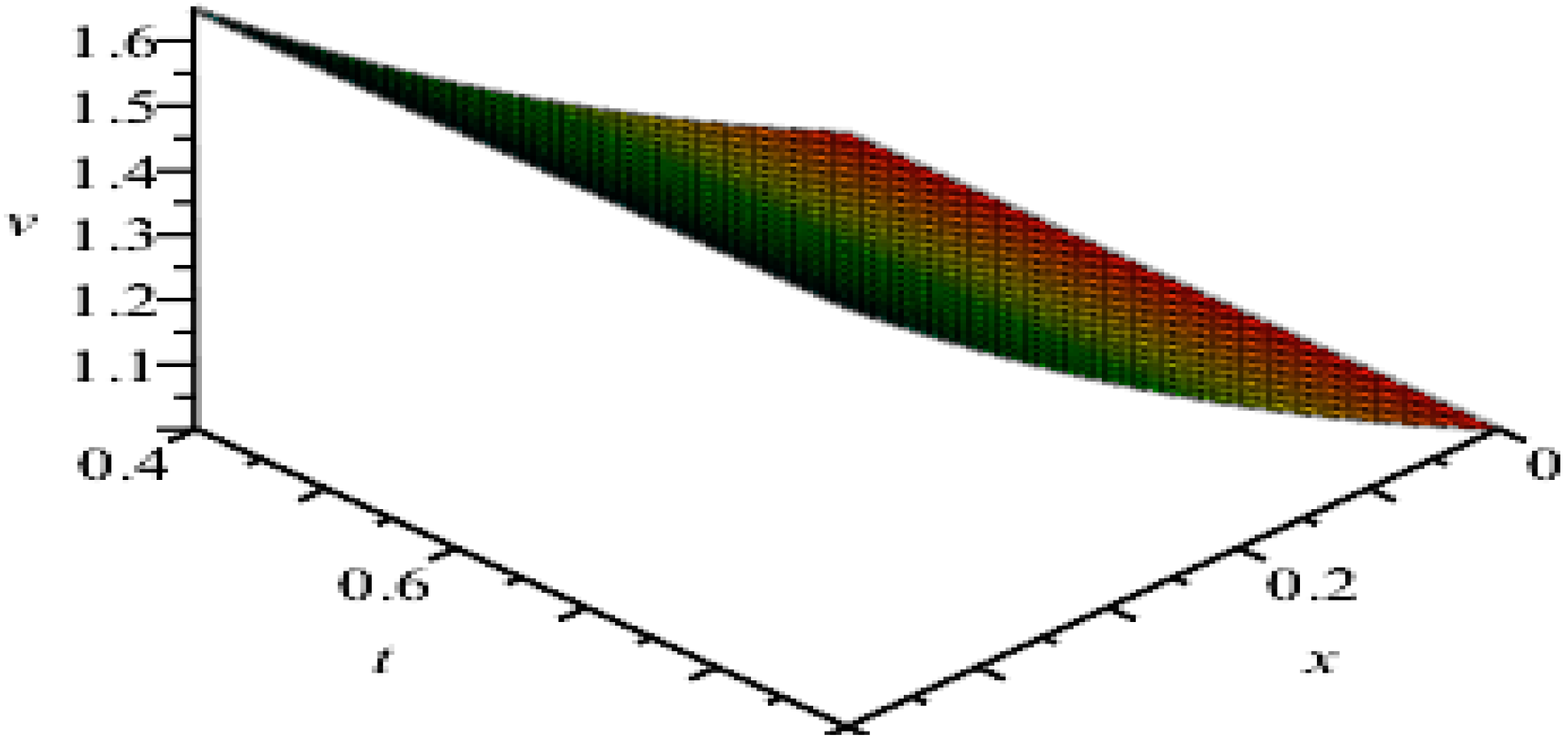
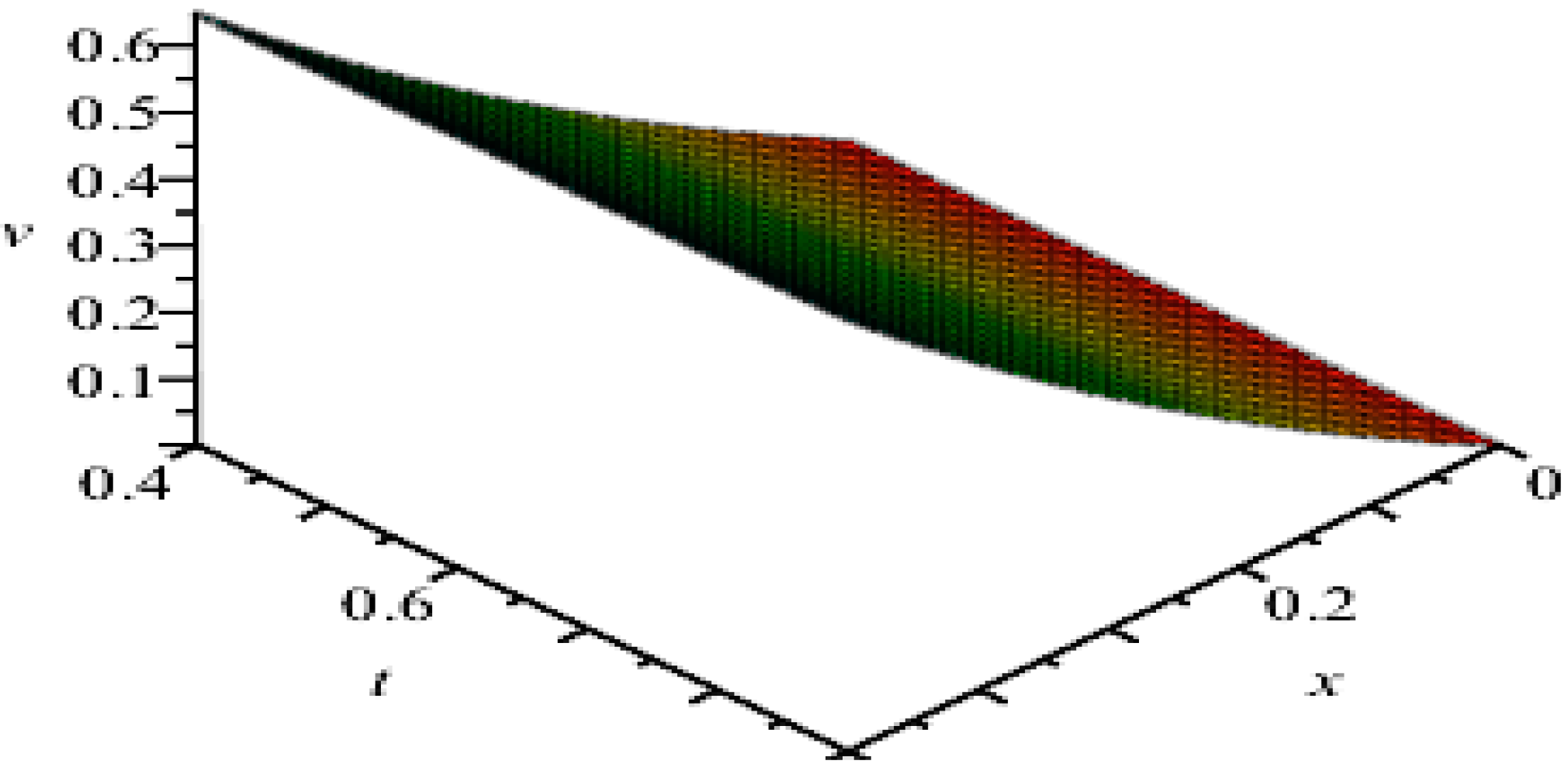
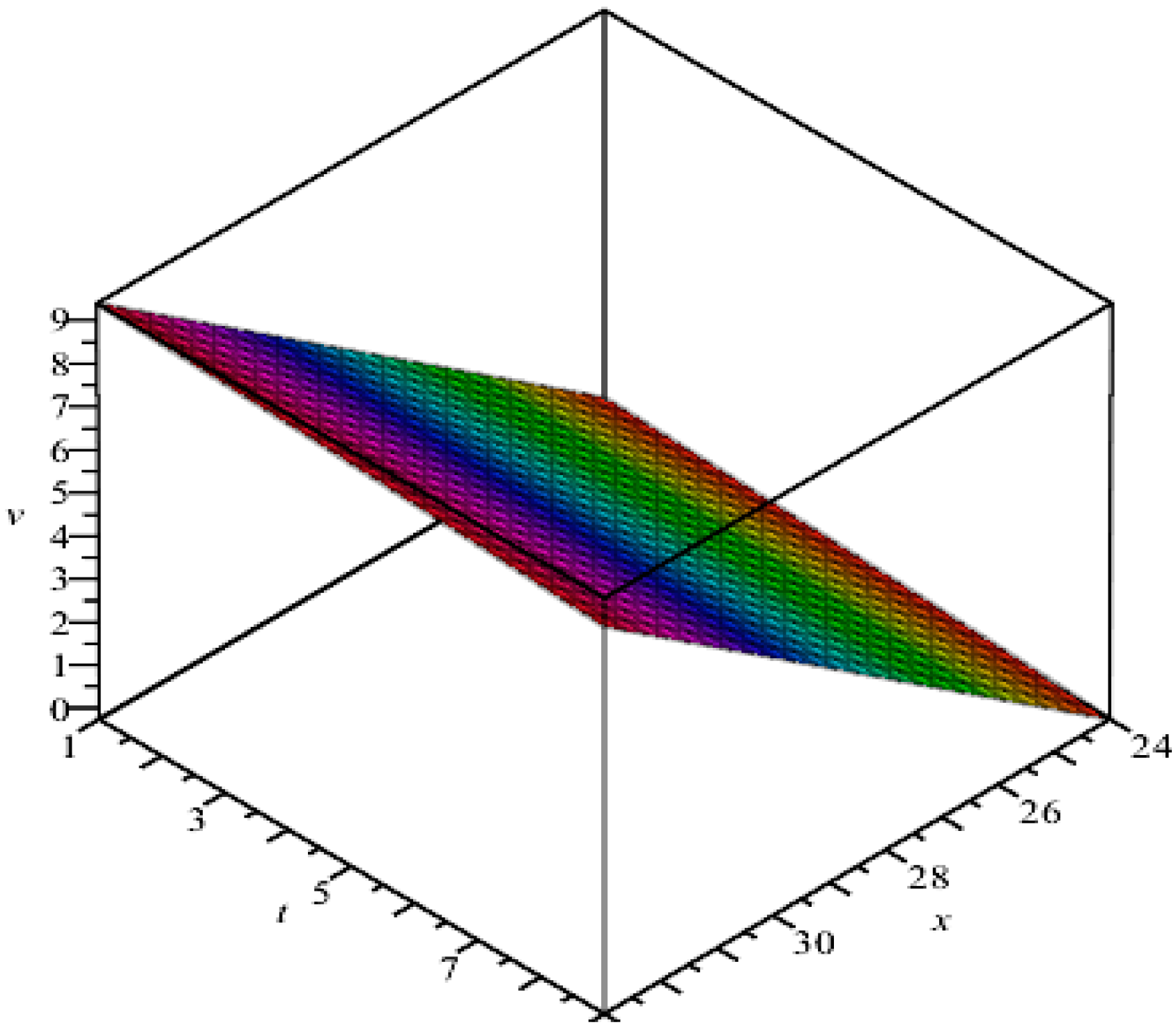
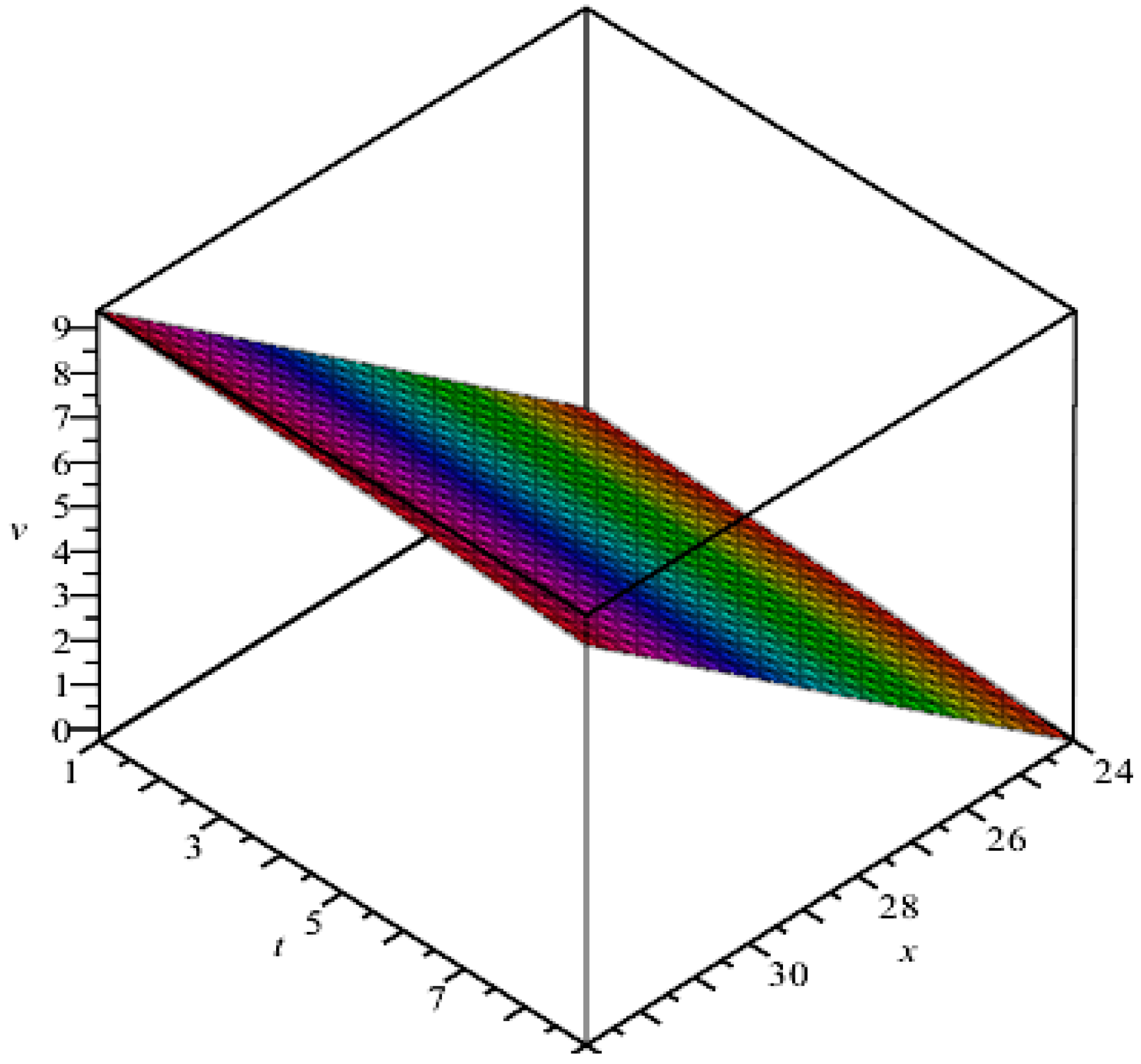
5. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Political Econ. 1973, 81, 637–354. [Google Scholar] [CrossRef]
- Owoloko, E.A.; Okeke, M.C. Investigating the Imperfection of the B-S Model: A Case Study of an Emerging Stock Market. Br. J. Appl. Sci. Technol. 2014, 4, 4191–4200. [Google Scholar] [CrossRef]
- John, J.C.H. Options, Futures, and Other Derivatives, 9th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2014. [Google Scholar]
- Ugbebor, O.O.; Edeki, S.O. On Duality Principle in Exponentially Le’vy Market. J. Appl. Math. Bioinform. 2013, 3, 159–170. [Google Scholar]
- Yao, K. A no-arbitrage theorem for uncertain stock model. Fuzzy Optim. Decis. Mak. 2015, 14, 227–242. [Google Scholar] [CrossRef]
- Chen, X.W. American option pricing formula for uncertain financial market. Int. J. Oper. Res. 2011, 8, 32–37. [Google Scholar]
- Li, S.; Peng, J. A new stock model for option pricing in uncertain environment. Iran. J. Fuzzy Syst. 2014, 11, 27–41. [Google Scholar] [CrossRef]
- Jiao, D.Y.; Yao, K. An interest rate model in uncertain environment. Soft Comput. 2015, 19, 775–780. [Google Scholar] [CrossRef]
- Oksendel, B. Stochastic Differential Equation; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Brzezniak, Z.; Zastawniak, T. Basic Stochastic Processes; Springer Verlag: Heidelberg, Germany, 1998. [Google Scholar]
- Zheng, Y. On Stochastic Differential Equation and Modified Black–Scholes Option Pricing Model. Available online: http://ssrn.com/abstract=1091823 (accessed on 9 October 2015).
- Smeureanu, I.; Fanache, D. A Linear Algorithm for Black–Scholes Economic Model. Rev. Inform. Econ. 2008, 1, 150–156. [Google Scholar]
- Cen, Z.; Le, A. A robust and accurate finite difference method for a generalized Black–Scholes equation. J. Comput. Appl. Math. 2011, 235, 3728–3733. [Google Scholar] [CrossRef]
- Mosneagu, A.M.; Dura, G. Numerical Approximation of Black–Scholes Equation. Ann. Alexandru Ioan Cuza Univ. Math. 2010, 56, 39–64. [Google Scholar]
- Uddin, M.K.S.; Ahmed, M.; Bhowmik, S.K. A Note on Numerical Solution of Linear Black–Scholes Model. GANIT J. Bangladesh Math. Soc. 2013, 33, 103–115. [Google Scholar] [CrossRef]
- Agliardi, R.; Popivanov, P.; Slovova, A. On Nonlinear Black–Scholes Equations. Nonl. Anal. Differ. Eq. 2013, 1, 75–81. [Google Scholar]
- Jodar, L.; Peris, P.S.; Cortes, J.C.; Sala, R. A new direct method for solving the Black–Scholes Equation. Appl. Math. Lett. 2005, 18, 29–32. [Google Scholar] [CrossRef]
- Qiu, Y.; Lorenz, J. A nonlinear Black–Scholes Equation. Int. J. Bus. Perform. Supply Chain Model. 2009, 1, 33–40. [Google Scholar] [CrossRef]
- Elbeleze, A.A.; Kilicman, A.; Taib, B.M. Homotopy Perturbation Method for Fractional Black–Scholes European Option Pricing Equations Using Sumudu Transform. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, D.; Singh, J. Numerical Computation of Fractional Black–Scholes Equation arising in Financial Market. Egypt. J. Basic Appl. Sci. 2014, 1, 177–183. [Google Scholar] [CrossRef]
- Ahmad, J.; Shakeel, M.; UI Hassan, Q.M.; Mohyud-Din, S.T. Analytical Solution of Black–Scholes Model Using Fractional Variational Iteration Method. Int. J. Modern Math. Sci. 2013, 5, 133–142. [Google Scholar]
- Kumar, S.; Yildirin, A.; Khan, Y.; Jafari, H.; Sayevand, K.; Wei, L. Analytical Solution of Fractional Black–Scholes European Option Pricing Equations Using Laplace Transform. J. Fract. Calc. Appl. 2012, 2, 1–9. [Google Scholar]
- Bohner, M.; Sanchez, F.H.M.; Rodriguez, S. European Call Option Pricing Using the Adomian Decomposition Method. Adv. Dyn. Syst. Appl. 2014, 9, 75–85. [Google Scholar]
- Allahviranloo, T.; Behzadi, S.S. The use of iterative methods for solving Black–Scholes equations. Int. J. Ind. Math. 2013, 5, 1–11. [Google Scholar]
- Biazar, J.; Goldoust, F. The Adomian Decomposition Method for the Black–Scholes Equation. In Proceedings of the 3rd International Conference on Applied Mathematics and Pharmaceutical Sciences (ICAMP’2013), Singapore, Singapore, 29–30 April 2013; pp. 321–323.
- Edeki, S.O.; Adinya, I.; Ugbebor, O.O. The Effect of Stochastic Capital Reserve on Actuarial Risk Analysis via an Integro-differential equation. IAENG Int. J. Appl. Math. 2014, 44, 83–90. [Google Scholar]
- Demiray, S.T.; Bulut, H.; Belgacem, F.B.M. Sumudu Transform Method for Analytical Solutions of Fractional Type Ordinary Differential Equations. Math. Probl. Eng. 2014, 2014. [Google Scholar] [CrossRef]
- Kanth, A.S.V.R.; Aruna, K. Comparison of two Dimensional DTM and PDTM for solving Time-Dependent Emden-Fowler Type Equations. Int. J. Nonlinear Sci. 2012, 13, 228–239. [Google Scholar]
- Dogan, N.; Erturk, V.S.; Akin, O. Numerical Treatment of Singularly Perturbed Two-Point Boundary Value Problems by Using Differential Transformation Method. Discrete Dyn. Nat. Soc. 2012, 2012. [Google Scholar] [CrossRef]
- Chen, C.K.; Ho, S.H. Solving partial differential equations by two-dimensional differential transform method. Appl. Math. Comput. 1999, 106, 171–179. [Google Scholar] [CrossRef]
- Jang, M.J.; Chen, C.L.; Liu, Y.C. Two-dimensional differential transform for partial differential equations. Appl. Math. Comput. 2001, 121, 261–270. [Google Scholar] [CrossRef]
- Sen, A.K. An Application of the Adomian decomposition method to the transcient behavior of a model of biochemical reaction. J. Math. Anal. Appl. 1988, 131, 232–245. [Google Scholar] [CrossRef]
- Mousa, M.M.; Ragab, S.F. Application of the Homotopy Perturbation Method to Linear and Nonlinear Schrodinger Equations. Verlag Z. Naturforschung Tubingen 2008, 63, 140–144. [Google Scholar] [CrossRef]
- Jang, B. Solving linear and nonlinear initial value problems by the projected differential transform method. Comput. Phys. Commun. 2010, 181, 848–854. [Google Scholar] [CrossRef]
- Ahmed, S.A.; Elzaki, T.M. A Comparative Study of Sumudu Decomposition Method and Sumudu Projected Differential Transform Method. World Appl. Sci. J. 2014, 31, 1704–1709. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Edeki, S.O.; Ugbebor, O.O.; Owoloko, E.A. Analytical Solutions of the Black–Scholes Pricing Model for European Option Valuation via a Projected Differential Transformation Method. Entropy 2015, 17, 7510-7521. https://doi.org/10.3390/e17117510
Edeki SO, Ugbebor OO, Owoloko EA. Analytical Solutions of the Black–Scholes Pricing Model for European Option Valuation via a Projected Differential Transformation Method. Entropy. 2015; 17(11):7510-7521. https://doi.org/10.3390/e17117510
Chicago/Turabian StyleEdeki, Sunday O., Olabisi O. Ugbebor, and Enahoro A. Owoloko. 2015. "Analytical Solutions of the Black–Scholes Pricing Model for European Option Valuation via a Projected Differential Transformation Method" Entropy 17, no. 11: 7510-7521. https://doi.org/10.3390/e17117510
APA StyleEdeki, S. O., Ugbebor, O. O., & Owoloko, E. A. (2015). Analytical Solutions of the Black–Scholes Pricing Model for European Option Valuation via a Projected Differential Transformation Method. Entropy, 17(11), 7510-7521. https://doi.org/10.3390/e17117510




