Local Fractional Homotopy Perturbation Method for Solving Non-Homogeneous Heat Conduction Equations in Fractal Domains
Abstract
:1. Introduction
2. The LFDO
- (a)
- ,
- (b)
- ,
- (c)
- , provided .
| Special functions defined on Cantor sets | ||
| C | 0 | |
3. Analysis of the Method
4. On Solutions of the NHCEs

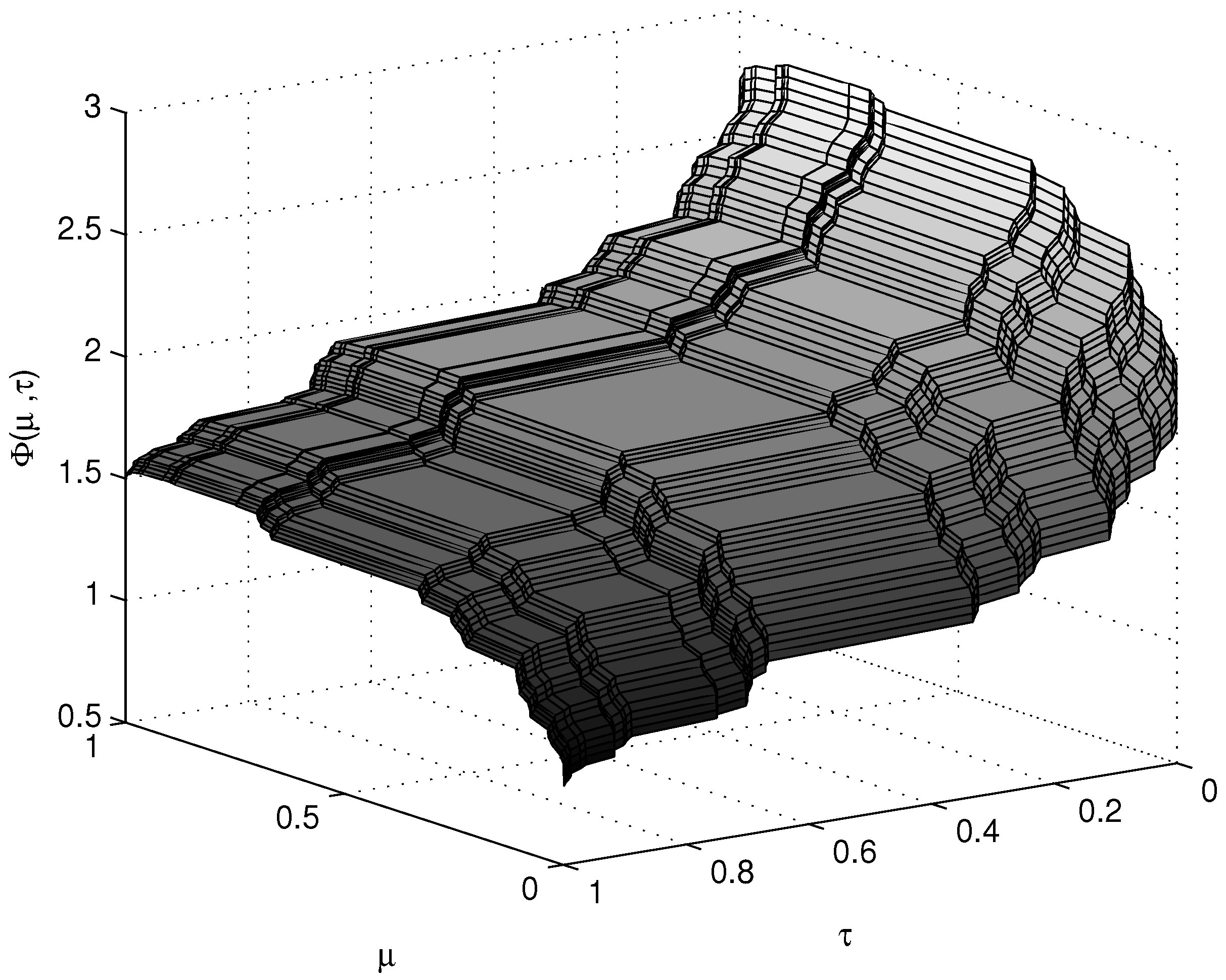
5. Discussion
| PDEs | NSs | |
|---|---|---|
| HHCE | ||
| NHCE | ||
| IVCs |
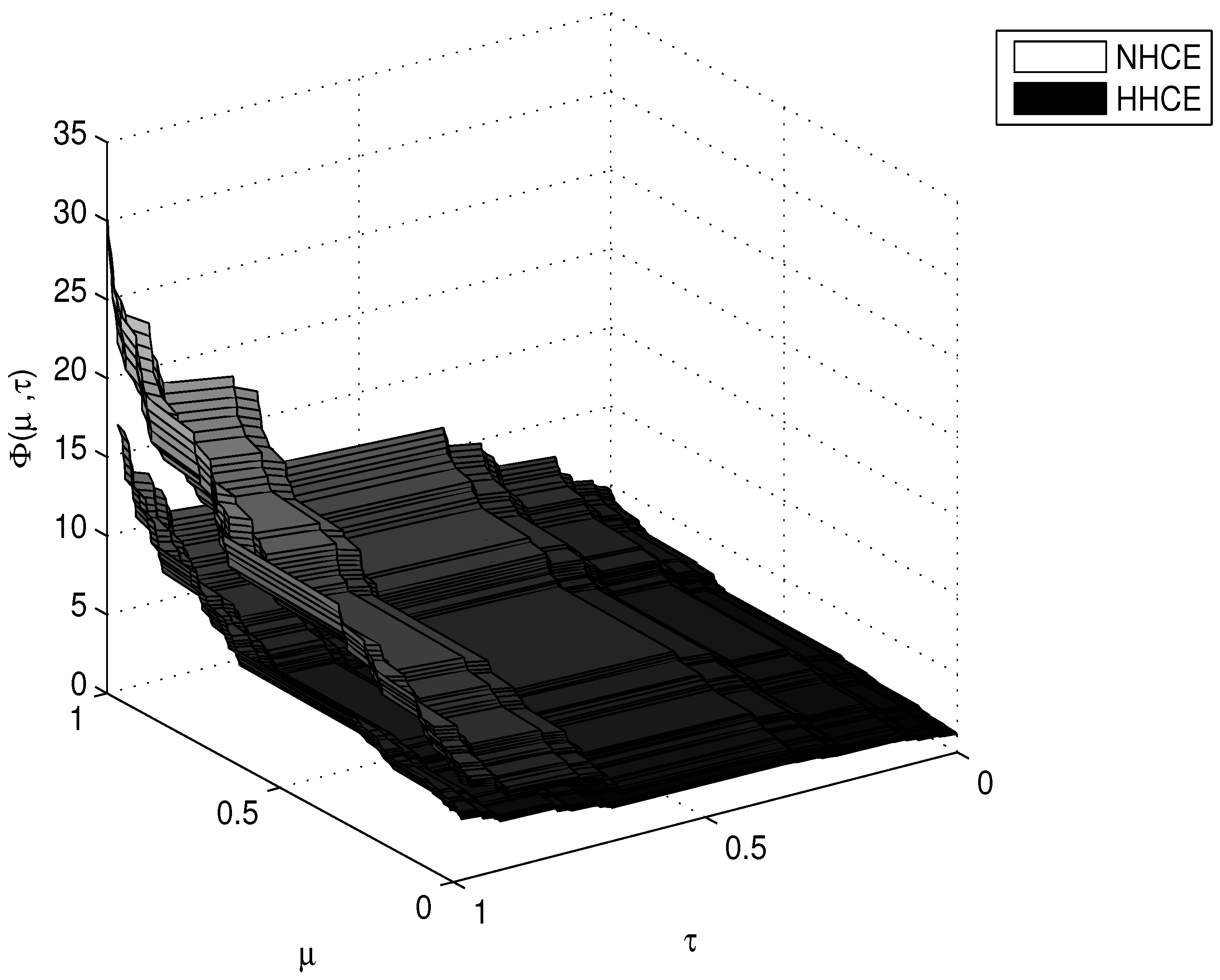
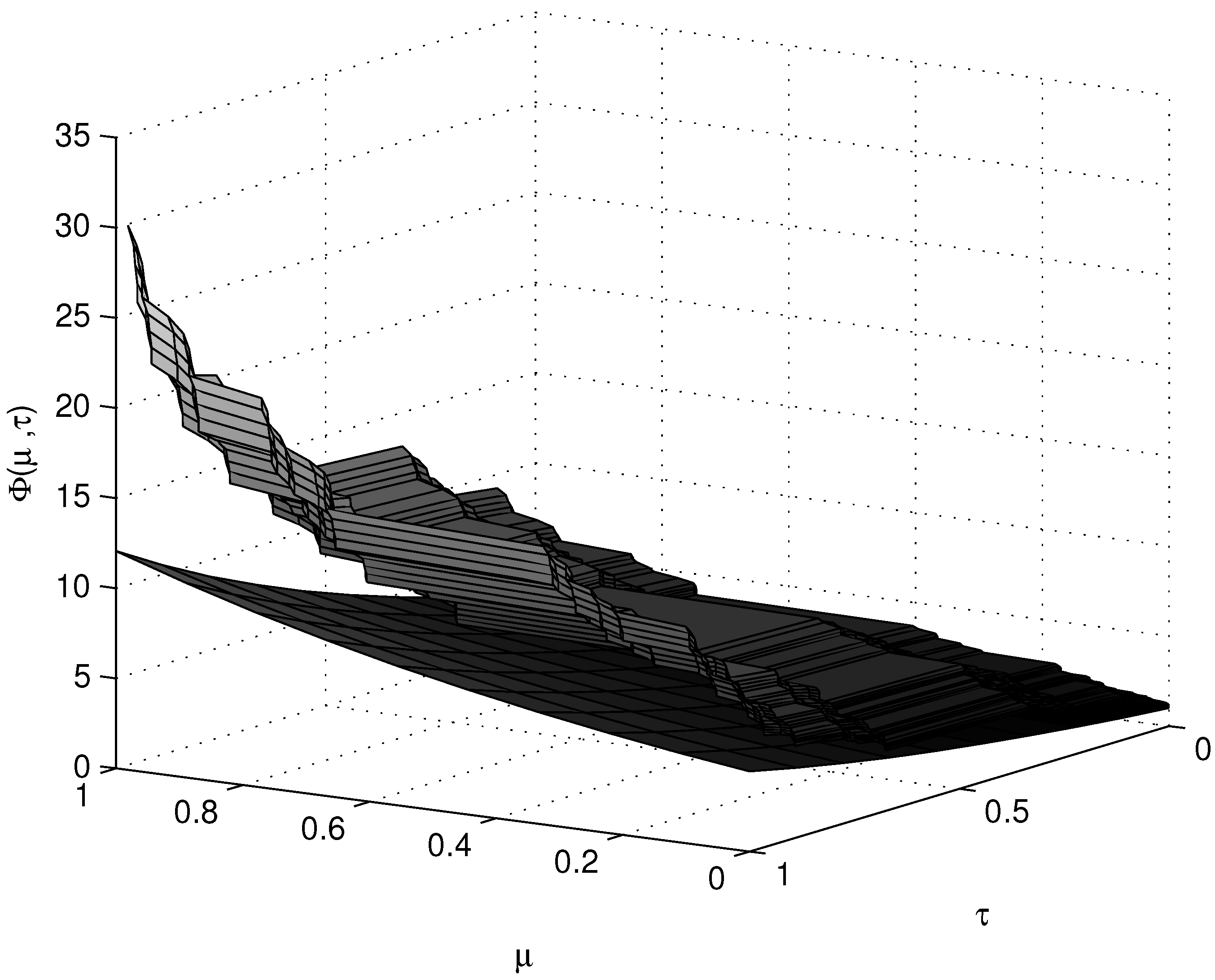
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Grassberger, P.; Nadler, W.; Yang, L. Heat conduction and entropy production in a one-dimensional hard-particle gas. Phys. Rev. Lett. 2002, 89, 180601. [Google Scholar] [CrossRef]
- Kim, S.K.; Lee, W.I. Solution of inverse heat conduction problems using maximum entropy method. Int. J. Heat Mass Transf. 2002, 45, 381–391. [Google Scholar] [CrossRef]
- Kolenda, Z.; Donizak, J.; Hubert, J. On the minimum entropy production in steady state heat conduction processes. Energy 2004, 29, 2441–2460. [Google Scholar] [CrossRef]
- Bautista, O.; Méndez, F.; Martinez-Meyer, J.L. (Bejan’s) early vs. late regimes method applied to entropy generation in one-dimensional conduction. Int. J. Therm. Sci. 2005, 44, 570–576. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Hristov, J. An approximate analytical (integral-balance) solution to a nonlinear heat diffusion equation. Therm. Sci. 2015, 19, 723–733. [Google Scholar] [CrossRef]
- Ortigueira, M.D. Fractional Calculus for Scientists and Engineers; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Baleanu, D.; Machado, J.A.T.; Luo, A.C. Fractional Dynamics and Control; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Ubriaco, M.R. Entropies based on fractional calculus. Phys. Lett. A 2009, 373, 2516–2519. [Google Scholar] [CrossRef]
- Kilbas, A.A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Essex, C.; Schulzky, C.; Franz, A.; Hoffmann, K.H. Tsallis and Rényi entropies in fractional diffusion and entropy production. Phys. A Stat. Mech. Appl. 2000, 284, 299–308. [Google Scholar] [CrossRef]
- Li, X.; Essex, C.; Davison, M.; Hoffmann, K.H.; Schulzky, C. Fractional diffusion, irreversibility and entropy. J. Non-Equilib. Thermodyn. 2003, 28, 279–291. [Google Scholar] [CrossRef]
- Magin, R.; Ingo, C. Entropy and information in a fractional order model of anomalous diffusion. Syst. Identif. 2012, 16, 428–433. [Google Scholar]
- Machado, J.T. Entropy analysis of integer and fractional dynamical systems. Nonlinear Dyn. 2010, 62, 371–378. [Google Scholar]
- Zhang, Y.; Baleanu, D.; Yang, X. On a local fractional wave equation under fixed entropy arising in fractal hydrodynamics. Entropy 2014, 16, 6254–6262. [Google Scholar] [CrossRef]
- Yang, X.J. Advanced Local Fractional Calculus and Its Applications; World Science: New York, NY, USA, 2012. [Google Scholar]
- Xu, S.; Ling, X.; Cattani, C.; Xie, G.N.; Yang, X.J.; Zhao, Y. Local fractional Laplace variational iteration method for nonhomogeneous heat equations arising in fractal heat flow. Math. Probl. Eng. 2014, 2014, 914725. [Google Scholar] [CrossRef]
- Yang, X.J.; Srivastava, H.M. An asymptotic perturbation solution for a linear oscillator of free damped vibrations in fractal medium described by local fractional derivatives. Commun. Nonlinear Sci. Numer. Simul. 2015, 29, 499–504. [Google Scholar] [CrossRef]
- Yang, X.J.; Srivastava, H.M.; He, J.H.; Baleanu, D. Cantor-type cylindrical-coordinate method for differential equations with local fractional derivatives. Phys. Lett. A 2013, 377, 1696–1700. [Google Scholar] [CrossRef]
- Cattani, C.; Srivastava, H.M.; Yang, X.-J. Fractional Dynamics; Emerging Science Publishers: Berlin, Germany, 2015. [Google Scholar]
- Ahmad, J.; Mohyud-Din, S.T. Solving wave and diffusion equations on Cantor sets. Proc. Pak. Acad. Sci. 2015, 52, 71–77. [Google Scholar]
- Yang, X.J.; Machado, J.T.; Hristov, J. Nonlinear dynamics for local fractional Burgers’ equation arising in fractal flow. Nonlinear Dyn. 2015, 80, 1661–1664. [Google Scholar] [CrossRef]
- Baleanu, D.; Srivastava, H.M.; Yang, X.J. Local fractional variational iteration algorithms for the parabolic Fokker-Planck equation defined on Cantor sets. Prog. Fract. Differ. Appl. 2015, 1. [Google Scholar] [CrossRef]
- Yang, X.J.; Baleanu, D.; Srivastava, H.M. Local fractional similarity solution for the diffusion equation defined on Cantor sets. Appl. Math. Lett. 2015, 47, 54–60. [Google Scholar] [CrossRef]
- Zhang, Y.Z.; Yang, A.M.; Long, Y. Initial boundary value problem for fractal heat equation in the semi-infinite region by Yang-Laplace transform. Therm. Sci. 2014, 18, 677–681. [Google Scholar] [CrossRef]
- Liu, H.Y.; He, J.H.; Li, Z.B. Fractional calculus for nanoscale flow and heat transfer. Int. J. Numer. Methods Heat Fluid Flow 2014, 24, 1227–1250. [Google Scholar]
- Srivastava, H.M.; Golmankhaneh, A.K.; Baleanu, D.; Yang, X.J. Local fractional Sumudu transform with application to IVPs on Cantor sets. Abstr. Appl. Anal. 2014, 2014, 620529. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Cattani, C.; Zhong, W.P. Signal processing for nondifferentiable data defined on Cantor sets: A local fractional Fourier series approach. Adv. Math. Phys. 2014, 2014, 561434. [Google Scholar]
- Yang, X.J.; Srivastava, H.M.; Cattani, C. Local fractional homotopy perturbation method for solving fractal partial differential equations arising in mathematical physics. Rom. Rep. Phys. 2015, 67, 752–761. [Google Scholar]
- He, J.H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- Ganji, D.D. The application of He’s homotopy perturbation method to nonlinear equations arising in heat transfer. Phys. A 2006, 355, 337–341. [Google Scholar] [CrossRef]
- Özis, T.; Yildirim, A. Traveling wave solution of Korteweg-de Vries equation using He’s homotopy perturbation method. Int. J. Nonlinear Sci. Numer. Simul. 2007, 8, 239–242. [Google Scholar] [CrossRef]
- Shakeri, F.; Dehghan, M. Inverse problem of diffusion equation by He’s homotopy perturbation method. Phys. Scr. 2007, 75, 551–556. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Cattani, C.; Yang, X.-J. Local Fractional Homotopy Perturbation Method for Solving Non-Homogeneous Heat Conduction Equations in Fractal Domains. Entropy 2015, 17, 6753-6764. https://doi.org/10.3390/e17106753
Zhang Y, Cattani C, Yang X-J. Local Fractional Homotopy Perturbation Method for Solving Non-Homogeneous Heat Conduction Equations in Fractal Domains. Entropy. 2015; 17(10):6753-6764. https://doi.org/10.3390/e17106753
Chicago/Turabian StyleZhang, Yu, Carlo Cattani, and Xiao-Jun Yang. 2015. "Local Fractional Homotopy Perturbation Method for Solving Non-Homogeneous Heat Conduction Equations in Fractal Domains" Entropy 17, no. 10: 6753-6764. https://doi.org/10.3390/e17106753
APA StyleZhang, Y., Cattani, C., & Yang, X.-J. (2015). Local Fractional Homotopy Perturbation Method for Solving Non-Homogeneous Heat Conduction Equations in Fractal Domains. Entropy, 17(10), 6753-6764. https://doi.org/10.3390/e17106753








