Extension of the Improved Bounce-Back Scheme for Electrokinetic Flow in the Lattice Boltzmann Method

Abstract

In this paper, an improved bounce-back boundary treatment for fluid systems in the lattice Boltzmann method [Yin, X.; Zhang J. J. Comput. Phys. 2012, 231, 4295–4303] is extended to handle the electrokinetic flows with complex boundary shapes and conditions. Several numerical simulations are performed to validate the electric boundary treatment. Simulations are presented to demonstrate the accuracy and capability of this method in dealing with complex surface potential situations, and simulated results are compared with analytical predictions with excellent agreement. This method could be useful for electrokinetic simulations with complex boundaries, and can also be readily extended to other phenomena and processes.

1. Introduction

With growing interest in bio-Micro Electro Mechanical Systems (MEMS) and bio-Nano Electro Mechanical Systems (NEMS) applications and fuel cell technologies, electrokinetic flows have become one of the most important non-mechanical techniques in the application of microfluidics and nanofluidics [1,2]. Electro-osmotic flow (EOF) is a promising approach to drive the microfluidics under an external electric field, such as sample injection, chemical reaction, species separation and energy supply [3,4]. Due to these important applications, EOF in microchannels has received interesting attention [5,6,7,8,9,10,11].

Electro-osmotic flow (EOF) is a basic electrokinetic phenomenon, where an electrical double layer (EDL) is formed due to the interaction between an electrolyte solution and a dielectric surface [12]. From the macroscopic point of view, the EOFs are governed by the Navier–Stokes (NS) equations for fluid flow and the Poisson–Boltzmann equation for the electrical potential. Many studies have been carried out on electro-osmotic flow in microchannel. The lattice Boltzmann method (LBM) has been generally accepted as a useful simulation method for complex flows [13,14,15]. The LBM approach is advantageous in dealing with complex boundary geometries [16,17] and could be potentially more efficient with advanced computational technologies. Because of its distinctive advantages over conventional numerical methods, the lattice Boltzmann method has introduced to simulate electro-osmotic flow in micro devices. Warren [18] made the first attempt to apply the LBM to solve the Navier–Stokes equations for the solution, while the conservation equation for each ionic species and the Poisson equation for the electrical potential were solved via the “moment propagation” method. He and Li [19] proposed a lattice Boltzmann scheme for analyzing the electrochemical processes in an electrolyte based on a locally electrically neutral assumption. With a multiple-component LBM model, this scheme has also been utilized to study the electrohydrodynamic drop deformation in an electric field [20]. The electrokinetic flows in microchannels is simulated by the lattice Boltzmann method with one-dimensional linearized solution of the Poisson–Boltzmann equation [5,7,8]. Melchionna and Succi [21] solved the nonlinear Poisson–Boltzmann equation by an efficient multi-grid technique and then predicted the flow behavior using a lattice Boltzmann scheme. The multi-grid technique has great efficiency to solve the nonlinear Poisson–Boltzmann equation; however it has rarely been extended for complex geometries [22]. Recently, The LBM has been applied to study the mixing enhancement in heterogeneously charged microchannels [23,24,25,26,27,28] and the roughness and cavitation effects in electro-osmotic microfluidics [29,30].

As with other numerical methods, boundary conditions play crucial roles for the simulation validity and stability. However, unlike the tremendous efforts in developing accurate boundary treatments for LBM models for fluid flows and convection-diffusion systems [31,32,33,34,35,36], boundary methods for LBM models of electric field have not been addressed adequately. Typical electric field LBM simulations are performed in regular domains with flat boundaries aligned along the lattice grid lines. Several studies have considered rough surfaces [26,30]; however, the rough surfaces were actually modeled as flat, stair-like patches. Recently, Yin and Zhang [32] developed an improved bounce-back method for fluid flows, which is discussed in [37,38,39].

In this paper, an improved bounce-back method for fluid flows [32] is extended to simulate the electrokinetic flows with arbitrary boundary shapes. Numerical simulations demonstrate that the boundary treatments have accurately represented the spatial geometry as well as the surface potential. An example calculation is also performed to illustrate the application of our boundary treatment for electrokinetic studies. This study could be useful for LBM simulations of electric fields in systems with complex surface geometry and surface conditions.

2. Macroscopic Governing Equations for EOF

For incompressible EOF in microfluidic channel, the governing equations including the continuity equation and the momentum equation can be described as follows:

$$\nabla \cdot u=0$$

(1)

$$\rho \frac{\partial u}{\partial t}+\rho u\cdot \nabla u=-\nabla P+\rho \upsilon {\nabla }^{2}u\text{+}F$$

(2)

where $u$ is the velocity vector, $\rho$ is the density of solution, $P$ is the pressure, $\upsilon$ is the kinetic viscosity of the flow, $F$ represents the external force and is given as:

$$F={\rho }_{e}E$$

(3)

where ${\rho }_e$ is the net charge density, and $E$ is the external electric field.

The drive force of the EOF is indicated by the body force term (${\rho }_{e}E$) in the momentum equation and is caused by the action of the induced electrical field on the net charge density in the EDL region. EDL theory [40] related the electrostatic potential and the ion distribution in the bulk solution can be well approximated by the Poisson equation as follows:

$${\nabla }^2\psi =-\frac{{\rho }_e}{\epsilon {\epsilon }_0}$$

(4)

where $\psi$ is the electrical potential, $\epsilon$ and ${\epsilon }_0$ are the dimensionless dielectric constant and permittivity of vacuum, respectively.

For the flows over a non-conducting stationary surface, the ion distribution can be well approximated by the Boltzmann distribution:

$$n_i=n_{i,\infty }\sinh \left(-\frac{z_{i}e\psi }{k_{b}T}\right)$$

(5)

where $n_i$ is the ionic number concentration of the $i$-th species, $n_{i,\infty }$ is the ion concentration in the bulk solution, $z_i$ is the valence of type-$i$ ions, $e$ is the charge of an electron, $k_b$ is the Boltzmann constant and $T$ is the absolute temperature. For a symmetric electrolyte ($z_i=z$ and $n_{i,\infty }=n_{\infty }$) considered in the present study, the net charge density is given as follows:

$${\rho }_e=-2n_{\infty }ze\sinh \left(\frac{ze\psi }{k_{b}T}\right)$$

(6)

Combining Equations (4) and (6) yields the nonlinear Poisson–Boltzmann distribution for the EDL potential in the dilute electrolyte solution:

$${\nabla }^2\psi =\frac{2n_{\infty }ze}{\epsilon {\epsilon }_0}\sinh \left(\frac{ze\psi }{k_{b}T}\right)$$

(7)

For the surfaces with low surface electric potentials, the Debye–Hückel approximation ($\sinh \left(\frac{ze\psi }{k_{b}T}\right)\approx \frac{ze\psi }{k_{b}T}$) can be applied and the Poisson–Boltzmann equation can be linearized to:

$${\nabla }^2\psi =\frac{2n_{\infty }{z}^2{e}^2}{\epsilon {\epsilon }_0{k}_{b}T}\psi ={\kappa }^2\psi$$

(8)

where:

$$\kappa =\sqrt{\frac{2n_{\infty }{z}^2{e}^2}{\epsilon {\epsilon }_0{k}_{b}T}}$$

(9)

and its reciprocal ${\kappa }^{-1}$, the so-called Debye length, is usually used as a measure of the EDL thickness in Debye–Hückel theory.

3. Numerical Method

The numerical method adopted in this work requires the solution of the Navier–Stokes equations for fluid flow and the Poisson–Boltzmann equation for electric potential distribution. A lattice structure D2Q9 with complex boundary conditions is proposed to solve the governing equations using two LBM model, corresponding to the fluid flow and electric potential, respectively. It is necessary to introduce the LB evolution equations and the boundary treatments in this section.

3.1. Lattice Boltzmann Model for the NS Equations

The evolution equation corresponding to the NS equations with external force is given as:

$$f_{\alpha }(x+e_{\alpha }\Delta t,t+\Delta t)-f_{\alpha }(x,t)=-\frac{1}{{\tau }_f}\left[f_{\alpha }(x,t)-f_{\alpha }^{eq}(x,t)\right]+\Delta t{F}_{\alpha }$$

(10)

where $f_{\alpha }(x,t)$ is the distribution function for the flow fields at location $x$ and time $t$ and the subscript $\alpha$ indicates the lattice direction. $\Delta t$ is the time step. The parameter ${\tau }_f$ is the relaxation time for the density distribution function. $F_{\alpha }$ is the forcing term corresponding to the applied external electric field.

In order to recover the correct NS equation, the density equilibrium distribution in this work can be typically expressed as:

$$f_{\alpha }^{eq}={\omega }_{\alpha }\rho \left[1+3\frac{e_{\alpha }\cdot u}{c^2}+9\frac{{\left(e_{\alpha }\cdot u\right)}^2}{2c^4}-\frac{3u^2}{2c^2}\right]$$

(11)

where $c$ is the lattice speed defined as $\Delta x/\Delta t$, $\Delta x$ the lattice grid size. For the D2Q9 lattice model, the lattice weight factors depends on the length of the corresponding lattice vector, and is given by ${\omega }_0=4/9$, ${\omega }_{1-4}=1/9$, ${\omega }_{5-8}=1/36$.

The relaxation time for fluid flow is related with the fluid viscosity by:

$${\tau }_f=\frac{3\upsilon }{c\Delta x}+0.5$$

(12)

The forcing term caused by the interaction of the EDL field with the externally applied electrical field is incorporated into the discrete Boltzmann equation by following the method described:

$$F_{\alpha }=\left(1-\frac{1}{2{\tau }_f}\right){\omega }_{\alpha }\left[\frac{3\left(e_{\alpha }-u\right)}{c^2}+\frac{9\left(e_{\alpha }\cdot u\right)}{c^4}{e}_{\alpha }\right]\cdot F$$

(13)

The Chapman–Enskog expansion can be used to recover the macroscopic NS equations, and Macroscopic quantities such as the density and fluid velocity can then be evaluated from the distribution functions as:

$$\rho ={\displaystyle \sum _{\alpha }{f}_{\alpha }}$$

(14)

$$\rho u={\displaystyle \sum _{\alpha }{e}_{\alpha }{f}_{\alpha }}+\frac{\Delta t}{2}F$$

(15)

3.2. Lattice Boltzmann Model for Poisson–Boltzmann Equation

Here, to solve the Poisson–Boltzmann equation, we adopt an LBM algorithm proposed by Oulaid et al. [41] because of its good numerical accuracy. The Poisson–Boltzmann equation can be considered as a convection-diffusion equation at the steady state. A lattice distribution function $g_{\alpha }$ is introduced, and its evolution is described by the following lattice Boltzmann equation:

$$g_{\alpha }(x+e_{\alpha }\Delta t,t+\Delta t)-g_{\alpha }(x,t)=-\frac{1}{{\tau }_g}\left[g_{\alpha }(x,t)-g_{\alpha }^{eq}(x,t)\right]+\Delta t{G}_{\alpha }+\frac{\Delta t^2}{2}{\overline{D}}_{\alpha }{G}_{\alpha }$$

(16)

where $g_{\alpha }(x,t)$ is the distribution function for electric potential. ${\tau }_g$ is the relaxation time for the electric potential distribution function. $G_{\alpha }$ is related to the net charge term in Equation (4) by:

$$G_{\alpha }=-{\omega }_{\alpha }\chi \frac{{\rho }_e}{\epsilon {\epsilon }_0}$$

(17)

and the operator ${\overline{D}}_{\alpha }={\partial }_t+\theta e_{\alpha }\cdot \nabla$, with $\theta \in \left[0,1\right]$ as a parameter for different schemes. Both the minimum and maximum values of $\theta$ (0 and 1) have been tested with diffusion and convection-diffusion systems, and no significant influence on the solution accuracy is found. In this work we use a forward scheme for the temporal derivative with $\theta =1$ for simplicity:

$${\overline{D}}_{\alpha }{G}_{\alpha }=\frac{G_{\alpha }\left(x,t\right)-G_{\alpha }\left(x-e_{\alpha }\Delta t,t-\Delta t\right)}{\Delta t}$$

(18)

The electric potential $\psi$ can be calculated from the distribution functions by:

$$\psi ={\displaystyle \sum _{\alpha }{g}_{\alpha }}$$

(19)

and the equilibrium distribution $g_{\alpha }^{eq}$ of electrical potential evolution function is:

$$g_{\alpha }^{eq}={\omega }_{\alpha }\psi$$

(20)

Following the spirit for the fluid flow, the following differential equation through the Chapman–Enskog analysis can be derived:

$$\frac{\partial \psi }{\partial t}=\chi {\nabla }^2\psi \text{+}\chi \frac{{\rho }_e}{\epsilon {\epsilon }_0}$$

(21)

and the solution to the Poisson Equation (4) can be obtained at the steady state of the simulation when the partial differential term on the left-hand side approaches zero. The potential diffusivity in Equation (21) is defined as:

$$\chi =\frac{\left(2{\tau }_g-1\right)c\Delta x}{6}$$

(22)

3.3. Boundary Conditions

As with any other numerical methods, correct and accurate boundary treatments play a crucial role in LBM simulation. Many useful schemes for boundary condition have been developed for solving different physical problems. To model the fluid-solid interaction on the complex geometries, the mid-point bounce-back scheme [30] is used for the flow field. As shown in Figure 1, the link between the fluid node $x_f$ and the solid node $x_s$ intersect the physical boundary at $x_b$. The fraction of the intersected link in the solid domain region is $\Delta =\left|x_s-x_b\right|/\left|x_s-x_f\right|$.

Figure 1. Schematic illustrations for the mid-point bounce-back scheme.

Figure 1. Schematic illustrations for the mid-point bounce-back scheme.

As we known, the evolution equations consist of two computational steps:

Collision:

$${\phi }_{\alpha }^{\ast }(x,t)-{\phi }_{\alpha }(x,t)=-\frac{1}{\tau }\left[{\phi }_{\alpha }(x,t)-{\phi }_{\alpha }^{eq}(x,t)\right]$$

(23a)

Streaming:

$${\phi }_{\alpha }(x+e_{\alpha }{\delta }_t,t+{\delta }_t)={\phi }_{\alpha }^{\ast }(x,t)$$

(23b)

with ${\phi }_{\alpha }=f_{\alpha }$ or $g_{\alpha }$. When implementing the boundary conditions with LBM, the difficulty is how to finish the collision and streaming steps at the boundaries. In Figure 1, after the collision step at the fluid node $x_f$, the distribution function $f_{\alpha }^{\ast }$ leave $x_f$, and is then assumed to be bounce-back at the midpoint $x_m$ in the reversed direction and with a modified magnitude as $f_{\overline{\alpha }}$:

$$f_{\overline{\alpha }}=f_{\alpha }^{\ast }-\frac{2\rho {\omega }_{\alpha }}{c_s^2}{u}_m\cdot e_{\alpha }$$

(24)

where $e_{\overline{\alpha }}=-e_{\alpha }$, $u_m$ is the midpoint velocity at the point $x_m$ to be determined.

For $\Delta \le 1/2$, the midpoint $x_m$ locates between $x_b$ and $x_f$, and the midpoint velocity $u_m$ can be readily obtained with a linear interpolation:

$$u_m=\frac{\frac{1}{2}{u}_b+(\frac{1}{2}-\Delta )u_f}{1-\Delta }$$

(25)

where $u_b$ is the imposed boundary velocity at the intersection point $x_b$, and $u_f$ is the flow velocity calculated at the fluid node $x_f$. For $\Delta >1/2$, the midpoint $x_m$ is in the solid domain and therefore an extrapolation is needed to obtain velocity $u_m$:

$$u_m=\frac{\frac{3}{2}{u}_b-(\Delta -\frac{1}{2})u_{ff}}{2-\Delta }$$

(26)

where $u_{ff}$ is the velocity at the fluid point $x_{ff}$.

Following the above velocity boundary treatment, here, we use the electric potential ${\psi }_m$ at the midpoint to calculate the electric potential distribution function at the bounce-back nodes:

$$g_{\overline{\alpha }}(x_f,t+\delta t)=-g_{\alpha }^{+}(x_f,t)+2{\omega }_{\alpha }{\psi }_m$$

(27)

with the midpoint electric potential ${\psi }_m$ obtained via:

$${\psi }_m=\{\begin{array}{l}\frac{\frac{1}{2}{\psi }_b+(\frac{1}{2}-\Delta ){\psi }_f}{1-\Delta }\hspace{1em}\hspace{1em}\Delta \le 1/2\\ \frac{\frac{3}{2}{\psi }_b-(\Delta -\frac{1}{2}){\psi }_{ff}}{2-\Delta }\hspace{1em}\hspace{0.17em}\Delta >1/2\end{array}$$

(28)

where ${\psi }_b$ is the imposed boundary electric potential at the intersection point $x_b$, ${\psi }_f$ is the electric potential calculated at the fluid node $x_f$, and ${\psi }_{ff}$ is the electric potential at the fluid point $x_{ff}$.

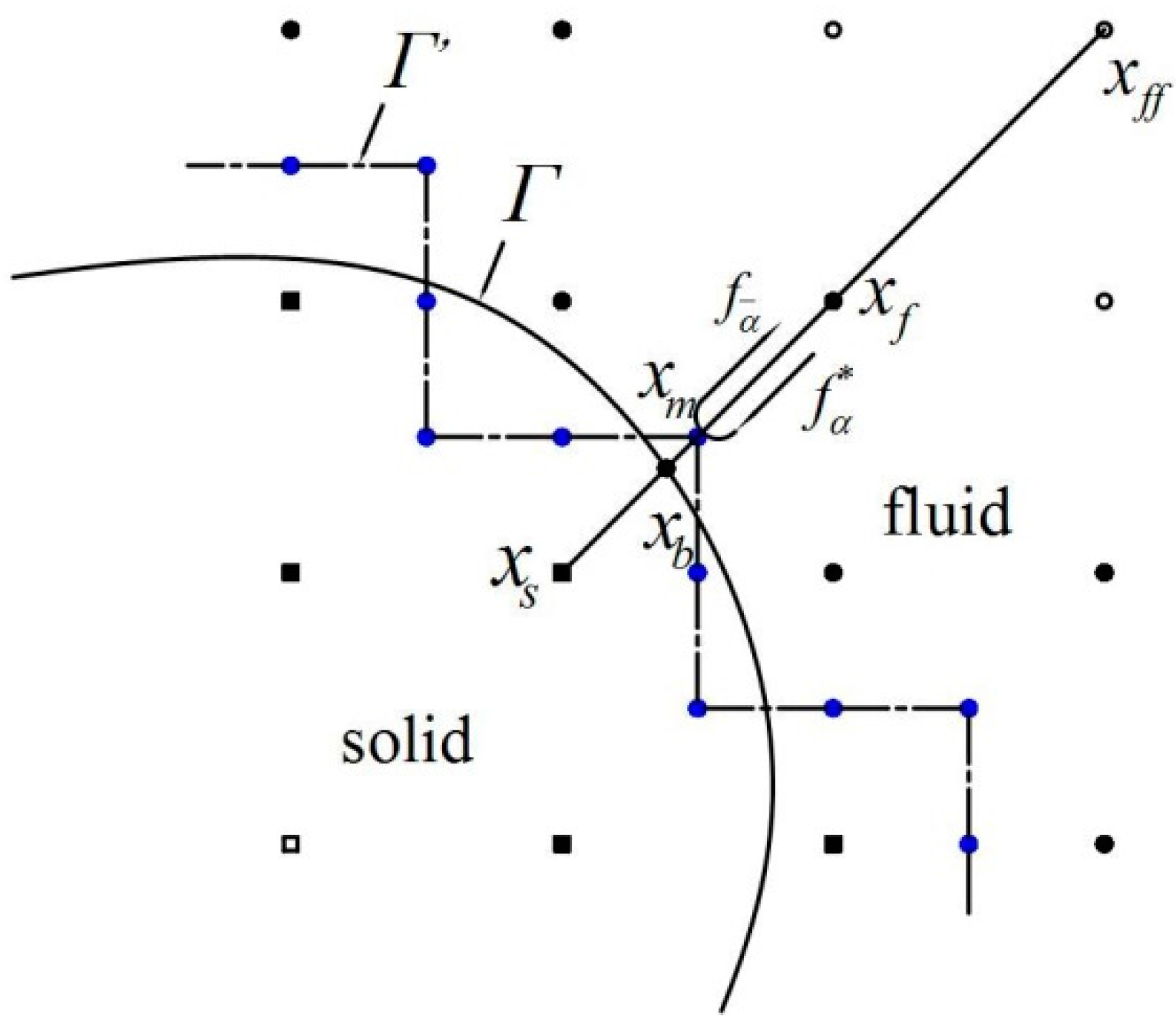
4. Validation and Discussions

4.1. Electric Potential with Flat Surface

First, we apply the improved bounce-back scheme to calculate the potential profile between two parallel plates, both of constant potential, immersed in an electrolyte solution. Near the charged surfaces, ions in the electrolyte solution will be redistributed and the electric diffuse layer will be established. The ion charge density can be related to the local potential via the Boltzmann distribution. For surfaces with low surface potentials, the Debye–Huckel approximation can be applied and the Poisson–Boltzmann equation can be solved by Equation (8). The solution of this linearized Poisson–Boltzmann equation between two identical plates of a separation H is:

$$\psi (x)={\psi }_0\frac{\cosh (\kappa x)}{\cosh (\kappa H/2)}$$

(29)

where $x$ is the transverse location across the gap with $x=0$ at the centerline. We use ${\psi }_0=1$, $\kappa =0.02$, and different channel heigh $H=16,32,64,128$ in our simulation. The calculated potential profile is plotted in Figure 2. The symbols are results from LBM simulations, and the black lines are theoretical solutions predicted from Equation (29). Excellent agreement can be seen with different channel height between the simulation results and theory.

Figure 2. Electric potential distributions from our LBM simulation (symbols) and the analytical solution (black lines) with different height between two identically charged plates in an electrolyte solution.

Figure 2. Electric potential distributions from our LBM simulation (symbols) and the analytical solution (black lines) with different height between two identically charged plates in an electrolyte solution.

For a more quantitative analysis, the simulations with channel height $H=16$ and different offset ($\Delta \text{=}0.2$, $\Delta \text{=}0.5$, and $\Delta \text{=}0.7$) are implemented by the classical bounce-back treatment and the improved bounce-back treatment, as shown in Figure 3. When the offset $\Delta \text{=}0.5$, the results from different treatment are identical. When the offset $\Delta \text{=}0.2$ or $\Delta \text{=}0.7$, for the classical bounce-back methods, these different offset values have no influence on the electric potential distribution. However, the improved bounce-back method can correctly follow the theoretical solution.

Figure 3. Electric potential distributions from present treatment, classical Bounce-Back treatment and the analytical solution with different offset (red symbol $\Delta \text{=}0.5$; blue symbol $\Delta \text{=}0.7$; green symbol $\Delta \text{=}0.2$).

Figure 3. Electric potential distributions from present treatment, classical Bounce-Back treatment and the analytical solution with different offset (red symbol $\Delta \text{=}0.5$; blue symbol $\Delta \text{=}0.7$; green symbol $\Delta \text{=}0.2$).

As for typical LBM boundary models, the numerical accuracy is studied. We choose different channel heigh $H=16,32,64,128$ and calculate the error between the LBM results and theoretical solutions. The errors are plotted in Figure 4, and linear fitting are conducted in the logarithmic graph. The fitting slope is usually considered as the accuracy order of a numerical model. As show in Figure 5, the accuracy order is 1.97, about 2, indicating a second-order for this system by the improved bounce-back treatment.

Figure 4. The error for electric potential between two identically charged plates in an electrolyte solution.

Figure 4. The error for electric potential between two identically charged plates in an electrolyte solution.

Figure 5. Electric potential distributions between two coaxial circular surfaces.

Figure 5. Electric potential distributions between two coaxial circular surfaces.

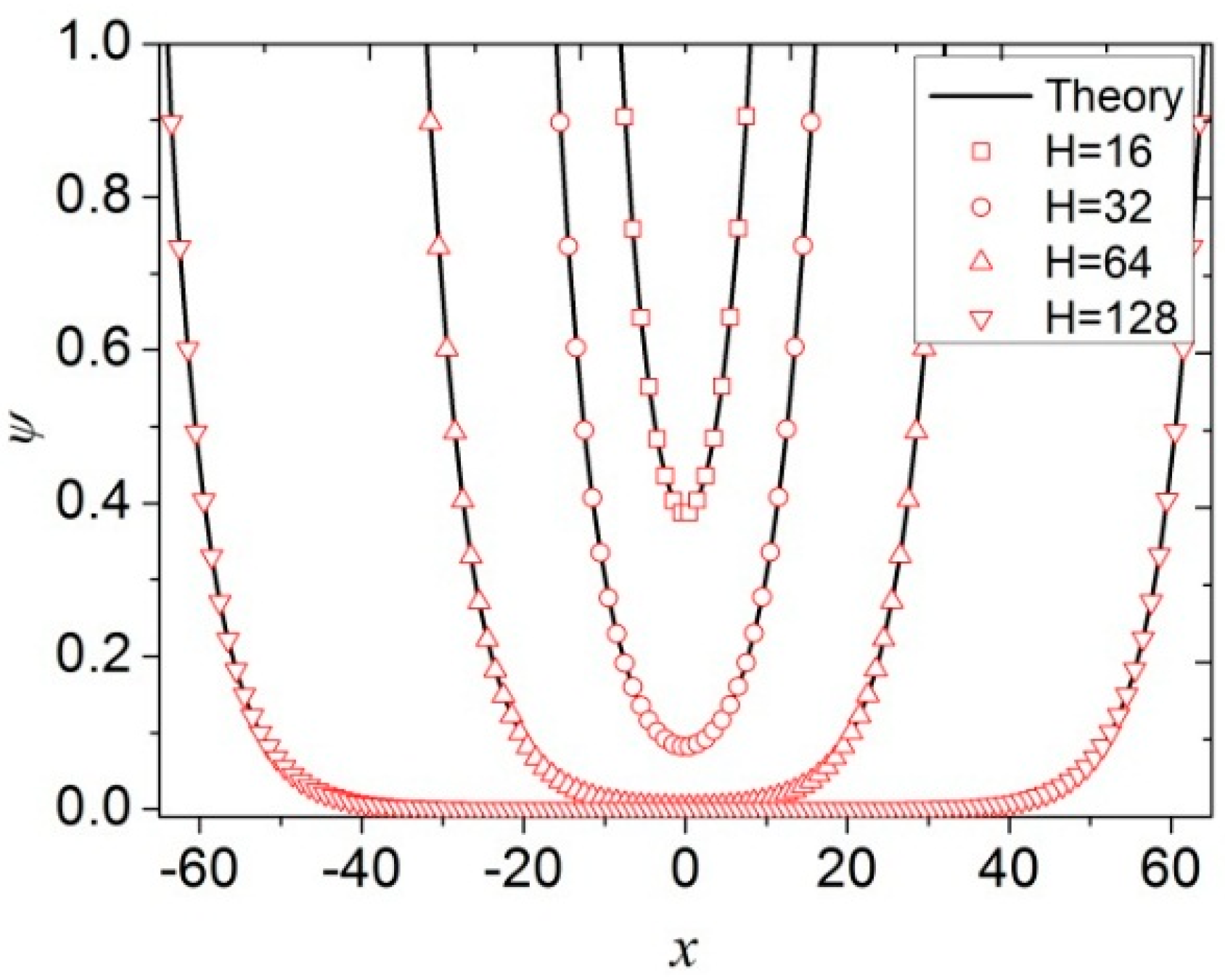
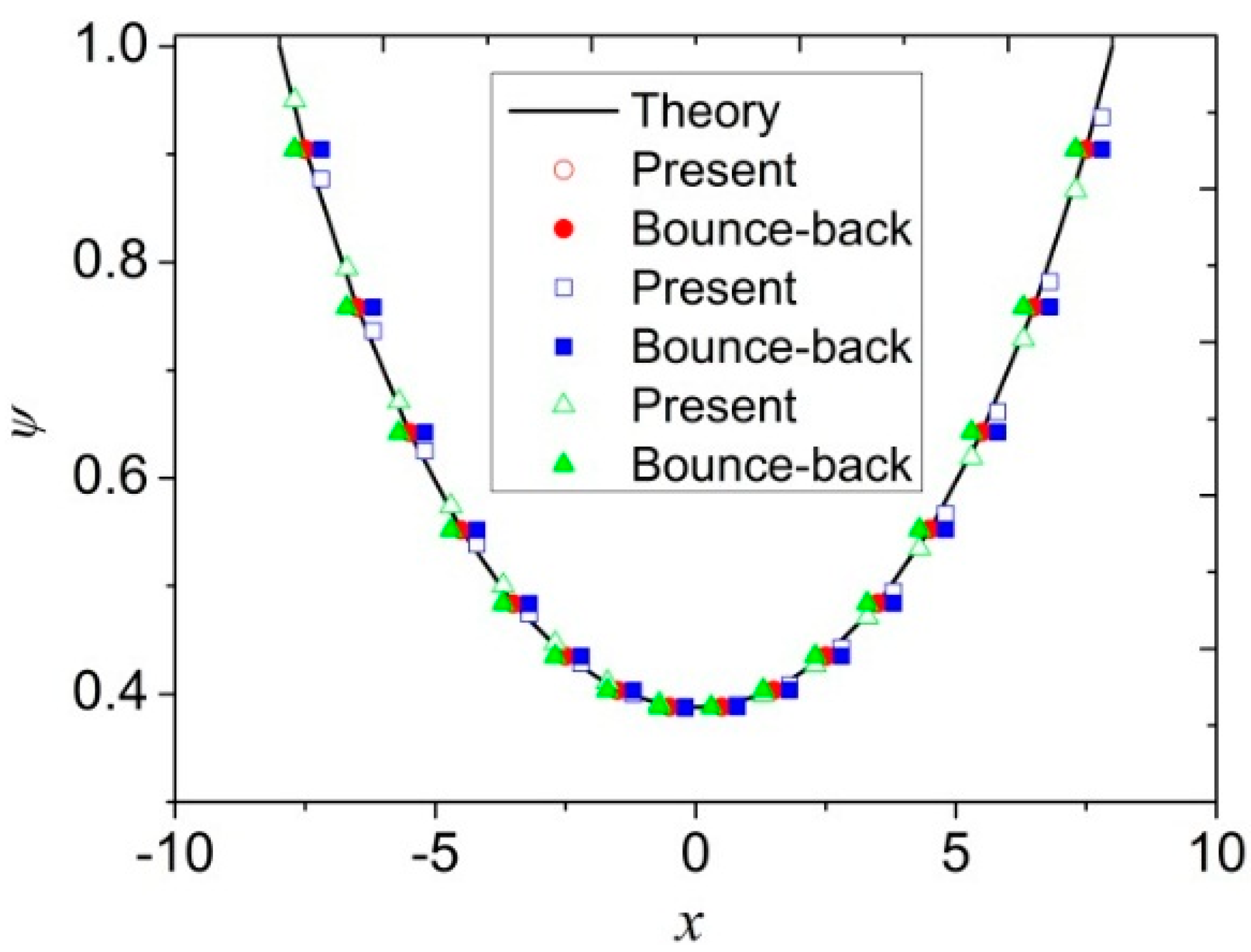
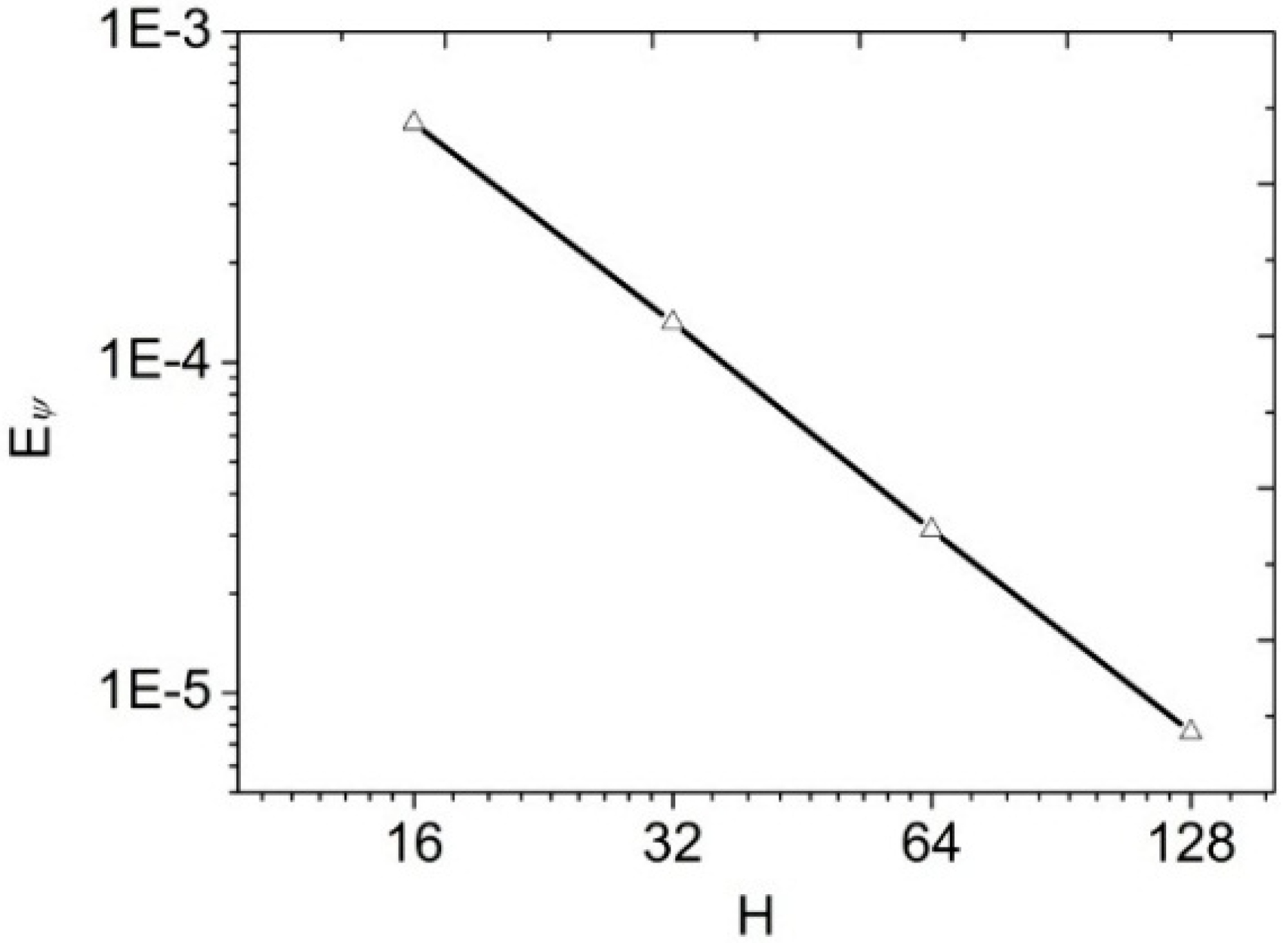
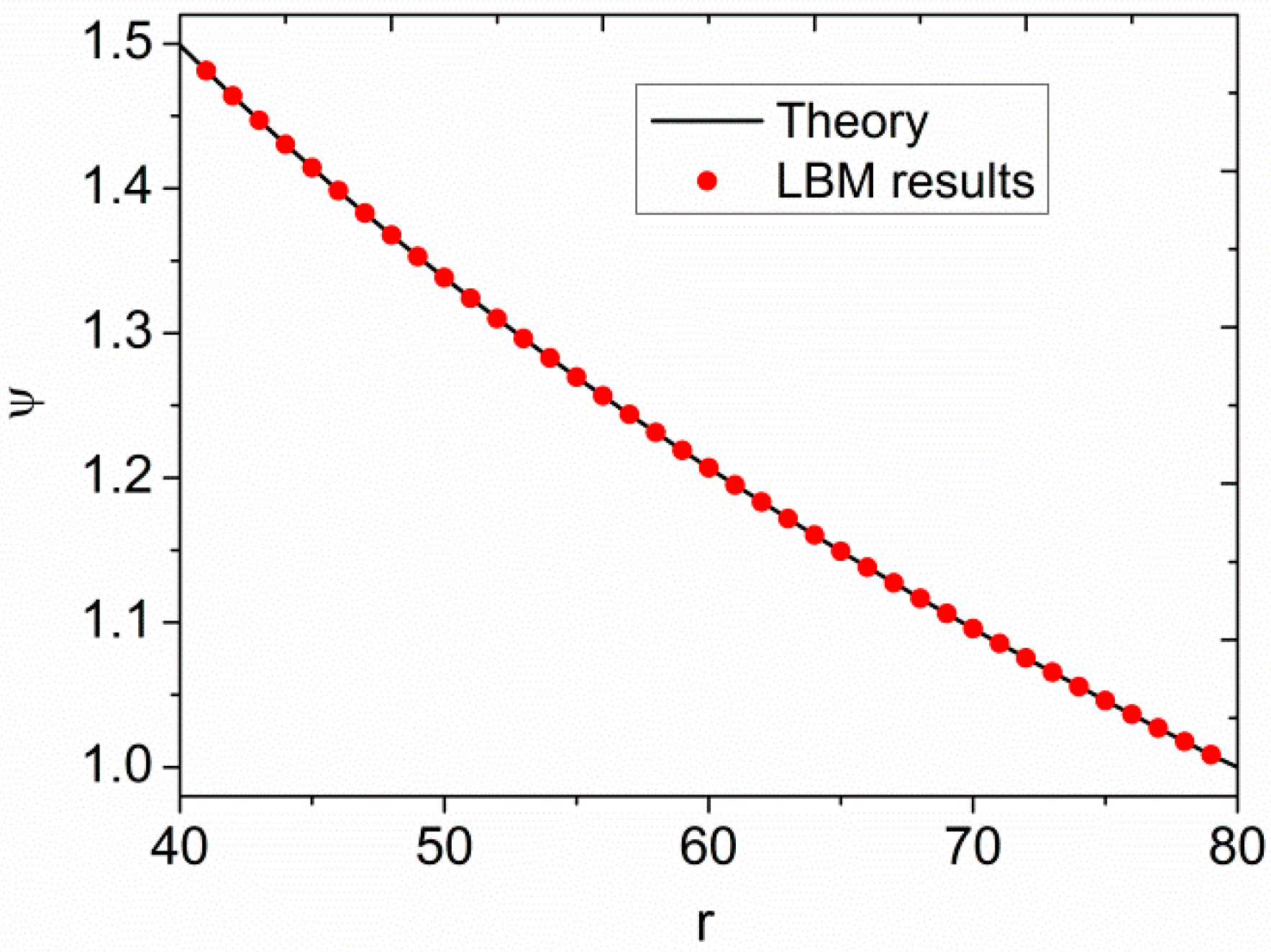
4.2. Electric Potential with Complex Geometry

Next, to examine the performance of our method for more complex boundary shapes and conditions, we consider the electric field between two coaxial circular surfaces with inner and outer radii $R_{in}$ and $R_{out}$, respectively. With no net charge, the general solution is given as:

$$\psi (r)=C_1\ln r+C_2$$

(30)

where the constants $C_1$ and $C_2$ can be determined by the boundary conditions on the surfaces. For the Dirichlet boundary conditions, the electric potential on both surfaces are $\psi (R_{in})={\psi }_1$ and $\psi (R_{out})={\psi }_2$.

The corresponding exact solution for this case is:

$$\psi (r)={\psi }_1+({\psi }_2-{\psi }_1)\frac{\ln (r/R_{in})}{\ln (R_{out}/R_{in})}$$

(31)

In the simulation, we set $R_{in}=40$, $R_{out}\text{=80}$, ${\psi }_1\text{=}1.5$ and ${\psi }_2\text{=}1$. The domain size is $201\times 201$ and the surfaces are put at the center of the domain. Simulation result for this system is plotted in Figure 3. We also find that the results agree well with analytical solution.

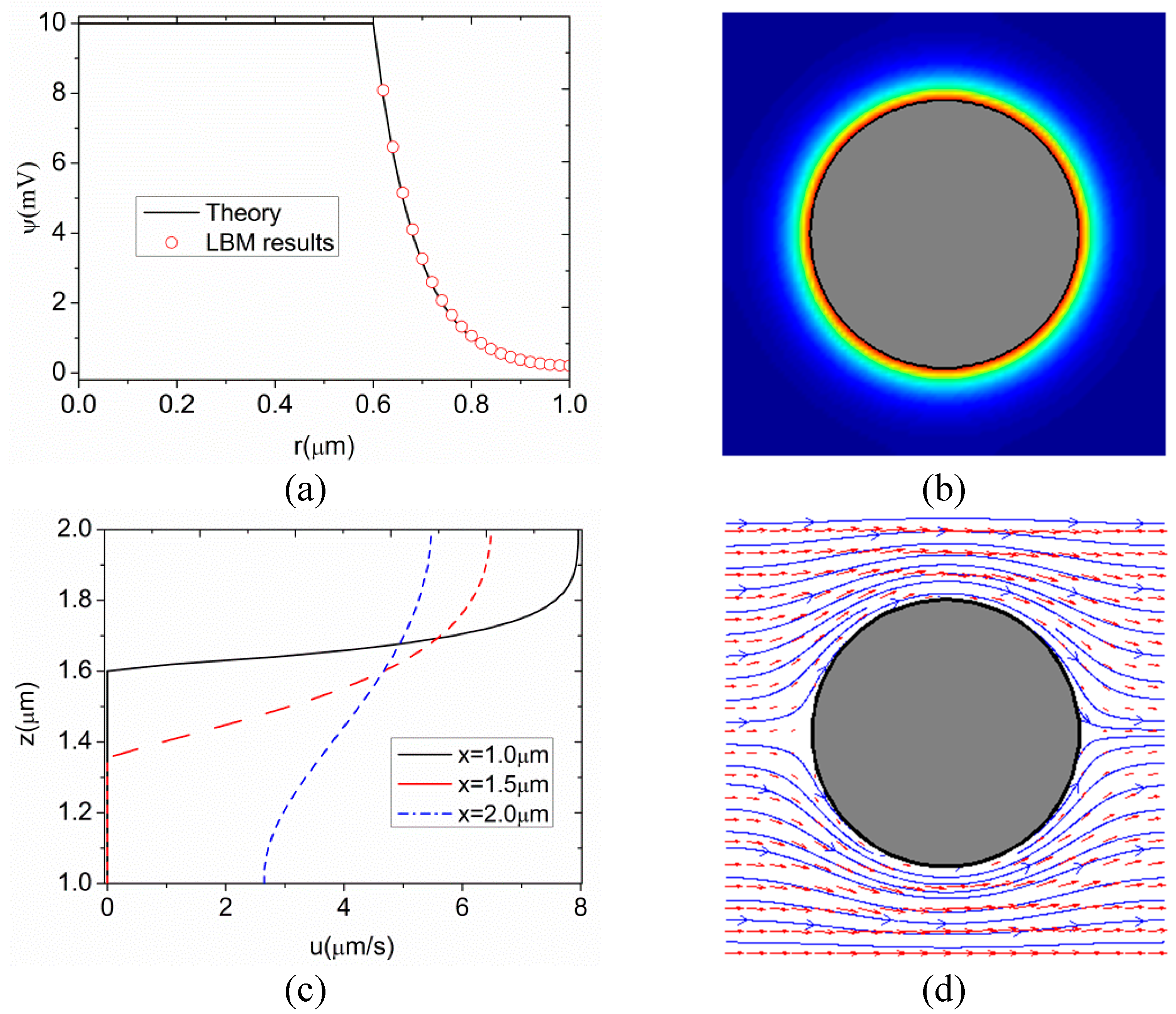
4.3. Application in Electro-Osmotic Flows

In this section, a charged spherical particle immersed in an electrolyte solution is considered with a side length of 2 μm. A $100\times 100\times 100$ uniform grid is used and the particle center $\left(x_c,y_c,z_c\right)$ locates at the center of the cubic domain. Detailed numerical results on electro-osmotic flow and the effects of variation of ionic concentration, the sphere radius, external electric field and electric potential on velocity profile are presented. The numerical results are also compared with analytical solutions. In the simulation, the Poisson–Boltzmann equation is solved to obtain a steady solution firstly. And then the Navier–Stokes equations with the external force term is solved. We select a symmetric solution with $z:z=1:1$ (for example, KCl, NaCl, etc.) and assume the solution has similar physical properties. The parameters are the ionic molar concentration $c_{\infty }=0.01M$, $n_{\infty }=c_{\infty }{N}_A$, where $N_A$ is Avogadro’s number, the dielectric constant of the solution $\epsilon {\epsilon }_0=6.95\times {10}^{-10}{\mathrm{C}}^2/Jm$, the temperature $T=273\mathrm{K}$, the density $\rho =1.0\times {10}^3\mathrm{kg}/m^3$, and the electric potential with ${\psi }_0$ as a constant. The external electric field is only applied in $x$-direction, i.e., $E=\left(E_x,0,0\right)$. The dimensionless relaxation time ${\tau }_f$ and ${\tau }_g$ are set to be 1.0. Periodic boundary conditions are applied in all the three directions, and hence the simulated system actually represents a cubic array of spheres uniformly distribution in space.

The algorithm and boundary treatment described in previous sections have been used to simulate the electric flow with curved boundary. For the purpose of validation, the solution of the Poisson–Boltzmann equation around a spherical particle with thin EDL layers is given as:

$$\psi \left(r\right)={\psi }_0\frac{R}{r}{e}^{-\kappa \left(r-R\right)}$$

(32)

where $r$ is the distance to the spherical center. We use ${\psi }_0=\text{10 mV}$ and $E_x=500\mathrm{V}/m$ in our simulation. The particle has a radius of R = 0.6 μm.

Figure 6a shows the electric potential as a function of the distance to the particle center. The red circles are from our LBM calculation and the black curve is the theory solution according to Equation (32). Good agreement can be observed between them. The potential distribution at $y=y_c$ is presented in Figure 6b. The distribution appears circularly symmetric and isotropic, and this is confirmed by the fact that all the simulated $\psi$~$r$ data points fall approximately on a single curve in Figure 6a.

When an external electric field is applied, an electric force $F$ will be generated in the electrolyte solution near the surface due to non-zero charge in that region, and the electrostatic force can thus induce fluid flows along the electric field direction. This phenomenon is called the electro-osmosis. Figure 6c displays the velocity component $u$ in the $y=y_c$ with different locations x = 1.0 μm, x = 1.5 μm, and x = 2.0 μm. Only the upper half (z ≥ zc = 1.0 μm) is shown for these symmetric curves. At x = 1.0 μm (black solid line), the velocity increases from 0 at the surface to a plateau value near the top boundary. This is similar to the typical plug-like velocity profile of electro-osmotic flows in straight channels, since the electric force only exists in the thin EDL near the surface. Away from this particular location, the cross-sectional area for the flow passage increases, and therefore the flow velocity decreases due to the mass conservation. The electro-osmotic flow streamlines in the $y=y_c$ plane are plotted in Figure 6d. The red arrows indicate the velocity magnitude and direction. The flow pattern is symmetric about both $x=x_c$ and $z=z_c$ due to the symmetric system geometry and the creeping electro-osmotic flow. These simulation results demonstrate that our method for electro-kinetic flows is useful.

Figure 6. The electric potential distribution (a) and (b) and electro-osmotic flow (c) and (d) around the spherical particle in the $\text{y}=y_c$ plane.

Figure 6. The electric potential distribution (a) and (b) and electro-osmotic flow (c) and (d) around the spherical particle in the $\text{y}=y_c$ plane.

5. Conclusions

In this paper, we have extended the improved bounce-back boundary treatment for LBM flow simulations to electric field simulations. Several simulations have also been performed to examine our boundary methods in term of ability to deal with complex boundary situations. An example simulation of electro-osmotic flow with a charge sphere particle immersed in an electrolyte solution has also been presented. Comparisons with theoretical predictions show excellent agreement for all simulations, and our method therefore could be useful for future electrokinetic simulations with complex boundary geometries. Furthermore, the boundary treatment in this work can be applied to LBM simulations for other processes and phenomena that can be described by similar differential equations.