We adopt a methodology that may help us to extract the structure of and appreciate the nature of the exergy flow paths associated with heat transfer, provide insight into ways of defining rational efficiency in exergy analysis and make the choice of environmental reference temperature somewhat more solid and method based, recognizing the significance of finite time in real thermodynamic processes that involve heat transfer. We start with the simplest case and develop the concepts progressively.
2.1. One Heat Source and One Heat Sink with Reversible Heat Transfer
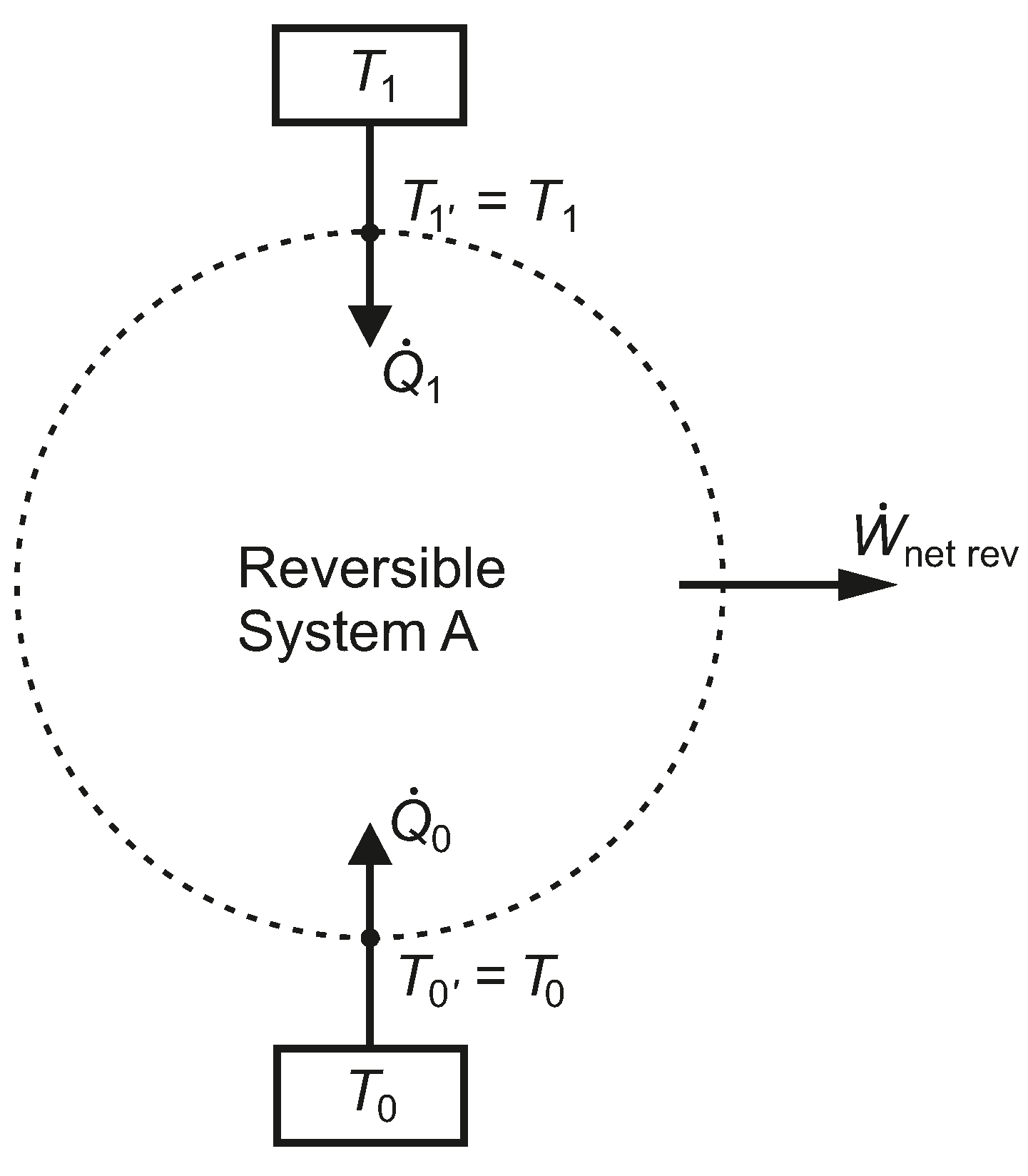
In
Figure 2, a system, A, has a net work interaction while exchanging heat with just two isothermal reservoirs, at temperatures
and
, where each thermal reservoir is linked to the boundary of the system, without any thermal resistance between them. For the moment, we assume the net work is an energy output and that
. We also assume that System A undergoes only reversible processes.
Figure 2.
A closed reversible system, A, bounded by two isothermal reservoirs, without intermediate thermal resistances.
Figure 2.
A closed reversible system, A, bounded by two isothermal reservoirs, without intermediate thermal resistances.
The thermal efficiency,
, is given by Equation (
5), and the net rate of work output is given by Equation (
6). This efficiency is known as the Carnot efficiency,
, as Sadi Carnot [
9] first described the concept of an idealized cycle of a heat engine system, based on reversible processes and with only infinitesimal temperature differences causing the heat transfer interactions between the system and two isothermal reservoirs. Carnot also pointed out that this maximum efficiency, expressing the “motive power” of the heat transfer rates, was independent of the particular working substance, whether solid, liquid, vapour or two-phase. The Carnot efficiency would be applicable for any net rate of work output of a reversible steady-state or cyclic device, operating between the two isothermal reservoirs, for which the assumption of zero or infinitesimal connecting thermal resistances held.
Now, we consider cases where the net work interaction is an energy input and where
may be greater than or less than
. Carnot [
9] (p.11) pointed out that the net work output of his idealized heat engine could be reversed, so that the energy taken from the source and that transferred to the sink could be returned, leaving no net effect on the heat engine system or its surroundings. The heat pump and refrigeration COPs of a reversible heat engine, operating in reverse, are given by Equations (
7) and (
8).
In Equation (
7),
and
are both negative, and the isothermal reservoir at temperature
is the heat sink at a temperature above
. In Equation (
8),
is negative, and the isothermal reservoir at temperature
is the heat source, which is at a temperature below
.
There remains a further case to be considered. Imagine we had an isothermal reservoir somewhere under the surface of the Earth at −100
C. Then, our heat engine could operate between ambient temperature,
, and that low-temperature reservoir, at
. This would be one of four different application cases that are possible. We could have:
a heat engine (which we denote as HE1) accepting heat transfer from a high temperature heat source at and rejecting heat at (if irreversible, the entropy transfer rate out at is greater than the entropy transfer rate in at ),
a heat engine (HE2) accepting heat transfer at and rejecting heat to a low temperature heat sink at (if irreversible, the entropy transfer rate out at is greater than the entropy transfer rate in at ),
a heat pump (which we denote as a reverse heat engine, Type 1, RHE1) rejecting heat to a high temperature sink at and accepting heat transfer at (if irreversible, the entropy transfer rate out at is greater than the entropy transfer rate in at ) or,
a refrigerator (RHE2) accepting heat transfer from a low temperature source at and rejecting heat at (if irreversible, the entropy transfer rate out at is greater than the entropy transfer rate in at ).
The Type 1 systems or devices (HE1 and RHE1) operate at temperatures that are mainly above ambient temperature, while Type 2 (HE2 and RHE2) operates mainly at temperatures below ambient temperature. In all four cases, entropy has to be balanced to respect the second law, which states that for a system that is undergoing no net change, the rate of entropy creation must be greater than or equal to zero and can only equal zero if there is no irreversibility occurring within the system. Where entropy is being created within the system, there must be a corresponding net rate of entropy rejection from the system. As a consequence, for a unique net rate of entropy transfer into the system (positive or negative) from the thermal energy reservoir at
(this reservoir either provides or accepts a rate of exergy transfer) and a unique rate of entropy generation within the system, there must be a unique rate of heat transfer into or out of the environmental isothermal reservoir at
: the existence of the environmental isothermal reservoir allows this balancing heat transfer rate to occur. It could be called a rate of anergy transfer, using the term proposed by Rant [
13]. It may be that progress in the field of exergy analysis and finite time thermodynamics has been held back by a lack of attention to anergy transfer.
Cases HE1 and HE2 are the heat engine cases where or . There is a net rate of exergy input associated with heat transfer at and a net rate of exergy output as work. RHE1 and RHE2 are the reverse heat engine cases where or . There is a net rate of exergy input as work and a net rate of exergy output associated with heat transfer at .
For a reversible HE2, where , the following expressions apply.
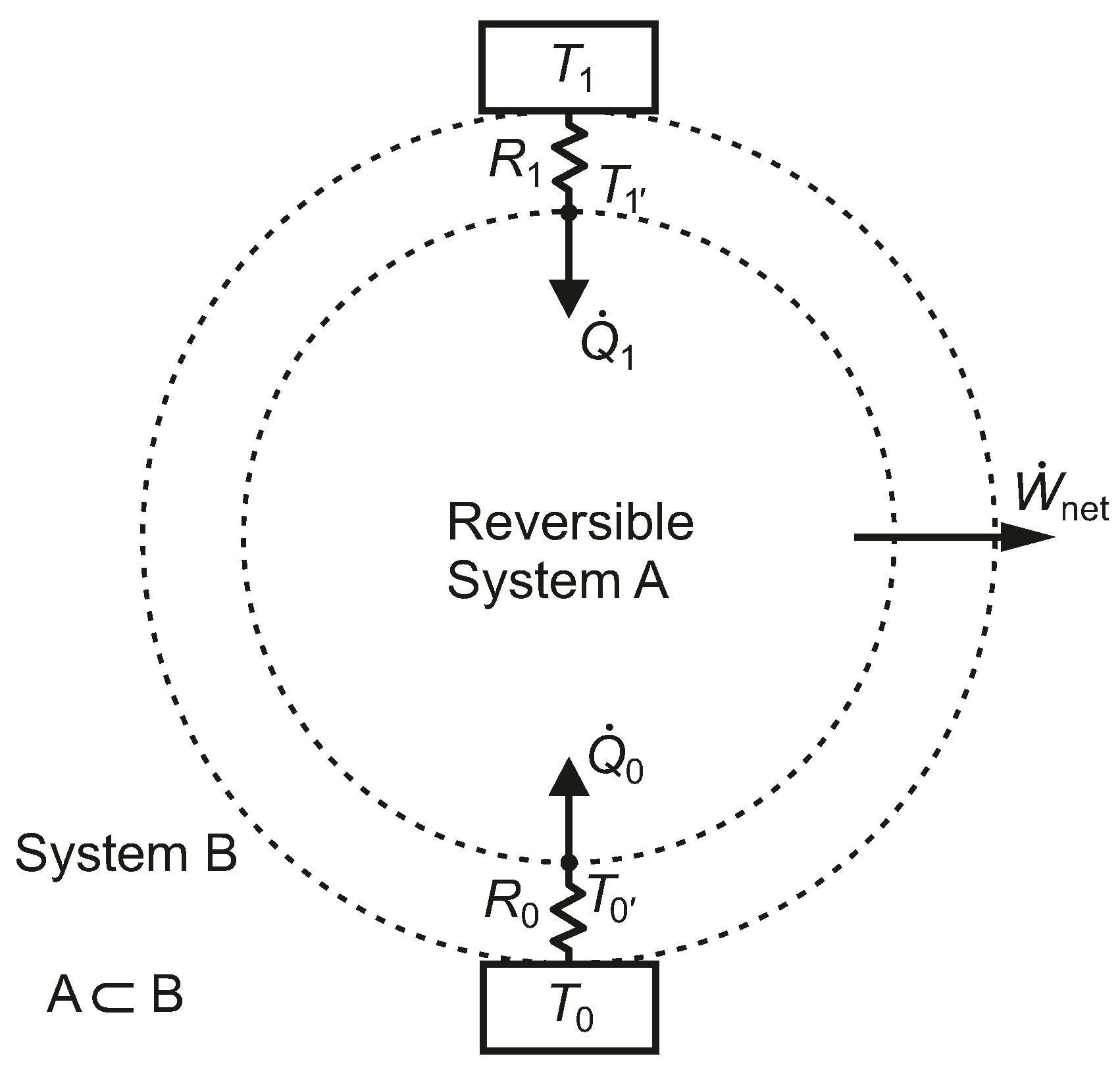
2.2. One Heat Source and One Heat Sink with Thermal Resistances
Assuming an HE1 heat engine (
), taking into account the temperature drops associated with heat transfer through resistances
and
in
Figure 3 and letting
, the thermal efficiency is given by Equation (
11) and the net power output by Equation (
12).
Figure 3.
A closed reversible system, A, bounded by two constant thermal resistances linked to isothermal reservoirs.
Figure 3.
A closed reversible system, A, bounded by two constant thermal resistances linked to isothermal reservoirs.
Assuming an HE2 heat engine (
), the thermal efficiency is given by Equation (
13) and the net power output by Equation (
14). We note that the thermal efficiency is still defined as the net rate of work output divided by the rate of heat input and that, in this case, the rate of heat input is
.
The heat pump and refrigeration COPs are given by Equations (
15) and (
16).
At this point, we define one more first law performance parameter that we will refer to subsequently as part of our second law analysis of HE2 heat engines. We use the engine COP of Equation (
17) for an HE2 to express the ratio of the net work output rate to the rate of heat rejection to the low temperature sink at
, where
. The work output rate is given by Equation (
18).
2.3. Heat Input Rate and Thermal Efficiency of a Heat Engine at Maximum Power
For an HE1 heat engine (where
) at maximum net power output, the rate of heat input is given by Equation (
19) and the thermal efficiency by Equation (
20).
Similar expressions can be written for an HE2 heat engine: Equations (
21) and (
22). We also provide Equations (
23) and (
24), as we regard
as the principal heat transfer rate.
Vaudret
et al. [
14] have traced the history of Equation (
20) to a 1929 book by Reitlinger and have included a scanned image of the relevant excerpt in their paper. Furthermore, an equation equivalent to Equation (
20) for thermal efficiency was provided by Novikov [
1], where
was the temperature at which heat transfer evolved in a nuclear reactor and
was the ambient temperature. As a simplification underlying this form of the equation, the working fluid cycle was assumed to be reversible. Novikov credited a number of other authors with developing this type of expression. Equation (
20) was popularized by Curzon and Ahlborn [
2], and their paper has been very widely cited.
Equations (
11), (
12) and (
16) were included (the last in two end-of-chapter problems) for the first time in the seventh edition (2013) of the popular heat and mass transfer textbook by Incropera
et al. [
15], emphasizing a growing appreciation of the structural relationship between the temperature differences associated with heat transfer interactions and optimization of plant performance—the papers by Novikov [
1] and Curzon and Ahlborn [
2] were cited. As an example, McGovern and Harte [
16,
17] included internal thermal resistances in exergy analyses of the operation of refrigeration compressors.
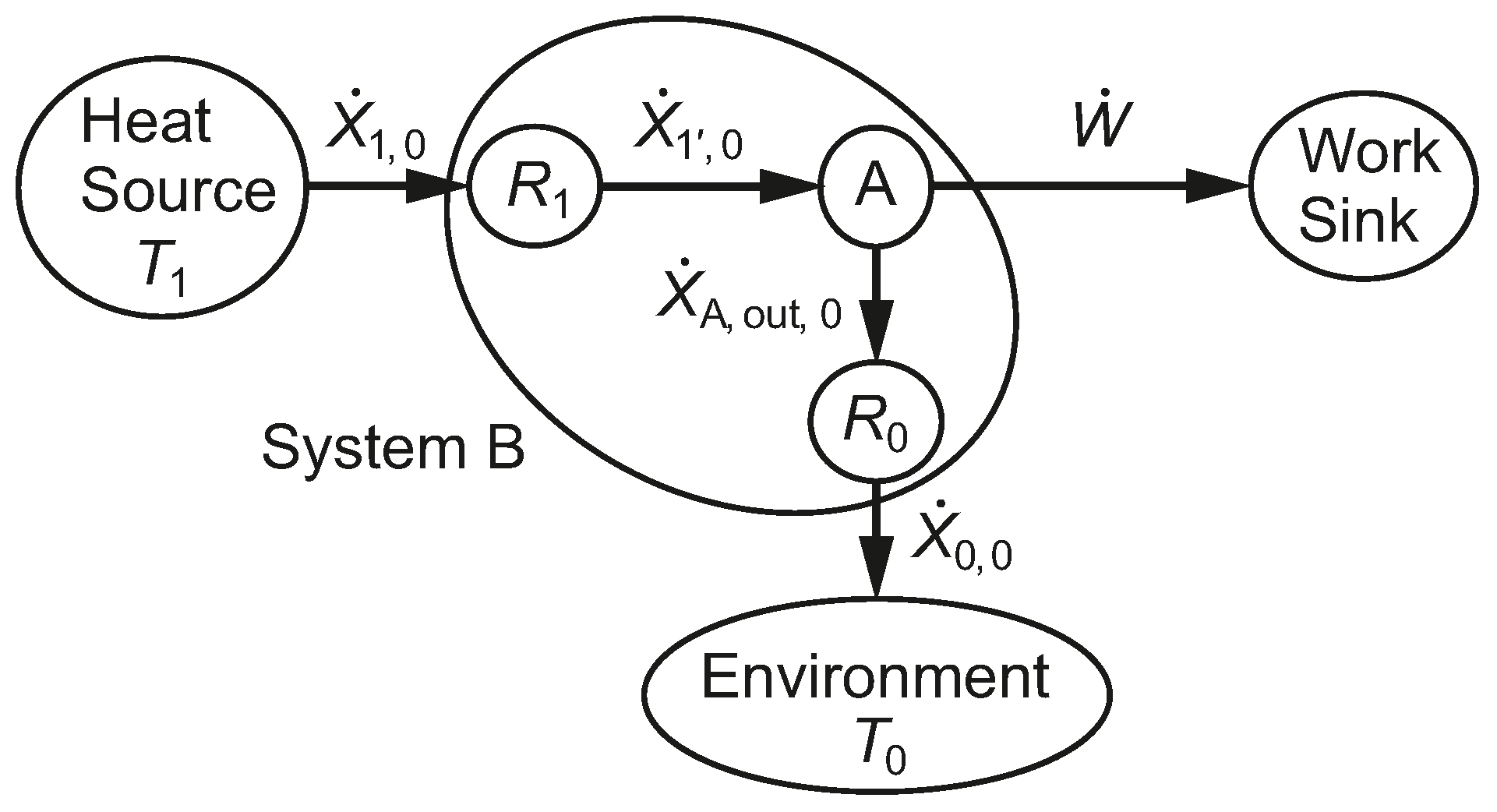
We note that System B in
Figure 3, which undergoes irreversible processes, has the same thermal efficiency as System A, which undergoes only reversible processes. The fact that both systems have the same thermal efficiency emphasizes the weakness of a first-law-only parameter, such as
, for characterizing the performance of the heat engine. Systems B and A also share the same heat pump or refrigeration COPs.
2.4. Exergy Analysis Principles to Be Applied
The equality of Clausius [
10], Equation (
25), applies to the reversible system, A, of
Figure 3, while his
inequality, Equation (
26), applies to the irreversible system, B, that includes the thermal resistances.
Here, we write Clausius’ expressions on a time rate basis for a closed, steady or cyclic system. If the system is steady, the summation is performed over the surface, requiring knowledge of the distribution of the heat flux and temperature. If the system is cyclic, the summation is performed over the surface and over time, requiring knowledge of the distribution of heat flux and temperature over the surface and over time. These expressions represent the second law of thermodynamics, while Equation (
27) represents the first law.
Equations (
25), (
26) and (
27) give rise to the Gouy–Stodola theorem, Equation (
28), a derivation of which is available in Bejan [
18] (Ch. 2). In this equation,
is the rate at which available work (also known as exergy) is destroyed, e.g., in System B in
Figure 3, and
is the rate of entropy generation within the system. In including a zero in the subscript label of
, Bejan explained and emphasized that the expressed rate at which available work is destroyed is with reference to an associated energy transfer rate (also known as an anergy transfer rate in this context) occurring at the specified environmental reference temperature
.
As Bejan [
18] (Ch. 2) explained, it is common to draw the boundary of an overall system being analysed in entropy generation minimization analysis (or in exergy analysis) conventionally, in such a way that the ultimate ‘balancing’ transfer of energy to or from the environment occurs at
. The Gouy–Stodola theorem applies for just this case, but is not applicable for systems, or particularly subsystems, subject to constraints, such as being adiabatically separated from the environment, or bounded by a surface over which different or varying temperatures exist, or being bounded by an external surface of the overall system over which different environmental temperatures exist. Any entropy creation within a closed, steady or cyclic system undergoing no net change will require entropy transfer out of the system somewhere on the boundary, at some temperature, or over some ranges of temperature. If the system is steady, the rate of entropy rejection must be contemporaneous with the rate of entropy creation. In addition to writing Equation (
28) with a zero in the identifying subscript of the lost work term, Bejan also provided an equation, equivalent to Equation (
29), that allowed the lost work to be expressed relative to an associated reference temperature,
, on a system or subsystem boundary where balancing heat transfer or balancing entropy transport or transfer occur to satisfy the inequality of Clausius. This could be for cases where we are interested in the performance of a subsystem in the context of its own local constraints. We borrow this concept in relation to the exergy transfer rate associated with a rate of heat transfer, which we refer to an appropriate boundary temperature, Equation (
30) and
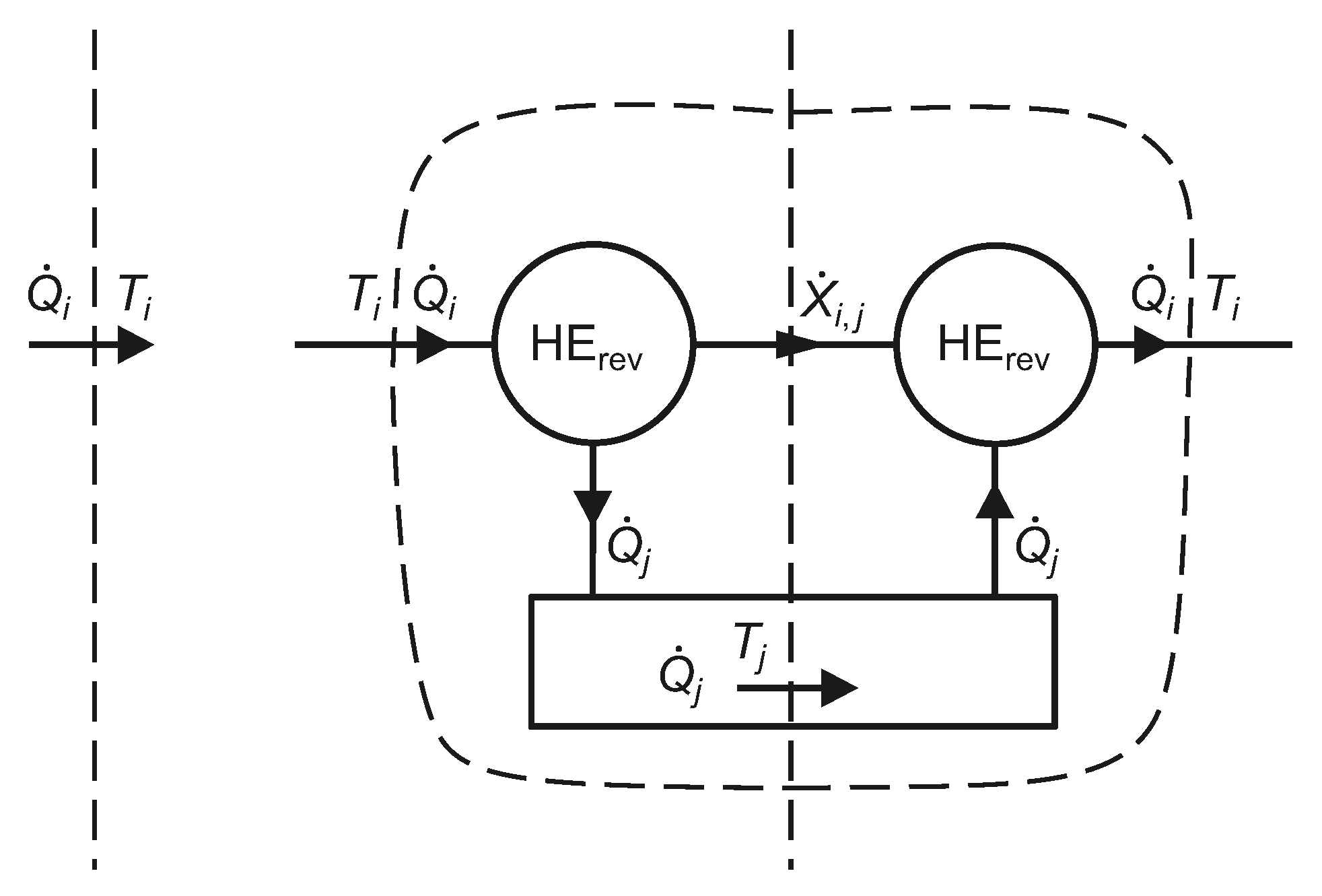
Figure 4.
From the Carnot efficiency of a reversible engine operating between isothermal reservoirs at
and
, the reversible shaft work associated with a heat transfer rate
at
is given by Equation (
30), as explained schematically in
Figure 4. The algebraic sign of the exergy transfer rate is automatically taken into account [
19], but care is needed in its interpretation. The exergy transfer rate
will have the same sign as
if
, but will have the opposite sign if
. In a vapour compression refrigeration plant, the energy transfer rate to the refrigerant in the evaporator is an input to the refrigeration system, but the corresponding exergy transfer rate is a negative input, which means that the exergy output rate is positive. Thus, Equation (
30) gives the exergy transfer rate,
, associated with an actual heat transfer rate in the context of the temperature
of an isothermal reservoir at which any required heat and entropy transfer to satisfy the inequality of Clausius can occur.
Figure 4.
The exergy transfer rate, , corresponding to a heat transfer rate at , relative to an isothermal reservoir at temperature (virtual reversible heat engines, HE, are employed).
Figure 4.
The exergy transfer rate, , corresponding to a heat transfer rate at , relative to an isothermal reservoir at temperature (virtual reversible heat engines, HE, are employed).
The rate of anergy transfer,
, associated with a rate of heat transfer at temperature
is given by Equation (
31). We note that the rate of anergy transfer is directly proportional to the reference temperature
(which is usually the same as
) and indirectly proportional to the temperature at which the heat transfer occurs. It follows from Equation (
31) that the rate of anergy transfer associated with a rate of heat transfer is always in the same direction as the heat transfer. We also note that the anergy rate of a rate of heat transfer at a given temperature equals the corresponding entropy transfer rate multiplied by the reference temperature for exergy and anergy
, which we call
if it applies for the entire composite system under consideration.
For our definition of rational efficiency,
η, we use the ratio, for a specified system, of the sum of the net exergy outputs to all exergy sinks, divided by the sum of the net exergy inputs from all exergy sources; Equation (
32). To be rigorous, we need to make the following stipulations. There can only be one or more sources or one or more sinks, not both, associated with the net work rate. Likewise, for any temperature or infinitesimal temperature range where heat transfer occurs over the boundary, there can only be one or more sources or one or more sinks, not both, for the associated exergy transfer rate. This definition is entirely boundary-based. If a net exergy output rate will ultimately be destroyed and is therefore not useful, we have the choice of extending the boundary into the reference environment to include that rate of exergy destruction, thereby eliminating it from the numerator of the rational efficiency.
In a seminal paper in 1986, Valero, Lozano and Muñoz [
20] introduced the concept of exergetic cost, defined as the amount of exergy per unit time required to produce a physical flow, and proposed a set of propositions relating to it as part of a theory of exergy saving. The concepts introduced amounted to a new way of looking at overall systems in terms of the laws of thermodynamics and the principles of economics. For costing and rational efficiency evaluation purposes, their proposition
2P, “…all the products of a generic equipment have the same unit exergetic cost” is key to addressing furcations (or forks) in the flow of exergy through an overall system or plant. Lozano and Valero published a comprehensive paper on the theory of exergetic cost in 1993 [
21]. In this publication, the corresponding proposition,
P4b, had the wording “…if a unit has a product composed of several flows, then the same unit exergetic cost will be assigned to all of them”.
We believe exergetic costing approaches, and exergonomic approaches built on them will be more widely used as understanding of the nature of exergy flow through systems deepens. The reference temperature is of central importance, as the numerical outcomes are dependent on it. McGovern [
22] focused on the structural issue of exergy recycles.
Now we point out the structural difference between a conventional mechanical efficiency of a power transmission system, such as a gearbox, and a rational efficiency according to Equation (
32). The mechanical efficiency (shaft power output over input) could be 95%. The rational efficiency would typically be zero (where the analysis boundary extends into the environment). However, in principle the rational efficiency of an improved version could be higher than even the mechanical efficiency. If the materials could withstand it, we could cause the heat rejection rate (energetically equivalent to 5% of the input shaft power) to occur at a very high temperature relative to the temperature of the surroundings,
, and the net rate of exergy output could come arbitrarily close to the net input of mechanical power (input minus output shaft power).
2.5. Exergy Analysis of a Reversible System Linked without Thermal Resistances to Its Heat Source and Sink
We now apply exergy analysis to the reversible heat engine, A, described in
Section 2.1 and
Figure 2. We take
to be the temperature of the environment. The net rate of work
is equivalent to a rate of shaft work, so it is also a rate of exergy transfer. If
,
can only be zero, and all rates of exergy output are zero, so the rational efficiency is undefined and irrelevant. In all other cases, the rational efficiency is unity.
If
and
is positive, System A is a reversible heat engine (HE1) producing a net work output rate,
, according to Equation (
6). We apply Equation (
30) with
to find the rates of exergy transfer associated with
and with
,
i.e.,
and
. Hence, the rational efficiency is given by:
Similarly, if
and
is positive, System A is a reversible heat engine (HE2) producing a net work output rate. The rates of exergy transfer associated with
and with
are, once again,
and
. We note that in this case, the exergy input rate is associated with the energy output rate
. Hence, the rational efficiency is once again given as unity by Equation (
33).
If
and
is negative, System A is a reversible heat pump (RHE1) providing heat transfer to the isothermal reservoir at
. The rational efficiency is given by:
If
and
is negative, System A is a reversible refrigerator (RHE2) accepting heat transfer from the isothermal reservoir at
(an exergy output rate). The rational efficiency is given by:
2.6. Exergy Analysis of a Reversible System Linked to Its Heat Source and Sink by Thermal Resistances
We now apply exergy analysis to Heat Engine B described in
Section 2.2 and
Figure 3. If
,
can only be negative (
i.e., an exergy input rate) or zero. The rates of exergy output can only be zero, so the rational efficiency is zero when
is negative.
Using Equations (
2), (
13), (
15), (
16), (
17) and (
30), we obtain the following expressions for the rational efficiency where System B functions as a heat engine (denoted “eng”) or a heat engine operating in reverse (denoted “reng”, for “reverse engine”).
In
Figure 5 and
Figure 6 we provide sample rational efficiency plots
versus the principal heat transfer rates,
, for heat engines (HE1 and HE2), a heat pump (RHE1) and a refrigeration plant (RHE2), each corresponding to the overall system, B, in
Figure 3.
For a heat engine (
or
) at maximum net power output, the rational efficiency is given by Equation (
40).
Figure 5.
Rational efficiency versus the principal heat transfer rate, , for heat engines ( and ).
Figure 5.
Rational efficiency versus the principal heat transfer rate, , for heat engines ( and ).
Figure 6.
Rational efficiency versus the principal heat transfer rate, , for reverse heat engines ( and ).
Figure 6.
Rational efficiency versus the principal heat transfer rate, , for reverse heat engines ( and ).
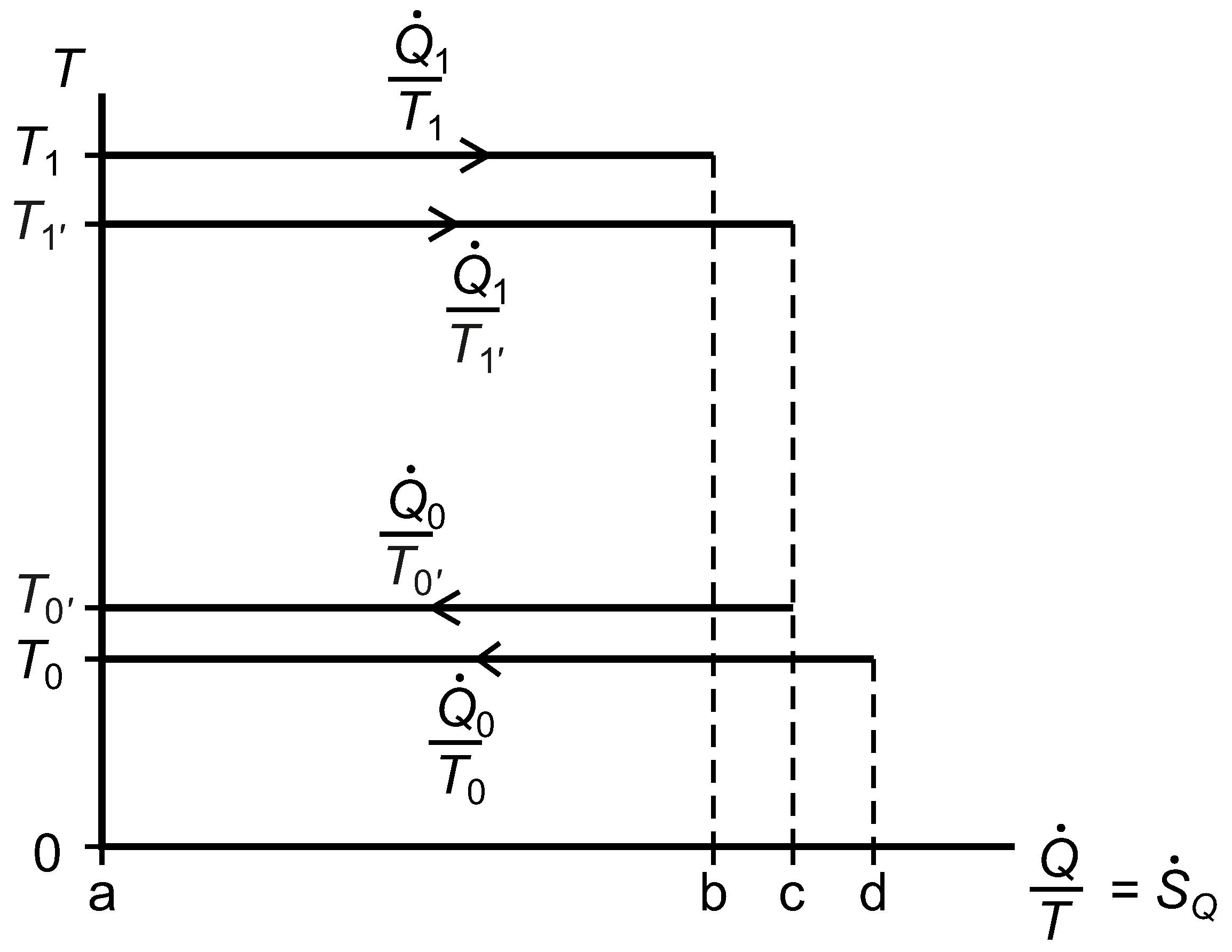
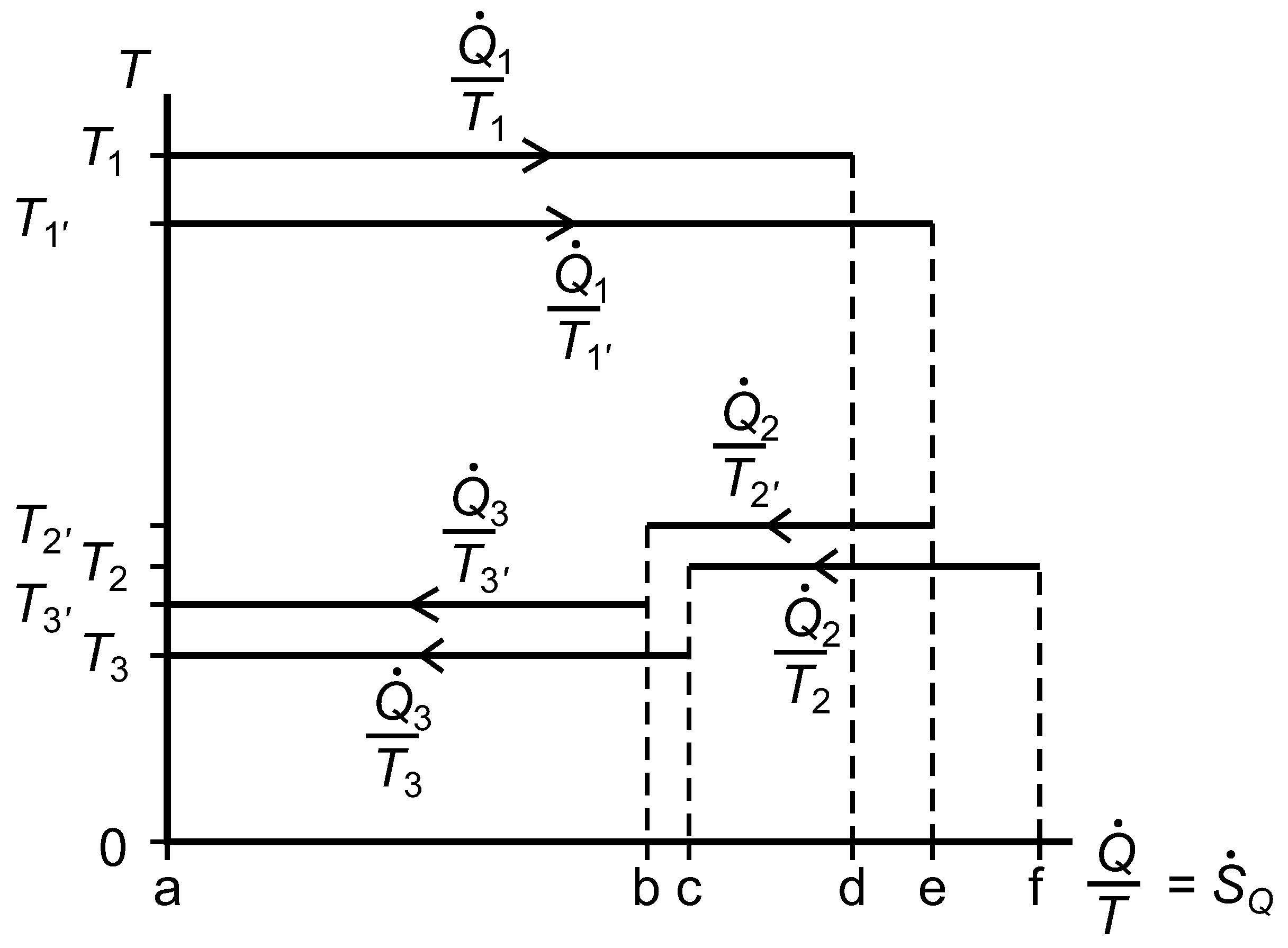
2.7. The Temperature versus Entropy Transfer Rate Diagram
We now consider the exergy analysis of the systems represented in
Figure 3 with reference to a diagram of temperature
versus entropy transfer rate for whichever system or subsystem we wish to focus on;
Figure 7. Clausius’ cyclic integral, Equation (
41), is applied over surface area and time to give the rate of entropy generation within any closed system or subsystem that undergoes no net change, and the Gouy–Stodola theorem, Equation (
28), allows us to calculate the rate of lost work.
Figure 7.
A diagram of temperature versus entropy transfer rates for a reversible heat engine linked by thermal resistances to two isothermal reservoirs, one of which is at the environmental temperature, .
Figure 7.
A diagram of temperature versus entropy transfer rates for a reversible heat engine linked by thermal resistances to two isothermal reservoirs, one of which is at the environmental temperature, .
For System B, with respect to the environmental isothermal reservoir at
, the lost work rate is given by Equation (
42) and the rate of exergy input is given by Equation (
43).
The rational efficiency of System B with respect to
is given by Equation (
44). The quantities in this expression correspond to positive and negative rectangular areas in
Figure 7.
We also provide rational efficiency expressions for Systems A,
and
with respect to their entropy balancing reference temperatures
,
and
, respectively; Equations (
45)–(
47).
We suggest that these relative rational efficiencies are appropriate parameters to quantify the second law performance of these component subsystems. In our case, System A is reversible, but in a more general case, it would have a relative rational efficiency less than one. We note that when analysed in relation to the entropy balancing reference temperatures for their own boundaries, systems and are exergy destruction sinks, which convert exergy to anergy.
We now provide rational efficiency expressions for Systems A and
with respect to the entropy balancing reference temperature of the composite System B,
; Equations (
48) and (
49) respectively.
Figure 8 shows the exergy transfer rates between the subsystems of System B. System A has one exergy input rate,
, and two exergy output rates,
and
. We refer to this as a bifurcation of the exergy transfer rate path. The relative magnitudes of the exergy output rates of System A are characterized by their exergetic furcation factors; Equations (
50) and (
51).
Figure 8.
A diagram of the exergy transfer rates for the reversible heat engine linked by thermal resistances to two isothermal reservoirs, one of which is at the environmental temperature, .
Figure 8.
A diagram of the exergy transfer rates for the reversible heat engine linked by thermal resistances to two isothermal reservoirs, one of which is at the environmental temperature, .
The overall rational efficiency of System B is expressed in terms of two subsystem rational efficiencies (the second of which is unity in this case) and one exergetic furcation factor; Equation (
52). We note that we can complete the entire analysis of System B and its subsystems, provided we have enough information to draw the temperature
versus entropy transfer rate diagram of
Figure 7.
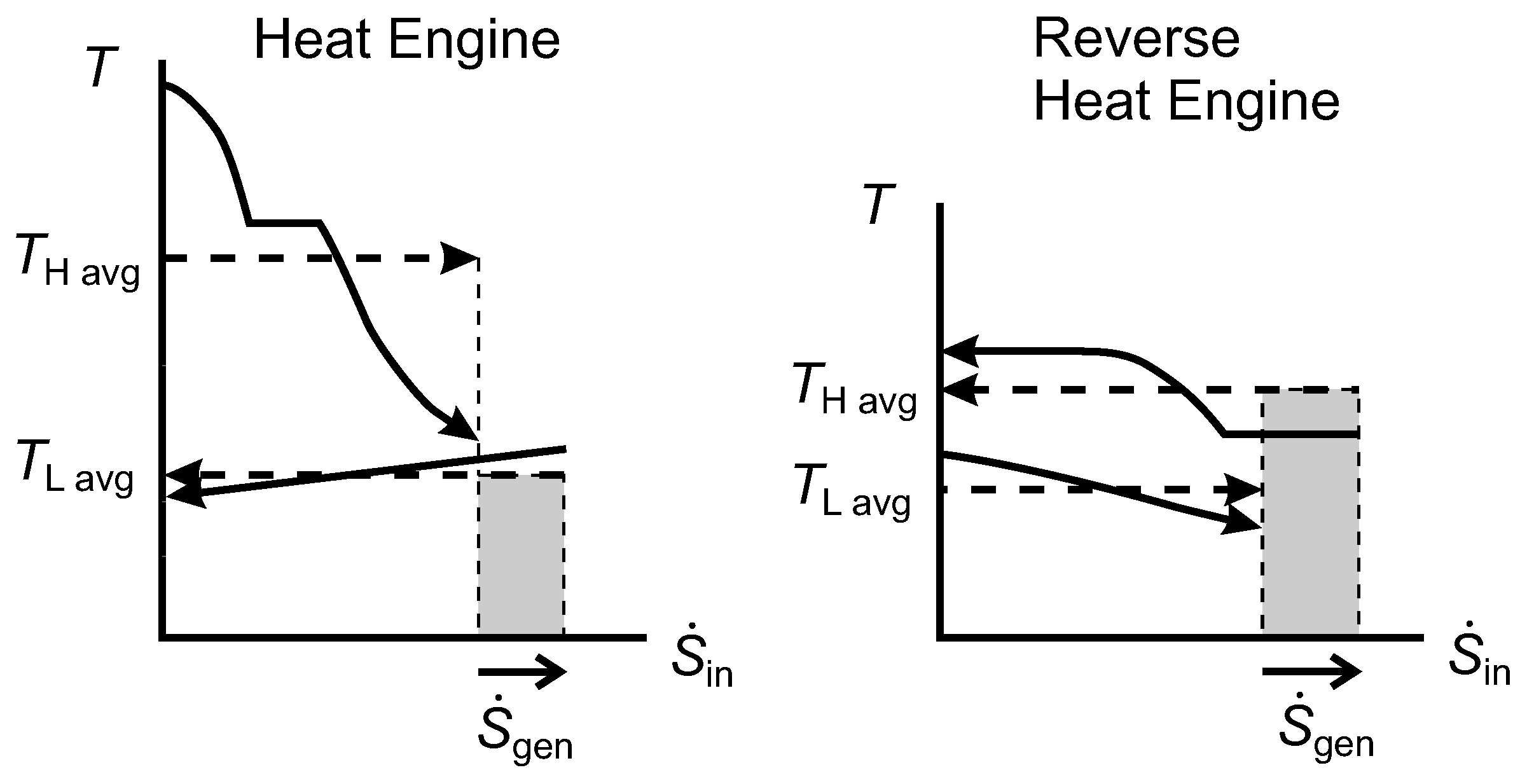
2.9. Lost Work Rate and the Diagram
Figure 9 shows
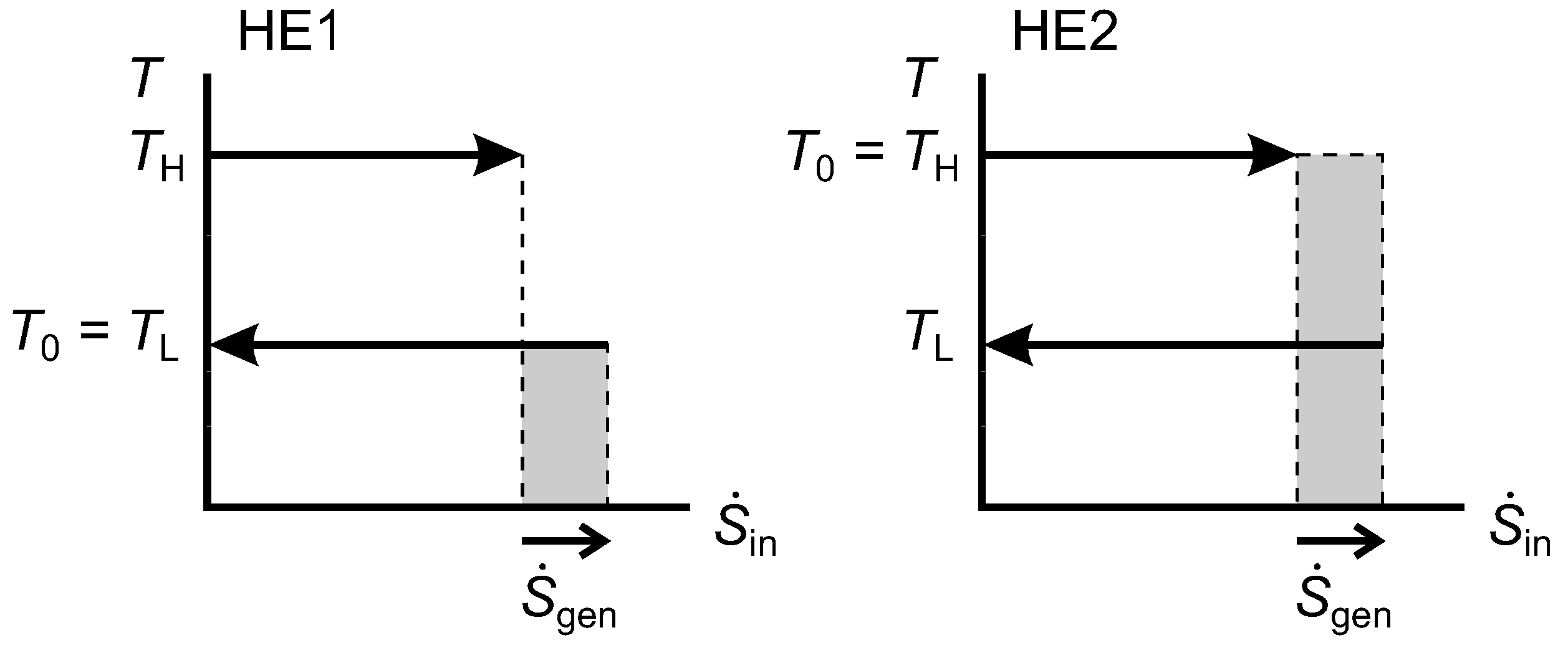
diagrams for an irreversible HE1 and an irreversible HE2 that each have one isothermal source and one isothermal sink. In both cases, the width of the shaded area gives the rate of entropy generation, which is positive. For HE1, we can show that the shaded rectangle is the lost work rate, as follows:
Figure 9.
Diagrams for an irreversible Heat Engine 1 (HE1) and an irreversible HE2.
Figure 9.
Diagrams for an irreversible Heat Engine 1 (HE1) and an irreversible HE2.
For HE2, the same expression for
applies, and we can obtain
using Equation(
29). Hence,
and we note that this is equal to the shaded area for HE2.
From Equation (
31) for both HE1 and HE2, we see that
(the shaded area shown for HE1) and that
(the shaded area shown for HE2). In HE1, the reservoir at
is the environmental thermal reservoir, so
would correspond to
in our notation for
Figure 3, while
would correspond to
. In HE2,
is the environmental temperature and
would correspond to
.
Similarly, for the reverse heat engines represented in
Figure 10, we show that the shaded region for RHE2 is equal to the lost work rate for it.
Figure 10.
Diagrams for an irreversible Reversed Heat Engine 1 (RHE1) and an irreversible RHE2.
Figure 10.
Diagrams for an irreversible Reversed Heat Engine 1 (RHE1) and an irreversible RHE2.
For RHE1, the same expression for
applies, and we can obtain
using Equation (
29). Hence,
and we note that this is equal to the shaded area for RHE1.
We note three special or limiting cases of the diagrams in
Figure 9 and
Figure 10. They do not pose any difficulties for the methodology, but is is helpful to be aware of them.
A reverse heat engine can operate between thermal reservoirs at
and
, but with only an infinitesimal heat transfer rate at
(regarded as a highly irreversible refrigerator), or at
again when
(regarded as a highly irreversible heat pump),
Figure 10.
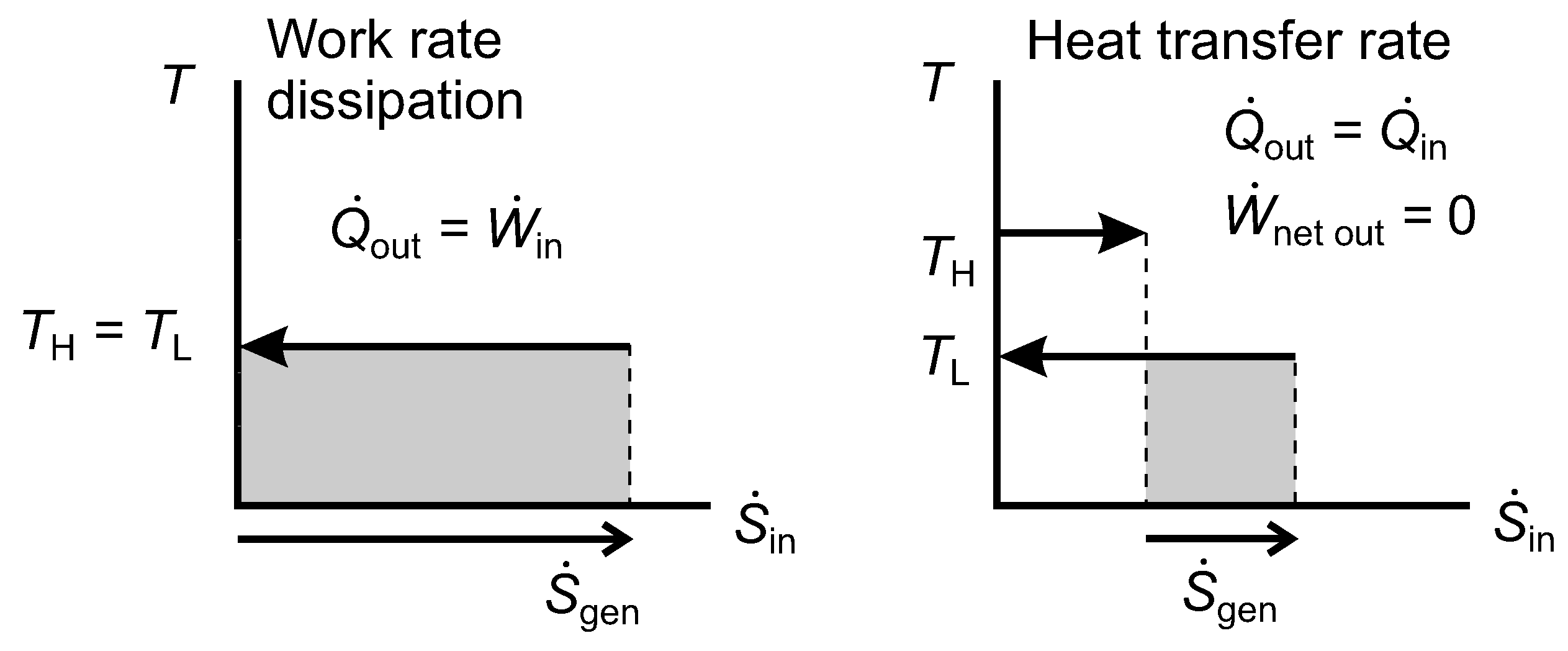
There can be a net rate of work input accompanied by a corresponding net rate of heat rejection at
, e.g., a brake or a churn;
Figure 11, work rate dissipation.
There can be internal heat transfer through the system in the direction from the hotter surface to the colder one with zero net work output (a thermal resistance);
Figure 11, heat transfer rate.
Externally, case 2 is infinitesimally different to case 1. Internally, the systems would differ. The highly irreversible heat pump or refrigerator would maintain a thermal gradient within the system, and part of the exergy destruction rate would be associated with internal heat conduction through that gradient, the remainder being associated with irreversibility in the reverse heat engine, also giving rise to internal heat conduction. In a fluid brake or dry friction brake, the exergy destruction rate would be associated with mechanical friction, giving rise to internal heat conduction. In an eddy current brake, the exergy destruction rate would be associated with electrical resistance, also giving rise to internal heat conduction.
Figure 11.
Diagrams of temperature versus entropy transfer rates for irreversible work rate dissipation, as in a brake, and heat transfer rate in a thermal resistance.
Figure 11.
Diagrams of temperature versus entropy transfer rates for irreversible work rate dissipation, as in a brake, and heat transfer rate in a thermal resistance.