1. Introduction
Determining the location of a sound source from subtle differences in intensity and/or temporal information,
i.e., sound localization, is crucial to the survival of many species and in human communication. In particular, the ability to detect the location from random signals with a fine temporal precision is essentially important for the extraction of such a kind of spatial information [
1]. The superior olive complex (SOC) in mammals is a center for sound localization and includes the medial superior olive (MSO) for interaural time difference (ITD) and the lateral superior olive (LSO) for interaural level difference (ILD) [
2]. This means that the SOC receives information from both ears. One group of nerve fibers innervating SOC comes from the spherical bushy neuron of the anteroventral cochlear nucleus (AVCN), preserving fine temporal information for ITD detection.
For a greater temporal precision, the spherical bushy neuron receives a supra-threshold stimulus coming from a couple of auditory nerve fibers (ANFs) onto the soma with a special morphology of pre-synapses, an endbulb of Held [
2–
4]. Moreover, the spherical bushy neurons not only have high-threshold potassium channels, but a different kind of potassium channel,
i.e., low-threshold potassium channels, to sharpen the waveform of action potentials [
5].
Nevertheless, a high level of spontaneous random activity has been observed in auditory brain stem nuclei in the absence of a sound stimulus [
6,
7]. Liberman has suggested that fibers with different spontaneous rates have different ascending projections in the cochlear nuclei [
8,
9]. However, it was still unknown why spontaneous random activity was observed in the cochlear nuclei,
i.e., a functional role of spontaneous random activity.
In recent years, it has been reported that spontaneous random activity, which occurs even in the absence of a sound stimulus, was beneficial to sound information transmission in inner hair cell synapses within the framework of some sort of stochastic resonance (SR) phenomena [
10]. In the literature, the authors have proposed a different type of SR that depends on the rates of spontaneous random activity more than the regular SR, which is a phenomenon observed when deterministic and random dynamics in some non-linear systems are coupled [
11–
18]. However, whether spontaneous random activity is beneficial to information transmission in the spherical bushy neuron of the AVCN that projects to the MSO for ITD detection with a microsecond temporal precision is still unclear.
In this paper, we test our hypothesis that spontaneous random activity can better enhance information transmission when the intensity of sinusoidal functions is set at a smaller value, i.e., a weaker sound level, within the framework of some sort of SR phenomena. We used computer simulations to investigate, from the information-theoretic perspective, how the resonance phenomenon that depends on the spontaneous spike rates can be observed when the intensity or frequency of sinusoidal functions is varied and the number of sodium channels (randomness) is varied. That is, our approach is based on computational neuroscience, using the information rates estimated from the entropy of inter-spike intervals (ISIs).
The neuron model used in the present paper was a stochastic version of the Hodgkin–Huxley (HH) model, which generated temporal jitter in response to identical stimuli [
19–
24], unlike the original HH model [
25]. A preliminary result was reported in the conference proceedings [
26,
27].
2. Methods
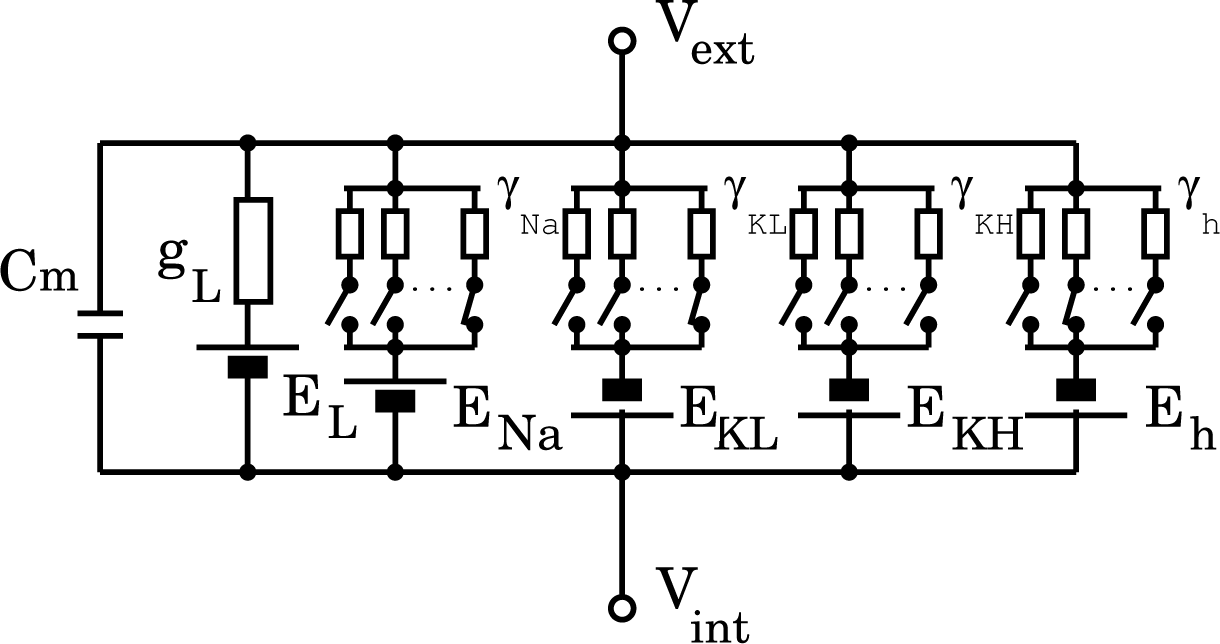
A spherical bushy neuron soma was represented by a single-compartment model in which the diameter of the soma,
d, was set at 21
μm and the capacity of cell membranes was 0.9
μF/cm2 [
28]. The modified Hodgkin–Huxley model consisted of four types of ion channels of sodium (Na) and high- and low-threshold potassium (KH, KL) and cation channels (h) with stochastic ion channel models. KH, KL and h channels play an important role in helping stabilize rhythmic responses to sinusoidal functions; the KH channel accelerates a repolarization phase; the KL channel shortens the membrane time constant; and the h channel stabilizes the resting membrane potential by lowering the membrane resistance [
28,
29]. The electrical equivalent circuit of the neuron model is shown in
Figure 1. The transmembrane potentials,
Vm(
t), the difference between extracellular and intracellular potentials, can be expressed by Kirchhoff’s current law as a function of time:
in which a scaling factor of 2 was adopted according to the literature [
28], and the resting potential,
Erest, was set at −65 mV, and where:
in which
Nx(
t) denote the number of open channels of each type (
x = Na, KL, KH, n, p, h). Each ion channel follows the discrete-state Markov processes with eight states for sodium channels, ten states for low-threshold potassium channels, six (3 × 2) states for high-threshold potassium channels and two states for cation channels. These channels were implemented by the channel number tracking algorithm [
23].
Equation (1) was solved numerically in terms of
Vm(
t) with the Runge–Kutta method [
30].
The state transition rate was multiplied by a value of 1/0.17, so that the temperature can be set at 38°C, where
ENa = 55 mV,
EK = −70 mV,
Eh = −43 mV, and
EL = −65 mV, according to the literature [
5]. The single conductance was expressed as follows:
where the parameters were set as follows:
Ssoma = 4
π(
d/2)
2,
,
,
,
,
,
ρNa = 6 channels/
μ m
2,
ρK = 2 channels/
μ m
2,
i.e.,
,
,
,
The number of channels was varied to investigate how the randomness of ion channels (intrinsic fluctuations) could affect information transmission, being set at
, 27,708 (
ρNa = 20), 83,126 (
ρNa = 60) and 166,253 (
ρNa = 120), given that the neuron model was asymptotically close to being deterministic as the number of channels increased.
The excitatory synaptic current
IANF (
t) ascending from the primary auditory nerve fiber was modeled as a filtered inhomogeneous Poisson process, assuming that refractory period was small enough, as:
where the equilibrium potential of excitatory synapses was set at
Ee = 0 mV, and the synapse conductance waveform was the alpha function expressed as:
where the time constant was set at
τe = 0.1 ms [
28] and the excitatory synaptic equilibrium potential was set at
Ee = 0 mV. The excitatory synaptic conductance,
, was set such that the excitatory synaptic current could become supra-threshold stimuli,
i.e., the firing efficiency (FE), defined by the number of spike firings divided by the number of stimulus presentations, could take a value of 1.0, accordingly
[
28]. This is because the objective of the present study is to investigate how spontaneous random activity can better enhance information transmission when the excitatory synaptic current stimulus is supra-threshold. We note that inhibitory synapses are not incorporated in this study, because pre-synaptic vesicle secretion is assumed to elicit post-synaptic spikes, although GABAergic and glycinergic synapses have been found in the descending pathway from sub-nuclei of the SOC to the cochlear nucleus [
31].
NANF (
t) in
Equation (4) denotes the counting process of an inhomogeneous Poisson process [
32], described by the following intensity function:
where the intensity function is modulated by the sinusoidal function:
where
λspon was varied as 5, 10, 25, 50, 75, 100 and 125 s
−1,
λc = 100, 200, 400 or 800 s
−1 and
f = 220, 880, 1760 or 3520 Hz, so as to investigate the dependency of sound intensity (
i.e.,
λc), as well as frequency characteristics within the human speech spectrum. In representing units, we note that the intensity or rate of temporal events randomly occurred according to an inhomogeneous Poisson process has units of
s−1,
i.e., counts per unit time, while the frequency of periodic sinusoidal function has units of Hz,
i.e., cycle per second.
The information rate of the spike trains was estimated to quantitatively evaluate information transmission by calculating the total and noise entropy, based on the ISI of the adjacent spike firing times,
T, in which the renewal point process [
32] was assumed, as follows [
33–
36]:
where
R denotes the spike firing rate (
i.e., the number of spike firings per unit time), and the total entropy of the ISI is expressed as:
and the noise entropy of the ISI is expressed as:
given the condition of the stimulating current,
IANF (
t), sampled from 30 realizations with the different sinusoidal phases generated by pseudo-random numbers between 0 and 2
π.
p(
Ti) and
p(
Ti|IANF (
t)) as a function of discrete intervals (bin),
Ti, denote the probability of the ISI and conditional probability of the ISI on the
IANF (
t), whereas in practical situations, the probability as a function of
Ti was estimated from the ISI histogram with a bin width of 0.5 ms.
E[ ] denotes the expectation operation, but in practical situations, 30 samples were averaged to calculate the noise entropy given the 30 sample realizations of
IANF (
t).
3. Results
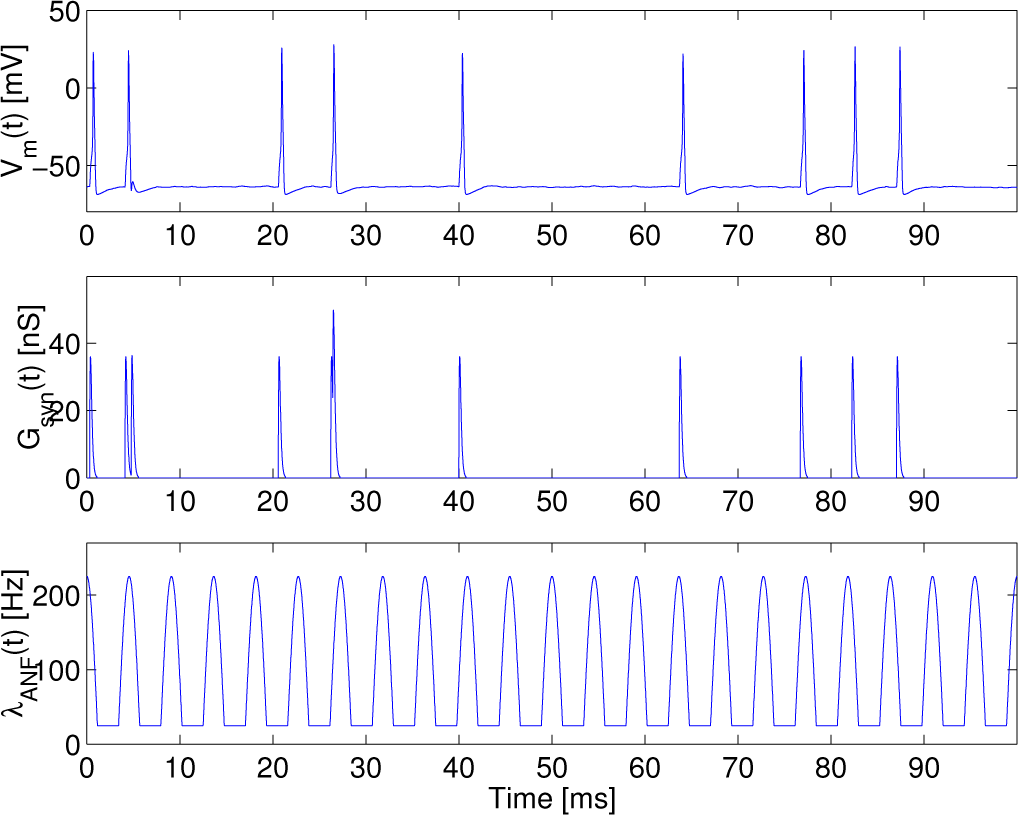
The transmembrane potential, the conductance of the excitatory synapse and the intensity function of an inhomogeneous Poisson process are depicted as a function of time in
Figure 2, when the synaptic conductance is set such that the synaptic current can become the supra-threshold stimulus, at
λc = 200 s
−1 and
f = 220 Hz.
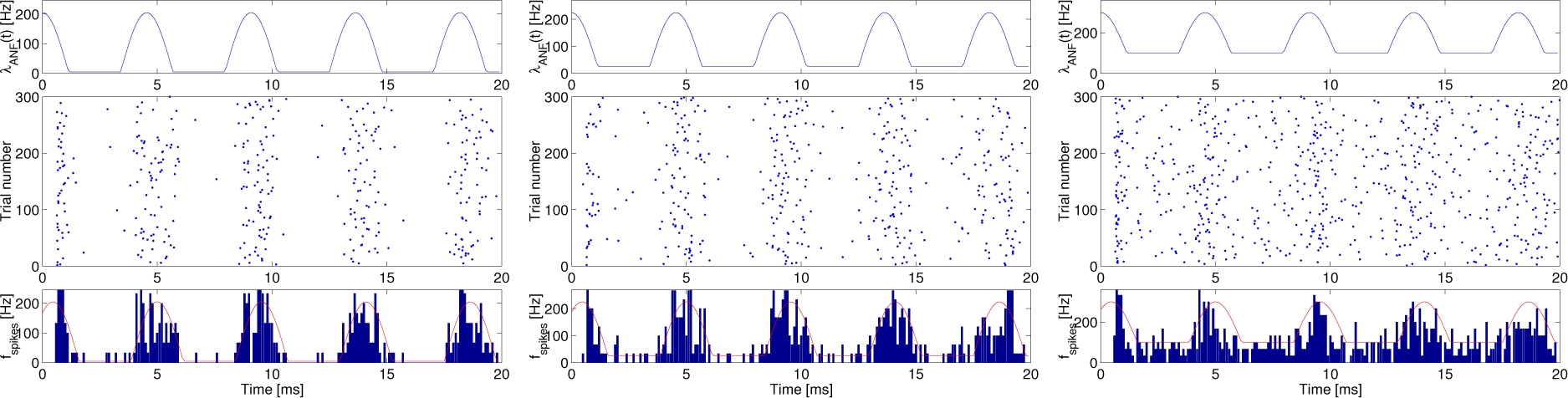
Figure 3 shows an intensity function (top), a raster plots of 300 realizations (middle), the post-stimulus time histogram (PSTH) as the estimated spike firing rates superimposed on the genuine value of the intensity function (bottom) as a function of time for 20 ms in the time length at
λspon = 5 (left), 25 (middle) and 100 (right) s
−1,
λc = 200 s
−1 and
f = 220 Hz.
The raster plot and PSTH can give us insight into a qualitative impression of a functional role of spontaneous random activity; however, they may not provide any quantitative evaluation. Instead, in order to do so, we adopted the information rates of the spike trains in response to the synaptic currents, driven by the primary auditory nerve.
The information rates were estimated by multiplying the mutual information to the spike firing rates according to
Equations (8)–
(10) in which the mutual information was estimated from observations of the ISI histograms, as the spontaneous rates,
λspon, were varied to 5, 10, 25, 50, 75, 100 and 125 s
−1.
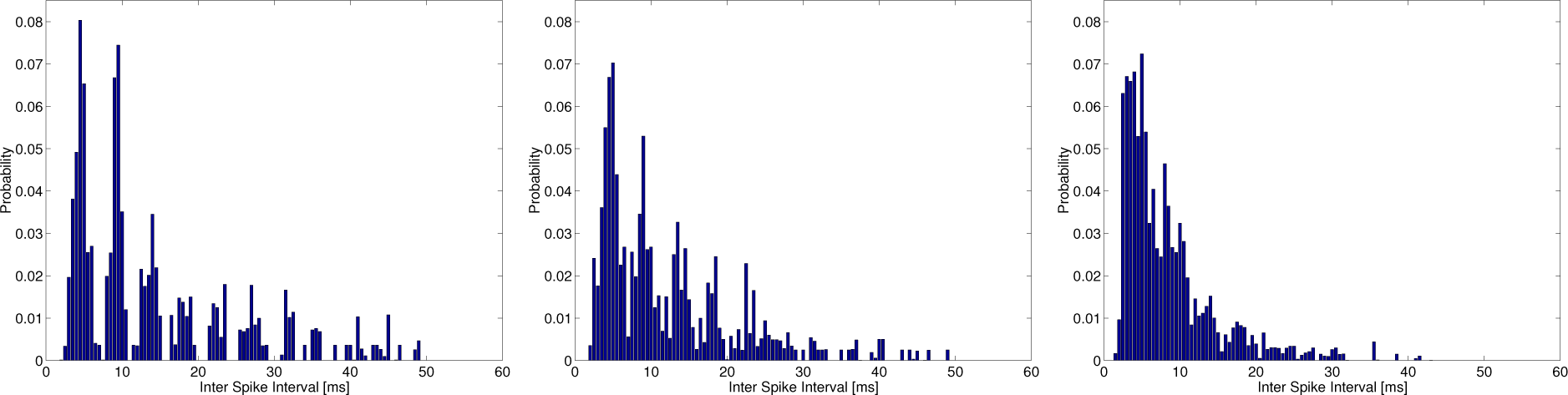
Figure 4 shows the typical ISI histograms used in estimating the total entropy at
λspon = 5 (left), 25 (middle) and 100 (right) s
−1 at
λc = 200 s
−1,
f = 220 Hz. The ISI histogram in the middle trace of
Figure 4 is similar to that observed in the cat primary auditory nerve [
37] and may comprise both random and periodic ISIs, since the intensity function in
Equations (6) and
(7) is composed of not only sinusoidal functions,
, but a constant value,
λspon, that generates the spontaneous random activity being modeled as a homogeneous Poisson process. However, the ISI histogram in the left of
Figure 4 is only composed of periodic ISIs.
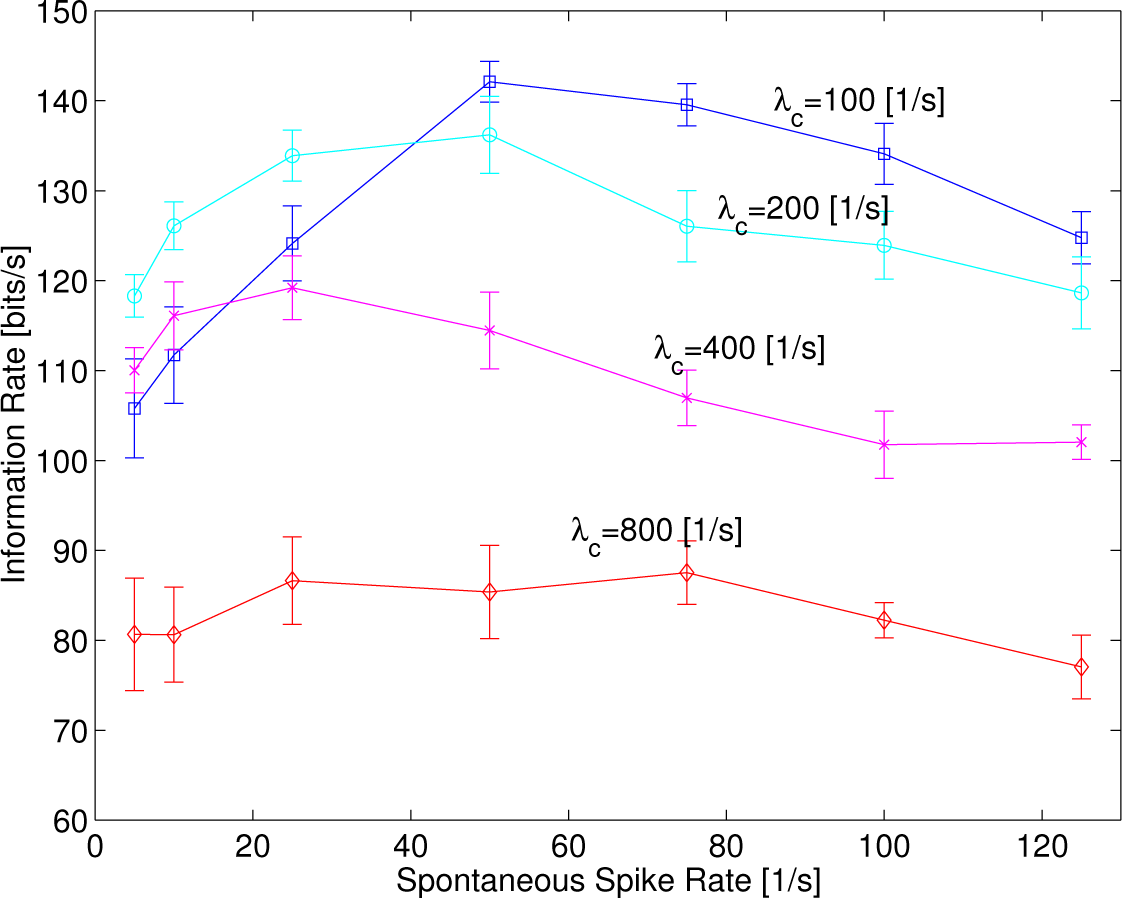
The mean of information rates estimated from five samples with error bars of the standard deviation is depicted in
Figure 5 as a function of the spontaneous rate
λspon in which the intensity of sinusoidal functions,
λc, is varied to 100, 200, 400 and 800 s
−1 at
f = 220 Hz.
The information rate increased, reached a maximum and then decreased as the spontaneous rate increased, like a typical curve of the regular SR, in which
λc = 100, 200 and 400 s
−1, while the sharpness of convex curves tended to decrease as
λc increased. This implies a resonance phenomenon that depends on the spontaneous rates, like those shown in [
26]. The maximum value of the information rates around
λspon = 25–50 s
−1 decreased as
λc increased. Eventually, the resonance curve disappeared in which
λc = 800, suggesting that spontaneous random activity did not work at all. The results show that random spontaneous activity can better help enhance information rates at a smaller intensity of sinusoidal functions,
λc,
i.e., a weaker sound signal.
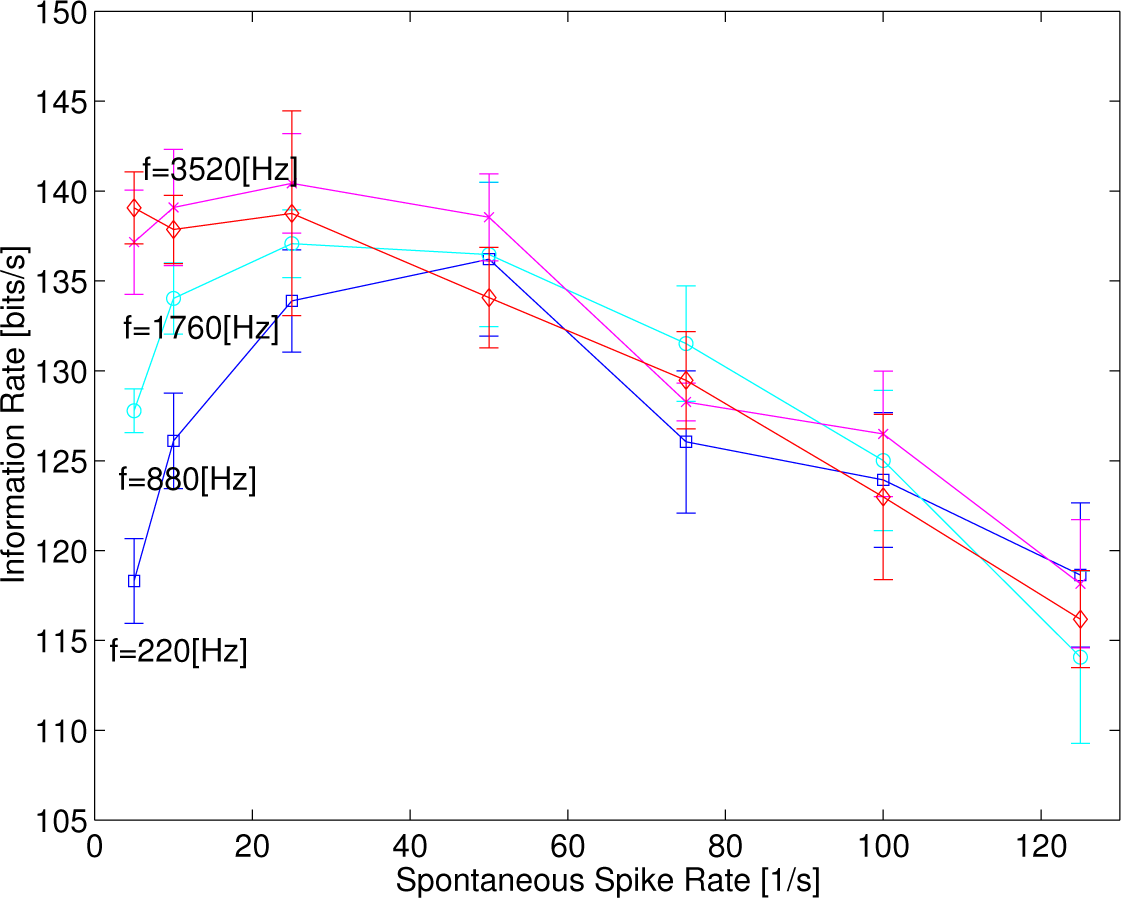
Figure 6 depicts the information rates as a function of the spontaneous rates at four different kinds of frequency of sinusoidal functions, 220, 880, 1760 and 3520 Hz at
λc = 200 s
−1, showing that the sharpness of convex curves tends to decrease as the frequency of sinusoidal functions increases. Eventually, the information rates decrease monotonically when
f = 3520 Hz, due possibly to the phase-locked responses disappearing.
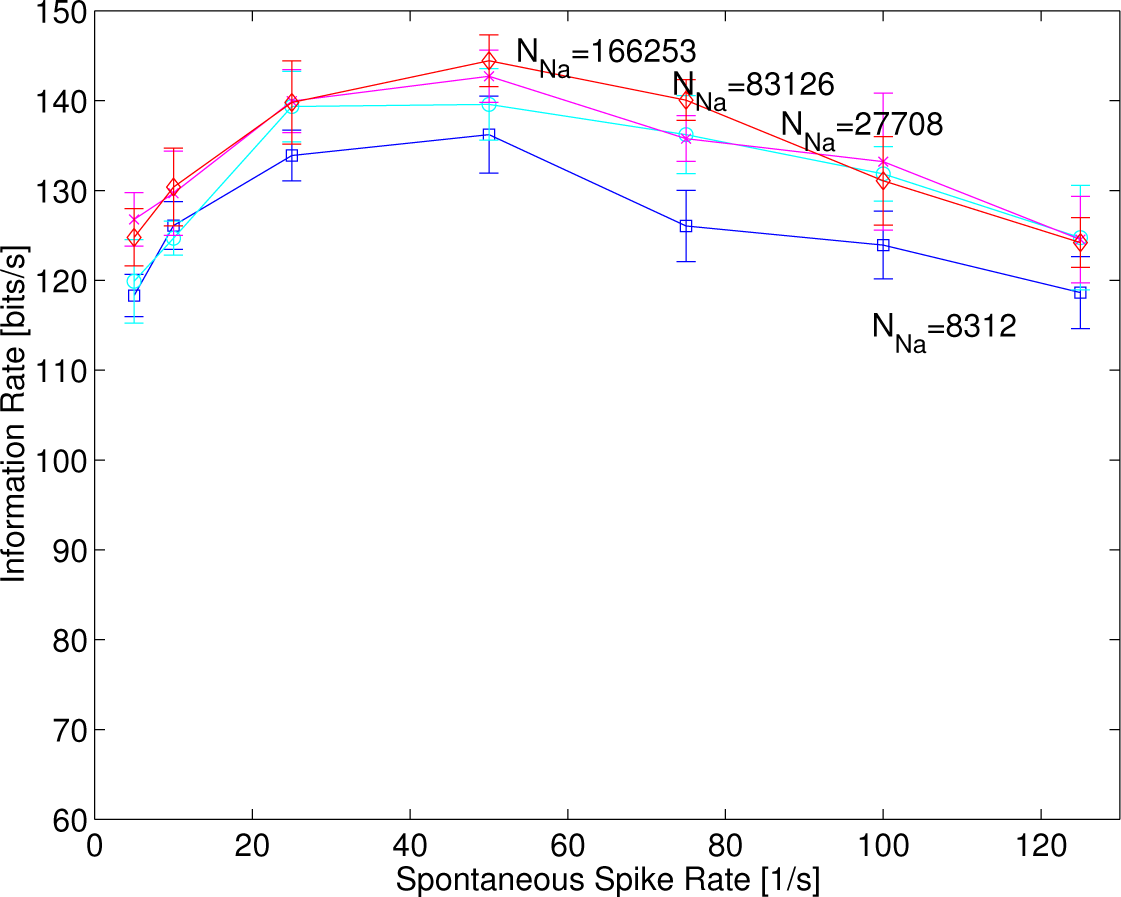
In order to investigate how much the stochasticity or randomness of ion channels affects some of the stochastic resonance with supra-threshold stimuli, the number of sodium channels was varied to 8312, 27,708, 83,126 and 166,253. This is because increasing the number of sodium channels lets the stochastic HH model approach asymptotically the deterministic original HH model, which cannot generate temporal jitter in response to identical stimuli at all. In
Figure 7, the resonance curves are observed, although the curve of 8312 was slightly smaller than those in others. This shows that the stochasticity or randomness of ion channels (intrinsic fluctuation) affects some of the stochastic resonance phenomenon less, which depends on the spontaneous rates, implying that some sort of stochastic resonance with supra-threshold stimuli was created by the randomness of the synaptic current events (extrinsic fluctuation).
4. Discussion
In the present paper, it was shown using computer simulations on the basis of a biophysically-realistic model of spherical bushy neurons stimulated by the supra-threshold synaptic currents that spontaneous random activity was able to better enhance information transmission, when the intensity of sinusoidal functions was set to a smaller value, i.e., a weaker sound level. The results also showed that this sort of resonance phenomenon was able to better enhance information transmission at a lower frequency of sinusoidal functions within a specific frequency range that gave a rise to the phase-locked responses, i.e., the first or second formant frequency of speech. This may imply support for our hypothesis that spontaneous random activity functions beneficially in information transmission within the framework of some sort of SR phenomena.
The resonance phenomenon of the information rates as a function of
λspon observed in the present study seems like a supra-threshold stochastic resonance (SSR) [
38–
41] as a function of the intensity of a Gaussian white noise, because the current applied is a supra-threshold stimulus. The synaptic current could be approximated by the Gaussian white noise; if the synaptic current having a smaller value of the time constant were small, the frequency of synaptic vesicle secretion would be large, such that the voltage fluctuation could not be so large (it is diffusion approximation: [
42–
46]). However, the structure or configuration of the neuron model in this sort of resonance phenomenon is quite different from that of the regular SSR, since the spherical bushy neuron model used is constructed by a single neuron, unlike a population or an array of neurons in the regular SSR. If the spontaneous random activity of the supra-threshold stimulus can be regarded as an extrinsic fluctuation, this sort of resonance phenomenon that depends the spontaneous rate in a single neuron structure can be classified into the SSR phenomena. Furthermore, this sort of resonance phenomenon with the supra-threshold stimulus seems to be categorized into the regular SR phenomenon, which helps enhance a weak sub-threshold stimulus, because this phenomenon can significantly enhance information transmission when the intensity of sinusoidal functions is set at a smaller value,
i.e., a weaker sound level, as is shown in
Figure 5.
It is likely that the stochasticity or randomness of the supra-threshold synaptic current events modeled by an inhomogeneous filtered Poisson process,
i.e., an extrinsic fluctuation, makes it possible to create this sort of resonance phenomenon, since a change in the number of ion channels of the stochastic HH model,
i.e., an intrinsic fluctuation, makes an alteration in the characteristics of the resonance curves less, as is shown in
Figure 7. That is, the stochastic ion channels of our model used in the present study contribute less to this sort of emerging resonance phenomenon, although they play an important role in generating temporal jitter in response to identical stimuli and likewise in computing the noise entropy from the spike trains.
It may follow from our results and the implications discussed in [
6–
9] that this sort of resonance phenomenon, which depends on the spontaneous rates, is adopted for a reliable synaptic transmission from an endbulb of Held pre-synapse to the post-synaptic neuron of spherical bushy cells with a fine temporal resolution. This is because any sub-threshold stimulus that yields extrinsic fluctuations cannot be squeezed into the spherical bushy neuron, due to the specific morphology of the endbulb of Held pre-synapse, unlike that in other synapses of the central nervous system. Likewise, it may be easy to imagine that this sort of resonance phenomenon can be used, as well, for the calyx of Held, which reliably transmits information on the sound level with a greater intensity resolution into the post-synaptic neuron of the medial nucleus of the trapezoid body (MNTB) that projects to the LSO for ILD detection.
In recent years, novel research regarding binaural cochlear implants, so as to not only improve the quality of speech recognition beyond that of monaural cochlear implants, but to better perform sound localization, has been reported by Delgutte [
47]. It follows from the findings presented in this paper that an appropriate value of the spontaneous spike rates, likewise, may help better determine the location of a sound source in binaural cochlear implants, giving rise to maximizing information transmission. The traditional understanding suggested by Liberman [
6–
9] must imply that a high level of spontaneous activity, even in the absence of sound stimuli, plays a pivotal functional role in information transmission for sound localization, like that artificially generated with a pulsatile stimulus developed in monaural cochlear implants.