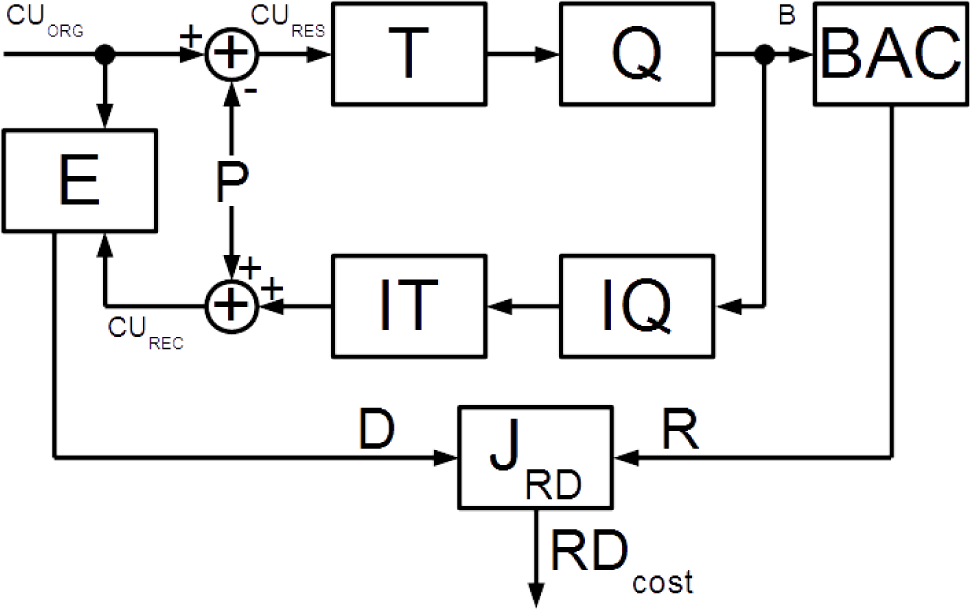
As soon as the separate context probability models are used for arithmetic coding of data B, the entropy of the symbols of different syntax groups should be handled separately. Generally, rate R estimation of data B can be divided into rate estimation of splitting information, prediction information and transformed residual information.
3.2. Prediction Data Rate Estimation
The information on intra-prediction also contains the indication of the CU partitioning on prediction units or PUs. Each PU is a region of pixels on a video frame to perform the single type of prediction. PU indicates the intra-prediction mode for luma and chroma samples separately.
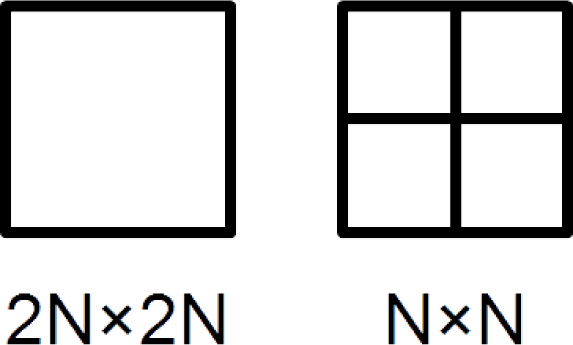
In the case of intra-prediction, there are two possible CU partitions of PUs: 2
N × 2
N or
N ×
N (
Figure 3). The 2
N × 2
N partitioning forms one PU with the size of the CU, while the
N ×
N partitioning forms four PUs with half the size of the CU being split. However, the
N ×
N intra-partitioning is only possible for the bottom-level CU of a minimal size within the given coding configuration.
The minimum size that the CU can have is 8 × 8 pixels. In the case of 2N × 2N partitioning, one PU covers the whole 8 × 8 CU, and in the case of N × N partitioning, four 4 × 4 PUs cover the 8 × 8 CU. It is also possible to restrict the minimum CU size to 16 ×16 or even 32 × 32, but this configuration does not find real applications.
The arithmetic coding of CU partitioning makes sense only for the CUs at the bottom level of the partitioning quadtree, i.e., 8 × 8 CUs. The SBAC codes one context-dependent symbol to indicate the PU partition mode. The value of one indicates the 2N × 2N partitioning, while the value of zero indicates the N × N partitioning.
Prediction data stored in a PU specify the intra-mode used for the prediction of luma samples within the PU. There are a total of 35 possible intra-prediction modes. Without arithmetic coding, the indication of the chosen intra-prediction mode would take six bits in the bitstream.
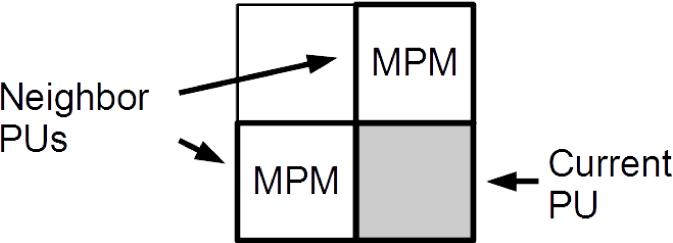
The SBAC distinguishes intra-prediction modes from the most probable modes (MPM) and the rest. To simplify the presentation of the arithmetic coding, we will refer to those that are “not MPM” as the least probable modes or LPM.
A list of MPM contains three elements. Generally, the MPM list depends on whether the left and the above neighbor PUs (
Figure 4) are available for the current PU. Their intra-prediction modes form two elements of the MPM list. Unavailable neighbor PUs or neighbor PUs with inter-prediction are substituted with the DC predictor. The derivation process for the rest of elements in the MPM list can be found in [
13].
The arithmetic coding of the PU intra-prediction mode starts with the context-dependent bin. When this bin is equal to one, the intra-prediction mode is included in the MPM list. When the bin is equal to zero, the intra-prediction mode is LPM. It takes 1–2 bypass bins to code the index of the corresponding intra-mode in the MPM list. In the case of LPM, it takes five bypass bins to code the remainder of the intra-prediction mode: given that the selected prediction mode is not one of the three MPM modes, only 35 − 3 = 32 = 25 possible modes are left.
It is not a problem to count the number of bypass-coded bins that directly corresponds to the number of bits in the coded sequence. At the same time, the accurate entropy estimation for the context-dependent bin is of a high value.
Intra-prediction of chroma samples is performed separately from the prediction of luma samples. Intra-prediction for chroma planes is indicated by the first PU in a CU in the case of 4:2:0 subsampling. However, the chroma intra-prediction mode depends on the one chosen for luma prediction and is indicated in the corresponding syntax element of the H.265/HEVC video sequence [
13]. The first bin of this syntax element is context-dependent. The value of zero unambiguously means that the chroma intra-prediction mode is identical to the luma intra-prediction mode of the first PU within a CU and that no other bins follow. The value of one means that the chroma intra-prediction mode is different from the luma intra-prediction mode. In this case, its value can be planar, DC, vertical, horizontal or vertical down-left (Mode 34) [
13]. In the latter case, the context-dependent bin is followed by the two bypass-coded bins.
We collected statistics on the average self-information of the described context-dependent bins with the HM v.13.0 [
10] reference encoder and JCT-VCtest video sequence set [
14,
15]. Class E* test sequences correspond to the older test set [
15], but we included them in our experiments for the completeness of the obtained results. The average results combined within Classes A–F [
14] of the sequences are given in
Table 1.
Obviously, 2N × 2N is the most probable partitioning mode for the bottom level CU, as soon as the self-information of the corresponding bin value is less than the self-information of the N × N partitioning bin value. On average, the indication of 2N × 2N partitioning takes 0.65 bits in the coded sequence, while the indication of N × N partitioning takes 2.06 bits. However, on several video sequences, the situation is different. For the sequences Cactus, Kimono (Class C) and Four People (Class E), N × N partitioning produces less bits per context-dependent bin compared to 2N × 2N partitioning. At the same time, Class C video sequence RaceHorses produces almost an identical number of bits for both partitioning modes. Those video sequences have more details, and 4 × 4-pixel prediction is used more often than in other sequences. Therefore, the obtained estimation of the entropy value when used in RDO will increase the RDcost of 4 × 4 prediction units, and they will be chosen less often. This influence of RDcost might change the frequency of N × N partitioning selection and provide a higher bit rate overhead for the mentioned video sequences.
Algorithm 1.
Estimation of the luma prediction header size.
Algorithm 1.
Estimation of the luma prediction header size.
![Entropy 16 06667f11]() |
The indication of the MPM happens more often for most of the test video sequences, providing the average self-information of the corresponding context-dependent bin equal to 0.58. There are no cases in the test video sequences set for which LPM is more probable. However, the sequences, PartyScene (Class C), RaceHorses, BQSquare and BlowingBubbles (Class D), have almost equal probability of MPM and LPM. The replacement of BAC-based estimation with the precalculated entropy estimation should force the encoder to increase the selection of MPM in the RDO process for those sequences.
The average self-information of the context-dependent bin to indicate the intra-prediction of the chroma plane is 0.36, which means that this value is the most probable and the most commonly used.
Algorithm 2.
Estimation of the chroma prediction header size.
Algorithm 2.
Estimation of the chroma prediction header size.
![Entropy 16 06667f12]() |
It looks reasonable to substitute the arithmetic coding of the prediction header with the bit counting procedure of bins after binarization. A bit counting of bypass-coded bins consists of counting the number of these bins, as they directly correspond to one bit on the input of SBAC. Bit counting of context-dependent bins is built upon the calculated average self-entropy of the bin values without consideration of the probability states of the context models of the arithmetic coder itself.
The algorithm of luma intra-prediction bit counting is given in
Algorithm 1, while the bit counting algorithm for the intra-prediction of the chroma plane is given in
Algorithm 2.
3.3. Residual Data Rate Estimation
Residual data (
CURES on
Figure 1) is the data left after the subtraction of predicted pixel values from the original pixel values of a coding unit. The residual pixel values are subject to discrete transform and quantization. Residual data coding in HEVC is performed on the level of a transform block (TB). TB is a matrix of transformed and quantized residuals. Its size can be 32 ×32, 16 ×16, 8 ×8 or 4 ×4. The coefficients are scanned in diagonal, horizontal or vertical order depending on the intra-prediction mode (
Figure 5). Any TB is scanned within 4 ×4 sub-blocks. The diagonal scan starts from the bottom right corner and proceeds to the top left corner, scanning each diagonal line in the direction from top right to bottom left. The scan pattern consists of a diagonal scan of the 4 ×4 sub-blocks and a diagonal scan within each of the 4 ×4 sub-blocks [
16]. Horizontal and vertical scans (
Figure 5) may also be applied in the intra-case for 4 ×4 and 8 ×8 TBs. The horizontal and vertical scans are defined row-by-row and column-by-column, respectively, within the 4 ×4 sub-blocks. The scan over the 4 ×4 sub-blocks is the same as within the sub-block.
Transform block coding in H.265/HEVC requires data relegation to eight syntax groups:
Significant coefficient flag (SC);
Significant coefficients group flag (SG);
Last significant coefficient position X (PX);
Last significant coefficient position Y (PY);
“Coefficient value greater that one” flag (G1);
“Coefficient value greater than two” flag (G2);
Coefficients signs (SIGNS);
Remaining coefficient level (RL).
At first, the XY position of the last significant coefficient in a scan order is determined and arithmetically coded (PX and PY). A coefficient group (CG) is defined as a set of 16 consecutive coefficients (corresponds to a 4 ×4 sub-block) in the scan order. A group having at least one non-zero coefficient is considered significant (SG). Second, each group of significant coefficients is coded by flags indicating whether the coefficients are significant (SC), thus forming a map of significant coefficients. Then, for each significant coefficient, a flag indicating whether its absolute value is greater than one (G1) is coded consequently. After that, for the first coefficient with an absolute value greater than one, an additional flag for whether its absolute value is greater than two is coded (G2). To determine the signs of the coefficients, a sign map (SIGNS) is coded. Finally, the remaining values of the coefficients (RL) are coded.
The symbols of each syntax group are coded with a separate probability context, except for SIGNS, RL and part of PX and PY. Those symbols are coded in the bypass mode: the probabilities of symbol 0 and symbol 1 are considered equal; therefore, the usual update of the SBAC state is skipped.
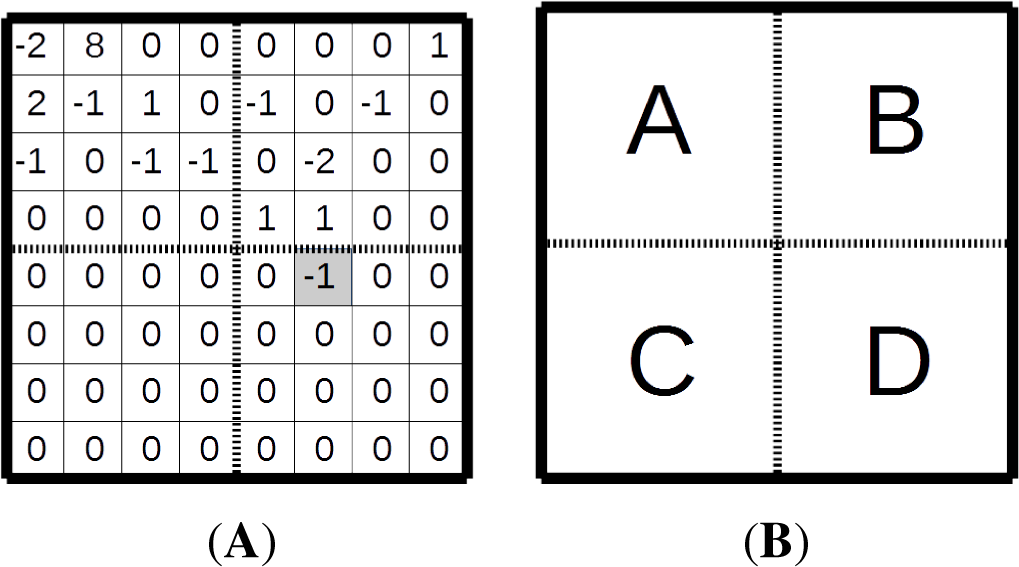
For example, let us consider the arithmetic coding of a sample 8 ×8 matrix of quantized transform coefficients depicted in
Figure 6A. The position (5;4) of the last significant coefficient, −1, is highlighted. It is coded first. Let us assume that the scanning order is diagonal. The TB has four 4 ×4 sub-blocks, A, B, C and D, in
Figure 6B. The first significant coefficient group, Group D, has a non-zero element. The significant coefficients group flag 1 is not coded, as it obviously equals one for the group containing the last significant coefficient. The map of significant coefficients does not include the last significant coefficient and consists of two flags, both zero. The absolute value of −1 is not greater than one; therefore the G1 flag equals zero. The final bin is the sign flag 1 of the coefficient.
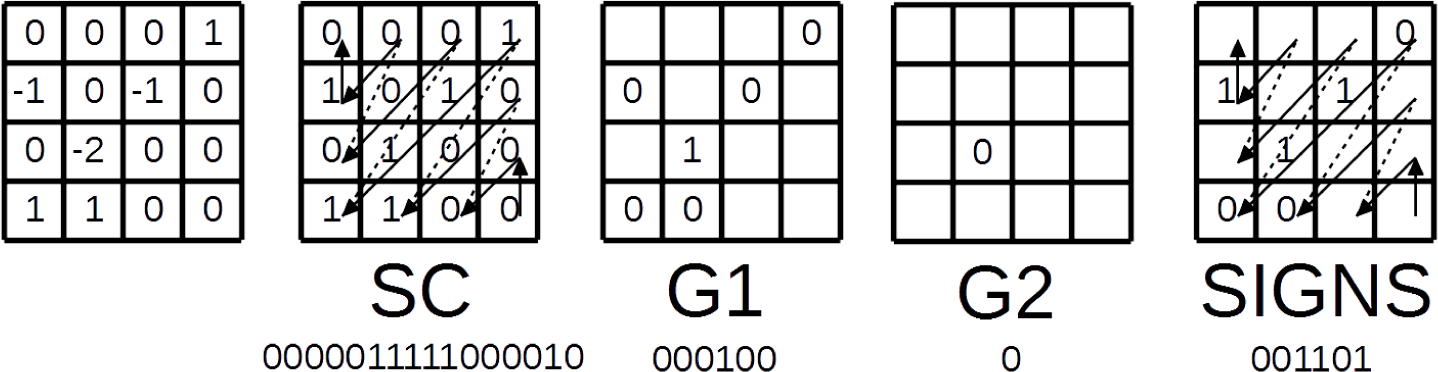
The next CG in diagonal scan order is Group B (
Figure 6B). It has non-zero coefficients; therefore, the SG flag is one. The coding of the map of significant coefficients is illustrated in
Figure 7. SC flag values and the bins on the input of SBAC are shown under the corresponding blocks on
Figure 7. For the significant coefficients, the flags of whether they are greater that one are coded. For this particular block, the G1 bins would be 000100. For the first coefficients greater than one, the G2 flag 0 is coded. Finally, the coefficient sign bins would be 001101.
The next CG in the diagonal scan order is Group C (
Figure 6B). It consists of zero coefficients; therefore, the SG flag is 0, and no more bins are coded for this group.
The coding of Group A (
Figure 6B) has the same order as Group B, so we would skip the detailed description.
The symbols generated to describe residual data are coded with SBAC using a total of seven context groups:
Significant coefficient flag (SC);
Significant coefficient group flag (SG);
Last significant position X (PX);
Last significant position Y (PY);
Coefficient value greater that one flag (G1);
Coefficient value greater than two flag (G2);
Bypass mode (BP)
In fact, each context group has several probability subgroups, but we omit them to simplify the algorithm.
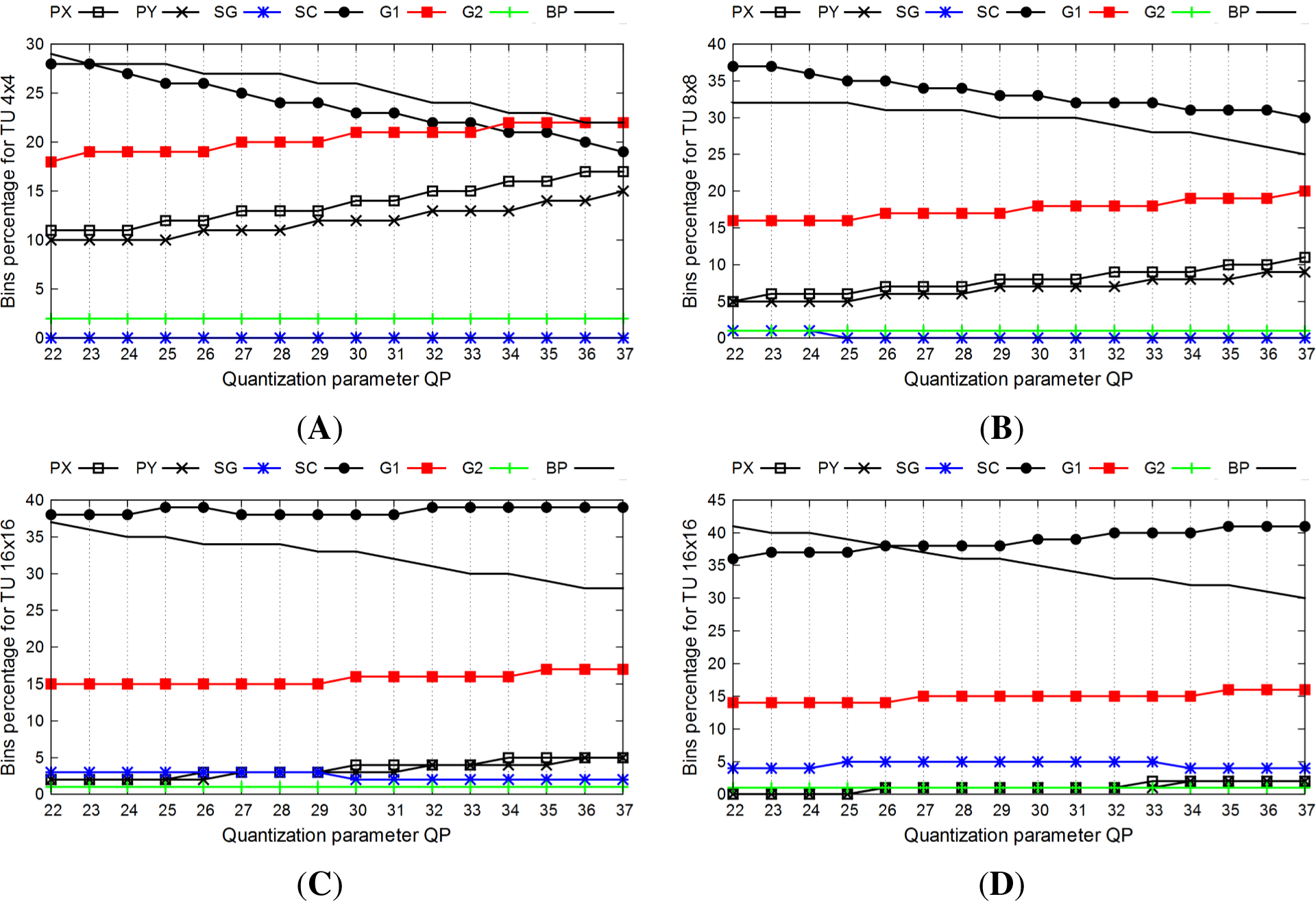
With the HM reference encoder, we collected the statistics on the number of bins by context groups on the input of SBAC for the JCT-VC test video sequences. The results are almost the same for all of the test sequences; therefore, in
Figure 8, we illustrate an example of a bin distribution by context groups for the BasketballDrill video sequence for 4 ×4, 8 ×8, 16 ×16 and 32 ×32 transform units (TUs). The bypass-coded bins and SC bins take most part of the message to arithmetically code: approximately 20–40% each. The higher the block size is, the less the part of the information on the last significant coefficient position taken. On 4 ×4 TUs, almost 20% of the bins are PX or PY. While on the 8 ×8 TUs, this information takes only 10% and even less on the bigger TUs. Furthermore, the percentage of those bins increases with the increase of the quantization parameter.
To get the value of
R, the full arithmetic coding must be performed. We suggest estimating the information entropy
H(
Bi) of the symbols
Bi within the
i–th context group [
4,
17]:
where
pi(
j) is the occurrence probability of the symbol
j ∈
Z, 0 ≤
j ≤ 1 in the message
Bi. Considering that
Ni = S(
Bi) is the total number of symbols in the message
Bi, the estimated bit rate will be:
where
H(
B7) = 1.0 for bypass-coded bins, and seven is the number of context groups.
We compared our estimation
with the real rate value
R(
B) for each estimated block in the HM reference encoder [
10] on the JCT-VC test sequences [
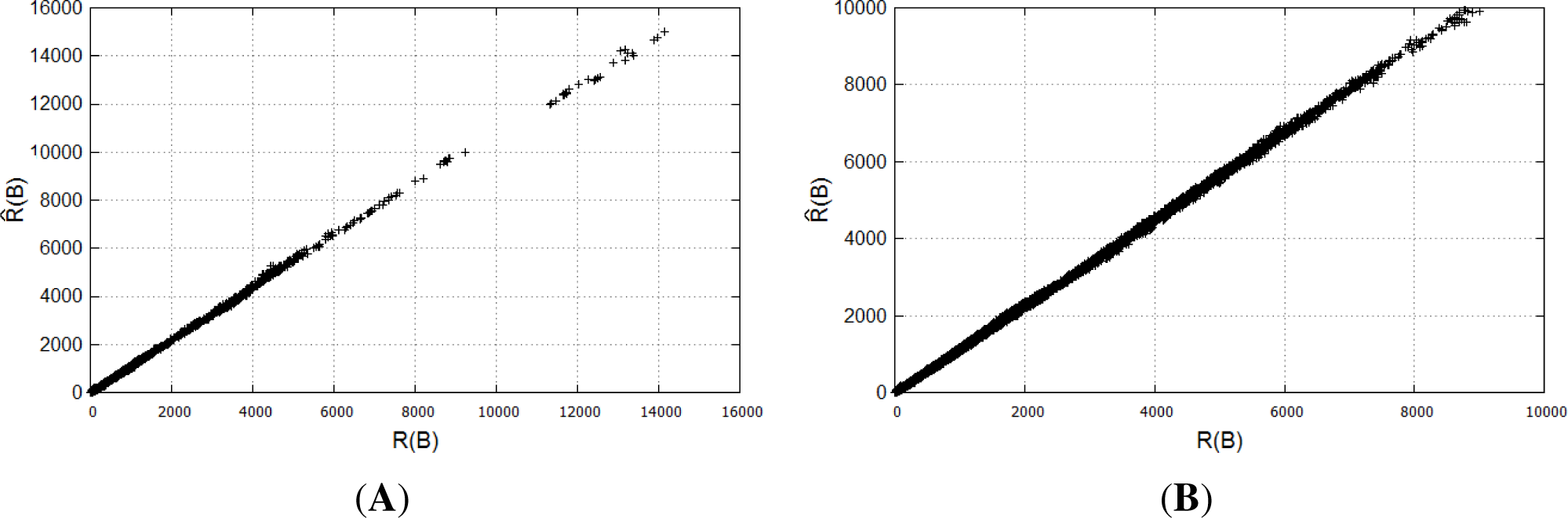
18]. A scatter plot showing the distribution of values
and
R(
B) for the BasketballDrill and PeopleOnStreet test sequences is given in
Figure 9. Estimation of
has almost a linear relation with
R(
B). On the JCT-VC test sequences, we gathered statistics on
R(
B) of a coding unit and its evaluation
. We estimated the correlation coefficient as:
where
is a covariance of
and
R(
B), while
and
σR are the corresponding standard deviations. The correlation coefficient between our estimation
and real value
R(
B) for all test sequences roughly equals 0.999.
A high correlation between the rate evaluation
and the real rate value
R(
B) provides an opportunity to accurately approximate a scatter plot of the rate estimation with a linear dependency
. Approximation parameters
a and
b determine the offset of the evaluation
. We evaluated the average values of the parameters
a and
b for the estimation
on the JCT-VC test sequences. The experiment showed that, on average, the value of
b → 0, and the value of
a ≈ 1.08. With the value of
a not equal to one, we overestimate the real value
R(
B), which is equivalent to the change of the parameter
λ in
Equation (1). Therefore, to compensate for the overestimation, we introduce the normalization coefficient
k =
1/
a = 0.93.