A Note on Distance-based Graph Entropies
Abstract
:1. Introduction
2. Preliminaries
3. Distance-Based Graph Entropies
Definition 1
Definition 2
Definition 3
Definition 4
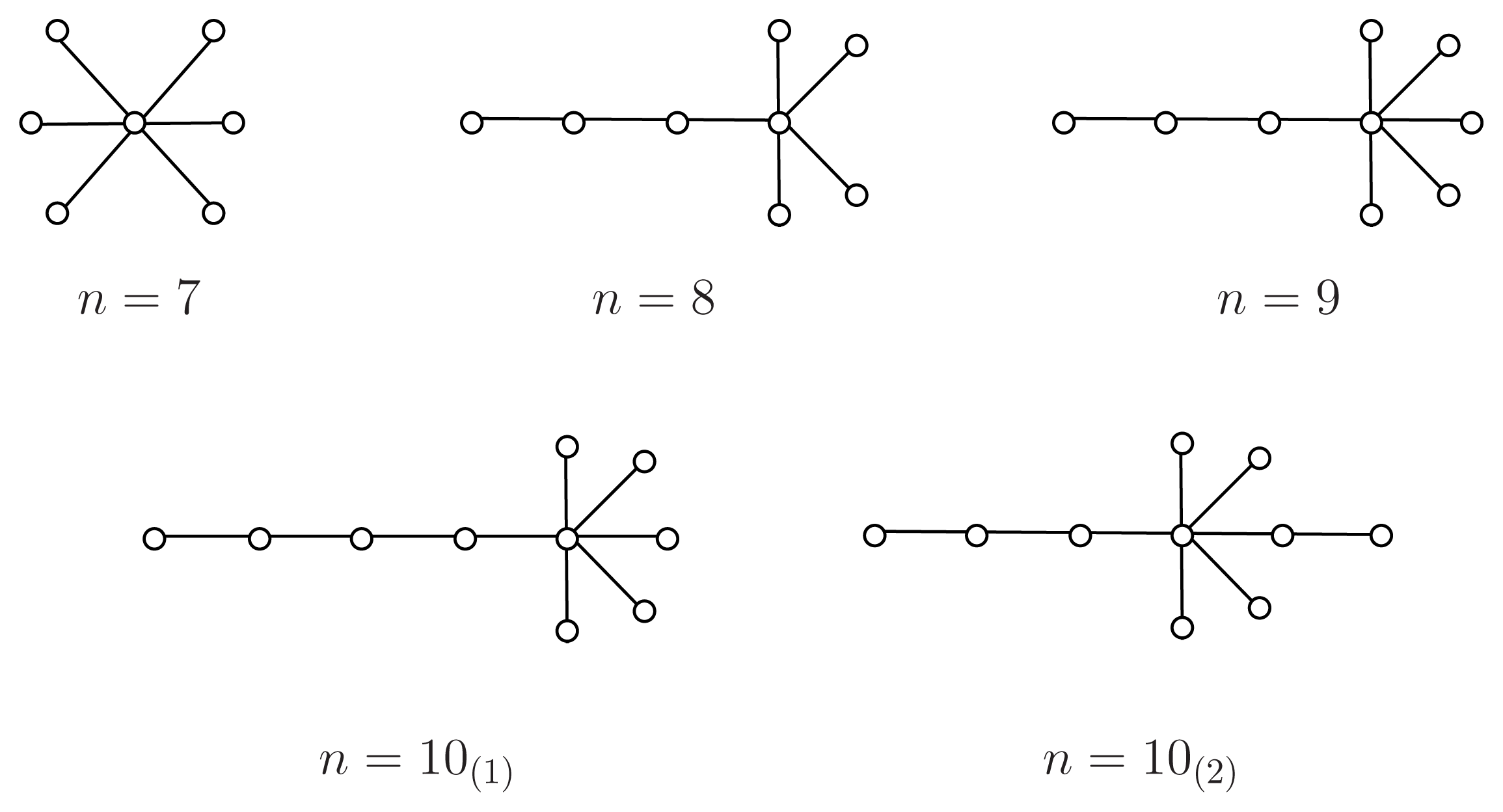
4. Results and Discussion
Proposition 5
Theorem 6
Proof
Conjecture 7
Theorem 8
Proof
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, OH, USA, 1949. [Google Scholar]
- Bonchev, D.; Rouvray, D.H. Complexity in Chemistry, Biology, and Ecology; Mezey,, P.G., Ed.; Mathematical and Computational Chemistry; Springer: New York, NY, USA, 2005. [Google Scholar]
- Bonchev, D. Information Theoretic Indices for Characterization of Chemical Structures; Research Studies Press: Chichester, UK, 1983. [Google Scholar]
- Holzinger, A.; Ofner, B.; Stocker, C.; Valdez, A.C.; Schaar, A.K.; Ziefle, M.; Dehmer, M. On graph entropy measures for knowledge discovery from publication network data. In Multidisciplinary Research and Practice for Information Systems; Proceedings of International Cross-Domain Conference and Workshop on Availability, Reliability, and Security, CD-ARES 2012, Prague, Czech Republic, 20–24 August 2012, Quirchmayer, G., Basl, J., You, I., Xu, L., Weippl, E., Eds.; Lecture Notes in Computer Science, Volume 7465; Springer: Berlin/Heidelberg, Germany, 2013; pp. 354–362. [Google Scholar]
- Dehmer, M. Information processing in complex networks: Graph entropy and information functionals. Appl. Math. Comput 2008, 201, 82–94. [Google Scholar]
- Dehmer, M.; Mowshowitz, A. A history of graph entropy measures. Inform. Sci 2011, 181, 57–78. [Google Scholar]
- Rashevsky, N. Life, information theory, and topology. Bull. Math. Biophys 1955, 17, 229–235. [Google Scholar]
- Trucco, E. A note on the information content of graphs. Bull. Math. Biol 1965, 18, 129–135. [Google Scholar]
- Dehmer, M.; Emmert-Streib, F. Structural information content of networks: Graph entropy based on local vertex functionals. Comput. Biol. Chem 2008, 32, 131–138. [Google Scholar]
- Dehmer, M.; Borgert, S.; Emmert-Streib, F. Entropy bounds for molecular hierarchical networks. PLoS ONE 2008, 3. [Google Scholar] [CrossRef]
- Mowshowitz, A. Entropy and the complexity of the graphs I: An index of the relative complexity of a graph. Bull. Math. Biophys 1968, 30, 175–204. [Google Scholar]
- Dehmer, M.; Mowshowitz, A.; Emmert-Streib, F. Advances in Network Complexity; Wiley-Blackwell: Weinheim, Germany, 2013. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Mowshowitz, A. Entropy and the complexity of graphs II: The information content of digraphs and infinite graphs. Bull. Math. Biophys 1968, 30, 225–240. [Google Scholar]
- Mowshowitz, A. Entropy and the complexity of graphs III: Graphs with prescribed information content. Bull. Math. Biophys 1968, 30, 387–414. [Google Scholar]
- Mowshowitz, A. Entropy and the complexity of graphs IV: Entropy measures and graphical structure. Bull. Math. Biophys 1968, 30, 533–546. [Google Scholar]
- Körner, J. Coding of an information source having ambiguous alphabet and the entropy of graphs. In Transactions of the Sixth Prague Conference on Information Theory, Statistical Decision Function, Random Processes; Walter de Gruyter: Berlin, Germany, 1973; pp. 411–425. [Google Scholar]
- Emmert-Streib, F.; Dehmer, M. Exploring statistical and population aspects of network complexity. PLoS ONE 2012, 7. [Google Scholar] [CrossRef]
- Cao, S.; Dehmer, M.; Shi, Y. Extremality of degree-based graph entropies. Inform. Sci 2014, 278, 22–33. [Google Scholar]
- Konstantinova, E.V. On some applications of information indices in chemical graph theory. In General Theory of Information Transfer and Combinatorics; Springer: New York, NY, USA, 2006. [Google Scholar]
- Costa, L.D.F.; Rodrigues, F.A.; Travieso, G.; Villas Boas, P.R. Characterization of complex networks: A survey of measurements. Adv. Phys 2007, 56, 167–242. [Google Scholar]
- Wiener, H. Structural determination of paraffin boiling points. J. Am. Chem. Soc 1947, 69, 17–20. [Google Scholar]
- Dehmer, M.; Kraus, V. On extremal properties of graph entropies. MATCH Commun. Math. Comput. Chem 2012, 68, 889–912. [Google Scholar]
- Shi, Y. Entropy lower bounds for quantum decision tree complexity. Inf. Process. Lett 2002, 81, 23–27. [Google Scholar]
- Dragomir, S.; Goh, C. Some bounds on entropy measures in information theory. Appl. Math. Lett 1997, 10, 23–28. [Google Scholar]
- Bondy, J.A.; Murty, U.S.R. Graph Theory; Springer: Berlin, Germany, 2008. [Google Scholar]
- Bonchev, D.; Trinajstić, N. Information theory, distance matrix and molecular branching. J. Chem. Phy 1977, 67, 4517–4533. [Google Scholar]
- Dehmer, M.; Varmuza, K.; Borgert, S.; Emmert-Streib, F. On entropy-based molecular descriptors: Statistical analysis of real and synthetic chemical structures. J. Chem. Inf. Model 2009, 49, 1655–1663. [Google Scholar]
- Abramov, O.; Lokot, T. Typology by means of language networks: Applying information theoretic measures to morphological derivation networks. In Towards an Information Theory of Complex Networks: Statistical Methods and Applications; Dehmer, M., Emmert-Streib, F., Mehler, A., Eds.; Springer: New York, NY, USA, 2011; pp. 321–346. [Google Scholar]
- Brandes, U. A faster algorithm for betweenness centrality. J. Math. Sociol 2011, 25, 163–177. [Google Scholar]
- Alizadeh, Y.; Andova, V.; Klavzar, S.; Skrekovski, R. Wiener dimension: Fundamental properties and (5,0)-nanotubical fullerenes. MATCH Commun. Math. Comput. Chem 2014, 72, 279–294. [Google Scholar]
- da Fonseca, C.M.; Ghebleh, M.; Kanso, A.; Stevanovic, D. Counterexamples to a conjecture on Wiener index of common neighborhood graphs. MATCH Commun. Math. Comput. Chem 2014, 72, 333–338. [Google Scholar]
- Dobrynin, A.A.; Entringer, R.C.; Gutman, I. Wiener index of trees: Theory and applications. Acta Appl. Math 2001, 66, 211–249. [Google Scholar]
- Hamzeh, A.; Iranmanesh, A.; Reti, T.; Gutman, I. Chemical graphs constructed of composite graphs and their q-Wiener index. MATCH Commun. Math. Comput. Chem 2014, 72, 807–833. [Google Scholar]
- Hrinakova, K.; Knor, M.; Skrekovski, R.; Tepeh, A. A congruence relation for the Wiener index of graphs with a tree-like structure. MATCH Commun. Math. Comput. Chem 2014, 72, 791–806. [Google Scholar]
- Knor, M.; Luzar, B.; Skrekovski, R.; Gutman, I. On Wiener index of common neighborhood graphs. MATCH Commun. Math. Comput. Chem 2014, 72, 321–332. [Google Scholar]
- Lin, H. On the Wiener index of trees with given number of branching vertices. MATCH Commun. Math. Comput. Chem 2014, 72, 301–310. [Google Scholar]
- Lin, H. Extremal Wiener index of trees with given number of vertices of even degree. MATCH Commun. Math. Comput. Chem 2014, 72, 311–320. [Google Scholar]
- Lin, H. A note on the maximal Wiener index of trees with given number of vertices of maximum degree. MATCH Commun. Math. Comput. Chem 2014, 72, 783–790. [Google Scholar]
- Ma, J.; Shi, Y.; Yue, J. On the extremal Wiener polarity index of unicyclic graphs with a given diameter. In Topics in Chemical Graph Theory; Gutman, I., Ed.; Mathematical Chemistry Monographs, No.16a; University of Kragujevac and Faculty of Science Kragujevac: Kragujevac, Serbia, 2014; pp. 177–192. [Google Scholar]
- Skrekovski, R.; Gutman, I. Vertex version of the Wiener theorem. MATCH Commun. Math. Comput. Chem 2014, 72, 295–300. [Google Scholar]
- Alon, N. On the number of subgraphs of prescribed type of graphs with a given number of edges. Isr. J. Math 1981, 38, 116–130. [Google Scholar]
- Alon, N. On the number of certain subgraphs contained in graphs with a given number of edges. Isr. J. Math 1986, 53, 97–120. [Google Scholar]
- Bollobás, B.; Erdös, P. Graphs of extremal weights. Ars Combin 1998, 50, 225–233. [Google Scholar]
- Bollobás, B.; Sarkar, A. Paths in graphs. Stud. Sci. Math. Hung 2001, 38, 115–137. [Google Scholar]
- Bollobás, B.; Sarkar, A. Paths of length four. Discret. Math 2003, 265, 357–363. [Google Scholar]
- Bollobás, B.; Tyomkyn, M. Walks and paths in trees. J. Graph Theory 2012, 70, 54–66. [Google Scholar]
- Holzinger, A.; Hortenhuber, M.; Mayer, C.; Bachler, M.; Wassertheurer, S.; Pinho, A.; Koslicki, D. On Entropy-based Data Mining. In Interactive Knowledge Discovery and Data Mining: State-of-the-Art and Future Challenges in Biomedical Informatics; Holzinger, A., Jurisica, I., Eds.; Lecture Notes in Computer Science, Volume 8401; Springer: Berlin/Heidelberg, Germany, 2014; pp. 209–226. [Google Scholar]

© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chen, Z.; Dehmer, M.; Shi, Y. A Note on Distance-based Graph Entropies. Entropy 2014, 16, 5416-5427. https://doi.org/10.3390/e16105416
Chen Z, Dehmer M, Shi Y. A Note on Distance-based Graph Entropies. Entropy. 2014; 16(10):5416-5427. https://doi.org/10.3390/e16105416
Chicago/Turabian StyleChen, Zengqiang, Matthias Dehmer, and Yongtang Shi. 2014. "A Note on Distance-based Graph Entropies" Entropy 16, no. 10: 5416-5427. https://doi.org/10.3390/e16105416
APA StyleChen, Z., Dehmer, M., & Shi, Y. (2014). A Note on Distance-based Graph Entropies. Entropy, 16(10), 5416-5427. https://doi.org/10.3390/e16105416





