Abstract
This paper deals with the leader-following consensus of multi-agent systems with matched nonlinear dynamics. Compared with previous works, the major difficulty here is caused by the simultaneous existence of nonidentical agent dynamics and unknown system parameters, which are more practical in real-world applications. To tackle this difficulty, a distributed adaptive control law for each follower is proposed based on algebraic graph theory and algebraic Riccati equation. By a Lyapunov function method, we show that the designed control law guarantees that each follower asymptotically converges to the leader under connected communication graphs. A simulation example demonstrates the effectiveness of the proposed scheme.
1. Introduction
By designing a distributed control law for simple agents with a limited communication range and processing power, a system of multiple agents (i.e., a multi-agent system) can perform complex tasks in a cooperative manner. Therefore, cooperative control of multi-agent systems has gained great interest in recent years and has been successfully applied to multisensor location and identification, multi-robot search and rescue and the formation control of multiple unmanned air vehicles [1,2]. The typical cooperative behaviors of multi-agent systems include consensus, formation control, rendezvous, flocking and containment control. Among them, consensus is a fundamental approach to realize other cooperative control. Roughly speaking, consensus means that all agents reach an agreement on a common value of interest (such as position, velocity, attitude, etc.) relying solely on local information from neighboring agents.
As a hot topic in the field of coordination control, seminal work on the consensus problem has been conducted by Vicsek et al. [3], Jadbabaie et al. [4], Olfati-Saber and Murray [5], Moreau [6], Ren and Beard [7], Olfati-Saber [8], Ren [9], Lin et al. [10] and Zhu and Yuan [11], to name just a few. For multi-agent systems with single-integrator dynamics, it has been demonstrated that consensus can be reached if and only if the undirected topology is connected or the directed topology contains a spanning tree [7]. For multi-agent systems with double-integrator or high-order dynamics, the convergence of consensus will be affected by not only communication topology, but also coupling strength between agents [9–11], which is somewhat different from the single-integrator case. It should be pointed out that the aforementioned consensus algorithms have been predominantly concerned with agents without their own dynamics. In other words, the time-evolution of agents is determined by the information exchange among them. However, multi-agent systems encountered in real-world applications can hardly be described by such integrator-based models, since many of them possess high-dimensional complicated dynamics.
Recent studies have begun to draw a connection between consensus and agent dynamics [12–19]. For example, Tuna [12] showed that an output feedback law exists under which coupled discrete-time linear systems synchronize asymptotically. The work of [17–19] discussed the leader-following consensus of multiple linear agents under time-varying topologies. Note that most of the existing results were restricted to agents with deterministic linear dynamics. A more interesting scenario is that agents have uncertain general nonlinear dynamics. Nevertheless, such a scenario has rarely been considered. Some exceptions include [20] for leadless consensus and [21,22] for leader-following consensus, where the solution was given under the restrictive assumption that nonlinear dynamics should satisfy a global Lipschitz-type condition. In other works [23,24], the leader-following consensus problem of multi-agent systems with heterogeneous matched nonlinear dynamics was considered by using adaptive control, but only approximate consensus behavior with bounded residual errors was achieved.
Motivated by the above discussion, here, we further consider the consensus problem of multi-agent systems with matched nonlinear dynamics in the presence of unknown parameters. The problem is investigated in a leader-following framework without imposing a global Lipschitz-type condition on agent dynamics. It should be noted that a relevant topic for this problem is the synchronization of complex network [12,17,25,26]. After quantifying the structure property of complex networks by defining various entropy measures (e.g., Shannon entropy, Gibbs entropy, Kolmogorov–Sinai entropy, structure entropy; see [27–31] and the references therein), lots of interesting techniques have been proposed to solve the synchronization problem of networked linear or nonlinear oscillators [32,33]. However, most of the previous synchronization analysis does not focus on the communication limitation, which thus is difficult to be extended to the consensus problem relying on both the communication limitation and the agent self-dynamics. The main contributions are three-fold. First, agent dynamics in this paper are in a matched nonlinear form, which contain integrator-type agent dynamics in the literature as special cases. Moreover, the nonlinear dynamics of agents are assumed to be nonidentical. Second, both the followers and the leader are allowed to contain unknown parameters, which are inevitable in real multi-agent systems due to imprecise measurements and interactions with an unknown environment. Finally, by parameterizing the unknown nonlinear dynamics of each agent with some basis functions, a distributed adaptive control law is designed based on local consensus error feedback for connected communication graphs. The Lyapunov function method together with a Riccati equation is employed to show that the proposed control law asymptotically regulates each follower agent (nonidentical, nonlinear and unknown) to the leader agent.
The remainder of the paper is organized as follows. Some background on graph theory, as well as the problem formulation are given in Section 2. In Section 3, we provide the consensus result on nonlinear multi-agent systems with a connected communication topology. A simulation example is presented in Section 4, followed by Section 5, which concludes this paper.
2. Preliminaries
Throughout the paper, the following notions will be used. || · || denotes the Euclidean norm. 1N (0N) is a vector in ℝN with elements being all ones (all zeros), and In (On) is the n × n identity matrix (zero matrix). diag{x1, …, xN} defines a diagonal matrix with diagonal entries x1 to xN. Denote by S > 0 (S < 0) that the matrix S is positive (negative) definite. ⊗ denotes the Kronecker product with well known properties (A ⊗ B)T = AT ⊗ BT, A ⊗ (B+C) = A ⊗ B+ A ⊗ C, (A ⊗ B)(C ⊗ D) = AC ⊗ BD, where A, B, C and D are matrices with appropriate dimensions. If not explicitly stated, we assume that the dimensions of the matrix used in this paper are compatible.
2.1. Graph Theory
Let ℊ = (
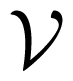 , ) be an undirected graph with a set of nodes
, ) be an undirected graph with a set of nodes
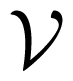 = {v1, …, vN} and a set of edges ⊆
= {v1, …, vN} and a set of edges ⊆
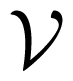 ×
×
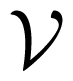 . The node indices belong to a finite index set = {1, …, N}. An edge of is denoted by an unordered pair (vi, vj), which means that node vi and vj can exchange information with each other. Let us define a weighted adjacency matrix
. The node indices belong to a finite index set = {1, …, N}. An edge of is denoted by an unordered pair (vi, vj), which means that node vi and vj can exchange information with each other. Let us define a weighted adjacency matrix
 = [αij ] ∈ ℝN×N as follows: αij = αji > 0 if (vi, vj) ∈ , otherwise αij = αji = 0. Moreover, we assume that αii = 0 for all i ∈ . The set of neighbors of node i is denoted by Ni = {j ∈ : (vi, vj) ∈ }. Define the degree matrix as D = diag{d1, …, dN} with di = ∑j∈Ni αij. The symmetric Laplacian matrix corresponding to the undirected graph ℊ is defined as L = D −
= [αij ] ∈ ℝN×N as follows: αij = αji > 0 if (vi, vj) ∈ , otherwise αij = αji = 0. Moreover, we assume that αii = 0 for all i ∈ . The set of neighbors of node i is denoted by Ni = {j ∈ : (vi, vj) ∈ }. Define the degree matrix as D = diag{d1, …, dN} with di = ∑j∈Ni αij. The symmetric Laplacian matrix corresponding to the undirected graph ℊ is defined as L = D −
 . A path is a sequence of unordered edges of the form (vi1, vi2), (vi2, vi3), …, where vij ∈
. A path is a sequence of unordered edges of the form (vi1, vi2), (vi2, vi3), …, where vij ∈
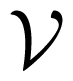 . The graph ℊ is called connected if there is a path between any two nodes.
. The graph ℊ is called connected if there is a path between any two nodes.
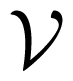 , ) be an undirected graph with a set of nodes
, ) be an undirected graph with a set of nodes
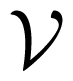 = {v1, …, vN} and a set of edges ⊆
= {v1, …, vN} and a set of edges ⊆
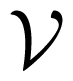 ×
×
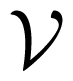 . The node indices belong to a finite index set = {1, …, N}. An edge of is denoted by an unordered pair (vi, vj), which means that node vi and vj can exchange information with each other. Let us define a weighted adjacency matrix
. The node indices belong to a finite index set = {1, …, N}. An edge of is denoted by an unordered pair (vi, vj), which means that node vi and vj can exchange information with each other. Let us define a weighted adjacency matrix
 = [αij ] ∈ ℝN×N as follows: αij = αji > 0 if (vi, vj) ∈ , otherwise αij = αji = 0. Moreover, we assume that αii = 0 for all i ∈ . The set of neighbors of node i is denoted by Ni = {j ∈ : (vi, vj) ∈ }. Define the degree matrix as D = diag{d1, …, dN} with di = ∑j∈Ni αij. The symmetric Laplacian matrix corresponding to the undirected graph ℊ is defined as L = D −
= [αij ] ∈ ℝN×N as follows: αij = αji > 0 if (vi, vj) ∈ , otherwise αij = αji = 0. Moreover, we assume that αii = 0 for all i ∈ . The set of neighbors of node i is denoted by Ni = {j ∈ : (vi, vj) ∈ }. Define the degree matrix as D = diag{d1, …, dN} with di = ∑j∈Ni αij. The symmetric Laplacian matrix corresponding to the undirected graph ℊ is defined as L = D −
 . A path is a sequence of unordered edges of the form (vi1, vi2), (vi2, vi3), …, where vij ∈
. A path is a sequence of unordered edges of the form (vi1, vi2), (vi2, vi3), …, where vij ∈
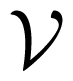 . The graph ℊ is called connected if there is a path between any two nodes.
. The graph ℊ is called connected if there is a path between any two nodes.2.2. Problem Formulation
The multi-agent system considered here is composed of N follower agents and a leader, having distinct n-th order dynamics. The dynamics of the i-th follower agent is described as:
where xi(t) = (xi1, xi2, …, xin)T ∈ ℝn is the state of agent i, ui(t) ∈ ℝm is the control input and fi(xi(t), t) ∈ ℝm is the matched nonlinear dynamics of agent i, which is assumed to be unknown. A ∈ ℝn×n and B ∈ ℝn×m are known matrices.
The leader, indexed as i = 0, has the following dynamic model:
where x0(t) = (x01, x02, …, x0n)T ∈ ℝn is the state of the leader and f0(x0(t), t) ∈ ℝm is an unknown continuous function.
The following assumptions are used throughout the paper.
Assumption 1
The unknown nonlinear dynamics fk(xk(t), t) is parameterized as:
where φk(xk, t) ∈ ℝr×m is the basis function matrix and θk ∈ ℝr is the unknown constant parameter vector to be estimated.
Assumption 2
The pair (A, B) is stabilizable.
In what follows, we use the undirected graph ℊ to model the information topology relation among N follower agents (labeled as vi, i ∈ ). Furthermore, we define an augmented graph
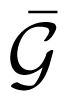 = (
= (
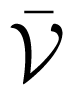 , ̄) to model the interaction topology between N followers and the leader (labeled as v0), where
, ̄) to model the interaction topology between N followers and the leader (labeled as v0), where
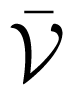 = {v0, v1, …, vN} and ̄ ⊆
= {v0, v1, …, vN} and ̄ ⊆
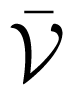 ×
×
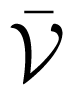 . To depict whether the followers are connected to the leader in
. To depict whether the followers are connected to the leader in
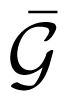 , we define a leader adjacency matrix
, we define a leader adjacency matrix
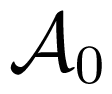 = diag{α10, …, αN0} ∈ ℝN×N, where αi0 > 0 if follower vi is connected to the leader across the communication link (vi, v0), otherwise, αi0 = 0. If we define a new matrix H = L+
= diag{α10, …, αN0} ∈ ℝN×N, where αi0 > 0 if follower vi is connected to the leader across the communication link (vi, v0), otherwise, αi0 = 0. If we define a new matrix H = L+
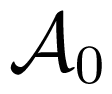 , the following lemma plays a key role in the sequel.
, the following lemma plays a key role in the sequel.
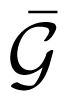 = (
= (
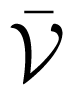 , ̄) to model the interaction topology between N followers and the leader (labeled as v0), where
, ̄) to model the interaction topology between N followers and the leader (labeled as v0), where
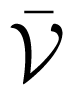 = {v0, v1, …, vN} and ̄ ⊆
= {v0, v1, …, vN} and ̄ ⊆
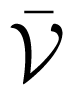 ×
×
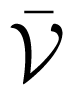 . To depict whether the followers are connected to the leader in
. To depict whether the followers are connected to the leader in
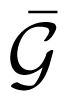 , we define a leader adjacency matrix
, we define a leader adjacency matrix
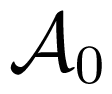 = diag{α10, …, αN0} ∈ ℝN×N, where αi0 > 0 if follower vi is connected to the leader across the communication link (vi, v0), otherwise, αi0 = 0. If we define a new matrix H = L+
= diag{α10, …, αN0} ∈ ℝN×N, where αi0 > 0 if follower vi is connected to the leader across the communication link (vi, v0), otherwise, αi0 = 0. If we define a new matrix H = L+
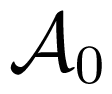 , the following lemma plays a key role in the sequel.
, the following lemma plays a key role in the sequel.Lemma 1
([34]): If undirected graph 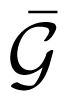 is connected, then the symmetric matrix H associated with
is connected, then the symmetric matrix H associated with 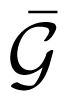 is positive definite.
is positive definite.
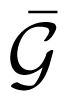 is connected, then the symmetric matrix H associated with
is connected, then the symmetric matrix H associated with 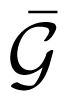 is positive definite.
is positive definite.3. Consensus Analysis
In this section, we start with the design of distributed adaptive controllers for follower agents, then the stability analysis of leader-following consensus of nonlinear multi-agent systems is presented.
3.1. Distributed Adaptive Controller Design
Under Assumption 1, the parameter vector θi of the unknown function fi(xi, t) is unavailable in the controller design. Instead, θi has to be estimated by each follower agent during the evolution. On the other hand, for consensus protocol design, it is assumed that only relative state information can be used. More precisely, the only obtainable information for follower vi is the local neighborhood consensus error [35]:
where αij and αi0 are defined in Section 2.
With these limitations, the control law for the i-th followers is designed as follows:
with
where c > 0 is the coupling strength and K ∈ ℝm×n is the feedback gain matrix to be designed later; θ̂i and θ̂0i are the estimations of the unknown parameters θi and θ0, respectively.
Substituting the designed control law (5)–(6) into the multi-agent system (1)–(2), the closed-loop system for the i-th follower and the leader can be expressed as:
and
where θ̃i = θ̂i − θi.
3.2. Stability Analysis
In order to analyze the performance of the designed consensus protocol, we define the consensus error between follower vi and the leader v0 as δi(t) ≜ xi(t)−x0(t). Then, from the closed-loop system (7)–(8), the dynamics of δi(t) can be obtained:
where
, Φf = diag{φ1, …, φN} and Φ0 = diag{φ0, …, φ0}.
Remark 1
The leader-following consensus problem of the multi-agent system (1)–(2) is solved by the control law (5)–(6) if and only if the equilibrium point δ(t) = 0 of the consensus error system (10) is asymptotically stable.
On the other hand, under Assumption 2, one can see that the following algebraic Riccati equation:
and the parameter adaptive law as:
Remark 2
Both the control law (5)–(6) and the adaptive law (13) are strictly distributed, in the sense that each follower only uses local information of neighboring followers and the leader if this follower is an informed agent. Thus, no centralized information is required, which is more practical for controller implementation.
Theorem 1
Consider the multi-agent system (1)–(2) under Assumptions 1 and 2. Assume that the communication graph 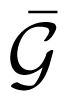 is connected and φk (k = 0, 1, …, N) are uniformly bounded. Then, the distributed control law (5)–(6) combined with the adaptive law (13) solves the leader-following consensus problem if the coupling strength c is chosen as:
is connected and φk (k = 0, 1, …, N) are uniformly bounded. Then, the distributed control law (5)–(6) combined with the adaptive law (13) solves the leader-following consensus problem if the coupling strength c is chosen as:
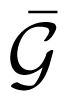 is connected and φk (k = 0, 1, …, N) are uniformly bounded. Then, the distributed control law (5)–(6) combined with the adaptive law (13) solves the leader-following consensus problem if the coupling strength c is chosen as:
is connected and φk (k = 0, 1, …, N) are uniformly bounded. Then, the distributed control law (5)–(6) combined with the adaptive law (13) solves the leader-following consensus problem if the coupling strength c is chosen as:where λmin(H) denotes the smallest eigenvalue of H.
Proof
Consider the following candidate Lyapunov function:
Since the graph
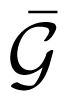 is connected, we know that H is positive definite from Lemma 1. Then, there exists a unitary matrix U ∈ ℝN×N, such that:
is connected, we know that H is positive definite from Lemma 1. Then, there exists a unitary matrix U ∈ ℝN×N, such that:
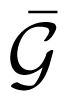 is connected, we know that H is positive definite from Lemma 1. Then, there exists a unitary matrix U ∈ ℝN×N, such that:
is connected, we know that H is positive definite from Lemma 1. Then, there exists a unitary matrix U ∈ ℝN×N, such that:where λi > 0 are eigenvalues of matrix H. With the state transformation δ̃ = (U ⊗ In)δ, we can continue (17) as follows:
Obviously, V̇ is negative semi-definite. Then, it follows that V (t) ≤ V (0), which indicates that δ, θ̃f, θ̃0 ∈ L∞. Hence, δ̇(t) ∈ L∞ due to (10) and the assumption that φj (j = 0, 1, …, N) are uniformly bounded. Moreover, from (18), one has:
that is to say, δ ∈ L2. According to Barbalat’s lemma [37], the trajectory of error system (10) starting from any initial conditions will converge to the origin asymptotically as t → ∞, which, in turn, indicates that limt→∞ ||xi(t) − x0(t)|| = 0, ∀ i ∈ . The proof is thus completed.
Remark 3
It is worthwhile to mention here that the leader-following consensus problem of multi-agent systems with heterogeneous unknown nonlinear dynamics was also investigated using adaptive control in [38,39] and fuzzy disturbance observer in [40], but they only consider agents with first-order dynamics. In this paper, the results in [38–40] were largely extended to the multi-agent systems with more general agent dynamics described by (1)–(2). Therefore, the results of this paper are expected to be a necessary complement to the consensus development of general nonlinear multi-agent systems.
4. Numerical Simulation
In this section, a numerical example is presented to illustrate Theorem 1. Consider a multi-agent system composed of five followers and a leader with a communication graph shown in Figure 1, in which the weights on each edge are assumed to be one. The Laplacian matrix L among five followers and the leader adjacency matrix
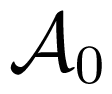 are given by:
are given by:
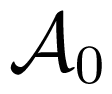 are given by:
are given by: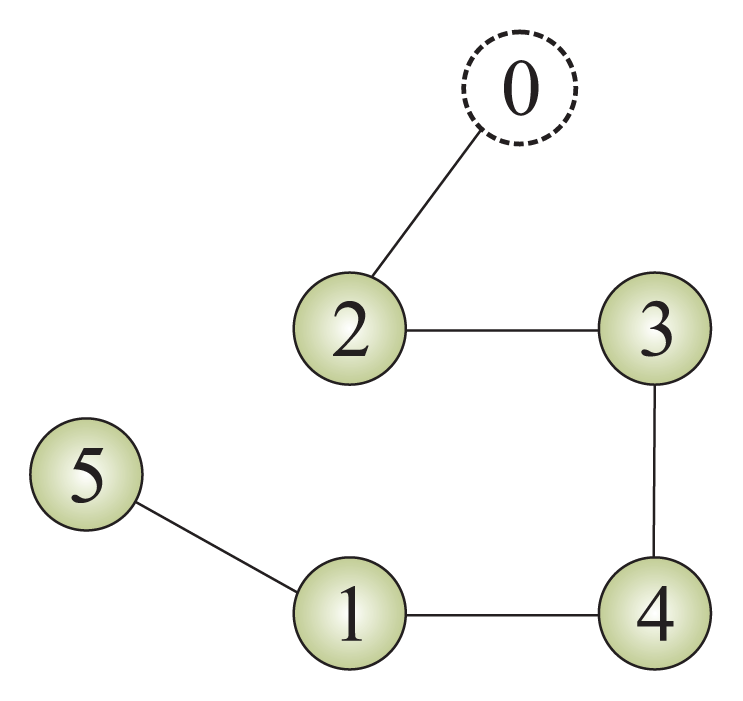
Figure 1.
Communication topology between the leader and the followers.
In simulation, each follower agent is modeled as the Chen chaotic system [41]:
where xi = [xi1, xi2, xi3]T are the state variables of the i-th (i = 1, …, 5) follower agent. It is known that the Chen system depicts a chaotic behavior when α = 35, β = 3 and γ = 28. Letting:
the Chen system in (19) can be written in the form of (1). Apparently, the pair (A, B) is stabilizable, and the nonlinear function f(xi, t) can be parameterized as
in Assumption 1 with:
Let the leader agent be described also by the Chen system with different unknown nonlinear dynamics:
where
with:
When the designed control law (5)–(6) and the adaptive law (13) are applied to this multi-agent system, the control gain K in (6) is selected according to the following procedure. Solving the algebraic Riccati equation (11) yields:
Then, the gain matrix K is designed as K = BT P. Thus, according to Theorem 1, when
, the leader-following consensus will be achieved using the distributed control law (5)–(6) combined with the adaptive law (13). The simulation results with c = 6.5 are shown in Figures 2 and 3, from which we can see that each follower described by (19) asymptotically converges to the leader described by (20), although there exist unknown parameters.
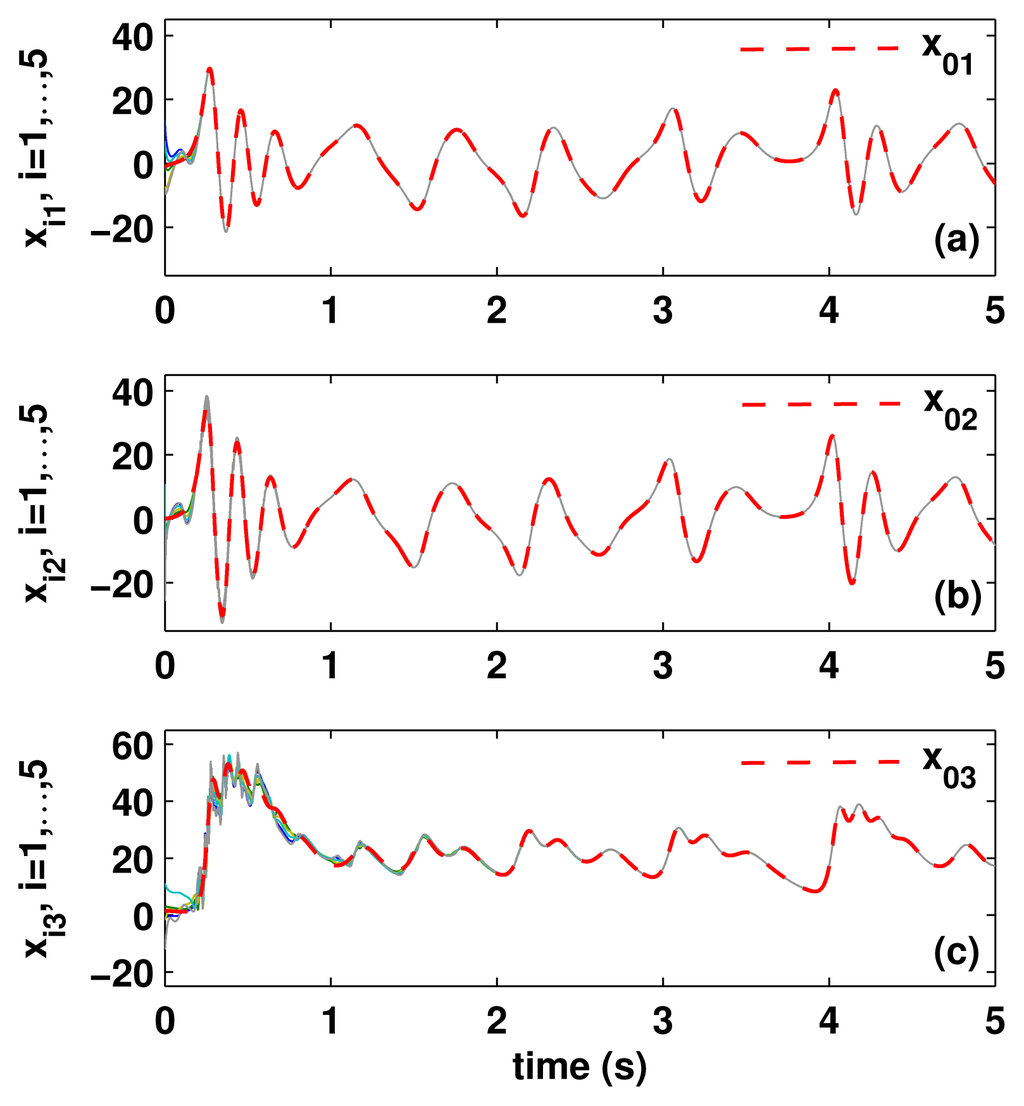
Figure 2.
State trajectories xk(t) (k = 0, 1, …, 5) of all followers and the leader.
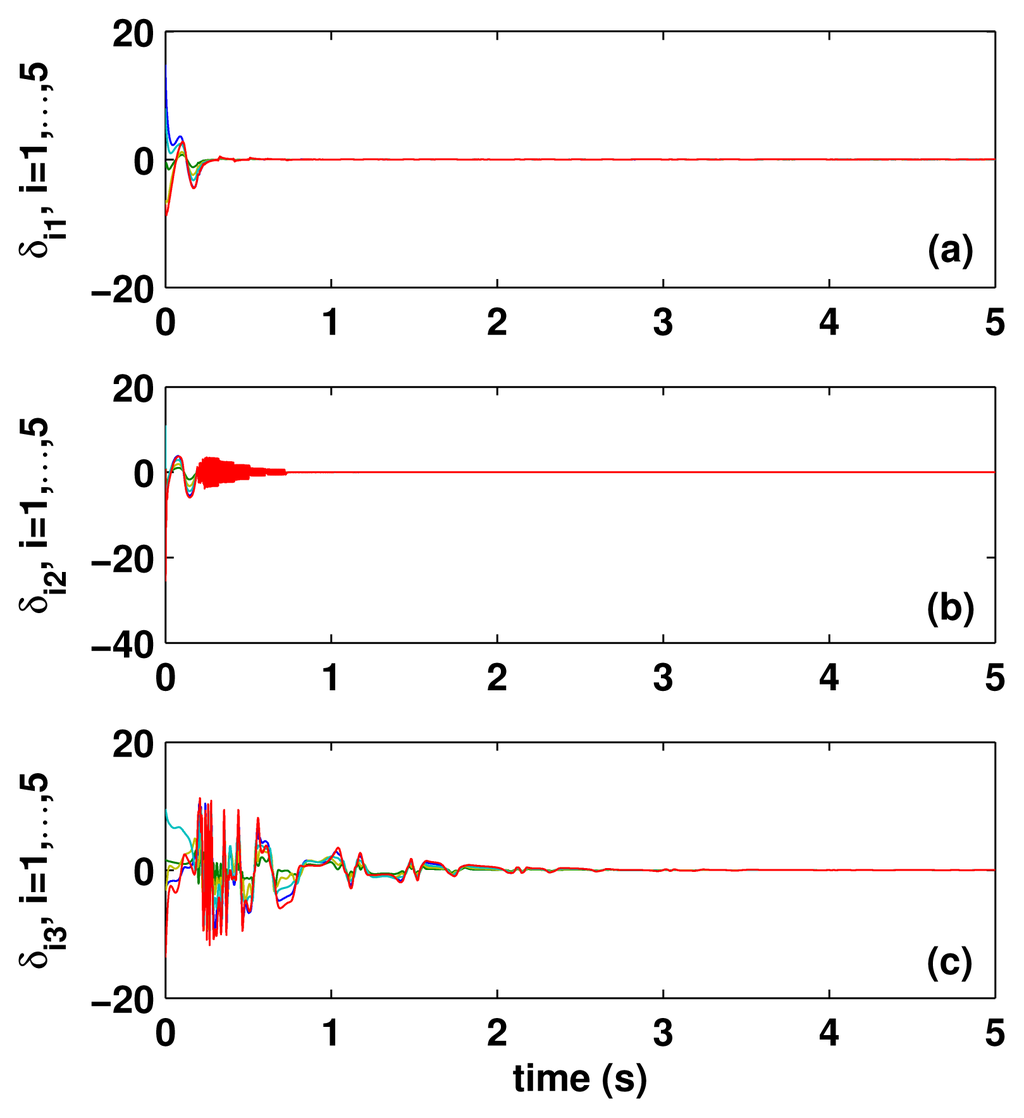
Figure 3.
Error trajectories δi(t) = xi(t) − x0(t) (i = 1, …, 5) between each follower and the leader.
5. Conclusions
In this paper, we have studied the leader-following consensus problem of multi-agent systems with unknown nonlinear dynamics. Compared with previous models, our system does not require individual agent dynamics to satisfy the global Lipschitz-type condition. Moreover, based on the local consensus error feedback, a distributed adaptive control law has been developed, which was proven to drive all of the followers to the leader under a undirected and connected communication topology. In the future, we will further apply the method proposed in this paper to multi-agent systems with more general agent dynamics and more general communication graphs.
Acknowledgments
This work was jointly supported by the Training Program for Outstanding Young Teachers in University of Guangdong Province (Grant No. Yq2013065), the China Postdoctoral Science Foundation (Grant No. 2013M540648), and the University Scientific and Technological Innovation Project of Guangdong Province (Grant No. 2013KJCX0068).
Author Contributions
All authors contributed to the initial motivation of the work, to the research and numerical experiments and to the writing. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Murray, R.M. Recent research in cooperative control of multivehicle systems. J. Dyn. Syst. Meas. Control 2007, 129, 571–583. [Google Scholar]
- Lewis, F.L.; Zhang, H.; Hengster-Movric, K.; Das, A. Cooperative Control of Multi-Agent Systems: Optimal and Adaptive Design Approaches; Springer-Verlag: London, UK, 2014. [Google Scholar]
- Vicsek, T.; Czirók, A.; Ben-Jacob, E.; Cohen, I.; Shochet, O. Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett 1995, 75, 1226–1229. [Google Scholar]
- Jadbabaie, A.; Lin, J.; Morse, A. Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Trans. Autom. Control 2003, 48, 988–1001. [Google Scholar]
- Olfati-Saber, R.; Murray, R. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar]
- Moreau, L. Stability of multi-agent systems with time-dependent communication links. IEEE Trans. Autom. Control 2005, 50, 169–182. [Google Scholar]
- Ren, W.; Beard, R.W. Consensus seeking in multiagent systems under dynamically changing interaction topologies. IEEE Trans. Autom. Control 2005, 50, 655–661. [Google Scholar]
- Olfati-Saber, R. Flocking for multi-agent dynamic systems: algorithms and theory. IEEE Trans. Autom. Control 2006, 51, 401–420. [Google Scholar]
- Ren, W. On consensus algorithms for double-integrator dynamics. IEEE Trans. Autom. Control 2008, 53, 1503–1509. [Google Scholar]
- Lin, P.; Li, Z.; Jia, Y.; Sun, M. High-order multi-agent consensus with dynamically changing topologies and time-delays. IET Control Theory Appl 2011, 5, 976–981. [Google Scholar]
- Zhu, J.; Yuan, L. Consensus of high-order multi-agent systems with switching topologies. Linear Algebra Appl 2014, 443, 105–119. [Google Scholar]
- Tuna, S.E. Synchronizing linear systems via partial-state coupling. Automatica 2008, 44, 2179–2184. [Google Scholar]
- Seo, J.H.; Shim, H.; Back, J. Consensus of high-order linear systems using dynamic output feedback compensator: Low gain approach. Automatica 2009, 45, 2659–2664. [Google Scholar]
- Li, Z.; Duan, Z.; Chen, G.; Huang, L. Consensus of multiagent systems and synchronization of complex networks: A unified viewpoint. IEEE Trans. Circuits Syst. I Regul. Pap 2010, 57, 213–224. [Google Scholar]
- Ma, C.; Zhang, J. Necessary and sufficient conditions for consensusability of linear multi-agent systems. IEEE Trans. Autom. Control 2010, 55, 1263–1268. [Google Scholar]
- Zhang, H.; Lewis, F.L.; Das, A. Optimal design for synchronization of cooperative systems: State feedback, observer and output feedback. IEEE Trans. Autom. Control 2011, 56, 1948–1952. [Google Scholar]
- Scardovi, L.; Sepulchre, R. Synchronization in networks of identical linear systems. Automatica 2009, 45, 2557–2562. [Google Scholar]
- Ni, W.; Cheng, D. Leader-following consensus of multi-agent systems under fixed and switching topologies. Syst. Control Lett 2010, 59, 209–217. [Google Scholar]
- Qin, J.; Yu, C.; Gao, H. Coordination for linear multiagent systems with dynamic interaction topology in the leader-following framework. IEEE Trans. Ind. Electron 2014, 61, 2412–2422. [Google Scholar]
- Li, Z.; Ren, W.; Liu, X.; Fu, M. Consensus of multi-agent systems with general linear and Lipschitz nonlinear dynamics using distributed adaptive protocols. IEEE Trans. Autom. Control 2013, 58, 1786–1791. [Google Scholar]
- Wen, G.; Duan, Z.; Chen, G.; Yu, W. Consensus tracking of multi-agent systems with Lipschitz-type node dynamics and switching topologies. IEEE Trans. Circuits Syst. I Regul. Pap 2014, 61, 499–511. [Google Scholar]
- Xu, W.; Cao, J.; Yu, W.; Lu, J. Leader-following consensus of non-linear multi-agent systems with jointly connected topology. IET Control Theory Appl 2014, 8, 432–440. [Google Scholar]
- Peng, Z.; Wang, D.; Zhang, H.; Sun, G. Distributed neural network control for adaptive synchronization of uncertain dynamical multiagent systems. IEEE Trans. Neural Netw. Learn. Syst 2014, 25, 1508–1519. [Google Scholar]
- Li, Z.; Duan, Z.; Lewis, F.L. Distributed robust consensus control of multi-agent systems with heterogeneous matching uncertainties. Automatica 2014, 50, 883–889. [Google Scholar]
- Lü, J.; Chen, G. A time-varying complex dynamical network model and its controlled synchronization criteria. IEEE Trans. Autom. Control 2005, 50, 841–846. [Google Scholar]
- DeLellis, P.; DiBernardo, M.; Garofalo, F. Novel decentralized adaptive strategies for the synchronization of complex networks. Automatica 2009, 45, 1312–1318. [Google Scholar]
- Demetriusa, L.; Manke, T. Robustness and network evolution-an entropic principle. Physica A 2005, 346, 682–696. [Google Scholar]
- Xiao, Y.-H.; Wu, W.-T.; Wang, H.; Xiong, M.; Wang, W. Symmetry-based structure entropy of complex networks. Physica A 2008, 387, 2611–2619. [Google Scholar]
- Anand, K.; Bianconi, G. Entropy measures for networks: Toward an information theory of complex topologies. Phys. Rev. E 2009, 80. [Google Scholar] [CrossRef]
- Mowshowitz, A.; Dehmer, M. Entropy and the complexity of graphs revisited. Entropy 2012, 14, 559–570. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J 1948, 27. [Google Scholar]
- Arenas, A.; Díaz-Guilera, A.; Kurths, J.; Moreno, Y.; Zhou, C. Synchronization in complex networks. Phys. Rep 2008, 469, 93–153. [Google Scholar]
- Kocarev, L. Consensus and synchronization in complex networks; Springer-Verlag: Berlin, Germany, 2013. [Google Scholar]
- Hong, Y.; Hu, J.; Gao, L. Tracking control for multi-agent consensus with an active leader and variable topology. Automatica 2006, 42, 1177–1182. [Google Scholar]
- Khoo, S.; Xie, L.; Man, Z. Robust finite-time consensus tracking algorithm for multirobot systems. IEEE/ASME Trans. Mechatron 2009, 14, 219–228. [Google Scholar]
- Lancaster, P.; Rodman, L. Algebraic Riccati Equations; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Slotine, J.J.; Li, W. Applied Nonlinear Control; Prentice Hall: Upper Saddle River, NJ, USA, 1991. [Google Scholar]
- Yu, H.; Xia, X. Adaptive consensus of multi-agents in networks with jointly connected topologies. Automatica 2012, 48, 1783–1790. [Google Scholar]
- Das, A.; Lewis, F.L. Distributed adaptive control for synchronization of unknown nonlinear networked systems. Automatica 2010, 46, 2014–2021. [Google Scholar]
- Lee, T.H.; Park, J.H.; Ji, D.H.; Jung, H.Y. Leader-following consensus problem of heterogeneous multi-agent systems with nonlinear dynamics using fuzzy disturbance observer. Complexity 2014, 19, 20–31. [Google Scholar]
- Chen, G.; Ueta, T. Yet another chaotic attractor. Int. J. Bifurc. Chaos 1999, 9, 1465–1466. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).