Performance Degradation Assessment of Rolling Element Bearings Based on an Index Combining SVD and Information Exergy
Abstract
:1. Introduction
2. Information Exergy
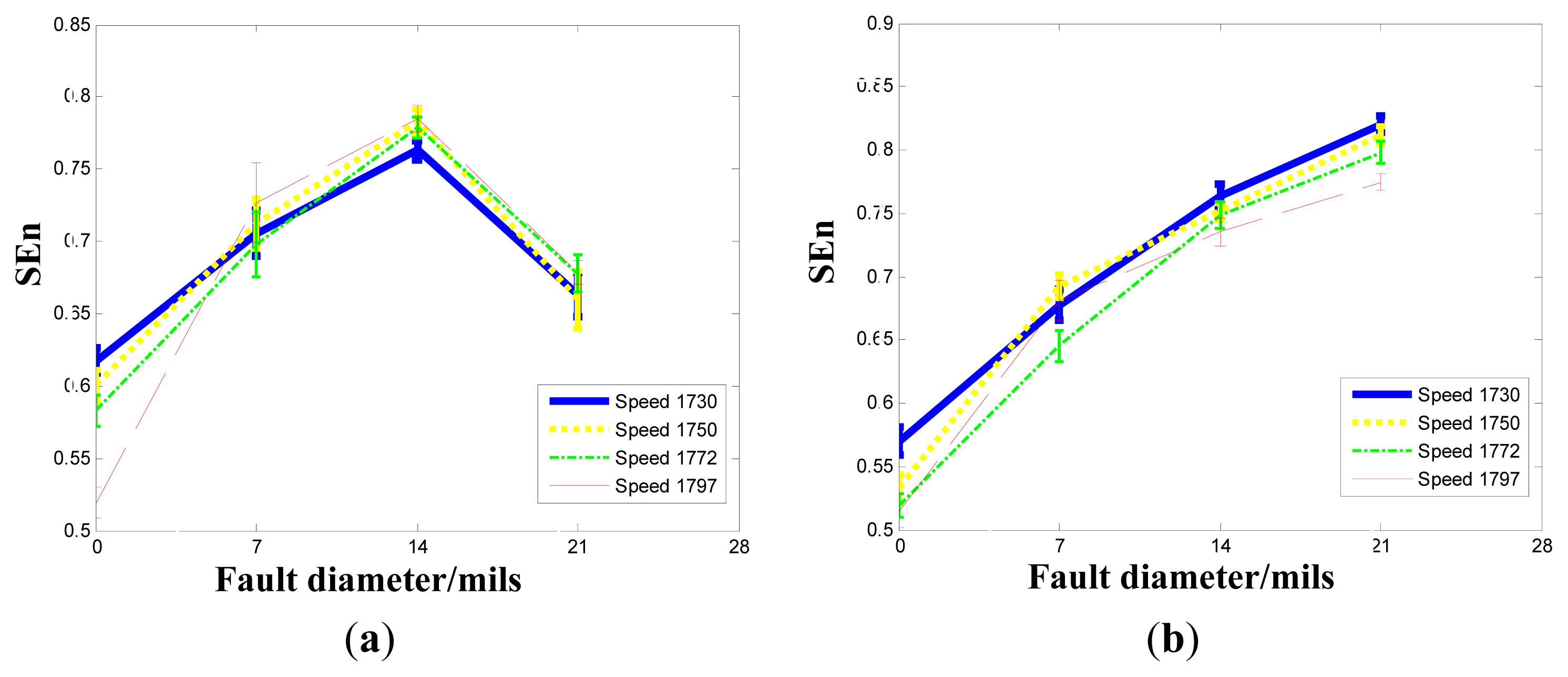
2.1. Generalized Information Entropy
2.2. Information Exergy
3. Information Exergy Index for Degradation Assessment
3.1. Information Exergy Index Combining SVD and Information Exergy
3.2. Degradation Assessment Based on the Proposed Information Exergy Index
4. Experimental Validation of Information Exergy Index
4.1. Experiment Description
4.2. Experimental Results and Analysis
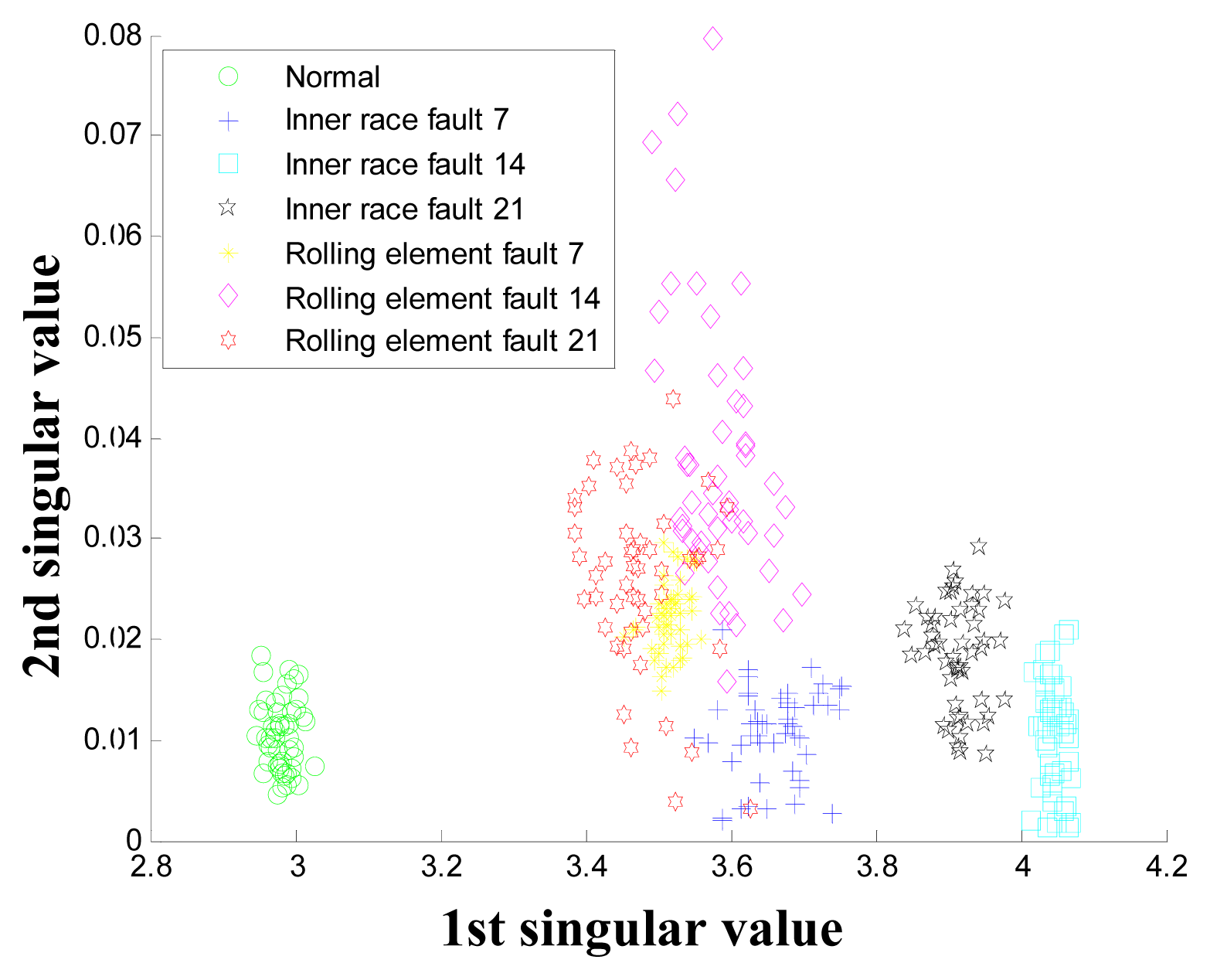
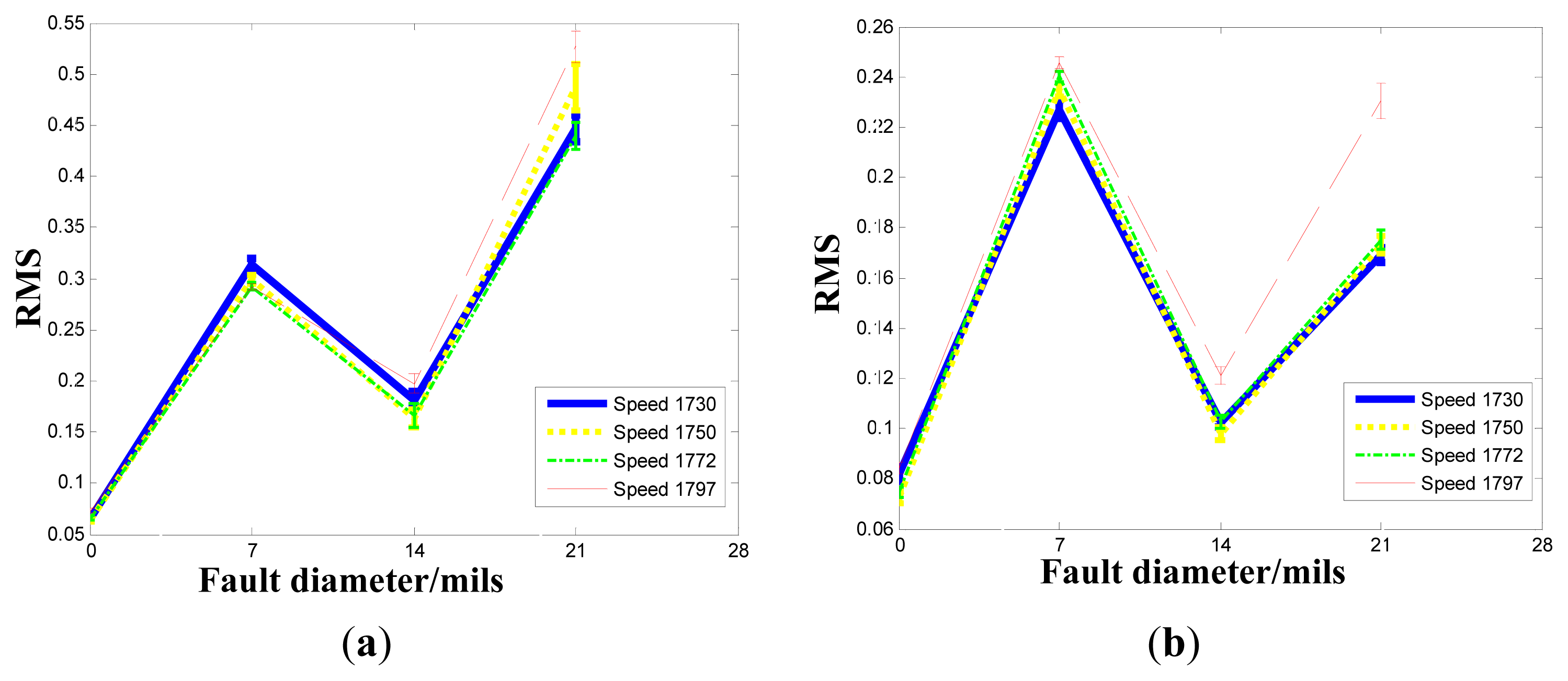
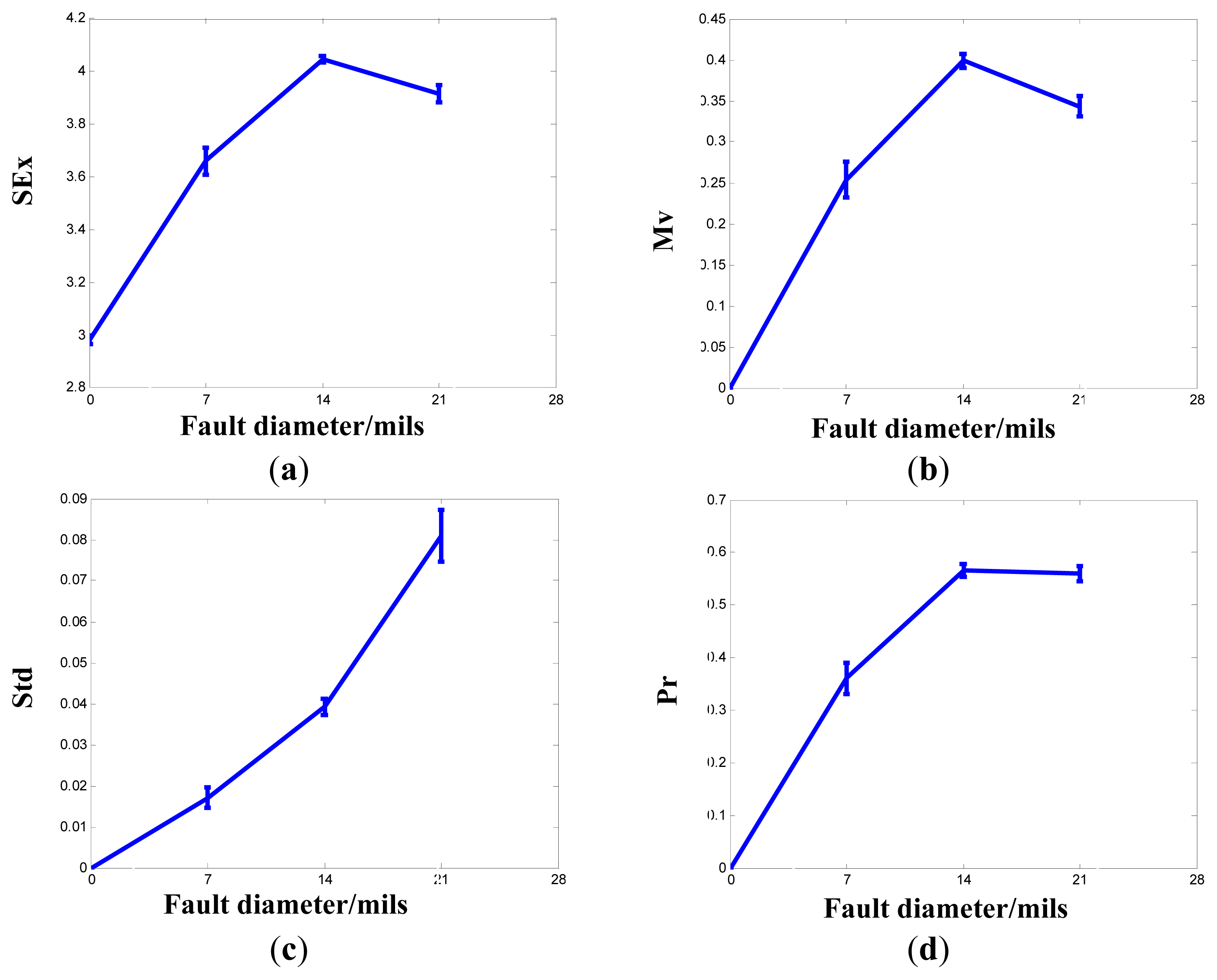
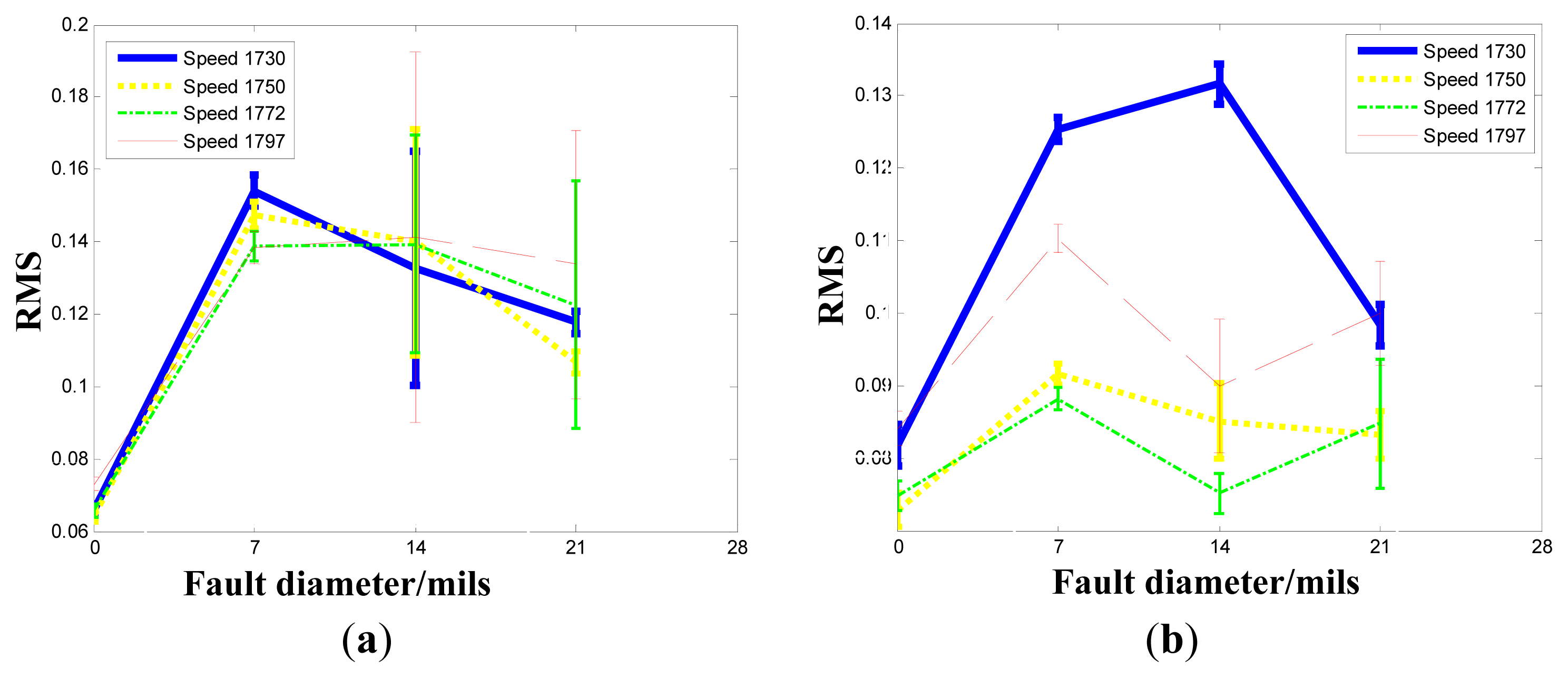
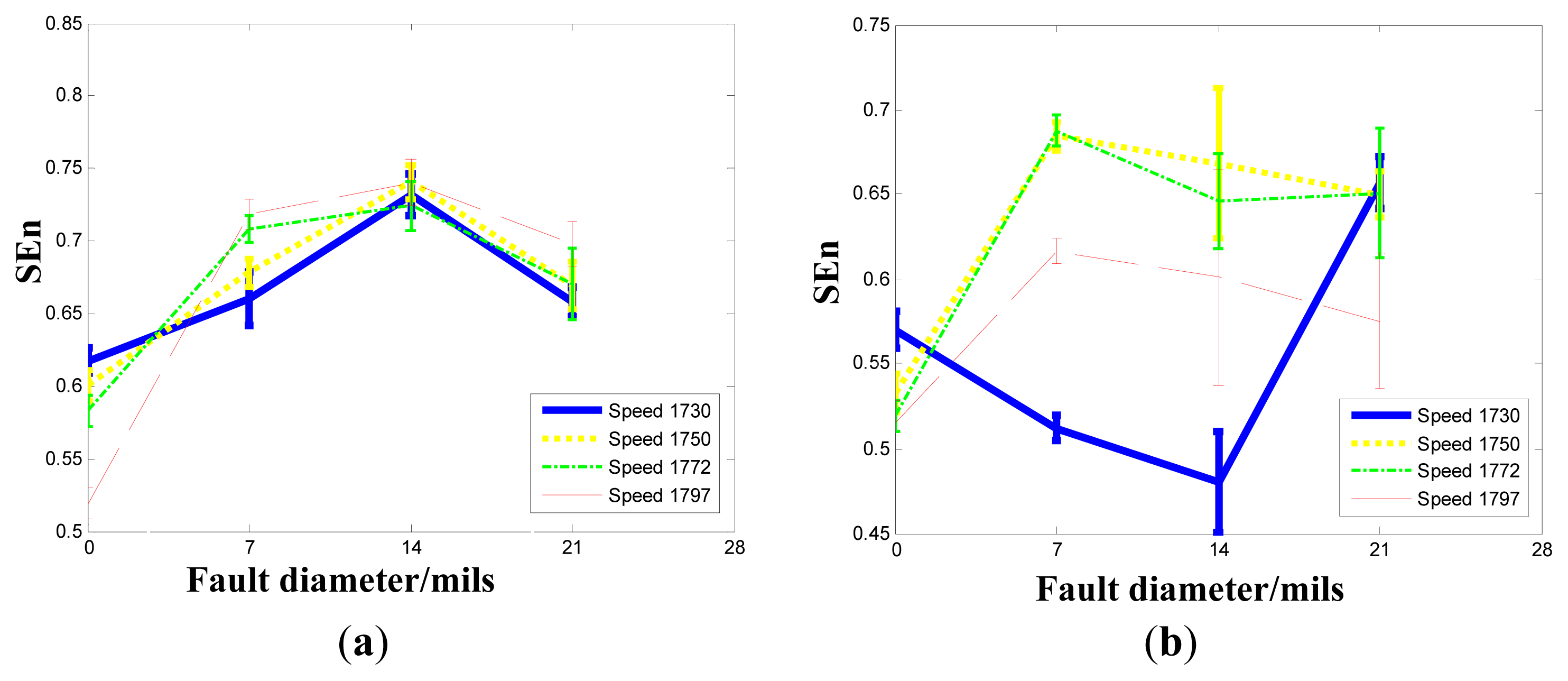
4.2.1. Inner Raceway Degradation Assessment
4.2.2. Rolling Element Degradation Assessment
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zio, E.; Gola, G. A neuro-fuzzy technique for fault diagnosis and its application to rotating machinery. Reliab. Eng. Syst. Saf 2009, 94, 78–88. [Google Scholar]
- Jardine, A.K.S.; Lin, D.M.; Banjevic, D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process 2006, 20, 1483–1510. [Google Scholar]
- Chen, B.; Yan, Z.L.; Chen, W. Defect detection for wheel-bearings with time-spectral kurtosis and entropy. Entropy 2014, 16, 607–626. [Google Scholar]
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics—A tutorial. Mech. Syst. Signal Process 2011, 25, 485–520. [Google Scholar]
- Liao, L.X.; Lee, J. A novel method for machine performance degradation assessment based on fixed cycle features test. J. Sound Vib 2009, 326, 894–908. [Google Scholar]
- Niu, G.; Yang, B.S.; Pecht, M. Development of an optimized condition-based maintenance system by data fusion and reliability-centered maintenance. Reliab. Eng. Syst. Saf 2010, 95, 786–796. [Google Scholar]
- Yan, R.Q.; Gao, R.X.; Wang, C.T. Experimental evaluation of a unified time-scale-frequency technique for bearing defect feature extraction. J. Vib. Acoust 2009. [Google Scholar]
- Tao, B.; Zhu, L.M.; Ding, H.; Xiong, Y.L. An alternative time-domain index for condition monitoring of rolling element bearings—A comparison study. Reliab. Eng. Syst. Saf 2007, 92, 660–670. [Google Scholar]
- Feng, Z.P.; Zuo, M.J.; Hao, R.J.; Chu, F.L.; Badaoui, M.E. Gear damage assessment based on cyclic spectral analysis. IEEE Trans. Reliab 2011, 61, 21–32. [Google Scholar]
- Pan, Y.N.; Chen, J.; Li, X.L. Spectral entropy: A complementary index for rolling element bearing performance degradation assessment. Proc. Inst. Mech. Eng. Part C: J. Mech. Eng. Sci 2009, 223, 1223–1231. [Google Scholar]
- Hong, H.B.; Liang, M. Fault severity assessment for rolling element bearings using the Lempel-Ziv complexity and continuous wavelet transform. J. Sound Vib 2009, 320, 452–468. [Google Scholar]
- Yu, J.B. Local and nonlocal preserving projection for bearing defect classification and performance assessment. IEEE Trans. Ind. Electron 2012, 59, 2363–2376. [Google Scholar]
- Liu, W.B.; Zhong, X.; Lee, J.; Liao, L.X.; Zhou, M. Application of a novel method for machine performance degradation assessment based on Gaussian mixture model and Logistic regression. Chin. J. Mech. Eng 2011, 24, 879–884. [Google Scholar]
- Shen, Z.J.; He, Z.J.; Chen, X.F.; Sun, C.; Liu, Z.W. A monotonic degradation assessment index of rolling bearings using fuzzy support vector data description and running time. Sensors 2012, 12, 10109–10135. [Google Scholar]
- Hong, S.; Zhou, Z.; Zio, E.; Hong, K. Condition assessment for the performance degradation of bearing based on a combinatorial feature extraction method. Digit. Signal Process 2014, 27, 159–166. [Google Scholar]
- Xu, R.Z.; Xie, L.; Zhang, M.C.; Li, C.X. Machine degradation analysis using fuzzy CMAC neural network approach. Int. J. Adv. Manuf. Technol 2008, 36, 765–772. [Google Scholar]
- Moghaddass, R.; Zuo, M.J. A parameter estimation method for a condition-monitored device under multi-state deterioration. Reliab. Eng. Syst. Saf 2012, 106, 94–103. [Google Scholar]
- Lee, S.; Li, L.; Ni, J. Online degradation assessment and adaptive fault detection using modified hidden Markov model. J. Manuf. Sci. Eng 2010. [Google Scholar]
- Hu, J.Q.; Zhang, L.B.; Liang, W. Dynamic degradation observer for bearing fault by MTS-SOM system. Mech. Syst. Signal Process 2013, 36, 385–400. [Google Scholar]
- Zhang, Y.; Zuo, H.F.; Bai, F. Classification of fault location and performance degradation of a roller bearing. Measurement 2013, 46, 1178–1189. [Google Scholar]
- Tamilselvan, P.; Wang, P.F. Failure diagnosis using deep belief learning based health state classification. Reliab. Eng. Syst. Saf 2013, 115, 124–135. [Google Scholar]
- Widodo, A.; Yang, B.S. Application of relevance vector machine and survival probability to machine degradation assessment. Expert Syst. Appl 2011, 38, 2592–2599. [Google Scholar]
- Safizadeh, M.S.; Latifi, S.K. Using multi-sensor data fusion for vibration fault diagnosis of rolling element bearings by accelerometer and load cell. Inf. Fusion 2014, 18, 1–8. [Google Scholar]
- Xiao, W.B.; Chen, J.; Dong, G.M.; Zhou, Y.; Wang, Z.Y. A multichannel fusion approach based on coupled hidden Markov models for rolling element bearing fault diagnosis. Proc. Inst. Mech. Eng. Part C: J. Mech. Eng. Sci 2012, 226, 202–216. [Google Scholar]
- Lin, Y.F.; Chen, M.Y.; Zhou, D.H. Online probabilistic operational safety assessment of multi-mode engineering systems using Bayesian methods. Reliab. Eng. Syst. Saf 2013, 119, 150–157. [Google Scholar]
- Li, Z.X.; Yan, X.P. Study on data fusion of multi-dimensional sensors for health monitoring of rolling bearings. Insight-Non-Destr. Test. Cond. Monit 2013, 55, 147–151. [Google Scholar]
- Pan, Y.N.; Chen, J.; Dong, G.M. A hybrid model for bearing performance degradation assessment based on support vector data description and fuzzy c-means. Proc. Inst. Mech. Eng. Part C: J. Mech. Eng. Sci 2009, 223, 2687–2695. [Google Scholar]
- Lybeck, N.; Marble, S.; Morton, B. Validating prognostic algorithms: A case study using comprehensive bearing fault data. Proceedings of the 2007 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10March 2007; pp. 1–9.
- Jiang, L.L.; Liu, Y.L.; Li, X.J.; Chen, A.H. Degradation assessment and fault diagnosis for roller bearing based on AR model and fuzzy cluster analysis. Shock Vib 2011, 18, 127–137. [Google Scholar]
- Zhang, B.; Sconyers, C.; Byington, C.; Patrick, R.; Orchard, M.; Vachtsevanos, G. A probabilistic fault detection approach: application to bearing fault detection. IEEE Trans. Ind. Electron 2011, 58, 2011–2018. [Google Scholar]
- Sawalhi, N.; Randall, R.B. Simulating gear and bearing interactions in the presence of faults: Part I. The combined gear bearing dynamic model and the simulation of localised bearing faults. Mech. Syst. Signal Process 2008, 22, 1924–1951. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Mob. Comput. Commun. Rev 2001, 5, 3–55. [Google Scholar]
- Wu, B.F.; Wang, K.C. Robust endpoint detection algorithm based on the adaptive band-partitioning spectral entropy in adverse environments. IEEE Trans. Speech Audio Process 2005, 13, 762–775. [Google Scholar]
- Yu, D.J.; Yang, Y.; Cheng, J.S. Application of time-frequency entropy method based on Hilbert-Huang transform to gear fault diagnosis. Measurement 2007, 40, 823–830. [Google Scholar]
- Wu, S.D.; Wu, C.W.; Wu, T.Y.; Wang, C.C. Bearing fault diagnosis based on multiscale permutation entropy and support vector machine. Entropy 2012, 14, 1343–1356. [Google Scholar]
- Ren, W.X.; Sun, Z.S. Structural damage identification by using wavelet entropy. Eng. Struct 2008, 30, 2840–2849. [Google Scholar]
- Sciubba, E.; Wall, G. A brief commented history of exergy from the beginnings to 2004. Int. J. Thermodyn 2007, 10, 1–26. [Google Scholar]
- Chen, F.; Huang, S.H.; Yang, T.; Gao, W.; He, G.Q. Information exergy diagnosis method of vibration faults of rotating machinery. J. Mech. Eng 2009, 45, 65–71. [Google Scholar]
- Zhang, B.; Zhang, L.J.; Xu, J.W.; Liu, J. Information exergy-based method for structural damage diagnosis. J. Vibroeng 2013, 15, 1606–1618. [Google Scholar]
- Rajwade, A.; Rangarajan, A.; Banerjee, A. Image denoising using the higher order singular value decomposition. IEEE Trans. Pattern Anal. Mach. Intell 2013, 35, 49–862. [Google Scholar]
- Shirali, G.A.; Mohammadfam, I.; Ebrahimipour, V. A new method for quantitative assessment of resilience engineering by PCA and NT approach: A case study in a process industry. Reliab. Eng. Syst. Saf 2013, 119, 88–94. [Google Scholar]
- Tamura, M.; Tsujita, S. A study on the number of principal components and sensitivity of fault detection using PCA. Comput. Chem. Eng 2007, 31, 1035–1046. [Google Scholar]
- Ocak, H.; Loparo, K.A. Estimation of the running speed and bearing defect frequencies of an induction motor from vibration data. Mech. Syst. Signal Process 2004, 18, 515–533. [Google Scholar]
- Zhang, L.J.; Xu, J.W.; Yang, J.H.; Yang, D.B.; Wang, D.D. Multiscale morphology analysis and its application to fault diagnosis. Mech. Syst. Signal Process 2008, 22, 597–610. [Google Scholar]
- Yu, J.B. Bearing performance degradation assessment using locality preserving projections. Expert Syst. Appl 2011, 38, 7440–7450. [Google Scholar]
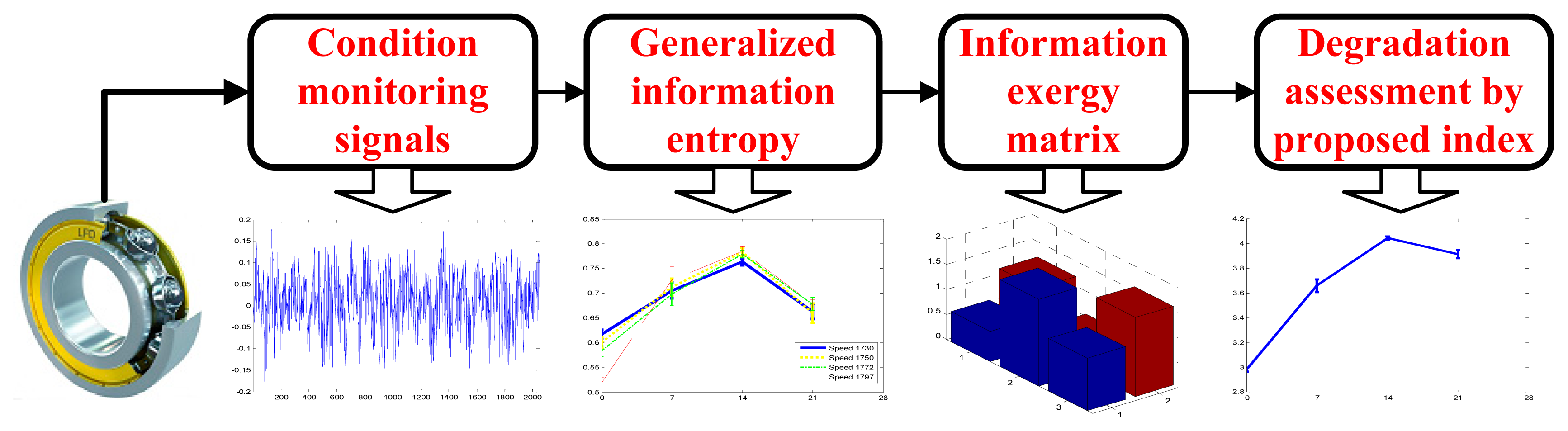


| Step 1 | Condition monitoring signals of multiple instants and multiple sensors are preprocessed for calculation of generalized information entropy, such as fast Fourier transform (FFT). |
| Step 2 | Specific generalized information entropy such as spectral information entropy of multi-instant and multi-sensor condition monitoring signals is calculated. |
| Step 3 | Information exergy matrix is constructed using the specific generalized information entropies of multiple instants and multiple sensors. |
| Step 4 | Information exergy index is extracted by SVD of the above information exergy matrix and singular value truncating. |
| Step 5 | Empirical relationship between information exergy index and degradation severity is established by clustering information exergy indices with known degradation severities. |
| Step 6 | Degradation severity is assessed by the established empirical relationship when new information exergy index is input. |
| Index | Normal | 7 Mils Fault | 14 Mils Fault | 21 Mils Fault |
|---|---|---|---|---|
| SEx | 2.9817(0.0060) * | 3.6606(0.0137) * | 4.0467(0.0034) * | 3.9153(0.0080) * |
| Mv | 0 | 0.2536(0.0845) | 0.3987(0.0208) * | 0.3432(0.0361) * |
| Std | 0 | 0.0170(0.1480) * | 0.0392(0.0487) * | 0.0810(0.0772) * |
| Pr | 0 | 0.3607(0.0812) * | 0.5659(0.0207) * | 0.5598(0.0259) * |
| Index | Normal | 7 Mils Fault | 14 Mils Fault | 21 Mils Fault |
|---|---|---|---|---|
| SEx | 2.9817(0.0040) * | 3.5170(0.0047) * | 3.5826(0.0094) * | 3.4769(0.0112) * |
| Mv | 0 | 0.1901(0.0569) * | 0.2147(0.0981) * | 0.1838(0.1247) * |
| Std | 0 | 0.0161(0.0749) * | 0.0221(0.1448) * | 0.0113(0.3443) * |
| Pr | 0 | 0.2697(0.0555) * | 0.3200(0.0770) * | 0.2648(0.1249) * |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhang, B.; Zhang, L.; Xu, J.; Wang, P. Performance Degradation Assessment of Rolling Element Bearings Based on an Index Combining SVD and Information Exergy. Entropy 2014, 16, 5400-5415. https://doi.org/10.3390/e16105400
Zhang B, Zhang L, Xu J, Wang P. Performance Degradation Assessment of Rolling Element Bearings Based on an Index Combining SVD and Information Exergy. Entropy. 2014; 16(10):5400-5415. https://doi.org/10.3390/e16105400
Chicago/Turabian StyleZhang, Bin, Lijun Zhang, Jinwu Xu, and Pingfeng Wang. 2014. "Performance Degradation Assessment of Rolling Element Bearings Based on an Index Combining SVD and Information Exergy" Entropy 16, no. 10: 5400-5415. https://doi.org/10.3390/e16105400
APA StyleZhang, B., Zhang, L., Xu, J., & Wang, P. (2014). Performance Degradation Assessment of Rolling Element Bearings Based on an Index Combining SVD and Information Exergy. Entropy, 16(10), 5400-5415. https://doi.org/10.3390/e16105400






