1. Introduction
One of the remarkable features of the organic world is the large diversity of plants and animals that exist and the high degree of adaptation of these organisms to their natural environment. The morphological, physiological and behavioral features that characterize this adaptation are not immutable states. These features evolve: They undergo directional and adaptive change as one population type replaces another over evolutionary time. The question which emerges from this observation is: Can this directional change in the morphology and physiology of organisms be explained in terms of a dynamic model which takes into account the fact that biopopulations are composed of genetically unique individuals?
Darwin’s answer to this problem was articulated in the
Origin of Species [
1]. The model of adaptation and evolution he proposed is based on three tenets, [
2]:
(Variation) Individuals in a population differ in terms of their morphology, behavior and physiology.
(Heredity) There exists a positive correlation between the physiology and behavior of ancestors and their descendants.
(Selection) The resources necessary for life vary in terms of their abundance and diversity. Individuals with different characteristics vary in their ability to acquire and convert these resources into net-offspring production.
These tenets entail that changes in the composition of populations are a consequence of variation in heritable differences, and selection acting on this variation. Evolutionary change is however limited by the existing modification. Continued evolution over the long term requires mutation, the constant generation of new heritable alternative forms. The concatenation of these two processes–mutation and natural selection will result, as Darwin argued, in changes within populations (microevolution), and concomitantly, in changes between populations (macroevolution). Microevolution and macroevolution thus involve different mechanisms, and unfold over different time scales.
Microevolution pertains to changes in the composition of populations due to mutation and natural selection. This process occurs on a time scale of generations, and is the mechanism which underpins the diversity of populations, adaptive changes and geographic variation. Macroevolution refers to changes in the composition of lineages due to speciation and extinction. This process unfolds on a geological time scale and is the mechanism which underlies directional trends in morphological and morphometric properties of species over large episodes of geological time.
A central element in Darwin’s argument is that all macroevolutionary processes have their origin in evolutionary change within populations, and hence are the result of natural selection acting on genotypic and phenotypic variation. This proposition, which has now been supported by comparative molecular studies of genotypic variation within and between species, indicates that evolutionary processes on both a ecological and geological time scales can be analyzed in terms of processes which occur at the individual level, Mayr [
3,
4].
The relation between the dynamics which drive microevolution and the patterns observed at the macroevolutionary level was clearly recognized by the pioneers in theoretical genetics, Fisher, Haldane and Wright. These authors recognized that the Darwinian dynamic involves two complementary events:
a cooperative process–the interaction within the organism of related alleles and the transmission of these allelic types to the offspring,
a competitive process–the interaction within the population of related phenotypes and the selection of a phenotypic trait according to its capacity to appropriate resources and invest these resources into offspring production.
The efforts of these pioneers to develop a mathematical model of Darwin’s theory focused initially on forging a synthesis of Mendel’s laws of particulate inheritance–the basic premise of the cooperative event–with various hypotheses regarding the dynamics of the competitive process.
The problem which the analysis of competition generated can be formulated in the following terms: what class of demographic parameters characterize Darwinian fitness, that is the capacity of a type to appropriate resources and invest these resources into offspring production?
The appropriation of resources and its reinvestment into offspring production can be factored into two actions, [
5].
- (a)
A resource-metabolic process: The acquisition of resources from the external environment and its conversion into reproduction and survivorship.
- (b)
A metabolic-demographic process: The transformation of the metabolic energy of the organism into demographic currency.
When the metabolic-demographic process is the dominant event, then the outcome of competition will be determined by the rate at which the organism transforms the abundant resources into net-offspring production. However, when the resource-metabolic process is the limiting factor, then the outcome of competition will be determined by the rate at which the organism acquires the exiguous resources and converts these resources into demographic currency.
Classical studies of the evolutionary process, Fisher [
6], implicitly assumed that the resource abundance is large, effectively infinite. This entails that the metabolic-demographic process was the determining agent of natural selection. This perspective was the basis for the proposition that Darwinian fitness is characterized by the rate at which the population transforms the metabolic energy into net-offspring production, a quantity now called the Malthusian parameter, in honor of Thomas Malthus’ contribution to population dynamics [
7].
Malthusian selection, the term we will use to describe the process of selection which involves the population growth rate, or one its surrogates, the net-reproductive rate, as the measure of Darwinian fitness, rapidly emerged as the dominant paradigm in evolutionary studies. The Malthusian selection principle, which asserts that the outcome of selection is predicted by the population growth rate, became the cornerstone in evolutionary studies of life-history [
8–
10], the evolution of senescence [
11], and the dynamics of infectious diseases [
12–
14]. Malthusian selection also played a central role in studies of the evolution of social behavior: The inclusive fitness concept of Hamilton (see [
15,
16]) is a weighted measure of an individual’s fitness and those of its relatives. It is essentially an extension of the classical fitness concept of Fisher to include the offspring production of the individual’s relatives.
Malthusian selection derives from the hypothesis that resource abundance is effectively
unlimited. In this case the dynamics of selection will be regulated primarily by the capacity to transform this unlimited resource into the production of new descendants. The models of selection described in [
5] implicitly assumed that resource abundance is
limited. In view of this constraint, the resource-metabolic process now becomes a critical factor in determining the outcome of selection. This new class of models showed that the outcome of competition between related types is now determined by the rate at which the population appropriates the exiguous resources. This rate can be analytically described by the statistical parameter, evolutionary entropy. This quantity, which has its origins in the ergodic theory of dynamical systems, describes the number of accessible pathways of energy flow between the individuals in the population. The discovery and characterization of the evolutionary entropy parameter was the basis for the claim that Darwinian fitness can be described in terms of an evolutionary analogue of the Gibbs-Boltzmann entropy.
The evolutionary entropy concept was originally introduced in the context of demographic models, [
17]. These are processes in which the individuals are parametrized in terms of their age, and the demographic variables, survivorship and fecundity.
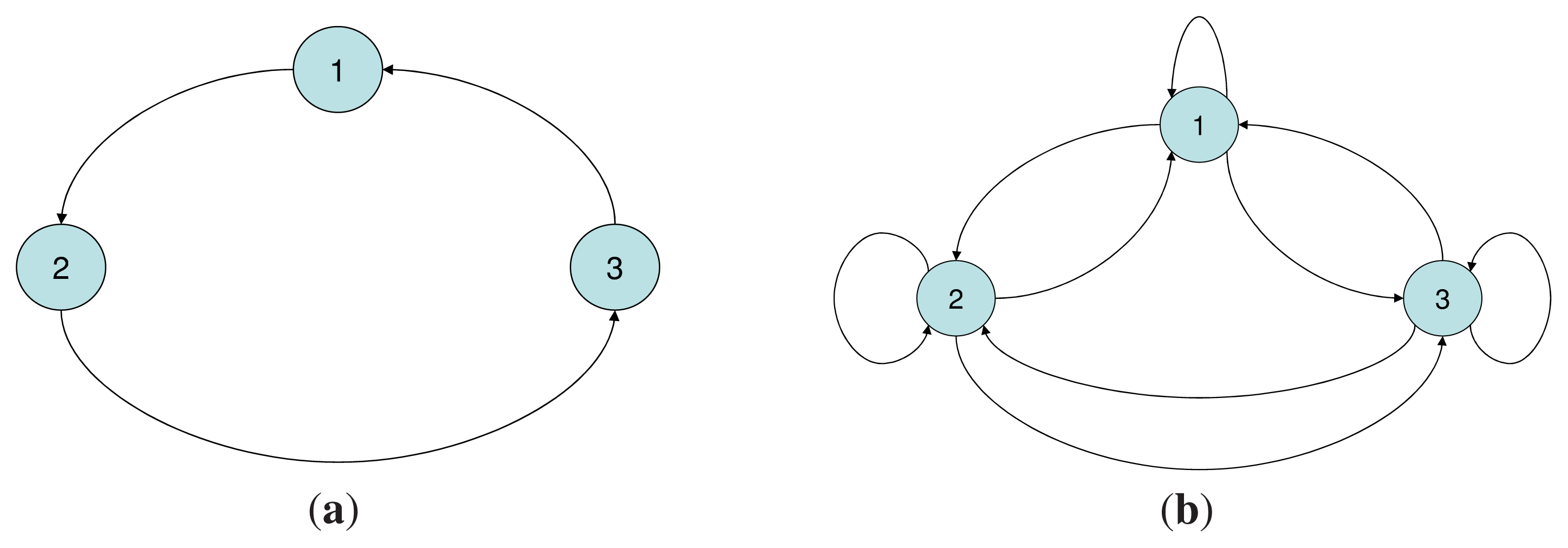
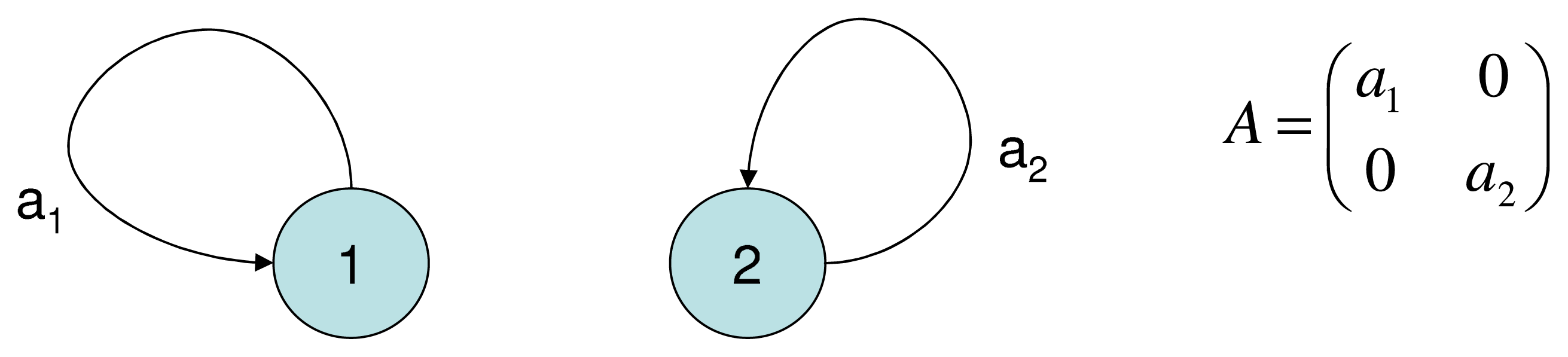
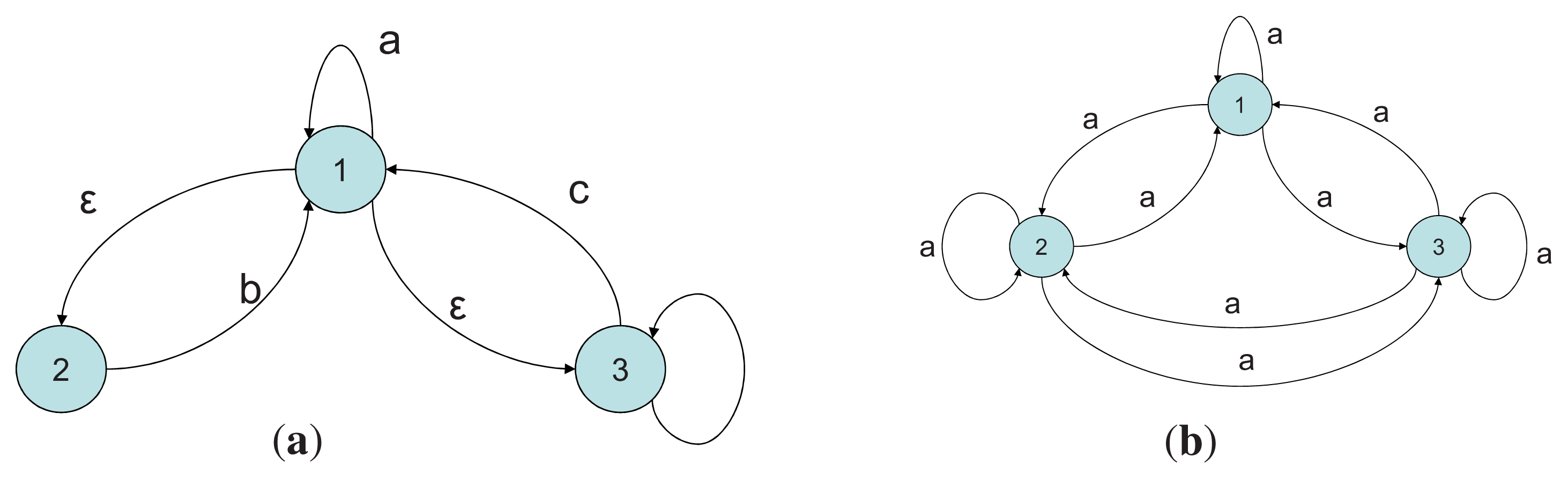
The demographic model is described as a directed graph where the nodes correspond to age-classes, and the links between the nodes describe the aging process–the transition from one age class to the next, and the reproductive process–the transition from a reproductive class to the class of newborns. If age is considered a measure of metabolic energy, then the transitions between the age-classes can be considered as a flow of energy from one age class to another. Evolutionary entropy, in the context of this model, describes the diversity of pathways of energy flow within the network. Annual plants (low entropy) are defined in terms of a unique reproductive event, and consequently a single pathway of energy flow. Perennials (high entropy) are populations with several reproductive events describing their life cycle. These systems define a network with several distinct pathways of energy flow.
Arnold, Demetrius and Gundlach [
18], Demetrius and Gundlach [
19], Demetrius, Gundlach and Ochs [
20] showed that the evolutionary entropy concept originally introduced in demographic systems can also be adduced to characterize the diversity of pathways of energy flow in other biological networks. Generically, one can associate to any network of interacting elements a macroscopic parameter, which describes the number of accessible pathways of energy flow within the system. This measure of network complexity represents the
rate at which the individual elements in the network appropriate and convert energy from the external environment into metabolic energy and reproductive capacity. Evolutionary entropy, which has its origin in the study of energy transformation in a population of living organisms, is thus distinct from thermodynamic entropy, a notion which has its origin in the study of energy transformation in aggregates of inanimate matter.
Thermodynamic entropy is a measure of the number of ways that the molecules in an aggregate of inanimate matter can be arranged to achieve the same total energy. This macroscopic index of the degree of disorder of a material aggregate characterizes the extent to which the total energy is spread throughout the aggregate and shared among the microscopic storage modes.
This review, which complements the earlier report described in Demetrius [
21], is a comparative study of three modes of selection–Malthusian, evolutionary entropic, and thermodynamic. Malthusian and evolutionary entropic selection refer to competition between living organisms for resources provided by the external environment. Thermodynamic selection refers to competition between molecules in an inanimate aggregate which is closed to the input of energy and matter.
In Malthusian selection, the resource provided by the environment is assumed to be unlimited in abundance. The outcome of competition under this resource constraint is determined by the rate at which the organisms convert resources into reproductive work. This rate is precisely the Malthusian parameter. Evolutionary entropic selection is concerned with the dynamics of competition under conditions where the resource abundance is limited. Competitive outcome, when limited resource constraint prevails, is decided by the rate at which an individual acquires energy from the environment and converts this energy into demographic currency. This rate is precisely the macroscopic parameter, evolutionary entropy.
Thermodynamic selection, in contrast to Malthusian and evolutionary entropic selection, occurs in a closed system. Each molecule in the system embodies a quantity of energy which is stored in the different microscopic storage modes–translational, rotational and vibrational. The interaction between the molecules results in an exchange of energy. Molecules are engaged in competition for the total energy in the system. The outcome of competition is described in terms of change in thermodynamic entropy, a measure of the extent to which the energy is spread among the different storage modes.
Malthusian selection provides the conceptual framework for studies of the evolutionary process as enunciated in the works of Fisher [
6]. Evolutionary entropic selection is the cornerstone of directionality theory, the analysis of the evolutionary models reviewed in [
21]. Thermodynamic selection is the process which underlies the statistical thermodynamics of Boltzmann and Gibbs.
These three modes of selection and the relations between them will be described in Sections 1.1 to 1.4. These sections provide a conceptual overview of the main tenets of directionality theory: We also furnish a historical account of earlier efforts, due to Lotka and Fisher, to develop an analytic model of evolutionary dynamics within the framework of the statistical thermodynamics of Boltzmann. This account is given in Sections 1.5 to 1.6.
1.1. Evolutionary Selection–Malthusian and Entropic
The analytical characterization of Darwinian fitness is central to any effort to develop a general theory of evolution by natural selection. Darwin had originally addressed the notion of fitness from the perspective of a naturalist. Selective advantage in Darwin’s terms includes a variety of behavioral features–attributes which are conditional on the environmental constraints which the organism experiences. In situations where competition involved the search for resources, fitness can be described by foraging capacity; when evasion of predators is the critical factor, fitness now involves vigilance and perceptual acuity. These behavioral features are highly qualitative proxies for the capacity to survive and reproduce–the demographic components of fitness. The approach adopted by the pioneers of population genetics abandoned Darwin’s naturalistic standpoint and considered individual birth and death rates as the fitness components which should be invoked in developing an analytic theory.
1.1.1. Malthusian Systems
Fisher’s demographic depiction of Darwinian fitness essentially ignored the environmental constraints which modulate competition, and proposed the Malthusian parameter as a measure of selective advantage.
According to Fisher [
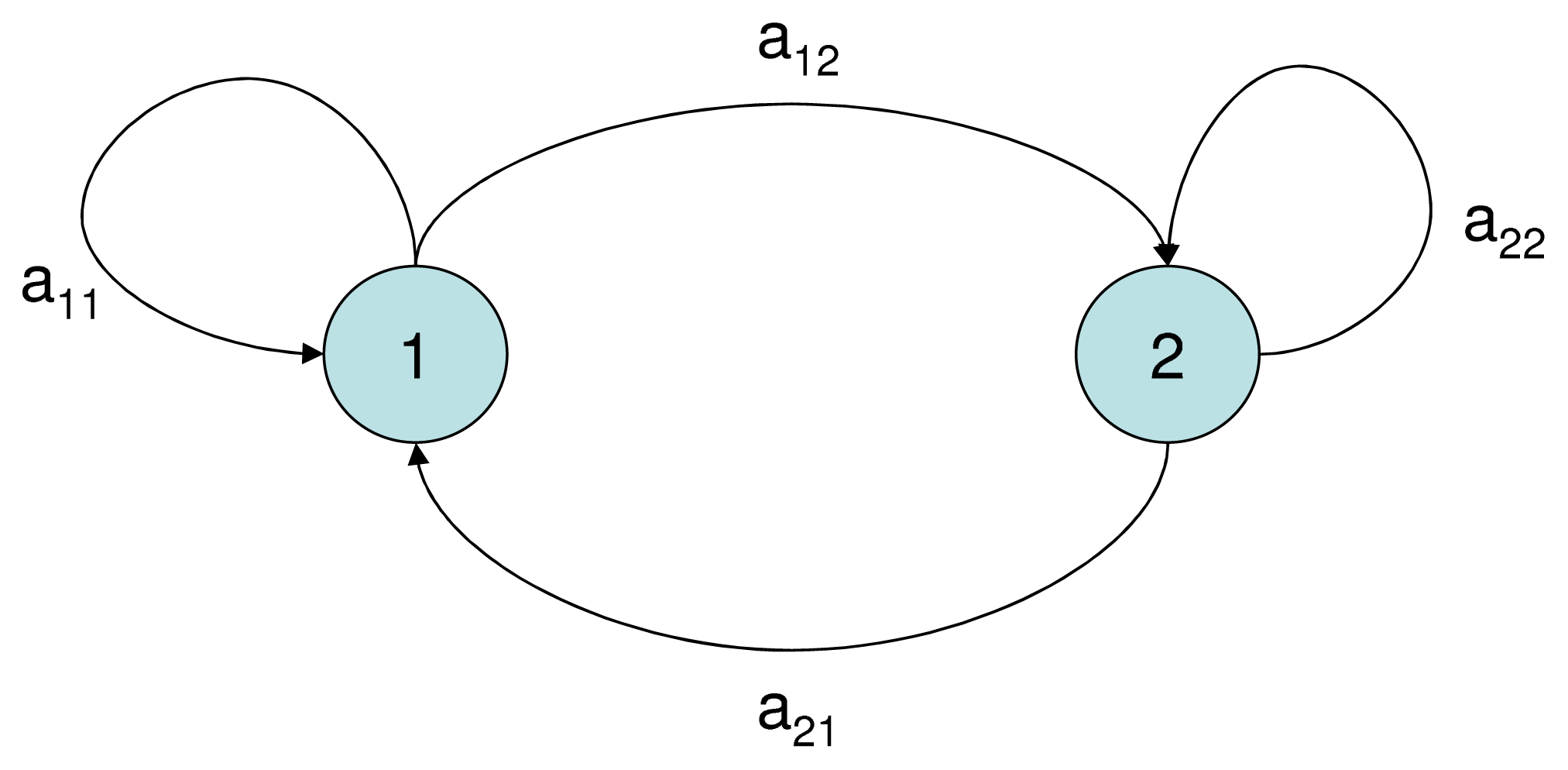
6], selective advantage, that is the capacity of a variant type to displace an incumbent in competition for resources, is given by
Here Δr = r*− r, where r and r* denote the population growth rate of the incumbent and variant type, respectively.
This index of selective advantage is the basis for the following proposition:
I (a) The Malthusian Selection Principle
Evolutionarily stable states of replicating populations maximize the population growth rate.
A population defined by individuals with a prescribed demographic condition, and concomitantly a certain genotypic composition, is said to be evolutionarily stable if it is invulnerable to invasion by a mutant type, that is a variant with a related demographic and genotypic composition. Evolutionarily stable populations will be characterized by a constancy in the growth rate, generation time, and physiological variables, such as metabolic rate. The growth rate will be a maximum, consistent with the nature and composition of the available resources.
The Malthusian selection tenet is an extremal principle. It is related to the Malthusian evolutionary principle, which describes evolutionary changes in population growth rate as one population type replaces another in processes driven by mutation and natural selection.
I (b) The Malthusian Evolutionary Principle
The population growth rate increases under mutation and selection, when resource abundance is unlimited.
The increase in growth rate which the Malthusian evolutionary principle describes, pertains to changes in demographic properties as new variants are introduced in the population and selection drives the population from one steady state to the next.
The Malthusian principles and related tenets based on various surrogates of the population growth rate, have emerged as crucial in efforts to develop a microevolutionary theory, and to apply the theory to the analysis of evolution on ecological and geological time scales. The Malthusian selection principle is now a mainstay in studies of processes such as the evolution of life-history, [
8–
10], and the evolution of cooperation, [
15,
16]. Certain demographic proxies of the Malthusian parameter, such as the net-reproduction rate, have also come to play an important role in epidemiological studies such as the spread of pathogens in animal and plant populations [
12–
14].
Although the Malthusian tenets have provided qualitative insights into these processes, it is now recognized that several of its predictions are inconsistent with empirical observations. The inconsistency is particularly acute in studies of the evolution of life span. For example, models based on the Malthusian principle predict that mortality rate will increase exponentially with age. However, in human populations, although a simple exponential curve–the Gompertzian distribution–provides a good fit for the mortality rate for most populations between ages 35 to 90, mortality rates after age 90 decelerates with age, defining what is called a mortality plateau [
22,
23].
The explanatory weakness and predictive limitations of the Malthusian models resides partly on assumptions which essentially ignore certain critical features of the dynamics of selection, namely:
resource abundance and its diversity,
finiteness of population size,
the variability in age and size at which individuals survive and reproduce.
Although these factors were a critical aspect of Darwin’s qualitative depiction of fitness, they were not completely integrated in analytic studies of the dynamics of selection as described in certain standard texts, see for example [
9,
10].
1.1.2. Evolutionary Entropic Systems
A fundamental aspect of evolutionary processes is the organism–environment dichotomy and the reciprocal nature of the interaction between organism and the environment. The environment impinges on the organism through its disposition of resources, whereas the organism responds to these environmental constraints through the variability in age and size at which individuals reproduce, [
24]. The reciprocity of the organism–environment interaction entails that a population will rarely be at demographic equilibrium. Accordingly, the mathematical formalism which has been developed to study phenomena close to equilibrium will not be applicable to analyze the class of dynamical systems which characterize evolutionary processes.
Studies of dynamical systems beginning in the 1970’s, and due mainly to the efforts of Bowen [
25], Ruelle [
26] and Sinai [
27], have provided new perspectives in the analysis of far from equilibrium systems by the discovery of certain connections between non-equilibrium statistical mechanics and the ergodic theory of dynamical systems. The concept which has played a seminal role in these developments is the Kolmogorov-Sinai or K-S entropy. This notion is a far reaching generalization of the Shannon entropy in information theory. The K-S entropy is an entropy rate. It depicts the maximal information per unit time associated with certain probabilistic dynamical systems. These dynamical systems are mathematical objects, called measure preserving transformations. They are defined in terms of a configuration space, a probability measure on the space, and a transformation on the configuration space which preserves the measure.
The non-equilibrium steady state of certain population processes in which individual birth and death rates are parametrized by age or size can be described as a probability measure on a configuration space, the space of genealogies, that is a recording of successive ancestors indexed by age, [
17,
28].
The entropy of the measure preserving transformation associated with the population process at steady state has emerged as a fundamental property of population dynamics. Three factors underlie this property: First, the entropy is an invariant of the dynamical system. This property means that statistically equivalent parametrizations of the population process in terms of age, size or metabolic state will yield the same value for entropy. Second, the entropy characterizes robustness, that is the rate at which population numbers return to the steady state condition after a random endogenous or exogenous perturbation. Thirdly, the entropy predicts the outcome of competition between related populations. Since the entropy of the population process determines the outcome of selection, we have appended the term evolutionary to distinguish the population concept from its thermodynamic analogue.
The evolutionary entropy concept can be illustrated by considering a model of a plant population in which individual birth and death rates are parametrized by age. In annuals–organisms in which reproduction occurs at a single stage in the life cycle, the flow of energy between the different age classes is described by a unique genealogy. This is a single reproductive cycle involving two stages, an initial stage which describes the seed of the plant, and a final stage which describes the mature plant. In perennials, organisms in which reproduction occurs at several distinct stages in the life cycle, the energy flow between the different age-classes is described by a multiplicity of genealogies, and consequently several distinct reproductive cycles. Evolutionary entropy is a measure of the multiplicity of reproductive cycles. In annuals, there is a unique reproductive cycle, hence a single pathway of energy flow and the entropy is zero. In perennials, the diversity of reproductive stages entails that the entropy will be positive.
The significance of the entropy concept in evolutionary theory derives from the fact that entropy predicts the outcome of competition between an incumbent population and a variant. This outcome is a stochastic event which is contingent on environmental constraints such as resource abundance and resource diversity: Selective advantage is now given by [
5,
29].
Here the parameters Φ and γ are demographic variables which define certain measures of resource constraints–its abundance and diversity, respectively. N denotes the population size and ΔS denotes the difference in entropy of the variant and ancestral type.
The measure of selective advantage given by
Equation (2) is the basis for the characterization of the outcome of natural selection in terms of the following rule [
5,
29]:
II (a) The Evolutionary Entropic Selection Principle
The evolutionarily stable states of a population are extremal states of entropy: maximum entropy, corresponding to resources which are constant in abundance and diverse in composition; minimum entropy, corresponding to resources which are singular and have variable abundance.
The evolutionary selection principle indicates that the resource constraints impose a critical effect on the outcome of selection, and hence on the class of demographic states which render the population invulnerable to invasion by variant types.
The entropic selection principle is the mainstay for long term studies of changes in population properties under mutation and selection. These long term changes are regulated by the resource constraints experienced during the history of the population, and can be qualitatively described by:
II (b) The Entropic Principle of Microevolution
(i) a unidirectional increase in entropy when resource is diverse and has constant abundance; (ii) a uni-directional decrease in entropy when resource is singular and undergoes large variation in abundance.
This principle pertains to global changes in the demographic properties of the population as the system evolves from one non-equilibrium steady state to another. These changes are driven by mutation, which continuously generates new variants in the population, and selection, which opts for types whose demographic properties are consistent with the resource constraints imposed by the environment.
1.1.3. Malthusian and Evolutionary Entropic Systems
The Malthusian principle is expressed in terms of a single parameter, the population growth rate. The principle is based on the assumption that the resource abundance is unlimited and population size is large, effectively infinite. When resource abundance is unlimited, then the outcome of selection is determined completely by the relative ability of the competing types to convert resources into net-offspring production. This capacity depends uniquely on the population growth rate. When population size is large, effectively infinite, then fluctuations in numbers are negligible and the outcome of selection is a deterministic process.
The evolutionary entropic principle, by contrast, is expressed in terms of four parameters: the entropy, the population size, and the resource abundance and resource diversity, respectively. This selection principle is derived on the assumption that resource abundance is limited and population size is finite. Now, when resource abundance is limited, the outcome of selection will be constrained by the relative ability of the competing types to acquire the exiguous resource from the external environment. This capacity to annex resources will depend on the robustness or stability of the population as measured by evolutionary entropy. When population size is finite, the fluctuations in population numbers induced by endogenous perturbations entail that the process of selection will now be a stochastic event.
These observations suggest that the Malthusian tenet, which assumes unlimited resources and infinite population size will be a limiting case of the entropic selection rule, which assumes limited resources and finite size. The relation is concisely expressed by the following proposition:
(A): The Malthusian principle is the limit, as the population size and resource abundance tends to infinity, of the entropic selection principle.
The entropic selection principle is not restricted to biological systems whose structure derives from demographic variability, that is differences in the age or developmental state at which individuals reproduce and die. The ergodic theory of dynamical systems has been exploited to analyze structures which derive from
(a) molecular heterogeneity, that is differences in the chemical composition of the substrates that define metabolic systems, and the differences in the rates at which substrates are transformed into products;
(b) ecological variability, that is the differences in the mode and intensity of interaction between the species in an ecosystem. The statistical parameter evolutionary entropy can also be defined for the metabolic and ecological networks associated with these systems, [
18–
20].
The various components–molecules, organisms, and populations–that constitute the metabolic, demographic and ecological systems, respectively, can also be considered in bioenergetic terms, namely, as isothermal chemical machines that transform resources from the environment into chemical energy. In this context, evolutionary entropy depicts a generic property of biological networks: it is a statistical parameter which describes the diversity of the pathways of energy flow between the individual elements that define the network.
1.2. Thermodynamic Selection
Thermodynamic entropy pertains to material aggregates–solids, liquids, gases. The molecules in the aggregate store translational, rotational, vibrational, and intermolecular energies which depend on the distance separating the molecules. Thermodynamic entropy is a measure of the extent to which the total energy is shared by the different storage modes [
30].
A crystalline solid has low entropy. The intermolecular forces are strong thus restricting the spread of energy to the neighborhood of certain fixed positions in the solid. A liquid has high entropy since the weakness of the forces between the molecules permits a larger spreading or sharing of the energy among the various storage modes.
The crowning achievement of Boltzmann’s statistical thermodynamics was his exploitation of the entropy concept to give a mechanistic rationale of the time asymmetric behavior of the flow of heat in material bodies.
Boltzmann’s thermodynamic entropy is a measure of the number of ways that the molecules in the system can be arranged to attain the same total energy. Boltzmann’s entropy agrees with the macroscopic thermodynamic entropy of Clausius when the system is at equilibrium. Macroscopic evolution in aggregates of inanimate matter is described by the directional change in the Boltzmann entropy, a quantity which increases and tends to a maximum. The time asymmetric behavior of the transduction of energy in macroscopic systems can thus be expressed by the following extremal principle.
(III) The Thermodynamic Selection Principle
The thermodynamically stable states of material aggregates are the states which maximize entropy.
Thermodynamic stability refers to the invariance in time of mechanical, chemical and thermal properties of the system. Maximum thermodynamic entropy denotes an energy distribution in which the degree of spreading and sharing of the energy among the microscopic states of the system is maximal.
The equilibrium state in thermodynamic systems is the outcome of a dynamic process involving collision between the particles that constitute the aggregate. This process is essentially driven by differences in the extent to which the total energy of a molecule is shared among the various microscopic storage modes. Accordingly, it can be considered, by analogy with evolutionary systems, a process of selection.
The thermodynamic selection process will be parametrized by what we will call, by formal analogy with
Equation (1), the selective coefficient, denoted
s, and we write
where ΔS̃ = S̃* − S̃, and S̃ and S̃* denote the thermodynamic entropy at time t and t + 1, respectively. The condition s > 0 describes the direction of spontaneous change in entropy in an isolated system.
1.3. Thermodynamic and Evolutionary Processes
Evolutionary selection and thermodynamic selection pertain to open and isolated systems, respectively.
The selection principle for evolutionary systems refers to biological networks: metabolic, demographic and ecological. These networks are open systems: they require resources from the external environment in order to drive their organization and maintain their integrity.
The microscopic variables that describe the properties of the individual elements that comprise these networks are quantities such as the age specific fecundity and mortality rates (demographic networks), enzymatic reaction rates (metabolic networks), speciation and extinction rates (ecological networks). The ergodic theory of dynamical systems provides a methodology for generating a class of macroscopic variables from the individual level parameters. The principal macroscopic variables can be described as follows.
- (a)
The growth rate r.
This macroscopic parameter describes energy yield per unit time. In the case of demographic networks, this quantity is the population growth rate.
- (b)
The cycle time T.
This macroscopic variable describes the mean recurrence time of the Markov chain associated with the network. In the case of demographic models, the mean recurrence time is the generation time, the mean age of mothers at the birth of their offspring.
- (c)
Evolutionary entropy S.
This quantity describes the number of pathways of energy flow within the network.
- (d)
The reproductive potential Φ.
This parameter describes the rate at which the organism appropriates energy from the external environment and converts this energy into metabolic activity.
Each of these macroscopic variables are functions of the microscopic parameters that describe the kinetic properties of the elements that compose the network. These four parameters are related by the identity
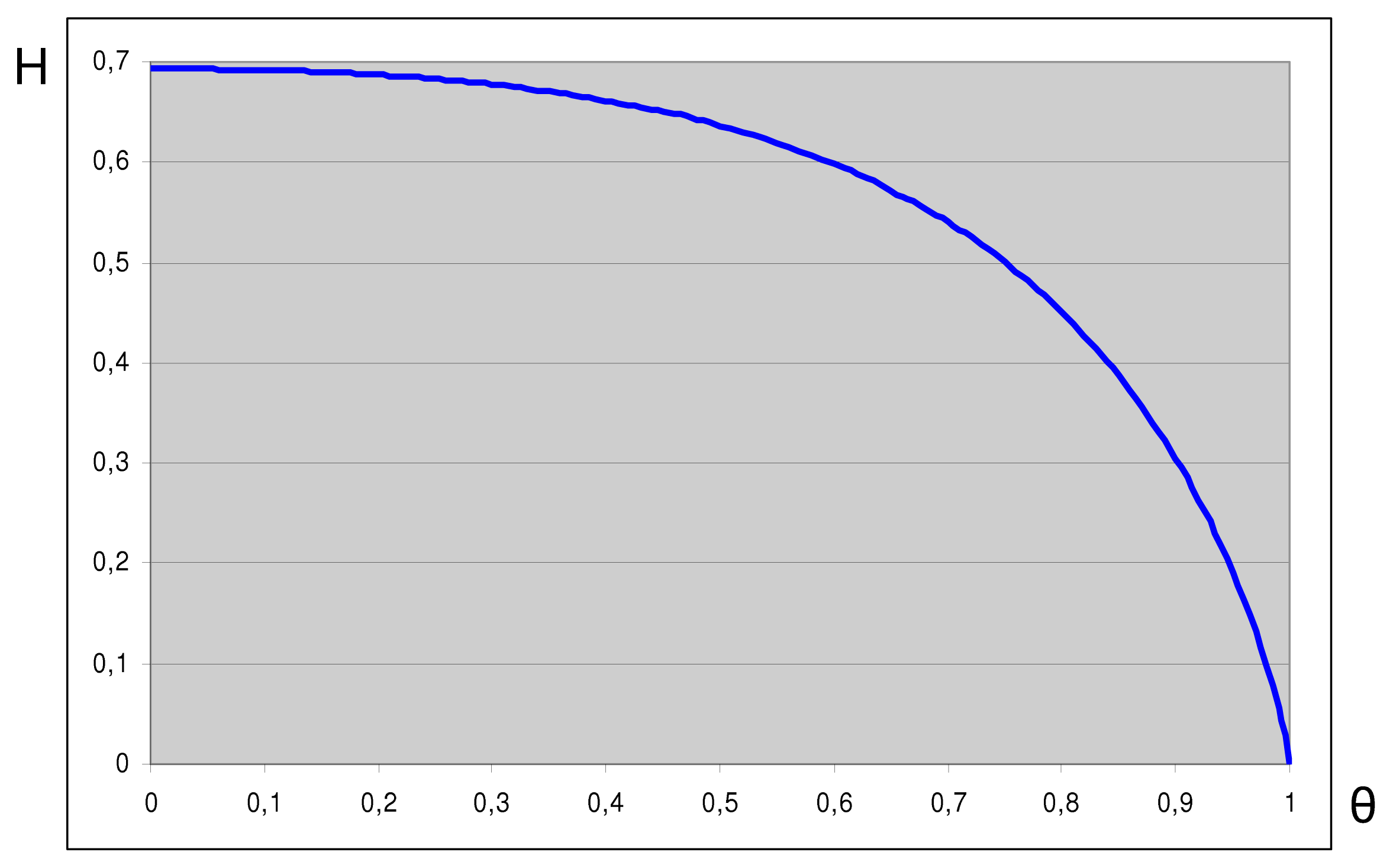
The quantity H = S/T describes the rate at which the organism appropriates energy from the external environment and transforms this energy into reproductive activity. The quantity H describes energy yield per unit resource.
The expression (
3) can be exploited to determine a relation between the change in evolutionary entropy,
dS, and the change in the metabolic rate
dP. If we consider perturbations which ensure that the cycle time
T remains constant, then the change
dS in entropy, induced by a change
dP in the metabolic rate, becomes, [
31]
The thermodynamic selection principle refers to competition within aggregates of inanimate matter. The elements that constitute these macroscopic aggregates are molecules. Each molecule stores energy in translational, vibrational and rotational modes. Statistical mechanics furnishes a methodology for characterizing the macroscopic variables that describe the material aggregate. These quantities are
- (a)
The free energy F̃.
Free energy is that component of the total energy of a system which is capable of doing work under isothermal conditions. Accordingly, the free energy can be considered as the potential energy of a system held at constant temperature.
- (b)
The temperature T̃.
This macroscopic variable describes the mean kinetic energy of the molecules that compose the system.
- (c)
Thermodynamic entropy S̃.
The entropy is a measure of the extent to which the total energy in the system is spread and shared among the different microscopic storage modes.
- (d)
Internal energy Ũ.
This quantity describes the total amount of energy in the molecules that compose the system.
The four thermodynamic variables are related by the identity:
Thermodynamic entropy also admits a macroscopic representation, analogous to
Equation (4). The relation, which was discovered by Clausius, identifies the change in entropy
dS̃, with the quantity of heat added
dQ̃, and the temperature
T̃A comparison of the identities (
3) and (
5), and the macroscopic characterizations of entropy given by
Equations (4) and
(6) indicates a formal correspondence between the thermodynamic and evolutionary parameters. This correspondence is given by
Table 1.
Thermodynamic theory and evolutionary theory are concerned with energy transformations in aggregates of inanimate matter and populations of living organisms, respectively. The two most fundamental parameters associated with the two theories are thermodynamic entropy and evolutionary entropy. In
Table 2, we contrast the statistical and macroscopic depictions of the two measures of entropy.
Now, the metabolic processes that regulate energy transformation in cells can be considered as a thermodynamic process, with temperature as the organizing variable, and as an evolutionary process, with generation time as the integrating parameter. In these processes, the inverse temperature is analytically related to the mean cycle time [
21]. We will appeal to this relation between temperature and generation time to establish the following proposition.
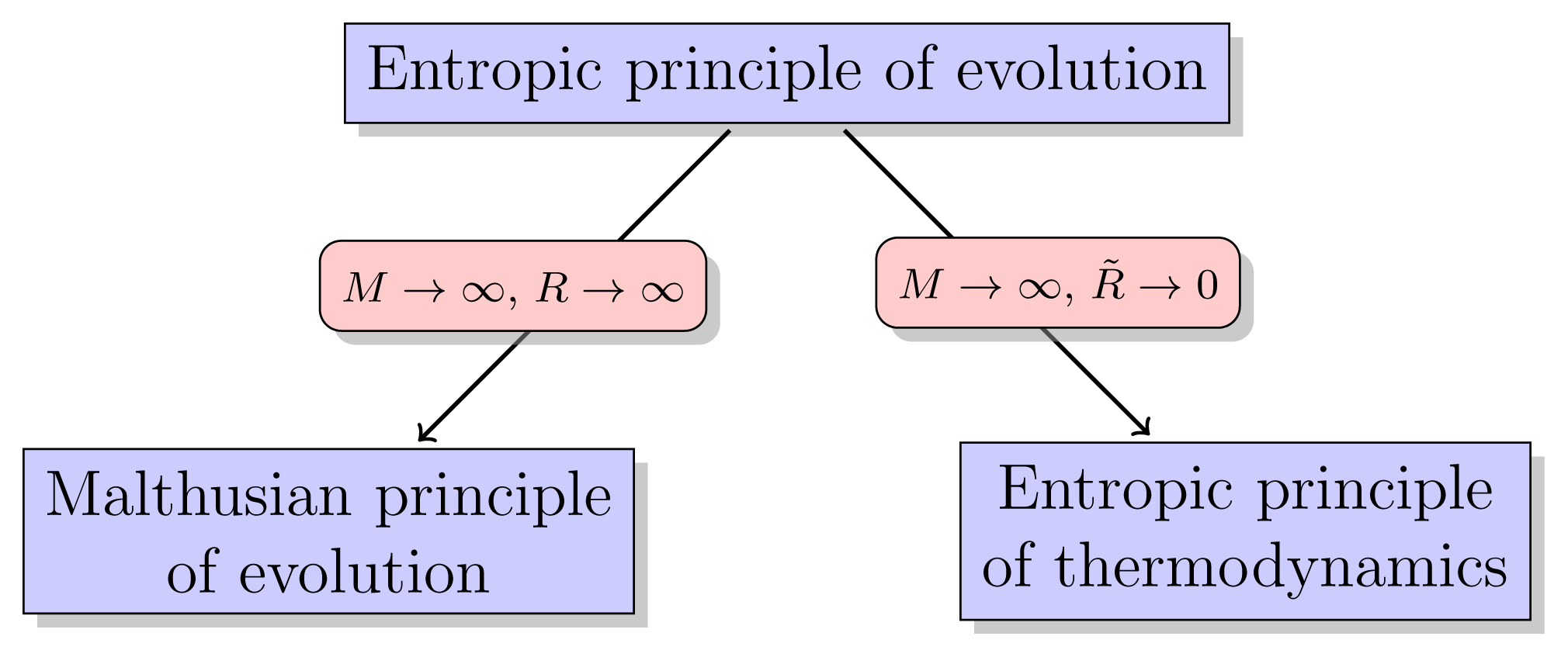
(B): The thermodynamic selection principle is the limit, as M → ∞, R̃ → 0, of the evolutionary selection principle.
The parameter M denote population size and R̃ denote the resource production rate. The condition R̃ → 0 means that the system, which was originally open to the input of energy and matter, now becomes a closed system.
1.4. The Selection Principles
We will distinguish between three modes of selection. The first two, evolutionary entropic selection and Malthusian selection, pertain to populations of metabolic entities: metabolic networks, cells and higher organisms. Evolutionary entropic selection is defined for populations subject to limited resource conditions and finite population size. Malthusian selection is defined for populations subject to unlimited resource conditions and large, effectively infinite size. The third mode of selection pertains to aggregates of inanimate matter, solids, liquids and gases. The systems in this case are isolated, and selection is said to be thermodynamic.
Now, according to the evolutionary entropic principle, the evolutionarily stable states are extremal states of entropy–maximum entropy, corresponding to constant resources, minimum entropy corresponding to resources with large variation in abundance.
The Malthusian selection principle and the thermodynamic selection principle, as indicated by the propositions (A) and (B), are both limiting cases of the evolutionary entropic tenet. Selection in the Malthusian model occurs when resource abundance is unlimited and population size is effectively infinite. The evolutionary stable states are states which maximize the population growth rate.
Selection in the thermodynamic model refers to systems which are closed to the input of energy and matter. The system is assumed to be large, consisting of an infinite number of particles. The thermodynamically stable condition is now described by states which maximize thermodynamic entropy.
The analytic relationship between the evolutionary entropic principle and the two tenets–the Malthusian principle and the thermodynamic principle–is described in
Figure 1.
1.5. Historical Digression: Mendel and Malthus
The Darwinian evolutionary process can be considered as involving two complementary events. The first is natural selection–competition between phenotypically related types for the available resources. The second is the transmission of inheritance–cooperation between related types in the transfer of the genetic endowment.
The selection event occurs during the period when the variant types generated by mutation are introduced in the population–the invasion process. The outcome of competition which defines the invasion process is determined by the relative capacity of the resident and variant types to acquire resources and to convert these resources into offspring production.
Darwin, whose understanding of the competition process was largely influenced by Malthus, assumed that the outcome of selection is determined by the rate of increase of population numbers–a property now called the Malthusian parameter.
The transmission of inheritance is described by the recombination of variant and incumbent types to generate a new array of types–the establishment process. Cooperation of parental alleles defines the recombination event. It is determined by the rules of inheritance which dictates the transmission of phenotypic traits from parent to offspring.
Darwin invoked the prevailing model of blending inheritance as the rule which describes the transmission of characters. According to this model, which seemed consistent with Darwin’s investigation of domesticated organisms, the characters of parents were blended in the offspring. Hence, the genotype of the offspring of a cross will be intermediate between those of the two parents.
It is of some historical interest that Malthusian selection and the blending of parental heredities, two basic premises of Darwin’s theory, are both fundamentally flawed, although both seem highly consistent with empirical observations. The plausibility of both principles derives from the fact that they are both valid under certain idealized situations. The Malthusian principle is indeed valid when resources are unlimited in abundance and population size is effectively infinite. The theory of blending inheritance is a viable effective explanatory model when the number of genes specifying a character is large, effectively infinite.
Mendel’s model was proposed in 1840. The model, however, was largely ignored until its rediscovery by de Vries and Correns in 1900. However, the significance of Mendel’s theory was only fully appreciated when it was recognized that the theory of blending inheritance can be considered a limiting case of Mendel’s atomic model. This can be formally depicted in terms of the following proposition.
(I) The principle of blending inheritance is the limit, as n → ∞, where n is the number of genes controlling a character, of the principle of particulate inheritance.
This proposition accounted for the observation that quantitative traits such as height and weight appear to be the result of the fusion of different types. Consequently, the theory of blending inheritance can be understood as an approximation to Mendel’s model of particular inheritance.
The Malthusian principle of selection was proposed in 1930, [
6]. It has for several decades dominated studies in evolutionary demography. This dominance derives in large part from its apparent rapport with studies of competition under laboratory conditions. However, several anomalies in other empirical contexts were documented. For example, studies of selection in bacterial populations indicate that certain bacterial strains with lower growth rate can replace ancestral strains.
The analytical foundation for the entropic principle of selection was described in 1974, [
17]. The principle resolved several anomalies in evolutionary genetics, [
29], and explained various observations regarding the spread of pathogenic strains of microorganisms under various classes of ecological constraints, [
32]. The principle also explained certain phenomena such as the existence of a mortality plateau in human population–a condition which is inconsistent with the Malthusian framework, [
29].
The resistance to the acceptance of the entropic principle, [
33,
34], hinges on the fact that the Malthusian proposition is a valid tenet under certain idealized conditions. A critical factor in the gradual erosion of this resistance is the recognition, which this review delineates, of the formal relation between the Malthusian proposition and the entropic principle.
(II) The Malthusian principle of selection is the limit, as N → ∞, R → ∞, where N denotes population size, and R denotes resource abundance, of the entropic principle of selection.
This proposition implies that the Malthusian tenet is an approximation to the entropic selection principle, an approximation whose validity increases as the resource abundance and population size increase.
The entropic selection principle and Mendel’s theory of particulate inheritance formalize the competitive and cooperative processes that comprise Darwin’s theory. Directionality theory is the integration of these two tenets in a mathematical model. The theory aims to explain the biological diversity and the adaptation and stability of biological systems at levels of organization–molecular, cellular and multicellular, of increasing complexity, and operating over time scales–generational, ecological and geological, of increasing amplitude.
1.6. Historical Digression: Lotka, Fisher
Irreversibility of natural processes in aggregates of inanimate matter is a common phenomenon. The canonical example of an irreversible process is the tendency of energy to migrate as heat from hotter to colder bodies. The mechanism driving such directional change has been completely elucidated, due primarily to the work of Clausius and Boltzmann. Clausius showed that the irreversibility of natural processes implied the existence of a macroscopic parameter which he called entropy. Boltzmann gave a statistical characterization of the Clausius entropy and established that the entropy increases in isolated systems.
Directional change in macroscopic population variables in living systems is also a ubiquitous phenomenon. The parameter that has played a critical role in studies of directionality in processes involving living organisms is size, typically the body size of an adult organism. Cope [
35] seems to have been the first to systematically analyze changes in body size over evolutionary time. Using fossil data, Cope observed that there is a tendency towards size increase within certain lineages. More recent studies of the fossil data has shown that the increase in body size is not a universal property. There exist several lineages where size decreases. One of the more striking examples of this variation in directional changes in body size is given by the equid lineage. The studies, as documented by Alberdi
et al. [
36], indicate an increase in size in North America, and a decrease in size in Europe during the Paleocene era. The ecological conditions in America and Europe were significantly different during that period. This suggests that directional changes in body size are conditional on ecological constraints.
Recent experimental investigations of mutation and natural selection based on populations of polynucleotides, Domingo
et al. [
37] have shown that directional changes in size at the molecular level are also highly contingent on environmental conditions. Domingo
et al. [
37] reviewing experimental studies in Spiegelman [
38] and Eigen [
39] showed that when resources are limited and constant, size, as measured by sequence length of polynucleotide, increases. However, when resources are abundant, size decreases.
The problem of irreversibility in populations of living organisms, as documented in organismic and molecular evolution, can be formulated as follows: Does there exist a biological analogue of thermodynamic entropy whose change under mutation and selection will explain the directionality observed in living systems?
Analogues of the entropic principle in thermodynamics which have been proposed to address this question have been developed from two complementary perspectives–the first bioenergetic, proposed by Lotka [
40], the second demographic, advanced by Fisher [
6]. Both viewpoints are now recognized to have serious limitations.
1.6.1. Bioenergetic Considerations—Lotka and the Thermodynamic Paradigm
Lotka’s analysis of the problem of directionality was based on a characterization of Darwinian fitness in terms of the efficiency with which organisms transform the free energy of the resources into metabolic energy. The organisms that prevail are those that capture and use energy at a rate and with an efficiency which exceeds the rate and efficiency of competing types. Lotka exploited this measure of fitness to show that changes in the distribution of energy and matter, as one population type replaces another, can be described by the following precept:
(I) The rate of circulation of matter throughout the system increases under natural selection.
Lotka’s principle was embraced by several theoretical biologists as a fundamental rule with implications for the understanding of adaptation and evolutionary trends at various levels of biological organization, molecular, cellular and ecological, (Wicken [
41], Ulanowicz [
42], Schneider and Kay [
43]).
The analytical basis for Lotka’s principle derives from a postulate, called the thermodynamic paradigm for living systems, Schneider and Kay [
43]). According to this postulate, the patterns of biological evolution are phenomenological manifestations of the Second Law of Thermodynamics (for an appraisal of this perspective, see Schneider and Sagan [
44]). The thermodynamic paradigm underscores the distinction between isolated systems, which are closed to the input of energy and matter, and open systems which exist in a world of energy and material fluxes.
Energy transformation in isolated systems is governed by the laws of equilibrium thermodynamics. Entropy in classical thermodynamics can be expressed by the Clausius relation
Here dS̃ denotes the change in entropy, dQ̃ the heat added to the system and T̃ the absolute temperature.
Thermodynamic selection refers to competition between the individual molecules for the total energy contained in the material aggregate. Hence the selective advantage s, is given by
Here ΔS̃ is the difference, at successive times, in the extent of energy spreading within the microscopic storage modes associated with each molecule.
Energy transformations in
open systems are contingent on the action of energy and material fluxes on the steady state configurations of the system. In systems where the steady states are close to the equilibrium configuration—this includes physical systems such as the Benard cell—energy transformation can by analyzed in terms of the formalism of dissipative structures, Nicolis and Prigogine [
45].
Wicken [
41], Schneider and Kay [
43] have argued that the formalism of dissipative structures is also applicable to far from equilibrium systems, that is systems, like living organisms, that are dependent on fluxes of matter and energy from the external environment in order to maintain their organization.
The application of the formalism of dissipative structures to evolutionary theory is based on the assumption that the thermodynamic concept, entropy production, defined for physico–chemical systems, see Nicolis and Prigogine [
45], can be considered a measure of the efficiency with which biosystems appropriate energy from the environment and distribute this energy throughout the various units that compose the system. Systems endowed with a greater efficiency will have a selective advantage, hence the entropy production of the system will increase as more efficient types replace their less efficient competitors. Consequently, the rate of circulation of matter and energy in the system, a measure of the entropy production rate, will also increase.
This thermodynamic model of the evolutionary process has been adduced in studies of ecosystem dynamics to propose various correlations between temperature and ecosystem parameters such as species diversity, and ecosystem productivity. However, empirical studies of the relations between these thermodynamic and ecosystem parameters are not consistent with the various claims advanced by the proponents of the model. For example, contrary to the predictions of the thermodynamic paradigm, there is no correlation between the temperature of ecosystems and their productivity.
Although heat is the most familiar mode of energy transfer in aggregates of inanimate matter, it is an inefficient means of transferring energy in living organisms. This inefficiency issues from the fact that the maximum work which may be obtained from a heat engine is given by the equation
Here
q is the heat absorbed, and
T2 and
T1 are the absolute temperatures of the aggregates of matter between which the heat passes. Since there are no significant differences between the different parts of a cell or between the different tissues in an organism, cells cannot function as heat engines, Lehninger [
46].
The isothermal nature of living organisms imposes certain fundamental limitations on the thermodynamic paradigm invoked by Lotka as a model for understanding the dynamics of selection in biotic systems.
1.6.2. Demographic Systems—Fisher and the Malthusian Paradigm
The demographic approach to formalizing Darwinian fitness has its origin in Malthus’ study of population dynamics. The main thrust of Malthus’ theory was the distinction between the exponential growth of a population and the linear growth of resources. Malthus argued that, in view of these qualitative differences in growth rate, populations will eventually be subject to resource limitations—a condition which would lead to intense competition. This observation entailed a struggle for resources as a mechanism for evolutionary change—an implication Darwin explicitly acknowledged in The Origin of Species.
Inspired partly by Darwin’s acknowledgment, Fisher [
6] proposed the population growth rate, which he canonized as the Malthusian parameter, as a measure of Darwinian fitness. The main contribution of Fisher to the formalization of Darwin’s argument is the fusion of the Malthusian demographic models with the Mendelian laws of inheritance to study changes in
mean fitness, that is the mean population growth rate, under natural selection. This contribution is expressed in the following proposition, Fisher [
6].
(II) The mean fitness of a population increases under natural selection.
The above statement ascribes a direction to the process of natural selection—a property which Fisher considered to be analogous to the increase in entropy which characterizes the thermodynamic selection principle in inanimate matter.
The measure of selective advantage in the Fisherian model is given by
Here Δr is the difference in growth rate between the incumbent and the variant type.
This measure of selective advantage is the rationale for the Malthusian selection principle: The outcome of competition between related populations is a deterministic process which is predicted by the population growth rate.
The Malthusian tenet which formed the cornerstone of Fisher’s model, has been cited as the cardinal rule for elucidating the dynamics of evolutionary processes in several contexts: molecular and viral evolution, Domingo
et al. [
37]; the evolution of life history, Charlesworth [
47], Roff [
9], Houston and McNamara [
48]; the evolution of aging, Hamilton [
11]. However, the implications of the Malthusian principle are often inconsistent with empirical observations. For example, the Malthusian models predict that mortality rates in natural populations should increase exponentially with age—the Gompertzian distribution. However, large scale studies of senescence in several animal and in modern human populations have revealed mortality rates that level off at advanced ages—the so called mortality plateau, Carey
et al. [
49].
This fundamental limitation of the Malthusian parameter as a measure of fitness was only recently elucidated, [
5,
29]. These studies show that the Malthusian parameter predicts the outcome of selection only under idealized conditions, namely, when resources are unlimited and population size is large, effectively infinite. When resources are limited, and vary in abundance and composition, and when population size is finite, the outcome of selection is now determined by the rate at which organisms appropriate resources from the external environment, a property which is analytically described by evolutionary entropy, [
5].
2. Organization of Paper
Directionality theory is a mathematical model of the Darwinian theory of evolution by variation and natural selection. The key concept in directionality theory is evolutionary entropy, a statistical parameter which describes the rate at which organisms appropriate resources from the external environment and the efficiency with which these resources are reinvested into net-offspring production. The mathematical basis of the evolutionary entropy concept and the relation of the concept to thermodynamic entropy is described in Section 3.
Classical models of the evolutionary process characterize the population dynamics in terms of two macroscopic parameters, population growth rate and generation time. Experimental studies of competition between populations indicate that these two parameters predict the outcome of selection only under certain restricted class of ecological constraints. In Section 4 we exploit the ergodic theory of dynamical systems to show that the prediction of the outcome of selection under general ecological constraints requires a new class of macroscopic variables, in particular, the quantity evolutionary entropy.
Section 5 exploits this evolutionary entropy concept to study the dynamics of competition for resources between related populations–an incumbent population and a variant. The outcome of competition is described in terms of the following tenet:
The entropic selection principle
When resources are constant in abundance and diverse in composition, variants with increased entropy will have a selective advantage and increase in frequency. When resources vary in abundance and resource composition is singular, variants with decreased entropy will have a selective advantage and increase in frequency.
Section 6 reviews the relation between complexity and stability in the context of biological networks—metabolic, demographic and ecological. Complexity is characterized in terms of evolutonary entropy, and stability by the rate at which the population returns to the steady state after a random endogenous or exogenous perturbation. The relation between these two macroscopic properties is expressed by
The complexity-stability theorem
Changes in evolutionary entropy and changes in stability are positively correlated.
Evolutionary entropy is a statistical measure of the number of accessible pathways of energy flow within the population. The complexity–stability theorem, Demetrius, Gundlach and Ochs [
50], thus reflects the intuitive notion that as the number of pathways of energy flow increases, the resilience of the population to endogenous and exogenous perturbations also increases.
The entropic selection principle and the complexity-stability theorem are the main precepts that describe the evolutionary dynamics of metabolic, demographic and ecological networks. These include populations of replicating molecules, age and size-structured populations, communities of interacting species.
The entropic selection principle and the complexity–stability theorem also apply to the analysis of social networks, that is populations of organisms whose resource allocation among themselves is determined by certain rules of cooperation. The analytic study of the evolutionary dynamics of social behavior, which we call the Entropic theory of sociality, can be developed from both genetic and phenotypic perspectives.
The genotypic viewpoint was introduced by Hamilton, [
51], and has its origin in models of classical population genetics. Hamilton’smodel, called
Inclusive fitness theory, considers the individual as the uni of selection. The evolution of social behavior is analyzed in terms of the genes that determine the social interaction between pairs of individuals–the performer of the behavior and its recipient. The fundamental parameter in this study is the coefficient of kinship–the genetic relatedness between actor and recipient. Fitness in this model is described in terms of net-offspring production. The fitness associated with the social network is the sum of the fitness of the actor and the fitness of the recipient–a quantity which is weighted by the coefficient of kinship.
The cornerstone of Inclusive fitness theory is Hamilton’s rule. This asserts that the evolution of altruism and selfishness, two cardinal measures of sociality, can be qualitatively described as follows.
- I(a)
When genetic relatedness is high, altruism will have a selective advantage.
- I(b)
When genetic relatedness is low, selfishness will have a selective advantage.
The phenotypic perspective regarding social behavior described in this review considers a population of individuals as the unit of selection. A social network is described in terms of a directed graph where the nodes correspond to individuals and the links between nodes represent the nature and intensity of the interaction. The analysis of the evolution of social behavior in this model is based on what we have called:
The Entropy–Sociality Rule
Evolutionary entropy parametrizes the position of a population along a sociality–continuum: low entropy depicting a network consisting of individuals with selfish dispositions, high entropy characterizing a network consisting of individuals with cooperative dispositions.
Our analysis of the evolution of social behavior distinguishes between the ecological constraints (limited and unlimited resources), and the demographic conditions (finite and infinite population size) which determine the selective process.
This study is developed in Section 7. The rules which we derive are classified according to the resource constraints which operate. These rules and can be qualitatively annotated as follows:
- (a)
Limited resources
When resource abundance is limited and population size is finite, the outcome of selection will be decided by the capacity of individuals to appropriate resources from the environment. The selective process will be regulated by the level of resource abundance and its degree of heterogeneity. The predicted correlation between resource patterns and behavioral dispositions can be described as follows.
- II(a)
When resource abundance is constant, and resource composition diverse, cooperative traits will have a selective advantage.
- II(b)
When resource is subject to large variation in abundance, and resource composition is singular, selfish traits will have a selective advantage.
- (b)
Unlimited resources
When resource abundance is unlimited and population size is large, effectively infinite, the level of resource abundance is no longer a decisive factor in the selective process. Darwinian fitness, the capacity of a type to contribute to the ancestry of the next generation, will now depend on the rate at which the organisms convert the available resources into offspring production. Phenotypic relatedness now emerges as a critical factor in deciding the outcome of selection. The evolutionary rules describing social behavior can now be depicted as follows.
- III(a)
When phenotypic relatedness is high, cooperation will have a selective advantage.
- III(b)
When phenotypic relatedness is low, selfishness will have a selective advantage.
Now Hamilton’s rule, as expressed by (I), derives from models of classical population genetics. These models implicitly assume that resources are unlimited and that population size is large, effectively infinite. In Section 8, we will extend the domain of application of Inclusive fitness theory by incorporating the effects of resource constraints and population size on Hamilton’s model. We will show, in the framework of this gene-centric model, that the evolution of altruism and selfishness can be described in terms of propositions which are analogous to (II) and (III). The propositions are as follows:
- (IV)(a)
When resources are of limited abundance, and population size is finite, the evolution of social behavior is conditional on the resource constraints, namely the degree of variation in abundance and the heterogeneity in composition
- (IV)(b)
When resources are of unlimited abundance, and population size is large, effectively infinite, then the evolution of social behavior is contingent on the genetic relatedness.
These results indicate that Hamilton’s rule, which is derived from the assumption that the genetic evolution of social behavior is determined exclusively by the degree of genetic relatedness, refers uniquely to conditions where resource abundance is unlimited, and population size is large, effectively infinite. Our analysis indicates that when resource abundance is limited and population size is finite, genetic relatedness is no longer the deciding factor. This observation, which makes explicit the domain of application of Inclusive fitness theory, can be summarized in terms of the following dictum.
Hamilton’s Rule and the Entropic Principle of sociality: Hamilton’s rule is the limit, as resource abundance and population size tend to infinity, of the entropic principle of sociality.
The above proposition entails that Hamilton’s rule, and its various elaborations proposed by recent investigators, see, for example, Bourke [
15], is an
approximation to the entropic principle of sociality–an approximation whose validity increases, as resource abundance and population size increase.
Section 9 appeals to a new theory of bioenergetics–quantum metabolism–to derive analytic relations between evolutionary entropy and a suite of organism and population level parameters. An analytical relation between entropy and body size, which emerges from these studies, will be a central element in the analysis of microevolutionary and macroevolutionary trends in body size.
Section 9–11 are concerned with evolutionary dynamics on ecological and geological time scales. The evolutionary process on these time scales involves the integration of an invasion dynamics, which is described by the entropic selection principle, and an establishment process, which involves the laws of Mendelian inheritance. Section 9 appeals to the entropic selection principle and the laws of Mendelian inheritance to derive the fundamental theorem of evolution, and a class of directionality principles for evolutionary change under speciation and extinction, [
21].
The fundamental theorem of evolution
- A(i)
When resources are constant in abundance and diverse in competition, evolutionary entropy increases.
- A(ii)
When resources undergo large variation in abundance and is singular, evolutionary entropy decreases.
These principles pertain to long term changes in entropy as one population type replaces another due to the continual action of mutation and selection.
Certain aspects of this microevolutionary principle have been evaluated using demographic data of Swedish and French populations during the last 200 years [
52,
53]. These studies have been shown to be consistent with the fundamental theorem of evolution.
The study of evolutionary dynamics as concisely described in terms of the rules A(i) and A(ii), is based on the analysis of changes in the genotypic and phenotypic composition of a population as new types are introduced by mutation and the population composition reordered by selection. The model imposes certain critical ecological and demographic constraints: resource abundance is limited, and population size is finite. The changes in entropy described by the two tenets refer to global shifts in population composition as the system evolves from one non-equilibrium state to another under the mutation–selection regime.
The Fisherian model of the evolutionary process, as articulated by the fundamental theorem of natural selection, entails that mean fitness increases. The theorem is concerned with changes in genotypic and phenotypic composition under a single force, namely selection. The changes in genotypic composition due to mutation–a central factor in the process described by the entropic principle of evolution–is ignored in Fisher’s model. The Fisherian analysis implicitly assumes certain critical ecological and demographic constraints, namely, resource abundance is unlimited and population size is large, effectively infinite. The changes in genotypic and phenotypic composition are characterized in terms of changes in the mean Malthusian parameter, the measure of fitness adduced in the model.
Now, as we have established in [
29], the Malthusian selection principle, the tenet which underlies the Fisherian analysis, is the limit, as resource abundance and population size tend to infinity, of the entropic selection principle. We can therefore appeal to this correspondence between Malthusian selection and entropic selection to relate Fisher’s theorem with the fundamental theorem of evolution:
Fisher’s selection theorem and the fundamental theorem of evolution: The increase in mean fitness is the limit, as resource abundance and population size tend to infinity, and the mutation rate tends to zero, of the fundamental theorem of evolution.
Higher level or macroevolutionary processes such as speciation, and extinction–background and mass extinction, are analyzed in Section 10 and 11 as emergent properties of the microevolutionary events of mutation and natural selection. Background extinction pertains to the gradual demise of species due primarily to biotic factors. Mass-extinction–a relatively rare event–pertains to the demise of complete clades and phyletic lineages–a process driven primarily by abiotic forces.
These macroevolutionary changes are expressed in terms of the following proposition.
Directionality Principles: Speciation and Background Extinction
The rate of change of mean entropy is equal to the covariance in entropy and the net-diversification rate.
Two distinct dynamical changes in mean entropy can be inferred from the above Proposition.
- B(i)
When the net-diversification rate and the entropy are positively correlated, the mean entropy increases.
- B(ii)
When the net-diversification rate and the entropy are negatively correlated, the mean entropy decreases.
The macroevolutionary change which also implicates mass extinction events can be described by a related principle:
Directionality Principle: Speciation, Background and Mass Extinction
The maximum entropy of species in a clade increases as one clade replaces another over geological time.
The three classes of directionality principles can be adduced to predict evolutionary changes in morphometric variables, namely, adult body size, on ecological time scales; mean body size, and maximum body size on geological time scales. The changes in body size can be inferred from the directional trends in entropy and can be annotated as follows:
- (I)
Directional trends in adult body size under mutation and selection.
- (i)
Body size increases when resources are constant in abundance and diverse in composition.
- (ii)
Body size decreases when resources vary in abundance and is singular in composition.
- (II)
Directional trends in mean body size under speciation and background extinction.
- (i)
Mean body size increases when the net-diversification rate and body size are positively correlated.
- (ii)
Mean body size decreases when the net-diversification rate and body size are negatively correlated.
- (III)
Directional trends in maximum body size under speciation, background extinction, and mass extinction: The maximum body size increases as one clade replaces another at successive epochs of geological time.
Directionality theory is an analytic study of energy transformation in living organisms. The organizing parameters are evolutionary entropy, a measure of the diversity of the pathways of energy flow within the population, and generation time, the mean turn-over time of the metabolic processes in the population.
Thermodynamic theory is the analytic study of energy transformation in inanimate matter. The organizing parameters are thermodynamic entropy, a measure of the diversity of energy states in a material aggregate, and temperature, the mean kinetic energy of the particles in the aggregate.
In Section 12 we will establish an analytic relation between evolutionary entropy and thermodynamic entropy. We will appeal to this relation to establish a correspondence between the thermodynamic selection principle and the fundamental theorem of evolution.
We will show that, when the rate of change in resource abundance tends to zero, and population size tends to infinity, the fundamental theorem of evolution reduces to the thermodynamic selection principle. This correspondence establishes a link between the thermodynamic processes that regulate energy transformation in inanimate matter, and the evolutionary processes that determine energy transformation in living organisms. The link, which we call the Continuation Rule, is the mainstay of a new class of models of the emergence of life from inanimate matter.
3. Entropy: Origin and Properties
Heterogeneity in the developmental state at which individuals in a population pass through the various stages of their life-cycle is an intrinsic property of all organisms. This variability, which is encoded in the genome, has its origin in the processes that underlie the ontogeny of the individual. In cellular systems, it results from the random inequalities between cells, such as the unequal distribution of metabolic components which occur at cell division. In multicellular and higher organisms, this variability is a consequence of the small random variations in the sequence of developmental events that transform the zygote into an adult. Accordingly, any genetically homogeneous population of organisms will be characterized by a heterogeneity in individual birth and death rates.
The ergodic theory of dynamical systems was exploited to provide a quantitative measure of this heterogeneity. This measure of energy flow in living organisms was called evolutionary entropy, on account of its formal relation with the statistical measure thermodynamic entropy.
3.1. Thermodynamic Entropy
Heat flows from hotter bodies to colder bodies and not the other way round. This empirical observation and the efforts to explain it in mechanistic terms was the driving force behind the development of thermodynamic theory. Clausius showed that this directionality in the flow of heat energy implied the existence of a property which he called entropy, and denoted S̃. By appealing to mathematical arguments and physical principles, Clausius established a fundamental relation between the entropy change dS̃ and the change in heat energy dQ̃ which occurs in a material aggregate at a given temperature, T̃.
The entropy concept, as introduced by Clausius, is a phenomenological observable whose change at given absolute temperature is determined by the amount of heat energy supplied to the system. In order to obtain a mechanistic explanation of the directional change in the flow of heat, one needs a mathematical model which will relate the microscopic behavior of the particles that compose the material aggregate with macroscopic properties such as temperature. The model introduced by Boltzmann and Gibbs considered the material aggregate–solid, liquid or gas–as composed of individual particles whose state is described by their position and velocity.
The statistical thermodynamics of Gibbs and Boltzmann is based on two mathematically equivalent descriptions of the diversity in energy states of the individual particles. These measures of diversity, which coincide with the Clausius entropy when certain equilibrium conditions are satisfied, are called the Gibbs entropy S̃G, and the Boltzmann entropy S̃B.
The Gibbs entropy S̃G
Here p̃j denotes the probability that a randomly chosen particle is in energy state j.
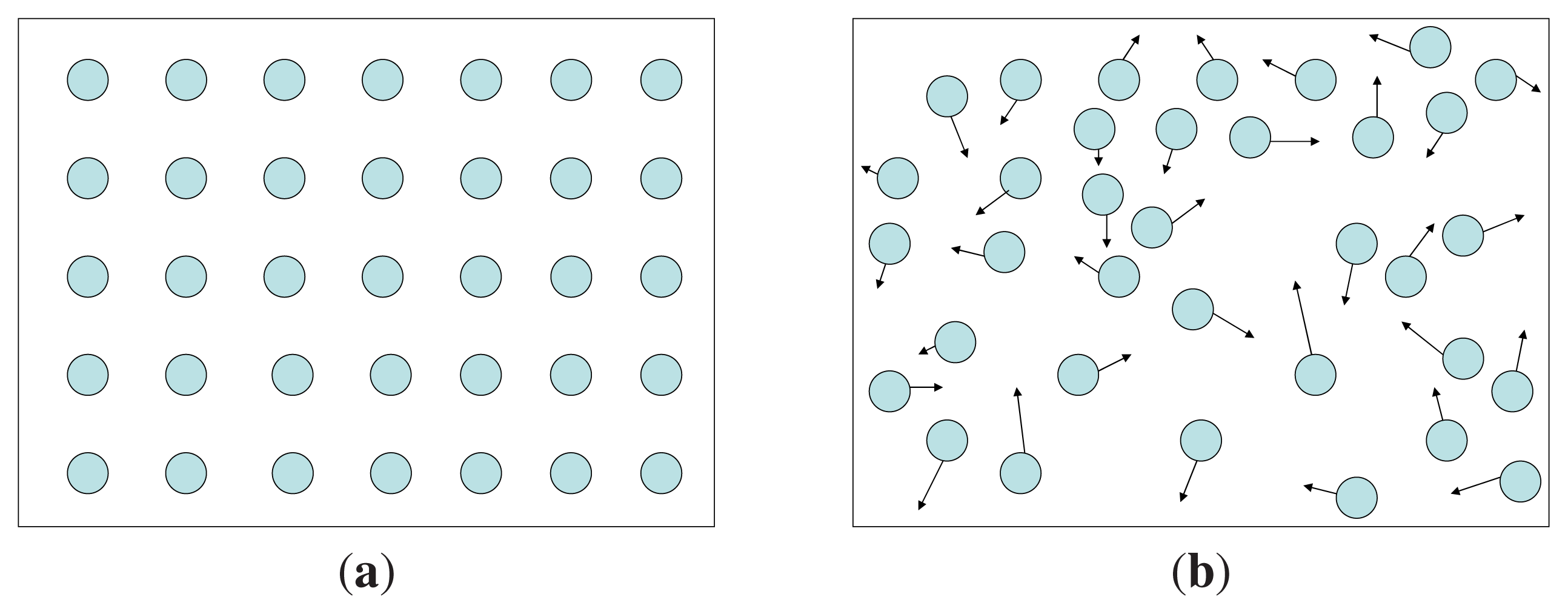
A solid has low entropy since the constituent particles occupy fixed positions in the aggregate. A gas has high entropy since the particles are free to move around.
Figure 2(a) and (b) describe the distributions of particles in a solid and a gas, respectively.
The entropy
S̃G describes the extent to which the energy is spread out among the accessible microstates. In
Figure 2(a) energy is spread out among few microstates and
S̃G is small, in
Figure 2(b) energy is spread out among a large number of microstates and
S̃G is large.
The Boltzmann entropy, denoted S̃B, is given by
Here k is Boltzmann’s constant, and W denotes the number of microstates consistent with a given macrostate. In a solid, W is small, hence so is S̃B. In gases, W is large, hence S̃B is also large.
Boltzmann’s singular contribution to thermodynamic theory rests on establishing two analytical facts.
- (a)
The entropy S̃B increases as the material aggregate evolves from one non-equilibrium state to an equilibrium condition. This mathematical result embodies the thermodynamic principle: The equilibrium states of material aggregates are the states which maximize thermodynamic entropy.
- (b)
At equilibrium, the Boltzmann entropy and the Clausius entropy coincide. The Clausius entropy is expressed in terms of the property heat, and the macroscopic variable temperature. The relationship between the Boltzmann entropy and the Clausius entropy, when integrated with Boltzmann’s theorem, provides a mechanistic explanation of the Second Law of Thermodynamics.
3.2. Evolutionary Entropy
Heat is the most common agency by which energy is transformed in inanimate systems. It is not, however, an effective mode of energy transfer in living organisms–which are essentially isothermal. Living organisms do not operate as thermal machines since there are no significant differences in temperature either at the cellular level or at the tissue level.
The energy-transforming activities in a cell, for example, can be described in terms of a flow of chemical energy from organic substrates to those energy-requiring processes necessary for the functioning of the cell. These energy-transforming processes are isothermal, nevertheless, they are characterized by a certain directionality. This property can be illustrated by considering a population of replicating cells transforming the energy of foodstuff into chemical work. A population which is initially synchronous, that is all cells in the population pass through the cell cycle at the same rate, will gradually become asynchronous, a condition described by the cells passing through the cycle at different rates. The transition from synchrony to asynchrony is a characteristic feature of all populations of replicating cells. The phenomenon corresponds to a change in the distribution of the flow of chemical energy within the population. The shift from a synchronous to an asynchronous system entails the existence of a mathematical property which we call evolutionary entropy, denoted
S. By appealing to certain allometric rules which relate cell size to metabolic rate and cycle time, we established a fundamental relation between changes in evolutionary entropy
dS, and the change in metabolic rate
dP which occurs in a population with a given generation time
T [
31],
A mechanistic explanation of the directionality described by the transition from synchrony to asynchrony requires a mathematical model which incorporates the kinetic behavior of the individual cells in the population. The model invoked in [
17,
20] addressed this problem by considering the population as consisting of individual cells whose kinetics is parametrized in terms of the rates at which the cells pass through the different stages of the cell cycle. The objective of this model was the derivation of statistical descriptors of asynchrony and the use of these descriptors to explain the spontaneous change from synchrony to asynchrony.
3.2.1. Statistical Measures: Cell Cycle Model
The ergodic theory of dynamical systems presents a mathematical framework for generating macroscopic level properties from the array of interacting lower level entities: The application of this formalism to populations of replicating cells whose position in the cell dycle is parametrized by age, has given rise to two mathematically equivalent statistical measures which coincide with the bioenergetic variable described by
Equation (11).
The first statistical measure, an analogue of the Gibbs entropy, is given by
Here
d denotes the number of age classes. The quantity
pj denotes the probability that the mother of a randomly chosen daughter cell is in the state
j. The entropy
S thus describes the uncertainty in the age of the mother of a randomly chosen newborn cell. A synchronous population has zero entropy; an asynchronous population has positive entropy.
Figure 3 describes synchronous and asynchronous populations, respectively.
The nodes in both graphs correspond to age or cell cycle stage. In
Figure 3(a), cell division occurs at a single stage in the cell cycle. Here, the cells in the population pass through the different stages of the cell cycle at the same rate. We have
p1 =
p2 =
. . . =
pd−1 = 0,
pd = 1. Thus the entropy is
S = 0.
In
Figure 3(b) cell division may occur at several distinct stages in the cell cycle. Here we have
pj ≥ 0 for 1 ≤
j ≤
d − 1 and
pd ≤ 1, thus the entropy
S is positive.
The second statistical measure, an analogue of the Boltzmann entropy, is given by
Here W* denotes the number of typical lineages or genealogies generated by a cell in the population. The term genealogy corresponds to a recording of the successive ancestors of a cell in the population.
In
Figure 3(a), each cell generates a unique genealogy, which can be expressed by the sequence
Here W* = 1 and S = 0.
In
Figure 3(b), the genealogies which are generated by a cell in state 1 are
There is an uncountable number of genealogies generated by state 1. The number of typical genealogies, W*, will satisfy the condition W* > 1. Hence we have S > 0.
The expressions given by
Equations (12) and
(13) also pertain to populations of cells or organisms whose state is parametrized by a physiological condition, which leads to graphical representations of the form given by
Figure 2(a), (b).
3.2.2. Statistical Measures: General Model
An important generalization of the cell cycle model–which includes metabolic networks or ecological systems–can be described in terms of a strongly connected graph,
G, see
Figure 4.
Let Ω denote the set of all paths of the graph G. Such paths are denoted by
where each xi represents the state of an element in the population. Each path is called, as in the cell cycle model, a genealogy as it represents a recording of successive ancestral states of particular individuals.
At steady state, the dynamical behavior of the system will be described by a probability measure μ on Ω, which is invariant under the transformation τ : Ω → Ω, defined by (τx)i = xi+1 for i ∈ ℤ.
Evolutionary entropy for this class of models is the Kolmogorov-Sinai entropy
Hμ(
τ ), see Billingsley [
54]. There exists a large class of models, where the interaction between the elements which define the graph is of a form which entails that the measure
μ is Markov and given by a stochastic matrix
P = (
pij) together with the corresponding stationary distribution
π = (
πi). In this case evolutionary entropy, denoted
H, becomes
The entropy H describes the diversity of pathways of energy flow between the elements that compose the network.
The entropy
H can also be described as the asymptotic rate of increase of the number of typical genealogies, an expression analogous to
Equation (13).
Let Ω(t) denote the set of genealogies generated by a single individual during the interval (0, t) and let E denote a subset of Ω(t). We associate with the set E a probability measure as follows. Consider an element z ∈ E, where
and write [z] = {x ∈ Ω : xi = zi for 0 ≤ i ≤ t − 1}. Let μt define a measure on Ω(t) via μt(E) = ∑z∈E μ([z]). Then the effective population size N* (t) is defined by
for small ɛ > 0. The effective size describes the minimal number of genealogies whose total probability exceeds 1 − ɛ. The Shannon-McMillan-Breiman Theorem can be applied to show that
It follows from W* = limt→∞[N*(t)]1/t that
The expressions (
14) and (
15) thus represent two equivalent statistical characterizations of entropy.
In
Figure 5(a) the probability measure
μ on the space of genealogies Ω can be described in terms of the stochastic matrix
P, which is
In
Figure 5(b) the probability measure
μ is described by the stochastic matrix
P given by
and W̃* = 3. Hence both entropy measures yield the value log 3.
Figure 5(a), (b) also illustrate the depiction of entropy as a measure of the diversity of pathways of energy flow. In
Figure 5(a), there is a unique path as described by the cycle 1 2 3.
Figure 5(b) indicates a multiplicity of paths.
3.3. Thermodynamic Entropy and Evolutionary Entropy
Thermodynamic theory in its largest sense is concerned with the rules which govern the flow and distribution of energy within and between various material aggregates: solids, liquids and gases
The theory has its origin in empirical observations concerning the conversion of the chemical energy of fuels into the kinetic energy of steam engines. Accordingly, a critical distinction is made between the classical or phenomenological thermodynamics, which is concerned with macroscopic depictions of energy transformations, and statistical thermodynamics, which analyzes energy transformation in terms of quantities which describe the molecular dynamics and organization of the macrocopic properties.
The central concepts in classical thermodynamics are the temperature, T̃, the heat energy Q̃, and the phenomenological entropy S̃, discovered by Clausius in the studies of the Carnot models of energy conversion.
Clausius integrated physical observations and mathematical analysis to show that changes in entropy
dS̃ are related to the temperature
T̃ and the change
dQ̃ in heat energy. The relation between these quantities is given by
Equation (8).
Statistical thermodynamics is an analytical theory based on algorithmic rules for expressing the phenomenological variables in classical thermodynamics in terms of the dynamical properties of the molecules that constitute the material aggregate. The Clausius entropy, for example, admits a statistical representation. This statistical descriptor is given in terms of the number of microstates consistent with a given macroscopic state, a property which defines the statistical measure of entropy introduced by Gibbs and Boltzmann. An important observable in statistical thermodynamics is the free energy, denoted F̃. This quantity satisfies a variational principle which entails an analytic relation between the free energy, the mean energy, Ũ, the Gibbs-Boltzmann entropy S̃ and the temperature, T̃. We have the identity
Evolutionary theory in its largest sense is concerned with the rules which govern the flow and distribution of chemical or metabolic energy within and between populations of replicating organisms. Directionality theory is a mathematical model of the evolutionary process. The central concepts in the theory are the generation time T, the mean turn-over time of the chemical reactions within the organism and the mass-specific metabolic rate P.
The integration of bioenergetic observations and mathematical analysis entailed the existence of a property, evolutionary entropy, whose change is related to the generation time and the metabolic rate according to
Equation (11).
The ergodic theory of dynamical systems was exploited to derive statistical characterizations of the macroscopic variable evolutionary entropy. An important parameter in this study is the population growth rate denoted r. This quantity is known to satisfy a variational principle which is formally analogous to the minimization of the free energy in statistical mechanics. This variational principle entails that the population growth rate can be expressed as the sum of an energy function, called the reproductive potential and denoted Φ, and an entropy rate S/T. We have
The function Φ is called the reproductive potential.
The relations (
8), (
11) and the relations (
16), (
17) suggest a formal correspondence between the thermodynamic variables, the free energy, the mean energy, the thermodynamic entropy, and the temperature, and the population parameters–growth rate, reproductive potential, evolutionary entropy and the generation time.
The relations described in
Table 1 indicate that the thermodynamic and the evolutionary selection principles are formally analogous. We will show in Section 10 that in the case of networks which can be analyzed from both thermodynamic and evolutionary perspectives, we have, when resource production,
R → 0, and population size,
M → ∞ the condition
This relation indicates that the thermodynamic principle can be seen as a limiting case of the evolutionary principle. This observation has important implications for understanding in energetic terms the transition from an aggregate of inanimate matter to a system consisting of metabolic and replicating entities.
4. Macroscopic Variables in Biological Networks
Statistical mechanics is a mathematical framework for describing how higher level patterns may emerge from the activity and the interaction between the lower-level elements. The microscopic world of a gas are the individual molecules whose dynamics can be parametrized by their position and velocity. The macroscopic variables are quantities such as the mean energy, the temperature, and the entropy.
The formalism developed by Gibbs and Boltzmann, which relates the macroscopic variables with the cooperative interaction of the atoms and molecules in the microscopic world of physical systems can be generalized to analyze the relation between macroscopic variables and the kinetic variables of biopopulations [
18,
20].
4.1. The Dynamics of Biological Networks
Biological networks with non-linear dynamics can be described by the difference equation [
20]
Here
A(
t) = (
aij(
t) is a matrix whose entries
aij(
t) are functions of the distribution
u(
t). A particular example is the total population size
N(
t) = ∑
i ui(
t). The relation (
18) can be illustrated with two well known examples.
(1) Demographic models
The elements ui(t) denote the number of individuals in age-class (i) at time t. The matrix assumes the form
Here mi(t) denotes the mean number of offspring produced by individuals in the i-th age class; bi(t) represent the proportion of individuals that survive from age class (i) to age class (i + 1).
(2) Cell cycle models
The elements ui(t) now denote the number of individuals in stage (i) of the cell cycle. Assuming that mitosis only occurs at states (d−1) and (d) in the cell cycle, and that the transition between states of the cell cycle are of the form j → j + 1, or j → j + 2, we have
4.2. The Steady State
We will assume that the systemevolves to a steady state. At steady state the process is now represented by the constant matrix A = (aij) with aij > 0.
Let S = {1, 2, . . . , d} and
We now introduce the space of configurations
The configuration space Ω is called the space of genealogies. It denotes the set of all infinite backward paths of the graph associated with the matrix.
Now let
τ : Ω → Ω, (
xk) ↦ (
x̃k), where
x̃k =
xk+1 be the shift map, and let
M denote the set of probability measures which are invariant under the shift
τ. Let
μ denote the natural probability measure on Ω when the steady state of
Equation (18) is attained. This measure
μ is known to satisfy a variational principle, see [
18]: It is the probability measure that maximizes
Here Hμ(τ) is the Kolmogorov-Sinai entropy for the system (Ω, μ, τ) and the function ϕ : Ω → ℝ is given by
The probability measure μ is known to be a Markov measure. Analytically, it is described in terms of the Markov-matrix P = (pij), where
Here v = (vi) is the left eigenvector corresponding to the largest eigenvalue (in absolute terms) λ of the matrix A.
4.3. The Macroscopic Variables
The variational principle given by
Equation (20) indicates that the process at steady state can be described in terms of the dynamical system (Ω
, μ, ϕ) where the function
ϕ is given by
Equation (21), and the measure
μ is determined by the Markov chain induced by the matrix
P given by
Equation (22).
The statistical mechanics formalism furnished algorithms for generating a family of macroscopic variables using the function ϕ and the measure μ.
(i) The growth rate
Consider the function
and write
where for given (x0, x1, . . . , xn) we denote by x* any point in Ω with
for i = 0, 1, . . . , n.
In correspondence with the famous Perron-Frobenius Theorem the limit
exists under rather general conditions for the potential
ϕ. Here
λ is the dominant eigenvalue of the transition matrix
A. In view of the variational principle given by
Equation (20), we have, see [
18], that
where H = Hμ(τ) and Φ = ∫ ϕdμ.
The statistical parameter H denotes the Kolmogorov–Sinai entropy of the dynamical system(Ω, μ, ϕ).
(ii) Evolutionary entropy
The term evolutionary entropy describes the entropy H when the measure μ is Markov. In this instance, the measure can be represented in terms of a probability matrix P = (pij) with a stationary distribution. The entropy H is now given by
We now evaluate
Equation (25) in the case of a demographic network and then for a general biological network.
Demographic networks
We consider the network given by
Equation (19) and assume that the age-specific fecundity and survivorship variables are constant, that is
mi(
t) =
mi,
bi(
t) =
bi. Write
The number lj represents the proportion of individuals surviving to age j.
Let λ denote the dominant eigenvalue of the matrix A: This quantity is the unique positive real root
defines a probability distribution for the age of parents.
With the help of the probability distribution given by the
pj, we can express the elements of the Markov matrix
P = (
pij) in terms of (
pj). This enables a computation of
H as given by
Equation (25), and we have
The quantity S is a measure of the number of reproductive cycles in the demographic network and describes the degree of iteroparity. The quantity T is the generation time, the mean age of mothers at the birth of their offspring.
General networks
An analogue of
Equation (27) holds in the case of general biological networks [
54].
We consider the directed graph G associated with the Markov matrix P = (pij). We now fix once and for all a vertex a ∈ X, where X = (1, 2, . . . , d). We now consider the set of all states, denoted X̃, and defined by
A state ã ∈ X̃ is a path on the graph G, which starts at a and ends at a, and does not visit a in the middle.
Write
The quantity pã is the probability of a given cycle which starts at a.
We can appeal to Abramov’s theorem in ergodic theory to show, see [
55], that
Here |ã| = n for the n such that
This depiction of
H, which is of the same form as
Equation (27), elucidates the distinction between the two entropy measures
H and
S. The quantity
S is a measure of the number of replicative cycles in the network. The quantity
T is the cycle times mean return time of the Markov process.
(iii) The reproductive potential and other indices
The relation given by
Equation (23) can be used to generate a new class of macroscopic variables.
Let
λ(
δ) denote the dominant eigenvalue of the matrix
A(
δ), where
and
r(
δ) = log
λ(
δ). As shown in [
20], we have
where
Here
![Entropy 16 05428f19]()
and Var
n denote the expectation and the variance with respect to the measure
μn on finite symbol sequences of length
n of the form (
x0, x1, . . . , xn), which is given by
The quantities H, Φ, σ2 and κ represent a suite of macroscopic variables. The quantity Φ is called the reproductive potential, σ2 the demographic variance, and κ the correlation index.
5. The Entropic Selection Principle
The entropic selection principle constitutes a set of rules which describe the outcome of competition between an incumbent population and a variant type. The rules assert that the outcome is conditional on certain constraints on the resources and predicted by evolutionary entropy. Qualitatively, the rules contend that (a) when resources are constant and limited, variants with increased entropy will prevail and increase in frequency; (b) when resources undergo large variations in abundance, variants with decreased entropy will be dominant.
5.1. Incumbent and Variant Populations
Our analysis of competition will be described in terms of a dynamic interaction between two classes of populations–an incumbent, whose dynamics at steady state is given by (Ω, μ, ϕ) and a variant, whose dynamics at steady state is given by (Ω, μ*, ϕ*). In order to express the notion that the variant is derived from the incumbent by a mutation, we will impose the following condition, assuming δ having small absolute value:
where
The biological rationale for the above constraints are discussed in [
32].
Let r, H, σ2 denote the macroscopic parameters that describe the incumbent and r(δ), H(δ), σ2(δ) the corresponding parameters for the variant. Write
The relations given in
Equation (28) entails assuming Φ ≠ 0,
γ ≠ 0 that
where γ = 2σ2 + κ. In particular, we can conclude for small δ the following relations:
These implications will play a crucial role in the next section where we determine criteria for invasion of a variant type.
5.2. Invasion-Extinction Dynamics
The condition for the increase in frequency and ultimate fixation of the invading population is evaluated by considering the stochastic dynamics of the frequency of the invader. For this purpose a continuous time diffusion approximation is used in order to consider
Here N(t) denotes the population size of the resident population and N* (t) the population size of the invader, where N* (t) ≪ N(t) and t ∈ ℝ+.
For analyzing the dynamics of
p(
t) techniques of diffusion approximation, see Feller [
56], are integrated with the techniques of ergodic theory (cf. Arnold, Demetrius and Gundlach [
18]). This approach rests on a central limit theorem asserting that for the natural measure
μ and for any
a ∈ ℝ
Thus asymptotically the deviations of the sample path Snϕ for one genealogy from the mean for n → ∞ can be approximated by Brownian motion with variance σ2t for a continuous time evolution. Thus we assume that the sample path Snϕ corresponding to a randomly chosen individual can be described by Brownian motion and hence by a diffusion equation. In fact, we assume that the whole population can be described this way and that large deviations from the mean lose significance when the size of the population increases. This corresponds to observations of statistical entities and in particular of real population behavior.
Consequently we consider p(t) as a stochastic process by treating the dynamics of the population sizes N(t) and N* (t) as diffusion processes with infinitesimal moments obtained as
where we denote by
![Entropy 16 05428f20]()
the expectation. In the determination of the second infinitesimal moment we invoke the observation that if
N becomes large the influence of fluctuations becomes small and hence the process becomes deterministic. Thus we have made the assumption that the change in log
N(
t) in the time interval Δ
t due to fluctuations is caused by Brownian motion with variance
. We can therefore describe the evolution of the density
f(
N, t) of the process
N(
t) by the solution of the Fokker-Planck equation
Equivalently, we could also characterize N(t) as a solution of the stochastic differential equation
We get respective representations for the process N* (t) and its density f* (N*, t), namely
We assume that the processes N(t) and N* (t) evolve simultaneously and stochastically independently. Then we obtain for
that the stochastic differential equations for N and N* are equivalent to
If we assume that M is constant, then p is given by a diffusion process with drift
and variance
The diffusion process has a density ψ which solves the Fokker-Planck equation
and has natural boundary conditions
corresponding to the cases that
p = 0 (extinction of the mutant population) and
p = 1 (extinction of the incumbent population). For any initial value
ψ(
p, 0) there exists a unique solution (Feller [
56]).
We denote by P(y) the probability that the diffusion process leads to an absorption in the state 1 (extinction of the incumbent population). By appealing to the backward Kolmogorov equation of the diffusion process and integration it follows that
where
Except in the degenerate–and for large M unusual–case of
, P′ (y) cannot vanish and the convexity of P can be determined in terms of s only, and it is easy to show that s > 0 implies the convexity of P, s < 0 implies the concavity of P. The degree of curvature of P depends on the magnitude of s, i.e., on the values of Δr, Δσ2 and M, as can be seen from the following graphs, obtained by numerical calculation for some suitable choices of Δσ2/σ*2 and Ms/Δσ2 and showing the dependence of P(y), the ultimate invasion probability, on y, the initial frequency of the mutant:
These observations on the relationship between the signs of Δr and Δσ2, and the curvature of P entail that for almost all initial values of p very close to 0 the solution p is absorbed in 0 for any possible perturbation, if
5.3. Evolutionary Stability
Evolutionary stability refers to the condition that no mutant population can invade into an incumbent population,
i.e., all mutant populations will eventually become extinct. In the previous section we have seen that this situation can only occur under two conditions on the change of macroscopic parameters Δ
r and Δ
σ2. The selective advantage
s̃ can be expressed in terms of changes in a single macroscopic variable, namely Δ
H when Φ ≠ 0,
γ ≠ 0. This new index is obtained by appealing to the perturbation relations given by
Equations (29)–
(32). We obtain
The criteria for invasion of a mutant will now be given by
Table 3.
Thus the main result on invasion dynamics and evolutionary stability of populations can be summarized by the following entropic selection principle.
Theorem 5.1
A population is evolutionarily stable, if its entropy is extremal, namely maximal in the case of Φ < 0, γ > 0 and minimal in the case of Φ > 0, γ < 0, respectively.
These entropic selection rules indicate that evolutionarily stable states correspond to extremal states of evolutionary entropy. Evolutionary entropy is positively correlated with demographic stability, the rate at which the population returns to the steady state condition after a random perturbation [
50]. Consequently, the evolutionarily stable state will be also characterized by states of extremal demographic stability.
5.4. Selection Principle and Resource Constraints
The analysis of the effect of resource constraints on the outcome of selection will be based on the following assumption: The resource abundance R and the total population size M are in dynamical equilibrium.
Consistent with
Equations (34) and
(35), we will also assume that the dynamics of the population size
N is determined by the growth rate,
r, and the demographic variance
σ2, respectively.
The outcome of competition between the ancestral type X and the variant type X*depends on two factors:
- (1)
Resource-metabolic process: The relative capacity of the two types to acquire the resources which the environment avails. This property will depend on the metabolic efficiency of the organisms and their capacity to acquire the energy of the resources and to transformthis energy into metabolic energy.
- (2)
Metabolic-demographic process: The relative capacity of the types to convert the metabolic energy of the organism into net-offspring production
The relative contribution of these two factors to the outcome of selection will depend on the resource abundance R. When R is large, effectively infinite, the changes Δr and Δσ2 will not be correlated with changes ΔR in resource abundance. In this case, the competitive outcome will be completely regulated by the metabolic-demographic process. However, when resource abundance is finite, the changes Δr and Δσ2 will both be correlated with the change ΔR in resource abundance and hence the resource-metabolic process becomes a critical factor in determining selective outcome.
We will distinguish between these two factors in delineating the effect of resource abundance, finite or infinite, on the dynamics of selection.
(I) Resource abundance infinite
When this condition prevails, the metabolic-demographic process determines selective outcome. Accordingly, the outcome will now depend on the demographic variables Δr, Δσ2 and the population size M.
When the population size M is infinite, the selective process will be completely determined by Δr. The selective advantage now becomes
When M is finite, the measure of selective advantage is now a function of Δr, Δσ2 and M,
(II) Resource abundance finite
When this condition prevails, the resource-metabolic process now becomes a critical factor in deciding the outcome of competition. Let us assume that the dynamical changes in resource abundance R can be described in terms of two parameters, resource production rate and resource diversity, respectively. Now when resource abundance is finite, the changes ΔR will induce changes in the net-reproduction function and consequently, correlated changes Δr and Δσ2 in the growth rate and the demographic variance, respectively. Now if r(δ) and σ2(δ) are the resulting parameters after changes in r and σ2 due to a perturbation of magnitude δ in the net-reproduction function, we have
Since the resource abundance is limited, we conclude that
Moreover Φ and γ, which are demographic parameters, will be correlated, and hence characterize the resource variables, production rate and diversity, respectively.
Now the rate at which the population returns to its steady state condition after a random perturbation in the individual parameters, is given by evolutionary entropy H. The parameter ΔH will now describe the relative capacity of the two types to respond to changes in resource abundance.
Accordingly, when resource abundance is finite, the outcome of competition between the incumbent and variant type will now be contingent on the parameters Φ and γ, and predicted by ΔH.
When
M is
infinite, the measure of selective advantage can be inferred from
Equation (39), and becomes
Hence,
- (i)
when Φ < 0, ΔH > 0 or Φ > 0, ΔH < 0, s > 0, and the variant increases in frequency,
- (ii)
when Φ > 0, ΔH > 0 or Φ < 0, ΔH < 0, s < 0 and the variant decreases in frequency.
When M is finite, the measure of selective advantage now becomes
Hence
, ΔH > 0 or
, ΔH < 0 implies s̃ > 0, and the variant increases in frequency. Whereas
, ΔH < 0 or
, ΔH > 0 implies s̃ < 0 and the variant decreases in frequency.
The relation between the resource conditions (finite and infinite), population size
M, and the various measures of selective advantage is summarized in
Table 4.
We can appeal to the characterization given in
Table 4 to assert the following proposition:
The Malthusian principle and the entropic selection principle—a relation: The Malthusian principle is the limit as resource abundance and population size tend to infinity of the entropic selection principle.
Since Fisher’s discovery of the Malthusian principle in 1930, the notion that the population growth rate predicts the outcome of natural selection has been the basis for most evolutionary studies. The relation between the Malthusian and the entropic principle we have described indicates that the Malthusian principle represents an approximation to the entropic principle. The validity of the approximation will increase with increasing population size and increasing resource abundance. The explanatory power of the Malthusian model in evolutionary biology, is based on the fact that in many experimental and laboratory contexts, population size is indeed large and resources are indeed abundant. In the natural populations however, resources are often limited, and population size is small. In this case the evolutionary entropic principle now becomes the critical tenet for understanding the dynamics of evolutionary change.
5.5. Demographic Parameters and Resource Constraints
We will now appeal to the description of the reproductive potential Φ and the demographic index
γ to show that when resource abundance is finite, the sign of Φ can be invoked to represent different degrees of resource abundance, whereas the sign of
γ can be used to characterize different degrees of resource diversity. The empirical and computational support for the correlation between the demographic parameters and the resource constraints is established in [
29].
(A) Reproductive potential Φ as index of resource abundance
Hence Φ < 0 ⇒ r < H and Φ > 0 ⇒ r > H.
Since
r denotes population growth rate, the rate of increase in population size, and
H characterizes population stability, the rate of return of populations to their steady state condition after a perturbation, we can infer from
Equation (43) that the following characterizations of the reproductive potential obtain:
The condition Φ < 0 characterizes equilibrium species. These populations are described by a relatively constant population size and inhabit environments where resources are constant and limited. The relation Φ > 0 describes opportunistic species. Population size in this case can undergo large variations and the resources fluctuate in abundance.
(B) Demographic index γ as a measure of resource diversity
The demographic index
γ is related to the demographic parameters
σ2 and
κ according to the identity, see [
20],
The variance σ2 is positive, whereas κ as a measure of the skewness of the random variable log ϕ can assume both positive and negative values.
The condition Φ ≪ 0, represents a large skewness in the net-reproductive function and entails γ < 0, whereas κ ≈ 0 or κ > 0, a flatness in the net-reproductive function, implies γ > 0. These relations entail:
γ < 0: peaked distribution in net-reproductive function–a homogeneous resource type (singular resource),
γ > 0: a flat distribution in net reproductive function–a heterogeneous resource type (diverse resources).
The property
γ < 0 describes
univalent systems. This defines a homogeneous resource with low diversity, whereas
γ > 0 characterizes
multivalent systems. The available resources in this case are heterogeneous and diverse. The constraints which the resource abundance and the resource diversity imposes on the demographic variables Φ and
γ are summarized in
Table 5.
6. Complexity and Stability of Biological Networks
The complexity–stability dichotomy in biological systems has its origin in studies of integrative medicine. These investigations aimed to elucidate the mechanisms which organisms exploit to maintain their functionality, despite large endogenous and exogenous perturbations. The two main contributors to these studies were the French experimentalist, Claude Bernard [
57] and the American physiologist, Walter Cannon [
58]. Bernard introduced the notion of constancy of the
Milieu Interieure to describe the capacity of organisms to maintain their metabolic integrity when subject to various stresses induced by the interaction with the environment. This stability, according to Bernard, was a result of the high degree of connectance of themetabolic networks in living organisms. The large diversity of pathways that define the networks was proposed as the factor which buffered the system against perturbations, and ensured constancy of energy production despite random variations in the reaction kinetics. Cannon introduced the term homeostasis to describe the capacity of a metabolic network to maintain its functionality. The factors which ensured homeostasis was attributed to the topology of the regulatory network.
The empirical observations of Bernard and Cannon can be considered the basis for the hypothesis that the robustness of cellular and metabolic networks are correlated with the diversity of the pathways of energy flow between the individual elements.
The contrast between complexity, as a measure of the connectance of a biological network, and stability, as characterizing its response to perturbations, later emerged as a central theme in ecology. The significance of the complexity–stability hypothesis as a fundamental biological property is largely due to Elton [
59] who provided empirical evidence to show that the robustness of ecological networks is typically greater in communities described by a high degree of connectance between the species.
The empirical observations of Elton has been the stimulus for several analytical studies of the complexity–stability hypothesis in the context of ecological models. One of the first efforts to develop a formal analysis of the problem is due to MacArthur [
60]. Heuristic arguments were adduced to show that the complexity of the network, as defined in terms of number of species and the number of trophic levels, was positively correlated with stability.
MacArthur’s model, despite its highly qualitative nature, emerged as a important contribution to ecological studies as it furnished a powerful heuristic, and a proximate mechanism for understanding the empirical observations of Elton.
May [
61], in an effort to introduce a more rigorous framework for studying the relation between complexity and stability, appealed to earlier computational studies due to Gardner and Ashby [
62], and proposed a model where the interaction coefficients between species are described as random variables fixed in time. May appealed to certain properties of large random matrices to claim that increasingly severe constraints must be imposed on the distribution of the interspecific coefficients to ensure the stability of the ecological community. The argument, as advanced in [
61], contends that, as the connectance of the network or the average interaction strength between the species increases, the transition from stability to instability is sharp.
May’s proposition, based on extensive numerical studies, runs counter to MacArthur’s result which was derived by a heuristic argument and formulated in highly qualitative terms. The stability concepts invoked in the two classes of models, however, are based on quite different criteria. Stability in Mac Arthur’s model describes “the amount of choice which energy has in following the paths up through the food web”. In May’s model, a network is defined to be stable if and only if all eigenvalues of the community matrix associated with the network have negative real parts. This notion of stability has considerable explanatory power in studies of systems which are isolated, or closed to the action of external forces. However, this characterization of stability becomes less significant in the case of systems, biological networks for example, whose steady states are described by non-equilibrium constraints.
The model proposed in Demetrius, Gundlach and Ochs [
50] was formulated in order to provide a general mathematical framework for the empirical observations documented in the studies by Bernard, Cannon and Elton, and also to furnish an evolutionary understanding for the large differences in stability observed in studies of biological networks.
Our analysis appealed to recent developments in the ergodic theory of dynamical systems and the theory of large deviations to formally characterize the notions of complexity and stability. We assume that the dynamical system associated with the network is at steady state, and is described in terms of the mathematical object (Ω, μ, ϕ). Here Ω denote the configuration space of genealogies; ϕ represents a potential function on Ω, and μ denotes the Gibbs measure associated with ϕ.
Now, the complexity of a network can be qualitatively described in terms of the connectance of the network, and the intensity of interaction between the nodes. We will appeal to the ergodic theory of dynamical systems to describe these properties in terms of the entropy of the dynamical system (Ω, μ, ϕ).
The robustness of a biological network describes its capacity to maintain its functionalities in the face of internal and external perturbations. Large deviation theory, Ellis [
63], Young [
64], can be adduced to obtain an analytic depiction of robustness in terms of the rate at which the system returns to the steady state configuration after a random perturbation.
We will show that the entropy
H, and the robustness,
R are analytically related. This result, [
50], called the complexity-stability theorem, asserts.
The quantities ΔH and ΔR denote the changes in entropy and robustness which are generated as a result of a change in the microscopic parameters that define the network.
The complexity–stability theorem given by
Equation (44) implies that evolutionary entropy
H, predicts the macroscopic response of the system to a spontaneous fluctuation. The application of this result to elucidate the response of biological networks to external perturbations is based on the fluctuation–dissipation theorem in statistical mechanics. According to this result, Kubo [
65], the response of a system in thermodynamic equilibrium to a small external perturbation is equivalent to its relaxation after a spontaneous fluctuation. We can apply this result and the relation given by
Equation (41), to establish that evolutionary entropy determines the response of the system to any endogenous or exogenous perturbation. Hence evolutionary entropy is a proximate cause of network stability, and parametrizes the resilience of the system and its capacity to maintain its functionalities after random perturbations.
6.1. Complexity and Evolutionary Entropy
The complexity of a biological network denotes, in qualitative terms, the extent to which the behavior of the components of the network are correlated. The concept thus involves properties such as: the connectance of the network, the intensity of interaction between the nodes, and the size of the network.
Any analytic measure of complexity should be an increasing function of size and should: (a) attain its minimum value when the network is described my a unique cycle; (b) for fixed size, increase with the clustering of the nodes and the intensity of the interaction between the nodes; and (c) attain its maximum value when all nodes are connected to each other by a path of unit length.
Fig 9 denote three graphs with the same number of nodes but with different connectance between the nodes.
According to our prescription, any complexity measure, C, should satisfy the properties C(a) < C(b) < C(c).
We will show that the dynamical entropy of the model (Ω, μ, ϕ) satisfies the complexity criteria that we have postulated. If we denote the entropy by H, we observe that
and H(a) = 0, H(c) = log 3.
In general, if d denote the number of nodes in the network, we have
The characterization of entropy H as a measure of complexity rests on the analytical fact that H describes the asymptotic rate of increase of the number of “typical” genealogies generated by the network.
In the case of a given network, the genealogies generated up to time t can be ordered in terms of their frequencies. According to the Shannon-McMillan theorem, when t is large, the genealogies will fall into two classes: (i) a class S1 where each genealogy has approximately the same frequency, (ii) a class S2 where the sum of the probabilities of the genealogies belonging to this class is ɛ. The class S1 constitutes the typical genealogies. At time t, the number in this class is approximately etH.
The notion of typical genealogies can be formalized as follows. Let Ω(t) denote the set of genealogies generated during the time interval (0, t), and let E denote a subset of Ω (t). We will use the measure μ on Ω to associate with the set E a probability measure, which we denote by μE.
Consider an element z ∈ E where
and write
We now write
We now introduce a quantity N* (t) defined by
N* (t) describes the minimal number of genealogies generated up to time t, whose probability exceeds (1 − ɛ). This quantity, by definition, is the typical number of genealogies up to time t.
The relation between the entropy
H and the network complexity is an immediate consequence of the Shannon-McMillan theorem, Billingsley [
54],
A heuristic interpretation of
Equation (45) can be expressed as follows. We assert that for arbitrarily small
ɛ > 0, and
δ > 0, and for sufficiently large
t, all genealogies can be separated into classes
S1 and
S2 such that:
- (a)
for every genealogy x in class S1
- (b)
the sum of the probabilities of genealogies belonging to the class S2 is less then δ.
For all genealogies x ∈ S1 we have that
is close to H. Hence, all genealogies of the class S1 have approximately the same probability, namely e−tH. This means that the number of genealogies in this class, the typical genealogies, is approximately etH.
6.2. Robustness and the Fluctuation Decay Rate
Robustness pertains to the invariance of the macroscopic properties of the system in the face of endogenous and exogenous perturbations. The nature of these perturbations will be conditioned by the biological network, its level of organization and its structure.
The mathematical formalism of large deviation theory, Young [
64], Ellis [
63], provides a basis for describing the robustness of a biological network. The network is represented by the mathematical object (Ω
, μ, ϕ). We now introduce the mean value Φ, defined by:
Write
Here τ denote the shift transformation on the space of genealogies.
By the Birkhoff ergodic theorem,
Now write
The quantity Pn(ϕ) represents the deviation or fluctuation of the sample mean
from the normalized average value.
Given ɛ > 0, consider the probability Qn(ɛ) that the sample mean
differs from the mean value by more than ɛ, that is
We have by the ergodic theorem
The convergence to zero is at least exponential. Hence for any ɛ > 0, there exist positive constants C and M, such that for every n,
In order to depict the fluctuation decay rate, we ask: How fast on a logarithmic scale does the value Qn(ɛ) go to zero? The rate is given by
The quantity is a measure of the relaxation of the system after a spontaneous fluctuation.
The significance of as a measure of robustness depends on the Fluctuation dissipation theorem (FDT) in statistical mechanics. According to the FDT, there exists an explicit relation between the fluctuation properties of a thermodynamic system and its linear response which involves non-equilibrium quantities. The theorem relates the dissipation of dynamics at equilibrium with macroscopic response to exogenous perturbations. We can exploit this theorem to infer that constitutes a measure of the response of macroscopic properties of the biological network to external perturbations.
6.3. Entropy and Robustness: The Complexity–Stability Theorem
The complexity–stability theorem asserts that the entropy
H, and the fluctuation decay rate
, are positively correlated. The proof of will appeal to a class of analytic results in large deviation theory, due to Young [
64] and Ellis [
63]. We first give a heuristic argument which elucidates the theorem before proceeding to its proof.
The heuristic argument will depend critically on the characterization of
H given by
Equation (45). We note from
Equation (46) that
H embodies information regarding the asymptotic value of the minimal number of genealogies whose total probability exceeds 1 −
ɛ.
Now, it should be evident from
Equation (46) that the
greater the minimal number of genealogies whose total number exceeds 1 −
ɛ, the
smaller will be the measure of the set of genealogies that deviate up to
ɛ from the behavior of the typical genealogy. In view of the asymptotic representation of
N* (
t) and
Qn(
ɛ) given by
Equations (45) and
(48), we conclude that the larger the entropy, the more rapid the fluctuation decay rate. This is essentially the meaning of the positive correlation between
H and
which the theorem asserts.
We now proceed to a precise statement of the theorem and its formal proof. We will consider the network as described by the dynamical system (Ω, μ, ϕ) with entropy H. We will consider perturbations of the form
We let μ(δ) denote the measure associated with the function ϕ(δ) and let H(δ) denote the perturbed entropy.
Let and ( δ) denote the fluctuation decay rates of the original and the perturbed system. Write
We will establish the following result.
Theorem
The evolutionary entropy H and the fluctuation decay rate are positively correlated, that is
for sufficiently small δ.
The proof of our result draws from certain characterizations of in terms of a variational principle.
In order to find a characterization of we first define the more general decay rates
for arbitrary subsets E of the real line. The case we are mostly interested in corresponds to E = {s : |s − ϕ| > ɛ}. Consider the function
where ν denotes a probability measure in Ω which is invariant under the shift operator τ.
As shown, for example in Bowen [
25], the pressure
P(
ϕ) satisfies a variational principle and is given by
Write
and consider the function kϕ(s) defined by
Applying the definition of G(ν) and taking into account that we have to restrict our attention to measures with ∫ ϕdν= s, we obtain
As shown by Young [
64], the functions
(
ϕ,
E) and
̄(
ϕ,
E) defined in
Equations (50a) and
(50b) can be expressed by the relations
and
Moreover, the function
kϕ defined by
Equation (51) satisfies the following relations:
kϕ is continuous, and by the variational principle given in
Equation (20)kϕ(Φ) = 0.
The continuity of
kϕ implies that in the case
E = {
s : |
s −Φ| >
ɛ} with some fixed
ɛ > 0, the lim sup and lim inf in
Equations (50a) and
(50b) are actually limits and therefore
Let us now consider the perturbed system defined by the potential described by
Equation (49). Since
an application of the ergodic theorem yields
for genealogies x with probability one with respect to μ(δ), the unique equilibrium state corresponding to ϕ(δ).
Using ϕ( δ) = (1 + δ)ϕ and dividing by 1 + δ, we obtain
Genealogies for which the sample mean
after finite time n, deviates by more than ɛ from the expected mean value ∫ ϕdμ(δ), are thus characterized by
which is equivalent to
Let
denote the measure of the set of genealogies where the sample mean
differs from the mean value Φ(δ) by more than ɛ. Analogously to the above considerations for the unperturbed model, we find that
decays exponentially with rate
The last term sup {hν(τ) : ν τ-invariant, ∫ϕdν = Φ − ɛ} is independent of δ since
Analogously,
Combining
Equations (56) and
(57) applied with
δ=
δ1 and
δ = 0, we obtain with Δ
=
(
δ1) −
(0) and Δ
H =
hμ(δ1)(
τ) −
hμ(
τ)
and hence the desired result
for sufficiently small ɛ.
The expression (
52) relates the entropy, a measure of the connectance of the biological network, with robustness, the rate at which the system returns to the steady state after a spontaneous fluctuation. Now, according to the fluctuation-dissipation theorem in statistical mechanics, the response of a system to external perturbations is correlated with the internal fluctuations of the system in the absence of the disturbance, Kubo [
65].
The external perturbations of biological networks are highly dependent on the level of biological organization considered. These perturbations include:
- (a)
The removal of critical reactants in a metabolic network.
- (b)
The invasion of a pathogen in a demographic network.
- (c)
The extinction of certain species in an ecological network.
We can integrate the fluctuation–dissipation theorem of statistical mechanics with the fluctuationstability theorem to predict that the response of biological networks to these classes of external perturbations is determined by evolutionary entropy. The complexity–stability theorem thus furnishes a simple numerical index, namely entropy, for ranking networks according to their robustness, and hence their vulnerability to extinction.
6.4. The Evolution of Robustness
The distinction between proximate and ultimate causations of biological systems has been discussed by Mayr [
3], who attributes the distinction, in the context of ecological systems, to David Lack [
66].
Proximate causes relate the function of the system as well as its development, to the various local forces that regulate it. Proximate mechanisms deal with the genetic programs that determine the function or behavioral property of the system. Ultimate causes, on the other hand, purport to explain the origin and history of the developmental and genetic programs that regulate the behavior of the system. The complexity–stability theorem articulates the relation between the topology of the biological network and its response to perturbation. The theorem thus depicts a proximate cause for the stability of biological networks.
In order to characterize the evolutionary rationale for network stability, we will appeal to the entropic selection principle. According to this principle, the outcome of competition between an incumbent and a variant type is predicted by evolutionary entropy, and is contingent on the resource constraints, namely, its abundance and diversity. This principle can be integrated with the complexity–stability theorem to derive what we will call the:
According to this principle, the measure of selective advantage s, is now given by
Here ΔR denote the difference in robustness between the variant and the incumbent population.
The relation
Equation (59) yields an evolutionary argument for the large difference in the stability of biological networks. We observe from
Equation (59), that when
s > 0, we have the following conditions on the various parameters:
We infer from (a) and (b) a condition for the prevalence of robustness in terms of the ecological factors that regulate the dynamics of selection among competing networks.
The condition (a) entails that when resources are constant in abundance, (Φ < 0), and diverse in composition (γ > 0), networks with increased stability will have a selective advantage.
By contrast, condition (b) implies that when resources vary in abundance (Φ > 0), and is singular in composition (γ < 0), networks with decreased stability will have a selective advantage.
7. The Evolution of Cooperation
Sociality is a very common feature in groups of living organisms. The ability to cooperate and to perform acts which confer benefits to recipients and incur costs to the donor is ubiquitous. Cooperation can be observed in colonies of single celled organisms; marine invertebrates, which consist of individuals specialized to perform different roles; and insect societies [
15,
16,
67]. The phenomenon is also observed in human culture [
68].
The understanding of this behavior has derived largely from studies of the social insects: ants, bees, wasps and termites. The complex division of labour between members of the insect societies can be described in terms of three modes of organization: solitary, quasi-social, and eusocial. The degree of cooperation varies between each of these three modes. The extent to which the individual members of the group cooperate can be parametrized in terms of patterns of resource allocation.
- (a)
Solitary: Resource allocation in the population is uniquely to self.
- (b)
Quasi-social: In insects which display this trait, nesting is communal, with the nest site being shared by more than one adult female. Members in this colony allocate resources to both self and non-self.
- (c)
Eusocial: Social organization involves reproductive division of labor, that is only some individuals reproduce. The division into reproductive and non-reproductive castes means that certain individuals, the non-reproductives, allocate no resources to self.
The prevalence of these three modes of sociality varies. Solitary and quasi-social behavior are quite common. However, eusocial behavior is rare. Empirical studies of the ecological conditions under which these different modes of sociality are observed indicate that the incidence is largely modulated by the habitat, or more precisely, the resource conditions that characterize the habitat. For example, a high degree of cooperation or sociality is prevalent in insects living in stable resource limited environments, while solitary behavior is typical of species living in marginal habitats, where resources vary in abundance. One of the fundamental problems in studies of cooperation concern the evolutionary basis for this correspondence between various levels of sociality and the environmental constraints.
Studies of the evolution of sociality have been largely dominated by Hamilton’s inclusive fitness theory. The model revolves around the notion that selection on a gene for social behavior is contingent on two properties.
- (i)
The effects of the gene on the direct fitness of the bearer
- (ii)
The effects of the gene on the fitness of individuals who are genetically related to the bearer
Hamilton’s model is a natural extension of the classical Wright–Fisher models of population genetics to situations where the unit of selection is now defined in terms of a group of genetically related individuals. Hamilton’s rule asserts that any social trait will be favored by natural selection if and only if the sum of its direct and indirect fitness effects exceeds zero, [
51]. Fitness, in the context of these models is measured in terms of viability or reproductive success.
Inclusive fitness theory has generated considerable insight and qualitative understanding of social behavior, in particular, cooperation among the social insects. The theory, structured as it is around the basic assumptions of classical population genetics, has necessarily inherited certain limitations of this class of models. These limitations derive largely from the assumption that population size is large, effectively infinite, and resources are unlimited in abundance.
Critics of the Inclusive fitness theory, see for example, Bowles and Gitnis [
67], Wilson [
68], Wilson and Hölldobler [
69] have pointed to several common phenomena which are not readily accommodated within the framework of the model. These phenomena include:
- (1)
The prevalence of cooperative behavior in groups larger than the immediate family.
A recognized example of this phenomenon is cooperation among
Homo sapiens. Human cooperation is known to extend beyond the immediate family to include strangers. Laboratory experiments indicate that cooperation also occurs in interactions which are unlikely to be repeated, and in situations where no reputational gains are conferred by cooperative behavior, [
67].
- (2)
The rareness of eusociality and the ecological dominance of eusocial insects.
Eusociality is an advanced level of colonial organization described by division of labor between reproductive and non-reproductive castes, overlapping generation and cooperative care for the young. The eusocial condition is known to be rare. There exist only 15 taxonomic families of eusocial species in a phylogeny consisting of 2600 families [
68]. This phylogenetic rarity is inconsistent with the hypothesis that genetic relatedness is the primary mechanism which determines the evolution of cooperation.
- (3)
The correlation between eusociality and resource constraints.
The analysis of the Hymenopera and other species of insects indicate that all species that have attained eusociality live in fortified nest sites. In the early stages leading towards eusocial behavior the nest sites are generally guarded by workers. Moreover, a constant and dependable food resource is generally within foraging range of the workers [
68,
69]. The correlation between these resource constraints and the incidence of eusociality suggests that ecological factors may play a dominant role in the evolution of cooperation.
According to the theory of Inclusive fitness, genetic relatedness is the central factor which drives the spread of social traits. The formal structure of the model, and the various extensions that have been proposed, are based on a gene-centric view of social evolution. This perspective implicitly ignores the effect which constraints on the abundance and the composition of the resources may impose on the evolution of sociality.
Directionality theory is a generalmodel of the evolutionary process which takes into account the effect of ecological and demographic factors on the outcome of natural selection. The model considers both the effects of resource abundance and resource composition on the dynamics of selection. We will adduce the formalism of directionality theory to develop a general model of social evolution which considers the effect of variations in resource abundance and resource composition on social behavior. The model we propose is called the entropic theory of sociality. Our analysis considers the evolution of cooperation from both phenotypic and genotypic perspectives. In the first class of models, Section 7.1–7.4, the population is considered as the unit of selection. The second class of models, Section 8, is effectively an extension of the theory of inclusive fitness. In this analysis, the individual is considered as the unit of selection.
7.1. Evolutionary Entropy and Sociality
We consider a population as consisting of a group of individuals who interact through the allocation and sharing of resources. The interaction can be described by a weighted directed graph, where the weighted edges correspond to the intensity of the interaction between the individuals. The graph can be identified with an adjacency matrix A = (aij) ≥ 0. The coefficient aij, i ≠ j, is a measure of the contribution of individuals in class (j) to the net-reproductive success of individuals in class (i), while aii denotes the contribution of class (i) to its own reproductive success.
Let λ denote the dominant eigenvalue of A, and u = (ui) the eigenvector associated with λ:
We write
The evolutionary entropy H associated with the network is given by
Here π = (πi) is the stationary distribution of the matrix P = (pij).
We will illustrate the relation between entropy and the degree of sociality by considering the three classes of networks representing the interaction between the social insects. Without loss of generality, we consider a system defined by two nodes corresponding to donor and recipient:
The elements a11, a22 denote the contribution to self, whereas a12, a21 denote the contribution to non-self.
(a) Solitary networks
There are no contributions from self to non-self; all distributions are directed to self; H = 0.
(b) Completely social networks
Contributions to self and non-self are equal; H = log 2.
(c) Eusocial system
Eusociality is a special case of cooperation where one group of individuals–the non-reproductives– allocate no resources to self and invest all resources to non-self. The entropy is
where
7.2. Evolutionary Entropy as a Measure of Social Organization
Cooperation pertains to an engagement with other individuals in a social network in a mutually beneficial way. The social network in this context is defined in terms of interacting classes or groups of individuals. The individuals in each group are assumed to belong to the same age, or social class, or in general, defined by some common attribute.
We assume that the different groups appropriate resources from the external environment and allocate these resources to other groups according to certain norms of social behavior. The norms are said to be cooperative if they satisfy the following conditions.
- (a)
Reciprocity: This property describes the extent to which there exist differences between the allocation of one group to another group. When complete reciprocity obtains, group A allocates to group B the same amount that group B allocates to group A.
- (b)
Equitability: This norm describes the extent to which there exist differences between the allocation of one group to itself, and its allocation to non–self. In the case of a network consisting of two classes, A and B, complete equitability obtains when group A allocates the same amount to A, as it allocates to B.
The significance of evolutionary entropy in studies of the evolution of sociality is based on the fact that small changes in the norms, reciprocity and equitability, are positively correlated with changes in evolutionary entropy. This property can be formalized in terms of the following tenet:
Entropy-Sociality Rule
Evolutionary entropy parametrizes the position of a population along a sociality continuum defined in terms of the norms: reciprocity, and equitability.
Low entropic networks are described by weak reciprocity and low equitability. Networks with high entropy are characterized by strong reciprocity, high equitability.
The relation between entropy and the norms of cooperation can be illustrated by considering the dependence of entropy on reciprocity. We assume a symmetric interaction matrix
The coefficient a1 describes resource allocation to self, and a2 describes allocation of resources to non-self.
We write a1 = (1 −θ)a2 where 0 < θ < 1. The parameter θ denotes deviation from reciprocity. The entropy becomes
We note, see
Fig 14, that
H is a concave decreasing function of
θ, with 0 ≤
H ≤ log 2. The maximum value for
H is attained when
θ = 0, corresponding to complete reciprocity in resource allocation.
Figure 15(a) and 15(b) describe networks with low and high entropy, respectively. In
Figure 15(a), resources are allocated almost exclusively to (
1). Groups (
2) and (
3) receive small amounts
ɛ, from (
1), but contribute amounts
b and
c to (
1). In
Figure 15(b), resources are equitably distributed to (
1), (
2) and (
3).
7.4. The Evolution of Cooperation
We will now appeal to the entropic selection principle to study the evolution of cooperation under two classes of resource constraints, namely, limited abundance and unlimited abundance. We will show that when resource abundance is limited, then the outcome of selection is determined by the level of resource abundance and the heterogeneity of its composition. When resource abundance is unlimited, the outcome of selection will be contingent on relatedness.
Limited Resource Abundance, Finite Population Size
The measure of selective advantage in models of the evolution of sociality is given by,
The condition s > 0 entails
We can infer from (i) and (ii) the following set of rules which relate the resource constraint, as defined by Φ and γ, with changes in the degree of sociality, as characterized by evolutionary entropy.
We infer from (i) and (ii) the following constraints on resource abundance and resource composition
- I(a)
When resources are constant in abundance and diverse in composition, cooperation will have a selective advantage and increase in frequency.
- I(b)
When the resource varies in abundance and is singular in composition, selfishness will have a selective advantage and increase in frequency.
Unlimited resource Abundance; Infinite Population Size
When M → ∞, R → ∞, the measure of selective advantage is now given by
Now, Φ < 0 ⇒ Δr.ΔH > 0; Φ> 0 ⇒ Δr.ΔH < 0.
We conclude that since the selective advantage is now determined by the growth rate, r, we can infer from the above implications the following rules:
- (a)
When Φ < 0, cooperation has a selective advantage and will increase in frequency.
- (b)
When Φ > 0, selfishness has a selective advantage and will increase in frequency.
Now Φ = r − H. Hence Φ < 0 ⇒ r < H; Φ > 0 ⇒ r > H.
Now the phenotypic relatedness ρ is given by ρ= π1. Since
we obtain
where
Now
We can therefore infer from the tenets (a) and (b) given above, the following rules relating phenotypic relatedness with the spread of cooperation or selfishness.
- II(a)
When Φ > r/H̃, cooperation will have a selective advantage and increase in frequency.
- II(b)
When Φ < r/H̃, selfishness will have a selective advantage and increase in frequency.
The tenets (I) and (II) regarding the evolution of cooperation and selfishness indicate the critical effect of resource abundance on the spread of the different behavioral traits. When resource abundance is limited, the outcome of selection is determined by the rate at which resources are appropriated from the external environment. In this case, the outcome of competition will be determined by the degree of variation in resource abundance and the heterogeneity in resource composition.
However, when resource abundance is unlimited, the outcome of selection is decided by the rate at which resources are converted into commodities which confer individual benefits. Relatedness now becomes the critical factor in the spread of cooperative and selfish dispositions.
8. A Genetic Theory of the Evolution of Social Behavior
Hamilton proposed a classification of social behavior in terms of the gain or loss of offspring induced by the performance of the behavior. The model distinguishes between an actor X and a recipient Y. In Hamilton’s model X performs some action on Y. Each individual experiences a change in their expected offspring number as a result of the action. Four types of social action are distinguished—mutualism, altruism, selfishness and spite.
Mutualism is defined as the social action in which both partners X and Y gain offspring from the action. Altruism is defined as the social action in which the actor X loses offspring and the recipient Y gains offspring. Selfishness is defined as a social action in which X profits and Y incurs a loss, whereas spite corresponds to the condition where both X and Y incur losses.
8.1. Inclusive Fitness Theory
In this section we consider Hamilton’s rule in terms of the traits altruism and selfishness, and we will appeal to the formalism of directionality theory to extend the theory by incorporating the effect of environmental factors on social behavior. We will distinguish between two classes of ecological and demographic constraints.
(i) limited resources, finite population size; (ii) unlimited resources, infinite population size.
We will show that when resource abundance is limited and population size is finite, then the evolution of cooperation is independent of genetic relatedness, and is determined uniquely by the degree of variation in resource abundance, and the degree of heterogeneity in resource composition. However, when resource abundance is unlimited and population size infinite, then genetic relatedness determines the evolution of cooperation.
We will consider a social network as defined in terms of the matrix
This can be illustrated graphically as in
Figure 16, where
X1 denotes the donor and
X2 the recipient.
We let a1 and a2 denote the change in net-offspring number induced by the social behavior. We distinguish between the actor X1 and the recipient X2 by assuming that a1 ≠ a2. Without loss of generality, we will assume that a2 < a1.
We consider a change in the interaction between X1 and X2 and assume that the social network that describes the variant is given by the matrix
Here α1 and α2 are assumed to be small and to be represented by α1 = ln(a1)δ and α2 = ln(a2)δ for |δ| small and the dynamics of the network can be included in the context of our entropic selection approach. As a further consequence, |α1 −α2| = |δ| | log(a1/a2)| is always much smaller than | log(a1/a2)|.
Now let H and H*denote the entropy of A and A*, respectively:
where
Write
and
Then it follows that
Since α1 and α are assumed small (and |α1 −α2| much smaller than | log(a1/a2)|), we have the following implications:
The dispositions, altruism and selfishness can be described in terms of constraints on the parameters
α1 and
α2. The classification, adapted from Hamilton [
51] and Bourke [
15] is as follows.
Altruism: (α1 > 0, α2 < 0). Altruistic behavior is a social action in which the actor, the altruist, incurs a cost α1, and confers a benefit α2 to the recipient.
Selfishness: (α1 < 0, α2 > 0). Selfish behavior is defined as a social action in which the actor profits, and the recipient incurs a loss.
We will have recourse to this classification in deriving a set of conditions for the evolution of altruism and selfishness. The crux of our analysis is the distinction between the following two canonical classes of resource and demographic constraints.
- (A)
Limited resources, finite population size: The measure of selective advantage under this class of ecological-demographic conditions is
The relation
Equation (61) entails the following conditions which ensure the spread of the variant trait:
By appealing to the characterization of altruism (α1 > 0, α2 < 0), and selfishness (α1 < 0, α2 > 0), we can infer a class of rules which specify the ecological constraints which will generate the two modes of behavior, altruism and selfishness. The rules are as follows:
- A(i)
Diverse resources, constant abundance: altruism will have a selective advantage and will spread.
- A(ii)
Singular resource, variable abundance: selfishness will have a selective advantage and will spread.
- (B)
Unlimited resources, infinite population size: The measure of selective advantage when this ecological-demographic situation prevails is,
Here r denotes the population growth rate. Now if λ and λ* denote the dominant eigenvalue of the matrices A and A*, we have
Now Δr > 0 represents the condition for the evolution of a social action. Since ΔrΔλ > 0, we conclude that the evolution of sociality is now determined by the conditions
Let ρ denote the genetic relatedness of X1 to X2. This quantity is defined by the probability of sharing a focal gene over and above the average probability. Hence
Accordingly, we can express ρ, in terms of the fitness parameters, a1 and a2 namely
.
The criteria for the evolution of altruism and selfishness can be derived from the above equation which becomes,
We will now show that when resource abundance is unlimited and population size is large, effectively infinite, the spread of a social trait now depends on the relation between the degree of relatedness ρ, and the cost-benefit ratio.
In the case of altruism, we write
α1 =
c, the cost incurred by the actor, and
α2 = −
b, the benefit which accrues to the recipient. We obtain from
Equation (63) the following result.
- B(i)
If ρb > c, then altruism will have a selective advantage and will increase in frequency.
In the case of selfishness, we now write
α1 = −
c, to represent the benefit gained by the actor, and
α2 =
b to describe the cost incurred by the recipient. We now obtain by appealing to
Equation (63) the following result:
- B(ii)
If αb < c, then selfishness will have a selective advantage and will increase in frequency.
The proposition expressed by B(i) and B(ii) represents Hamilton’s rule.
8.2. Inclusive Fitness Theory and the Entropic Theory of Sociality
Hamilton’s theory of inclusive fitness is an extension of classical population genetics to analyze the evolution of social behavior. These genetic models which have their origin in the pioneering studies of Fisher, Haldane and Wright, implicitly assume that resource abundance is unlimited and that population size is large, effectively infinite. Darwinian fitness in this context is characterized by the capacity of an organism to convert the available resources into net-offspring production and is measured by netreproduction rate or some surrogate of this property.
Selective advantage in the framework of these models can be described by
Here r denotes net-offspring production.
The entropic principle of sociality issues from a model which explicitly considers the organism– environment interaction in the study of competition between resident and variant types. Consequently, resource abundance and resource diversity now become critical components in the competition process. Darwinian fitness is now characterized by the efficiency of the organism to acquire energy from the external environment–a condition which is regulated by the abundance of the resource, and its temporal variation and diversity.
Selective advantage is now given by
We have shown analytically that these twomeasures of selective advantage are related as the following diagram indicates
Here R denote the resource abundance and M the population size.
This limiting condition entails the following property:
Inclusive fitness theory and the Entropic theory of Sociality
The theory of inclusive fitness is the limit, as resource abundance and population size tend to infinity, of the entropic theory of sociality.
One of the anomalies of inclusive fitness theory is the large scale cooperation observed among genetically unrelated individuals. The entropic theory of sociality indicates that the nature and intensity of this cooperation is modulated by external factors, namely resource abundance and resource diversity. Hamilton’s model ignores these essential constraints. Inclusive fitness theory thus represents an approximation to the entropic theory of sociality. The validity of the approximation is contingent on the resource constraints and population size. When resource abundance is unlimited and the population size is large, effectively infinite, the predictions of both theories are equivalent.
9. Directionality Theory: Micorevolutionary Trends–Ecological Time Scale
The evolutionary process which unfolds on an ecological time scale can be analyzed in terms of two events.
An invasion dynamic. This event involves the introduction of new variants in the population and the subsequent competition between the incumbent and the variant type for the available resources.
An establishment dynamic. Its main signature is the generation of new types by Mendelian segregation and the interaction of the array of genotype with the external environment.
The entropic principle specifies the outcome of the invasion process. Cooperation between the new variant and the incumbent results in the generation of new types. The Mendelian principle of inheritance is the rule which governs the distribution of types. The frequency of the types will change contingent on the ecological constraints.
The integration of these processes was described in Demetrius [
70]. The model assumed that the phenotypic traits were controlled by a single locus. The incumbent population has genotype AA, the variant is described by a genotype Aa. The microevolutionary dynamics studies the change in entropy as the dynamical system evolves from one steady state configuration described by the incumbent population with entropy
H, to a new steady state condition, which is now defined by a composite population with entropy
H̃.
This composite population will in general be polymorphic, comprising the incumbent, the successful mutant–which initially will be rare–and the various genotypes generated by mating between the incumbent and the mutant.
We are interested in evaluating the change ΔH = H̃ − H, under various classes of ecological constraints. We will first describe the dynamics of the incumbent population, defined by the genotype AA.
9.1. The Dynamics of the Incumbent
We consider a nonlinear age-dependent model of population growth. Let u(x, t) denote the number of individuals of age x at time t. The population size N(t) at time t is given by
The changes in the function u(x, t) are determined by μ(x,N), the age-specific death rate, and m(x,N), the age-specific birth rate at population size N.
The dynamics of u(x, t) is
The entropy H of the population at steady state will be a function of the age-specific birth and death rate at steady state.
We will now assume that a variant population with genotype Aa has invaded the incumbent population. Mating between the variant Aa and the incumbent AA will result in the production of genotypes AA, Aa and aa. These three types comprise the composite population. The Mendelian laws will specif the birth rate of the population described by each of the genotypes. The dynamics of selection will depend on the response of the different genotypes to the ecological and resource constraint.
9.2. The Composite Population
We assumed random mating between the two genotypes.
In sexual reproduction, the frequency of types generated by random mating is specified by
Table 6. Here m and f denote male and female types.
The selective dynamics of the genotypes x1 = AA, X2 = Aa, X3 = aa can be analyzed in continuous time, in terms of the following functions
These functions describe the number of genotypes.
The dynamical equations for the changes in numbers ui(x, t) of the genotype Xi are given by
Here μi(x, t) denotes the mortality function of the genotype Xi. This typically is a function of the resource constraints that regulates population growth.
The birth rate
ui(0,
t) of the genotypes are obtained from the Mendelian laws given in
Table 6. The model generally assumes that the birth rate
ui(0,
t) requires that
the fecundity of a mating between a given pair of individuals is determined uniquely by age and genotypes,
mating is at random with respect to age and genotype.
Write
where U(x, t) = u1(x, t) + 2u2(x, t) + u3(x, t).
We can now appeal to the Mendelian laws of inheritance given in
Table 6 to express
ui(
x,
t) in terms of the fecundity functions
mi(
x,
t) and
μi(
x,
t).
The equilibrium solution of
Equation (64) describes the ultimate effect of the selection process on this initial increase of the mutant.
We will assume that the system evolves to a polymorphism which will be described by the presence of all threee genotypes X1, X2 and X3.
9.3. The Fundamental Theorem of Evolution
The directional change in entropy as the system evolves from one steady state to the next is derived by a comparison of the entropy H in the steady state defined by the presence of the incumbent X1, and the entropy Ĥ in the steady state defined by the composite population X1, X2 and X3. Write Δ̂H = Ĥ − H, the change in entropy as the system evolves from one steady state to the next and write ΔH = H* − H, where H* denotes the entropy of the variant type.
According to the entropic selection principle, the deterministic criterion for the invasion of the variant type is given by
Now, an analysis of the dynamical system given by
Equation (64) shows that
This asserts that the local change in entropy ΔH (due to the invasion process), and the global change in entropy, Δ̂H (due to the establishment process) are positively correlated.
We can now appeal to
Equations (65) and
(66) to predict long term changes in entropy as the incumbent population AA is replaced by the composition population consisting of the three genotypes AA, Aa and aa.
We infer the following implications
If Φ < 0, γ > 0, then Δ̂H < 0 that is, the entropy increases.
If Φ > 0, γ < 0, then Δ̂H < 0 that is, the entropy decreases.
In view of the characterization of Φ and γ in terms of resource abundance and diversity, we can now infer long term changes in entropy under mutation and natural selection–the Fundamental Theorem of Evolution.
- I (a)
If resource composition is diverse (γ > 0) and resource abundance constant (Φ < 0), then the entropy increases as the system evolves from one steady state to the next.
- I (b)
If resource composition is singular (γ < 0) and resource abundance variable (Φ > 0), then the entropy decreases as the system evolves from one steady state to the next.
The relation between resource constraints and long term directional changes in entropy under the microevolutionary process of mutation and selection is described in
Table 7.
9.4. Empirical Considerations
The fundamental theorem of evolution which
Table 7 delineates has been empirically evaluated using plant populations [
73], human populations [
52,
53], and an analysis of the equid lineage [
74]. The analysis using plant population is based on demographic data of 56 species of plants. A statistical analysis of correlations between entropy,
S, and the parameter called the reproductive potential, Φ, generated results which were consistent with a uni-directional increase in entropy under resource conditions defined by constant abundance (Φ
< 0), and a uni-directional decrease in entropy under resource conditions defined by variable abundance (Φ
> 0).
The analysis based on human populations [
52,
53] was complicated by the effect of cultural factors on the evolutionary dynamics in modern human populations. The statistical analysis was nevertheless robust enough to decode trends in evolutionary entropy which are consistent with the FTE.
The study using the equid lineage appeals to the fact that evolutionary entropy is analytically related to body size. We can therefore infer from the FTE that body size increases, when resources are diverse in composition and has constant abundance, and decreases, when resources are singular in composition and has variable abundance.
These predictions regarding trends in body size were evaluated using data from the equid lineage during the Plio-Pleistocene. The analysis was based on a comparative study of trends in body size in North America and in Europe. An appeal to various sources which documented the ecological and resource conditions which prevailed in the two continents during the Plio-Pleistocene indicates that the North American equid lineage was subject to resources of constant abundance and diverse composition, while the European lineage was characterized by variable resource abundance and singular composition. The FTE predict that body size in the equid lineage will increase in North America and decrease in Europe. The data described in [
36] was consistent with these predictions.
9.5. The Fundamental Theorem of Natural Selection (FTS) and the Fundamental Theorem of Evolution (FTE)
The central tenet of Darwin’s theory of evolution is the gradual replacement of one population type by another through the action of the following processes.
- (i)
The production of variation:
Mutation is the primary mechanism generating variation. It is a random event. Once allelic variation has been introduced, the total diversity of genotypes may be increased as a result of genetic recombination.
- (ii)
The action of selection:
This process—differential survival and reproduction—is a non-random event. In every generation only a small percentage of individuals will survive to reproductive age. Selection discriminates between the various types in a population according to their capacity to annex resources from the external environment, and to transform these resources into reproductive activities.
Fisher’s fundamental theorem of natural selection and the fundamental theorem of evolution are propositions which aim to formalize the Darwinian process by analyzing the genotypic and phenotypic changes which occur during evolution. The two propositions differ in terms of the assumptions made regarding the forces driving the changes in population composition.
(I) The fundamental theorem of natural selection (FTS)
The central assumptions of the FTS is the local nature of the genotypic and phenotypic changes, and the mechanism of selection. The model considers selective changes occurring on a time scale in which the production of new variation by mutation can be ignored. The changes in population composition are induced uniquely by differences in the capacity of the organism to invest existing resources into reproduction and survivorship. This assumption entails two modes of selection; Malthusian, which pertains to selection due to differences in the growth rate of the types; and viability, which pertains to selection due to differences in the individual probability to survive to reproductive age.
Studies of changes in population composition under Malthusian selection typically assume asexual haploid populations. The mean fitness w̄ is given by
Here wj denote the Malthusian parameter of type Xj, and pj denote its frequency.
The extension of these studies to diploid population presents analytical problems in view of the genetic complexities generated by Mendelian factors. Consequently, when diploid populations are considered, the analysis is often restricted to viability selection.
The standard model of diploid populations and viability selection considers alleles A1, A2, . . . , Ak at an autosomal locus. If Pii denote the relative frequency of the homozygotes, and 2Pij the relative frequency of heterozygotes, then the frequency of the allele Ai is
The mean fitness is now given by
The analysis of changes in the frequency of types under both modes of selection leads to the following proposition
Here Δw̄ = w̄′ − w̄, the change in mean fitness from one generation to the next.
The relation (
67) asserts the following proposition:
Mean fitness increases under natural selection.The extensions of
Equation (67) to situations based on interactions at several loci all assume viability selection. These extensions, and their relations with the fundamental theorem of natural selection, have been reviewed and discussed in Edwards [
71] and Ewens [
72].
(II) The fundamental theorem of evolution (FTE)
The FTE considers genotypic and phenotypic changes as driven by two processes: (a) the introduction of new variations by mutation, (b) the discrimination between variant and incumbent types by selection. The selection process is due to differences in the capacity of organisms to appropriate resources from the environment, and to transform these resources into metabolic and reproductive work. This mode of selection leads to the characterization of fitness by evolutionary entropy.
The FTE integrates the entropic selection principle with the laws of Mendelian inheritance to analyze changes in evolutionary entropy as one population replaces another over evolutionary time. The changes in evolutionary entropy are illustrated in
Figure 17.
Here H1 denotes the entropy of the incumbent at steady state, and H2 the entropy of the new composite population at steady state. According to the FTE, the change ΔH = H2 − H1 is conditional on the resource constraint. this is described by the directionality principle:
Evolutionary entropy increases (ΔH > 0) when resource abundance is constant and composition diverse; evolutionary entropy decreases (ΔH < 0), when resource abundance is variable and composition is singular.
The FTE can be considered a synthesis of Mendelian genetics, demography and ecology to furnish a mathematical model of Darwin’s theory of evolution by variation and natural selection.
(III) The FTS and the FTE—implications
Darwin’s theory of evolution is a qualitative model of directional changes in the properties of populations as one type replaces another under the action of variation and selection. Directional transitions are not unique to the organic world. Changes in the macroscopic properties of material objects, such as solids, also have a directional component.
Consider an insulated container in which two blocks of copper, one hot and the other cold, are sealed together. There will be spontaneous flow of heat from the hot body to the cold body until both reach some intermediate temperature. This directional property which this spontaneous physical change depict is the Second Law of Thermodynamics. The law was explained by Boltzmann in terms of a model of statistical mechanics of interacting particles. The cornerstone of Boltzmann’s work was the quantity, thermodynamic entropy, denoted S̃, a measure of the spreading of energy throughout the energy storage modes of the material aggregate.
Directionality in inanimate material aggregates is characterized by the condition
This describes an increase in thermodynamic entropy as the system moves from one initial state, where the individual blocks have different temperatures, to an equilibrium state where both blocks have the same temperature.
Fisher considered the FTS, which describes a uni-directional change in mean fitness, as a biological analogue of the Second Law of thermodynamics. According to Fisher:
“It will be noticed that the fundamental theorem of natural selection bears some remarkable resemblances to the Second Law of Thermodynamics. Both are properties of populations, or aggregates, true irrespective of the nature of the units which compose them; both are statistical laws; each requires the constant increase of a measurable quantity, in the one case, the entropy of a physical system, and in the other the fitness measured by the Malthusian parameter of a biological population.”
The remarkable resemblance Fisher has postulated does not hold up to a critical scrutiny.
Thermodynamic entropy, the statistical measure adduced in Boltzmann’s directionality theorem, is a valid measure of the spread of energy within the microscopic storage modes of a material aggregate. The increase in thermodynamic entropy which Boltzmann’s analysis establishes, offers a statistical mechanics explanation of the Second Law. Boltzmann’s theorem thus represents a valid mechanistic rationale for empirical observation that the spontaneous flow of heat is uni-directional, namely from hotter to colder bodies.
The Malthusian parameter, the concept cited in Fisher’s theorem, is an aggregate measure of individual birth and death rates. This measure describes the rate at which an organism converts resources into net-offspring production. The Malthusian parameter, thus describes the outcome of natural selection under a special class of ecological constraints, namely those defined by unlimited resource condition. When resources are unlimited, the capacity of the organism to appropriate energy from the external environment does not impact on the outcome of selection. The deciding factor, when this resource constraint obtains, is the efficiency in converting the metabolic energy of the organism into reproductive activity.
Evolution in natural populations generally unfold under conditions where resources are limited in abundance. Accordingly, the Malthusian parameter, the mainstay in the Fisherian analysis, does not generally predict selective outcome.
These observations indicate that Fisher’s theorem does not represent a valid explanation of the changes in population composition induced by the force of natural selection. Fisher’s theorem, in sharp contrast to Boltzmann’s theorem, is not consistent with empirical observations concerning changes in the various properties that describe natural populations.
The formulations of the FTS based on Malthusian selection and viability selection pertain to local or instantaneous changes in mean fitness. This mode of selection ignores ecological constraints and consequently is unable to explain the long term changes in genotypic and phenotypic composition observed in natural populations.
The FTE, in sharp contrast to the FTS, integrates Mendelian genetics with demography and ecology to explain the changes in population composition as new variants are introduced in the population by mutation, and then screened by natural selection.
Table 8 summarizes the different properties of the FTS and the FTE.
10. Directionality Theory: Evolutionary Trends on a Geological Time Scale
Microevolution pertains to the changes in the genotypic and phenotypic composition of populations over an ecological time scale. This evolutionary process pertains to changes within a population or within a phyletic lineage. The changes in population composition are driven by mutation and natural selection.
The entropic selection principle is the basis for the quantitative understanding of microevolutionary patterns. This principle, as we have observed, gives a mechanistic explanation of processes such as the evolution of life history, the evolution of sociality, and the origin and proliferation of cancer cells.
Macroevolution pertains to the changes in the species composition of clades over geological time scales. This evolutionary process is driven by speciation–the formation of new species, and extinction, the demise of species or complete biota.
The history of life when viewed on a geological time scale has a directionality component. This property can be described by changes in mean body size within clades, and changes in the maximum body size over the whole history of life.
Mean body size increases in most phyletic lineages. This fact, now called Cope’s rule, see Cope [
35], has been observed originally in clades of Cenozoic mammals. The largest known representative among these taxonomic groups are usually geologically younger than their smaller relatives.
Newell [
76], in later studies, showed that the increase in mean size also holds in many invertebrates. Among foraminferans, arthropods, echinoderms, all widely separated lineages, there exist a distinct trend towards size increase. The increase in mean body size, however, is not universal. Among brachiopods, bryozoans, there is little increase in size. Some of the lineages are known to show a distinct stability of size over geological time. The study of body size evolution in Cretaceous molluscs by Jablonski [
77] indicates both patterns of size increase and decrease.
Maximum body size, that is the maximum size attained by species within a clade, does however show a uni-directional increase. The recent period level compilation of the largest known fossil organisms show that maximum size increased by 16 orders of magnitude over the past 3.5 billion years [
78].
The entropic selection principle, the organizing tenet in explaining the adaptation of populations on a microevolutionary level, is also the basis for explaining the adaptation of species and directional trends observed on a macroevolutionary level. The significance of the entropic selection principle in understanding macroevolutionary change derives from the fact, underscored by Mayr [
4] that all macroevolutionary processes unfold in populations and genotypes of individuals, and are thus the emergent features of microevolutionary events. Speciation and extinction–macroevolutionary events–can therefore be analyzed in terms of the dynamics of allelic variation within populations, and competition between populations.
We will therefore apply the formalism developed in the study of microevolution to establish certain correlations between evolutionary entropy and the macroevolutionary parameters, speciation rates and extinction rates. We will then exploit these correlations to derive a class of macroevolutionary principles which describe changes in mean entropy and maximum entropy over geological time. These principles constitute the evolutionary rationale for the trends in mean and maximum body size documented in the fossil record.
10.1. The Dynamics of Speciation
Speciation is the process by which new lineages arise. The process has two aspects: (i) the gradual change from an ancestral to a derived species; (ii) the splitting of a species to generate two derived species, Coyne and Orr [
79].
The speciation rate is expressed as the number of new species produced per existing species per time period–typically a million years. The inverse of this number is the mean waiting time for the transformation of one species into another. This quantity is the average period elapsing between the origin of a new lineage and the reproductive isolation of the lineage. Hence the waiting time measures the interval between the emergence of a new mutation and the ultimate fixation of the mutant.
The mean waiting time is proportional to the mean time to fixation of a mutant allele. We will exploit methods introduced in [
80,
81] to show that the mean waiting time
τ is given by
Here
N denotes the population size and
σ2 the demographic variance. We will then use
Equation (68) to derive a relation between the speciation rate and evolutionary entropy.
10.1.1. Mean Fixation Time
We consider a population X1 with demographic parameters (r, H, σ2, Φ) and the mutant X2 defined by the parameter (r*, H*, σ2*, Φ*). Let f(p, t) denote the probabilitiy that the mutant allele X2 becomes fixed by the t-th generation, given that its frequency is p at time t = 0. Write f(p) = limt→∞ f(p, t). Then f(p) denotes the probability of ultimate fixation.
Consider the quantity
Then
represents the mean fixation time, that is the average number of generations until the mutant allele with initial frequency becomes fixed in the population, [
80].
Now, see [
20], the function
f(
p, t) satisfies the Kolmogorov backward equation
where
and
We can obtain an ordinary differential equation for
T(
p) as follows: We differentiate each term in
Equation (70) with respect to
t, and we multiply each of the resulting terms by
t. By integrating the terms with respect to
t from 0 to ∞, we obtain
Under the natural assumption that
vanishes at t = ∞ it follows that
Equation (72) can now be integrated to yield an expression for
T(
p). We write
where
Then
The boundary conditions are lim
p→0 T(
p) =
a for some finite
a, and
T(1) = 0. From
Equation (73), the mean time to fixation
τ(
p) =
T(
p)
/f(
p) can be calculated as
10.1.2. Entropy and Speciation Rate
We will assume throughout that speciation is driven by allopatric processes, that is complete geographic isolation of the two species, see Mayr [
3]. Allopatric speciation is often subdivided into two modes:
vicariant speciation, in which reproductive isolation evolves after the geographic range splits into two or more largely isolated populations, and
peripatric speciation, in which reproductive isolation evolves after an isolated habitat is colonized by a few individuals, or a small population becomes geographically isolated, beyond the periphery of the parential population. We will assume, following Mayr [
3] that the peripatric mode of speciation is the dominant mode.
The peripatric isolate will be described by a small population size and a gene pool which is statisticallly different from the parental gene pool. The ecological niche the isolate occupies will be much narrower than the niche of the parental population.
This restriction on the niche breadth and the population size means that variations in resource abundance may be ignored and that the principal environmental factors which will influence the speciation dynamics will be the resource diversity as described by the parameter : We establish the following relations between rate of speciation and entropy:
- I (a)
If γ < 0, then the rate of speciation is positively correlated with entropy.
- I (b)
If γ > 0, then the rate of speciation is negatively correlated with entropy.
We will assume that the rate of speciation, denoted
α, is inversely related to the mean waiting time for the fixation of an allele. We can then infer from
Equation (68), the relation
where c is a positive constant.
Now, from
Equation (31), we have that
γ < 0 ⇒ Δ
σ2Δ
S̃ > 0 and
γ > 0 ⇒ Δ
σ2Δ
S̃ < 0. We conclude that
when γ < 0, Δα ΔS̃ > 0 and speciation rate is positively correlated with entropy;
when γ > 0, Δα ΔS̃ < 0 and speciation rate is negatively correlated with entropy.
Now, evolutionary entropy is positively correlated with body size. The model thus predicts that the nature of the correlations between speciation rate and body size will be contingent on the demographic resource constraint γ. We have that when γ < 0–a singular resource–speciation rate will increase with body size. However, when γ > 0–corresponding to species utilizing diverse resources–speciation rate will decrease as body size increases.
10.2. The Dynamics of Extinction
Species extinction represents the other component that determines changes in the composition of clades. Species extinction has two signatures: background extinction and mass extinction [
3]. Background extinction refers to the steady demise of individual species. This steady extinction derives from certain intrinsic limits of the genetic constitution of the population to adapt to changes in the environment which may occur during the species evolutionary history. These changes may involve the arrival of a new competitor or the invasion of a new pathogen.
Mass extinction pertains to the annihilation of a large proportion of the biota–this process occurring in a very short time on a geological time scale. Although background extinction is driven primarily by biotic factors and natural selection, and mass extinction is due primarily to physical factors such as changes in climate or the chemical composition of the terrestrial atmosphere, both extinction processes can be analyzed in terms of a similar mathematical formalism.
We will show that for a population of size N with growth rate r, and demographic variance σ2, the probability of ultimate extinction, denoted ω, is given by
We will then appeal to this expression to obtain relations between the extinction probability and entropy, for extinction under background and mass-extinction regimes.
The derivation of
Equation (75) considers a population of size
N(
t) subject to fluctuations induced by the demographic structure. We therefore assume that the change in log
N(
t) in the interval Δ
t due to fluctuations is caused by Brownian motion with variance
σ2Δ
t/N(
t). We can therefore describe the evolution of the density
f(
N, t) of the process by the solution of the Fokker-Planck equation, see Demetrius, Gundlach and Ochs [
20], given by
This equation can be solved explicitly, see Feller [
56].
The probability ω(t) that the population dies out before time t, is given by
It was shown in Feller [
56] that
We can appeal to
Equation (77) to establish certain correlations between extinction rates and entropy under background and mass extinction regimes.
10.3. Background Extinction
The extinction of species under this regime is a steady and gradual process. Extinction derives from the inability of the population to adapt sufficiently rapidly to the changing ecological conditions.
In our analysis of this process, we assume that rN = C and write
We will now use
Equation (78) to show that the direction of the correlation between extinction rate
β and entropy is contingent on the demographic parameter
γ.
Let β denote the extinction rate, and assume that Δω Δβ > 0, that is probability of ultimate extinction ω, and the extinction rate β, are positively correlated. We now show the following.
(II) (a) when γ < 0, the changes in extinction rate and the changes in entropy are positively correlated,
(II) (b) when γ > 0, the changes in extinction rate and the changes in entropy are negatively correlated,
By appealing to the series of relations, see Section 5.1,
Evolutionary entropy is related to body size. This empirical and analytical fact [
31] can be integrated with the patterns described by
Equations (79) and
(78) to predict correlations between extinction rate and body size.
Since
γ is a measure of habitat or resource diversity, we can infer from
Equations (79) and
(78) the following patterns.
When resource is singular, weak habitat diversity, extinction rate will increase with increasing body size.
When resource is diverse, strong habitat diversity, extinction rate will decrease with increasing body size.
We can now appeal to the macroecolgocial perspective [
82,
83] to predict relations between extinction rate and body size on islands and on continents.
Islands and continents differ largely in terms of habitat or resource diversity which is typically weak when habitat range is small and strong when habitat size is large. Accordingly, we have the following extinction patterns for the two habitats.
- (a)
Islands: Extinction rate will increase with increasing body size. Computational studies of this extinction pattern, indicate that the body size frequency distribution induced will be log-normal.
- (b)
Continents: Extinction rate will decrease with increasing body size. Numerical studies of this extinction pattern indicate a body size frequency distribution which is strongly right skewed.
Empirical studies of body size frequency distribution on islands are known to vary from log-normal to weakly right skewed, whereas the distribution patterns on continents are strongly right skewed, [
83]. These observations are indicative of a certain robustness as regards the constraints on habitat diversity on correlations between extinction and body size.
10.4. Mass Extinction
Mass extinction refers to the demise of species, complete lineages or biota by physical factors such as the large and widespread changes in climatic conditions.
The factors which induce these events are episodic in nature. The effect of mass extinction regimes will typically be described by a large decrease in population size with minimal effects on the life-history properties of the population.
In evaluating the dynamics of mass-extinction, we will therefore evaluate the effects of this event on changes in population size N and changes in ω, the probability of ultimate extinction. We have
Hence
Now Δ
ω Δ
β > 0, where
β is the extinction rate. Since evolutionary entropy
S̃ is negatively correlated with popolation size
N, we conclude from
Equation (81) the following.
11. Directionality Principles in Macroevolution
Macroevolutionary change, that is changes in the composition of clades on an geological time scale, are determined by speciation and extinction processes. The extinction process has two signatures: background events and mass extinction events.
The anaytic relations between speciation-extinction events and evolutionary entropy give a framework for evaluating changes in entropy on a geological time scale.
Mass extinctions are relatively rare events when contrasted with the process of background extinction. The events are in effect decoupled from each other; background extinction acting over a large span of geological time, whereas mass extinction relegated to small intervals of geological times.
In the study of changes in species composition over geological time we distinguish between two phases
an episode defined uniquely by speciation and background extinction–a process which unfold over several million years;
an extended phase involving speciation and the alternation of background and mass extinction regimes–a process which occurs over billion of years.
11.1. Speciation and Background Extinction
Our model considers a clade consisting of several distinct lineages. We let Ni(t) denote the number of species in the lineage Xi at time t and we let S̃i denote the entropy of species in the lineage Xi. Each lineage characterizes a group of species with common phenotypic and adaptive properties and hence common speciation and extinction rates. The mean entropy S̃ of the species in the clade is given by
where
Here pi(t) denotes the frequency of the lineage Xi at time t.
Let αi and βi denote the speciation and extinction rates of the lineage Xi. Write μi = αi − βi and
Then we obtain from
and with the help of
that
the covariance of the entropy and the speciation-extinction rate.
and hence
We will now assume that the evolutionary process is driven uniquely by peripatric speciation, as in the model proposed by Mayr [
3]. According to the peripatric model, the speciation event occurs typically at peripheral isolates. In the case of the peripatric model, we have the following speciation and extinction conditions:
Let μi denote the net-diversification rate,
We call the lineage type 1, if
and type 2, if
- (I)
In the case of type 1 clades, we have
- (II)
In the case of type 2 clades, we have
11.2. Speciation and Alternation of Background and Mass Extinction
Background extinction represents the steady extinction of species due to biotic factors. This extinction process is a continuous and steady event induced by the inability of species to respond to local changes in their environment. Such environmental changes are generated, typically, by the introduction of new predators or the invasion of a new pathogen.
Quite distinct from the steady demise of individual species are the mass extinction events. Such processes derive from physical factors. They result in the extermination in a very short time of a large proportion of the biota.
The mean entropy of the species in a clade at any point in time, constitutes a useful parameter for describing macroevolutionary changes when speciation and background extinction are the two processes driving changes in the species distribution of clade. The analysis given in Section 11.1 shows that the mean entropy increases in type 1 lineages and decreases in type 2 lineages.
However, when the macroevolutionary process is analyzed on a geological time scale which includes mass-extinction events, a useful measure of directionality is the maximum entropy, Ŝ, defined by
Here S̃i is the entropy of a species in the clade.
The maximum value given in
Equation (89) is evaluated at steady state and is assessed by considering all the species in the clade.
We will assume that the macroevolutionary process is described by the alteration of speciation-background extinction with mass-extinction events. Since we are concerned with directional changes int the maximum entropy Ŝ, we will restrict the analysis to type 1 lineages, that is lineages whose mean entropy increases over geological time in a dynamic driven by speciation-background extinction events.
The change in mean entropy due to the alternation of speciation-background extinction with mass-extinction in the case of type 1 lineages can be represented by the graphs shown in
Figure 18.
E1 and E2 represent mass extinction events. The graphs X1, X2 and X3 describe the change in mean entropy which occurs within the clade over the period of geological time.
In order to model the alternation of background and mass extinction events, we assume that as a result of a mass extinction event, a large fraction of the lineages become extinct. The system after the mass extinction event will be described by a new ancestral clade with mean entropy S1. Since mass extinction events occur on a much shorter time scale than background extinction events, we may assume S1 > S0, that is the mean entropy of the new ancestral lineage exceeds the mean entropy of the preceding ancestral lineage. Speciation and background extinction will then drive the new clade to a state described by increased mean entropy.
If
, where S* denotes the maximum entropy of species in the new clade, we infer from the above argument that
We conclude that in the process where mass-extinction events alternate with the process of speciation and background extinction we have
where Δ̃S = Ŝ* − Ŝ.
11.3. The Evolution of Mean Body Size
The directionality principles for the mean entropy and the maximum entropy can be used to predict directional trends in body size. The predictions derive from the fact that entropy and body size are analytically related. We have, as discussed earlier, the relation
We can now appeal to
Equations (86) and
(88) to infer the following trends for mean body size.
In type 1 lineages, mean body size increases.
In type 2 lineages, mean body size decreases.
Directionality theory thus accounts for the non-universality of Cope’s rule. Our analysis indicates that directional trends in body size–an increase or decrease–is highly contingent on the correlation between net-diversification rate and entropy–a property which is dependent on demographic constraints. These constraints are in effect the result of the ecological forces which prevail during the evolutionary history of the species.
11.4. The Evolution of Maximum Body Size
The maximum size of organisms has increased enormously since the origin of life more than 3.5 billion years ago [
84]. The relation between entropy and body size entails that the change in maximum size can be explained in terms of the principle of selection for maximum entropy as given by
Equation (90).
This principle asserts that when mass-extinction events alternate with the process of speciation and background extinction, the maximum entropy of species in a clade will increase. We conclude that maximum body size increases over geological time.
The blue whale is the largest animal that has ever existed on earth; the giant sequoia the largest plant. These organisms are both the descendants, through processes of mutation, selection and speciation of prokaryotic organisms that originated 3.5 million years ago. During this period there has been size changes within groups–an increase in
mean body size within certain lineages: a decrease in
mean body size within other lineages. However, as indicated by
Figure 18, the maximum sizes attained at any geological period increases. The maximum sizes are reached by progressive size increases within each clade. Accordingly the over-all size change derives from the emergence of successive clases, their extinction by mass extinction events and their replacement by new clades. The maximum size, at each geological period will be attained from a different major group of organism.
The empirical evidence indicates that over geological time, the maximum sizes are attained from a different major group of organisms. In the case of plants, they are, for instance, lycopos, gymnosperms and angiosperms; In the case of animals, the major groups are dinosaurs, mammals [
84]. These maximum sizes were attained by progressive size increases within each clade. This suggests that the overall size change over geological time is a consequence of the sequential emergence of different successive taxonomic groups and differential extinction of these groups by mass extinction events.
12. Evolutionary Dynamics and Thermodynamics
Thermodynamic theory in its widest sense can be considered as the analysis of changes in energy distribution in aggregates of inanimate matter in so far as these changes are due to differences in temperature. Evolutionary theory in its widest sense can be considered as the study of changes in the energy distribution of aggregates of living matter, in so far as these changes are regulated by differences in cycle time.
12.1. The Entropic Principles: A Characterization
Inanimate matter manifests itself primarily as three distinct states–solid, liquid and gas. These states differ in their physical attributes–a property which is largely dependent on the degree of organization of the constituent molecules. The reasons for these differences in physical attributes and the rules that govern the transition from one state to another are described by thermodynamic theory. The central concepts of the theory are the temperature, which describes the mean kinetic energy of the constituent molecules and thermodynamic entropy. The entropy S̃ is related to temperature T̃ by the Clausius expression
Here dQ̃ denotes the energy supplied as heat, and dS denotes the change in entropy.
Thermodynamic entropy has a statistical representation, namely,
Here p̃j denote the probability that a randomly chosen particle in the aggregate is in energy state j.
The Second Law of Thermodynamics, the fundamental tenet of the theory, states that in an isolated system, all transformations proceed towards a state of equilibrium defined by maximum entropy. Accordingly, thermodynamically stable states are characterized by states which maximize entropy.
Living organisms are entities which are far from thermodynamic equilibrium. These systems transform the free energy of the external environment into chemical energy which is used to maintain the metabolic activity of the system. A prokaryotic cell, a simple example of living matter, can be considered as a metabolic network organized within a membrane structure. The molecular organization that defines a cell is strikingly different from the organization observed in an inanimate aggregate. The reasons for these differences can be understood in terms of directionality theory. The fundamental concepts in this theory are the generation time, that is the mean turnover time of the macromolecules in the cell, and evolutionary entropy. The entropy S̃ is related to the cycle time T̃ according to the expression
Here dP denotes the change in metabolic rate induced by the change in activity of the metabolic process, and dS denotes the change in evolutionary entropy.
The entropy S also has a statistical representation, namely
Here pj denotes the probability that the precursor of a randomly chosen metabolite in the network is in energy state j.
The directionality principle for evolutionary entropy describes the changes in the distribution of energy within the cell. These changes are contingent on the abundance and diversity of the external resources which the cell converts into chemical energy used for biosynthesis. The main tenets of the theory assert:
When resources are constant, limited and of large diversity, all transformations proceed towards states of increasing entropy, the steady state being defined by maximum entropy;
When resources are subject to large variations in abundance and its diversity is weak, all transformations proceed towards a state of decreasing entropy, the steady state is now defined by minimum entropy.
Consequently, the evolutionarily stable states are described by extremal states of entropy–maximum entropy, when resources are constant and limited, minimum entropy when resources undergo large variations in abundance.
We will appeal to the depiction of thermodynamic and evolutionary entropy given by
Equations (91) and
(92) to show that the thermodynamic principle is the limit, as the resource production rate tends to zero and the population size tends to infinity, of the evolutionary entropic principle.
13. The Entropic Principles: An Analytic Relation
Directionality in energy flow in material aggregates under isolated conditions involves two parameters, temperature and thermodynamic entropy. Irreversibility is specified by the condition that,
as the system evolves towards a state of thermodynamic equilibrium.
Directionality in energy flow in living systems–which are metabolic replicating systems–involves the parameters cycle time and evolutionary entropy. Irreversibility under these constraints is contingent on the resource constraints.
If we assume that the population size is large so that the effect of resource diversity can be ignored, then the change in evolutionary entropy will depend uniquely on the resource abundance and we obtain the following relations:
We will now show that when R̃ → 0, where R̃ denote the resource supply rate, we have
The derivation is based on an analysis of energy transformation within a living cell, the fundamental unit of biological systems. Such energy transformation can be analyzed in terms of both the thermodynamic and evolutionary formalism.
Our analysis is based on a system in which irreversible processes are confined to a region (I) which is small compared to the surrounding (II). We may consider (I) as an aqueous solution of several thousand chemical substances contained within a membrane structure that is permeable to both matter and energy.
Substrates which are present in (II) will enter (I). These substrates will undergo reaction and are returned to (II) as products. We imagine (II) as a portion of the local environment.
We assume that the region (II) is well mixed so that the temperature T̃ and other thermodynamic parameters are constant.
Metabolic activity in (I) can be expressed in terms of a network of chemical reactions. We assume that the activity in the network is maintained away from equilibrium by the input of energy and matter from regions (II).
Provided there is a constant flux of energy into the model system, new values of concentrations and flow will emerge. The system will evolve to a steady state condition where the concentration of the substrates remain constant.
Let
T denote the mean cycle time of the chemical reaction network. As shown in Demetrius [
5], at steady state, the mean cycle time
T will be inversely related to the temperature
T̃. We have
Here h denotes Planck’s constant, k, the Boltzmann’s constant and ρ an effective activation energy.
Now the mass-specific metabolic rate
P and the generation time
T, will satisfy the allometric relations, Demetrius and Tuszynski [
85],
where α and α̃ are the proportionality constants and β the scaling exponent.
We conclude that
Let Ẽ denote the energy being produced in (II) and E the energy created by the occurence of irreversible processes in (I).
We assume that
where A is a constant. This condition entails that the resource production rate, R̃ = 0.
We will assume that the energy Ẽ is proportional to the temperature T̃ and write
Now dS = − TdP, and
where k is a numerical constant.
Let Δ
S and Δ
S̃ denote the change in thermodynamic and evolutionary entropy, respectively. We conclude from
Equation (99) that
15. Conclusions
Inanimate material aggregates and living organisms, at various levels of organization–cellular and populational, both manifest, when observed over certain particular time scales, changes which have a strong directional component.
The canonical example of directional change in the inanimate world is the flow of heat in isolated systems: heat always flows from hotter bodies to colder bodies and not the other way round. The mechanistic understanding of this process derives from the pioneering efforts of Carnot, Clausius and Boltzmann. This understanding is embodied in the Second Law of Thermodynamics which states that in an isolated system, all transformations proceed irreversibly towards a state of maximum thermodynamic entropy. Thermodynamic entropy is a statistical measure of structural organization in an aggregate of inanimate matter. This quantity describes the number of ways the molecules in the material aggregate can be arranged to achieve the same total energy. Thermodynamic entropy also describes the extent to which energy is distributed over all the microscopic storage modes of the system.
Macroevolutionary change in the history of life is embodied in the fossil record. This record indicates a uni-directional increase of maximum body size of organisms since the initial appearance of life more than 3.5 billion years ago. A mechanistic, albeit, qualitative understanding of this directionality was advanced by Darwin in terms of the principle of variation and selection. Darwin’s central insight was the introduction of the concept, fitness, a measure of the capacity of a type to extract energy from the external environment and to convert this energy into net-offspring production.
A quantitative model of Darwin’s argument is incarnated in directionality theory, a mathematical model of microevolutionary and macroevolutionary processes based on evolutionary entropy as the measure of fitness. Evolutionary entropy is a statistical measure of dynamic organization in an aggregate of metabolic entities. These entities include: the substrate and products that form the elements of a metabolic network; the organisms that are the units of an age-structured or size-structured population; the individuals that define the cooperative units in a social network. The entropy, in the context of these models, describes the number of pathways of energy flow within the network. Evolutionary entropy also characterizes the rate at which energy from the external environment is appropriated, and then transformed into activities which contribute to the persistence and integrity of the network.
The fundamental tenets of directionality theory, as regards population of replicating organisms, pertain to the dynamics of evolutionary change under mutation and natural selection. These tenets can be qualitatively described in terms of the following rules.
When resources are diverse, and constant in abundance, all changes proceed towards a state of maximum entropy.
When resources are singular, and undergo large variation in abundance, all changes proceed towards a state of minimum entropy.
Accordingly, the laws which govern energy transfer in aggregates of inanimate matter and in aggregates of living matter are distinct. In thermodynamic systems, the transitions are towards a state of maximum entropy. In evolutionary systems, the transitions are towards states of maximum or minimum entropy: the direction of change being contingent on the environmental constraints. However, the thermodynamic and evolutionary laws are related. The thermodynamic principle is the limit, as population size tends to infinity and resource production rate tends to zero, of the evolutionary tenet. This thermodynamic–evolutionary dichotomy has important implications towards the understanding of the principles which underlie the transition from inanimate reactive molecules to a living cell.
 and Varn denote the expectation and the variance with respect to the measure μn on finite symbol sequences of length n of the form (x0, x1, . . . , xn), which is given by
and Varn denote the expectation and the variance with respect to the measure μn on finite symbol sequences of length n of the form (x0, x1, . . . , xn), which is given by the expectation. In the determination of the second infinitesimal moment we invoke the observation that if N becomes large the influence of fluctuations becomes small and hence the process becomes deterministic. Thus we have made the assumption that the change in log N(t) in the time interval Δ t due to fluctuations is caused by Brownian motion with variance
. We can therefore describe the evolution of the density f(N, t) of the process N(t) by the solution of the Fokker-Planck equation
the expectation. In the determination of the second infinitesimal moment we invoke the observation that if N becomes large the influence of fluctuations becomes small and hence the process becomes deterministic. Thus we have made the assumption that the change in log N(t) in the time interval Δ t due to fluctuations is caused by Brownian motion with variance
. We can therefore describe the evolution of the density f(N, t) of the process N(t) by the solution of the Fokker-Planck equation