Analysis and Visualization of Seismic Data Using Mutual Information
Abstract
:1. Introduction
2. Mathematical tools
2.1. Gutenberg-Richter Law
2.2. Mutual Information
2.3. K-means Clustering
2.4. Hierarchical Clustering
3. Analysis Global Seismic Data
| Region number | Region name | Number of events | Minimum Magnitude | Maximum Magnitude | Average Magnitude |
|---|---|---|---|---|---|
| 1 | Alaska-Aleutan arc | 38,976 | 0.9 | 8.0 | 3.7 |
| 2 | Southeastern Alaska to Washington | 19,389 | 0.3 | 7.1 | 2.6 |
| 3 | Oregon, California and Nevada | 26,188 | 0.0 | 7.6 | 2.9 |
| 4 | Baja California and Gulf of California | 7,621 | 1.1 | 7.2 | 2.7 |
| 5 | Mexico-Guatemala area | 29,991 | 1.9 | 7.9 | 3.9 |
| 6 | Central America | 20,524 | 0.0 | 7.5 | 3.8 |
| 7 | Caribbean loop | 48,592 | 0.7 | 7.3 | 3.0 |
| 8 | Andean South America | 81,209 | 1.2 | 8.5 | 3.5 |
| 9 | Extreme South America | 2,544 | 0.0 | 6.3 | 3.2 |
| 10 | Southern Antilles | 6,102 | 0.3 | 7.5 | 4.4 |
| 11 | New Zealand region | 58,270 | −0.1 | 8.1 | 3.2 |
| 12 | Kermadec-Tonga-Samoa Basin area | 50,129 | 1.7 | 8.1 | 4.1 |
| 13 | Fiji Islands area | 23,723 | 1.0 | 7.2 | 4.0 |
| 14 | Vanuatu Islands | 29,062 | −1.4 | 7.9 | 4.1 |
| 15 | Bismarck and Solomon Islands | 29,600 | −1.4 | 8.0 | 4.0 |
| 16 | New Guinea | 24,991 | −0.2 | 7.8 | 4.0 |
| 17 | Caroline Islands area | 5,016 | 0.0 | 7.0 | 4.1 |
| 18 | Guam to Japan | 33,998 | 1.2 | 7.5 | 3.7 |
| 19 | Japan-Kuril Islands-Kamchatka Peninsula | 865,579 | 0.0 | 8.3 | 1.6 |
| 20 | Southwestern Japan and Ryukyu Islands | 583,992 | 0.1 | 7.4 | 1.1 |
| 21 | Taiwan area | 285,357 | −0.8 | 7.9 | 2.2 |
| 22 | Philippine Islands | 31,277 | 0.0 | 8.4 | 3.9 |
| 23 | Borneo-Sulawesi | 34,279 | 0.0 | 7.5 | 4.0 |
| 24 | Sunda arc | 46,430 | 0.0 | 8.4 | 4.0 |
| 25 | Myanmar and Southeast Asia | 7,853 | 0.0 | 7.4 | 3.1 |
| 26 | India-Xizang-Sichuan-Yunnan | 29,361 | −0.6 | 8.0 | 2.7 |
| 27 | Southern Xinjiang to Gansu | 15,464 | 0.0 | 8.0 | 2.9 |
| 28 | Lake Issyk-Kul to Lake Baykal | 32,330 | 1.3 | 7.4 | 2.6 |
| 29 | Western Asia | 21,621 | 0.0 | 8.1 | 3.2 |
| 30 | Middle East-Crimea-Eastern Balkans | 220,607 | 3.1 | 8.4 | 2.7 |
| 31 | Western Mediterranean area | 194,094 | −0.5 | 7.2 | 1.9 |
| 32 | Atlantic Ocean | 37,502 | −0.3 | 7.0 | 2.8 |
| 33 | Indian Ocean | 12,848 | 0.0 | 7.7 | 4.1 |
| 34 | Eastern North America | 15,104 | −2.1 | 7.3 | 2.7 |
| 35 | Eastern South America | 67 | 0.0 | 5.7 | 4.3 |
| 36 | Northwestern Europe | 91,190 | 0.0 | 5.9 | 1.6 |
| 37 | Africa | 49,370 | 0.0 | 7.4 | 2.5 |
| 38 | Australia | 7,759 | 2.2 | 6.5 | 2.5 |
| 39 | Pacific Basin | 3,003 | 2.3 | 7.0 | 2.9 |
| 40 | Arctic zone | 18,786 | 2.1 | 6.9 | 2.4 |
| 41 | Eastern Asia | 13,790 | 1.6 | 7.8 | 2.6 |
| 42 | Northeast. Asia, North. Alaska to Greenland | 6,823 | 1.8 | 7.6 | 3.1 |
| 43 | Southeastern and Antarctic Pacific Ocean | 6,943 | 0.0 | 7.1 | 4.3 |
| 44 | Galápagos Islands area | 2,351 | −0.6 | 6.4 | 4.2 |
| 45 | Macquarie loop | 1,743 | 2.2 | 7.8 | 4.3 |
| 46 | Andaman Islands to Sumatera | 20,762 | 0.9 | 9.2 | 4.0 |
| 47 | Baluchistan | 4,101 | 0.3 | 7.6 | 3.9 |
| 48 | Hindu Kush and Pamir area | 39,669 | 0.0 | 7.3 | 3.0 |
| 49 | Northern Eurasia | 60,082 | 1.1 | 5.9 | 1.4 |
| 50 | Antarctica | 64 | 1.9 | 5.5 | 4.0 |
3.1. K-means Analysis Based on G-R Law Parameters
| Region number | a | b | R |
|---|---|---|---|
| 1 | 8.7 | 1.08 | 0.99 |
| 2 | 6.5 | 0.88 | 0.99 |
| 3 | 7.0 | 0.89 | 0.99 |
| 4 | 7.5 | 1.06 | 0.99 |
| 5 | 8.4 | 1.10 | 0.98 |
| 6 | 8.4 | 1.12 | 0.99 |
| 7 | 8.6 | 1.19 | 0.99 |
| 8 | 8.9 | 1.08 | 0.99 |
| 9 | 7.4 | 1.08 | 0.97 |
| 10 | 8.3 | 1.07 | 0.92 |
| 11 | 7.6 | 0.97 | 0.99 |
| 12 | 9.4 | 1.15 | 0.97 |
| 13 | 9.3 | 1.24 | 0.97 |
| 14 | 8.5 | 1.02 | 0.98 |
| 15 | 8.5 | 1.02 | 0.98 |
| 16 | 8.6 | 1.05 | 0.96 |
| 17 | 8.3 | 1.16 | 0.97 |
| 18 | 9.5 | 1.27 | 0.98 |
| 19 | 9.0 | 1.06 | 0.99 |
| 20 | 8.0 | 1.05 | 0.99 |
| 21 | 7.6 | 0.95 | 0.99 |
| 22 | 8.9 | 1.11 | 0.98 |
| 23 | 9.3 | 1.18 | 0.96 |
| 24 | 9.2 | 1.14 | 0.98 |
| 25 | 7.4 | 0.99 | 0.99 |
| 26 | 8.1 | 1.07 | 0.99 |
| 27 | 7.3 | 0.97 | 0.99 |
| 28 | 7.2 | 0.96 | 0.99 |
| 29 | 8.3 | 1.12 | 0.98 |
| 30 | 8.4 | 1.12 | 0.97 |
| 31 | 8.3 | 1.18 | 0.98 |
| 32 | 9.1 | 1.21 | 0.99 |
| 33 | 8.8 | 1.16 | 0.98 |
| 34 | 7.4 | 1.10 | 0.96 |
| 35 | 6.9 | 1.24 | 0.97 |
| 36 | 8.1 | 1.35 | 0.98 |
| 37 | 8.3 | 1.14 | 0.99 |
| 38 | 7.6 | 1.15 | 0.97 |
| 39 | 7.6 | 1.07 | 0.98 |
| 40 | 7.9 | 1.11 | 0.98 |
| 41 | 7.1 | 0.94 | 0.99 |
| 42 | 6.8 | 0.96 | 0.98 |
| 43 | 8.4 | 1.10 | 0.96 |
| 44 | 8.9 | 1.32 | 0.98 |
| 45 | 7.1 | 0.94 | 0.91 |
| 46 | 8.0 | 1.00 | 0.99 |
| 47 | 7.5 | 1.05 | 0.99 |
| 48 | 8.7 | 1.19 | 0.99 |
| 49 | 6.1 | 0.97 | 0.94 |
| 50 | 6.0 | 1.09 | 0.98 |
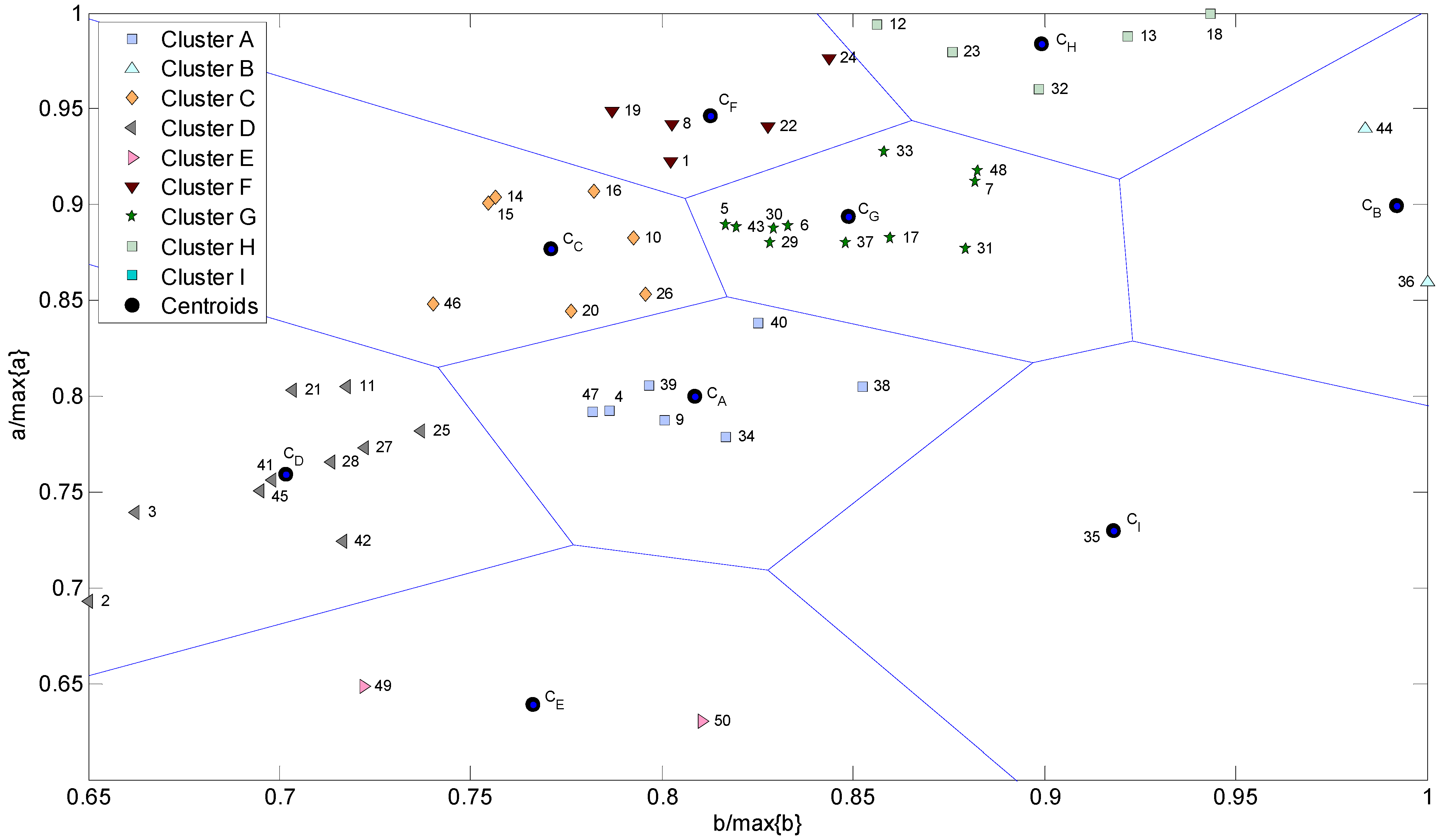

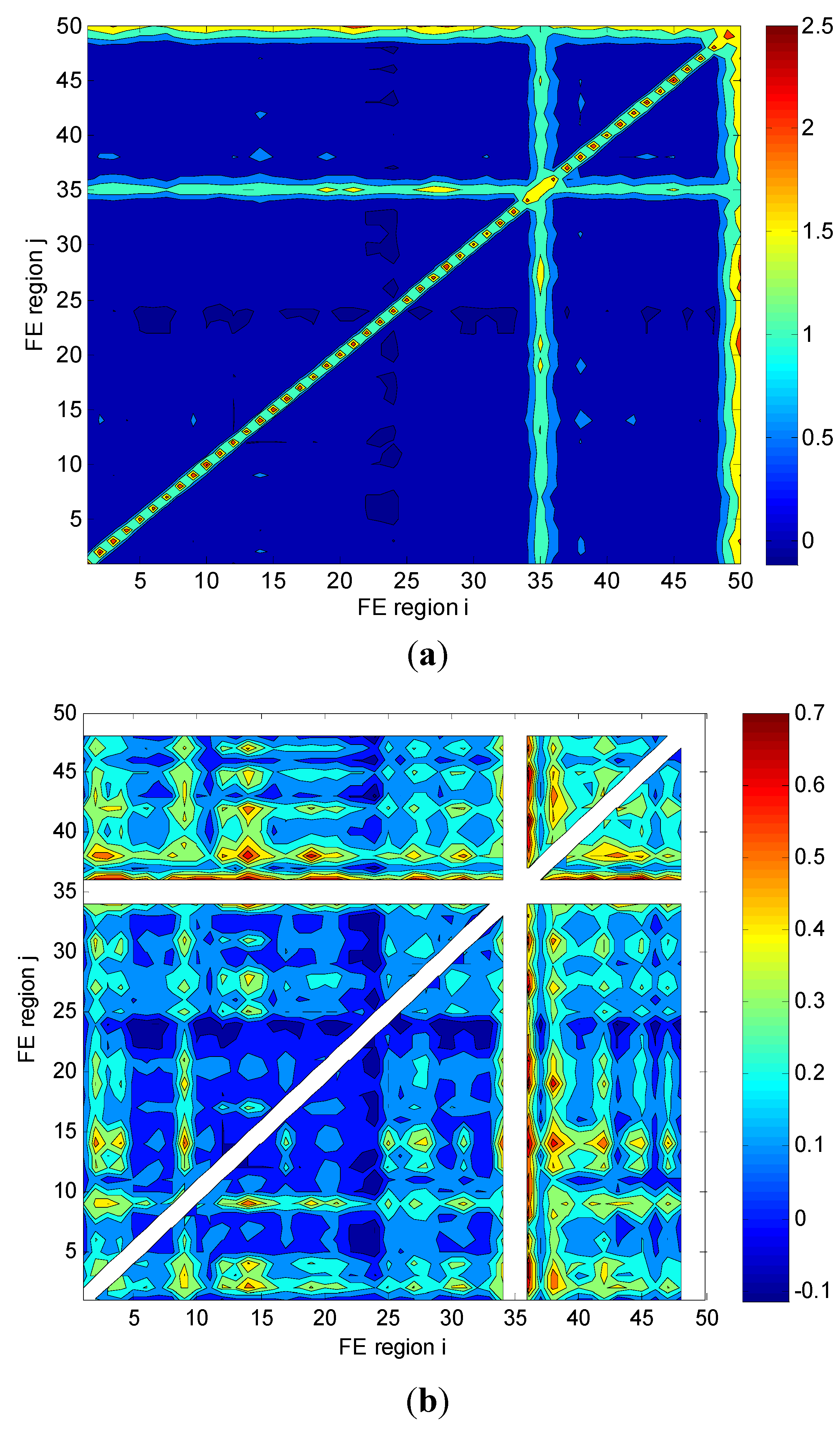
3.2. Analysis by Means of Mutual Information
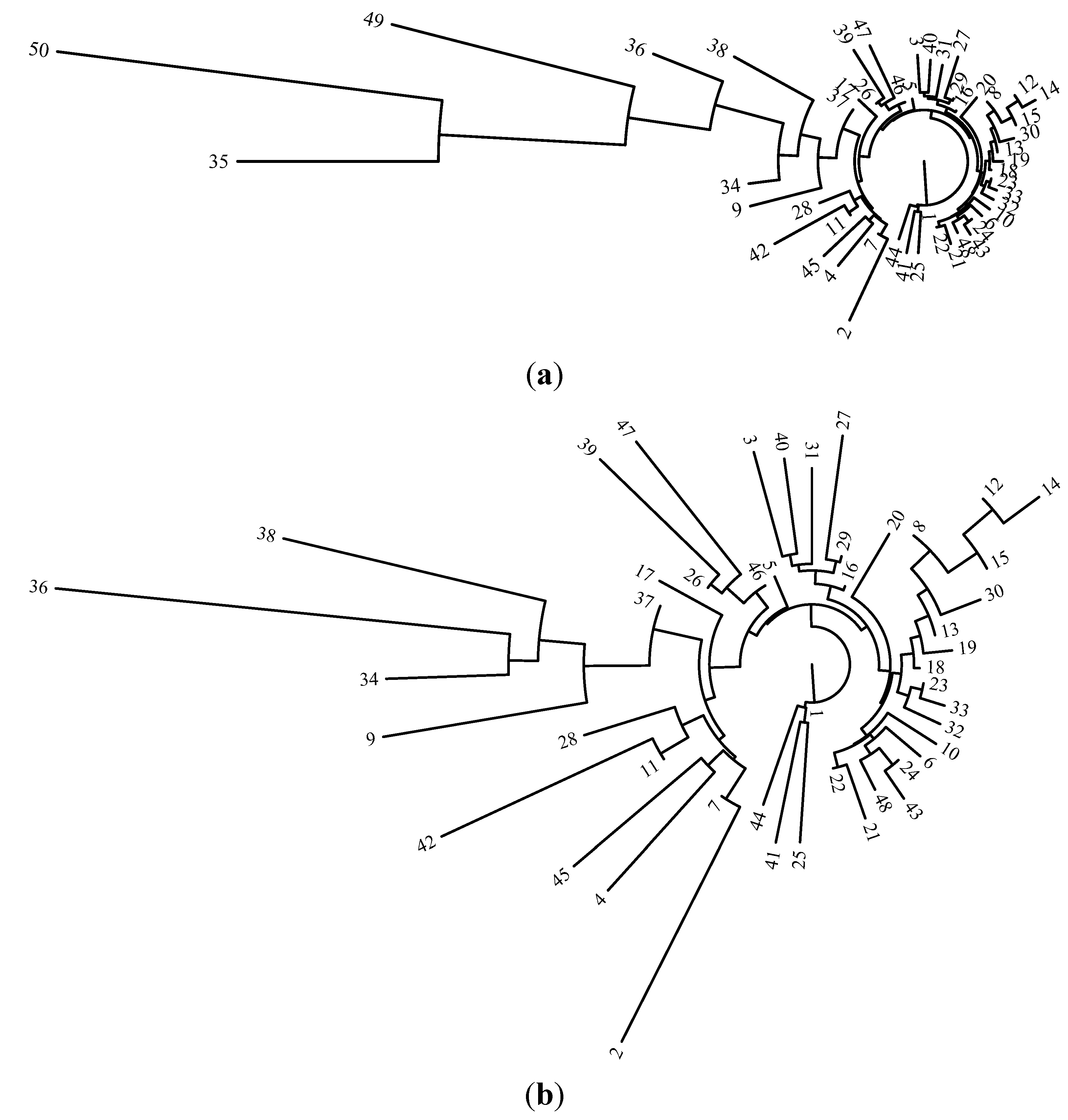
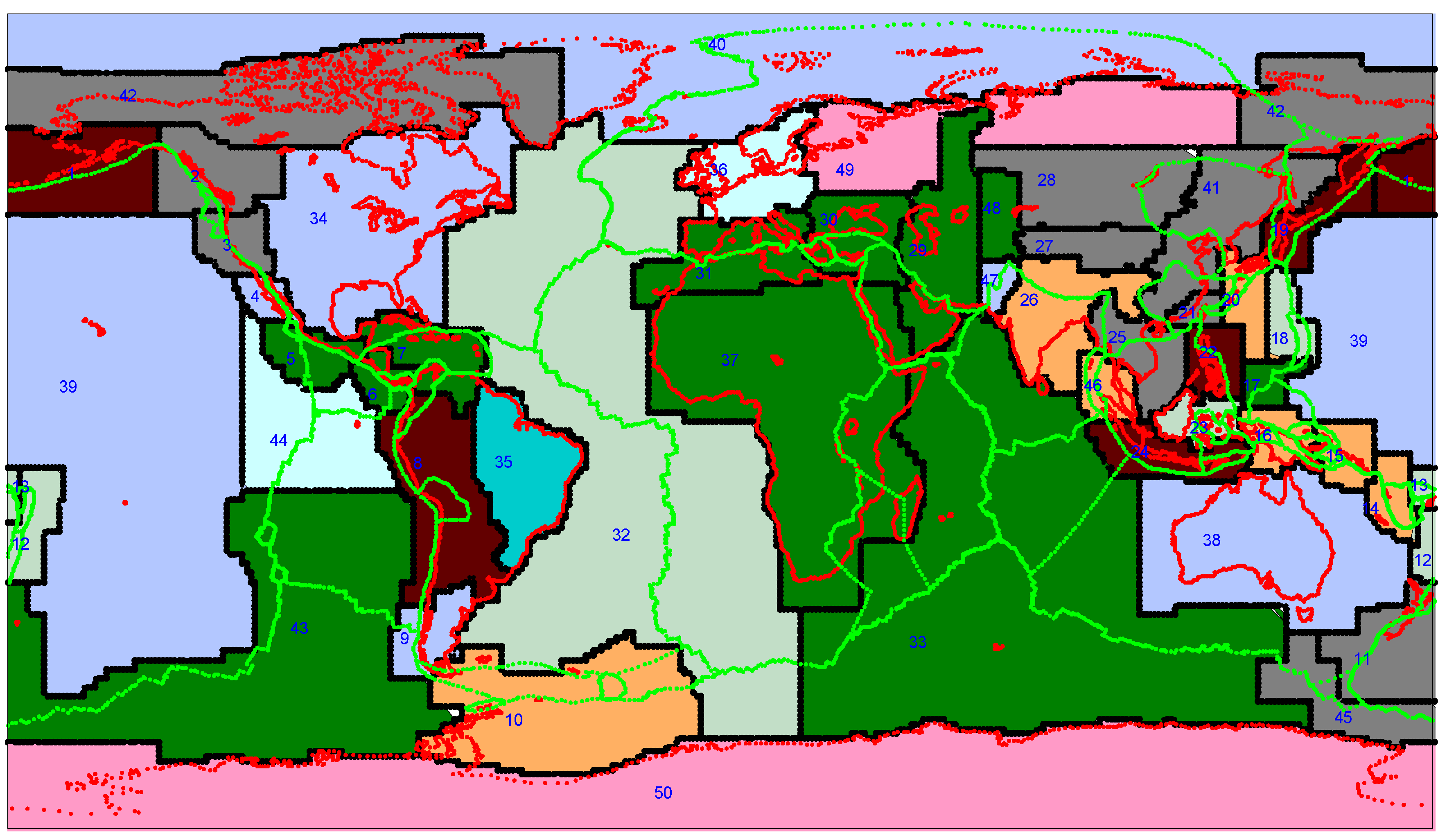
4. Analysis of Rectangular Grid-Based Regions

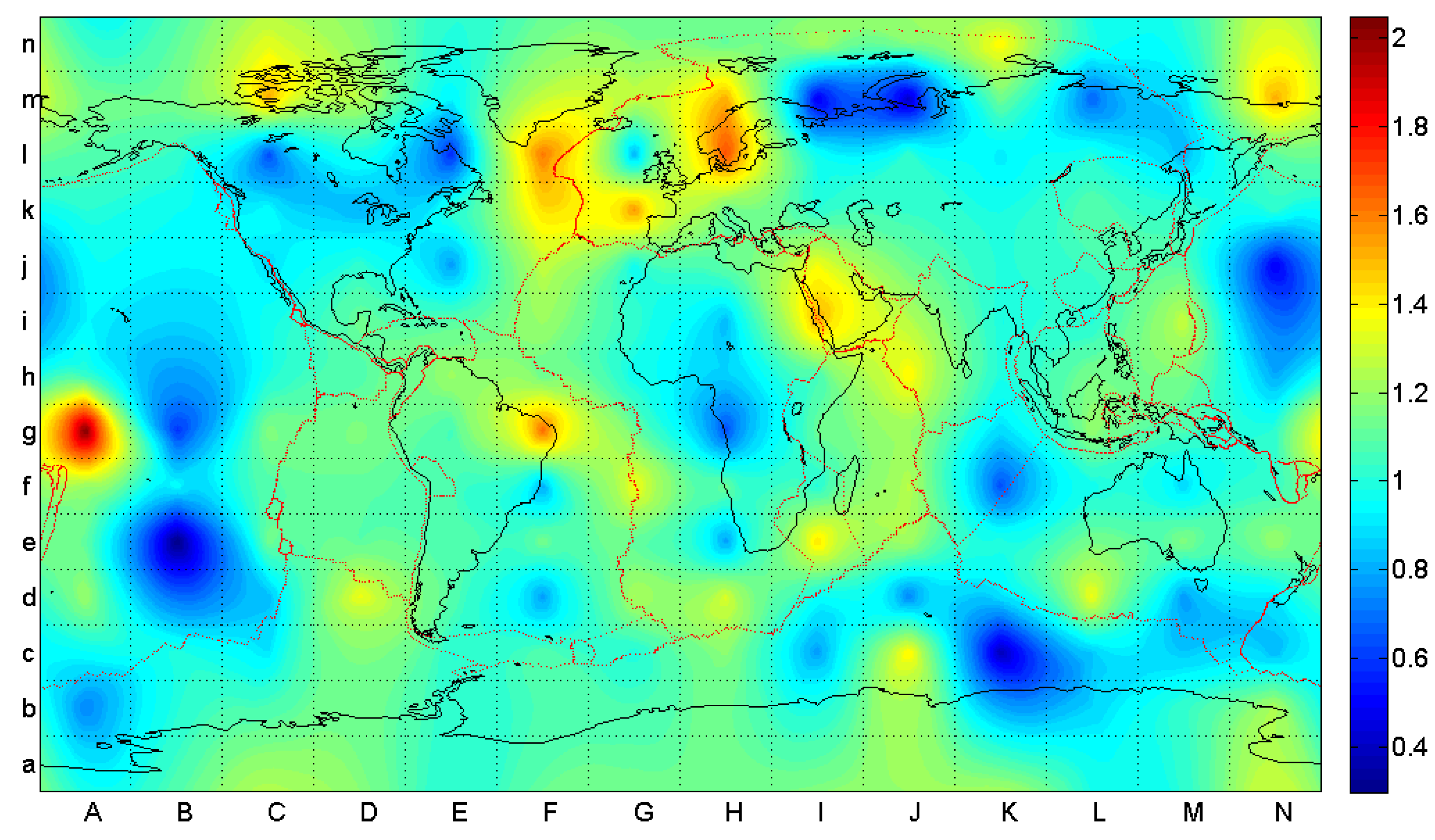
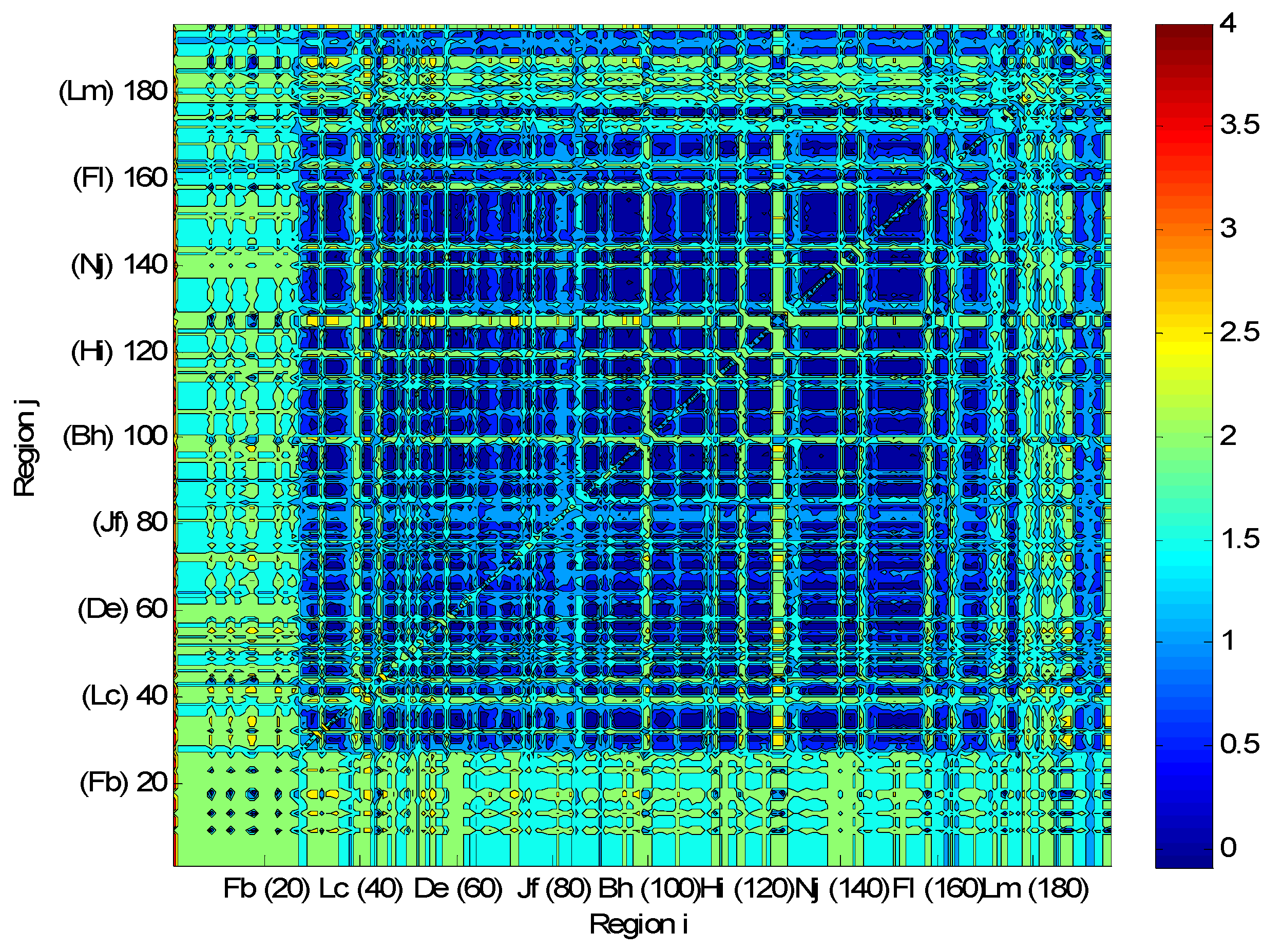
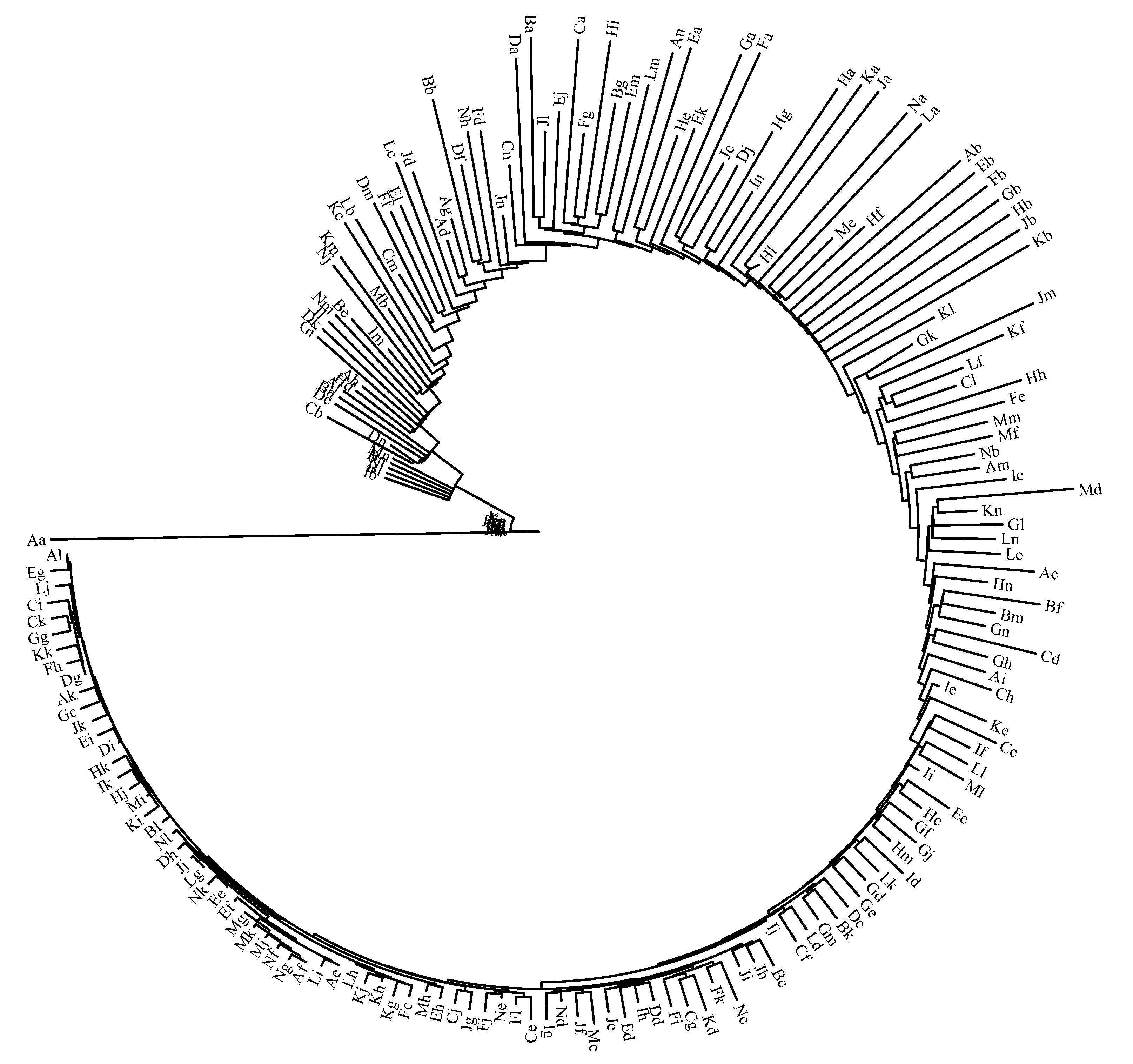
5. Conclusions
Conflicts of Interest
References
- Ghobarah, A.; Saatcioglu, M.; Nistor, I. The impact of the 26 December 2004 earthquake and tsunami on structures and infrastructure. Eng. Struct. 2006, 28, 312–326. [Google Scholar] [CrossRef]
- Marano, K.; Wald, D.; Allen, T. Global earthquake casualties due to secondary effects: a quantitative analysis for improving rapid loss analyses. Nat. Hazards 2010, 52, 319–328. [Google Scholar] [CrossRef]
- Lee, S.; Davidson, R.; Ohnishi, N.; Scawthorn, C. Fire following earthquake—Reviewing the state-of-the-art modelling. Earthq. Spectra 2008, 24, 933–967. [Google Scholar] [CrossRef]
- Bird, J.F.; Bommer, J.J. Earthquake losses due to ground failure. Eng. Geol. 2004, 75, 147–179. [Google Scholar] [CrossRef]
- Cavallo, E.; Powell, A.; Becerra, O. Estimating the direct economic damages of the earthquake in Haiti. Econ. J. 2010, 120, 298–312. [Google Scholar] [CrossRef]
- Tseng, C.-P.; Chen, C.-W. Natural disaster management mechanisms for probabilistic earthquake loss. Nat. Hazards 2012, 60, 1055–1063. [Google Scholar] [CrossRef]
- Wu, J.; Li, N.; Hallegatte, S.; Shi, P.; Hu, A.; Liu, X. Regional indirect economic impact evaluation of the 2008 Wenchuan Earthquake. Environ. Earth Sci. 2012, 65, 161–172. [Google Scholar] [CrossRef]
- Keefer, P.; Neumayer, E.; Plümper, T. Earthquake propensity and the politics of mortality prevention. World Dev. 2011, 39, 1530–1541. [Google Scholar] [CrossRef]
- Zamani, A.; Agh-Atabai, M. Multifractal analysis of the spatial distribution of earthquake epicenters in the Zagros and Alborz-Kopeh Dagh regions of Iran. Iran J. Sci. Technol. 2011, A1, 39–51. [Google Scholar]
- Sornette, D.; Pisarenko, V. Fractal plate tectonics. Geophys. Res. Lett. 2003. [Google Scholar] [CrossRef]
- Bhattacharya, P.; Chakrabarti, B.; Kamal. A fractal model of earthquake occurrence: Theory, simulations and comparisons with the aftershock data. J. Phys. Conf. Ser. 2011, 319, 012004. [Google Scholar] [CrossRef]
- De Rubeis, V.; Hallgass, R.; Loreto, V.; Paladin, G.; Pietronero, L.; Tosi, P. Self-affine asperity model for earthquakes. Phys. Rev. Lett. 1996, 76, 2599–2602. [Google Scholar] [CrossRef] [PubMed]
- Hallgass, R.; Loreto, V.; Mazzella, O.; Paladin, G.; Pietronero, L. Earthquake statistics and fractal faults. Phys. Rev. E 1997, 56, 1346–1356. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Christopoulos, S.-R.G. Natural time analysis of the centennial earthquake catalog. Chaos 2012, 22, 023123. [Google Scholar] [CrossRef] [PubMed]
- Turcotte, D.L.; Malamud, B.D. International Handbook of Earthquake and Engineering Seismology; Jennings, P., Kanamori, H., Lee, W., Eds.; Academic Press: San Francisco, CA, USA, 2002; p. 209. [Google Scholar]
- Kanamori, H.; Brodsky, E. The physics of earthquakes. Rep. Prog. Phys. 2004, 67, 1429–1496. [Google Scholar] [CrossRef]
- Stein, S.; Liu, M.; Calais, E.; Li, Q. Mid-continent earthquakes as a complex system. Seismol. Res. Lett. 2009, 80, 551–553. [Google Scholar] [CrossRef]
- Lennartz, S.; Livina, V.N.; Bunde, A.; Havlin, S. Long-term memory in earthquakes and the distribution of interoccurrence times. Europhys. Lett. 2008, 81, 69001. [Google Scholar] [CrossRef]
- El-Misiery, A.E.M.; Ahmed, E. On a fractional model for earthquakes. Appl. Math. Comput. 2006, 178, 207–211. [Google Scholar] [CrossRef]
- Lopes, A.M.; Tenreiro Machado, J.A.; Pinto, C.M.A.; Galhano, A.M.S.F. Fractional dynamics and MDS visualization of earthquake phenomena. Comput. Math. Appl. 2013, 66, 647–658. [Google Scholar] [CrossRef]
- Sornette, A.; Sornette, D. Self-organized criticality and earthquakes. Europhys. Lett. 1989, 9, 197–202. [Google Scholar] [CrossRef]
- Shahin, A.M.; Ahmed, E.; Elgazzar, A.S.; Omar, Y.A. On fractals and fractional calculus motivated by complex systems. 2009. [Google Scholar]
- Rocco, A.; West, B.J. Fractional calculus and the evolution of fractal phenomena. Physica A 1999, 265, 535–546. [Google Scholar] [CrossRef]
- Samko, S.; Kilbas, A.; Marichev, O. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: London, UK, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Kilbas, A.; Srivastava, H.M.; Trujillo, J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J. Fractional Calculus: Models and Numerical Methods; Series on Complexity, Nonlinearity and Chaos; World Scientific Publishing: Singapore, Singapore, 2012. [Google Scholar]
- International Seismological Centre (2010) On-line Bulletin, Internatl. Seis. Cent., Thatcham, UK. Available online: http://www.isc.ac.uk (accessed on 12 June 2013).
- Gutenberg, B.; Richter, C.F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar]
- Christensen, K.; Olami, Z. Variation of the Gutenberg-Richter b values and nontrivial temporal correlations in a spring-block model for earthquakes. J. Geophys. Res. 1992, 97, 8729–8735. [Google Scholar] [CrossRef]
- Ogata, Y.; Katsura, K. Analysis of temporal and spatial heterogeneity of magnitude frequency distribution inferred from earthquake catalogues. Geophys. J. Int. 1993, 113, 727–738. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Posadas, A.; Hirata, T.; Vidal, F.; Correig, A. Spatio-temporal seismicity patterns using mutual information application to southern Iberian peninsula (Spain) earthquakes. Phys. Earth Planet. Inter. 2000, 122, 269–276. [Google Scholar] [CrossRef]
- Telesca, L. Tsallis-based nonextensive analysis of the southern California seismicity. Entropy 2011, 13, 1267–1280. [Google Scholar] [CrossRef]
- Mohajeri, N.; Gudmundsson, A. Entropies and scaling exponents of street and fracture networks. Entropy 2012, 14, 800–833. [Google Scholar] [CrossRef]
- Matsuda, H. Physical nature of higher-order mutual information: Intrinsic correlations and frustration. Phys. Rev. E 2000, 62, 3096–3102. [Google Scholar] [CrossRef]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef] [PubMed]
- Vastano, J.A.; Swinney, H.L. Information transport in spatiotemporal systems. Phys. Rev. Lett. 1988, 60, 1773–1776. [Google Scholar] [CrossRef] [PubMed]
- Fraser, A.M. Reconstructing attractors from scalar time series: A Comparison of singular system and redundancy criteria. Phys. D 1989, 34, 391–404. [Google Scholar] [CrossRef]
- Herzel, H.; Schmitt, A.O.; Ebeling, W. Finite sample effects in sequence analysis. Chaos Soliton Fractals 1994, 4, 97–113. [Google Scholar] [CrossRef]
- Tenreiro Machado, J.A.; Costa, A.C.; Quelhas, M.D. Entropy analysis of DNA code dynamics in human chromosomes. Comput. Math. Appl. 2011, 62, 1612–1617. [Google Scholar] [CrossRef]
- Tenreiro Machado, J.A.; Costa, A.C.; Quelhas, M.D. Shannon, Rényie and Tsallis entropy analysis of DNA using phase plane. Nonlinear Anal. Real World Appl. 2011, 12, 3135–3144. [Google Scholar] [CrossRef]
- Matsuda, H.; Kudo, K.; Nakamura, R.; Yamakawa, O.; Murata, T. Mutual information of Ising systems. Int. J. Theor. Phys. 1996, 35, 839–845. [Google Scholar] [CrossRef]
- Mori, T.; Kudo, K.; Tamagawa, Y.; Nakamura, R.; Yamakawa, O.; Suzuki, H.; Uesugi, T. Edge of chaos in rule-changing cellular automata. Phys. D 1998, 116, 275–282. [Google Scholar] [CrossRef]
- Feldman, D.P.; Crutchfield, J.P. Measures of statistical complexity: Why? Phys. Lett. A 1998, 238, 244–252. [Google Scholar] [CrossRef]
- Wicks, R.T.; Chapman, S.C.; Dendy, R.O. Mutual information as a tool for identifying phase transitions in dynamical complex systems with limited data. Phys. Rev. E 2007, 75, 051125. [Google Scholar] [CrossRef]
- Kwapieńa, J.; Drożdż, S. Physical approach to complex systems. Phys. Rep. 2012, 515, 115–226. [Google Scholar] [CrossRef]
- Arabie, P.; Hubert, L. Cluster analysis in marketing research. In Advanced Methods in Marketing Research; Bagozzi, R.P., Ed.; Blackwell: Oxford, UK, 1994; p. 160. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer-Verlag: New York, NY, USA, 2006. [Google Scholar]
- Park, U.; Jain, A.K. Face matching and retrieval using soft biometrics. IEEE Trans. Inf. Forensics Secur. 2010, 5, 406–415. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: New York, NY, USA, 1991. [Google Scholar]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Kanungo, T.; Mount, D.M.; Netanyahu, N.S.; Piatko, C.D.; Silverman, R.; Wu, A.Y. An efficient K-means clustering algorithm: Analysis and implementation. IEEE Trans. Pattern Anal. 2002, 24, 881–892. [Google Scholar] [CrossRef]
- Jain, A.K.; Dubes, R. Algorithms for Clustering Data; Prentice-Hall: Englewood Cliffs, NJ, USA, 1988. [Google Scholar]
- Johnson, S.C. Hierarchical clustering schemes. Psychometrika 1966, 32, 241–254. [Google Scholar] [CrossRef]
- Gower, J.C.; Ross, G.J.S. Minimum spanning trees and single linkage cluster analysis. Appl. Stat. 1969, 18, 54–64. [Google Scholar] [CrossRef]
- Ward, J.H., Jr. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Flinn, E.A.; Engdahl, E.R.; Hill, A.R. Seismic and geographical regionalization. Bull. Seismol. Soc. Am. 1974, 64, 771–993. [Google Scholar]
- Flinn, E.A.; Engdahl, E.R. A proposed basis for geographical and seismic regionalization. Rev. Geophys. 1965, 3, 123–149. [Google Scholar] [CrossRef]
- Zhao, X.; Omi, T.; Matsuno, N.; Shinomoto, S. A non-universal aspect in the temporal occurrence of earthquakes. New J. Phys. 2010, 12, 063010. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Omi, T.; Kanter, I.; Shinomoto, S. Optimal observation time window for forecasting the next earthquake. Phys. Rev. E 2011, 83, 026101. [Google Scholar] [CrossRef]
- Felsenstein, J. PHYLIP, version 3.6; free phylogeny inference package; Distributed by the author; Department of Genome Sciences, University of Washington: Seattle, Washington, DC, USA, 2005. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Machado, J.A.T.; Lopes, A.M. Analysis and Visualization of Seismic Data Using Mutual Information. Entropy 2013, 15, 3892-3909. https://doi.org/10.3390/e15093892
Machado JAT, Lopes AM. Analysis and Visualization of Seismic Data Using Mutual Information. Entropy. 2013; 15(9):3892-3909. https://doi.org/10.3390/e15093892
Chicago/Turabian StyleMachado, José A. Tenreiro, and António M. Lopes. 2013. "Analysis and Visualization of Seismic Data Using Mutual Information" Entropy 15, no. 9: 3892-3909. https://doi.org/10.3390/e15093892
APA StyleMachado, J. A. T., & Lopes, A. M. (2013). Analysis and Visualization of Seismic Data Using Mutual Information. Entropy, 15(9), 3892-3909. https://doi.org/10.3390/e15093892






