Permutation Complexity and Coupling Measures in Hidden Markov Models
Abstract
:1. Introduction
2. The Duality between Words and Permutations
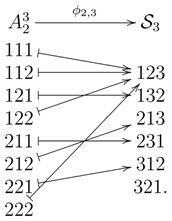 This example illustrates the following two properties of the map, : first, can be a proper subset of . As one can see from Theorem 1 below, is a proper subset of , if and only if . Second, two different words can have the same permutation type.
This example illustrates the following two properties of the map, : first, can be a proper subset of . As one can see from Theorem 1 below, is a proper subset of , if and only if . Second, two different words can have the same permutation type.- (i)
- Given a permutation, , we decompose the sequence, , of length L into maximal ascending subsequences. A subsequence, , of a sequence, , of length L is called a maximal ascending subsequence if it is ascending, namely, , and neither nor is ascending;
- (ii)
- If is a decomposition of into maximal ascending subsequences, then a word, , is defined by:We define . Note that , because π is the permutation type of some word, . Thus, we have . Hence, is well-defined as a map from to .
- (i)
- For every ,where if . In particular, , if and only if ;
- (ii)
- Let us put:Then, restricted on is a map into and restricted on is a map into . They form a pair of mutually inverse maps. Furthermore, we have:
3. A Result on Finite-State Finite-Alphabet Hidden Markov Models
- (i)
- for any and ;
- (ii)
- for any ;
- (iii)
- and for any .
4. Permutation Complexity and Coupling Measures
4.1. Fundamental Lemma
4.2. Excess Entropy
4.3. Transfer Entropy and Momentary Information Transfer
4.4. Directed Information
- (i)
- This is the permutation analogue of the equality:
- (ii)
- Here:and:The symbol, D, denotes the one-step delay. is the corresponding permutation analogue. The second equality is the permutation analogue of the equality . Since coincides with the transfer entropy rate, the first equality is just the equality between the transfer entropy rate and the symbolic transfer entropy rate (or the rate of one-step TERV) proven in Proposition 6, given the second equality;
- (iii)
- where is called the instantaneous information exchange rate and is defined by:and:From the last expression of , we can obtain:is the corresponding permutation analogue and called the symbolic instantaneous information exchange rate;
- (iv)
- Namely, the symbolic directed information rate decomposes into the sum of the symbolic transfer entropy rate and the symbolic instantaneous information exchange rate. This follows immediately from (ii), (iii) and the equality saying that the directed information rate decomposes into the sum of the transfer entropy rate and the instantaneous information exchange rate:
- (v)
- This is the permutation analogue of the equality saying that the mutual information rate between and is the sum of the directed information rate from to and the transfer entropy rate from to :where:is the mutual information rate and is its permutation analogue, called the symbolic mutual information rate. It is known that they are equal for any bivariate finite-alphabet stationary stochastic process [19]. Thus, the symbolic mutual information rate between and is the sum of the symbolic directed information rate from to and the symbolic transfer entropy rate from to .
- (i’)
- This is the permutation analogue of the equality:
- (ii’)
- The second equality is the permutation analogue of the equality:The quantities, and , are called the causal conditional transfer entropy rate and the symbolic causal conditional transfer entropyrate, respectively.
- (iii’)
- where is called the causal conditional instantaneous information exchange rate. The second equality is the permutation analogue of the equality:is the permutation analogue and is called the symbolic causal conditional instantaneous information exchange rate;
- (iv’)
- This is the permutation analogue of the following equality:
- (v’)
- This is the permutation analogue of the equality:where:is the causal conditional mutual information rate and is its permutation analogue, called the symbolic causal conditional mutual information rate. It can be shown that:if is the output process of an HMM with an ergodic internal process.
5. Discussion
- (i)
- for any , , if and only if ;
- (ii)
- for any , , if and only if .
- (i’)
- for any , , if and only if ;
- (ii’)
- for any , , if and only if .
Acknowledgments
Conflicts of Interest
References
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, e174102. [Google Scholar] [CrossRef]
- Amigó, J.M. Permutation Complexity in Dynamical Systems; Springer-Verlag: Berlin/ Heidelberg, Germany, 2010. [Google Scholar]
- Bahraminasab, A.; Ghasemi, F.; Stefanovska, A.; McClintock, P.V.E.; Kantz, H. Direction of coupling from phases of interacting oscillators: A permutation information approach. Phys. Rev. Lett. 2008, 100, e084101. [Google Scholar] [CrossRef]
- Cao, Y.H.; Tung, W.W.; Gao, J.B.; Protopopescu, V.A.; Hively, L.M. Detecting dynamical changes in time series using the permutation entropy. Phys. Rev. E 2004, 70, e046217. [Google Scholar] [CrossRef]
- Kugiumtzis, D. Partial transfer entropy on rank vectors. Eur. Phys. J. Special Topics 2013, 222, 401–420. [Google Scholar] [CrossRef]
- Nakajima, K.; Haruna, T. Symbolic local information transfer. Eur. Phys. J. Special Topics 2013, 222, 421–439. [Google Scholar] [CrossRef]
- Rosso, O.A.; Larrondo, H.A.; Martin, M.T.; Plastino, A.; Fuentes, M.A. Distinguishing noise from chaos. Phys. Rev. Lett. 2007, 99, e154102. [Google Scholar] [CrossRef]
- Amigó, J.M.; Keller, K. Permutation entropy: One concept, two approaches. Eur. Phys. J. Special Topics 2013, 222, 263–273. [Google Scholar] [CrossRef]
- Bandt, C.; Keller, G.; Pompe, B. Entropy of interval maps via permutations. Nonlinearity 2002, 15, 1595–1602. [Google Scholar] [CrossRef]
- Keller, K.; Sinn, M. A standardized approach to the Kolmogorov-Sinai entropy. Nonlinearity 2009, 22, 2417–2422. [Google Scholar] [CrossRef]
- Keller, K.; Sinn, M. Kolmogorov-Sinai entropy from the ordinal viewpoint. Phys. D 2010, 239, 997–1000. [Google Scholar] [CrossRef]
- Keller, K. Permutations and the Kolmogorov-Sinai entropy. Discr. Cont. Dyn. Syst. 2012, 32, 891–900. [Google Scholar] [CrossRef]
- Keller, K.; Unakafov, A.M.; Unakafova, V.A. On the relation of KS entropy and permutation entropy. Phys. D 2012, 241, 1477–1481. [Google Scholar] [CrossRef]
- Unakafova, V.A.; Unakafov, A.M.; Keller, K. An approach to comparing Kolmogorov-Sinai and permutation entropy. Eur. Phys. J. Special Topics 2013, 222, 353–361. [Google Scholar] [CrossRef]
- Amigó, J.M.; Kennel, M.B.; Kocarev, L. The permutation entropy rate equals the metric entropy rate for ergodic information sources and ergodic dynamical systems. Phys. D 2005, 210, 77–95. [Google Scholar] [CrossRef]
- Amigó, J.M. The equality of Kolmogorov-Sinai entropy and metric permutation entropy generalized. Phys. D 2012, 241, 789–793. [Google Scholar] [CrossRef]
- Haruna, T.; Nakajima, K. Permutation complexity via duality between values and orderings. Phys. D 2011, 240, 1370–1377. [Google Scholar] [CrossRef]
- Haruna, T.; Nakajima, K. Permutation excess entropy and mutual information between the past and future. Int. J. Comput. Ant. Sys. 2012, in press. [Google Scholar]
- Haruna, T.; Nakajima, K. Symbolic transfer entropy rate is equal to transfer entropy rate for bivariate finite-alphabet stationary ergodic Markov processes. Eur. Phys. J. B 2013, 86, e230. [Google Scholar] [CrossRef]
- Haruna, T.; Nakajima, K. Permutation approach to finite-alphabet stationary stochastic processes based on the duality between values and orderings. Eur. Phys. J. Special Topics 2013, 222, 383–399. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Feldman, D.P. Regularities unseen, randomness observed: Levels of entropy convergence. Chaos 2003, 15, 25–54. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, A.; Schreiber, T. Information transfer in continuous processes. Phys. D 2002, 166, 43–62. [Google Scholar] [CrossRef]
- Pompe, B.; Runge, J. Momentary information transfer as a coupling measure of time series. Phys. Rev. E 2011, 83, e051122. [Google Scholar] [CrossRef]
- Marko, H. The bidirectional communication theory—A generalization of information theory. IEEE Trans. Commun. 1973, 21, 1345–1351. [Google Scholar] [CrossRef]
- Massey, J.L. Causality, Feedback and Directed Information. In Proceedings of International Symposium on Information Theory and Its Applications, Waikiki, HI, USA, 27–30 November 1990.
- Anderson, B.D.O. The realization problem for hidden Markov models. Math. Control Signals Syst. 1999, 12, 80–120. [Google Scholar] [CrossRef]
- Walters, P. An Introduction to Ergodic Theory; Springer-Verlag: New York, NY, USA, 1982. [Google Scholar]
- Seneta, E. Non-Negative Matrices and Markov Chains; Springer: New York, NY, USA, 1981. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Arnold, D.V. Information-theoretic analysis of phase transitions. Complex Syst. 1996, 10, 143–155. [Google Scholar]
- Bialek, W.; Nemenman, I.; Tishby, N. Predictability, complexity, and learning. Neural Comput. 2001, 13, 2409–2463. [Google Scholar] [CrossRef] [PubMed]
- Feldman, D.P.; McTague, C.S.; Crutchfield, J.P. The organization of intrinsic computation: Complexity-entropy diagrams and the diversity of natural information processing. Chaos 2008, 18, e043106. [Google Scholar] [CrossRef] [PubMed]
- Grassberger, P. Toward a quantitative theory of self-generated complexity. Int. J. Theor. Phys. 1986, 25, 907–938. [Google Scholar] [CrossRef]
- Li, W. On the relationship between complexity and entropy for Markov chains and regular languages. Complex Syst. 1991, 5, 381–399. [Google Scholar]
- Shaw, R. The Dripping Faucet as a Model Chaotic System; Aerial Press: Santa Cruz, CA, USA, 1984. [Google Scholar]
- Löhr, W. Models of Discrete Time Stochastic Processes and Associated Complexity Measures. Ph.D. Thesis, Max Planck Institute for Mathematics in the Sciences, Leipzig, Germany, 2010. [Google Scholar]
- Frenzel, S.; Pompe, B. Partial mutual information for coupling analysis of multivariate time series. Phys. Rev. Lett. 2007, 99, e204101. [Google Scholar] [CrossRef]
- Amblard, P.O.; Michel, O.J.J. On directed information theory and Granger causality graphs. J. Comput. Neurosci. 2011, 30, 7–16. [Google Scholar] [CrossRef] [PubMed]
- Ash, R. Information Theory; Wiley Interscience: New York, NY, USA, 1965. [Google Scholar]
- Staniek, M.; Lehnertz, K. Symbolic transfer entropy. Phys. Rev. Lett. 2008, 100, e158101. [Google Scholar] [CrossRef]
- Kugiumtzis, D. Transfer entropy on rank vectors. J. Nonlin. Sys. Appl. 2012, 3, 73–81. [Google Scholar]
- Kramer, G. Directed Information for Channels with Feedback. Ph.D. Thesis, Swiss Federal Institute of Technology, Zurich, Switzerland, 1998. [Google Scholar]
- Amblard, P.O.; Michel, O.J.J. Relating Granger causality to directed information theory for networks of stochastic processes. 2011; arXiv:0911.2873v4. [Google Scholar]
- Dahlaus, R.; Eichler, M. Causality and graphical models in time series analysis. In Highly Structured Stochastic Systems; Green, P., Hjort, N., Richardson, S., Eds.; Oxford University Press: New York, NY, USA, 2003; pp. 115–137. [Google Scholar]
- European Physical Journal Special Topics on Recent Progress in Symbolic Dynamics and Permutation Complexity. Eur. Phys. J. 2013, 222, 241–598.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Haruna, T.; Nakajima, K. Permutation Complexity and Coupling Measures in Hidden Markov Models. Entropy 2013, 15, 3910-3930. https://doi.org/10.3390/e15093910
Haruna T, Nakajima K. Permutation Complexity and Coupling Measures in Hidden Markov Models. Entropy. 2013; 15(9):3910-3930. https://doi.org/10.3390/e15093910
Chicago/Turabian StyleHaruna, Taichi, and Kohei Nakajima. 2013. "Permutation Complexity and Coupling Measures in Hidden Markov Models" Entropy 15, no. 9: 3910-3930. https://doi.org/10.3390/e15093910
APA StyleHaruna, T., & Nakajima, K. (2013). Permutation Complexity and Coupling Measures in Hidden Markov Models. Entropy, 15(9), 3910-3930. https://doi.org/10.3390/e15093910



