Entropy Measures of Street-Network Dispersion: Analysis of Coastal Cities in Brazil and Britain
Abstract
:1. Introduction
2. Study Area
- The three Brazilian cities have been growing rapidly in the last decades on account of their popularity for tourism. By contrast, the three British cities, historically very popular as resort cities, have developed over a much longer time and at different rates from the Brazilian cities. These differences, which are clearly reflected in the geometric properties of the street networks, provide unique opportunities to explore the mechanisms and constraints that affect the geometric properties of different street networks developing at different rates.
- All the cities are located at the coast and have very clear boundaries in the form of curved shorelines and a mountainous hinterland that acts to constrain their geographical expansion (Figure 1 and Figure 2). The curvature varies between the shorelines, as is reflected in the differences in their radii of curvature (Figure 3).
- The availability of high quality Landsat images and Google-Earth views for Brazilian cities and geographic information data for British cities make it possible to digitize and carry out a detailed geographical analysis of street networks.
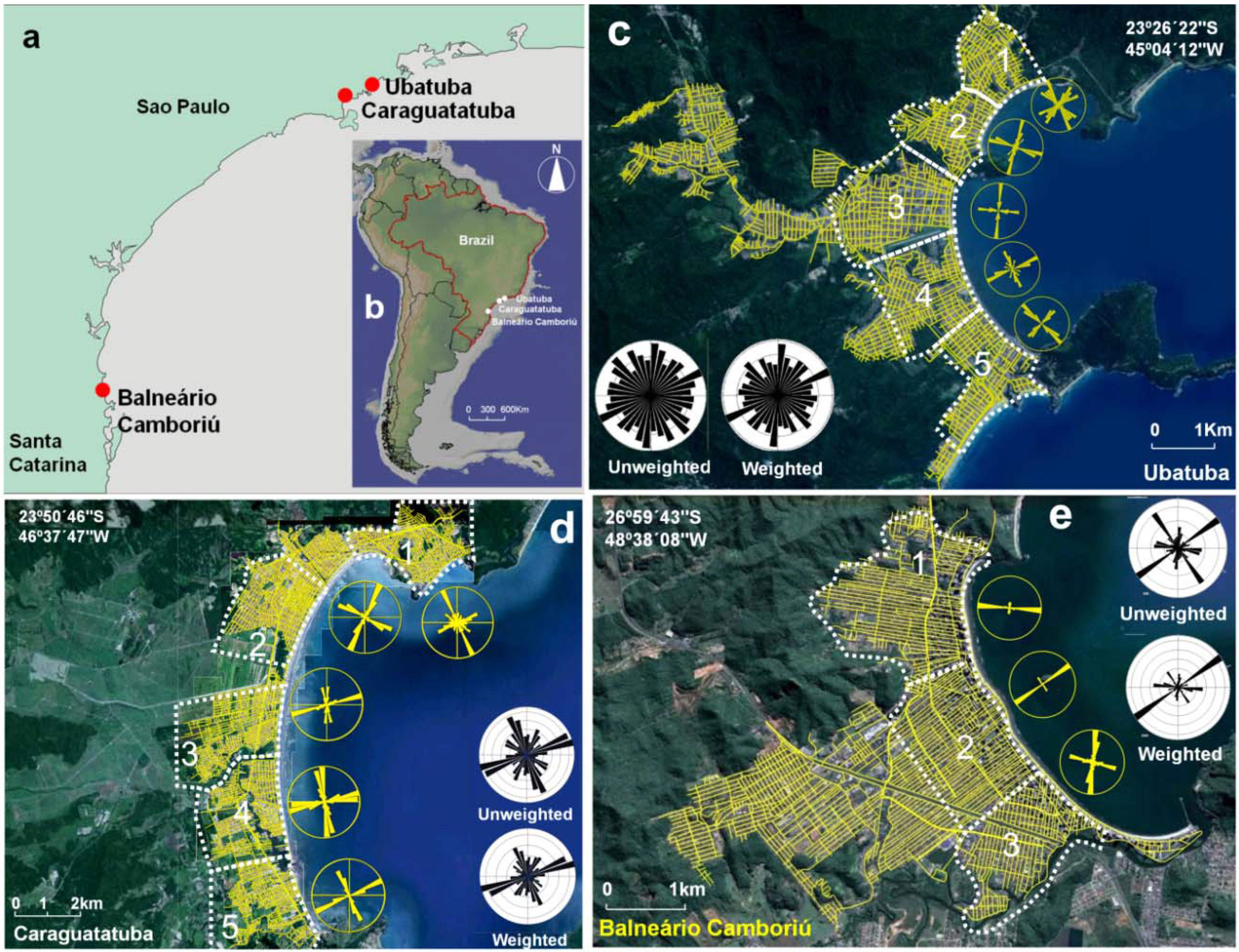

3. Data and Methods of Analysis
3.1. Data
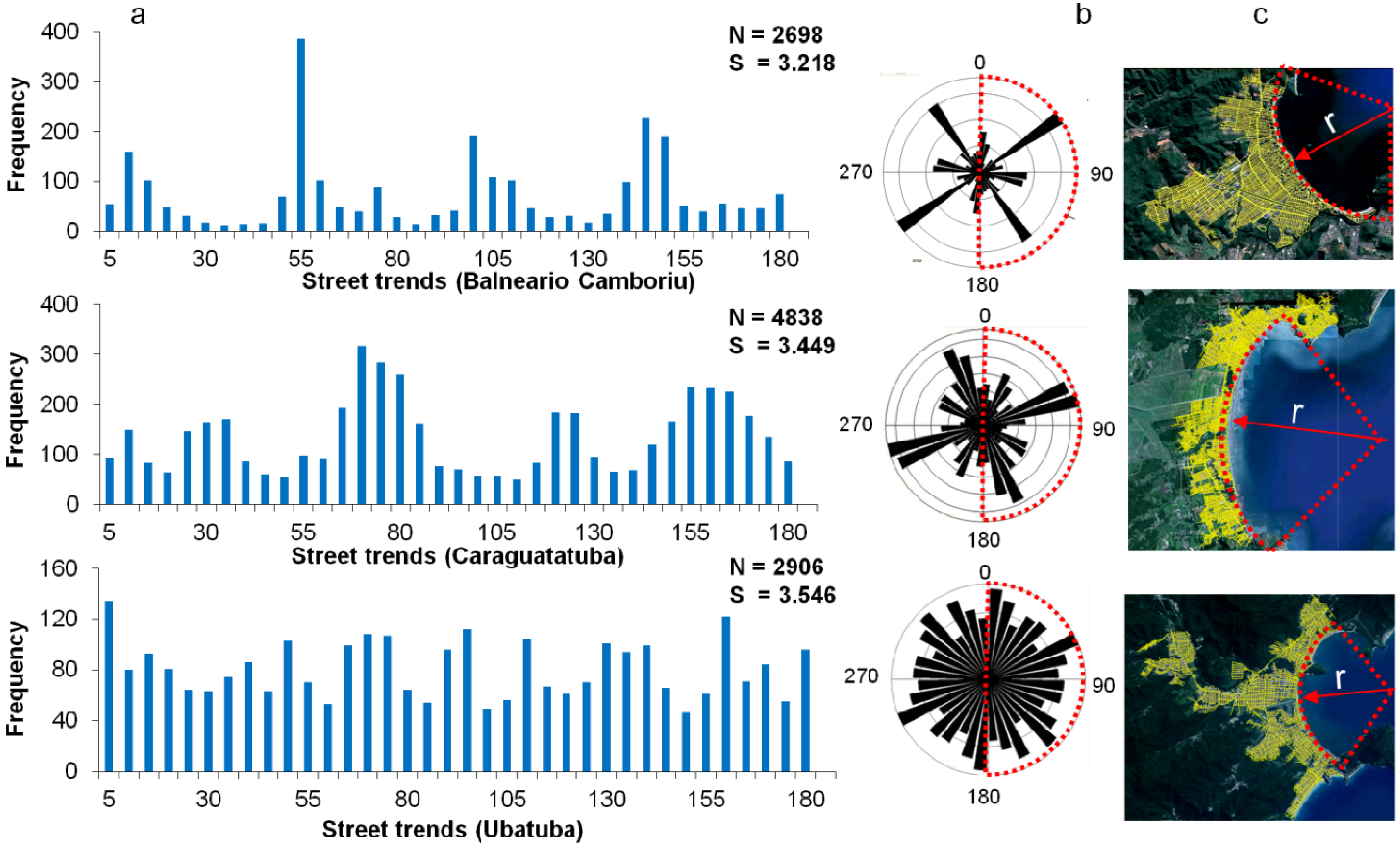
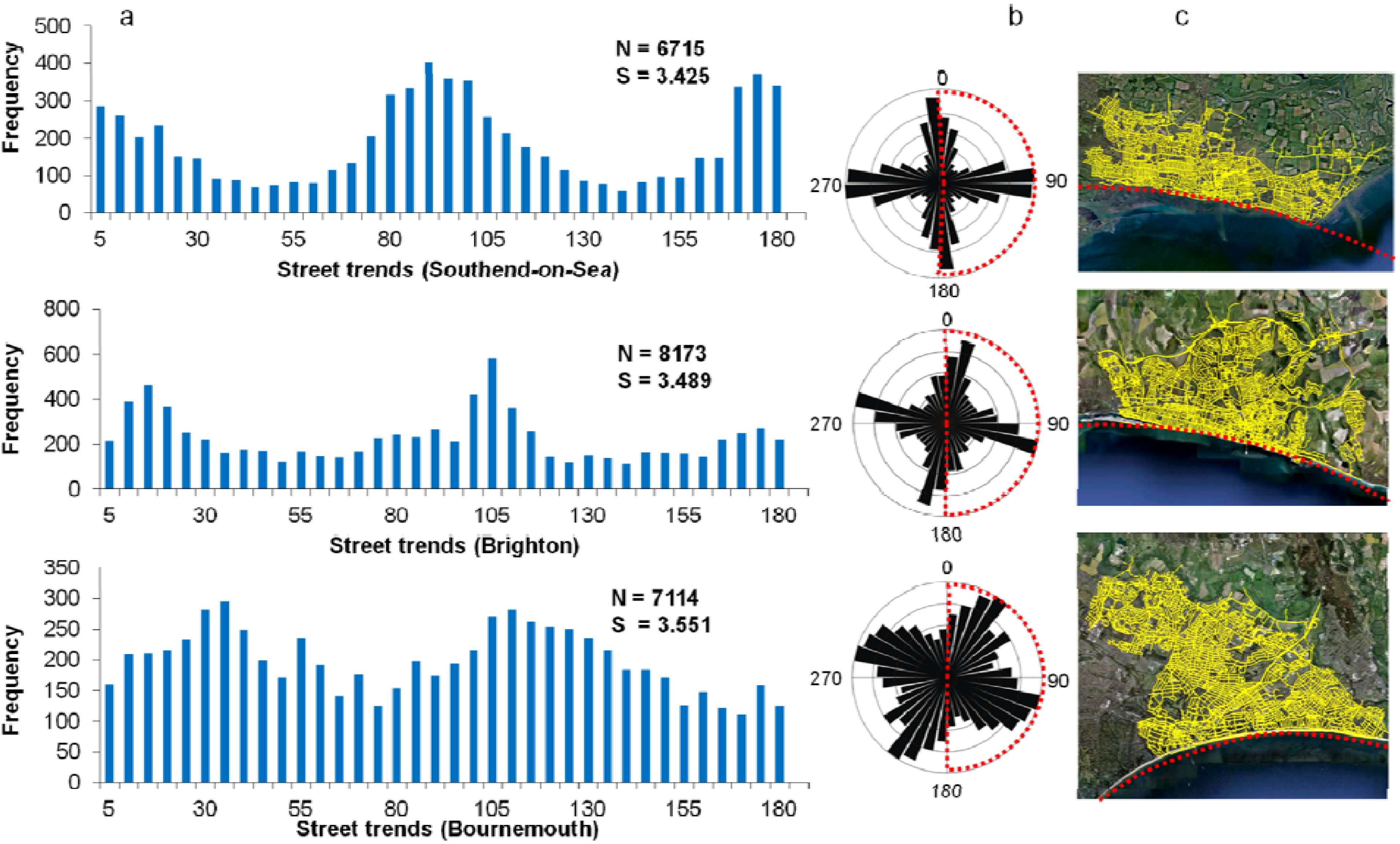
3.2. Directional Statistics
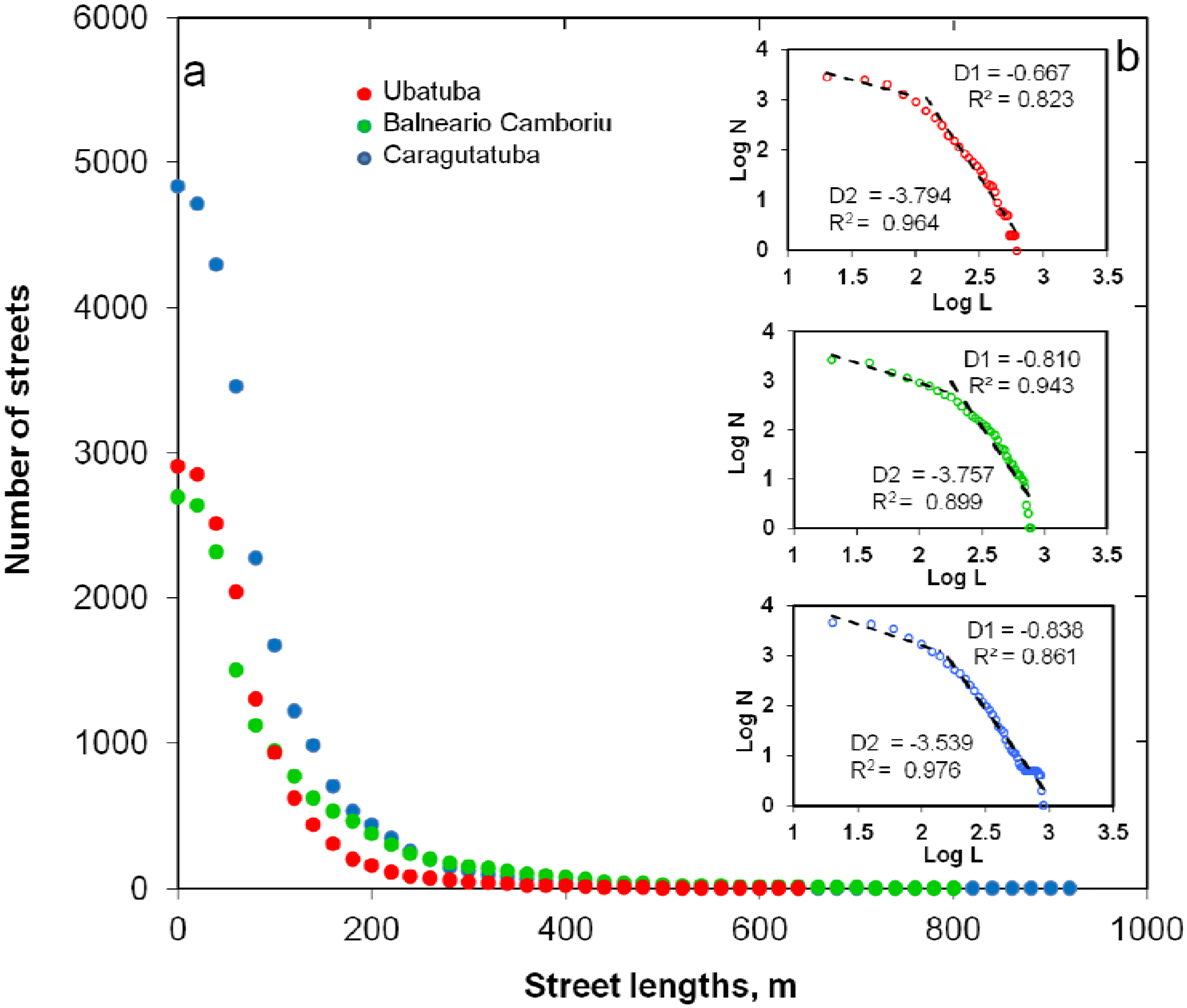
3.3. Street Length Distribution
3.4. Entropy Analysis
4. Results
| City | Number of streets | Radius of curvature | Scaling exponent | Xmin | Orientation entropy | Lengthrange | Average length | Length entropy |
|---|---|---|---|---|---|---|---|---|
| Ubatuba | 2906 | 2.35 | 2.605 | 106 ± 6 | 3.546 | 9–624 (615) | 92 | 2.237 |
| a | – | – | 0.667 | – | – | 9–100 (91) | 61 | 1.721 |
| b | – | – | 3.794 | – | – | 100–624 (524) | 159 | 2.282 |
| Caraguatatuba | 4838 | 9.3 | 2.583 | 146 ± 25 | 3.449 | 9–901 (892) | 101 | 2.389 |
| a | – | – | 0.838 | – | – | 9–140 (131) | 72 | 1.943 |
| b | – | – | 3.539 | – | – | 140–901 (761) | 217 | 2.523 |
| Balneario Camboriu | 2698 | 3.74 | 2.18 | 164 ± 57 | 3.218 | 6–794 (788) | 109 | 2.632 |
| a | – | – | 0.81 | – | – | 6–160 (154) | 68 | 2.041 |
| b | – | – | 3.757 | – | – | 160–794 (634) | 275 | 2.753 |
| Southend-on-Sea | 6715 | 39 | 2.366 | 157 ± 63 | 3.425 | 4–1651 (1647) | 86 | 2.568 |
| a | – | – | 0.872 | – | – | 4–160 (156) | 56 | 2.003 |
| b | – | – | 2.875 | – | – | 160–1651 (1491) | 273 | 2.969 |
| Brighton & Hove | 8173 | 30 | 2.15 | 150 ± 30 | 3.489 | 4–1869 (1865) | 87 | 2.658 |
| a | – | – | 0.763 | – | – | 4–120 (116) | 48 | 1.814 |
| b | – | – | 2.515 | – | – | 120–1869 (1749) | 234 | 3.184 |
| Bournemouth | 7114 | 12 | 2.515 | 142 ± 40 | 3.551 | 4–952 (948) | 82 | 2.395 |
| a | – | – | 0.881 | – | – | 4–140 (136) | 55 | 1.906 |
| b | – | – | 3.518 | – | – | 140–952 (812) | 230 | 2.658 |
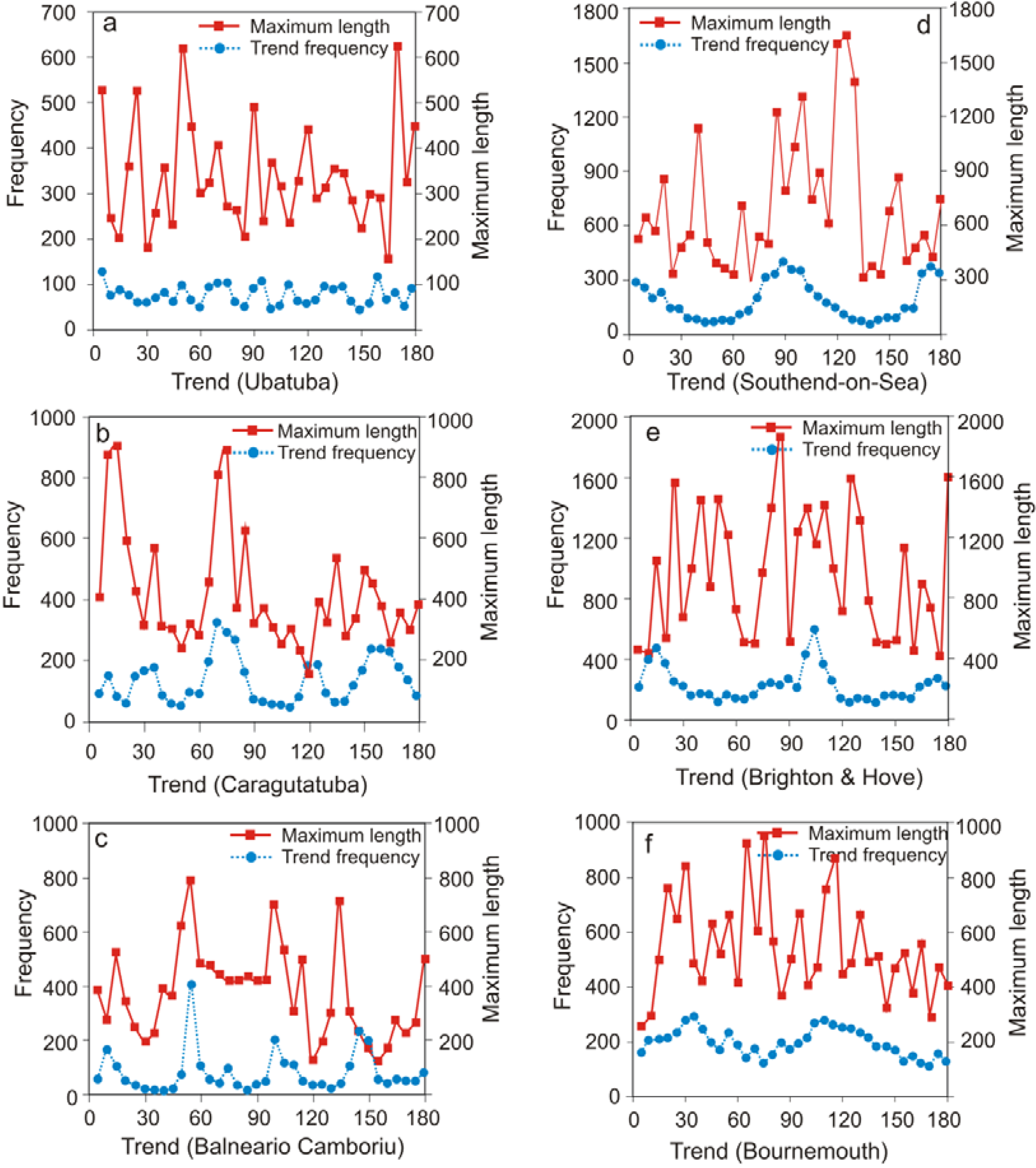
4.1. Street Trends
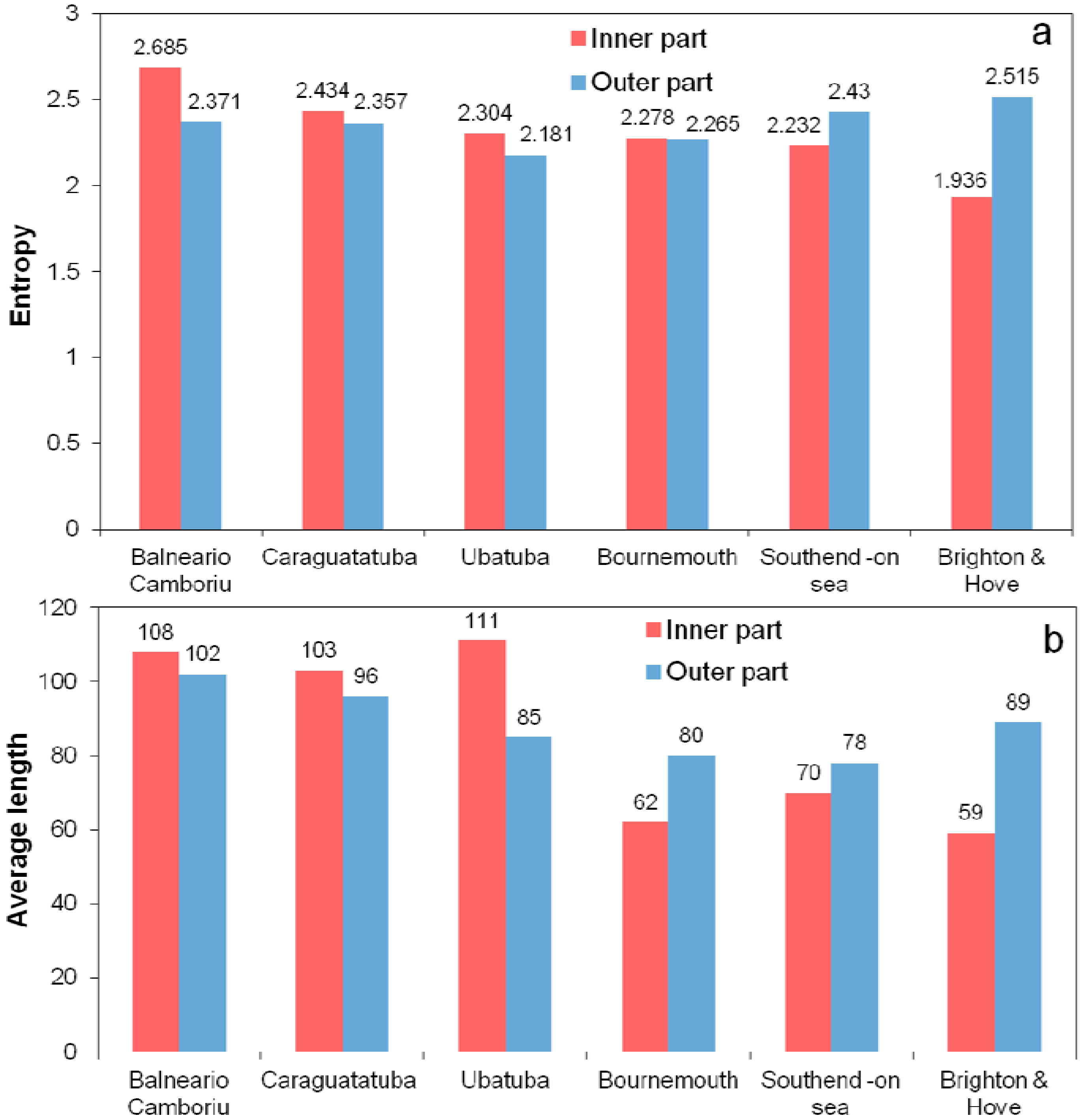
4.2. Street Lengths
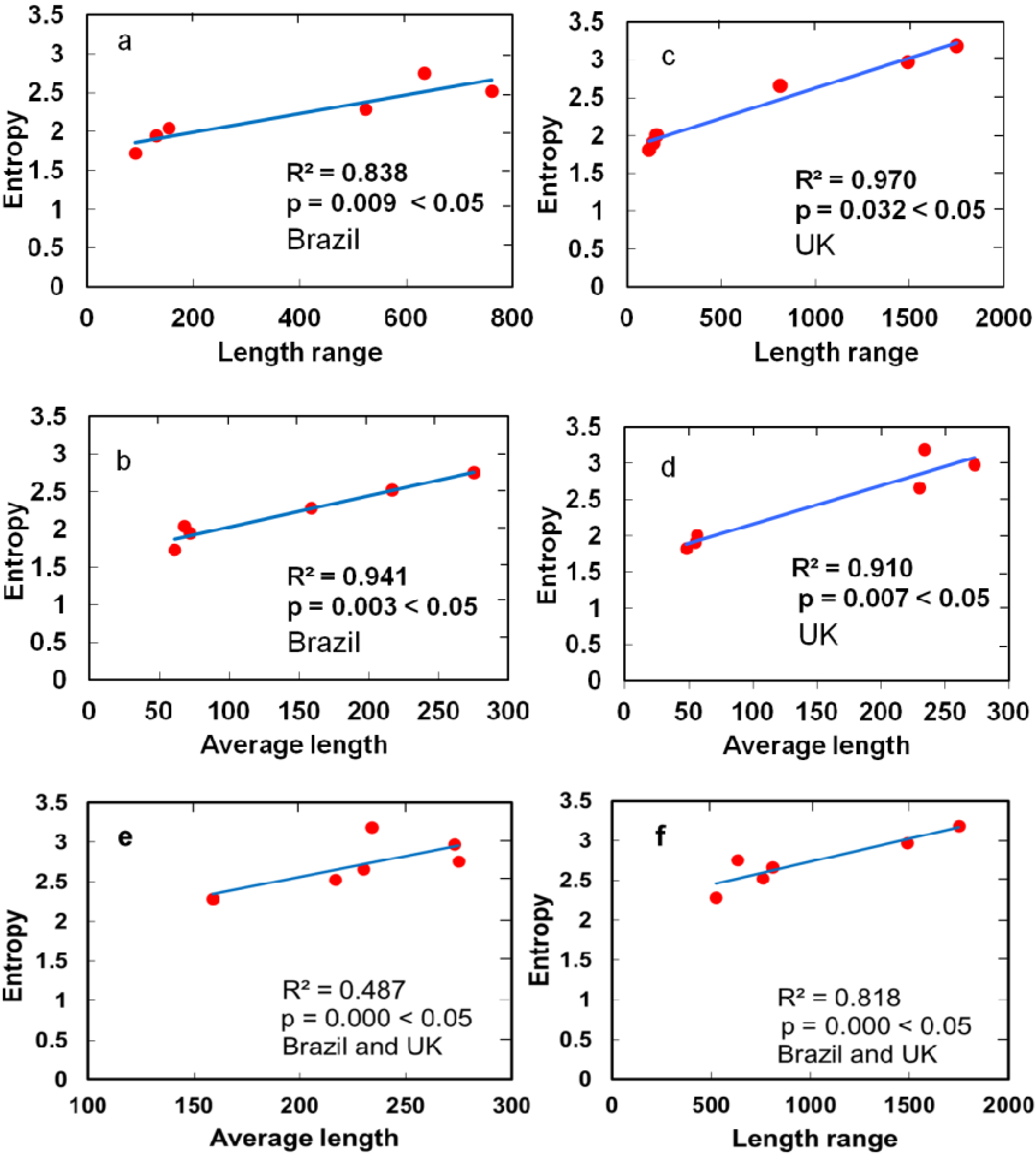
5. Discussion
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Kostof, S. The City Shaped: Urban Patterns and Meanings Through History; Thames and Hudson: London, UK, 1991. [Google Scholar]
- Batty, M.; Longley, P. Fractal Cities: A Geometry of Form and Function; Academic Press: London, UK, 1994. [Google Scholar]
- Batty, M. The size, scale, and shape of cities. Science 2008, 319, 769–771. [Google Scholar] [CrossRef] [PubMed]
- Levinson, D.; Huang, A. A positive theory of network connectivity. Environ. Plann. B 2012, 39, 308–325. [Google Scholar] [CrossRef]
- Scellato, S.; Cardillo, A.; Latora, V.; Porta, S. The backbone of a city. Eur. Phys. J. B 2006, 50, 221–225. [Google Scholar] [CrossRef]
- Hepcan, S.; Hepcan, C.C.; Kilicaslan, C.; Ozkan, M.B.; Kocan, N. Analyzing landscape change and urban sprawl in a Mediterranean coastal landscape: a case study from Izmir, Turkey. J. Coastal Res. 2013, 29, 301–310. [Google Scholar] [CrossRef]
- Shpuza, E. Urban shapes and urban grids: A comparative study of Adriatic and Ionian coastal cities. In Proceedings of the 6th Space Syntax Symposium, Istanbul, Turkish, 12–15 June 2007; pp. 009–12.
- Shpuza, E. Evolution of street networks in Adriatic and Ionian coastal cities 1769–2007. In Proceedings of the 7th International Space Syntax Symposium, Stockholm, Sweden, 8–11 June 2009.
- Mohajeri, M.; French, J.R.; Batty, M. Evolution and entropy in the organization of urban street patterns. Ann. GIS 2013, 19, 1–16. [Google Scholar] [CrossRef]
- Leopold, L.A.; Langbein, W.B. The Concept of Entropy in Landscape Evolution. US Geological Survey Professional Paper 500-A; US Government Printing Office: Washington DC, WA, USA, 1962; pp. 14–19.
- Wilson, A.G. Entropy in urban and regional modelling: Retrospect and prospect. Geogr. Anal. 2010, 42, 364–394. [Google Scholar] [CrossRef]
- Wilson, A.G. Entropy in Urban and Regional Modelling; Pion: London, UK, 1970. [Google Scholar]
- Levinson, D. Network structure and city size. PLoS One 2012, 7, e29721. [Google Scholar] [CrossRef] [PubMed]
- Xie, F.; Levinson, D. Topological evolution of surface transportation networks. Comput. Environ. Urban 2009, 33, 211–223. [Google Scholar] [CrossRef]
- Jat, M.K.; Garg, P.K.; Khare, D. Monitoring and modelling of urban sprawl using remote sensing and GIS techniques. Int. J. Appl. Earth Obs. 2007, 10, 26–43. [Google Scholar] [CrossRef]
- Ghanghermeh, A.; Roshan, G.; Orosa, J.A.; Calvo-Rolle, J.L.; Costa, A.M. New Climatic Indicators for Improving Urban Sprawl: A Case Study of Tehran City. Entropy 2013, 15, 999–1013. [Google Scholar] [CrossRef]
- Ramachandra, T.V.; Bharath, H.A.; Durgappa, D.S. Insights to urban dynamics through landscape spatial pattern analysis. Int. J. Appl. Earth Obs. 2012, 18, 329–343. [Google Scholar]
- Batty, M. Spatial entropy. Geogr. Anal. 1974, 6, 1–31. [Google Scholar] [CrossRef]
- Martins, R.D.A. Double exposure on the northern coast of the São Paulo State, Brazil. In Proceedings of the Berlin Conferences on Human Dimensions of Global Environmental Change, Berlin, Gemary, 8–9 October 2010.
- Ferreira, L.C.; Barbi, F.; Martins, R.D.A.; Teixeira, L.R.; Urbinatti, A.M. Governing climate change in Brazilian coastal cities: Risks and strategies. In Proceedings of Colorado Conference on Earth System Governance: Crossing Boundaries and Building Bridges, Fort Collins, CO, USA, 17–20 May 2011.
- Nicolodi, J.L.; Pettermann, R.M. Vulnerability of the Brazilian coastal zone in its environmental, social, and technological aspects. J. Coastal Res. 2011, 64(Special Issue), 1372–1379. [Google Scholar]
- Moura, N.J., Jr.; Ribeiro, M.B. Zipf law for Brazilian cities. Physica A 2005, 367, 441–448. [Google Scholar] [CrossRef]
- Ferreira, J.C.; Silva, L.; Polette, M. The coastal artificialization process: Impacts and challenges for the sustainable management of the coastal cities of Santa Catarina. J. Coastal Res. 2009, 59, 1209–1213. [Google Scholar]
- Rodrigues da Silva, A.N.; da Silva Costa, M.; Macedo, M.H. Multiple views of sustainable urban mobility: The case of Brazil. Transp. Policy 2008, 15, 350–360. [Google Scholar]
- Rodrigues da Silva, A.N.; Costa, G.C.F.; Brondino, N.C.M. Urban sprawl in Brazil and transportation energy use. Energy Sustainable Dev. 2007, 11, 171–185. [Google Scholar]
- Rodrigues da Silva, A.N. Transport geography in Brazil. J. Trans. Geogr. 2012, 22, 324–326. [Google Scholar] [CrossRef]
- IBGE. Available online: http://www.ibge.gov.br/home/estatistica/populacao/censo2010/ (accessed on 4 March 2013).
- Ordnance Survey. Available online: http://www.ordnancesurvey.co.uk/oswebsite/.co.uk/ (accessed on 8 October 2012).
- Haklay, M. How good is volunteered geographical information? A comparative study of OpenStreetMap and Ordnance Survey datasets. Environ. Plann. B 2009, 37, 682–703. [Google Scholar]
- EDINA. Available online: http://www.edina.ac.uk/ (accessed on 2 May 2012).
- Jiang, B.; Claramunt, C. Topological analysis of urban street networks. Environ. Plann. B 2004, 31, 151–162. [Google Scholar] [CrossRef]
- Newman, M. E. J. Power laws, Pareto distributions and Zipf’s law. Contemp. Phys. 2005, 46, 323–351. [Google Scholar] [CrossRef]
- Jiang, B. Topological pattern of urban street networks: universality and peculiarity. Physica A 2007, 384, 647–655. [Google Scholar] [CrossRef]
- Masucci, A.P.; Smith, D.; Crooks, A.; Batty, M. Random planar graphs and the London street network. Eur. Phys. J. B 2009, 71, 259. [Google Scholar]
- Chan, S.H.Y.; Donner, R.V.; Lammer, S. Urban road networks—spatial networks with universal geometric features? Eur. Phys. J. B 2011, 84, 563–577. [Google Scholar] [CrossRef]
- Ebdon, D. Statistics in Geography, 2nd ed.; Blackwell: Oxford, UK, 1985. [Google Scholar]
- Shaw, G.; Wheeler, D. Statistical Techniques in Geographical Analysis; Wiley: New York, NY, USA, 1985. [Google Scholar]
- Swan, A.R.H.; Sandilands, M. Introduction to Geological Data Analysis; Blackwell: Oxford, UK, 1995. [Google Scholar]
- Smith, M.J.; Goodchild, M.F.; Longley, P. Geospatial Analysis: A Comprehensive Guide, 3rd ed.; Troubador Publishing Ltd.: Leicester, UK, 2009. [Google Scholar]
- Nemec, W. The shape of the rose. Geology 1988, 59, 149–152. [Google Scholar] [CrossRef]
- GeOrient. Available online: http://www.holcombecoughlinoliver.com/ (accessed on 8 June 2012).
- Schroeder, M. Fractals, Chaos, Power Laws; W.H. Freeman: New York, NY, USA, 1991. [Google Scholar]
- Peitgen, H.O.; Jurgens, H.; Saupe, D. Chaos and Fractals, 2nd ed.; Springer Verlag: New York, NY, USA, 2004. [Google Scholar]
- Pisarenko, V.; Rodkin, M. Heavy-Tailed Distributions in Disaster Analysis; Springer: Heidelberg, Germany, 2010. [Google Scholar]
- Barabasi, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [PubMed]
- Clauset, A.; Chalizi, R.C.; Newman, M.E.J. Power-law distributions in empirical data. Soc. Ind. Appl. Math. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Hughes, I.G.; Hase, T.P.A. Measurements and Their Uncertainties; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Berendsen, H.J.C. Data and Error Analysis; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Han, D.D.; Qian, J.H.; Ma, Y.G. Emergence of double scaling law in complex systems. Europhys. Lett. 2011, 94, 28006. [Google Scholar] [CrossRef]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Stamps, A.E. Entropy and visual diversity in the environment. J. Archit. Plan. Res. 2004, 21, 239–256. [Google Scholar]
- Nelson, P. Biological Physics: Energy, Information, Life; W.H. Freeman: New York, NY, USA, 2006. [Google Scholar]
- Volkenstein, M.V. Entropy and Information; Birkhauser: Berlin, Germany, 2009. [Google Scholar]
- Desurvire, E. Classical and Quantum Information Theory; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Figueiredo, L. Continuity Lines: An investigation of urban form through street networks. Ph.D. Thesis, University College London, London, UK, 2009. [Google Scholar]
- Goodman, S. A dirty dozen: Twelve p-value misconceptions. Semin. Hematol. 2008, 45, 135–140. [Google Scholar] [CrossRef] [PubMed]
- Wickers, A. What is P-Value Anyway? Addison-Wesley: Boston, MA, USA, 2010. [Google Scholar]
- Brillouin, L. Science Uncertainty and Information; Academic Press: New York, NY, USA, 1964. [Google Scholar]
- Blundell, S.J.; Blundell, K.M. Concepts in Thermal Physics; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Sethna, J.P. Statistical Mechanics: Entropy, Order, Parameters, and Complexity; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Mohajeri, N.; Gudmundsson, A. Entropies and scaling exponents of street and fracture networks. Entropy 2012, 14, 800–833. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Mohajeri, N.; French, J.R.; Gudmundsson, A. Entropy Measures of Street-Network Dispersion: Analysis of Coastal Cities in Brazil and Britain. Entropy 2013, 15, 3340-3360. https://doi.org/10.3390/e15093340
Mohajeri N, French JR, Gudmundsson A. Entropy Measures of Street-Network Dispersion: Analysis of Coastal Cities in Brazil and Britain. Entropy. 2013; 15(9):3340-3360. https://doi.org/10.3390/e15093340
Chicago/Turabian StyleMohajeri, Nahid, Jon R. French, and Agust Gudmundsson. 2013. "Entropy Measures of Street-Network Dispersion: Analysis of Coastal Cities in Brazil and Britain" Entropy 15, no. 9: 3340-3360. https://doi.org/10.3390/e15093340
APA StyleMohajeri, N., French, J. R., & Gudmundsson, A. (2013). Entropy Measures of Street-Network Dispersion: Analysis of Coastal Cities in Brazil and Britain. Entropy, 15(9), 3340-3360. https://doi.org/10.3390/e15093340




