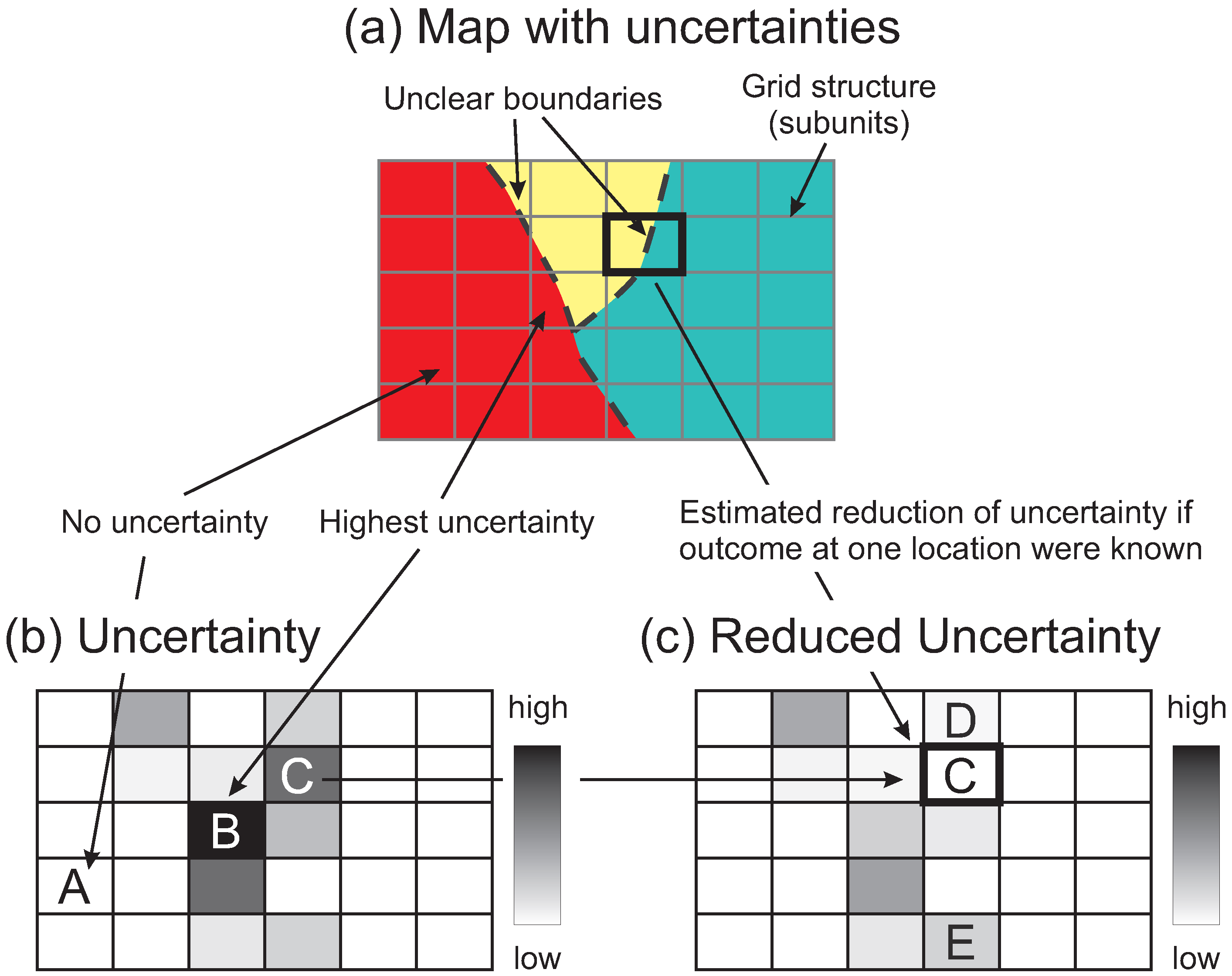
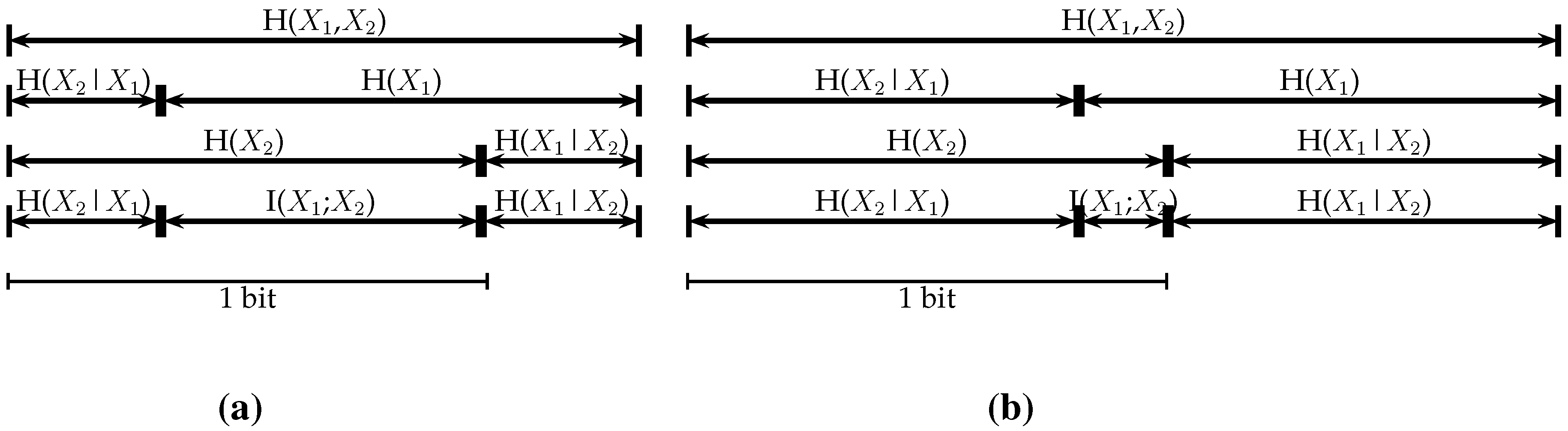The measures of information theory are now applied to evaluate uncertainty correlations and the potential reduction of uncertainty in a typical geological scenario. The example is intentionally kept simple for a clear presentation of the concepts. Applications to other fields should be directly transferrable. Generally, the measures can be applied to study uncertainties and their correlation in all types of spatial uncertainty estimation where the required (multinominal) probability tables for each combination of outcomes are available (as used in Equations (
4) and (
5)). For simple cases, it would be possible to obtain these probabilities from analytical estimations. However, in more complex settings, the probabilities can be estimated from multiple simulation results, for example derived as a result of a Monte Carlo simulation approach [
19]. One spatial modelling research field where simulations under uncertainty are becoming increasingly applied is structural geological modelling.
Several methods addressing the analysis and visualisation of subsurface structural uncertainties have been developed in recent years (e.g., [
11,
12,
13,
23,
24,
25]). Structural geological models, reflecting the result of geological history over millions of years, are inherently three-dimensional and contain complex correlation structures, for example due to offset along a fault, or multiple folding patterns. It was thus previously proposed to use information entropy as a measure of uncertainty in these models [
2]. In this section, a simple geological model will be used to review the interpretation of information entropy as a measure of uncertainty in a spatial setting. Next, the information theoretic measures for the interpretation of uncertainty correlations described before will be used to determine uncertainty reduction in several scenarios.
3.1. Analysis of Uncertainties at a Potential Drilling Location
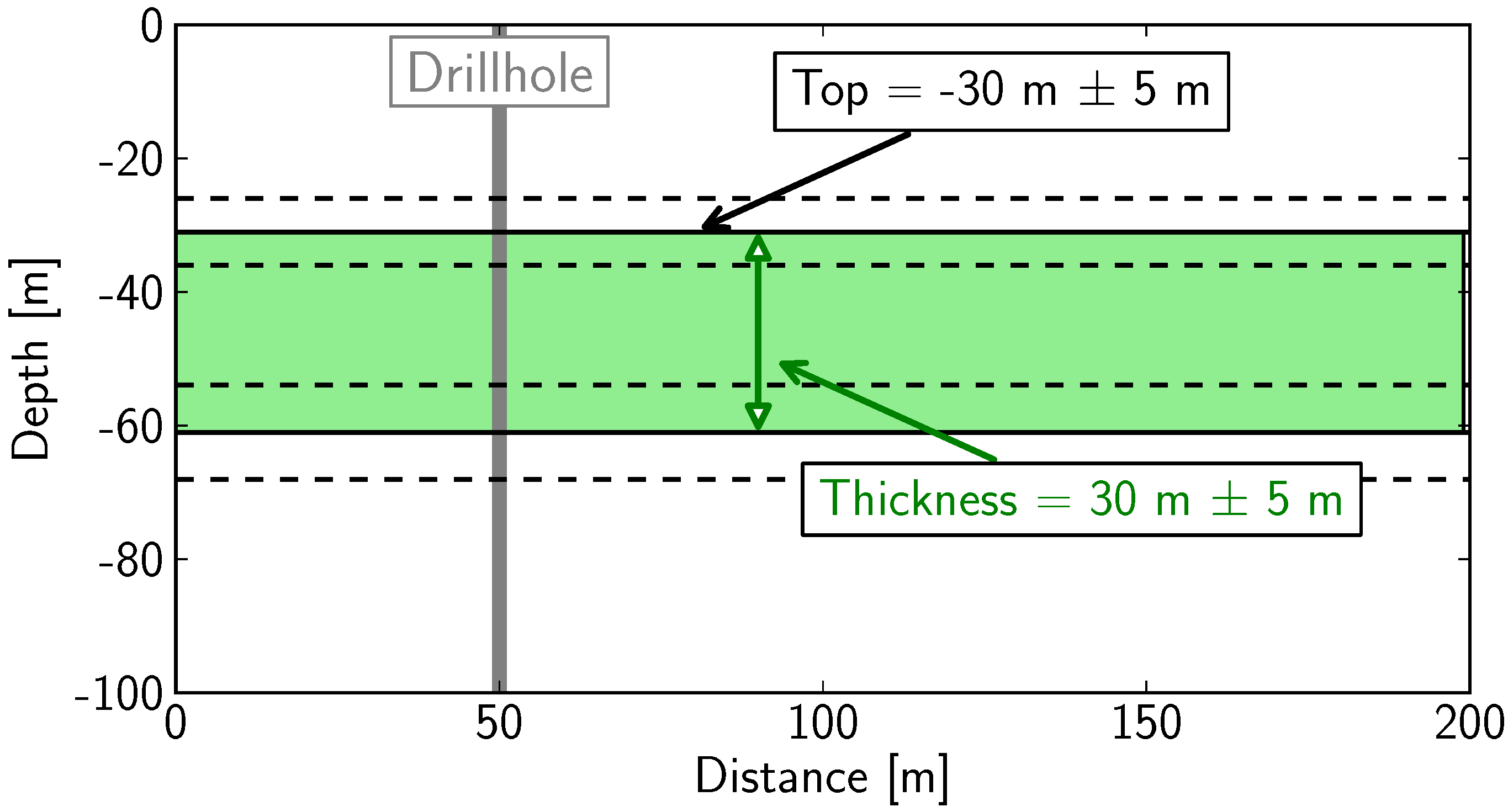
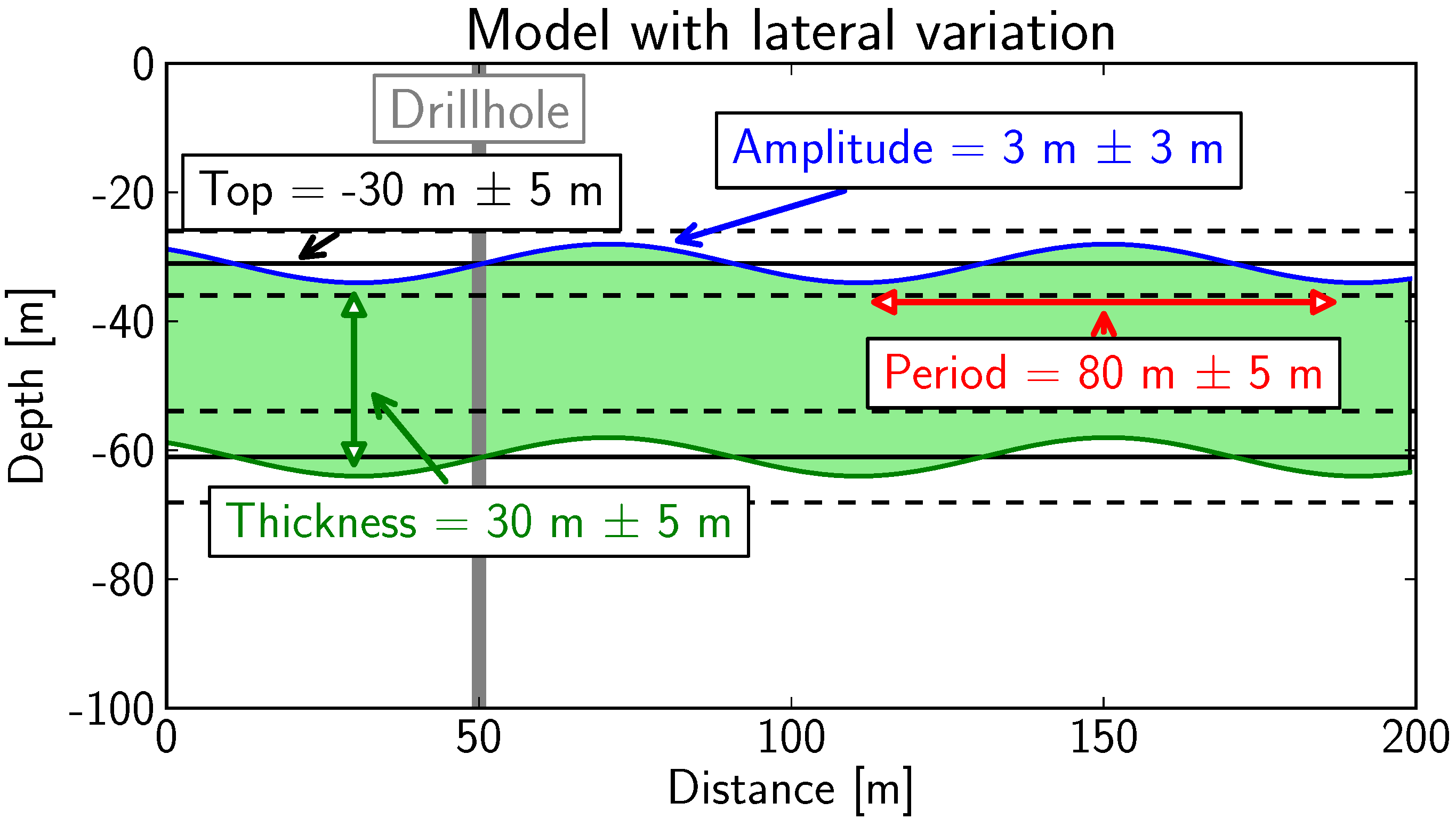
Consider a typical exploration case where drilling should be performed at a location for a specific geological layer at depth (for example a mineralised layer). We assume that information about the approximate depth of the layer and an estimation of the thickness exists, potentially derived from intersections of the layer in other drill-holes in the vicinity. Based on this information, it is estimated that the top of the layer is expected at a depth of 30
, with a standard deviation of 5
, assuming a normal distribution. Furthermore, the layer is expected to have a thickness of 30
, again with a standard deviation of 5
. Furthermore, depth and thickness are considered independent. From the addition of both distributions it can then be derived that the base of the layer is expected at 60
, with a standard deviation of approximately 7
. This setting is schematically visualised in
Figure 2.
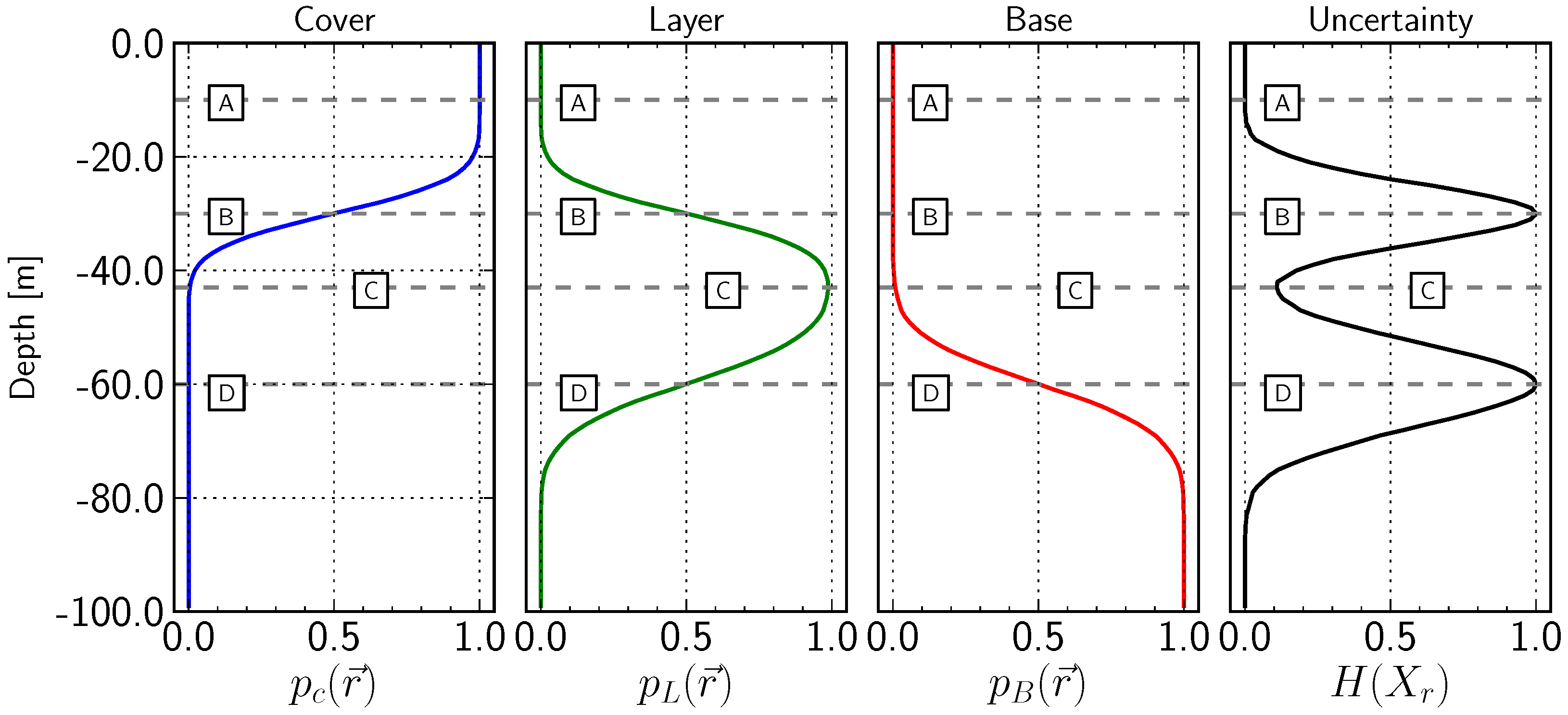
In the following, the focus will be on the analysis of uncertainties at this potential drill-hole location. The probabilities to obtain each of the geological units (the cover, the layer of interest, and the base layer) are derived from 1000 simulated model realisations. For the numerical analysis, the model is gridded to cell sizes of 10
by 10
. Results are shown in
Figure 3. Please note that depth is downwards, as customary in representations of drill-hole data. The forth graph shows the information entropy
at each position
r, calculated from the probabilities using Equation (
4). Note that, in this case, only the
z-value at position
changes.
Figure 3.
Probability distribution of geological units ( for the cover layer, for the layer of interest and for the base) at depth in drill-hole example, and the corresponding information entropy ; the dashed gray lines and the labels indicate important positions in the graph: A: , : no uncertainty; at B and D, H = 1, two outcomes equally probable ( at B, at D); C: minimum of uncertainty for layer; see text for further description.
Figure 3.
Probability distribution of geological units ( for the cover layer, for the layer of interest and for the base) at depth in drill-hole example, and the corresponding information entropy ; the dashed gray lines and the labels indicate important positions in the graph: A: , : no uncertainty; at B and D, H = 1, two outcomes equally probable ( at B, at D); C: minimum of uncertainty for layer; see text for further description.
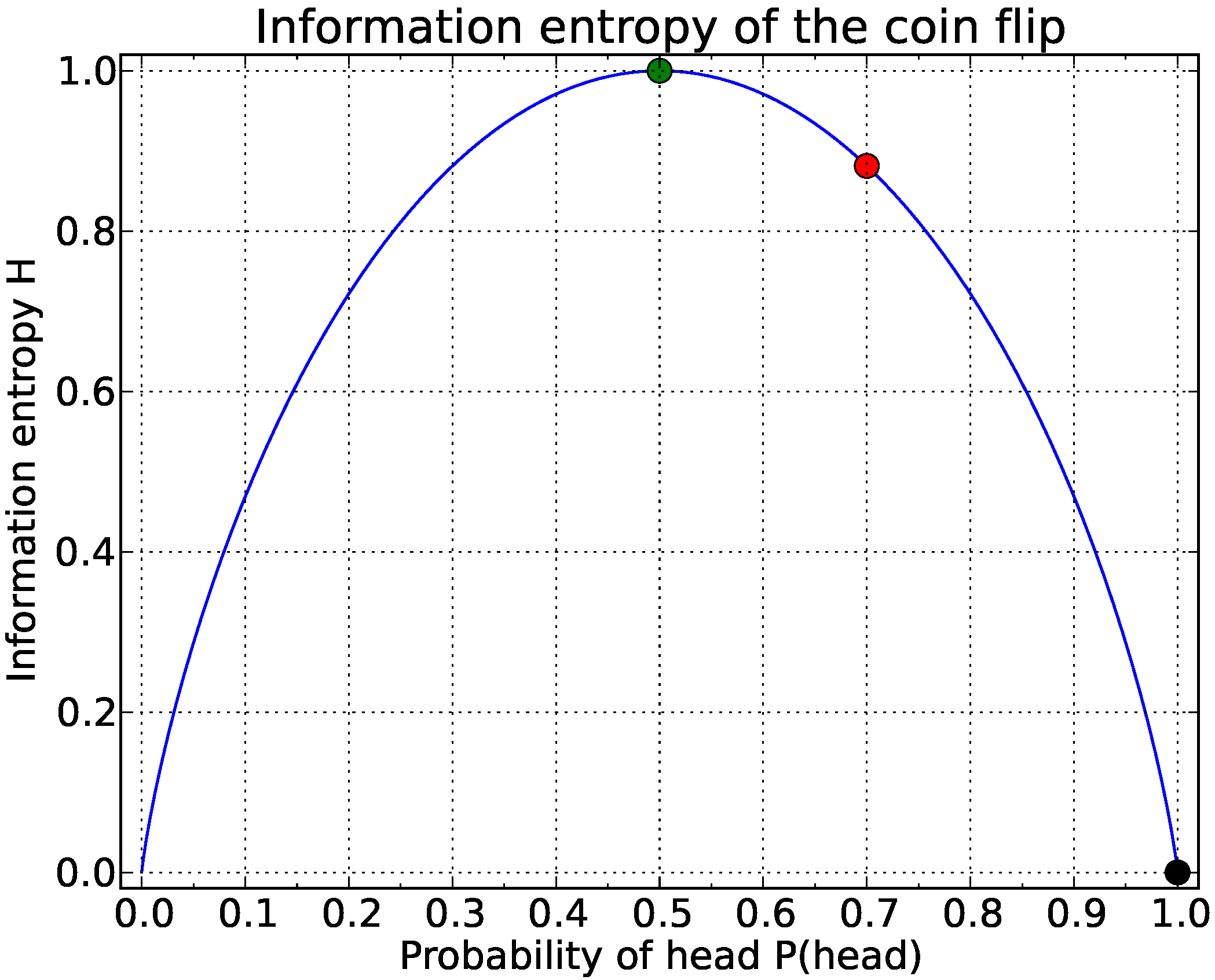
An interpretation of the information entropy graph is instructive to highlight the use of this quantity as a measure of uncertainty. Several key points are highlighted in
Figure 3 with dashed lines and labels. At the depth of the dashed line (label A), only one outcome is possible: the “Cover” unit with a probability of
, and the corresponding information entropy at this depth is zero, meaning that no uncertainty exists. The information entropy reaches its maximum value for two possible outcomes (
) at the two lines with labels B and D, where two outcomes are equally probable (
at B,
at D). In this case, these positions are equivalent to the expected values of the upper and lower boundary of the geological layer of interest. Both of these outcomes are as expected from the setup of the problem described above (
Figure 2).
It is interesting to note, however, that the lowest uncertainty in the range of the layer of interest is not exactly between the expected positions of the top and lower boundary (which would be at 45
), but actually shallower, at around 43
(label C in
Figure 3). The reason for the shallower position is that, as shown above, the position of the lower boundary has a higher standard deviation and this leads to a relatively lower uncertainty closer to the top boundary. In this case, the position corresponds to the highest probability of the layer of interest (green graph); however, this is not necessarily the general case.
3.2. Uncertainty Correlation between Two Locations at Depth
After the analysis of uncertainties with information entropy at single locations, correlations of uncertainty between different positions are evaluated in the next step. In order to determine the correlations in detail, the joint probability tables for all outcomes are determined from the simulation results for all combinations of locations. From these tables, all relevant information theoretic measures can be calculated using Equations (
5)–(
12). What is evaluated here is, therefore, how gaining knowledge about one specific location in the subsurface is related to uncertainties at all other locations. The important aspect is that these analyses are performed on the basis of the joint probability table and that no specific outcome has to be assumed, as the uncertainty correlations are a part of the underlying model.
Two types of spatial correlations of uncertainties can be expected:
In each of the areas of highest uncertainty (label B and D in
Figure 3), knowing the outcome at one point will necessarily reduce the uncertainty in the surrounding areas. This is due to the set-up of the example simulation (representing here, for example, geological expert knowledge) where the boundary position in the subsurface is simulated as normally distributed around an expected value.
Uncertain areas about the top and the base of the layer of interest should be correlated and knowing the outcome in the uncertain area about the top of the layer should influence uncertainties about the base, and vice versa. Although this correlation might be counter-intuitive, it follows from the set-up of the model with the top of the layer of interest defined, and the thickness considered uncertain (and not the base of the layer).
Each discrete cell in the model is considered as a separate random variable. In a first step, the joint and conditional entropy for all pair-wise combinations of all cells along the potential drill-hole location are evaluated. The results of the analysis are shown in
Figure 4 and
Figure 5. Each point in the visualised matrices corresponds to a pair of depth values (
at the location of the variable
and
at the position of the variable
). The colour bar in all of the following figures is set to highlight the
step levels (for values
, at least
(joint) outcomes are possible). Note that an additional step is included in every range to highlight changes within this step (e.g., between
and
at
. As in the figures before, depth is represented from top to bottom on the y-axis. The representation of the joint entropy (
Figure 4) reveals a pattern that is similar to the information entropy of one variable: it is high in the areas of uncertainty, in the range of the top of the layer at 25–35
(label A) and near the base of the layer at around 55–65
(label B). It is interesting to note that the joint entropy reaches its maximal value for position pairs between the top and the base layer (e.g., at label C).
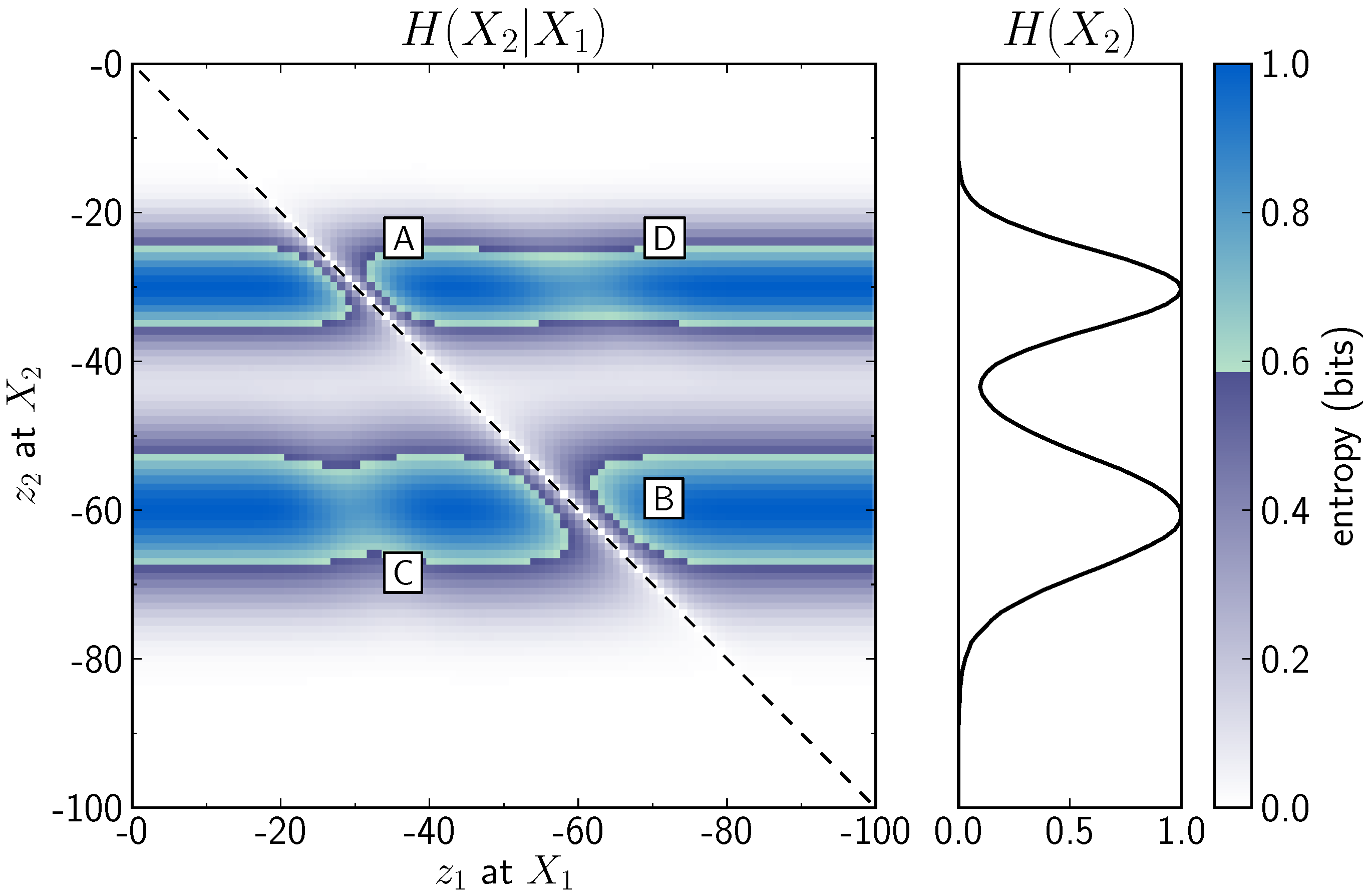
The conditional entropy of a cell in the subsurface, represented as variable
at a depth of
, given the outcome of a variable
at a depth
is represented in
Figure 5. The figure can be interpreted in a way that the vertical slice at a position
corresponds to the remaining uncertainty depth profile (for all values
), given the information of variable
at a depth
. The conditional entropy highlights the same features that could be expected from the analysis of the joint entropy: the high uncertainties around the top and the base of the layer are reduced when spatially close outcomes are known (labels A and B), and, additionally, the uncertainties around the base of the layer are reduced when areas near the top are known (label C), and vice versa (label D). However, the important distinction is that conditional entropy can directly be interpreted as a reduction of uncertainty, and that the value at each location is lower or equal to the initial information entropy (Equation (
9)). This important feature will be evaluated in more detail below. For comparison, the plot on the right in
Figure 5 shows the values of information entropy at depth. It is equivalent to the plot in
Figure 3. An important additional aspect of the conditional entropy is also highlighted in the figure: as opposed to the joint entropy, conditional entropy is not a symmetrical measure,
.
Figure 4.
Joint entropy between two variables at different z-values (depth in drill-hole). Labels correspond to important features, explained in detail in the text. The colour bar is set to reflect increments of , with an additional subdivision between two steps for visualisation purposes. Joint entropy is a symmetrical measure, the dashed line represents .
Figure 4.
Joint entropy between two variables at different z-values (depth in drill-hole). Labels correspond to important features, explained in detail in the text. The colour bar is set to reflect increments of , with an additional subdivision between two steps for visualisation purposes. Joint entropy is a symmetrical measure, the dashed line represents .
In addition to the evaluation of uncertainty reduction, an important aspect of spatial uncertainty estimation is to determine how uncertainties are correlated, or which locations share information about uncertainties in space. The joint entropy in
Figure 4 provides an indication of correlation; however, it is strongly dependent on the information entropy in each of the considered cells and therefore difficult to interpret. It has, for example, the disadvantage that pairs that certainly do not share any information, for example cases where the information entropy of one value is zero, can still be greater than zero (see, for example, the (0,60) pair,
etc.).
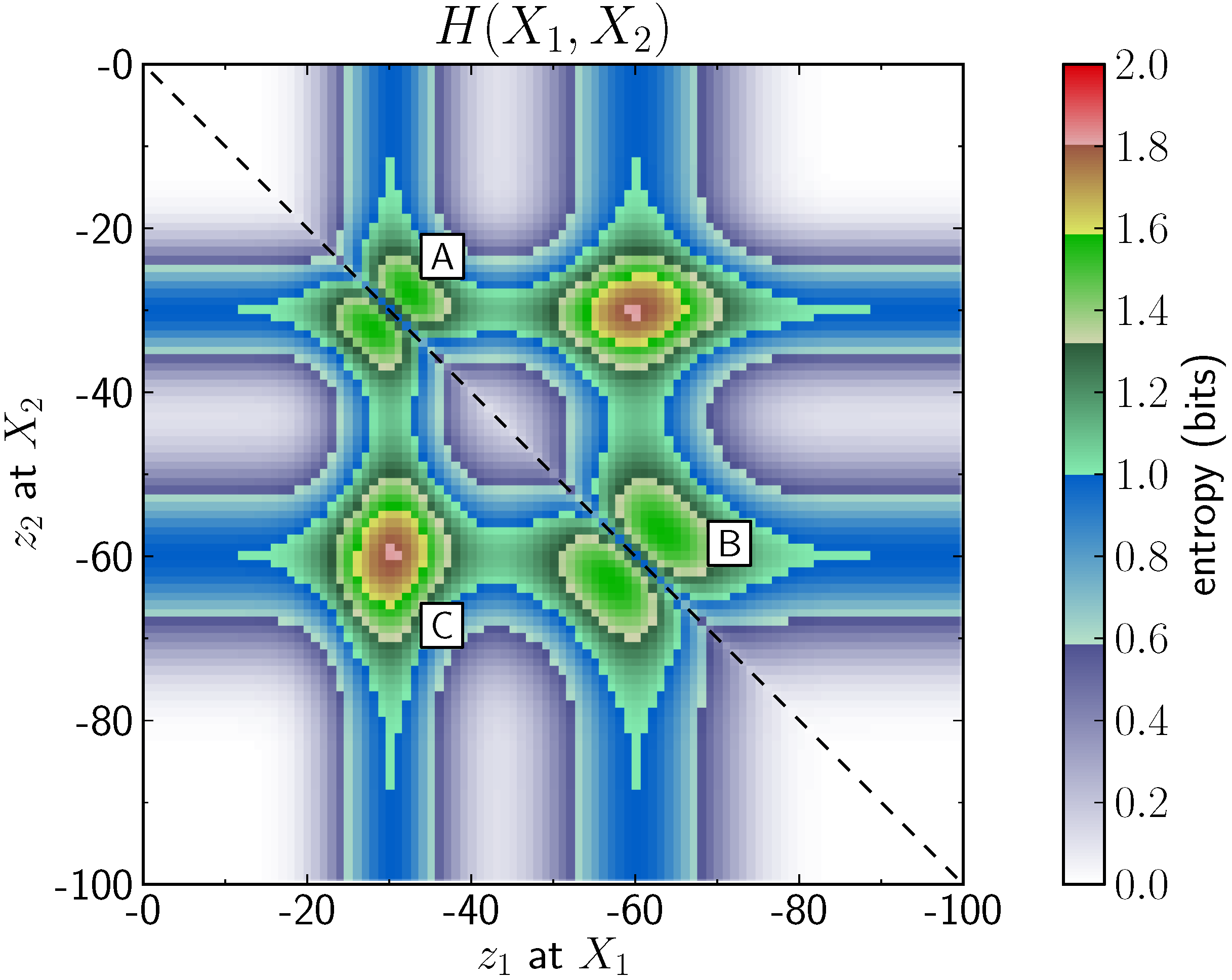
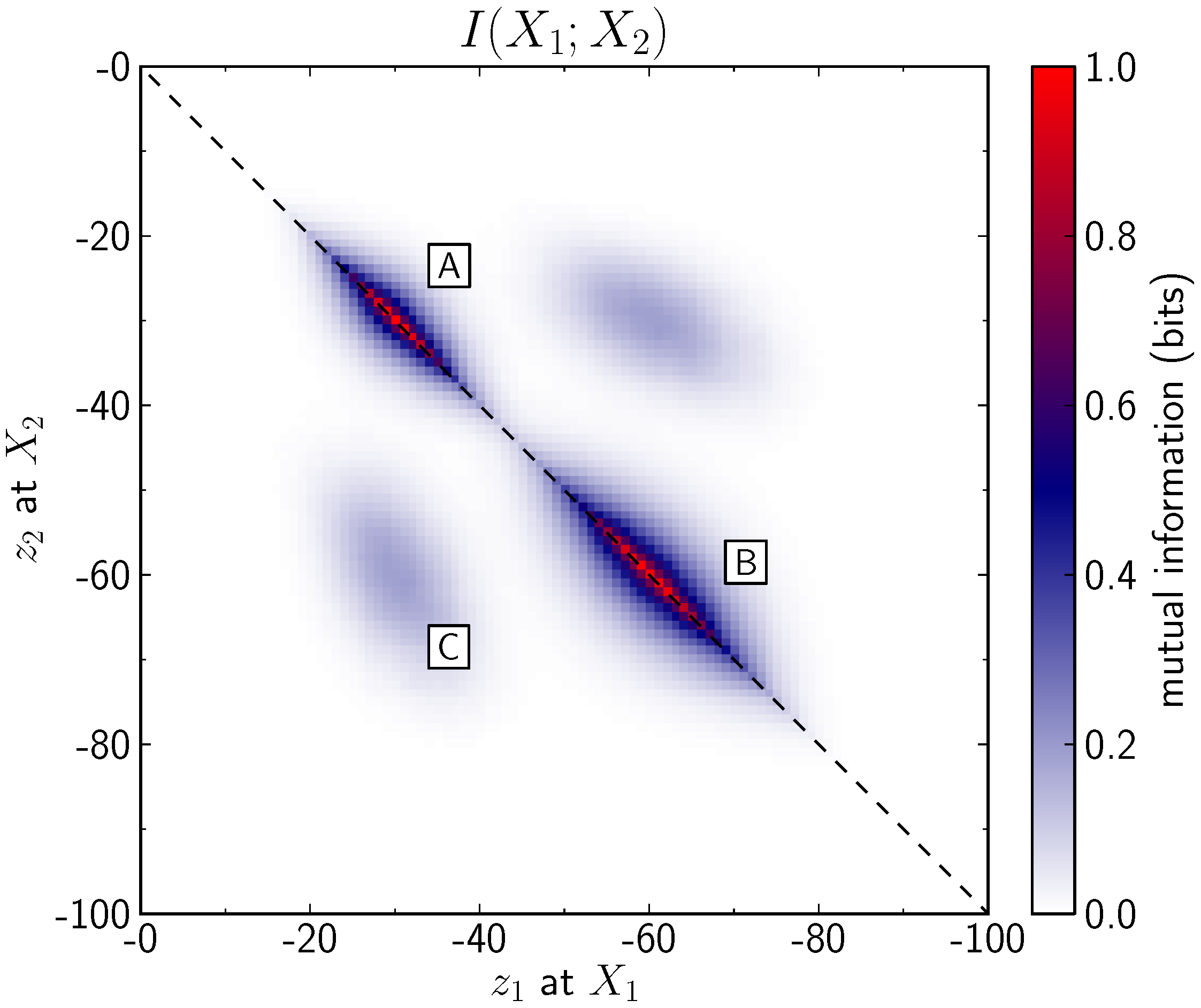
A more suitable measure for the interpretation of uncertainty correlations is mutual information. From Equation (
12) it is apparent that it takes into account the information entropy of both variables, reduced by the joint entropy between them. An evaluation of the mutual information between all pairs of variables in the drill-hole example is shown in
Figure 6. All the expected correlations are here clearly visible. The highest amount of shared information exists in cells close to each other, in the uncertain areas about the top (label A) and the base (label B) of the layer. In addition, the correlation between cells around the top and the base of the layer are apparent (label C), although clearly those correlations are weaker than the correlations at labels A and B. The figure also shows the symmetric nature of the mutual information.
Figure 5.
Conditional entropy of one variable at depth, given the information of another variable . It is interesting to note that the entropies around are reduced when information around a depth of is obtained (label C) and vice versa (label D). The figure also clearly shows that conditional entropy is not symmetrical. The colour bar is set to reflect increments of .
Figure 5.
Conditional entropy of one variable at depth, given the information of another variable . It is interesting to note that the entropies around are reduced when information around a depth of is obtained (label C) and vice versa (label D). The figure also clearly shows that conditional entropy is not symmetrical. The colour bar is set to reflect increments of .
Figure 6.
Mutual information between two random variables and at different z-positions in the drill-hole example. Variables close to each other with high entropy share a large amount of information (labels A and B). However, it is also interesting to note that variables at locations close to the top share information with variables around the base of the layer (label C). Mutual information is a symmetrical measure, the dashed line represents the symmetry axis, .
Figure 6.
Mutual information between two random variables and at different z-positions in the drill-hole example. Variables close to each other with high entropy share a large amount of information (labels A and B). However, it is also interesting to note that variables at locations close to the top share information with variables around the base of the layer (label C). Mutual information is a symmetrical measure, the dashed line represents the symmetry axis, .
3.3. Interpretation of the Relationship between all Measures
The examples before showed how the different measures from information theory provide insights into a variety of aspects of uncertainties and their spatial correlation in the subsurface. However, the relationships between the measures can be difficult to interpret. For clarification, two examples will be evaluated in more detail.
In the example of uncertainties in the drill-hole, it was shown that the joint entropy between a locations of
and
(Label C in
Figure 4) was higher than the joint entropy between close points, for example between
and
, whereas the mutual information behaves in the opposite way. This important difference is due to the information entropy of each variable by itself. For a visualisation of the relationships, all pair-wise information theoretic measures for those cases are represented in the diagrams in
Figure 7.
Figure 7.
Graphical representation of the relationships between information entropy, joint entropy, conditional entropy, and mutual information (after [
17]). The
z values correspond to the actual depth values in the drill-hole example and the corresponding pair-wise entropy measures, see
Figure 4,
Figure 5 and
Figure 6. (
a)
at
= 30
,
at
= 31
; (
b)
at
= 30
,
at
= 60
.
Figure 7.
Graphical representation of the relationships between information entropy, joint entropy, conditional entropy, and mutual information (after [
17]). The
z values correspond to the actual depth values in the drill-hole example and the corresponding pair-wise entropy measures, see
Figure 4,
Figure 5 and
Figure 6. (
a)
at
= 30
,
at
= 31
; (
b)
at
= 30
,
at
= 60
.
In the diagrams, the interpretation of joint entropy is clearly visible: the information entropy of each outcome by itself (
and
) is approximately the same in both cases. However, in the case of the close points in
Figure 7a, both points share more information, reflected in a higher mutual information
, than in the case of the points that are further separated (
Figure 7b). Also, the joint entropy is small for the former case, as well as the conditional entropies,
and
. Therefore, gaining information at
will lead to a higher reduction of uncertainty in the surrounding cells, at the top of the layer, than in the cells around the base of the layer that are further away, exactly as it would intuitively be expected in this setting.
3.4. Application of Multivariate Conditional Entropy to Determine Entropy Reduction during Drilling
The interpretation of uncertainties in the pair-wise comparison shown before provided an insight into the correlation between two locations. The analysis has successfully highlighted the fact that uncertainties about the top surface of the layer are correlated with uncertainties of the base. In a practical sense, however, it is often of interest to consider the overall reduction of uncertainty when the values at multiple locations are known. As an example, in the case of the drill-hole application before, if we were to actually drill at this location, we would obtain information along the entire drill path, and not only at the deepest location. As the entropies along the path can be expected to be correlated (as shown in this case in
Figure 6), the sum of the conditional entropies provides only an upper bound and would therefore lead to an underestimation of the remaining uncertainties. The correct measure to determine the remaining entropies is the multivariate conditional entropy (Equation (
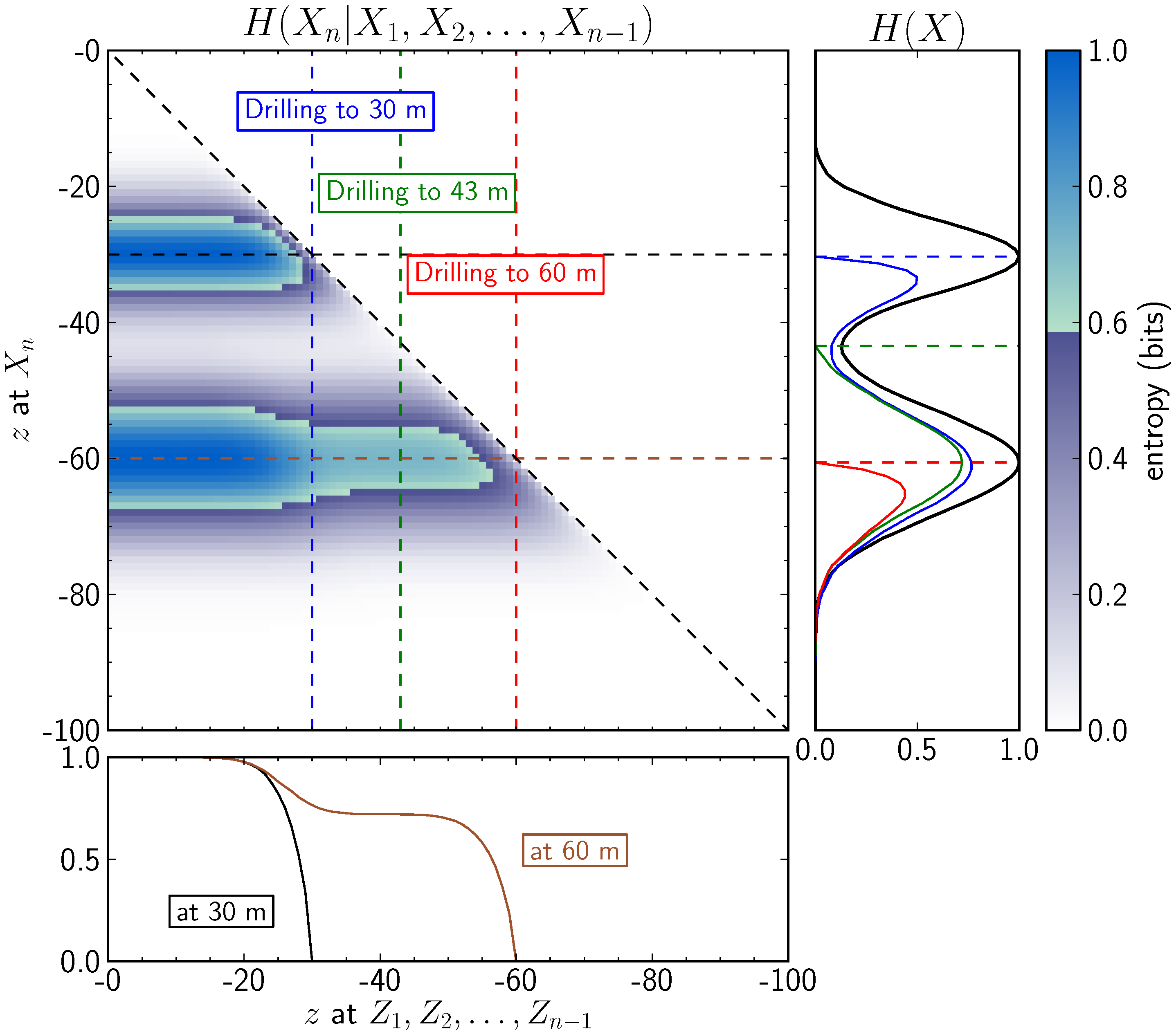
17)) of each cell in the model space, given the information of all cells along the drill path. The results are presented in
Figure 8. In essence, the matrix visualisation is comparable with the pairwise conditional entropy plot in
Figure 5. However, values in y-direction now represent the
remaining uncertainties at a depth
z, given the information of all variables
at shallower depths
. According to the definition of conditional entropy, values along a horizontal slice therefore have to decrease monotonically, reflecting the fact that uncertainties can only be reduced when new information is gained. This behaviour is shown for conditional entropies at the locations of highest uncertainty, at 30
and 60
, in the subfigure at the bottom in
Figure 8. After the drill path reached the cell, the remaining uncertainty at this location is, as expected, reduced to zero.
Figure 8.
Reduction of conditional entropy during information gain; the matrix visualisation is comparable with
Figure 5 but shows here the remaining uncertainty of a variable
at a position
, given the information of all variables
at shallower positions
; the bottom figure shows cuts in x-direction through the matrix, at the positions of highest uncertainty (30
and 60
); the right figure shows conditional entropy profiles with remaining uncertainties after drilling to 30
, 43
, and 60
.
Figure 8.
Reduction of conditional entropy during information gain; the matrix visualisation is comparable with
Figure 5 but shows here the remaining uncertainty of a variable
at a position
, given the information of all variables
at shallower positions
; the bottom figure shows cuts in x-direction through the matrix, at the positions of highest uncertainty (30
and 60
); the right figure shows conditional entropy profiles with remaining uncertainties after drilling to 30
, 43
, and 60
.
The subfigure on the right of
Figure 8 shows conditional entropy profiles of remaining uncertainties, given a drilling to a specific depth. In addition, the black line shows the model information entropy, as the initial state of uncertainty. It is clearly visible that, after drilling to a depth to 30
(blue line), uncertainties are reduced not only about the top surface of the layer but also about the base of the layer (at around 60
). Further drilling to the expected centre of the layer at around 43
(green line) does not reduce uncertainty significantly more. The red line, finally, shows the remaining uncertainties that can be expected after drilling to the expected base of the layer, at 60
.
This example clearly shows how information theoretic measure can be used not only to quantify uncertainties at specific locations at depth but also to evaluate how uncertainties—and information—are correlated in space. Making use of this estimation of correlation, it is then possible to determine how gaining information in one part of the model will reduce uncertainties in other areas.
3.5. Determination of Structural Correlations of Uncertainty in a Higher Dimension
In the previous example, we considered uncertainties for the 1-D case at a potential drilling location. The logical extension of this example is to consider the uncertainty reduction not only along this drill-hole, but also in areas further away from the drilling location. In order to evaluate the application of the information theoretic measures in this context, the previous conceptual geological model is extended into higher dimensions. The uncertainty correlations in a typical geological structure, i.e., a fold, will be evaluated. In a simplified conceptual form, a fold can be considered as a sinusoidal layer that is formed due to the compression of a stiff layer in a soft matrix, for example as a result of a compressional tectonic event. For the case of gentle folding, the structure can be assumed to be strictly symmetric. As in the one-dimensional case before, prior geological knowledge about the structure of the folding might exist, for example from comparison with field observations, and geological assumptions.
Four additional parameters are introduced to simulate the effect of the folded layer: the fold amplitude, defined by a normal distribution with a mean of 3
and a standard deviation of 3
, and the fold period, with a mean period of 80
and a standard deviation of 5
. In addition, the lateral position of the fold is randomly changed (see
Figure 9).
We will now compare the spatial reduction of uncertainty for both geological scenarios, the example of the planar surface of
Figure 2, essentially equivalent to the 1-D case studied above, and the case of the additional folding, represented in
Figure 9. As before, a total of 1000 models were randomly generated for each scenario with a cell resolution of 10
. Probability fields for each possible outcome were estimated from the simulated realisations. Results of this analysis are presented in the top row of
Figure 10. The left column corresponds to the model with the planar surface (
Figure 10a), and the right column to the model with a potential sinusoidal surface (
Figure 10b). Please note that these figures now actually represent vertical cross-sections in space, with depth along the y-axis, and distance along the x-axis, as opposed to the pair-wise location comparison in
Figure 4,
Figure 5 and
Figure 6. The first row of figures represents the information entropy (Equation (
1)) for both scenarios. The information entropy is almost identical for both cases, with remaining differences due to the shape of the sine function, and numerical noise.
Figure 9.
Extension of the example model to simulate folded top and base surfaces of the central layer.
Figure 9.
Extension of the example model to simulate folded top and base surfaces of the central layer.
The following rows in
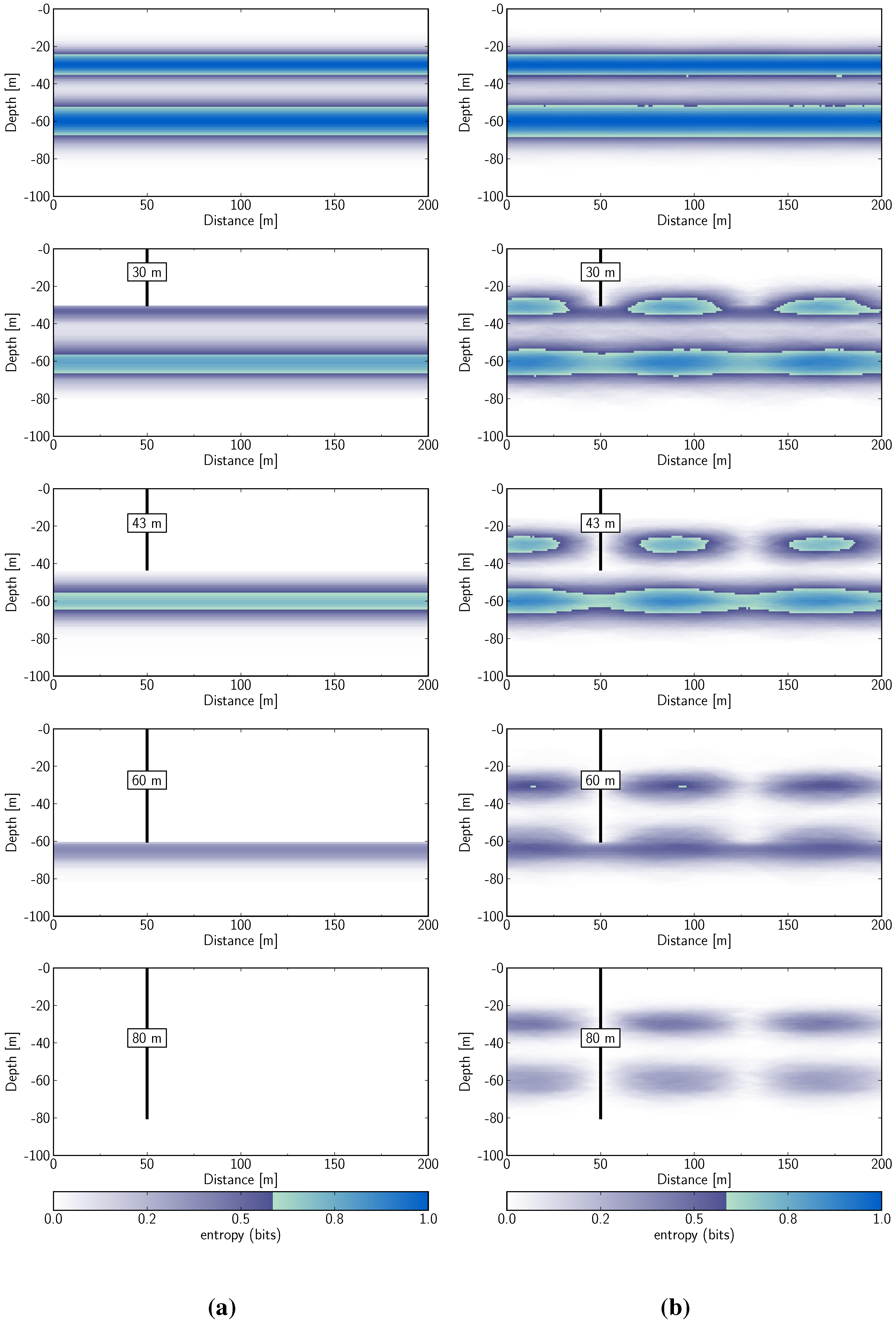
Figure 10a represent the multivariate conditional entropy of each location in the model, given the combined information of all cells that are part of the drill-hole, calculated with Equation (
18). These figures can be interpreted as the uncertainty reduction that can be expected with the information gained during drilling (here at an arbitrary location at 50
). The spatial characteristics of uncertainty reduction for the case of the planar surface in
Figure 10a is a lateral extrusion of the 1-D example, analysed in detail in
Figure 8, with corresponding steps of “drilling depth” (directly comparable with the curves in the right subfigure of
Figure 8). As expected, as soon as we reach a specific drilling depth, uncertainties above this depth are reduced to zero. As soon as the drilling depth extends below a position where the lower boundary can reasonably be expected (at 80
), everything has to be known and there are no remaining uncertainties.
The characteristics of uncertainty reduction are different for the case of the potential sinusoidal surface, shown in
Figure 10b. The first obvious difference is the fact that clear lateral variations of uncertainty reduction exist. In the case of the drilling to 30
, significant uncertainties remain at a lateral distance of approximately 40
from the drill-hole location. However, the conditional entropy also shows that the uncertainty is then reduced again at a distance of approximately 80
. Both aspects nicely reflect the sinusoidal lateral variation used as an input for the simulation (
Figure 9). Drilling to the depth with the highest probability of the layer, at around 43
, leads only to a small further uncertainty reduction. However, drilling to 60
, around the depth of the expected base of the layer, clearly reduces uncertainties about the base. Another interesting observation is that drilling to the base of the layer also reduces the remaining uncertainties around top surface even further. Finally, even after drilling through the entire depth of the potential layer, uncertainties remain in the sinusoidal model, as shown in the bottom of
Figure 10b. The multivariate conditional entropy clearly highlights the differences in uncertainty and their spatial correlation between the restricted case of planar surfaces, where all uncertainties would be completely resolved, and the additional lateral uncertainty added by the potential folding of the layer.
Figure 10.
Spatial distribution of conditional entropy, indicating uncertainty reduction during drilling. (
a) Planar surfaces (
Figure 2); (
b) Folded surfaces (
Figure 9).
Figure 10.
Spatial distribution of conditional entropy, indicating uncertainty reduction during drilling. (
a) Planar surfaces (
Figure 2); (
b) Folded surfaces (
Figure 9).
The study highlighted the application of measures from information theory to evaluate different aspects of spatial uncertainty: the analysis and quantification of uncertainties in space, the evaluation of uncertainty correlations between two locations, and finally the analysis of how additional information could be expected to reduce uncertainties in space. The most relevant aspects are summarised in
Table 1. The different measures are assigned to important “steps” in the analysis as used in the evaluation before. In a different context, only a subset of these analyses might be performed. Step I identifies the initial part of an uncertainty study: the quantification and visualisation of uncertainties in space. The information entropy of one variable has been applied previously to visualise and quantify spatial uncertainties [
1,
2,
14], and joint entropy is the logical extension to two variables. Step II addresses the question of uncertainty correlation and analyses how much information two variables, or in the spatial context, two locations, share. It is also directly evident from the representation of the relationships between the measures in
Figure 7 that for cases where two variables share no information, having the information at one location will not reduce uncertainties at the other location. The uncertainty reduction itself is performed with the measures of conditional entropy, step III in
Table 1. The important aspect of conditional entropy is that it provides a direct estimation of the remaining uncertainty at one location, given additional data at one or more (for the multivariate case) other locations in space. To close the loop, this remaining uncertainty estimate is directly comparable with the initial uncertainty, estimated with information entropy in step I. All measures combined provide consequently a coherent framework for the analysis and quantification of spatial uncertainties, their correlation, and potential reductions of uncertainties with additional information.
Table 1.
Application of information theoretic measures for uncertainty estimation, correlation analysis, and estimations of uncertainty reduction.
Table 1.
Application of information theoretic measures for uncertainty estimation, correlation analysis, and estimations of uncertainty reduction.
| Step | Measure | Use | Variables | Spatial Interpretation |
|---|
| I | Information entropy | Uncertainty quantification | Single variable | Analysis of uncertainty at one location |
| | Joint entropy | Uncertainty quantification | Two variables | Analysis of combined uncertainty at two locations |
| II | Mutual information | Correlation analysis | Two variables | Estimate of information shared between two different locations in space |
| III | Conditional entropy | Uncertainty reduction | Two variables | Estimate of how information at one location would reduce uncertainty in space |
| | Multivariate conditional entropy | Uncertainty reduction | Multiple variables | Estimate of how information at multiple locations would reduce uncertainty in space |