Multiscale Interactions betweenWater and Carbon Fluxes and Environmental Variables in A Central U.S. Grassland
Abstract
:1. Introduction
2. Methods
2.1. Site Description
2.2. Field Measurements and Processing
2.3. Multiscale Information Theory Metrics
3. Results and Discussion
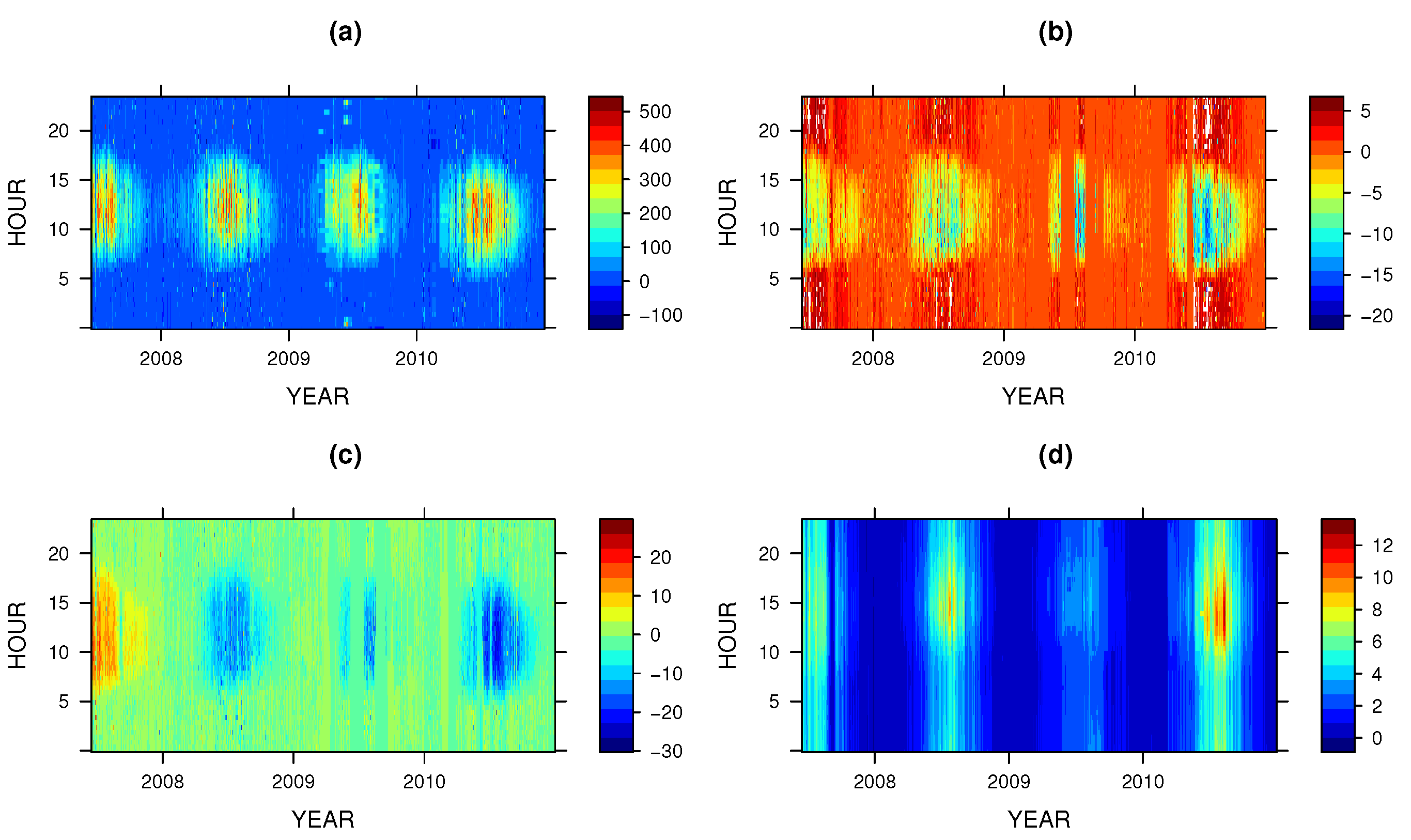
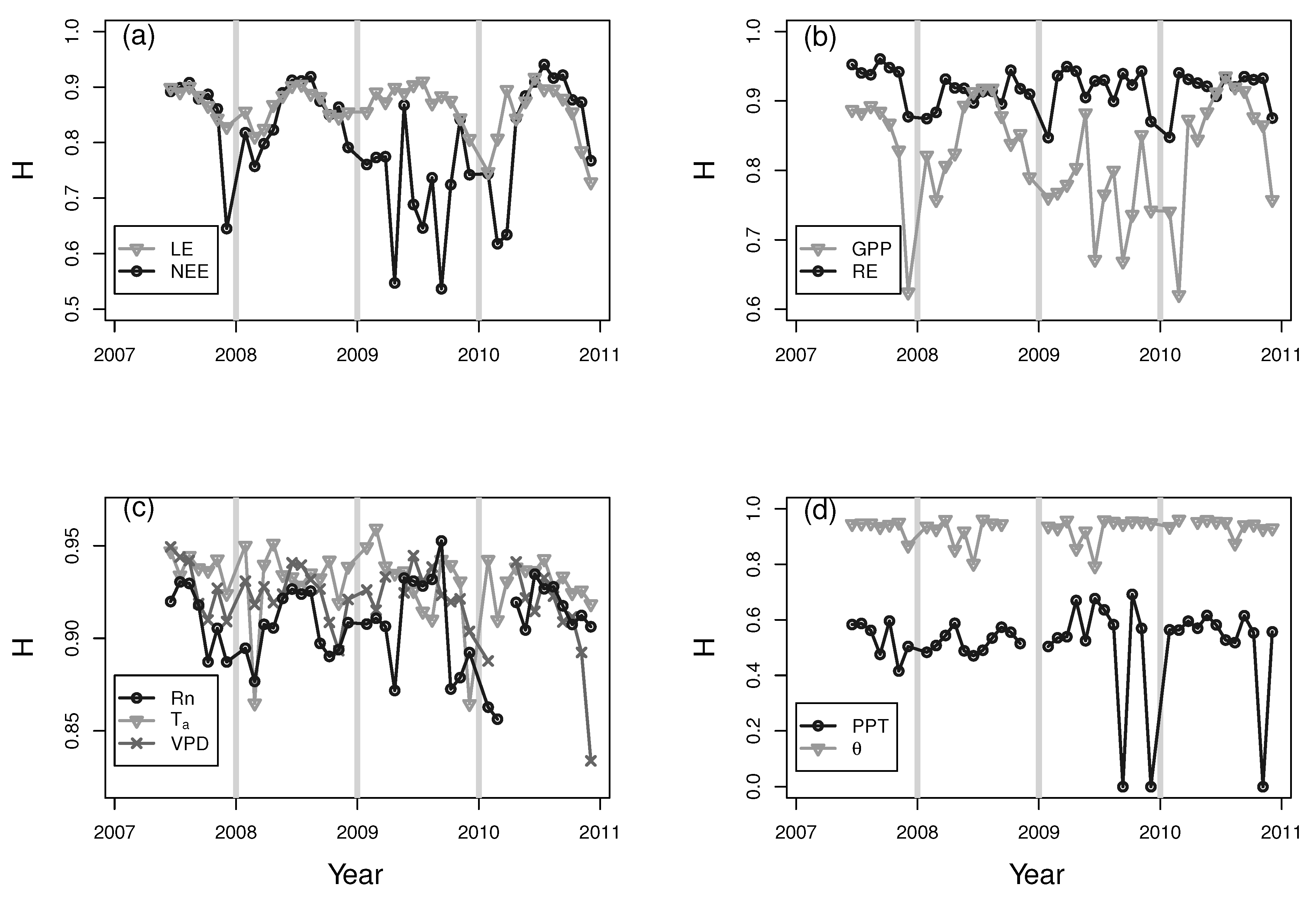
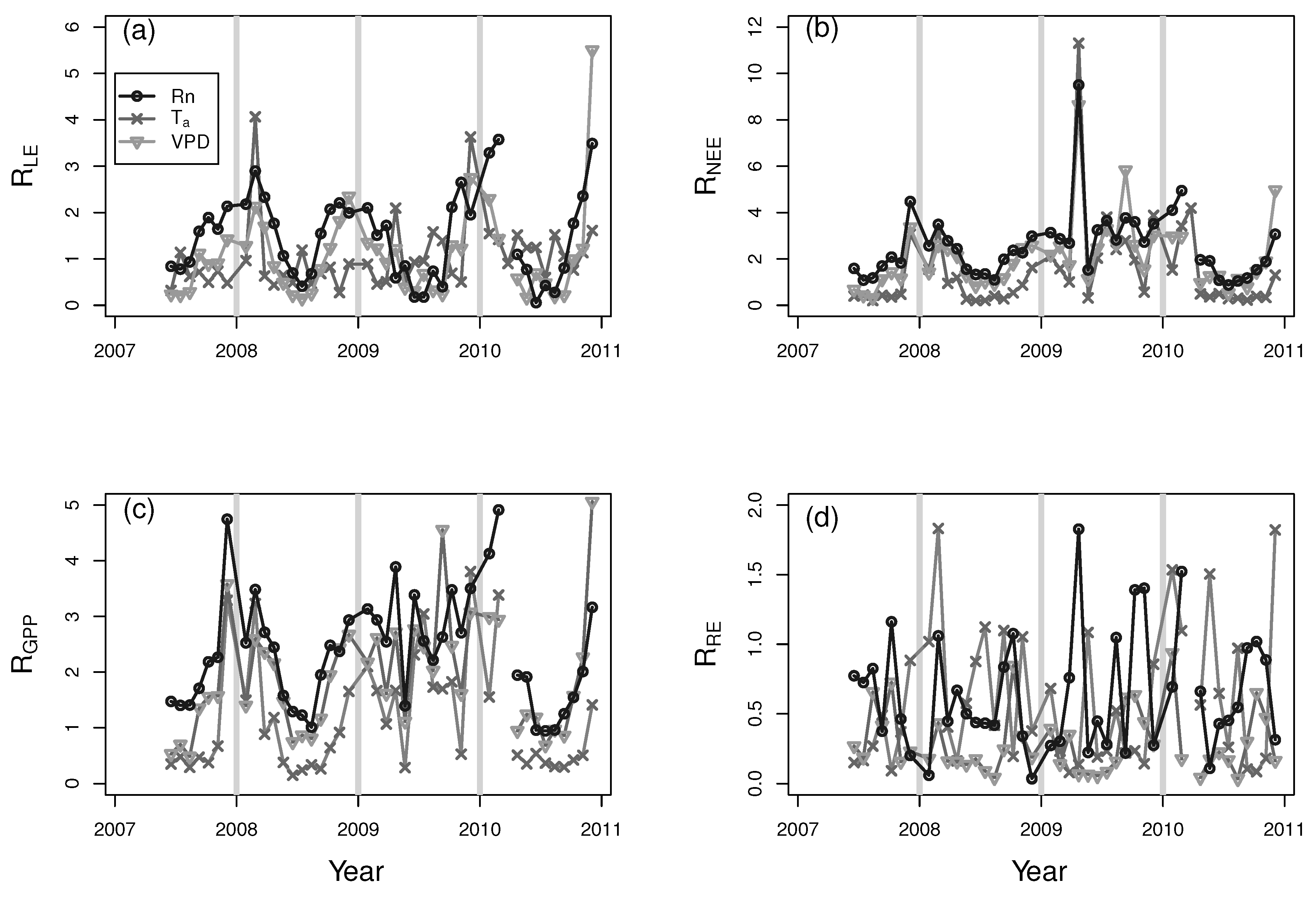

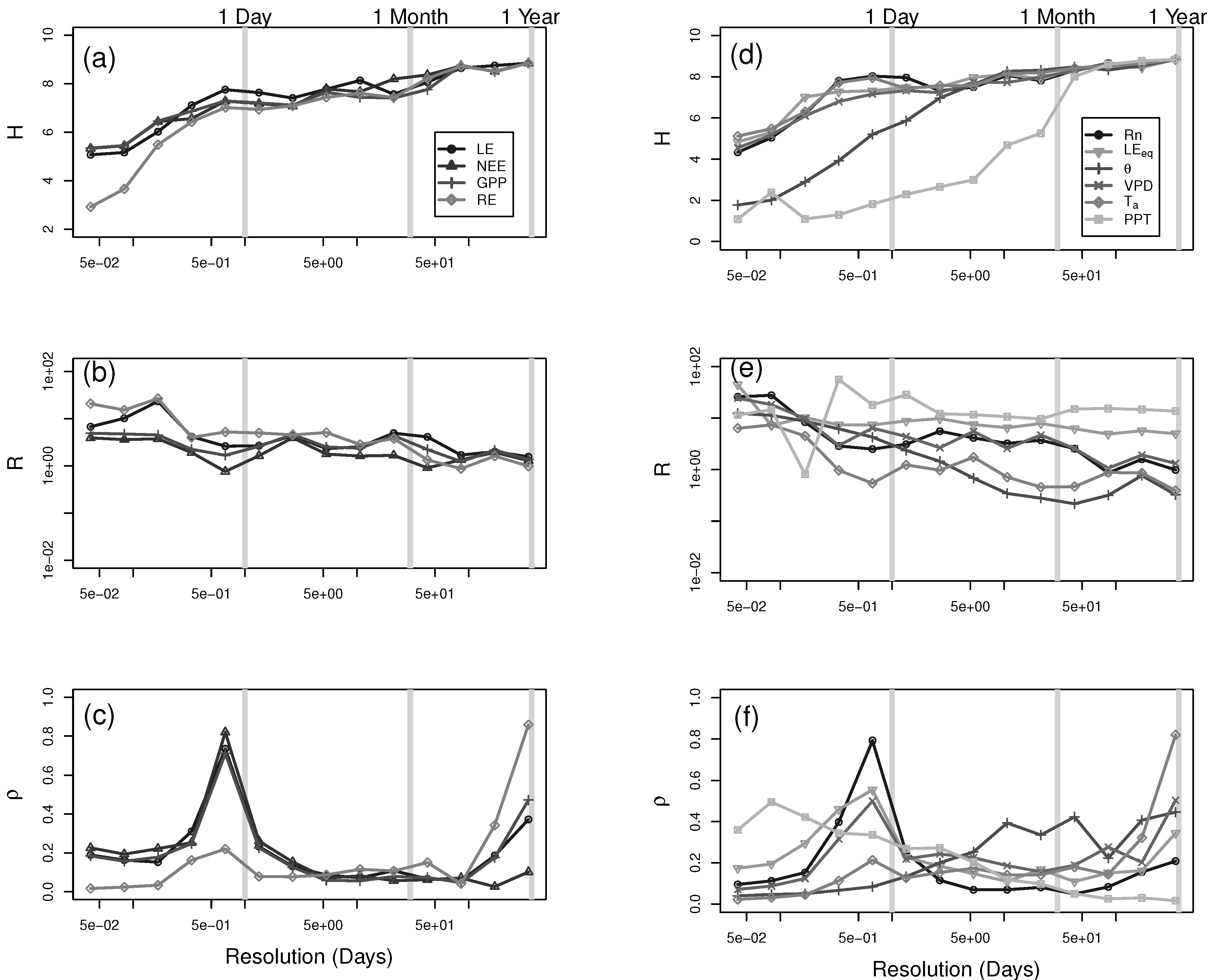
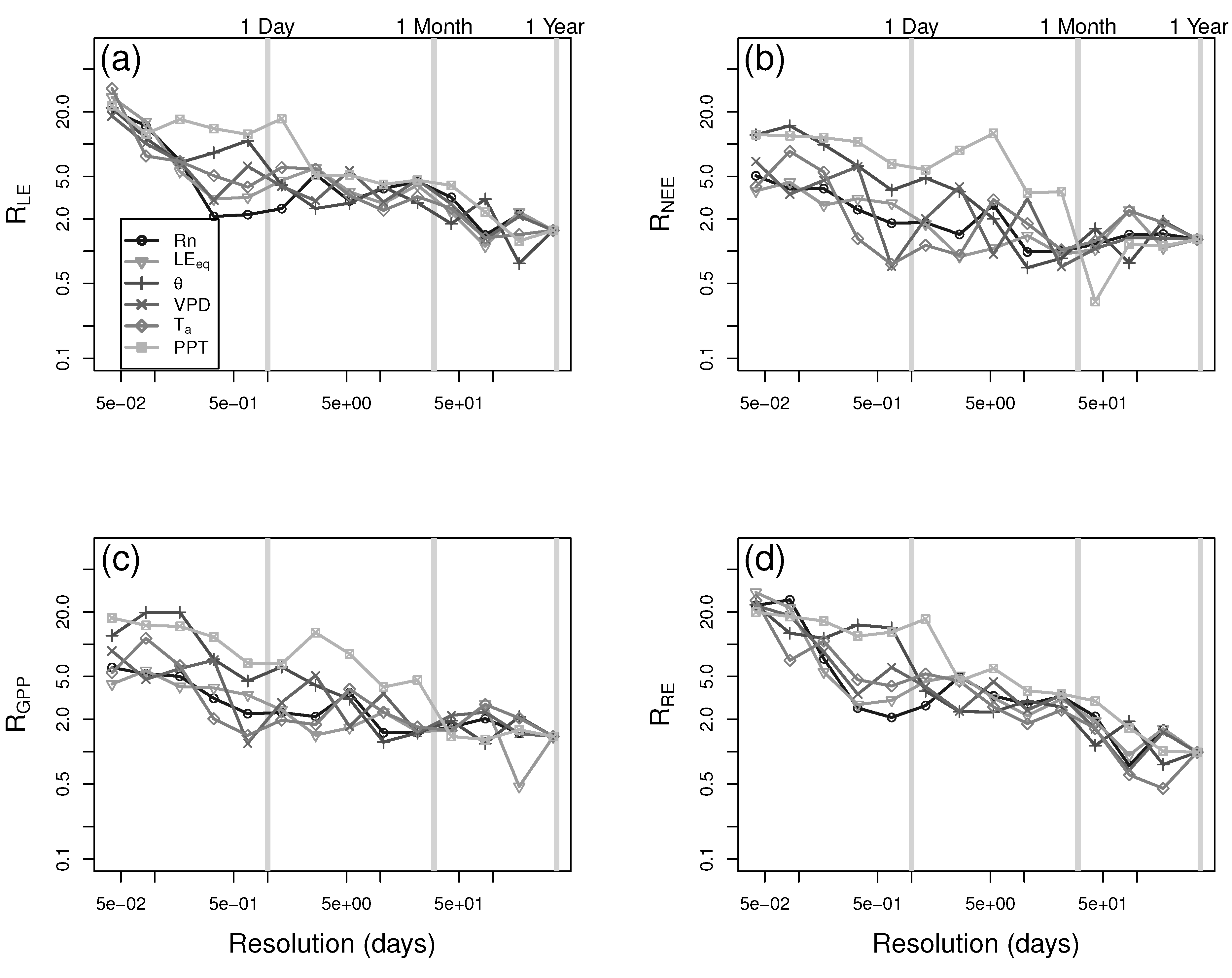
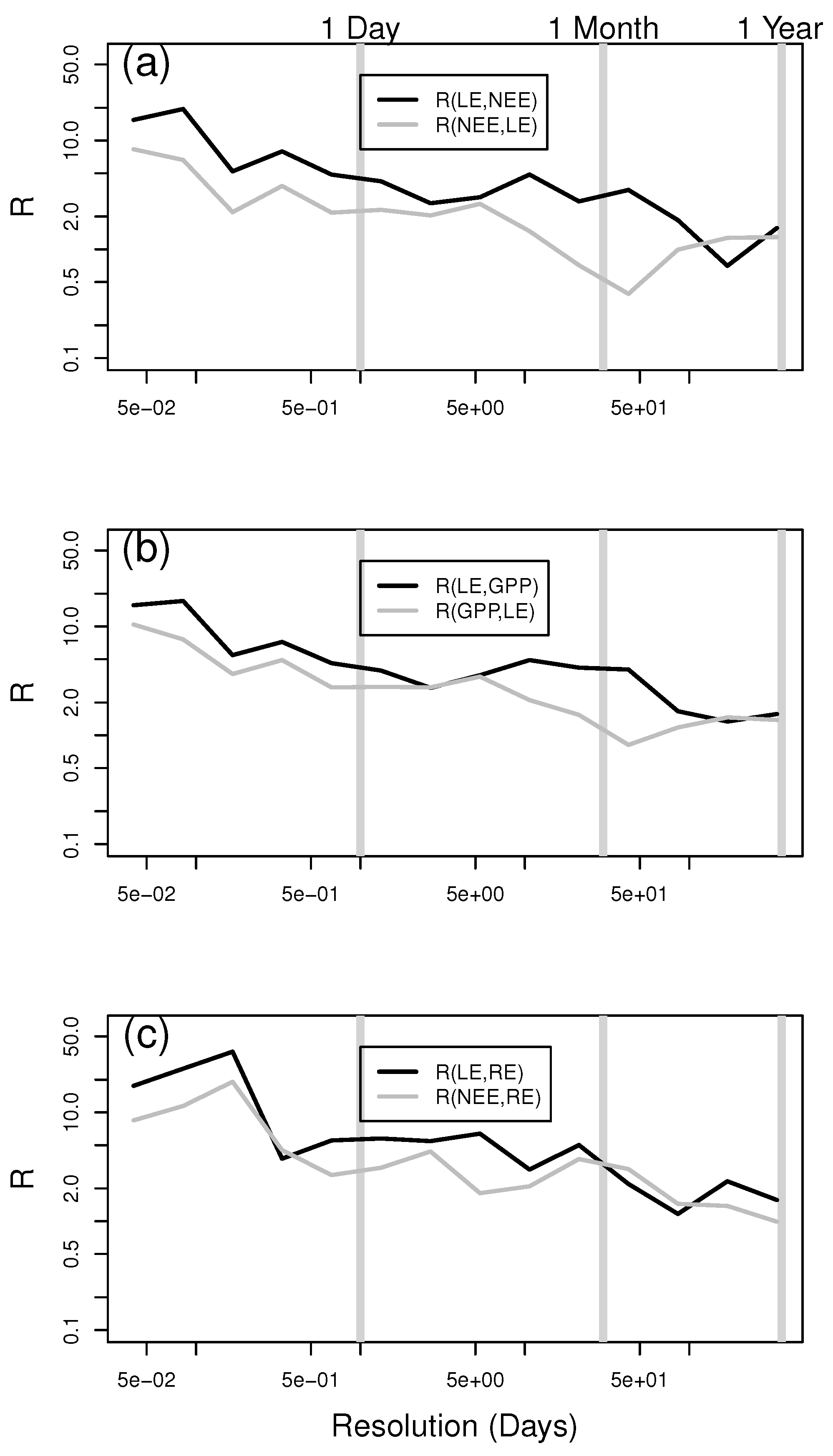
4. Conclusions
Acknowledgments
References
- Mahecha, M.D.; Reichstein, M.; Jung, M.; Seneviratne, S.I.; Zaehle, S.; Beer, C.; Braakhekke, M.C.; Carvalhais, N.; Lange, H.; Le Maire, G.; Moors, E. Comparing observations and process-based simulations of biosphere-atmosphere exchanges on multiple time-scales. J. Geophys. Res. 2010. [Google Scholar] [CrossRef]
- Katul, G.; Lai, C.T.; Schafer, K.; Vidakovic, B.; Albertson, J.; Ellsworth, D.; Oren, R. Multiscale analysis of vegetation surface fluxes: From seconds to years. Adv. Water Resour. 2001, 24, 1119–1132. [Google Scholar] [CrossRef]
- Stoy, P.; Katul, G.; Siqueira, M.; Juang, J.; McCarthy, H.; Kim, H.; Oishi, A.; Oren, R. Variability in net ecosystem exchange from hourly to inter-annual time scales at adjacent pine and hardwood forests: A wavelet analysis. In Tree Physiology; Duke Univ, Nicholas Sch Environm & Earth Sci: Durham, NC 27708 USA, 2005; pp. 887–902. [Google Scholar]
- Vargas, R.; Detto, M.; Baldocchi, D.; Allen, M. Multiscale analysis of temporal variability of soil CO2 production as influenced by weather and vegetation. Glob. Chang. Biol. 2010, 16, 1589–1605. [Google Scholar] [CrossRef]
- Hong, J.; Kim, J. Impact of the Asian monsoon climate on ecosystem carbon and water exchanges: A wavelet analysis and its ecosystem modeling implications. Glob. Chang. Biol. 2010, 17, 1900–1916. [Google Scholar] [CrossRef]
- Stoy, P.C.; Richardson, A.D.; Baldocchi, D.D.; Katul, G.G.; Stanovick, J.; Mahecha, M.D.; Reichstein, M.; Detto, M.P.; Law, B.E.; Wohlfahrt, G.; et al. Biosphere-atmosphere exchange of CO2 in relation to climate: A cross-biome analysis across multiple time scales. Biogeosciences 2009, 6, 2297–2312. [Google Scholar] [CrossRef]
- Mahecha, M.D.; Reichstein, M.; Lange, H.; Carvalhais, N.; Bernhofer, C.; Grünwald, T.; Papale, D.; Seufert, G. Characterizing ecosystem-atmosphere interactions from short to interannual time scales. Biogeosciences 2007, 4, 743–758. [Google Scholar] [CrossRef]
- Richardson, A.; Hollinger, D.; Aber, J.; Ollinger, S.; Braswell, B. Environmental variation is directly responsible for short- but not long-term variation in forest-atmosphere carbon exchange. Glob. Chang. Biol. 2007, 13, 788–803. [Google Scholar] [CrossRef]
- Cowan, I. Fit, fitter, fittest: Where does optimisation fit in? Silva Fenn. 2002, 36, 745–754. [Google Scholar] [CrossRef]
- Hopkins, A.; Del Prado, A. Implications of climate change for grassland in Europe: Impacts, adaptations and mitigation options: A review. Grass Forage Sci. 2007, 62, 118–126. [Google Scholar] [CrossRef]
- Soussana, J.F.; Luscher, A. Temperate grasslands and global atmospheric change: A review. Grass Forage Sci. 2007, 62, 127–134. [Google Scholar] [CrossRef]
- Scurlock, J.; Hall, D. The global carbon sink: A grassland perspective. Glob. Chang. Biol. 1998, 4, 229–233. [Google Scholar] [CrossRef]
- Cleland, E.E.; Chiariello, N.R.; Loarie, S.R.; Mooney, H.A.; Field, C.B. Diverse responses of phenology to global changes in a grassland ecosystem. Proc. Natl. Acad. Sci. USA 2006, 103, 13740–13744. [Google Scholar] [CrossRef] [PubMed]
- Li, S.G.; Eugster, W.; Asanuma, J.; Kotani, A.; Davaa, G.; Oyunbaatar, D.; Sugita, M. Response of gross ecosystem productivity, light use efficiency, and water use efficiency of Mongolian steppe to seasonal variations in soil moisture. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Chou, W.; Silver, W.; Jackson, R.; Thompson, A.; Allen-Diaz, B. The sensitivity of annual grassland carbon cycling to the quantity and timing of rainfall. Glob. Chang. Biol. 2008, 14, 1382–1394. [Google Scholar] [CrossRef]
- Fay, P.A.; Kaufman, D.; Nippert, J.B.; Carlisle, J.D.; Harper, C.W. Changes in grassland ecosystem function due to extreme rainfall events: Implications for responses to climate change. Glob. Chang. Biol. 2008, 14, 1600–1608. [Google Scholar] [CrossRef]
- Petrie, M.D.; Brunsell, N.A. The role of precipitation variability on the ecohydrology of grasslands. Ecohydrology 2012, 5, 337–345. [Google Scholar] [CrossRef]
- Chen, X.; Rubin, Y.; Ma, S.; Baldocchi, D. Observations and stochastic modeling of soil moisture control on evapotranspiration in a Californian oak savanna. Water Resour. Res. 2008, 44, W08409. [Google Scholar] [CrossRef]
- Polley, H.W.; Emmerich, W.; Bradford, J.A.; Sims, P.L.; Johnson, D.A.; Saliendra, N.Z.; Svejcar, T.; Angell, R.; Frank, A.B.; Phillips, R.L.; et al. Precipitation regulates the response of net ecosystem CO2 exchange to environmental variation on united states rangelands. Rangel. Ecol. Manag. 2010, 63, 176–186. [Google Scholar] [CrossRef]
- Petrie, M.D.; Brunsell, N.A.; Nippert, J.B. Climate change alters growing season flux dynamics in mesic grasslands. Theor. Appl. Climatol. 2012, 107, 427–440. [Google Scholar] [CrossRef]
- Hu, Z.; Yu, G.; Fu, Y.; Sun, X.; Li, Y.; Shi, P.; Wang, Y.; Zheng, Z. Effects of vegetation control on ecosystem water use efficiency within and among four grassland ecosystems in china. Glob. Chang. Biol. 2008, 14, 1609–1619. [Google Scholar] [CrossRef]
- Makela, A.; Berninger, F.; Hari, P. Optimal control of gas exchange during drought: Theoretical analysis. Ann. Bot. 1996, 77, 461–467. [Google Scholar] [CrossRef]
- Hari, P.; Makela, A.; Pohja, T. Surprising implications of the optimality hypothesis of stomatal regulation gain support in a field test. Aus. J. Plant Phys. 2000, 27, 77–80. [Google Scholar]
- Reichstein, M.; Tenhunen, J.D.; Roupsard, O.; Ourcival, J.M.; Rambal, S.; Miglietta, F.; Peressotti, A.; Pecchiari, M.; Tirone, G.; Valentini, R. Severe drought effects on ecosystem CO2 and H2O fluxes at three Mediterranean evergreen sites: Revision of current hypotheses? Glob. Chang. Biol. 2002, 8, 999–1017. [Google Scholar] [CrossRef]
- Van der Tol, C.; Meesters, A.G.C.A.; Dolman, A.J.; Waterloo, M.J. Optimum vegetation characteristics, assimilation, and transpiration during a dry season: 1. Model description. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Cava, D.; Contini, D.; Donateo, A.; Martano, P. Analysis of short-term closure of the surface energy balance above short vegetation. Agric. For. Meteorol. 2008, 148, 82–93. [Google Scholar] [CrossRef]
- Wever, L.; Flanagan, L.; Carlson, P. Seasonal and interannual variation in evapotranspiration, energy balance and surface conductance in a northern temperate grassland. Agric. For. Meteorol. 2002, 112, 31–49. [Google Scholar] [CrossRef]
- Aires, L.; Pio, C.P.; Pereira, J.P. The effect of drought on energy and water vapour exchange above a mediterranean C3/C4 grassland in Southern Portugal. Agric. For. Meteorol. 2008, 148, 565–579. [Google Scholar] [CrossRef]
- Aires, L.P.; Pio, C.P.; Pereira, J.S.P. Carbon dioxide exchange above a Mediterranean C3/C4 grassland during two climatologically contrasting years. Glob. Chang. Biol. 2008, 14, 539–555. [Google Scholar] [CrossRef]
- Polley, H.; Dugas, W.; Mielnick, P.; Johnson, H. C3–C4 composition and prior carbon dioxide treatment regulate the response of grassland carbon and water fluxes to carbon dioxide. Funct. Ecol. 2007, 21, 11–18. [Google Scholar] [CrossRef]
- Brunsell, N.A. Characterization of land-surface precipitation feedback regimes with remote sensing. Remote Sens. Environ. 2006, 100, 200–211. [Google Scholar] [CrossRef]
- Jones, A.R.; Brunsell, N.A. Energy balance partitioning and net radiation controls on soil moisture–Precipitation feedbacks. Earth Interact. 2009, 13, 1–25. [Google Scholar] [CrossRef]
- Brunsell, N.A.; Schymanski, S.J.; Kleidon, A. Quantifying the thermodynamic entropy budget of the land surface: Is this useful? Earth Syst. Dyn. 2011, 2, 87–103. [Google Scholar] [CrossRef]
- Paw, U.K.; Baldocchi, D.; Meyers, T.; Wilson, K.B. Correction of eddy-covariance measurements incorporating both advective effects and density fluxes. Bound.-Layer Meteorol. 2000, 97, 487–511. [Google Scholar] [CrossRef]
- Webb, E.; Pearman, G.; Leuning, R. Correction of flux for density effects due to heat and water vapour transfer. Q. J. R. Meteorol. Soc. 1980, 106, 85–100. [Google Scholar] [CrossRef]
- Foken, T.; Wichura, B. Tools for quality assessment of surface-based flux measurements. Agric. For. Meteorol. 1996, 78, 83–105. [Google Scholar] [CrossRef]
- Lloyd, J.; Taylor, J. On the temperature dependence of soil respiration. Funct. Ecol. 1994, 8, 315–323. [Google Scholar] [CrossRef]
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A.; et al. On the separation of net ecosystem exchange into assimilation and ecosystem respiration: Review and improved algorithm. Glob. Chang. Biol. 2005, 11, 1424–1439. [Google Scholar] [CrossRef]
- Kumar, P.; Foufoula-Georgiou, E. Wavelet analysis for Geophysical applications. Rev. Geophys. 1997, 35, 385–412. [Google Scholar] [CrossRef]
- Kleeman, R. Measuring dynamical prediction utility using relative entropy. J. Atmos. Sci. 2002, 59, 2057–2072. [Google Scholar] [CrossRef]
- Katul, G.; Lai, C.; Albertson, J.; Vidakovic, B.; Schäfer, K.; Hsieh, C.; Oren, R. Quantifying the complexity in mapping energy inputs and hydrologic state variables into land-surface fluxes. Geophys. Res. Lett. 2001, 28, 3305–3307. [Google Scholar] [CrossRef]
- Ruddell, B.J.; Kumar, P. Ecohydrologic process networks: 1. Identification. Water Resour. Res. 2009, 45, 1–22. [Google Scholar] [CrossRef]
- Ruddell, B.L.; Kumar, P. Ecohydrologic process networks: 2. Analysis and characterization. Water Resour. Res. 2009, 45, 1–14. [Google Scholar] [CrossRef]
- Freedman, J.; Fitzjarrald, D.; Moore, K.; Sakai, R. Boundary layer clouds and vegetation-atmosphere feedbacks. J. Clim. 2001, 14, 180–197. [Google Scholar] [CrossRef]
- De Ridder, K. Land surface processes and the potential for convective precipitation. J. Geophys. Res. 1997, 102, 30085–30090. [Google Scholar] [CrossRef]
- Juang, J.-Y.; Katul, G.G.; Porporato, A.; Stoy, P.C.; Siqueira, M.S.; Detto, M.; Kim, H.-S.; Oren, R. Eco-hydrological controls on summertime convective rainfall triggers. Glob. Chang. Biol. 2007, 13, 887–896. [Google Scholar] [CrossRef]
- Brunsell, N.A.; Jones, A.R.; Jackson, T.L.; Feddema, J.J. Seasonal trends in air temperature and precipitation in IPCC AR4 GCM output for Kansas, USA: Evaluation and implications. Int. J. Climatol. 2010, 30, 1178–1193. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Brunsell, N.A.; Wilson, C.J. Multiscale Interactions betweenWater and Carbon Fluxes and Environmental Variables in A Central U.S. Grassland. Entropy 2013, 15, 1324-1341. https://doi.org/10.3390/e15041324
Brunsell NA, Wilson CJ. Multiscale Interactions betweenWater and Carbon Fluxes and Environmental Variables in A Central U.S. Grassland. Entropy. 2013; 15(4):1324-1341. https://doi.org/10.3390/e15041324
Chicago/Turabian StyleBrunsell, Nathaniel A., and Cassandra J. Wilson. 2013. "Multiscale Interactions betweenWater and Carbon Fluxes and Environmental Variables in A Central U.S. Grassland" Entropy 15, no. 4: 1324-1341. https://doi.org/10.3390/e15041324
APA StyleBrunsell, N. A., & Wilson, C. J. (2013). Multiscale Interactions betweenWater and Carbon Fluxes and Environmental Variables in A Central U.S. Grassland. Entropy, 15(4), 1324-1341. https://doi.org/10.3390/e15041324



