1. Introduction
Receiver operating characteristic (ROC) curve analysis provides a basis for describing the performance of a diagnostic indicator when deployed in a binary diagnostic test. ROC curve analysis has found application in clinical medicine, veterinary medicine and crop protection (
e.g., [
1,
2,
3]). For a comprehensive overview of the methodology, see [
4,
5].
For the purpose of the present work, an outline description of the process by which an ROC curve may be derived allows us to introduce our terminology and notation. We refer generically to data provided by the diagnostic indicator as “risk scores”. During the process of characterizing a diagnostic indicator, a risk score is recorded for each of a number of experimental subjects. Each subject is also classified definitively as either a “case” (
e.g., subject is diseased) or a “control” (
e.g., subject is healthy) by a gold standard assessment (independent of the putative indicator). The ultimate goal of the experimental procedure as described is to provide a basis for decision-making in practice that does not require reference to the gold standard. When the decision in question is binary, an ROC curve is a useful summary of the performance of the diagnostic indicator [
6].
We now have a number of subjects, and two values for each: a risk score provided by means of the diagnostic indicator and the true status (case or control) provided by the gold standard. We can present the results graphically as frequency distributions of risk scores plotted separately for cases and controls. It is normal practice to calibrate the output of the diagnostic indicator so that higher risk scores tend to be associated with case status, and lower risk scores tend to be associated with control status. Typically, then, the mean of the distribution of risk scores for cases is larger than the mean of the distribution of risk scores for controls.
An ROC curve is, in essence, a summary of the (normalized) frequency distributions of risk scores for cases and controls. In this article, we are concerned with the properties of ROC curves based on continuous parametric models for the distributions of risk scores (
e.g., [
5,
7]). In practice, then, model parameters must be estimated from the experimental data; we do not describe this part of the analysis. For a continuous indicator variable
X we refer to the resulting probability density functions (pdfs) as
f1(
x) (for cases) and
f2(
x) (for controls). The corresponding cumulative distribution functions (cdfs) are
F1(
x) and
F2(
x), respectively.
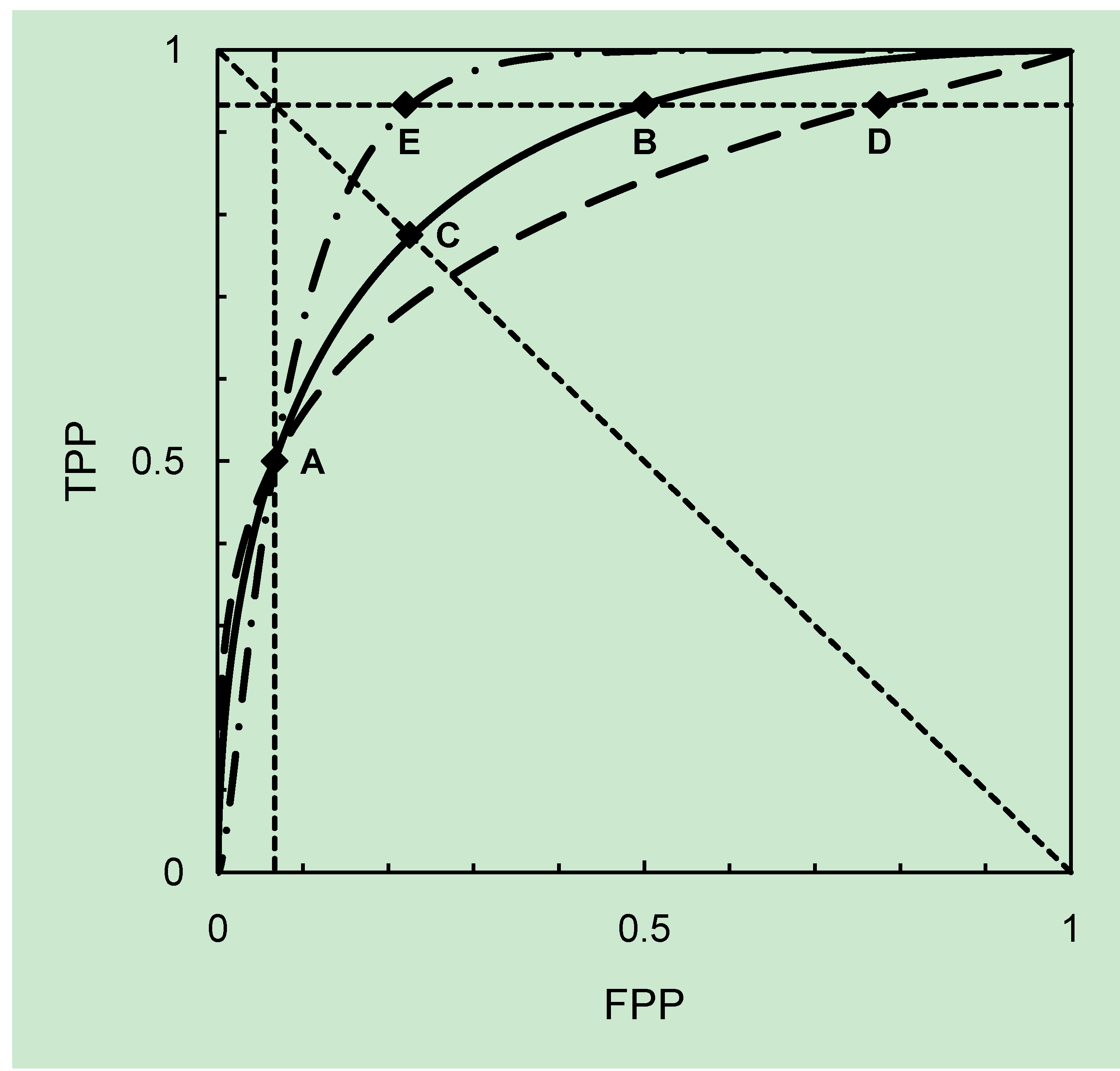
Now, consider the graphical plot of the pdfs of risk scores plotted separately for cases and controls. A diagnostic indicator and a threshold risk score together constitute a diagnostic test. In the process of developing a diagnostic test, our task is to characterize a threshold on the risk score scale such that subjects with risk scores above the threshold will be treated, and subjects with risk scores at or below the threshold will not be treated. The problem is that, typically, the distributions of risk scores for cases and controls overlap, so that there is no unequivocal “best” threshold risk score. Consider a particular choice of threshold risk score, and recall that we are working with the pdfs of risk scores for cases and controls. The proportion of cases correctly classified is the true positive proportion (TPP) and the proportion of controls correctly classified is the true negative proportion (TNP). The false negative proportion is FNP = 1 − TPP and the false positive proportion is FPP = 1 − TNP. The values of these proportions change with the choice of threshold risk score.
An ROC curve is a graphical plot of
TPP [=1 −
F1(
x)] against
FPP [=1 −
F2(
x)], with pairs of
TPP and
FPP values obtained by allowing a single threshold risk score to vary over the range of the indicator variable. Thus, points along the curve represent potential thresholds on the scale of the indicator variable, from each of which a binary test may be characterized. An ROC curve can therefore provide a useful summary of the characteristics of an indicator variable used as the basis for a binary test. Depending on the choice of model for risk scores for cases and controls, it may be possible to write down an analytical equation for the ROC curve, but this is immaterial in the present context. ROC curves that are monotone increasing above the main diagonal of the plot over the whole domain are sometimes referred to as “proper” ROC curves (see,
e.g., Section 4.6 in [
1]). Some continuous parametric ROC curves are proper, some are not; for example, it is well-known that the bi-Normal ROC curve is not in general proper, while the bi-gamma ROC curve is proper [
8].
While on the one hand the ROC curve represents a summary of the distributions of risk scores for cases and controls, on the other there are methods by which a summary of the ROC curve itself is sought [
7,
9]. By far the most common single-figure ROC curve summary measure in use is the area under the curve (AUC) as an index of diagnostic accuracy (
e.g., [
10]). Briefly, the idea is that diagnostic indicators with ROC curves which pass close to the top left-hand corner of the graphical plot of
TPP against
FPP (high AUC) provide tests for which
TPP and
TNP are both high, offering good discrimination between cases and controls. Diagnostic indicators with ROC curves close to the main diagonal of the plot of
TPP against
FPP (low AUC) have little to offer in terms of discrimination between cases and controls. However, in the present context, the AUC is unsuitable for use in the description of the symmetry properties of ROC curves. It is not difficult to see that ROC curves with the same AUC may have different symmetry properties (
e.g., Figure 2A in [
11]; Figure 2 in [
12]).
This article describes the symmetry properties of some parametric ROC curves based on continuous distributions. The article is set out as follows. The generic symmetry properties of ROC curves are described graphically. The application of the Kullback-Leibler divergence is outlined within the context of the present work. Some useful properties of the Pareto distribution are illustrated. The symmetry properties of bi-Normal, bi-exponential and bi-gamma ROC curves are analyzed. A general discussion is provided.
3. The Bi-Normal ROC Curve
For a continuous indicator variable X we have for cases and for controls, in which denote the mean and variance, respectively, of f1(x); and denote the mean and variance, respectively, of f2(x). The indicator variable is calibrated so that μ1 > μ2.
First we consider the symmetric bi-Normal ROC curve. For such curves, the standard deviations of the case and control distributions are equal,
[
1]. Also, for symmetric ROC curves in general, the KLDs are equal
[
17], and for the symmetric bi-Normal ROC curve in particular,
[
23]. For a numerical example, consider Killeen and Taylor’s Figure 1 (top) in [
14]. In this example, the distribution of risk scores for cases
f1(
x) is Normal with mean
μ1 = 3.4 and standard deviation
σ1 = 1 and the distribution of risk scores for controls
f2(
x) is Normal with mean
μ2 = 2 and standard deviation
σ2 = 1. The resulting ROC curve is geometrically symmetric [
14] and
I(
f1,
f2) =
I(
f2,
f1) = 0.980 nits.
Asymmetric bi-Normal ROC curves are discussed by Green and Swets [
13], Pepe [
1] and Marzban [
24]. In the terminology of the present article, bi-Normal ROC curves are
TPP-asymmetric when
and
TNP-asymmetric when
. Writing in the context of applications of bi-Normal indicators in clinical epidemiology, Pepe [
1] notes that the distribution of risk scores for controls is typically less dispersed than the distribution of risk scores for cases, in which case a typical bi-Normal ROC curve would be
TPP-asymmetric (
e.g., Figure 4.1 in [
1], where
).
The KLDs are now (
e.g., [
15]):
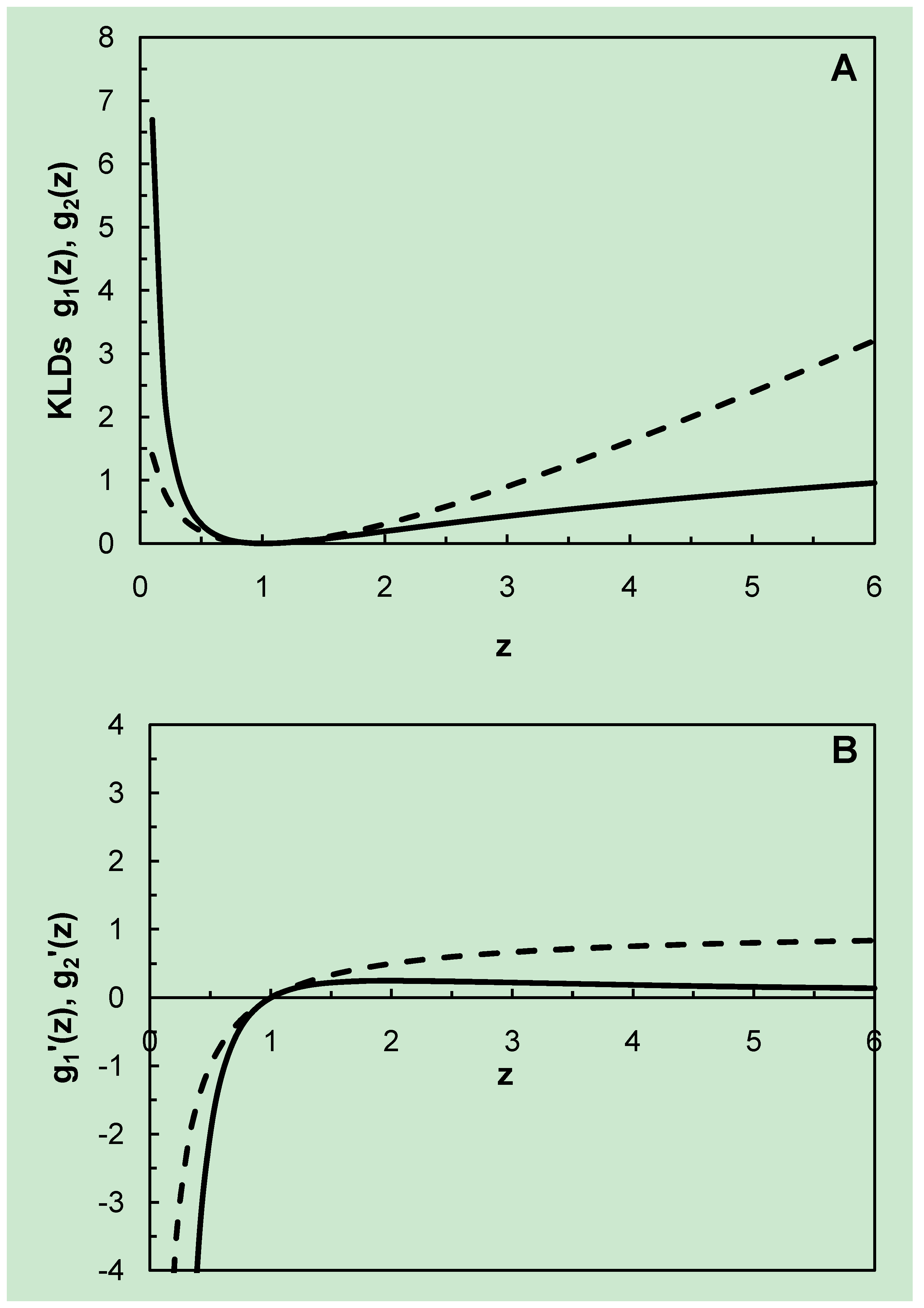
Let
, and we can write these as:
We compare this with the situation when
,
, and the ROC curve is symmetric. For
TPP-asymmetry, we have
; then
and (referring to
Figure 2A) we can see that
. For
TNP-asymmetry
; then
and (referring again to
Figure 2A)
. The inclusion of the factor ½ does not affect the inequality portrayed. Thus, for
TPP-asymmetry, we have
and for
TNP-asymmetry, we have
. This is illustrated in
Figure 3, using values of
μ1 and
μ2 from Killeen and Taylor (Figure 1 in [
14]). We note also from
Figure 3 that the point where the two curves intersect characterizes the symmetric ROC curve with
I(
f1,
f2) =
I(
f2,
f1) = 0.980 nits.
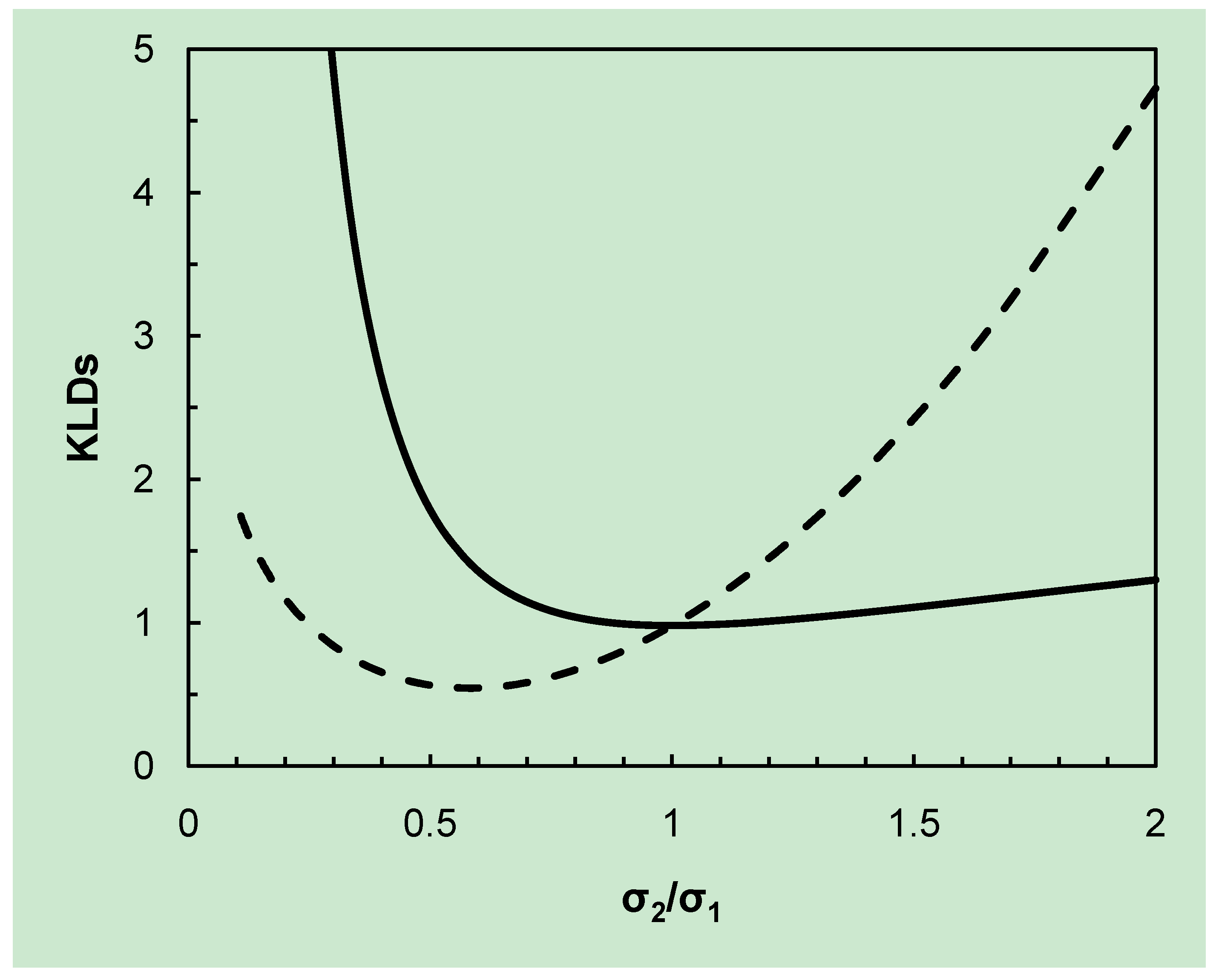
Figure 3.
Analysis of a bi-Normal ROC curve. The graph shows the Kullback-Leibler divergences I(f1,f2) (the solid line) and I(f2,f1) (the dashed line) for two Normal densities; f1(x) for cases has μ1 = 3.4 and σ1 is varied over a range that includes σ1 = 1, and f2(x) for controls has μ2 = 2.0 and σ2 = 1. When σ2/σ1 = 1, I(f1,f2) = I(f2,f1) and the corresponding ROC curve is symmetric about the negative diagonal. When σ2/σ1 < 1, I(f1,f2) > I(f2,f1) and the corresponding ROC curve is TPP-asymmetric; when σ2/σ1 > 1, I(f2,f1) > I(f1,f2) and the corresponding ROC curve is TNP-asymmetric.
Figure 3.
Analysis of a bi-Normal ROC curve. The graph shows the Kullback-Leibler divergences I(f1,f2) (the solid line) and I(f2,f1) (the dashed line) for two Normal densities; f1(x) for cases has μ1 = 3.4 and σ1 is varied over a range that includes σ1 = 1, and f2(x) for controls has μ2 = 2.0 and σ2 = 1. When σ2/σ1 = 1, I(f1,f2) = I(f2,f1) and the corresponding ROC curve is symmetric about the negative diagonal. When σ2/σ1 < 1, I(f1,f2) > I(f2,f1) and the corresponding ROC curve is TPP-asymmetric; when σ2/σ1 > 1, I(f2,f1) > I(f1,f2) and the corresponding ROC curve is TNP-asymmetric.
4. The Bi-Exponential ROC Curve
We deal with the bi-exponential ROC curve in passing, since it turns out to be a special case of the constant-shape bi-gamma ROC curve, below. Here, we have exponential densities for cases and controls (
e.g., [
25]), respectively:
. The indicator variable is calibrated so that the mean of the case distribution is larger than the mean of the control distribution, which requires
. A graphical plot of 1−
F1(
x) against 1−
F2(
x) then provides the ROC curve. Such ROC curves are
TPP-asymmetric (as described in
Figure 1) (see,
e.g., Figure 1 in [
25]).
Asadi
et al. (Table 13.1 in [
26]) provide a table of distributions related to the Pareto distribution by fixed transformation. Note that in the notation of Asadi
et al. [
26], our Pareto parameterization
. Then, following Asadi
et al. [
26], we obtain KLDs for two exponential distributions as follows:
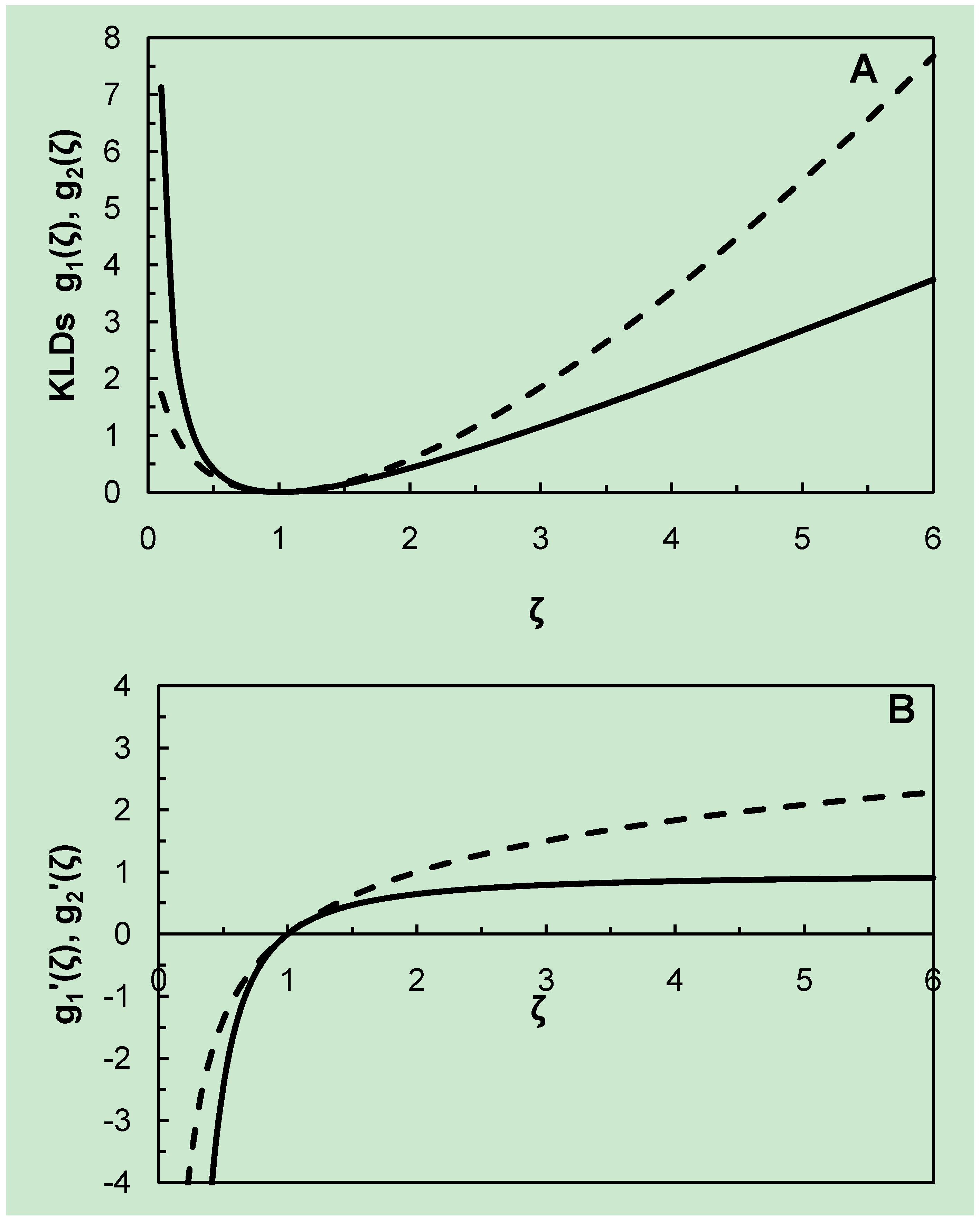
Let
and refer to
Figure 2A. For a useful ROC curve we require
, so we are only interested in the part of
Figure 2A where
z <1, and here we have
. For
, the case and control distributions are identical,
, and the corresponding ROC curve follows the main diagonal of the plot; such diagnostic indicators offer no discrimination between cases and controls.
6. Discussion
For continuous parametric ROC curves, we can define symmetry conditions. Notwithstanding, it is sometimes rather difficult to tell from a graphical plot whether an empirical ROC curve is actually symmetrical or only approximately so (
e.g., Figure 2 in [
24]). It is harder to define asymmetry conditions for continuous parametric ROC curves, although often relatively easy to tell from a graphical plot when an empirical ROC curve is asymmetric (
e.g., Figure 2 in [
10]). Marzban [
24] asks if asymmetry can be explained in terms of the underlying case and control distributions, and concludes that asymmetry in an ROC curve “can be attributed to unequal widths of the underlying distributions”. What is lacking is an independent assessment of asymmetry for comparison with the statistical assessment based on the relative dispersion of the case and control distributions. Here, we bring together a graphical definition of asymmetry (
Figure 1) with an analysis of the KLDs for the case and control distributions for some examples of continuous parametric ROC curves.
The main findings are as follows. Bi-Normal ROC curves may be symmetric,
TPP-asymmetric or
TNP-asymmetric. For symmetric bi-Normal curves, we have
; for
TPP-asymmetric curves,
; and for
TNP-asymmetric curves,
. Of particular interest is the point of intersection of the two curves in
Figure 3. The fact that at this point we have
indicates the existence of symmetric curves that lie above the main diagonal of the bi-Normal ROC plot. This in itself is not surprising, of course, but it is noted here for reference below.
Bi-exponential ROC curves may only be
TPP-asymmetric. For these
TPP-asymmetric curves,
. In this case the KLDs are equal only when
(referring to
Figure 2), indicating that (unlike the bi-Normal case) there is no symmetric curve that lies above the main diagonal of the bi-exponential ROC plot.
Bi-gamma ROC curves may be
TPP-asymmetric or
TNP-asymmetric. A constant-shape bi-gamma ROC curve is always
TPP-asymmetric and
. For the constant-scale bi-gamma ROC curve we considered the case of
λ = 1. This is always
TNP-asymmetric and
. In both cases (
i.
e., constant-shape and constant-scale) the KLDs are equal only when
(referring to
Figure 2A and
Figure 4A), indicating that (unlike the bi-Normal case) there is no symmetric curve that lies above the main diagonal of the bi-gamma ROC plot.
The choice of operational threshold on an ROC curve amounts to specification of the error rates (
FPP and
FNP=1 −
TPP) of the resulting diagnostic test. Recalling
Figure 1 (for example), we can see that the symmetry properties of an ROC curve influence the trade-off between these error rates that is of interest in the process of choosing a threshold. ROC curve symmetry and both kinds of asymmetry are observed empirically in the study of disease diagnostics. This is beyond the scope of summaries based on area under curve calculations. As noted by Marzban [
24], the ROC curve is a two-dimensional representation of a diagnostic indicator, so a single-figure summary measure cannot characterize all its properties. Further difficulties with the area under the ROC curve as a summary measure of performance of a diagnostic indicator are discussed in [
34]. Our work so far, relating to continuous parametric ROC curves, indicates the following. First, although the KLD is usually not a symmetric quantity [
35], it is noteworthy that for an ROC curve based on
f1(
x) (for cases) and
f2(
x) (for controls) that is symmetric about the negative diagonal,
I(
f1,
f2) =
I(
f2,
f1) [
17]. Second, although the lack of symmetry of the KLD has been referred to as a nuisance in applications [
36], in this particular study we find that the asymmetry of the KLD usefully characterizes the asymmetry of bi-Normal and bi-gamma ROC curves.