Utilizing the Exergy Concept to Address Environmental Challenges of Electric Systems
Abstract
:1. Introduction
2. Dual View of Electromagnet System
2.1. Energy and Exergy Balances
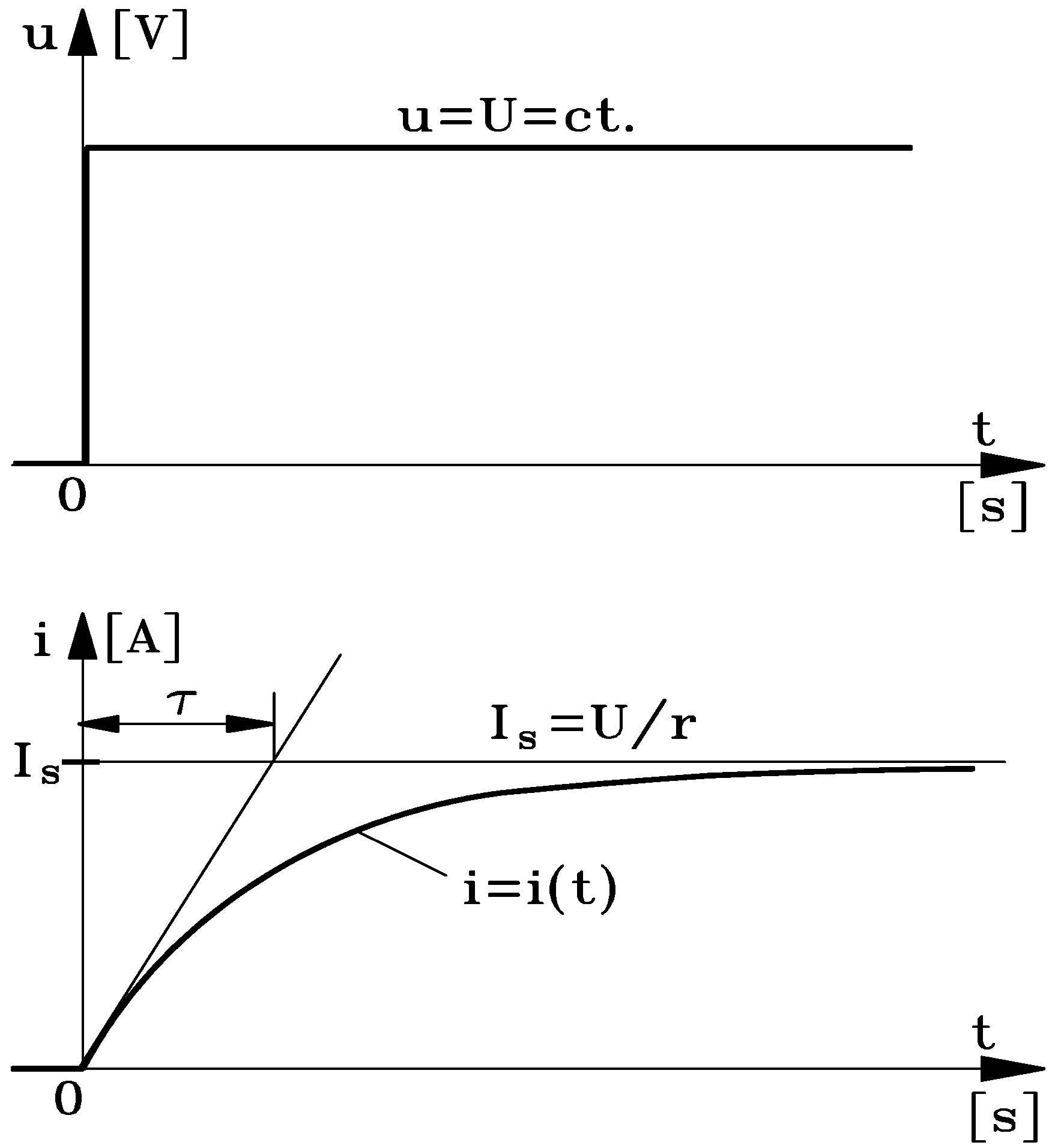
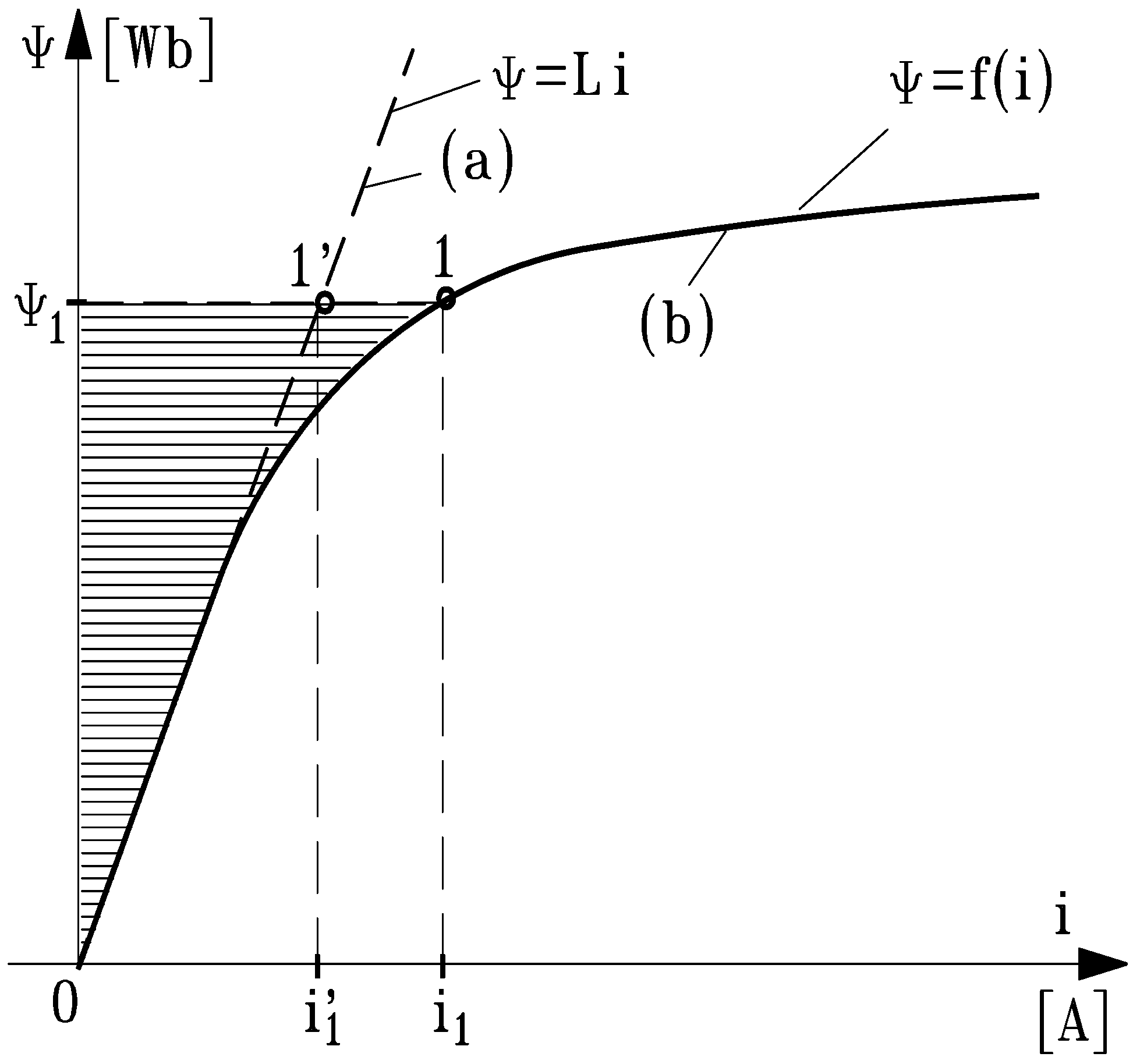

2.2. Useful Mechanical Work of Armature in Movement
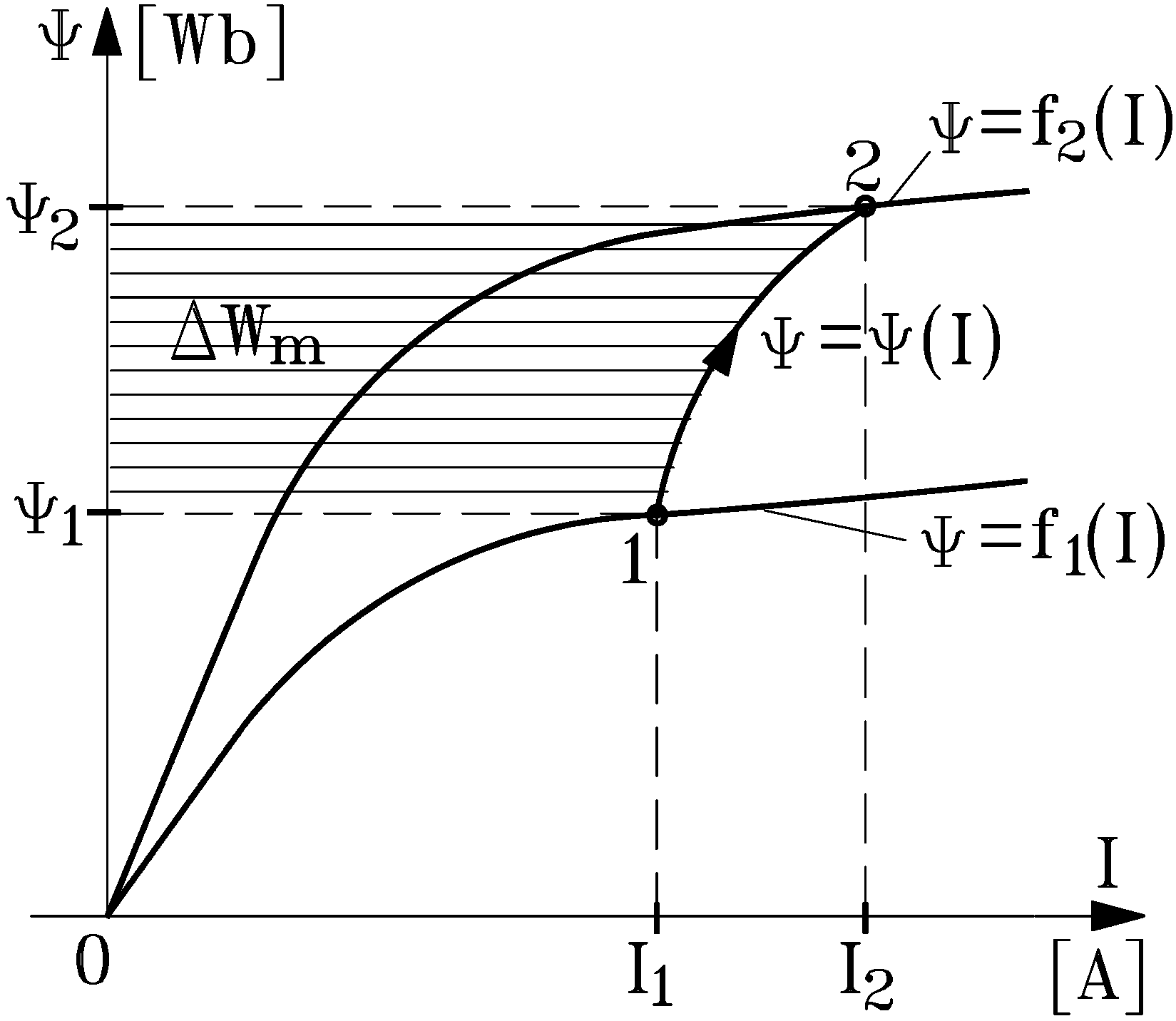
- at a constant current I = I1 = const., when the evolution is described by the straight line or
- at a constant flux Ψ = Ψ1 = const., when the evolution follows the straight line .
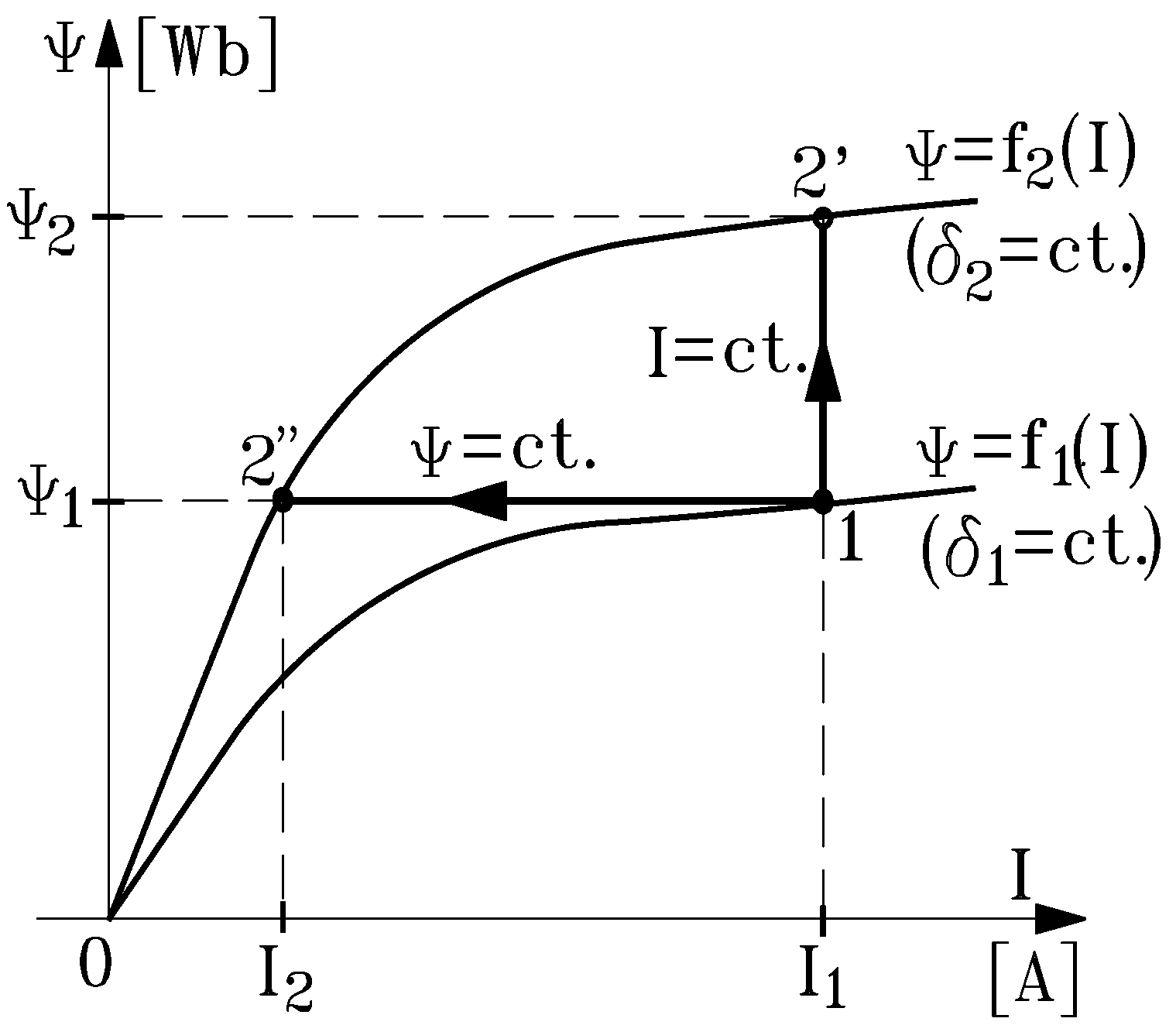
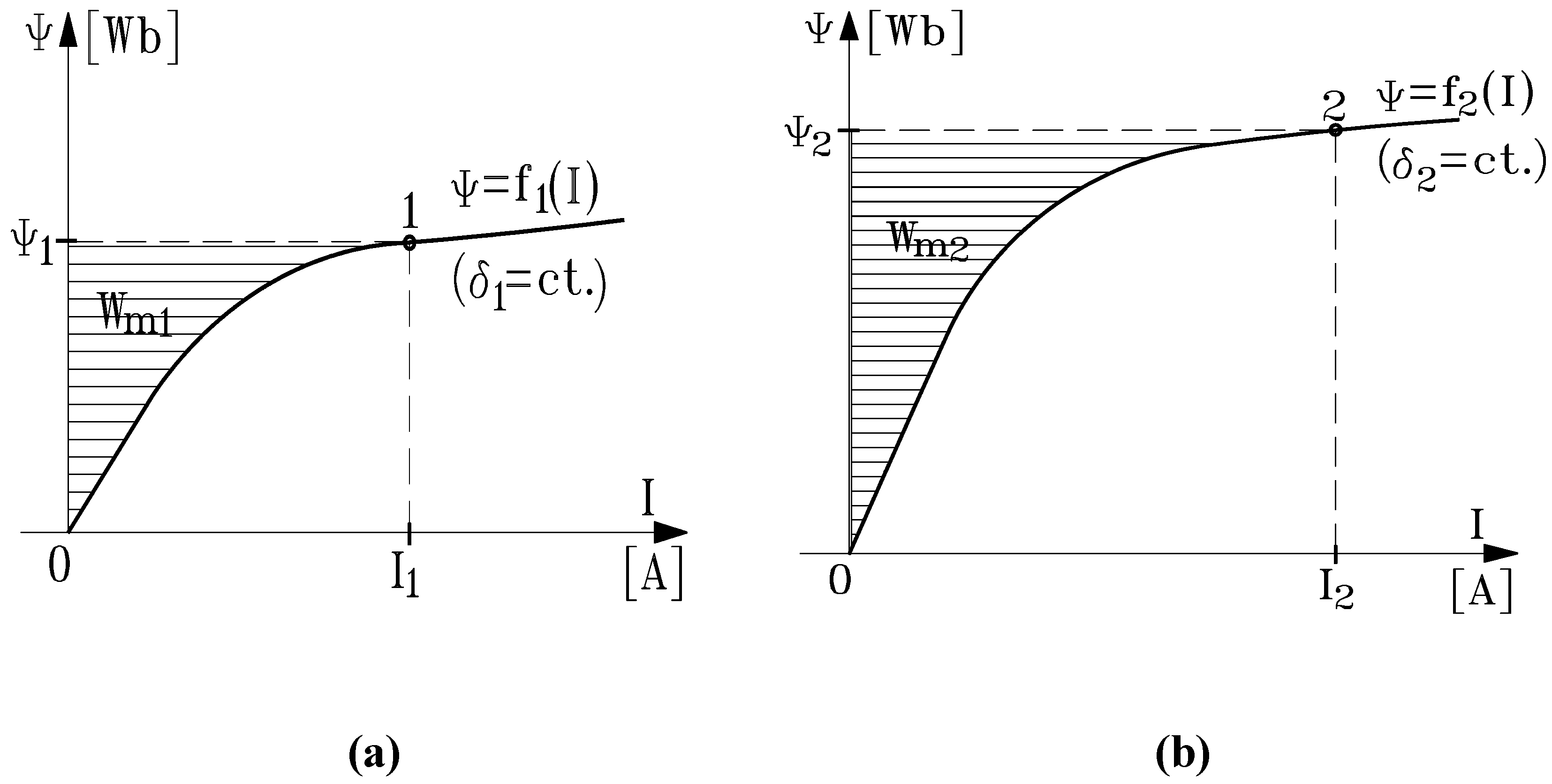
- a)
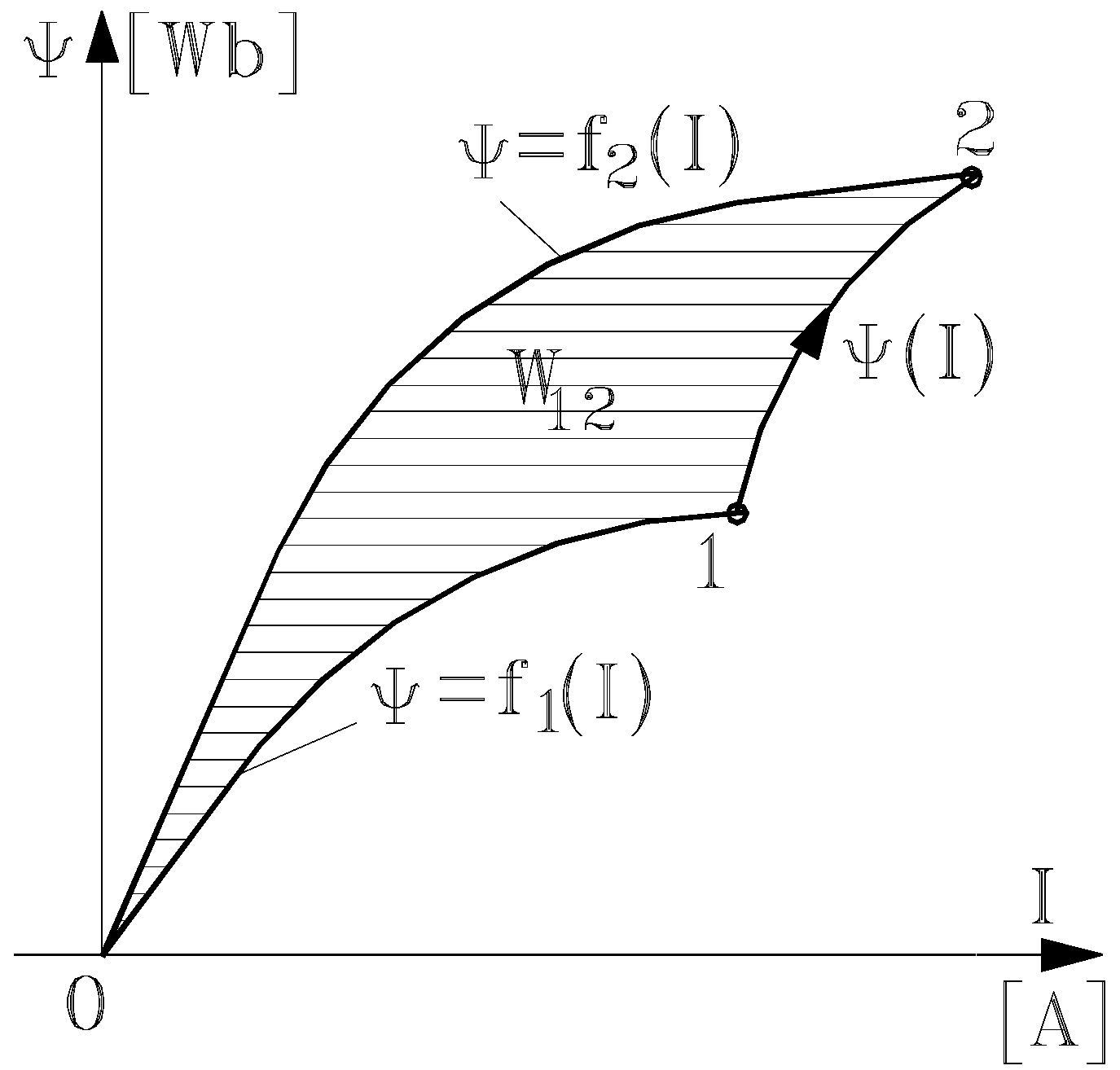
- W12 = W12' at I = const. (when the evolution is along the straight line ), where
- b)
- W12 = W12" at Ψ = const. (when the evolution is along the straight line ), where
- (1)
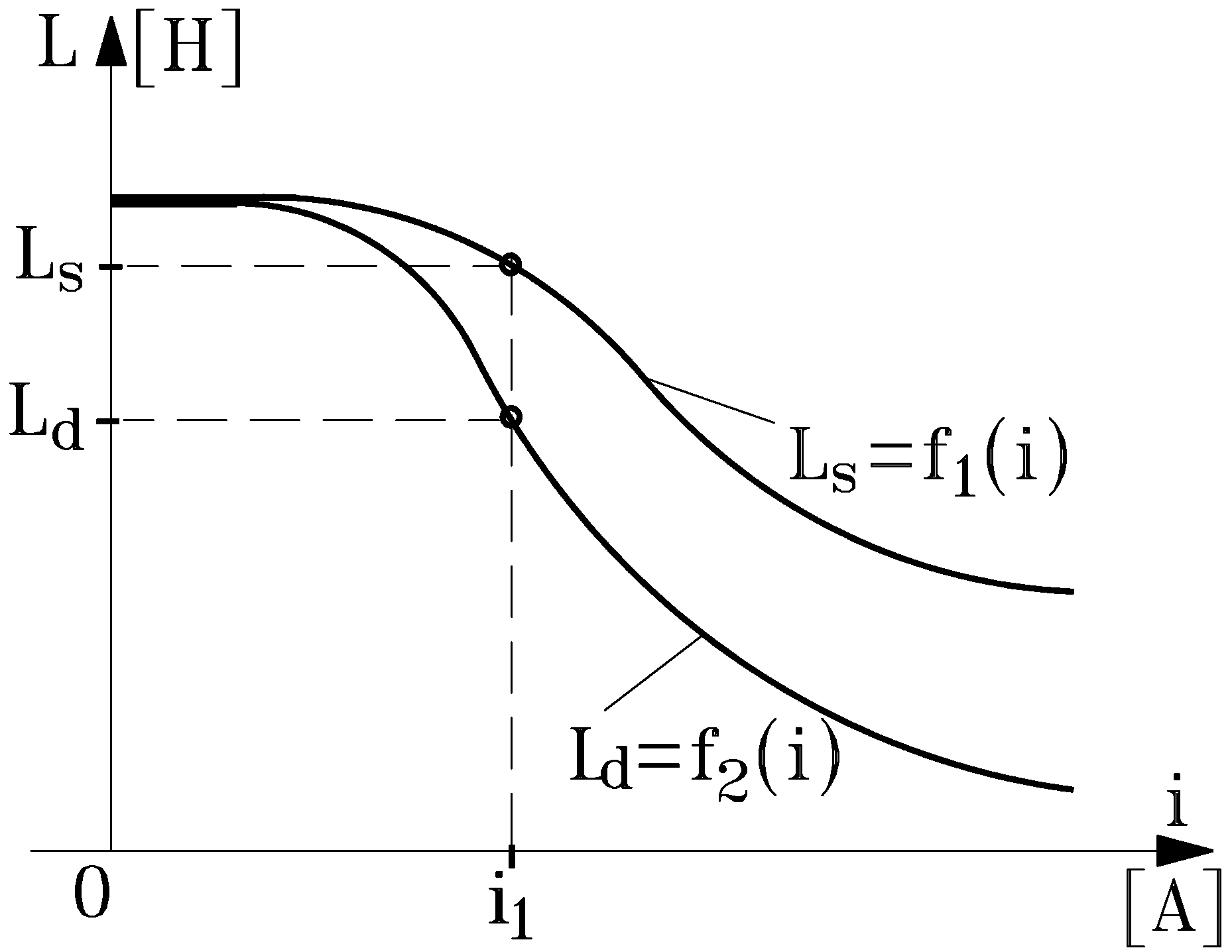
- Due to the existence of two inductances (static Ls and dynamic Ld), the “risk” of the double interpretation appears often. Only if the coils do not have a ferromagnetic core (when Ψ = f(i) is a straight line) are the two inductances (static and dynamic) the same, i.e., Ls = Ld = L and This result implies that, during the transient process of the industrial ecosystem moving among multiple stable states, it is advantageous to work with the dynamic inductance rather than the static inductance.
- (2)
- Graphical interpretations have been obtained theoretically of the classical formulas for the calculation of mechanical work, both at constant current (I = const.) and at constant flux (Ψ = const).
- (3)
- With the general expression for the embedded magnetic energy, the mechanical work expressions W12' from Equation (14) and W12" from Equation (15) (performed for the armature in motion) can be written in a unitary mode with the following expressions:
2.3. Electromagnet Force and Torque
2.3.1. Electromagnet Operation with Constant Current-turns
2.3.2. Electromagnet Operation with Constant Magnetic Flux
2.3.3. Discussion of Forces
3. Discussion of Electromagnetic Quantities as Environmental Parameters
4. Conclusions
References
- Dincer, I.; Rosen, M.A. Exergy: Energy, Environment and Sustainable Development; Elsevier: Oxford, UK, 2007. [Google Scholar]
- Rosen, M.A. A concise review of energy-based economic methods. In Proceeding of 3rd IASME/WSEAS International Conference on Energy & Environment, Cambridge, UK, February 2008; pp. 136–142.
- Wall, G. Exergy Tools. In Proceeding of the Institution of Mechanical Engineers, Part A: J. Power and Energy, March 2003; pp. 125–136.
- Rosen, M.A.; Bulucea, C.A. Assessing electrical systems via exergy: a dualist view incorporating technical and environmental dimensions. In Proceeding of 6th WSEAS International Conference on Engineering Education, Rhodes, Greece, July 2009; pp. 116–123.
- Wall, G. Exergy, ecology and democracy: concepts of a vital society or a proposal for an exergy tax. In Presented at 2nd European Congress on Economics and Management of Energy in Industry, Estoril, Portugal, April 1994.
- Wall, G. Introduction to life support systems and sustainable development. available at: http://www.exergy.se/ftp/ilsssd.pdf accessed on 15 January 2012.
- Szargut, J. Exergy Method: Technical and Ecological Applications; WIT Press: Southampton, UK, 2005. [Google Scholar]
- Moran, M.J. Availability Analysis: A Guide to Efficient Energy Use, revised ed.; American Society of Mechanical Engineers: New York, NY, USA, 1989. [Google Scholar]
- Szargut, J. International progress in second law analysis. Energy 1980, 5, 709–718. [Google Scholar] [CrossRef]
- Edgerton, R.H. Available Energy and Environmental Economics; D.C. Heath: Toronto, Canada, 1982. [Google Scholar]
- Brodyanski, V.M.; Sorin, M.V.; Le Goff, P. The Efficiency of Industrial Processes: Exergy Analysis and Optimization; Elsevier: New York, NY, USA, 1994. [Google Scholar]
- Yantovskii, E.I. Energy and Exergy Currents: An Introduction to Exergonomics; Nova Science Publishers: New York, NY, USA, 1994. [Google Scholar]
- Rosen, M.A.; Dincer, I. Exergy analysis of waste emissions. Int. J. Energy Research 1999, 23, 1153–1163. [Google Scholar] [CrossRef]
- Rosen, M.A. Energy- and exergy-based comparison of coal-fired and nuclear steam power plants. Exergy, An Inter. J. 2001, 1, 180–192. [Google Scholar] [CrossRef]
- Chen, G.Q.; Chen, B. Extended-exergy analysis of the Chinese society. Energy 2009, 34, 1127–1144. [Google Scholar] [CrossRef]
- Chen, G.Q.; Jiang, M.M.; Yang, Z.F.; Chen, B.; Ji, X.; Zhou, J.B. Exergetic assessment for ecological economic system: Chinese agriculture. Ecol. Model. 2009, 220, 397–410. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, G.Q. Physical sustainability assessment for the China society: exergy-based systems account for resources use and environmental emissions. Renew. Sust. Energ. Rev. 2010, 14, 1527–1545. [Google Scholar] [CrossRef]
- Ji, X.; Chen, G.Q.; Chen, B.; Jiang, M.M. Exergy-based assessment for waste gas emissions from Chinese transportation. Energ. Policy 2009, 37, 2231–2240. [Google Scholar] [CrossRef]
- Rosen, M.A.; Bulucea, C.A. Using exergy to understand and improve the efficiency of electrical power technologies. Entropy 2009, 11, 820–835. [Google Scholar] [CrossRef]
- Nicola, D.A.; Rosen, M.A.; Bulucea, C.A.; Brindusa, C. The exergetic and environmental impact assessment of underground electric train braking. P. I. Mech. Eng. F-J. Rai. 2010. [Google Scholar] [CrossRef]
- Allenby, B.R. Industrial Ecology: Policy Framework and Implementation; Prentice-Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Allenby, B.R. Industrial ecology, information and sustainability. Foresight 2002, 2, 163–171. [Google Scholar] [CrossRef]
- Ayres, R.U. Industrial metabolism. In Technology and Environment; Ausubel, J.H., Sladovich, H.E., Eds.; National Academy Press: Washington, DC, USA, 1989; pp. 23–49. [Google Scholar]
- Graedel, T.E.; Allenby, B.R. Industrial Ecology; Prentice Hall: Upper Saddle River, NJ, USA, 1995. [Google Scholar]
- Graedel, T.E. On the concept of industrial ecology. Annu. Rev. Energ. Env. 1996, 21, 69–98. [Google Scholar] [CrossRef]
- Connelly, L.; Koshland, C.P. Two aspects of consumption: using an exergy-based measure of degradation to advance the theory and implementation of industrial ecology. Resour. Conserv. Recy. 1997, 19, 199–217. [Google Scholar] [CrossRef]
- Holling, C.S.; Schindler, D.W.; Walker, B.W.; Roughgarden, J. Biodiversity in the functioning of ecosystems. In Biodiversity Loss; Perrings, C., Maler, K.-G., Folke, C., Holling, C.S., Jansson, B.-O., Eds.; Cambridge University Press: Cambridge, UK, 1995; pp. 44–83. [Google Scholar]
- Coulon, I.; Jufer, M. Introduction à l'électrotechnique (Introduction to Electrotechnics), 5th ed.; Piesses Politechniques Romandes: Lausanne, Switzerland, 1989. [Google Scholar]
- Nicola, D.A.; Bulucea, C.A. Electrotehnica, masini si echipamente electrice (Electrotechnics, Electrical Machines and Equipment); SITECH Publishing House: Craiova, Romania, 2005. [Google Scholar]
- Bulucea, C.A.; Nicola, D.A. Introducere în electrotehnica si echipamente electrice (Introduction to Electrotechnics and Electrical Equipment); SITECH Publishing House: Craiova, Romania, 2004. [Google Scholar]
- Nicola, D.A.; Rosen, M.A.; Bulucea, C.A.; Brandusa, C. Sustainable energy conversion in electrically driven transportation systems. In Proceedings of 6th WSEAS International Confenence on Engineering Education, Rhodes, Greece, July 2009; pp. 124–132.
- Mastorakis, N.E.; Bulucea, C.A.; Nicola, D.A. Modeling of three-phase induction motors in dynamic regimes according to an ecosystem pattern. In Proceeding of 13th WSEAS International Confenence on Systems, Rhodes, Greece, July 2009; pp. 338–346.
- Bulucea, C.A.; Nicola, D.A.; Mastorakis, N.E.; Rosen, M.A. Understanding electric industrial ecosystems through exergy. In Recent Researches in Energy and Environment: Proceedings of 6th IASME/WSEAS International Confenence on Energy and Environment, Cambridge, UK, February 2011; pp. 182–191.
- Nguyen, B.; Mohabeer, S.; Lai, V.; Lander, E. Evaluation of Electromagnetic Field Intensity in the City of Toronto. Report for Industry Canada, Spectrum Management, Ontario Regional Engineering. Canada, June 2002. [Google Scholar]
- Electromagnetic Compatibility – the EMC Directive 89/336/EEC, 1992. available at: http://www.ictregulationtoolkit.org/en/publication.3286.html/ accessed on 10 May 2012.
- Guide to the Implementation of Directives Based on the New Approach and the Global Approach, European Commission, 2000. available at: http://ec.europa.eu/enterprise/policies/single-market-goods/files/blue-guide/guidepublic_en.pdf accessed on 12 May 2012.
- VITO&BIOIS, Report on Distribution and Power Transformers, Contract N°. S12.515810 call ENTR/2008/039. Sustainable Industrial Policy – Building on the Ecodesign Directive – Energy-Using, Product Group Analysis. September 2010. available at: http://www.ebpg.bam.de/de/-ebpg_medien/entr2/402_studyd_10-10_part1-7.pdf accessed on 20 January 2012.
- Wuppertal Institute for Climate, Environment, Energy and SEEDT Partners, Policies and Measures Fostering Energy-Efficient Distribution Transformers: Report from the EUIEE Project “Strategies for Development and Diffusion of Energy-Efficient Distribution Transformers – SEEDT”. Project No. EIE/05/056/SI2.419632, Project prepared by Topalis, F. (coordinator); Irrek, W.; Targosz, R.. July 2008. available at: http://seedt.ntua.gr/dnl/SEEDT_project_report.pdf (accessed on 12 June 2012).
- Bulucea, C.A.; Nicola, D.A.; Mastorakis, N.E.; Dondon, P.; Bulucea, C.A.; Cismaru, D.C. Fostering the sustainability of power transformers. Recent Researches in Environmental & Geological Sciences. In Proceedings of 7th WSEAS International Conference on Energy and Environment, Kos, Greece, July 2012; pp. 72–81.
- Portier, C.J.; Wolfe, M.S. NIEHS Working Group Report of National Institute of Environmental Health Sciences of US National Institutes of Health: Assessment of Health Effects from Exposure to Power-Line Frequency Electric and Magnetic Fields. United States Department of Energy and the National Institute of Environmental Health Sciences/National Institutes of Health: Brooklyn Park, Minnesota, 16–24 June 1998. available at: http://www.niehs.nih.gov/health/assets/docs_a_e/assessment_of_health_effects_from_exposure_to_powerline_frequency_electric_and_magnetic_fields.pdf accessed on 25 July 2012. [Google Scholar]
- AGNIR. Electromagnetic fields and the risk of cancer. Report of an Advisory Group on Non-ionising Radiation. Doc. NRPB 1992, 3, 1–138. [Google Scholar]
- Wertheimer, N.; Leeper, E. Electrical wiring configurations and childhood cancer. Am. J. Epidemiol. 1979, 109, 273–284. [Google Scholar] [PubMed]
- Wertheimer, N.; Leeper, E. Magnetic field exposure related to cancer subtypes. Ann. NY Acad. Sci. 1987, 502, 43–54. [Google Scholar] [CrossRef] [PubMed]
- Gamberale, F.; Anshelm Olson, B.; Eneroth, P.; Lindh, T.; Wennberg, A. Acute effects of ELF electromagnetic fields: a field study of linesmen working with 400 kV power lines. British J. Ind. Med. 1989, 46, 729–737. [Google Scholar] [CrossRef]
- Asanova, T.P.; Rakov, A.N. The health status of people working in the electric field of open 400–500 KV switching structures. Gig. Tr. Prof. Zabol. 1966, 10, 50–52. [Google Scholar] [PubMed]
- Armstrong, B.; Thériault, G.; Guénel, P.; Deadman, J.; Goldberg, M.; Heroux, P. Association between exposure to pulsed electromagnetic fields and cancer in electric utility workers in Quebec, Canada, and France. Am. J. Epidemiol. 1994, 140, 805–820. [Google Scholar] [PubMed]
- Arnetz, B.B. Technological stress: psychophysiological aspects of working with modern information technology. Scand. J. Work Environ. Health 1997, 23, 97–103. [Google Scholar] [PubMed]
- Bell, G.B.; Marino, A.A.; Chesson, A.L. Alterations in brain electrical activity caused by magnetic fields: detecting the detection process. Electroencephalogr. Clin. Neurophysiol. 1992, 83, 389–397. [Google Scholar] [CrossRef]
- Sastre, A.; Cook, M.R.; Graham, C. Nocturnal exposure to intermittent 60 Hz magnetic fields alter human cardiac rhythm. Bioelectromagnetics 1998, 19, 98–106. [Google Scholar] [CrossRef]
- Liden, S. Sensitivity to electricity - a new environmental epidemic. Allergy 1996, 51, 519–524. [Google Scholar] [PubMed]
- Sandström, M.; Lyskov, E.; Berglund, A.; Medvedev, S.; Mild, K. Neurophysiological effects of flickering light in patients with perceived electrical hypersensitivity. JOEM 1997, 39, 15–22. [Google Scholar] [PubMed]
- Savitz, D.A.; Boyle, C.A.; Holmgreen, P. Prevalence of depression among electrical workers. Am. J. Ind. Med. 1994, 25, 165–176. [Google Scholar] [CrossRef] [PubMed]
- Directive 2004/40/EC of the European Parliament and of the Council – Electromagnetic Fields and Waves, of 29 April 2004 on the minimum health and safety requirements regarding the exposure of the workers to risks arising from electromagnetic fields and waves. available at: http://osha.europa.eu/en/legislation/directives/exposure-to-physical-hazards/osh-directives/direc-tive-2004-40-ec-of-the-european-parliament-and-of-the-council/ accessed on 17 March 2012.
- Report of World Health Organization. Extremely Low Frequency Fields. Environmental Health Criteria, Geneva, World Health Organization. available at: http://www.who.int/peh-emf/publications/Complet_DEC_2007.pdf accessed on 5 February 2012.
- International Commission on Non-Ionizing Radiation Protection (ICNIRP). Exposure to Static and Low Frequency Electromagnetic Fields, Biological Effects and Health Consequences (0-100 kHz); Matthes, R., McKinlay, A.F., Bernhardt, J.H., Vecchia, P., Eds.; ICNIRP: Oberschleissheim, Germany, 2003. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bulucea, C.A.; Rosen, M.A.; Nicola, D.A.; Mastorakis, N.E.; Bulucea, C.A. Utilizing the Exergy Concept to Address Environmental Challenges of Electric Systems. Entropy 2012, 14, 1894-1914. https://doi.org/10.3390/e14101894
Bulucea CA, Rosen MA, Nicola DA, Mastorakis NE, Bulucea CA. Utilizing the Exergy Concept to Address Environmental Challenges of Electric Systems. Entropy. 2012; 14(10):1894-1914. https://doi.org/10.3390/e14101894
Chicago/Turabian StyleBulucea, Cornelia A., Marc A. Rosen, Doru A. Nicola, Nikos E. Mastorakis, and Carmen A. Bulucea. 2012. "Utilizing the Exergy Concept to Address Environmental Challenges of Electric Systems" Entropy 14, no. 10: 1894-1914. https://doi.org/10.3390/e14101894
APA StyleBulucea, C. A., Rosen, M. A., Nicola, D. A., Mastorakis, N. E., & Bulucea, C. A. (2012). Utilizing the Exergy Concept to Address Environmental Challenges of Electric Systems. Entropy, 14(10), 1894-1914. https://doi.org/10.3390/e14101894





