1. Introduction
According to Aristotle, it is our ability to reason which sets humans apart from the rest of the animal kingdom. The understanding and manipulation of our environment that has made us so successful has only been possible through this unique ability. Reasoning underpins every human advancement and is used on a daily basis even if only trivially. Yet surprisingly, although reasoning is fundamental to the functioning and evolution of our species, we have had great difficulty in producing a satisfactory explanation of the mechanism that governs a large portion of this reasoning; namely inductive reasoning.
The difficulty of any attempt at unraveling the inner workings of the human mind should be appreciated. Some have even argued that a complete understanding of the human mind is beyond the capabilities of the human mind [
1]. Understanding how we reason is however an area in which significant progress has been made.
Reasoning is often broken down into two broad categories. Firstly there is deductive reasoning which can be thought of as the process of drawing logically valid conclusions from some assumed or given premise. Deductive reasoning is the type of reasoning used in mathematical proofs or when dealing with formal systems. Although this type of reasoning is obviously necessary, it is not always adequate.
When reasoning about our world we often want to make predictions that involve estimations and generalizations. For this we use inductive reasoning. Inductive reasoning can be thought of as drawing the “best” conclusions from a set of observations. Unfortunately these observations are almost always incomplete in some sense and therefore we can never be certain of the conclusions we make. This process is analogous to the scientific process in general. In science, rules and models are found by generalizing patterns observed locally. These models are then used to understand and predict our environment which in turn allows us to benefit, usually with great success. But like inductive inference, scientific hypotheses can never be completely validated, so we can never know whether they are true for certain. The difference between reasoning inductively or deductively can also be simply thought of as the difference between reasoning about the known or the unknown.
Philosophically speaking the fundamental goal of inductive reasoning is to gain a deeper awareness of how we should maintain rational beliefs and predictions in the face of uncertainty and the unknown observations or problems of the future. In some sense a history of inductive reasoning is a history of questioning and attempting to understand our own thought processes. As early as 300BC Epicurus was interested in how we judge competing theories for some given observations [
2]. This led him to postulate his principle of multiple explanations which stated that we should never disregard a consistent theory. William of Occam countered this with his with well-known “Occam’s razor” which advised that all but the simplest theory consistent with the observations should be discarded [
3]. Hume later stated the problem of induction explicitly for the first time
“What is the foundation of all conclusions from experience?” [
4]. He also set about questioning the validity of such conclusions. Hume’s problem led Bayes and Laplace to make the first attempts at formalizing inductive inference which has become the basis for Bayesianism. This is a school of thought that requires making an explicit choice in the class of explanations considered and our prior belief in each of them. Bayesianism has, in turn, fueled further attempts at formalizing induction.
To say that the history of induction has been contentious is an understatement [
5]. There have been many attempts at formalizing inductive reasoning [
6] that address specific situations and satisfy many of the intuitive properties we expect of induction. Unfortunately most of these attempts have serious flaws or are not general enough. Many of the results regarding induction have been controversial and highly contested, which is not particularly surprising. By its very nature induction deals with uncertainty, subjectivity and challenging philosophical questions, and is therefore highly prone to discussion and debate. Even if a result is formally sound, its philosophical assumptions and applicability in a range of situations are often questioned.
In 1964 Ray Solomonoff published the paper
“A Formal Theory of Inductive Inference” [
7]. In this paper he proposed a universal method of inductive inference which employs the Bayesian framework and his newly created theory of algorithmic probability. This method of Solomonoff induction appears to address the issues that plagued previous attempts at formalizing induction and has many promising properties and results. Solomonoff induction and related concepts are the central focus of this article.
The formalization of Solomonoff induction makes use of concepts and results from computer science, statistics, information theory, and philosophy. It is interesting that the development of a rigorous formalization of induction, which is fundamental to almost all scientific inquiry, is a highly multi-disciplinary undertaking, drawing from these various areas. Unfortunately this means that a high level of technical knowledge from these various disciplines is necessary to fully understand the technical content of Solomonoff induction. This has restricted a deep understanding of the concept to a fairly small proportion of academia which has hindered its discussion and hence progress.
In this article we attempt to bridge this gap by conveying the relevant material in a much more accessible form. In particular we have expanded the material in the dense 2007 paper
“On Universal Prediction and Bayesian Confirmation” [
8] which argues that Solomonoff induction essentially solves the induction problem. In addition to providing intuition behind the overall setup and the main results we also examine the philosophical motivations and implications of Solomonoff’s framework.
We have attempted to write this article in such a way that the main progression of ideas can be followed with minimal mathematical background. However, in order to clearly communicate concrete results and to provide a more complete description to the capable reader, some technical explanation is necessary.
By making this knowledge more accessible we hope to promote discussion and awareness of these important ideas within a much wider audience. Every major contribution to the foundations of inductive reasoning has been a contribution to understanding rational thought. Occam explicitly stated our natural disposition towards simplicity and elegance. Bayes inspired the school of Bayesianism which has made us much more aware of the mechanics behind our belief system. Now, through Solomonoff, it can be argued that the problem of formalizing optimal inductive inference is solved.
Being able to precisely formulate the process of (universal) inductive inference is also hugely significant for general artificial intelligence. Obviously reasoning is synonymous with intelligence, but true intelligence is a theory of how to act on the conclusions we make through reasoning. It may be argued that optimal intelligence is nothing more than optimal inductive inference combined with optimal decision making. Since Solomonoff provides optimal inductive inference and decision theory solves the problem of choosing optimal actions, they can therefore be combined to produce intelligence. This is the approach taken by the second author in developing the AIXI model which will be discussed only briefly.
1.1. Overview of Article
Here we will give a brief summary of the contents of this article.
Section 2 looks at the broader context of (universal) induction. At first we contrast it with deduction. We then argue that any inductive inference problem can be considered or converted to a sequence prediction problem. This gives justification for focusing on sequence prediction throughout this article. We also examine the relation between Solomonoff induction and other recent approaches to induction. In particular how Solomonoff induction addresses non-monotonic reasoning and why it appears to contradict the conclusion of no-free-lunch theorems.
Section 3 covers probability theory and the philosophy behind the varying schools of thought that exist. We explain why the subjective interpretation of probability is the most relevant for universal induction and why it is valid. In particular we explain why the belief system of any rational agent must obey the standard axioms of probability.
Applying the axioms of probability to make effective predictions results in the Bayesian framework which is discussed in depth in
Section 4. We look at what it means to be a Bayesian; why models, environments and hypotheses all express the same concept; and finally we explain the mechanics of the Bayesian framework. This includes looking at convergence results and how it can be used to make optimal Bayesian decisions. We also look briefly at continuous model classes and at making reasonable choices for the model class.
Section 5 gives an overview of some of the major historical contributions to inductive reasoning. This includes the fundamental ideas of Epicurus’s principle of multiple explanations and Occam’s razor. We also discuss briefly the criticisms raised by inductive skeptics such as Empiricus and Hume. Laplace’s contribution is then examined. This includes the derivation of his famous rule of succession which illustrates how the Bayesian framework can be applied. This rule also illustrates the confirmation problem that has plagued many attempts at formalizing induction. The cause of this problem is examined and we show that a recent claim by Maher [
9], that the confirmation problem can be solved using the axioms of probability alone, is clearly unsatisfactory. One of the most difficult problems with confirmation theory is the black ravens paradox. We explain why this counter-intuitive result arises and the desired solution.
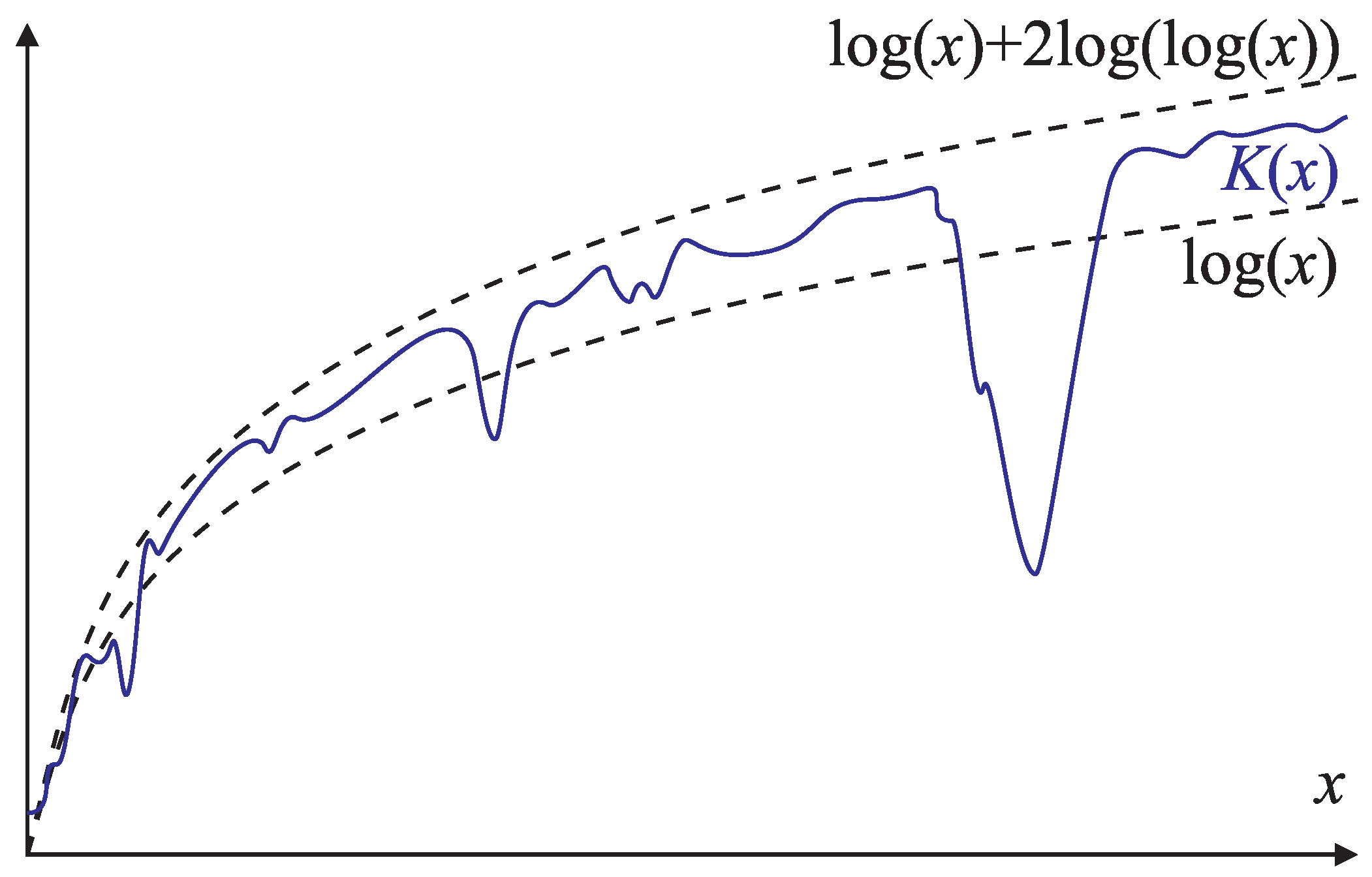
In order to understand the concept of Kolmogorov complexity which is integral to Solomonoff induction, it is necessary to briefly examine the fundamental concept of computability and the closely related Turing machine. The introduction of the theoretical Turing machine is in some ways considered the birth of computer science. We look at the basic idea of what a Turing machine is and how, through Solomonoff, it became an integral part of universal induction. The measure of complexity that Kolmogorov developed is a major part of algorithmic information theory. We examine the intuition behind it as well as some relevant properties.
In
Section 6 we discuss reasonable approaches to making a rational choice of prior as well as desirable properties for a prior to have. The universal prior involves the use of Kolmogorov complexity which we argue is highly intuitive and does justice to both Occam and Epicurus.
At this point, having introduced all the necessary concepts,
Section 7 gives an explanation of Solomonoff’s universal predictor. We examine two alternate representations of this universal predictor and the relationship between them. We also look at how this predictor deals with the problem of old evidence, the confirmation problem and the black ravens paradox.
Section 8 discusses several bounds for this universal predictor, which demonstrate that it performs excellently in general. In particular we present total, instantaneous, and future error bounds.
Section 9 looks at the value of Solomonoff induction as a gold standard and how it may be approximated and applied in practice. We mention a number of approximations and applications of either Solomonoff or the closely related Kolmogorov complexity. The extension of Solomonoff to universal artificial intelligence is also briefly covered.
Section 10 gives a brief discussion of some of the issues concerning Solomonoff induction as well as a review of the pros and cons, and concludes.
2. Broader Context
The work done on the problem of induction, both philosophically and formally, has been both vast and varied. In this article the focus is on using inductive inference for making effective decisions. From this perspective, having an effective method of prediction is sufficient. It is for this reason that this article focuses primarily on sequence prediction, rather than inference in the narrow sense of learning a general model from specific data. Even concept learning, classification, and regression problems can be rephrased as sequence prediction problems. After having clarified these relationships, we briefly look at Solomonoff induction in the context of some of the most significant concepts in recent discussions of inductive reasoning [
6] such as Bayesian learning versus prediction with expert advice, no-free-lunch theorems versus Occam’s razor, and non-monotonic reasoning.
2.1. Induction versus Deduction
There are various informal definitions of inductive inference. It can be thought of as the process of deriving general conclusions from specific observation instances. This is sort of dual to deductive inference, which can be thought of as the process of deducing specific results from general axioms. These characterizations may be a bit narrow and misleading, since induction and deduction also parallel each other in certain respects.
The default system for deductive reasoning is “classical” (first-order predicate) logic. The Hilbert calculus starts with a handful of logical axiom schemes and only needs modus ponens as inference rule. Together with some domain-specific non-logical axioms, this results in “theorems”. If some real-world situation (data, facts, observation) satisfies the conditions in a theorem, the theorem can be applied to derive some conclusions about the real world. The axioms in Zermelo-Fraenkel set theory are universal in the sense that all of mathematics can be formulated within it.
Compare this to the (arguably) default system for inductive reasoning based on (real-valued) probabilities: The Bayesian “calculus” starts with the Kolmogorov axioms of probability, and only needs Bayes rule for inference. Given some domain-specific prior and new data = facts = observations, this results in “posterior” degrees of belief in various hypotheses about the world. Solomonoff’s prior is universal in the sense that it can deal with arbitrary inductive inference problems. Hypotheses play the role of logical expressions, probability
corresponds to
X being false/true, and
to
X being true in some models but false in others. The general correspondence is depicted in
Table 1.
2.2. Prediction versus Induction
The above characterization of inductive inference as the process of going from specific to general was somewhat narrow. Induction can also be understood more broadly to include the process of drawing conclusions about some given data, or even as the process of predicting the future. Any inductive reasoning we do must be based on some data or evidence which can be regarded as a history. From this data we then make inferences, see patterns or rules or draw conclusions about the governing process. We are not really interested in what this tells us about the already observed data since this is in the past and therefore static and inconsequential to future decisions. Rather we care about what we are able to infer about future observations since this is what allows us to make beneficial decisions. In other words we want to predict the natural continuation of our given history of observations. Note that “future observations” can also refer to past but (so far) unknown historical events that are only revealed in the future.
From this general perspective, the scientific method can be seen as a specific case of inductive reasoning. In science we make models to explain some past data or observation history and these models are then used to help us make accurate predictions. As humans we find these models satisfying as we like to have a clear understanding of what is happening, but models are often overturned or revised in the future. Also, from a purely utilitarian point of view, all that matters is our ability to make effective decisions and hence only the predictions and not the models themselves are of importance. This is reminiscent of but not quite as strong as the famous quote by George Box that “Essentially, all models are wrong, but some are useful”.
We look now at some specific examples of how general induction problems can be rephrased as prediction problems.
2.3. Prediction, Concept Learning, Classification, Regression
In many cases the formulation is straight forward. For example, problems such as “what will the weather be like tomorrow?”, “what will the stock market do tomorrow?” or “will the next raven we see be black?” are already in the form of prediction. In these cases all that needs to be done is to explicitly provide any relevant historic data, such as stock market records or past weather patterns, as a chronological input sequence and then look for the natural continuations of these sequences. It should however be noted that a simple formulation does not imply a simple solution. For example, the chaotic nature of stock markets and weather patterns make it extremely difficult to find the correct continuation of this sequence, particularly more than a few time steps ahead.
More formally, in the field of machine learning, sequence prediction is concerned with finding the continuation of any given sequence . This may be used to represent a wide range of abstract problems beyond the obvious application to time series data such as historical weather or stock patterns. For instance, (online) concept learning, classification and regression can be regarded as special cases of sequence prediction.
Concept learning involves categorizing objects into groups which either do or do not possess a given property. More formally, given a concept
, it requires learning a function
such that for all
x:
Solomonoff induction only deals with the problem of sequence prediction; however, as we discuss in the next paragraph, sequence prediction is general enough to also capture the problem of concept learning, which itself is a specific case of classification. Although the setup and interpretation of classification using Solomonoff may be less intuitive than using more traditional setups, the excellent performance and generality of Solomonoff implies that theoretically it is unnecessary to consider this problem separately.
In machine learning, classification is the problem of assigning some given item x to its correct class based on its characteristics and previously seen training examples. In classification we have data in the form of tuples containing a point and its associated class . The goal is to correctly classify some new item by finding . As before, all data is provided sequentially with the new point appended at the end. In other words, the classification of x becomes “what is the next number in the sequence ?”. Technically this could be regarded as a specific case of regression with discrete function range, where the function we are estimating maps the items to their respective classes.
Regression is the problem of finding the function that is responsible for generating some given data points, often accounting for some noise or imprecision. The data is a set of (feature,value) tuples , ,..... In machine learning this problem is often tackled by constructing a function that is the “best” estimate of the true function according to the data seen so far. Alternatively, it can be formalized directly in terms of sequential prediction by writing the input data as a sequence and appending it with a new point for which we want to find the functional value. In other words the problem becomes: “What is the next value in the sequence ”. Although this approach does not produce the function explicitly, it is essentially equivalent, since for any x can be obtained by choosing .
2.4. Prediction with Expert Advice versus Bayesian Learning
Prediction with expert advice is a modern approach to prediction. In this setting it is assumed that there is some large, possibly infinite, class of “experts” which make predictions about the given data. The aim is to observe how each of these experts perform and develop independent predictions based on this performance. This is a general idea and may be carried out in various ways. Perhaps the simplest approach, known as follow the leader, is to keep track of which expert has performed the best in the past and use its prediction. If a new expert takes the lead, then your predictions will switch to this new leading expert. Naively, the performance of an expert can be measured by simply counting the number of errors in its predictions, but in many situations it is appropriate to use a loss function that weighs some errors as worse than others. A variant of this simple “follow the leader” concept is known as “follow the perturbed leader” in which our predictions mimic the leader most of the time but may switch to another with some specified probability [
10]. This technique gives a probability distribution rather than a deterministic predictor which can be advantageous in many contexts.
The traditional Bayesian framework discussed in this article uses a mixture model over a hypothesis or environment or model class, which resembles the “follow the perturbed leader” technique. This mixture model reflects our rational beliefs about the continuation of a sequence given the performance of each “expert” and, as we will see, performs very well theoretically. Solomonoff induction uses the Bayesian framework with the infinite class of “experts” given by all computable environments. This means that there is always an expert that performs well in any given environment which allows for good performance without any problem-specific assumptions.
2.5. No Free Lunch versus Occam’s Razor
This is in some way a contradiction to the well-known
no-free-lunch theorems which state that, when averaged over all possible data sets, all learning algorithms perform equally well, and actually, equally poorly [
11]. There are several variations of the no-free-lunch theorem for particular contexts but they all rely on the assumption that for a general learner there is no underlying bias to exploit because any observations are equally possible at any point. In other words, any arbitrarily complex environments are just as likely as simple ones, or entirely random data sets are just as likely as structured data. This assumption is misguided and seems absurd when applied to any real world situations. If every raven we have ever seen has been black, does it really seem equally plausible that there is equal chance that the next raven we see will be black, or white, or half black half white, or red etc. In life it is a necessity to make general assumptions about the world and our observation sequences and these assumptions generally perform well in practice.
To overcome the damning conclusion of these
no-free-lunch theorems in the context of concept learning, Mitchell introduced the following inductive learning assumption which formalizes our intuition and is essentially an implicit part of our reasoning [
12].
“Any hypothesis found to approximate the target function well over a sufficiently large set of training examples will also approximate the target function well over other unobserved examples.”
Similar assumptions can be made for other contexts but this approach has been criticized as it essentially results in a circular line of reasoning. Essentially we assume that inductive reasoning works because it has worked in the past but this reasoning is itself inductive and hence circular. Hume’s argument that this circularity invalidates inductive reasoning is discussed further in
Subsection 5.2. In fact this inductive learning assumption is closely related to what Hume called the principle of uniformity of nature. A principle he said we implicitly, but invalidly, assume.
If we prescribe Occam’s razor principle [
3] to select the simplest theory consistent with the training examples and assume some general bias towards structured environments, one can prove that inductive learning “works”. These assumptions are an integral part of our scientific method. Whether they admit it or not, every scientist, and in fact every person, is continuously using this implicit bias towards simplicity and structure to some degree.
Any agent, animal or machine, must make use of underlying structure in some form in order to learn. Although induction inherently involves dealing with an uncertain environment for which no hard guarantees can be made, it is clear that our world is massively structured and that exploiting structure in general is the best technique for performing well. By denying the relevance of this structure no-free-lunch theorems imply that general learning, and the concept of general intelligence, is essentially futile, which contradicts our experience. Solomonoff induction is witness to the possibility of general learning, assuming only some structure in the environment without having to specify which type of structure, and using Occam’s razor.
2.6. Non-Monotonic Reasoning
Non-monotonic reasoning is another concept that has been discussed recently in relation to induction. This concept attempts to solve the problem of formalizing common sense logic. When artificial intelligence researchers attempted to capture everyday statements of inference using classical logic they began to realize this was a difficult if not impossible task. The problem arises largely because of the implicit assumption of normality we often make to exclude exceptional circumstances. For example, it would be perfectly acceptable to make a statement such as “the car starts when you turn the key in the ignition” [
6]. Therefore if we let
be the predicate that we turn the key in the ignition in car
and
be the predicate that
x starts, then the previous sentence would be represented by the logical statement
. Of course there are many reasons why this might not be correct such as the fact that the car
x has no fuel or a mechanical problem. But these exceptions do not stop us making these types of statements because it is implicity assumed that this statement may only hold under normal conditions.
This assumption of normal conditions also leads to a logic that is non-monotonic in its arguments. Normally if the statement holds, then it follows logically that . However this rule may no longer hold using “normal case” reasoning. If is the predicate that x has no fuel then, although the statement is (normally) true, is (normally) not true, since the car will not start without fuel. Another example is that a general rule in our knowledge base may be that “birds can fly”. Therefore if x is a bird it is natural to assume that x can fly; however if x is a bird and x is a penguin then it is no longer correct to say that x can fly.
2.7. Solomonoff Induction
Solomonoff induction [
7] bypasses this issue entirely by avoiding the use of strict logical syntax which seems to be an inadequate tool for dealing with any reasonably complex or real-world environment. Non-monotonic statements such as the examples shown can be programmed in a variety of ways to effectively deal with “the normal case” and an arbitrary number of exceptional cases. This means that there exists a computable environment in Solomonoff’s universal class which will effectively describe the problem. The non-monotonicity of the environment will certainly affect its complexity and hence its prior but a simple non-monotonic environment will still have a reasonably high prior since there will be a reasonably short way of expressing it. More generally the complexity, and hence prior (see
Subsection 6.5), of a non-monotonic environment will depend on the variety and number of exceptions to the general rules, but this seems to be a desirable property to have. The implicit assumption of normality we use is due to our prior experience and knowledge of the real world. Initially, for an agent acting in an unknown environment, it seems reasonable that upon being told a general rule, it should assume the rule to hold in all cases and then learn the exceptional cases as they are observed or inferred. This is essentially how Solomonoff induction behaves.
Because of the fundamental way in which Solomonoff’s universal induction scheme continuously learns and improves from its experience, it may be argued that any useful computable approach to induction in one way or another approximates Solomonoff induction. In any case it appears to compare well with the above approaches. The major issue remains its incomputability and the difficulty of approximating Solomonoff in reasonably complex environments. This is discussed further in
Section 9.
3. Probability
In order to fully appreciate the Bayesian framework it is important to have some understanding of the theory of probability that it is based on. Probability theory has had a long and contentious history [
5,
13,
14]. Even today probability theory divides the scientific community with several competing schools of thought which stem largely from the different methods of dealing with uncertainty as it appears in different areas of science. The most popular of these are objective, subjective and frequentist which reflect fundamentally different philosophical interpretations of what probability means. Surprisingly it turns out that these interpretations lead to the same set of axioms and therefore these philosophical differences are of little importance in practical applications. It is however worth considering these differences when looking at our motivation in the context of induction.
In the following Ω is used to denote the sample space which is the set of all possible outcomes. An event is said to occur if the outcome is in E. For instance when throwing a die the sample space Ω is and an event E is some specific subset of these outcomes. For instance, the even numbers is the event and the set of numbers less than 3 is the event .
3.1. Frequentist
The frequentist approach is the most intuitive interpretation of probabilities, however it has several crippling drawbacks and is not applicable in many situations where we would like it to be. A frequentist defines the probability of an event as the limiting frequency of this event relative to the entire sample space Ω. Formally if is the number of times that event E occurs in n trials then . For example when throwing a die the probability of throwing a 6 is defined as the ratio of the number of throws that come up 6 to the number of throws in total as the number of throws goes to infinity. After many throws we expect this number to be close to . This is often one of the ways the concept of probability is taught, which is part of the reason that it appeals to our intuition. However when examined more closely it becomes apparent that this definition is problematic.
No matter how large n gets there is no guarantee that will converge to . Even if the die is thrown a million times it is conceivable although extremely unlikely that every roll will produce a 6 or that half the rolls will produce a 6. The best we can say is that as n increases, the probability that is arbitrarily close to also increases and will eventually get arbitrarily close to 1. Formally this is stated as converges to with probability 1. Unfortunately this gives rise to a circularity as the concept of probability is then used in defining probability.
Another problem with the frequentist approach is that there are many situations where it is not applicable. Consider the betting odds in a horse race. If the odds on a horse are, for instance, this is equivalent to saying that the probability that the horse will win is . This is certainly not the same as saying that the horse has won 1 in every 4 previous races. Instead it represents the bookies belief that the horse will win which depends on many factors. This probability as belief interpretation is the basis of the subjectivist’s understanding.
The error here may appear to be in associating probabilities with betting odds and it could be argued that strictly speaking the probability of the horse winning should be defined as the ratio of wins to overall races in the past, but this idea quickly becomes inconsistent. Clearly it makes no sense to equally weigh every race the horse has been in to find the probability of the horse winning this particular race. The races might therefore be restricted to those held on the same track and against the same horses, but since the weather and age of the horse might also be a factor there would be no other races with which to compare. This choice of reference class poses a very real problem in some practical situations such as medical diagnosis [
15]. The frequency approach is only really applicable in situations where we can draw a large number of samples from a distribution that is independent and identically distributed (i.i.d.) such as flipping a coin.
3.2. Objectivist
The objectivist interpretation is that probabilities are real properties of objects and of the world and therefore the objectivist believes that the world actually involves inherently random processes. This point of view has been largely supported by the success of quantum physics which states that there is true randomness present at a sub-atomic level. The most widely accepted set of axioms for objective probabilities are due to Kolmogorov [
16] and are given here.
Kolmogorov’s Probability Axioms.
If A and B are events, then the intersection , the union , and the difference are also events.
The sample space Ω and the empty set are events.
There is a function P that assigns non-negative real numbers, called probabilities, to each event.
and .
For a decreasing sequence of events with we have
In addition to the axioms there is the important definition of conditional probability. If
A and
B are events with
then the probability that event
B will occur under the condition that event
A occurred is
One of the problems with these axioms is that they only uniquely determine values for the null event and the event of the entire probability space. Although there are general principles for assigning values to other events, finding a universal formal method has been problematic. Applying general principles often requires some degree of subjectivity which can lead to debate. Kolmogorov complexity which is examined later provides a promising universal framework.
It has been argued [
17,
18] that the objective interpretation places too much faith in the ultimate truth of the quantum physics model. A simple example of randomness being incorrectly attributed to a process is the flipping of a coin. This is the standard analogy used in almost any situation where two outcomes occur with probability
each, with heads and tails representing the respective outcomes. This is because when we flip a coin the probability of heads is, for all practical purposes,
. Even in this article we used this example to represent a truly stochastic process, but in reality the probability of heads is actually (close to) 1 or 0 the moment the coin leaves your finger. This is because the process is not inherently random and if the exact initial conditions are known then the outcome can be calculated by applying the laws of physics. This statement is somewhat questionable as we may debate that an unknown breeze may affect the outcome or that our calculations would also need to consider the exact point that the coin lands which, if it was caught, would depend on the person. These objections are mute if we consider exact knowledge of initial conditions to include all local weather conditions and the persons state of mind. Without going into the question of free will the point is simply that we often use randomness to account for uncertainty in a model or a lack of adequate knowledge. Perhaps quantum physics is analogous to this in that although the model is currently very successful, there may be a time when the “inherent” randomness can be deterministically accounted for by a more accurate model.
In cases where the data is i.i.d., the objective probability is still identified with the limiting frequency, which is why these interpretations coincide for these cases. It is also possible to derive these axioms from the limiting frequency definition, however by using these axioms as a starting point the issues encountered by the frequentist are avoided.
3.3. Subjectivist
It is the subjectivist interpretation of probability that is most relevant in the context of induction, particularity in relation to agent based learning. The subjectivist interprets a probability of an event as a degree of belief in the event occurring and when any agent, human included, is attempting to learn about its environment and act optimally it is exactly this degree of belief that is important.
If a probability defines a degree of belief it must be subjective and therefore may differ from agent to agent. This may seem unscientific or unsatisfactory but when examined philosophically this interpretation has a strong case. To see this, consider Scott and Fred gambling in Las Vegas. While playing roulette they observe that the ball lands on 0 an abnormally high number of times causing them to lose significantly. Given that they are in a large well-known Casino, Fred thinks nothing of this abnormality believing that they have probably just been very unlucky. Scott on the other hand knows some of the employees at this particular Casino and has heard rumors of corruption on the roulette tables. This extra information can be thought of as observations that when combined with the statistical abnormality of the roulette table raises Scott’s belief that they have been victim to foul play. It is inevitable that, consciously or not, our analysis and interpretation of any situation will be biased by our own beliefs, experience and knowledge.
In a very formal sense this means that our probabilities are a function of our entire previous personal history and this is exactly how Solomonoff’s prediction scheme can be used. As a simple example consider Fred and Scott each independently drawing balls from an urn, with replacement, which contains black and white balls in an unknown ratio. Imagine that Fred draws 50 white balls and 20 black balls while Scott draws 30 white balls and 40 black balls. This is possible for any true ratio as long as there is a positive fraction of both black and white. Clearly Fred will believe that the ratio of white to black is approximately while Scott will believe that it is approximately . The point is that both of these beliefs are completely valid given their respective observations regardless of the true ratio.
Although we may accept that probabilities are subjective it is vital that there is a formal system that specifies how to update and manipulate these belief values. It is here that the subjective interpretation of probability has faced many criticisms as it was argued that subjective belief values do not obey formal mathematical rules or that the rules they do obey are also subjective making formalization difficult or impossible. It is a surprising and major result that any rational agent must update its beliefs by a unique system which coincides with that of limiting frequencies and objective probabilities.
The most intuitive justification for this is from a Dutch book argument which shows that if an agent’s beliefs are inconsistent (contradict the axioms) then a set of bets can be formulated which the agent finds favorable according to its beliefs but which guarantees that it will lose. The Dutch book argument is however not rigorous and there are several objections to it [
19]. The main issue rests on the implicit assumption that belief states uniquely define betting behavior which has been called into question since there are other psychological factors which can have an affect. For example in a game of poker it is often rational for a player to bet an amount that does not reflect his belief in winning the hand precisely because he is trying to bluff or convey a weak hand [
20]. In 1946 Cox published a theorem that gave a formal rigorous justification that
“if degrees of plausibility are represented by real numbers, then there is a uniquely determined set of quantitative rules for conducting inference” [
14] and that this set of rules is the same as those given by the standard probability axioms.
Cox’s Axioms for Beliefs.
The degree of belief in an event B, given that event A has occurred can be characterized by a real-valued function .
is a twice differentiable function of for .
is a twice differentiable function of and for .
This unification and verification of the probability axioms is a significant result which allows us to view the frequentist definition as a special case of the subjectivist interpretation. This means that the intuitively satisfying aspect of the frequentist interpretation is not lost but now obtains a new flavor. Consider again the case of determining the ratio of black to white balls in an urn through repeated sampling with replacement where the true ratio is
. As the urn is repeatedly sampled the relative frequency and hence subjective belief that the next ball is white will converge with probability 1 to
. Although this is the correct probability it is important to realize that it is still a belief and not an inherent property. In the unlikely but possible event that a white ball is sampled 1000 times the subjective probability/belief that the next ball will be white would be very close to 1.
This understanding of probability can be troubling as it suggests that we can never be certain of any truth about reality, however this corresponds exactly with the philosophy of science. In science it is not possible to ever prove a hypothesis, it is only possible to disprove it. No matter how much evidence there is for a hypothesis it will never be enough to make its truth certain. What are often stated as physical laws are actually only strongly believed and heavily tested hypotheses. Science is not impeded by this fact however. On the contrary, it allows for constant questioning and progress in the field and, although models may never be completely proven, it does not stop them being usefully applied.
4. Bayesianism for Prediction
To fully appreciate the historical attempts to solve the problem of induction and the corresponding discussions which fueled the field it is necessary to first understand the Bayesian framework. But before explaining the mechanics of the Bayesian framework it is worth having a brief look at what it means to be a Bayesian. Giving a precise explanation is difficult due to the various interpretations of Bayesianism [
13,
21], however all Bayesians share some core concepts.
Being a Bayesian is often simply associated with using Bayes formula but this is a gross simplification. Although Bayes formula plays an important role in the Bayesian framework it is not unique to Bayesians. The rule is directly derived from the axioms of probability and therefore its correctness is no more debatable than that of the axioms of probability.
More important to Bayesianism is Cox’s result that a rational belief system must obey the standard probability axioms. This is because a Bayesian is a subjectivist, believing that our beliefs and hence probabilities are a result of our personal history. In other works, what we believe today depends on what we believed yesterday and anything we have learnt since yesterday. What we believed yesterday depends on what we believed the day before, and so forth. Two individuals with very different histories may therefore hold different beliefs about the same event. This means that the probability of the event for each individual can be validly different from each other as long as they both updated their beliefs in a rationally consistent manner.
This rational updating process is at the core of Bayesianism. It may seem unscientific that different individuals can assign distinct yet valid probabilities but, as we have seen in
Subsection 3.3, this can be quite reasonable. There is a strong link to the frequentist approach here. If the two individuals are given the same observations, or at least observations from the same source, then their beliefs should eventually converge because their frequentist estimate should converge. Philosophically speaking, however, different individuals will never observe precisely the same observations. Each human has a unique experience of the world around them and therefore their beliefs will never be identical.
A Bayesian’s belief about events is governed by beliefs in the possible causes of those events. Everything we see has many possible explanations although we may only consider a few of them to be plausible. To be able to update beliefs consistently a Bayesian must first decide on the set of all explanations that may be possible. When considering a specific experiment this set of explanations, or hypotheses, need only explain the observations pertaining to the experiment. For example when flipping a coin to find its bias, the hypotheses may simply be all possible biases of the coin. For universal induction, we are interested in finding the true governing process behind our entire reality and to do this we consider all possible worlds in a certain sense. No matter what the problem is we can always consider it to consist of an agent in some unknown environment. In the coin example all irrelevant information is discarded and the environment simply consists of observing coin flips. It is useful to keep this general setup in mind throughout this article.
Lastly, the agent must have some prior belief in these explanations before the updating process begins. In other words before any observations have been made. Our beliefs today depend on beliefs yesterday which depend on the day before. But at some point there is no “day before” which is why some initial belief is required to begin the process. Over a long enough period these initial beliefs will be “washed out” but realistically they are important and should be chosen sensibly.
Summing up, a Bayesian holds beliefs about any possible cause of an event. These beliefs depend on all previously obtained information and are therefore subjective. A belief system that is entirely consistent with the Bayesian framework is obviously unrealistic as a model for human reasoning as this would require perfect logical updating at every instance as we continuously receive new information. There are also emotional and psychological factors that come into play for humans. Rather this is an idealized goal, or gold standard, which a Bayesian thinks we should strive for if we are to be completely rational.
4.1. Notation
In order to examine some of the more technical content and results it is necessary to first establish some notation. Throughout the article will represent the alphabet of the observation space being considered. This is simply the set of characters used to encode the observations in a particular situation. For example when flipping a coin and observing heads or tails, or or . An observation sequence is encoded as a string over the alphabet which is usually denoted x. In some cases we are interested in the length of x or some subsection of x. denotes a string of length n or, depending on context, the first n bits of x. denotes the mth bit of x. is the same as , meaning all bits before the nth bit. denotes the set of strings in this alphabet that have finite length. Therefore means x is any possible finite observation sequence.
In the Bayesian framework we deal with various environments, the class of all possible considered environments is denoted . It is assumed that one of these environments is the true environment which is denoted or simply μ. These hypotheses each specify distributions over strings x in the corresponding alphabet. This means that can be thought of as the probability of x according to environment . The concept of conditional probability is the same for these distributions with being the probability of observing x given that y was observed, under hypothesis . We have an initial belief in each of the environments in which is denoted . Note that probability and belief are used interchangeably in the Bayesian framework due to its subjectivist perspective. We may also be interested in our posterior belief in an environment after observing x. This is denoted .
4.2. Thomas Bayes
Reverend Thomas Bayes is a highly enigmatic figure in the history of mathematics. Very little is known of his life and few of his manuscripts survived. He only published one mathematical paper in his life, yet was elected to be a fellow of the royal society of London. On the 17th April 1761 Bayes died leaving unpublished an essay that would have a profound impact on the minds and methodologies of countless future scientists. This was not a discovery about the nature of our universe but rather a framework for how we can draw inferences about the natural world, essentially about how to rationally approach science. It was not until two years later that Bayes’ friend Richard Price posthumously published his “Essay towards solving a problem in the doctrine of chances” [
22] and it was not until many decades later that it began to have any major influence.
The problem as Bayes explicitly states it at the beginning of his essay is this:
Given: The number of times in which an unknown event has happened and failed
Required: The chance of its happening in a single trial lies somewhere between any two degrees of probability that can be named.
Intuitively Bayes was looking at the problem of inverse inference. At the time almost all applications of probability were to do with direct inference [
23]. These were cases where the initial mechanism and probabilities were known and the probability of some outcome was to be deduced. Bayes was instead interested in the case where experimental evidence was known but the true nature of the environment was unknown. In particular, given the number of successes and failures of an experiment what is the probability of success on the next trial?
The history of the development of inductive reasoning stretches over centuries with contributions from many great minds. It was actually through the apparently independent work of Laplace a decade later that the techniques of inverse probability gained widespread acceptance. Later we look at some of this history of inductive reasoning but here the focus is on the mechanics of the Bayesian framework which underlies most of the work in this field.
4.3. Models, Hypotheses and Environments
Whether we are testing hypotheses or modeling the world around us, science is fundamentally about understanding our environment in order to benefit from it in the future. Admittedly this statement may not be universally accepted, but it is from this utilitarian perspective that this article is written. This perspective is certainly influenced by the agent based setting of artificial intelligence. The entire field of economics, for example, is based on this assumption. In any case this abstract view of science is useful in order to see the relation with inductive inference. We can regard ourselves as agents maximizing some unknown reward function or utility. It is the complete generality of this utility that makes this assumption realistic. We may not be simply maximizing our bank balance, but the very fact that we have preferences between outcomes implies some in-built, possibly complex, reward function. Under this perspective, science is a tool for prediction which allows us to make decisions that maximize our utility; and models, environments and hypothesis are tools for science.
In looking at Bayesianism, it is important to realize that hypotheses, models and environments all express essentially the same concept. Although they may seem intuitively different they each express an explanation of some phenomenon at various levels of abstraction. A hypothesis is generally in relation to a specific experiment and is therefore quite a local explanation. A model is often used to explain a larger set of observations such as the movement of celestial bodies or the flow of traffic in a city, although models may be as comprehensive or specific as we like. Our environment may be thought of as a comprehensive model of our world, yet we can also use the term in reference to specific information relevant for some context such as a particular game environment. For example a chess environment consists of the current configuration of the pieces on the board and the rules that govern the game. The point here is that for the purposes of Bayesian learning no distinction is made between models, environments and hypotheses.
When thinking about a model or environment it is common to think of some meaningful underlying mechanism or program that governs the output we receive in the form of observations, however this is not necessary. At an abstract level, any complete hypothesis can be thought of as specifying a probability distribution over some observation set. In general the observations may not be independent so this distribution must be with respect to any previous observations generated by the environment. We consider this data to be encoded in a string over some finite alphabet which we denote , and the distribution is then over this alphabet. If the environment is deterministic then this distribution is simply concentrated to a single character of the alphabet at each step resulting in the probability of the correct string being one, or certain, and the probability of any other string being zero.
To illustrate this consider the simple environment of a fair coin being flipped. There are only two possible observations, either heads or tails so the alphabet is . In this case the observations are independent, so regardless of the observations seen so far the distribution given by this environment remains the same. For notation let E be some history sequence over and let be the distribution. Then we have, for any history E, and . If we consider the environment to instead be an ordered deck of cards then it is clear that if Z is some initial portion of the deck and a is the card following Z then and where is any other card in the deck. Since the card a following Z is obviously dependent on Z, it is clear that this distribution changes with the history Z. We call data sets that are drawn from independent distributions such as the coin flip, independent and identically distributed data, or i.i.d. for short.
In order to operate the Bayesian framework it is necessary to assume there is some class of hypotheses under consideration that contains the correct hypothesis . We will see that a countable class is sufficient for universal induction. Therefore, unless otherwise indicated, we (can) assume that is countable. Each of these hypotheses must be assigned some prior which represents the belief in this hypothesis before any data has been observed. For each we denote this prior by . This is something we do to a certain extent naturally. Imagine you see something unusual on the way to work such as an apartment block surrounded by police cars and an ambulance. Naturally you might consider a number of different explanations for this. Perhaps there was a break in, or a murder, or a drug bust. There is essentially a countless number of possible explanations you might consider which is analogous to the model class. Presumably one of these is correct and you would not consider them all to be equally likely. Your plausibility of each corresponds to the priors .
In order to be rigorous it is required that the hypothesis class be mutually exclusive and that the priors sum to one. That is . These requirements are simply equivalent to requiring that our belief system is rationally consistent. The prior belief in a particular observation string is the weighted sum of the beliefs in the string given by each hypothesis with weight proportional to the belief in that hypothesis. Formally where . This is a key concept, known as Bayes mixture, or marginal likelihood, which will be explained further. Note that the implicit dependence on “background knowledge” .
4.4. Bayes Theorem
Bayes theorem is used to update the belief in a hypothesis according to the observed data. This formula is easily derived from the definition of conditional probability.
A set of events is mutually exclusive and complete when any event in the sample space Ω must belong to one and only one event from this set. For example, any event
E along with it complement
form a mutually exclusive and complete set. Imagine you’re throwing a die and
E is the event of a 6. Obviously any throw must be in either the set
or its complement
. If Λ is a mutually exclusive and complete countable set of events, then
. This can be derived by using all and only Kolmogorov’s axioms of probability and the definition of conditional probability stated in
Section 3.3. Therefore Bayes theorem can be given in the form
Now let
be a hypothesis from class
, and
is be observational data. Since the model class
is required to be mutually exclusive and complete, Bayes formula can be expressed as follows
This is the posterior belief in
conditioned on data
is denoted
. The term
is the prior belief
and the term
is known as the likelihood. This likelihood is the probability of seeing the data
if hypothesis
is the true environment. But this is exactly how we defined the distribution given by hypothesis
and therefore
.
4.5. Partial Hypotheses
So far we have only considered complete hypotheses. These specify complete environments and therefore uniquely determine a probability distribution. In many cases however, we have hypotheses that only partially specify the environment. Instead they represent the set of all environments that satisfy some property, such as the property that some given statement is true.
For example consider a coin with some unknown bias θ, representing the probability the coin will land heads. We now flip the coin repeatedly to find its exact bias. An example of a complete hypothesis is the statement “the coin will land on heads of the time”, or . An example of an incomplete hypothesis is the statement “the coin will land heads somewhere between of the time and of the time”, or . It’s clear that the first hypothesis is a specific case of the second hypothesis. Now consider the statement “all ravens are black”. This is a partial hypothesis that consists of any environment where all ravens are black, or where there are no non-black ravens. This will be relevant when we examine the black ravens paradox.
It is important to be careful when dealing with these partial hypotheses. We showed that for a complete hypothesis we have . For a partial hypothesis this no longer holds since refers to a set of distributions and hence is undefined.
4.6. Sequence Prediction
From a metaphysical perspective it may be argued that our ultimate goal is to understand the true nature of the universe, or in this context to know which of the environment distributions is the true distribution , which will simply be denoted μ from now on. But since we are taking an agent based point of view, our aim is to make optimal decisions in terms of maximizing some utility function. From this more pragmatic perspective the primary concern is to make accurate predictions about the environment. This is called a prequential or transductive setting. Since the optimal predictions are given by the true distribution these approaches are not radically different; however, as we will see, it is not necessary to perform the intermediate step of identifying the correct distribution in order to make good predictions.
In some sense it is predictive power that has always been the primary function of science and reasoning. We know that realistically our scientific models may never be completely correct, however they are considered successful when they yield predictions that are accurate enough for our current purposes.
The goal is to make predictions that are optimal given the information available. Ideally this information extends to knowledge of the true environment μ in which case the optimal prediction is simply defined by this distribution, however this is rarely the case. Instead predictions must be based on some estimate of the true distribution which reflects an educated guess ρ of μ. Let all previous observational data be in the form of the string . Obtaining the posterior or predictive ρ-probability that the next observation will be is given by the conditional probability under ρ. Formally, . In the Bayesian framework this estimation is given by Bayes mixture ξ.
4.7. Bayes Mixture
If our class of hypotheses is countable then we can use the weighted average of all our hypotheses by their respective priors as our best guess estimation
ρ of the true environment
μ. This can be thought of as the subjective probability distribution as described above. Formally it is called Bayes Mixture and defined as follows
This definition makes perfect intuitive sense. The contribution of an environment
ν to the prediction of an observation
x is a combination of the prediction of
x under this environment
and the belief in this environment
. Imagine some environment
q predicts
x with certainty but your belief in this environment
is small, while all other environments in
predict
x with small probability. We would expect, as Bayes mixture implies, that the resulting probability of
x will remain small although larger than if
q was not considered at all.
Continuing with the poker example above, your opponent’s hand may be thought of as the unknown environment. The opponent may hold any hand and each of these corresponds to a particular hypothesis ν which you belief with probability . In this case consider the observation x to be the event that you win the hand. If there are still cards to be dealt then the prediction may be uncertain depending on how likely the remaining cards are to change the outcome. For example if you have three aces and ν is the hypothesis that the opponent has four diamonds, with one card to come, then since there is approximately chance that the next card will be a diamond which will make your opponents diamond flush beat your three aces. If there are no remaining cards then is simply one or zero depending on whether your hand is better or worse than hand ν respectively. Your beliefs may depend on psychological factors and previous betting but your final decision, if rational, should involve the estimation ξ over the various possible environments. Even if you have a sure belief that an opponent has a particular hand μ then this system remains consistent since ξ simply becomes the distribution given by μ. This is because , for all and therefore .
The probability of some observation under this Bayes mixture estimation can be thought of as its subjective probability since it depends on the priors which reflect our personal belief in the hypotheses before any data has been observed. If our belief
for some
ν, it does not contribute to
ξ and could equally well be dropped from
. Therefore, without loss of generality and consistent with Epicurus, we assume
from now on. An important mathematical property of this mixture model is its dominance.
This means that the probability of a particular observation under Bayes mixture is at least as great as its probability under any particular hypothesis in proportion to the prior belief in that hypothesis. This is trivial to see since the probability under Bayes mix is simply obtained by summing the probabilities under each hypothesis proportional to its prior and these are all non-negative. In particular this result applies to the true distribution
μ. This property is crucial in proving the following convergence results.
4.8. Expectation
Since our predications deal with possibly stochastic environments, expectation is an important concept in examining performance. When there is random chance involved in what rewards are gained, it is difficult to make guarantees about the effect of a single action. The action that receives a higher reward in this instance may not be optimal in the long run. As long as we have arbitrarily many tries, the best strategy is to choose the action that maximizes the expected reward. This is particularly relevant in relation to agent based learning.
In general, expectation is defined for some function
, which assigns a real value to an observation sequence of any length in the following way:
This can be thought of as the average value of a function under the true distribution. When we talk about maximizing an agent’s expected reward the function being considered is the agent’s utility function and this is generally the most important value. For example, when given the choice between a certain
or a
chance at
the rational choice is to take the latter option as it maximizes one’s expectation, assuming monetary value defines utility. Expectation is an essential concept for making good decisions in any stochastic environment.
In poker, for example, a good player uses expectation continuously, although the calculations may eventually become instinctual to a large degree. In general a player’s decision to continue in a hand depends on whether the expected return is larger than the amount the player must invest in the hand. In the case of Texas hold’em poker the true environment is the distribution given by the shuffled deck and the function is the expected return on some sequence of communal cards. It should also be noted that this is not a stationary environment: the distribution changes conditioned on the new information available in the communal cards.
4.9. Convergence Results
For the Bayesian mixture to be useful it is important that it performs well. As the accuracy of predictions is the primary concern, the performance of a distribution is measured by how close its predictions are to those of the true environment distribution. The analysis of this performance varies depending on whether the true environment is deterministic or stochastic.
Deterministic. In the deterministic setting the accuracy is easier to determine: As an observation either will or will not be observed, there is no uncertainty. For a deterministic environment it is sufficient to know the unique observation sequence
α that must be generated, since it contains all the information of the environment. Formally
for all
n where
is the initial
n elements of
α, and
for any
x that is not a prefix of
α,
i.e., there is no
n such that
. In this deterministic case the following results hold
Although the true distribution is deterministic, and perhaps even all environments in the hypothesis class
, this does not imply that Bayes mixture
ξ will be deterministic (see
Subsection 7.2).
Since an infinite sum of positive numbers can only be finite if they tend to zero, this result shows that the probability that the next observation will be predicted correctly under ξ, given all previous observations, converges rapidly to one. The sum of the probabilities that an incorrect, or off sequence, observation is predicted is bounded depending on our prior belief in the true environment α. If our prior belief is one, the true environment is known, then this constant is zero, meaning that we never make a mistake. This is not surprising as there is no uncertainty in our beliefs or the environment. For very small prior beliefs this bound grows larger which is again intuitive as the contribution of the true environment to the correct prediction will initially be small. However as long as the prior is non-zero, Bayes mixture performs well.
The seconds result shows that Bayes mixture will eventually predict arbitrarily many sequential observations correctly with probability approaching one. This means it is also an excellent multi-step look-ahead predictor.
Non-Deterministic. In non-deterministic environments there is always uncertainty about the observation sequence so we need to generalize our criterion for good performance. At each step the true environment is going to produce each observation with some probability, so ideally we want to predict each observation with this same probability. Therefore, in order to perform well, we want the distribution given by Bayes mixture to converge to the true distribution. To analyze this convergence a notion of distance between the two predictive distributions is required. For this we use the squared Hellinger distance.
This distance is dependent on the previously observed data because the distributions given by the environments are also dependent on this data. Intuitively two distributions are the same when they give equal probabilities to all possible observations, which is exactly the requirement for the Hellinger distance to be zero.
Even with this concept of distance the stochastic nature of the true environment makes mathematical guarantees difficult. For example a very unlikely sequence of observations may occur which causes Bayes mixture to be a lot further from the true distribution than we would expect. Because of this, results are given in terms of expectations. For example imagine a coin is flipped one hundred times and you are given the choice to receive for every heads and for every tails or every flip regardless. In the first case the only guarantee is that you will receive between and , however you know that the expectation is which is greater than the certain you would receive in the second case. Therefore expectation allows us to make decisions that will be beneficial in the long run.
It was shown in [
17,
24] that
As before the upper bound is a constant dependent on the prior belief in the true environment and the intuition is the same. This result implies that
will rapidly converge to
with probability one as
. In a stochastic environment “with probability one” is usually the strongest guarantee that can be made so this is a strong result. Roughly it states that the expected number of errors will be finite and Bayes mix will eventually be the same as the true predictive distribution.
4.10. Bayesian Decisions
We have seen that Bayes mixture acts as an excellent predictor and converges rapidly to the true environment. It is therefore not surprising that making decisions based on this predictor will result in excellent behavior. When making decisions however we are not concerned with the accuracy of our decisions but rather with the resultant loss or gain. We want to make the decision that will maximize our expected reward or minimize our expected loss.
In general, not all wrong predictions are equally bad. When predicting the rise and fall of stocks for example, a prediction that is off by only a fraction of a cent is probably still very useful while a prediction that is off by a few dollars may be hugely costly. As long as this loss is bounded we can normalize it to lie in the interval . Formally let be the received loss when has been predicted and was the correct observation.
Given this loss function the optimal predictor
for environment
ρ after seeing observations
is defined as the prediction or decision or action
that minimizes the
ρ-expected loss. This is the action that we expect to be least bad according to environment
ρ.
It should be noted that this optimal predictor may not give the prediction that is most likely. Imagine we have some test
T for cancer. The test result for a patient shows that there is a
chance that the patient has cancer. In other words we can consider
T to be the distribution where
. The loss incurred by not predicting cancer given that the patient does have cancer is 1 (after normalization), if the patient does not have cancer the loss is 0. On the other hand the loss incurred by predicting cancer if the patient does have cancer is
while if the patient does not have cancer the loss is a nominal
for premature treatment or further testing.
Given these values the
T-expected loss of predicting cancer is
The
T-expected loss of not predicting cancer is
Therefore
, the optimal predictor for
T, would choose to predict cancer even though there’s only a
likelihood, because it minimized the
T-expected loss.
Given this optimal predictor, the expected instantaneous loss at time
t and the total expected loss from the first
n predictions are defined as follows.
Obviously the best predictor possible is the optimal predictor for the true environment
, however as
μ is generally unknown, the best available option is the optimal predictor
for Bayes mixture
ξ for which the following result holds:
This means that the squared difference between the square roots of the total expected losses for
ξ and
μ is also bounded by a constant dependant on our initial belief. This result demonstrates that from a decision theoretic perspective the Bayesian mixture as a predictor performs excellently because it suffers loss only slightly larger than the minimal loss possible. The bound also implies that the instantaneous
of Bayes-optimal predictor
converges to the best possible
of the informed predictor
. In fact one can show that if a predictor performs better than
in any particular environment then it must perform worse in another environment. This is referred to as Pareto optimal in [
25].
4.11. Continuous Environment Classes
Although the results above were proved assuming that the model class is countable, analogous results hold for the case that the model class
is uncountable such as continuous parameter classes. For a continuous
the Bayesian mixture must be defined by integrating over
.
where
is (now) a prior probability
density over
. One problem with this is that the dominance
is no longer valid since the prior probability (not the density) is zero for any single point. To avoid this problem the Bayesian mixture is instead shown to dominate the integral over a small vicinity around the true environment
μ. By making some weak assumptions about the smoothness of the parametric model class
, a weaker type of dominance makes it possible to prove the following [
25,
26]:
This shows that even for a continuous
we get a similar bound. The added logarithmic term means that the sum to
n of the expected Hellinger distance is no longer bounded but grows very slowly. This is still enough to show that the distribution given by
ξ deviates from the true distribution
μ extremely seldom. The main point is that the effectiveness of the Bayesian framework is not significantly impaired by using a continuous class of environments.
4.12. Choosing the Model Class
The above results demonstrate that the Bayesian framework is highly effective and essentially optimal given the available information. Unfortunately the operation and performance of this framework is sensitive to the initial choice of hypothesis class and prior. As long as they are non-zero, the chosen priors will not affect the asymptotic performance of the Bayesian mixture as the observations eventually wash out this initial belief value. However in short-term applications they can have a significant impact.
The only restriction on the hypothesis class is that it must contain the true environment. This means any hypothesis that may be true, however unlikely, should be considered. On the other hand, having unnecessarily cumbersome classes will affect the prior values as they must sum to one. This means adding unnecessary hypotheses will subtract from the priors of relevant hypotheses. Since the bound of is proportional to the log inverse prior, having unnecessarily small priors leads to a high error bound which may affect short-term performance.
For these reasons, the general guideline is to choose the smallest model class that will contain the true environment and priors that best reflect a rational a-priori belief in each of these environments. If no prior information is available then these priors should reflect this lack of knowledge by being neutral or objective. In the case of universal induction however, there is essentially no thinkable hypothesis we can disregard, so we require a very large model class.
How to assign reasonable priors over model classes in general and the model class of essentially all possible explanations in particular is at the heart of the induction problem. We devote a whole own section to this intricate issue.
5. History
The history of the induction problem goes back to ancient times and is intimately tied to the history of science as a whole. The induction principle is at the core of how we understand and interact with our world and it is therefore not surprising that it was a topic of interest for numerous philosophers and scientists throughout history, even before the term induction was used or properly defined. It is however surprising that a formal understanding of induction is not given greater emphasis in education when it is, at least implicitly, of fundamental importance and relevance to all of science. In the following we will look at some of the most important historical contributions to inductive reasoning, including recent attempts at formalizing induction. We will also examine some of the major problems that plagued these attempts and later these will be re-examined in the context of universal induction to illustrate how Solomonoff succeeds where others have failed.
5.1. Epicurus
Some of the earliest writings on inductive reasoning are attributed to the ancient Greek philosopher Epicurus born roughly 341BC. Epicurus founded the philosophical school of Epicureanism which taught that observation and analogy were the two processes by which all knowledge was created. Epicurus’s most relevant teaching in regard to inductive reasoning is his principle of multiple explanations. This principle states that “if more than one theory is consistent with the data, keep them all”. Epicurus believed that if two theories explained some observed phenomenon equally well it would be unscientific to choose one over the other. Instead both theories should be kept as long as they both remain consistent with the data.
This principle was illustrated by one of his followers with the example of observing a dead body lying far away [
27]. In reasoning about the cause of death we may list all possible causes such as poison, disease, attack etc, in order to include the one true cause of death. Although we could reason that one of these must be the correct cause there is no way of establishing the true cause conclusively without further examination and therefore we must maintain a list of possible causes.
Similar reasoning is used in statistics to derive the principle of indifference which assigns equal prior probabilities to all models when there is no reason to initially prefer one over any other. Although there is clearly a certain validity in Epicurus’s reasoning, it seems unsatisfactory to believe equally in any hypothesis that accounts for some observed phenomenon. To see this consider that you have just looked at your watch and it is showing the time as 1 pm. It seems reasonable that you should therefore believe in the hypothesis that the time is in fact 1 pm and your watch is on time. But the hypothesis that it is actually 3 pm and your watch is two hours slow also explains the observations. It is also possible that a friend set your watch forward three hours as a joke and it is only 10 am. In fact it is possible to come up with ever more implausible scenarios which would equally account for your watch currently showing 1 pm and which would therefore, according to Epicurus, deserve equal consideration. So why then do we maintain a strong believe that our watch is correct and the time is actually 1 pm? If we were entirely true to Epicurus’s principle then a watch would have no use to us at all since any time would be equally possible regardless of the time shown. It is clear that our belief in a hypothesis is directly related to its plausibility and it is this idea of plausibility which we will further investigate.
Another problem with the principle of indifference is that it says nothing about how we should choose between conflicting predictions given by the various consistent models. Since our primary concern is making good predictions this is a serious issue.
5.2. Sextus Empiricus and David Hume
Sextus Empiricus was a philosopher born in 160 AD who gives one of the first accounts of inductive skepticism. He wrote
When they propose to establish the universal from the particulars by means of induction, they will effect this by a review of either all or some of the particulars. But if they review some, the induction will be insecure, since some of the particulars omitted in the induction may contravene the universal; while if they are to review all, they will be toiling at the impossible, since the particulars are infinite and indefinite. [
28]
This remains the simplest and most intuitive criticism of universal generalizations. Put simply it states that no universal generalization can ever be rigorously proven since it is always possible that an exception will be observed that will contradict this generalization. There is no flaw in this reasoning, however to believe that this argument invalidates induction is to misunderstand inductive reasoning. The argument does demonstrate that our belief in any universal generalization should never be , but this is widely accepted and does not hinder the formalization of an inductive framework. It does however give a sensible criterion which can be used to test the validity of an inductive method.
Sextus also gave an argument that resembles a better known argument due to Hume. Sextus wrote
“Those who claim for themselves to judge the truth are bound to possess a criterion of truth. This criterion, then, either is without a judge’s approval or has been approved. But if it is without approval, whence comes it that it is truthworthy? For no matter of dispute is to be trusted without judging. And, if it has been approved, that which approves it, in turn, either has been approved or has not been approved, and so on ad infinitum.” [
28]
Hume’s argument was that induction can not be justified because the only justification that can be given is inductive and hence the reasoning becomes circular. Although Hume and Empiricus reach the same conclusion, that induction can never be verified and is therefore inherently unreliable, they differ greatly in how they treat this conclusion.
Sextus believed that since there is no way affirming or denying any belief, we must give up any judgement about beliefs in order to attain peace of mind [
29]. It is worth mentioning that although he was a skeptic of induction, Empiricus’ philosophy was in many respects similar to the school of Bayesianism. Bayesians would agree that we should not hold any belief as certain (probability 1) or deny it entirely (probability 0;
cf. the confirmation problem in
Subsection 5.5), apart from logical tautologies or contradictions, respectively. Empiricus also believed that an objective truth of reality was unknowable and instead we can only be sure of our own subjective experiences. This is similar to the subjective interpretation of probability.
Hume on the other hand admits that using inductive inference, or at least reasoning by analogy, is an inevitable part of being human. He states
“having found, in many instances, that any two kinds of objects—flame and heat, snow and cold—have always been conjoined together; if flame or snow be presented anew to the senses, the mind is carried by custom to expect heat or cold, and to believe that such a quality does exist, and will discover itself upon a nearer approach. This belief is the necessary result of placing the mind in such circumstances” [
4]. Hume therefore concedes that although it can not be verified, induction is essential to our nature.
5.3. William of Ockham
The most important concept for inductive reasoning was famously posited by William of Ockham (or Occam) although the concept can not really be attributed to any person as it is simply an aspect of human nature. In its original form Occam’s razor is stated as “A plurality should only be postulated if there is some good reason, experience, or infallible authority for it”. A common interpretation is “keep the simplest theory consistent with the observations”. This principle is apparent in all scientific inquiry and in our day to day experience.
It is important to understand that a disposition towards simpler, or more plausible, explanations is simply common sense and should be entirely uncontroversial. For every observation we make on a day to day basis there is a multitude of possible explanations which we disregard because they are far too complex or unnecessarily convoluted to be plausible.
This was made clear in the example given above which made the point that even though there are various ways of accounting for a watch showing a certain time we remain convinced that it is the correct time. This is because the watch being correct is by far the simplest explanation. When Fred walks past some houses on a street numbered 1, 2, 3 respectively it would be natural for him to belief they are numbered in the standard manner however they may just as well be numbered according to the prime numbers which would have the natural continuation 5 rather than 4.
If you observe a street sign when searching for a house you have never visited before it is natural to assume it is correct rather than that it has been switched. It is even conceivable that you are witness to a vast hoax or conspiracy and all the signs you have seen have been changed. Perhaps the map you hold has itself been altered or you are coincidentally holding the one section that was misprinted in this edition or which Google maps got wrong. It is difficult to provide intuitive examples that do not seem entirely absurd but this is actually the point in some sense. A disposition towards simplicity is not only common sense, it is actually necessary for functioning normally in our world which overloads us with huge amounts information and countless conceivable explanations. People who place too much belief in unnecessarily complex ideas are often the ones labeled paranoid or illogical.
Occam’s razor is an elegant and concise formulation of this natural disposition, however it is still too vague to use formally. Both “simplest” and “consistent” require precise definitions, but this is difficult due to their inherent subjectivity. It is also worth noting that even two people observing the same phenomenon with precisely the same interpretation of Occam’s razor may draw different conclusions due to their past history. Generally speaking the observations referred to in Occam’s razor are from a specific experiment or phenomenon but philosophically they can be thought of as all the observations that make up an individual’s life and are therefore inevitably unique for each person. As a trivial example imagine Scott was walking with Fred down the street as he had seen the numbers 1, 2, 3 on the houses but Scott had previously observed that the next house on the street was numbered 5. Scott’s beliefs about the continuation of the sequence would then be different to Fred’s. He would be more inclined than Fred to believe the houses were numbered according to the primes. Having said this, Scott may still have a higher belief that the houses are numbered normally with the 4 absent for some unknown reason. This is because he has more evidence for the prime ordering than Fred but given his previous experience with house orderings the idea of a street with a prime ordering still seems more complex and hence less plausible than an explanation for the missing 4.
Few debate the validity of Occam’s razor, however it is exactly its subjective vague nature which has made it difficult to formalize. Various approaches to machine learning successfully apply a formal version of Occam’s razor relevant to the problem. For example when fitting a polynomial to some unknown function based on some noisy sample data we use a regularization term to avoid over-fitting. This means that the chosen solution is a trade off between minimizing the error and minimizing the complexity of the polynomial. This is not simply for aesthetic purposes; a polynomial that is chosen only to minimize the error will generally be far from the function that generated the data and therefore of little use for prediction. Unfortunately these methods are problem specific. Formalizing universal inductive reasoning requires a formal and universal measure of simplicity. As we will see this is exactly what Kolmogorov provides.
5.4. Pierre-Simon Laplace and the Rule of Succession
Laplace’s most famous contribution to inductive inference is his somewhat controversial rule of succession. For i.i.d. data where the outcome of each trial is either a success or a failure, this rule gives an estimation of the probability of success on the next trial. This is almost the same problem that Bayes formulated at the beginning of his essay.
Let
s be the number of successes,
f be the number of failures and
be the total number of trials, which is recorded in the binary string
x. The length of
x is the number of trials and each bit is either a 1 if the corresponding trial was a success or a 0 if it was a failure. For example if we have had
trials that were success, success, failure, success respectively then
,
, and
. The rule of succession states that the probability of success on the next trial is
The validity of this rule has been questioned but it follows directly from applying the Bayesian framework with a uniform prior and i.i.d. environment assumed. The derivation actually provides an informative illustration of how the Bayesian framework can be applied in practice. To see this, consider some stationary and independent experiments whose outcome we can categorize as either a success or a failure every time it is run, e.g., flipping a (biased) coin with heads being a success. In this case our model class
is the set of possible probabilities the experiment may give to success on a single trial. Let
be the true probability of success on a single trial. Since the experimental trials are stationary and independent,
remains constant, although our belief about
changes.
According to the definition of conditional probability we have where is the string with 1 appended at the end. The probability of any particular sequence x of failures and successes clearly depends on and is given by . The intuition behind this should be clear. Imagine you have a biased coin which gives heads with probability θ and hence tails with probability ). The probability of throwing heads s times is and the probability of throwing tails f times in a row is . Therefore, since the throws are i.i.d., the θ-probability of any sequence of throws with s heads and f tails is . For a regular, unbiased coin, the probability of heads is and therefore the probability of a sequence is . This means it depends only on the total number of throws.
We are now interested in the probability of some observation sequence
x. Since
θ is unknown we estimate the true probability using Bayes mixture which represents our subjective probability. This involves integrating over our prior belief density
to give
Note that we can not sum because the model class
is continuous and hence uncountable. Since we assume the prior distribution to be uniform and proper it must satisfy the following constraints
This results in the density,
. Therefore
The final equality is a known property of the Beta function. To find the conditional probability of success given this sequence we need to consider the sequence
with another success appended at the end. This is denoted
. The probability of this sequence
follows analogously from above since this sequence contains the same number of failures as
plus one more success. Therefore
The controversial and perhaps regretful example Laplace originally used to illustrate this rule was the probability that the sun will rise tomorrow given that it has risen in the past. Laplace believed that Earth was 5000 years old and hence that the sun had risen 1826213 times previously. Therefore by his rule the probability that the sun will rise tomorrow is
or equivalently the probability that it will not rise is
. In his original statement of the problem Laplace appended the example immediately with a note that this is only applicable if we knew nothing else about the mechanism of the sun rising, but since we know a lot about this mechanism the probability would be far greater. Unfortunately many ignored this accompanying explanation and claimed that the rule was invalid because this estimate for the sun rising was simply absurd. One counter example claimed that by the same reasoning the probability that a 10 year old child will live another year is
compared with an 80 year old man having probability
[
23] even though this clearly is a case where previous knowledge and lack of independence make the rule inapplicable.
5.5. Confirmation Problem
The confirmation problem involves the inability to confirm some particular hypothesis in the hypothesis class regardless of the evidence we observe for it. Usually the hypotheses considered when examining this problem are universal generalizations. Dealing with universal generalizations remains one of the most persistent challenges for systems of inductive logic.
As Empiricus argued, verifying any universal generalization is difficult because regardless of how many instances of something we observe, it is always possible that some unobserved instance will contradict any conclusions we may have drawn thus far. Therefore, finding a system that gives complete certainty in a universal generalization cannot be the actual goal since we know that this could not be justified unless we have observed every possible instance of the object about which the generalization was made. The problem is in finding a system that agrees with our intuition in all aspects of inductive logic. However satisfactory behavior regarding the confirmation of universal generalizations has evaded most proposed systems.
It should be noted that in this section and throughout the article we have used the term confirmation as it appears commonly in the literature [
9]. The meaning in this context is similar to what an unfamiliar reader may associate more closely with the term
“supports”. To make this clear, some evidence
E is said to confirm a hypothesis
H if the posterior probability of
H given
E is greater than before
E was observed. Unfortunately, as is illustrated in the next subsection, this definition is unsatisfactory in certain circumstances. An arbitrarily small increment in belief may not deserve to be labeled as confirmation, and so we call it weak confirmation. The confirmation problem is illustrated here using the above rule of succession.
When applicable, Laplace’s rule of succession seems to produce a reasonable estimate. It converges to the relative frequency, it is defined before any observations have been seen (for ) and it is symmetric. It is also not over-confident, meaning that it never assigns probability 1 to an observation. This satisfies Epicurus’s argument that no induction can ever be certain. Unfortunately there are some significant drawbacks, namely the zero prior problem. This zero prior problem is a specific instance of the more general confirmation problem.
The zero prior problem occurs because of the prior factor present in Bayes rule. For some hypothesis H and evidence E Bayes rule states . Therefore it is clear that if then regardless of the evidence E our posterior evidence must remain identically zero. This is why any hypothesis which is possible, no matter how unlikely, must be assigned a non-zero prior. When approximating the probability of success in the biased coin-flip example above, the hypothesis H corresponds to a particular θ, and the evidence E is the observation sequence x. Although the densities are non-zero for all θ, the probability of any particular θ is . Any proper density function must have zero mass at any point. This means that for any θ, the posterior no matter what the observation sequence. Imagine we are observing the color of ravens and θ is the percentage of ravens that are black. The hypothesis “All ravens are black” therefore might be associated with , but even after observing one million black ravens and no non-black ravens , which means we are still certain that not all ravens are black: . This is clearly a problem.
If we instead consider the composite or partial hypothesis for any arbitrarily small ε, then converges to 1 as the number of observed black ravens increases. This is called a soft hypothesis and intuitively it is the hypothesis that the percentage of black ravens is 1 or very close to 1. The reason our belief in this hypothesis can converge to 1 is that the probability is now the integral over a small interval which has a-priori non-zero mass and a-posteriori asymptotically all mass .
Instead of
it is also possible to formulate the hypothesis “all ravens are black” as the observation sequence of an infinite number of black ravens,
i.e.,
where a 1 is a black raven. This purely observational interpretation might be considered philosophically more appropriate since it considers only observable data rather than an unobservable parameter. However the same problem occurs. If
is a sequence of
n black ravens, then
. Therefore
This means that for any finite
k our belief in the hypothesis that we will observe
k more black ravens converges to 1 as the number of observed ravens
n tends to infinity, which is not surprising and conforms to intuition. Once we have seen 1000 black ravens we strongly expect that we will observe another 10 black ravens. However for the above hypothesis of “all ravens are black”
k is infinite and the probability
will be zero for any number
n of observed ravens. By making the reasonable assumption that the population of ravens is finite, and therefore that
k is finite, we may expect to fix the problem. This is the approach taken by Maher [
9]. However it still leads to unacceptable results which we examine further in the next subsection.
Since both forms of the universal generalization fail to be confirmed by the rule of succession there seem to be only two reasonable options.
We can simply accept that hypotheses corresponding to exact values of θ can not be confirmed, so instead soft hypotheses corresponding to small intervals or neighborhoods must be used. While we can successfully reason about soft hypotheses, we still have to decide what to do with the universal hypotheses. We would somehow have to forbid assigning probabilities to all-quantified statements. Assigning probability zero to them is not a solution, since this implies that we are certain that everything has exceptions, which is unreasonable. We can also not be certain about their truth or falsity. Bare any semantic, we could equally well eliminate them from our language. So focussing on soft hypotheses results in a language that either does not include sentences like “all ravens are black” or if they exist have no meaning. This makes the soft hypothesis approach at best inelegant and impractical if not infeasible.
The other solution is to assign a non-zero weight to the point
[
23]. This point mass results in an improper probability density however it does solve the confirmation problem. One such improper distribution is a 50:50 mixture of a uniform distribution with a point mass at 1. Mathematically we consider the distribution function
with
, which gives
. Using this approach results in the following Bayesian mixture distribution, again with
s successes,
f failures and
trials:
Therefore, if all observations are successes, or black ravens, the Bayesian mixture gives
, which is much larger than the
given by the uniform prior. Because of this both the observational hypothesis
and the physical hypothesis
can be confirmed by the observation of a reasonable number of black ravens. Formally, the conditional distribution of seeing
k black ravens after seeing
n black ravens is given by
and hence the observational hypothesis
is confirmed with each new observation. Our confidence in the hypothesis that all ravens are black after having observed 100 black ravens is about
. The first line also shows confirmation occurs for any finite population
k. As we would expect the physical hypothesis similarly gets confirmed with
. The new prior also has the property that once a non-black raven is observed, the posterior Bayesian distribution becomes the same as it would have been if a uniform prior had been assumed from the start, since
in this case.
So far we have considered a binary alphabet, but the idea of assigning prior point masses has a natural generalization to general finite alphabet. For instance if we instead consider the percentage of black, white and colored ravens, the results remain analogous.
It is immediately clear that the chosen “improper density” solution is biased towards universal generalizations, in this case to the hypothesis “all ravens are black”. The question is then why not design the density to also be able to confirm “no ravens are black”, or “exactly half the ravens are black”? It would be possible to assign a point mass to each of these values of θ but then why only these values? These values correspond to hypotheses that seem more reasonable or more likely and therefore which we want to be able to confirm. But ideally we want to be able to confirm any reasonable hypothesis, so the question becomes which points correspond to reasonable hypotheses?
It seems that we are intuitively biased towards hypotheses corresponding to simpler values such as rational numbers but we can argue that significant irrational fractions such as are also very reasonable. Deciding where to draw the line is clearly problematic but the universal prior which is described later provides a promising solution. It assigns non-zero probability to any computable number, and the class of computable numbers certainly contains any reasonable values θ. A non-computable θ corresponds to a non-computable hypothesis, which are usually not considered (outside of mathematics). It should also be noted that even if θ is incomputable, there are always arbitrarily close values which are computable and hence can be confirmed. Formally this means that the set of computable numbers is dense in the real numbers. The universal prior can therefore be seen as a logical extension of the above method for solving the confirmation problem.
Since this class of computable values is infinite, it may be asked why we do not go one step further and simply assign every value a non-zero point mass. The reason is that it is not mathematically possible. The reason comes down to the difference between countably infinite and uncountably infinite. Without going into depth consider the infinite sum . The property of creating an infinite sum that gives a finite value is only possible for countably infinite sums and since the set of real numbers in the interval is uncountably infinite it is not possible to assign values that form an everywhere non-zero prior.
5.6. Patrick Maher Does not Capture the Logic of Confirmation
In his paper “probability captures the logic of scientific confirmation” [
9] Patrick Maher attempts to show that by assuming only the axioms of probability it is possible to define a predicate that captures in a precise and intuitively correct manner the concept of confirmation. Maher chooses to use a conditional set of probability axioms based on that of von Wright, presumably for convenience.
Maher’s definition of confirmation is
Intuitively meaning that some evidence
E confirms a hypothesis
H when the probability of
H given
E and some background knowledge
D is greater than the probability of
H given
D alone. It is generally agreed that any attempt to define confirmation must consider background knowledge. This is illustrated in the following example by I.J. Good [
30].
Suppose our background knowledge is that we live in one of two universes. In the first there are 100 black ravens, no non-black ravens and 1 million other birds. In the second there are 1000 black ravens, 1 white raven and 1 million other birds. Some bird a is selected at random from all the birds and is found to be a black raven. It is not hard to see that in this case the evidence that a is a black raven actually lessens our belief that “all ravens are black” since it increases the probability that we are in the second universe where this is false.
Maher successfully shows that the above definition satisfies several desirable properties regarding our intuition of confirmation and scientific practice such as verified consequences and reasoning by analogy. Unfortunately this definition fails to satisfactorily solve the problem of universal generalizations. To illustrate this problem we again consider confirmation of the universal generalization “all ravens are black”. In particular, given that we have observed n black ravens what is our belief that all ravens are black?
Consider Theorem 9 from Maher’s paper. For this example we assume that
a is drawn at random from the population of ravens and we take the predicate
to mean that
a is black.
This means that regardless of the evidence, as long as its logically consistent, our belief in the universal generalization
remains zero. This is clearly a problem since although our belief in this generalization should not be
certain it should be greater than zero as long as the evidence does not contradict the generalization. In particular it should be possible to observe some evidence
E, such as many
x for which
holds, which leads to a significant posterior belief in this universal generalization.
The reason for this problem, under Maher’s construction, is that the probability that the next observed raven is black converges to one too slowly. After seeing a long enough sequence of black ravens our belief that the next one is black will become arbitrarily close to one but it is the rate of this convergence that is a problem. Because of this, the probability that all ravens are black remains zero regardless of our initial belief. A corollary of this is Maher’s Theorem 10 which, for any logical truth
T, states
Intuitively this means that there is no evidence that can be said to confirm a universal generalization. Consider to be the evidence E in Theorem 9. Since the posterior belief in the universal generalization must always remain zero for any evidence it is clear that this evidence can not increase the belief. Therefore it can not satisfy Maher’s above definition of confirmation.
In observing that the zero probability of universal generalizations stems from the infinite product in the proof of Theorem 9, Maher attempts to rectify the problem by considering only a finite population which he states is sufficient. Even if we accept the finiteness assumption, the solution he provides differs dramatically from accepted intuition. Theorem 11 is where we see the major flaw in Maher’s reasoning.
If there are only N ravens in existence then the universal generalization is equivalent to N individual observations . In other words, as long as there is some finite population N of ravens any observed subset n of ravens confirms the universal generalization. This is technically correct but we see from the following numerical example that it is unacceptable. In order to be fair to Maher the example is constructed similar to his own numerical example.
Let the population of ravens in the world be
and the number of observed ravens be
. The learning rate is
and we assume the initial belief that some raven is black to be an optimistic
. By Maher’s Proposition 19, the degree of belief in the black raven hypothesis can be computed as follows:
This means that after observing 1000 ravens which were all black our belief in the generalization
“all ravens are black” is still only
. In other words we are virtually certain that non-black ravens exist or equivalently that not all ravens are black. This is a clear contradiction to both common sense and normal scientific practice and therefore we must reject Maher’s proposed definition. This model of confirmation is too weak to achieve a reasonable degree of belief in the black ravens hypothesis. In contrast, in
Section 7.4 we show that Solomonoff exhibits strong confirmation in the sense that
P tends to 1. It may be believed that this result is due to this particular setup of the problem, however any continuous prior density and reasonable parameter values will encounter the same problem. In particular this includes Maher’s more sophisticated model for two binary properties, which mixes a Laplace/Carnap model for blackness times one for ravenness with a Laplace/Carnap model where the properties are combined to a single quaternary property. Observing a small fraction of black ravens is not sufficient to believe more in the hypothesis than in its negation, since the degree of confirmation in Maher’s construction is too small.
5.7. Black Ravens Paradox
We have used the typical example of observing black ravens to demonstrate the flaws of both Laplace and Maher in relation to confirmation but the full “black ravens paradox” is a deeper problem. It is deeper because even in a system that can confirm universal hypotheses, it demonstrates a further property that is highly unintuitive.
The full black ravens paradox is this: It has been seen that one desirable property of any inductive framework is that the observation of a black raven confirms the hypothesis that “all ravens are black”. More generally we would like to have the following property for arbitrary predicates
A and
B. The observation of an object
x for which
and
are true confirms the hypothesis “all
x which are
A are also
B” or
. This is known as Nicods condition which has been seen as a highly intuitive property but it is not universally accepted [
9]. However even if there are particular situations where it does not hold it is certainly true in the majority of situations and in these situations the following problem remains.
The second ingredient to this paradox is the interchangeability of logically equivalent statements in induction. In particular, consider two logically equivalent hypotheses and . If some evidence E confirms hypothesis then it logically follows that E also confirms , and vice versa. But any implication of the form is logically equivalent to its contrapositive . Therefore, taking the predicate to mean “is a raven” and to mean “is black”, this gives the following: The hypothesis , or “all ravens are black”, is logically equivalent to its contrapositive , or “anything non-black is a non-raven”.
The fact that any evidence for is also evidence for leads to the following highly unintuitive result: Any non-black non-raven, such as a white sock or a red apple confirms the hypothesis that “All ravens are black”.
This may be seen as evidence that there is a fundamental flaw in the setup being used here, but on closer examination it is not entirely absurd. To see this, consider the principle in a more localized setup. Imagine there is a bucket containing some finite number of blocks. You know that each of these blocks is either triangular or square and you also know that each block is either red or blue. After observing that the first few blocks you see are square and red you develop the hypothesis “all square blocks are red”. Following this you observe a number of blue triangular blocks. According to the above principle these should confirm your hypothesis since they confirm the logically equivalent contrapositive, “All non-red (blue) blocks are non-square (triangular)”. If the statement were false then there must exist a counter example in the form of at least some blue square block. As you observe that a growing number of the finite amount of blocks are not counter examples your probability/belief that they exist decreases and therefore the two equivalent hypotheses should be confirmed.
In this simplified case it is also easier to see the intuitive connection between the observation of blue triangular blocks and the hypothesis “all square blocks are red”. Even if there were an infinite number of blocks, which means the chance of a counter example does not obviously diminish, the confirmation of the hypothesis “all square blocks are red” by a blue triangular block seems reasonable. The reason for this is the following. If there is an infinite number of objects then there is always the same infinite number of objects that may be counter examples, but the longer we go without observing a counter example the more sure we become that they do not exist. This human tendency is implicity related to the assumption of the principle of uniformity of nature which is discussed briefly later. We expect that eventually the sample we see will be representative of the entire population and hence if there are no counter examples in this sample they should be unlikely in the wider population.
In our real-world example of black ravens we can argue for this principle analogously. When we see a white sock it is technically one more item that can no longer be a counter example to the hypothesis “all ravens are black”. And although there may be an incomprehensively huge number of possible objects in our universe to observe, there is still only a finite amount of accessible matter and hence a finite number of objects. But this does not seem to change our strong intuition that this result is ridiculous. No matter how many white socks or red apples we observe we do not really increase our belief that all ravens are black. The solution to this problem lies in the relative degree of confirmation. The above result only states that the belief in the hypothesis must increase after observing either a black raven or a white sock, it says nothing about the size of this increase. If the size of the increase is inversely proportional to the proportion of this object type in the relevant object population then the result can become quite consistent and intuitive.
Consider again the bucket of blocks. First imagine the number of square and triangular blocks is the same. In this case observing a red square block or a blue triangular block should provide roughly the same degree of confirmation in the hypothesis “all square blocks are red”. Now imagine that only of the blocks are square and are triangular. You have observed 20 blue triangular blocks and suddenly you observe a red square block. Intuitively, even if the blue triangular blocks are confirming the hypothesis “all red blocks are square”, it seems the observation of a red square block provides substantially more evidence and hence a much greater degree of confirmation. The higher the proportion of blue triangular blocks, the less confirmation power they have, while the smaller the proportion of blue blocks, the higher their confirmation power.
This also solves the problem of our intuition regarding black ravens. Black ravens make up a vanishingly small proportion off all possible objects, so the observation of a black raven gives an enormously greater degree of confirmation to “all ravens are black” than a non-black non-raven. So much so that the observation of a non-black non-raven has a negligible affect on our belief in the statement.
Unfortunately no formal inductive system has been shown to formally give this desired result so far. It is believed that Solomonoff Induction may be able to achieve this result but is has not been shown rigorously. Later we will argue the case for Solomonoff induction.
5.8. Alan Turing
In 1936 Alan Turing introduced the Turing machine. This surprisingly simple hypothetical machine turned out to be the unlikely final ingredient necessary for Solomonoff’s induction scheme as it allows for a universal and essentially objective measure of simplicity.
Turing’s aim was to capture the fundamental building blocks of how we undertake a task or procedure in a way that was general enough to describe a solution to any well defined problem. The final product is very minimal consisting of only a few core components. A Turing machine has a single work tape of infinite length which it can read from and write to using some finite number of symbols. The reading and writing is done by a read/write head which can only operate on one symbol at a time before either halting or moving to a neighboring symbol. The rest of the Turing machine is specific to the task and consists of the procedural rules. These rules can be represented by internal states with transitions that depend on what tape symbol is read and which in turn determine which tape symbol is written. These states can also be replaced by a look-up table that store the equivalent information. A comprehensive understanding of precisely how Turing machines work is not necessary for the purpose of this article as they are only dealt with on an abstract level. It is important however to have an intuitive understanding of their capabilities and properties.
It turns out that this simple construction is incredibly powerful. The Church–Turing Thesis states that “Everything that can be reasonably said to be computed by a human using a fixed procedure can be computed by a Turing machine”. There have been various attempts at defining precisely what a “fixed procedure” is, however all serious attempts have turned out to describe an equivalent class of problems. This class of computable functions or problems is actually large enough to include essentially any environment or problem encountered in science. This is because every model we use is defined by precise rules which can be encoded as an algorithm on a Turing machine. At a fundamental level every particle interaction is determined by laws that can be calculated and hence the outcome of any larger system is computable. The quantum mechanics model is problematic as it implies the existence of truly random natural processes but as long as a Turing machine is given access to a truly random source of input then even this model can be captured.
Although a Turing machine can be constructed for any computable task it is far from unique. For every task there is actually an infinite number of Turing machines that can compute it. For example there are an infinite number of programs that print “hello world”.
Strictly speaking Turing machines are hypothetical because of the requirement of an infinite work tape. Nevertheless we can think of a Turing machine as a computer with finite memory but which can be arbitrarily extended as it is required. Then the analogy of Turing machines and real computers actually becomes an equivalence. There are actually two valid analogies that can be drawn, which illustrates an interesting property of Turing machines. First consider the entire memory of the computer to be analogous to the work tape of the Turing machine and the program counter to be the position of the read/write head. Under this analogy the hardware makes up the procedural rules that govern how memory is written to and read from. Secondly consider some program running on this computer. Now only some of the physical memory corresponds to the work tape and the memory that holds the program instructions corresponds to the procedural rules. Not only are both of these analogies valid, they can both be true at the same time. A program can be thought of as a Turing machine for a specific task which is itself encoded in some language (ultimately binary) and a computer can be thought of as a Turing machine that simulates these encoded Turing machines.
This ability to create a Turing machine to simulate any other Turing machine is crucial to Solomonoff’s framework. Turing machines with this property are called Universal Turing machines and just as with any other task, there is an infinite number of them corresponding to the infinitely many ways of encoding a Turing machine as a string.
5.9. Andrey Kolmogorov
The same Kolmogorov who introduced the by now standard axioms of probability was also interested in universal notions of information content in or complexity of objects. Kolmogorov complexity quantifies the troublesome notion of complexity and hence also simplicity, which is crucial for a formal application of Occam’s razor. Before looking at Kolmogorov’s formal definition it is useful to review our intuitive understanding of simplicity.
Simplicity. The idea of simplicity is extremely broad as it can be applied to any object, model, function or anything that can be clearly described. It is exactly this idea of a description which is useful in finding a general definition. Let A be some arbitrary object, it could be as simple as a coffee mug. Let B be the same as A except with some added detail or information such as a word printed on the mug. Now it is natural to think of A as simpler than B because it takes longer to precisely describe B than A. This idea of description length turns out to be the most general and intuitive method for quantifying complexity.
Consider two strings x and y where x is a random thousand digit number and y is one thousand in a row. At first it may seem these two strings are just as complex as each other because they each take a thousand digits to describe however “one thousand in a row” is also a complete description of y which only requires twenty five characters. There are many possible descriptions of any string so a decision must be made as to which description to associate with the string’s complexity. Since there are always arbitrarily long descriptions the answer is to take the length of shortest possible description as the complexity measure. It is clear then that y is simpler than x since it has a far shorter description. x was also described with the short sentence “a random thousand digit number”but this was not a complete description. There are many numbers that could be a random thousand digit number but only one number is one thousand in a row. The shortest complete description of any 1000 digit random string is the string itself, hence about 1000 digits long.
Accepting that the simplicity of an object is given by its shortest possible description the issue of subjectivity remains in the choice of description language used. It is clear that the length of a description may be different in different languages and in the extreme case an arbitrarily complex string c can have an arbitrarily short description in a language constructed specifically for the purpose of describing c. This problem can be avoided by choosing a single unbiased language to use for all descriptions.
Kolmogorov Complexity. Kolmogorov’s idea was to use Turing machines to formally address the problem of subjectivity in the choice of description language. This is because a description of an object can be thought of as a procedure for producing an unambiguous encoding of that object. In other words a description is a program. Coming back to the previous example, a formal coding of “one thousand in a row” may be “for(i=0;i<1000;i++) printf(“9”);”.
There may of course be shorter descriptions but this at least gives an upper bound on the shortest description. The random number on the other hand would still have to be written out entirely which would result in a much longer shortest description “printf(“01100101...10011”);”. If x could be specified by a shorter description, then it would contain some structure, so by definition it would not be random.
By using programs we are again faced with the problem of choosing the programming language, however all programming languages are compiled to the native assembly language before being interpreted by the computer. Assembly (at least for RISC or Lisp processors) provides a rather unbiased, and surely universal language. This is now close to Kolmogorov’s formal definition. It is worth noting here that the extreme cases of languages tailored for a specific description is practically prevented by using assembly language. Consider the case where we attempt to “cheat” the system by hard-coding a long complex string such as c as a simple variable j in some new programming language. Although “print j” is now a simple description of c in this new language, when compiled to assembler the complexity of c becomes clear since the assembly code for this program will still need to contain its full description of the hard-coding of j.
A specific program in any language can be thought of as an encoding of a Turing machine and likewise a Turing machine can be thought of as a program. A Universal Turing machine can be used to simulate these encoded Turing machines or programs. This means that if a program/Turing machine p produces y when given x, then a universal Turing machine will also produce y when given x and p. Since native assembly language can represent any program it can be thought of as a particular Universal Turing machine. Therefore, taking the description with respect to assembly language is essentially the same as taking the description with respect to this particular Universal Turing machine. Since native assembly is written in binary we consider the description alphabet to be binary also.
Formally the Kolmogorov complexity of a string
x is defined as
Where
U is the Universal reference Turing machine, and
is the length of
p in binary representation.
In other words, the Kolmogorov complexity of x is the length of the encoding of the shortest program p that produces x when given as input to the Universal reference Turing machine.
Conditional Kolmogorov Complexity. In some cases it is necessary to measure the complexity of an object or environment relative to some given information. This is done using the conditional Kolmogorov complexity. Let
x be some string and imagine we want to measure the complexity of
x in relation to some previous knowledge, or side information,
y. The conditional Kolmogorov complexity is defined as follows
In other words it is the length of the shortest program to output
x given
y as extra input. This means that the information or structure present in
y may be used to shorten the shortest description of
x. If
y is uninformative or unrelated to
x then
will be essentially the same as
. However if
y contains a lot of the information relevant to
x then
will be significantly smaller. As an example consider an environment
that simply repeats a long complex sequence
y over and over.
will therefore be proportional to the complexity of
y. If, however, the side information
z contains at least one iteration of
y then it is easy to construct a simple short program that takes the relevant substring of
y and copies it repeatedly. Therefore
will be very small.
This introduction to Kolmogorov complexity was necessarily cursory. Kolmogorov complexity possesses many amazing properties and relations to algorithmic randomness and Shannon entropy. There are also many variations, and indeed throughout this work,
K stands for the prefix/monotone version if applied to finite/infinite strings. The differences are technically important, but are of no concern for us. The definition of
K has natural extensions to other non-string objects
x, such as natural numbers and functions, by requiring
U to produce some binary representation of
x. See [
27,
31] for a list of properties and a discussion of the graphical sketch of
K in
Figure 1.
Natural Turing Machines. The final issue is the choice of Universal Turing machine to be used as the reference machine. The problem is that there is still subjectivity involved in this choice since what is simple on one Turing machine may not be on another. More formally, it can be shown that for any arbitrarily complex string x as measured against the UTM U there is another UTM machine for which x has Kolmogorov complexity 1. This result seems to undermine the entire concept of a universal simplicity measure but it is more of a philosophical nuisance which only occurs in specifically designed pathological examples. The Turing machine would have to be absurdly biased towards the string x which would require previous knowledge of x. The analogy here would be to hard-code some arbitrary long complex number into the hardware of a computer system which is clearly not a natural design.
To deal with this case we make the soft assumption that the reference machine is natural in the sense that no such specific biases exist. Unfortunately there is no rigorous definition of natural but it is possible to argue for a reasonable and intuitive definition in this context. A universal Turing machine should be considered natural if it does not contain any extreme biases. In other words if it does not make any arbitrary, intuitively complex strings, appear simple. It is possible to make a reasonable judgement about this but it is preferable if there is a formal criterion which can be applied.
One possible criterion is that a reference machine is naturalif there is a short interpreter/compiler for it on some predetermined and universally agreed upon reference machine. If a machine did have an in-built bias for any complex strings then there could not exist a short interpreter/compiler. If there is no bias then we assume it is always possible to find a short compiler.
A bit more formally this is known as the short compiler assumption [
17] and can be stated as follows. “Given two
natural Turing-equivalent formal systems
and
there always exists a single
short program
I on
that is capable of interpreting all
programs”. This assumption is important in establishing the universality of Kolmogorov’s complexity measure. If string
x has Kolmogorov complexity
relative to system
then the upper bound of
is
where
is the length of the short interpreter. This follows simply from the fact that any
x can be encoded/described on
by using the encoding for
followed by the interpreter. There may of course be shorter descriptions but the shortest description is clearly at most this length. Analogous reasoning shows that
. This means that the Kolmogorov complexity of a string with respect to some system
F will be the same for any
natural F, within a reasonably small constant which is independent of the string being measured.
To make the above criterion formal it is necessary to quantify this concept of
short. The larger it is the more flexible this definition of
natural becomes. But there is a still a serious problem. The definition relies on the existence of “some predetermined and universally agreed on reference machine” which there is currently no consensus about. In deciding on which UTM to use for this definition it seems reasonable to choose the “most” natural UTM but this is obviously a circular endeavor. It may be argued [
17] that the precise choice of machine is not of critical importance as long as it is intuitively natural since, by the short compiler assumption, the complexity will remain approximately equal. From this perspective the practical and theoretical benefit of having some final fixed reference point outweighs the importance of making this fixed reference point “optimal” in some sense, since it has little practical impact and appears to be philosophically unsolvable.
This issue is one of the outstanding problems in algorithmic information theory [
32]. Fixing a reference machine would fix the additive and multiplicative constants that occur in many results and draw criticism to the field. Although it by no means solves the problem there is another useful way to view the issue.
The Kolmogorov complexity of a string depends only on the functionality of the universal reference machine and not its exact construction. That is, if there are two machines that, given the same input, always produce the same output, then they are said to be functionally equivalent and will result in the same Kolmogorov complexity for any string. The purpose of a universal Turing machine is only to simulate the Turing machine that is encoded as input and therefore the output of a universal Turing machine is uniquely defined by the Turing machine it is simulating (and the input for this Turing machine). This means that if two different UTM’s simulate the same Turing machine then they must produce the same output. If they both use the same encoding scheme then simulating the same Turing machine corresponds to having the same input and hence they must be functionally equivalent since the same input will always produce the same output. Since we only care about functionality, this observation shows that the choice of universal reference machine is equivalent to a choice of encoding scheme. The significance of this is that it is easier to argue for an intuitively natural encoding scheme than an intuitively natural Turing machine.
6. How to Choose the Prior
As previously shown, the Bayesian framework results in excellent predictions given a model class that contains the true environment and a reasonable prior assigned to each hypothesis . Unfortunately the framework gives no rigorous general method for selecting either this class or the priors. In the Bayesianism section we briefly discussed how to make a reasonable choice of model class and prior. Here we examine the prior in further detail; specifically general approaches and possible issues.
6.1. Subjective versus Objective Priors
A good prior should be based on reasonable and rational beliefs about all possible hypotheses before any evidence for them has been seen. This statement is somewhat ambiguous however since it is debatable which observations can be considered evidence. When looking at universal induction, every observation we make is potentially relevant; for particular experiments it can be hard to know in advance what is relevant. This stems fundamentally from the subjective interpretation of probability at the heart of Bayesianism. Because of this, a choice of prior often belongs to one of two categories. Firstly there are objective priors based on rational principles which should apply to anyone without any prior relevant knowledge. Secondly there are subjective priors that attempt to capture an agent’s personal relevant experience or knowledge. For example a subjective prior for some experiment may be significantly influenced by experience with similar experiments.
Solomonoff induction can deal with both approaches, leading to a model of universal induction. Obviously we require some form of objective prior before any observations have been made, since there is no available information to create a subjective prior. From this point on every observation is used to update beliefs and these new beliefs could be interpreted as subjective priors based on past experience, used for the next problem.
Consider again drawing black or white balls from an urn with some unknown ratio. Assume you start with a prior biased towards believing the ratio is . After observing 10 black balls in a row initially you may interpret the situation in two equivalent ways. Either you are 10 balls into this experiment and your belief has changed, or you are starting the experiment again but now your prior is skewed to a ratio with more black balls. More generally your posterior belief about each hypothesis H after observing E becomes your new prior for the observations following E.
6.2. Indifference Principle
Quantifying Epicurus’s principle of multiple explanations leads to the indifference principle which assumes that if there is no evidence favoring any particular hypothesis then we should weight them all as equally likely. When told that an urn contains either all black balls or all white balls and no other information, it seems natural to assign a probability of to each hypothesis before any balls have been observed. This can be extended to any finite hypothesis class by assigning probability to each hypothesis where is the number of hypotheses in .
For a continuous hypothesis class the analogous approach is to assign a uniform prior density which must integrate to 1 to be a proper probability density. This means that if the fraction of black balls in the urn is with no extra information, we assign a uniform density of to all θ, as seen in the derivation of the rule of succession. This does not mean that the agent is certain in any parameter, rather for any interval the belief that is given by the integral . Specifically, the belief in any exact value θ is zero which gives rise to the zero prior problem and hence the confirmation problem as discussed previously.
Furthermore, in some situations this indifference principle can not be validly applied at all. For a countably infinite class , the probability is zero which is invalid since the sum is identically zero. Similarly, for a continuous parameter over an infinite (non-compact) range, such as the real numbers, the density must be assigned zero which is again invalid since the integral would also be zero. Even when it can be applied, two further issues that often arise are reparametrization invariance and regrouping invariance.
6.3. Reparametrization Invariance
The idea of indifference and hence uniformity in a prior seems quite straight forward but a problem occurs if a different parametrization of a space is used. The problem is that if there are multiple ways of parametrizing a space then applying indifference to different choices of parametrization may lead to a different prior.
Imagine 1000 balls are drawn, with replacement, from an urn containing black and white balls. The number of black balls drawn out of these 1000 samples must obviously lie somewhere between 0 and 1001 and we denote this number k. It may be argued that since we know nothing it is reasonable to assume indifference over the 1000 possible values of k. This would result in a roughly equal prior over all values of θ. More specifically it would assign a prior of to every value in the set , where n is the total number of trials, in this case 1000.
On the other hand it may be argued that it is equally plausible to have a prior that is indifferent over every observable sequence of 1000 black or white balls. However, if each of these possible sequences are assigned equal probability then a very different prior is created. The reason for this is that there are far more possible sequences which contain approximately 500 black balls than there are sequences that contain nearly all black balls or nearly no white balls. In the extremes there is only one possible sequence for which and one possible sequence for which , but there are possible sequences for which . This means that indifference over every possible sequence leads to a prior over θ that is strongly peaked around . This peak is sharper for a higher number of trials.
Similarly it may seem equally valid to assume indifference over either θ or which would again lead to different priors. In some situations the “correct” choice of parametrization may be clear but this is certainly not always the case. Some other principles do not have this issue. Principles that lead to the same prior regardless of the choice of parametrization are said to satisfy the reparametrization invariance principle (RIP). Formally the criterion for the RIP is as follows.
By applying some general principle to a parameter θ of hypothesis class we arrive at prior . For example as above leads to by indifference. We now consider some new parametrization which we assume is related to θ via some bijection f. In this case we consider . Now there are two ways to arrive at a prior which focuses on this new parameter . Firstly we can directly apply the same principle to this new parametrization to get prior . For the indifference principle this becomes . The second way is to transform the original prior using this same bijection. When the prior is a density this transformation is formally given by . For this leads to . If then the principle satisfies the reparametrization invariance principle. It is clear from the example of that the indifference principle does not satisfy RIP in the case of densities.
It does however satisfy RIP for finite model classes . This is because for a finite class the prior for all and hence for any reparametrization f. A reparametrization in a finite class is essentially just a renaming that has no affect on the indifference.
6.4. Regrouping Invariance
Regrouping invariance can be thought of as a generalization of the concept of reparametrization invariance. This is because reparametrization involves a function that is a bijection and hence every instance of the transformed parameter corresponds to one and only one instance of the original parameter. Regrouping on the other hand involves a function that is not necessarily bijective and hence can lead to a many to one or one to many correspondence.
For example, the non-bijective function for leads to the regrouping . A more intuitive example can be seen if we again consider the observation of ravens. Previously only the binary information of a black or a non-black raven was recorded but we might also be interested in whether the raven was black, white or colored. In this case the population can not be parametrized with only one parameter θ as before. For i.i.d. data in general there needs to be as many parameters (minus one constraint) as there are possible observations. These parameters specify the percentage of the population that is made up by each observation. For the binary case only the percentage of black ravens θ was used but since the parameters must sum to one the percentage of non-black ravens is implicity defined by . Formally, for an i.i.d. space with d possible observations the parameter space is . In the binary case, the probability of a string with s successes and f failures was given by . In the case of d observations the probability of , with occurrences of observation i, is analogously given by .
The regrouping problem arises when we want to make inferences about the hypothesis “all ravens are black” when the setup is now to record the extra information of whether a raven is colored or white. Intuitively recording this extra information should not affect the outcome of reasoning about black ravens but unfortunately it does if we apply the principle of indifference. When we make an inference that only looks at the “blackness” of a raven, the observations are collapsed into blackness or non-blackness as before by mapping black to success and either white or colored to failure. We can then use the binary framework as before with . However, since we assumed indifference over the parameter vectors in this regrouping means that the prior belief is skewed towards higher proportions of non-black ravens and is therefore no longer indifferent. Indeed, constant for leads to for . This means that the indifference principle is not invariant under regrouping.
Because the function f is not bijective anymore, the transformation of the prior to some new parametrization now involves an integral or sum of the priors over all value of θ for which . Formally, for discrete class we have , and similarly for continuous parametric classes we have . As with reparametrization invariance before, for a principle to be regrouping invariant, we require that where is obtained by applying the same principle to the new parametrization.
It is generally considered highly desirable that a principle for creating priors is regrouping invariant, but intuitively it seems that this invariance is a difficult property to satisfy. Attempting to satisfy it for all possible regrouping leads to a predictor that is unacceptably overconfident. Formally this means that
which, as Empiricus argued, is an illogical belief unless we have observed every instance of a type. In fact, it was shown [
33] that there is no acceptable prior density that solves this problem universally.
Luckily the universal prior is not a density and one can show it approximately satisfies both, reparametrization and regrouping invariance [
8].
6.5. Universal Prior
The universal prior is designed to do justice to both Occam and Epicurus as well as be applicable to any computable environment. To do justice to Epicurus’ principle of multiple explanations we must regard all environments as possible, which means the prior for each environment must be non-zero. To do justice to Occam we must regard simpler hypotheses as more plausible than complex ones. To be a valid prior it must also sum to (less than or equal to) one. Since the prefix Kolmogorov complexity satisfies Kraft’s inequality, the following is a valid prior.
This prior is monotonically decreasing in the complexity of
ν and is non-zero for all computable
ν.
This elegant unification of the seemingly opposed philosophies of Occam and Epicurus is based only on these universal principles and the effective quantification of simplicity by Kolmogorov. The result is a prior that is both intuitively satisfying and completely objective.
When the bounds for Bayesian prediction of
Subsection 4.9 are re-examined in the context of the Universal Prior, we see that the upper bounds on the deviation of the Bayesian mixture from the true environment are
. This means it is proportional to the complexity of the true environment which is not surprising. In simple environments the convergence is quick while in complex environments, although the framework still performs well, it is more difficult to learn the exact structure and hence convergence is slower.
The universality of Kolmogorov complexity bestows the universal prior
with remarkable properties. First, any other reasonable prior
gives approximately the same or weaker bounds. Second, the universal prior approximately satisfies both, reparametrization and regrouping invariance [
8]. This is possible, since it is not a density.
7. Solomonoff Universal Prediction
Ray Solomonoff, born July 25th 1926, founded the field of algorithmic information theory. He was the first person to realize the importance of probability and information theory in artificial intelligence. Solomonoff’s induction scheme completes the general Bayesian framework by choosing the model class to be the class of all computable measures and taking the universal prior over this class. This system not only performs excellently as a predictor, it also conforms to our intuition about prediction and the concept of induction.
It should be appreciated that according to the Church-Turing thesis, the class of all computable measures includes essentially any conceivable natural environment. John von Neumann once stated “If you will tell me precisely what it is that a machine cannot do, then I can always make a machine which will do just that”. This is because, given any “precise” description of a task we can design an algorithm to complete this task and therefore the task is computable. Although slightly tongue in cheek and not quite mathematically correct, this statement nicely captures the universality of the concept of computability. There are of course imprecise ideas such as love or consciousness which can be debated, but if a system consists of clear-cut rules and properties then it is usually computable. According to the laws of physics our world is governed by precise, although not necessarily deterministic, rules and properties and indeed any physical system we know of is computable.
Unfortunately this is actually a slight simplification and the concept of infinity causes some technical issues. This is because, for a task to be formally computable it is required not only that it can be described precisely but also there is a program that completes this task in finite time, in other words it will always terminate. Due to the fundamentally finite nature of our universe this is not usually an issue in physical systems. However, in a more abstract environment such as the platonic world of math, the existence of infinite sets, infinite strings and numbers with infinite expansions means that this termination becomes more of an issue. In particular the sum over an infinite set of environments present in Bayes mixture can be incomputable and therefore one has to introduce a slightly broader concept of semi-computable. For a task to be semi-computable there must exist a program that will monotonically converge to the correct output but may never terminate. More formally, there is a Turing machine that outputs a sequence of increasing values which will eventually be arbitrarily close to the correct value, however we do not know how close it is and it may never output the correct value and/or may never halt.
7.1. Universal Bayes Mixture
Due to technical reasons it is convenient to choose
to be the class of all semi-computable so-called semi-measures. This extension of the class does not weaken its universality since any computable environment is also semi-computable. In fact we could further extend it to include all non-computable environments without changing the result because the universal prior for any non-computable environment is zero and therefore the prediction from any non-computable environment does not contribute. From here on this universal class is denoted
and the Bayesian mixture over this class using the universal prior, called the universal Bayesian mixture, is denoted
. Formally this is defined as before
where
is the universal prior. Since the class
is infinite, the Bayesian mixture
contains an infinite sum and therefore it is not finitely computable. It can however be approximated from below which means it is a semi-computable semi-measure and therefore a member of
itself. This property is one of the reasons that the extended model class was chosen. The proof that
is semi-computable is non-trivial and is important in establishing its equivalence with the alternative representation
M below.
7.2. Deterministic Representation
The above definition is a mixture over all semi-computable stochastic environments using the universal prior as weights. It is however possible to think about in a completely different way. To do this we assume in this subsection that the world is governed by some deterministic computable process. Since it is computable this process can be described by some program p which is described using less than or equal to ℓ bits. This is possible since every program must have finite length, however ℓ may be arbitrarily large. This upper bound ℓ on the length of p must of course be in relation to some universal reference Turing machine U, since each UTM uses a different encoding scheme which may affect the length of p.
As before the aim is to make the best possible predictions about observations x. Again this is done using a universal distribution over all binary strings x which reflect our beliefs in seeing those strings, even though the true environment p produces only one predetermined output string under this interpretation. In order to make the distribution universal it is important that there is no bias or assumptions made about the structure of the world. The string x represents the current observations or equivalently the initial output string of the true environment. At any point however we can not know whether the program has halted and the output string is complete or whether there is more output to come. More generally we say that a program p produces x if it produces any string starting with x when run on U. Formally this is written as . For this purpose programs that never halt are also permitted. Once it has produced a string starting with x it may continue to produce output indefinitely.
The probability of observing
x can be computed using the rule
. This sum is over all programs of length
ℓ. To remain unbiased, Epicurus’s principle is invoked to assign equal prior probability to each of these environments a priori. Since there are
of these programs they each get assigned probability
, so
for all
p of length
ℓ. As each of these programs
p is deterministic the probability
of producing
x is simply 1 if it does produces
x or 0 if it does not. Because
for any
p where
these programs can simply be dropped from the sum in the expression for
so it now becomes
This sum is still only over programs of length
ℓ, but there may be many shorter programs which also produce
x. Since the assumption was only that the world is governed by some program with less than or equal to
ℓ bits there is no reason not to also consider these shorter programs. Fortunately these programs are automatically accounted for due to the technical setup of the definition. If there is a program
p with length less than
ℓ then we can simply pad it out until it has length
ℓ without affecting how it operates and hence what it outputs. This padding can consist of any arbitrary binary string and therefore, importantly, the shorter
p is the more ways there are to pad it out to the full length. To be precise, for any program
p with
there are exactly
different ways to extend it and each of these
programs now have length
ℓ and output
x. This means that any program
p of length
contributes
to the above sum. This property means that the sum is actually over any program with length less than or equal to
ℓ and the contribution of a program depends on its true length.
Now since
ℓ can be arbitrarily large we extend this sum to be over any program of any length. Also, in order to avoid counting the same “core” programs multiple times we introduce the concept of a minimal program
p that outputs a string
x. A program is minimal if removing any bits from the end will cause it to not output
x, and hence programs with arbitrary padding are clearly not minimal. We can therefore rewrite the above sum as
where the sum is now over all minimal programs
p of arbitrary length. We call
the universal probability of
x.
can also be seen as the frequentist probability of
x as it corresponds to the total number of programs (minimal or non-minimal) of length
ℓ that produce
x, divided by the total number of programs of length
ℓ, in the limit as
.
This is a highly technical explanation of but there is a simpler way to think about it. The set of these arbitrary programs, without the restriction that they must produce x, is actually the set of all possible binary strings. This is because any binary input string for a universal Turing machine is considered to be a program, even though the vast majority of these programs will not produce any useful or meaningful result. The contribution of any particular program p with length is . It is no coincidence that this corresponds to the probability of producing this program by simply flipping a coin for each bit and writing a 1 for heads and a 0 for tails. This means that the contribution of a particular program corresponds to the probability that this program will appear on the input tape when the Universal Turing machine is provided with completely random noise. Now the set of programs that produce x is the set of programs which contribute to . Therefore is actually the probability of producing x when random noise is piped through some universal reference Turing machine U. This alternative representation of leads to some interesting insights.
Firstly, this entirely different approach to finding a universal probability of
x turns out to be equivalent to
. Even though
considers only deterministic environments and
sums over all semi-computable stochastic environments, they actually coincide, within a multiplicative constant which can be eliminated and henceforth will be ignored [
17]. The intuitive reason for this is that, roughly speaking, the stochastic environments lie in the convex hull of the deterministic ones. To see this consider the two points on the real line between 1 and 2. The convex hull of these two points is the set of points
c such that
where
and
. In other words any point in the convex hull is a mixture of 1 and 2 where the mixing coefficients, like a probability distribution, must sum to 1. This set of points is simply the interval
. Given three points in a plane, the convex hull is the filled-in triangle with vertices at these points. In the more abstract setting of deterministic environments the same intuition holds. As a simple example imagine you must open one of two doors and you know for a fact that one door has a cat behind it and the other door has a dog behind it. You are unsure which door holds which animal however, but you have a
belief that the first door is the door with the cat. This means that under your own Bayesian mixture estimation your belief that the first door holds a cat is
. This may seem trivial but it illustrates that by mixing deterministic environments, such as the two possibilities for the doors, the resulting estimation may be stochastic. The same principle holds for all computable deterministic environments. Every stochastic environment is equivalent to some mixture of deterministic environments. Also, since any mixture of stochastic environments is itself a stochastic environment, it is also equivalent to some mixture of deterministic environments.
The equivalence of
and
M is particularly surprising considering that
uses the universal prior, which favors simple environments, while
is based on Epicurus’s principle which is indifferent. On closer examination however, there is an interesting connection. In
the shortest program
p which produces
x clearly has the greatest contribution to the sum, since
is maximal when
is minimal. In fact another program
q which has length only 1 bit greater contributes only half as much since
In general a program with only
n more bits contributes only
as much as the shortest. It turns out that the contribution from this shortest program actually dominates the sum. But the length of the shortest program
p that produces
x is the Kolmogorov complexity
and therefore
is approximately equal to
which is the universal prior for
x. It is interesting that by starting with the indifference principle and using only logical deduction in the framework of Turing machines we arrive at a predictor that favors simple descriptions in essentially the same way as advocated by Occam’s razor. This can be seen as both an intuitively appealing characteristic of
and as a fundamental justification for Occam’s razor [
34].
7.3. Old Evidence and New Hypotheses
One of the problems with the Bayesian framework is dealing with new hypotheses H that were not in the original class . In science it is natural to come up with a new explanation of some data which cannot be satisfactorily explained by any of the current models. Unfortunately the Bayesian framework describes how to update our belief in a hypothesis according to evidence but not how to assign a belief if the hypothesis was created to fit the data. Several questions come to mind in trying to solve this problem such as “should old evidence be allowed to confirm a new hypothesis?” or “should we try to reason about our belief as if the evidence did not exist?”.
By choosing the universal class this problem is formally solved. Theoretically it can no longer occur since this class is complete in the sense that it already contains any reasonable hypothesis. Since the full mixture is however incomputable it is likely that an approximation will only consider a subset of this class, but this is not a problem as the universal prior is unaffected. If a “new” hypothesis H is considered then it is simply assigned its universal prior , and the evidence can then be used to update this prior as if it had been in the original approximation class. Although hypotheses can still be constructed to fit data they will automatically be penalized if they do so in a complex way. This is because if H is naively used to account for E then and hence, if E is complex, will be small. A hypothesis that naively accounts for E is similar to a program that “hard codes” the string corresponding to E.
For example in the ancient Greek’s geocentric model of planetary motion it was discovered that using perfect spheres for the orbits of the planets did not fit with the observed data. In order to maintain the highly regarded perfect sphere and the ideological point of the earth being the center of the universe, complex epicycles were added to the model to fit all observations. Finally, in the year of his death in 1543, Nicolaus Copernicus published a far more elegant model which sacrifices perfect spheres and placed the sun at the center of the solar system. Despite resistance from the church the undeniable elegance of this solution prevailed.
Generally, by following this method, a new hypothesis that accounts for some data in an elegant and general manner will be believed far more than a new hypothesis that is overly biased towards this particular data. This seems reasonable and corresponds with common practice.
7.4. Black Ravens Paradox Using Solomonoff
We will now look at the black raven’s paradox in relation to Solomonoff induction. First we will show that Solomonoff induction is able to confirm the hypothesis “all ravens are black”. We will then comment on the relative degree of confirmation under Solomonoff.
Laplace looked at the binary i.i.d. case of drawing balls from an urn. The confirmation problem in this case arose from the zero prior in any complete hypothesis due to the use of a prior density over the continuous class of hypotheses . Confirmation for the hypothesis was made possible by assigning an initially non-zero point probability mass to for . In this case there are only two possible observations, a white ball or a black ball. The parameter θ represents the proportion of black balls but we also have another parameter representing the proportion of white balls. This second parameter is implicity given by due to the constraint that they must sum to one. The two constraints on these parameters, that they must sum to one and lie in the interval , can be thought of as a one-dimensional finite hyperplane which is equivalent to a unit line.
In the black ravens paradox we have to define two predicates, Blackness and Ravenness. There are four possible observations: These are a black raven
, a non-black raven
, a black non-raven
and finally a non-black non-raven
,
i.e., the observation alphabet is
. Each of these types has an associated parameter that represents the proportion of the entire population which belong to each of the respective types. These parameters are denoted
respectively. This makes the setup significantly more complex to work with. Since any object must belong to one and only one of these types the corresponding parameter values must sum to one. A complete hypothesis is given by any valid assignment of each of these four parameters and therefore the model class is given by the following:
This space can be visualized as a three-dimensional finite hyperplane which is equivalent to a 3-simplex, as in
Figure 2, where each vertex corresponds to the hypothesis that one of the parameters make up all observations. Vertex
corresponds to the hypothesis that all objects are black ravens, Vertex
corresponds to the hypothesis that all objects are non-black non-ravens and so forth. The point in the very center of the probability simplex corresponds to the hypothesis
. Since non-black non-ravens make up the vast majority of objects in the real world, the correct hypothesis corresponds to a point very close to the vertex given by
.
We are now interested in the partial hypothesis given by the statement “all ravens are black”. This represents the set of any points where the statement is true. But the statement “all ravens are black” is logically equivalent to the statement “there are no non-black ravens”, and this occurs exactly when . Therefore our partial hypothesis represents the set . In the figure above this corresponds to the entire face H of the simplex that lies opposite the vertex at .
The question remains whether we are able to confirm this hypothesis using the universal prior. This requires that the hypothesis is assigned a non-zero prior. The universal prior in this case depends on the complexity of the values of each of the parameters. Intuitively, the integers 0 and 1 are the simplest numbers in the interval . Therefore the universal prior is going to favor hypothesis that have parameter values of 0 or 1. The hypotheses corresponding to each vertex have one parameter set to one and the rest set to zero, e.g., . These are the simplest valid assignments of the parameters and therefore have the highest prior. If a hypothesis lies on the face of the simplex then it implies that one of the parameters must be zero, as in . Therefore hypotheses lying on a face are also implicitly favored. Specifically, there are hypotheses corresponding to points on a face that are assigned a non-zero prior and therefore, . This means is assigned a non-zero prior as required. In fact any hypothesis that has computable values assigned to its parameters has a non-zero prior. Since these “computable” hypotheses are dense in the simplex, essentially any reasonable subset of this model class is assigned a non-zero prior.
The choice of class implicitly assumes that observations are sampled i.i.d: The probability of observing a sequence of n (non)black (non)ravens objects if is the true parameter is , where is the number of times, x has been observed. This i.i.d. assumption will be relaxed below.
The physical hypothesis
refers to the unobservable parameters
. Similarly as in the binary confirmation problem in
Section 5.5, we can introduce an equivalent observational hypothesis
that consists of all possible observation sequences consistent with the hypothesis that all ravens are black. One can show that
as well as
asymptotically get fully confirmed,
i.e.,
Let us now consider the universal mixture
, which is not limited to i.i.d. models. Clearly
includes all i.i.d. environments with computable parameter
, hence
M should be able to confirm the black raven hypothesis too. Indeed, consider any computable probability distribution
μ consistent with
,
i.e.,
for
. Let
be a sequence sampled from
μ, which by definition of
μ does not contain any non-black ravens. Then the convergence in total variation result from
Subsection 8.1 (choose
and exploit
) implies
That is, M strongly confirms the black raven hypothesis under any reasonable sampling process, of course provided no non-black ravens are observed. No i.i.d. or stationarity or ergodicity or other assumption is necessary. This is very favorable, since real-life experience is clearly not i.i.d. What remains to be seen is whether M also gets the absolute and relative degree of confirmation right. But the fact that Solomonoff induction can confirm the black raven hypothesis under very weak sampling assumptions even in infinite populations containing ravens and other objects is already quite unique and remarkable.
8. Prediction Bounds
Since Solomonoff’s approach is simply the Bayesian framework with the universal model class and prior, the bounds for Bayes mixture from
Section 4 remain valid for
, although it is now possible to say a little more. Firstly, since the bounds assume that
we can now say they hold for any computable environment
μ. Also, since
M and
coincide, the same bounds for
also hold for
M. This means that
and
M are excellent predictors given only the assumption that the sequence being predicted is drawn from some computable probability distribution which, as discussed, is a very weak assumption, and even this can be relaxed further.
8.1. Total Bounds
In particular the deterministic total bound from the Bayesianism section holds with
ξ replaced by
M. This means that in the case that the true distribution
μ is deterministic the following bound holds.
Since an infinite sum of positive numbers can only be finite if they tend to zero, this means that
. In other words, the predictions converge to the correct predictions. Indeed, convergence is rapid in the sense of
for all but a vanishing fraction of
t, which implies fast convergence in practice as long as the sequence is not too complex. The property of being able to predict the next observation of any deterministic computable sequence with high probability after viewing a relatively short initial segment of this sequence is a strong result.
Solomonoff’s stronger result [
35] generalizes this to sequences
x sampled from any arbitrary unknown computable distribution
μ. In particular the following bound holds
which implies that if
x is sampled from any
μ, the universal predictor
M rapidly converges to the true computable environment
μ with
μ-probability 1.
Both results consider one-step lookahead prediction but are easily extendible to multi-step lookahead prediction [
17]. Exploiting absolute continuity of
μ w.r.t.
M, asymptotic convergence can be shown even for infinite lookahead [
36] and any computable
μ:
All three results illustrate that eventually M will recognize any structure present in a sequence. This sequence may be as simple as an infinite string of 1’s or as complex as every 74th digit in the binary expansion of π which even a human would find very difficult to recognize. In the context of observing ravens, or days when the sun rises, the observation string can be thought of as a string of 1’s where 1 represents a black raven, or sun rise, and 0 represents a white raven, or no sun rise. In this case the convergence is particularly fast because is very small. Again this is not surprising: the more obvious or simple the structure in a sequence the better M performs.
8.2. Instantaneous Bounds
The previous bounds give excellent guarantees over some initial
n predictions but say nothing about the
nth prediction itself. In classes of environments that are independent and identically distributed (i.i.d.) it is also possible to prove good instantaneous bounds but in the general case this is more difficult. In many cases it is reasonable to think of the data as i.i.d. even if it is not strictly true. For example when observing ravens there are many factors that affect which raven gets observed, at the very least your location, however thinking of the observations as being drawn randomly from the entire population is a reasonable approximation. Sometimes it is useful to interpret uncertain or minor factors as noise over otherwise i.i.d. data. Unfortunately there are also many cases where it is not at all reasonable to consider the data as i.i.d. and for these more general cases the following bound for computable
x was proven in [
8]:
where
C is a constant which depends on the complexity of the environment but not on
n.
This means that the probability of an incorrect prediction depends on how much of the sequence has been seen as well as the complexity of the sequence. For simple strings this probability will quickly become small but for complex strings only a very weak guarantee can be given. If the string is very simple, in the sense that
, then
C will be small and hence the lower and upper bound will coincide within an irrelevant multiplicative constant, denoted by
below. In particular for
we get
Due to the non-monotonic nature of
this results in an interesting property. Because
dips when
n is simple,
spikes up. In other words
M expects a counter example to a universal generalization after a simple number of observations more than after a comparatively random number of observations. Although this may seem absurd there is a certain validity to being “cautious” of simple numbers.
When we examine the world around us there is structure everywhere. Countless patterns and regularities in what we see and hear, even if most of it evades our conscious attention. This may seem like a vague and subjective claim but it is actually verifiable. This underlying structure is the reason why fractal compressors, which operate by extracting simple recursive regularities from images, work so successfully [
37]. Interestingly they work particularly well on images of natural scenery because they contain large amounts of fractal structure. In fact there is a lot of structure in the sequences governing many natural processes such as the growth of a human embryo which doubles with each generation, or the arrangement of petals and leaves on certain plants which often obey simple mathematical rules such as the Fibonacci sequence. Not surprisingly this underlying structure is also found in the technological world. It has been verified, using Google to measure frequencies of integers [
38], that numbers with low Kolmogorov complexity occur with high probability on the internet.
Structure is closely related to Kolmogorov complexity. If a process or object is highly structured then this means we can write a short program to predict it or produce it. If a process has very little structure then it is closer to a random string and requires a much more verbose description or encoding. In the context of binary prediction with error probability bounded by , as above, this structure is reflected by the simplicity of n. The abundance of structure in the world means that simple numbers are more likely to be significant, which corresponds with the non-monotonic nature of . It should also be noted that although the above example considers binary prediction, analogous results hold for more general alphabets.
The non-monotonic bound of may still seem strange but it is important to realize that even at simple numbers our belief does not suddenly switch from a low belief in one observation to a high belief. Even for large simple n, is still quite small, so our belief in seeing a zero after ones is still almost negligible, but higher than after ones, a relatively random number of the same magnitude. In any case, the total bound ensures that the size and frequency of these “peaks” are quite limited.
It should also be noted that we have made the implicit assumption that we know exactly how many observations we have made so far. In reality however we often do not know n precisely. Consider all the black ravens you have ever observed. It’s likely that you know you have observed many black ravens but not likely you could recall the exact number. This means that if you were to apply the above method strictly you would have to formalize some prior distribution about your belief in the exact number of ravens you have observed and then take the average of the above method according to this prior. This averaging would smooth out the above mentioned peaks, so our belief in observing a different object would decrease more uniformly. In many real world situations where the above bound seems absurd, uncertainty in our precise observation history would cause a more uniform decrease as these peaks are washed out by Bayesian averaging.
8.3. Future Bounds
When looking at an agent’s performance it is often important to consider not only the total and instantaneous performance but also the total future performance bounds. In other words it can be important to estimate how many errors it is going to make from now on. Consider a general agent learning how to play chess from scratch. Obviously it will make a large number of errors initially as it does not even know the rules of the game so most of its moves will be invalid. More interesting is to examine the expected number of errors once it has learnt the rules of the game. There are many situations were it is reasonable for an agent or predictor to have some grace or learning period.
Formally, for a given sequence
and the Hellinger distance
defined in
Subsection 4.9 between
M and the true environment
μ, the future expected error is written as follows:
In general, there is no way of knowing how similar the future will be to the past. The environment may give the agent a long simple sequence of observations which it predicts well and then suddenly change to a complex unpredictable pattern. Here it is worth mentioning the relation to what Hume called the principle of uniformity of nature [
4]. He argued that induction implicitly assumes this principle which states that the future will resemble the past. But the only way to verify this principle is through induction which is circular reasoning and therefore induction cannot be proven. As we will see however, the future bound does not assume this principle but rather accounts for it through a factor that measures the divergence of the future from the past.
In the total bound (), a sudden switch to a more complex sequence is accounted for by the Kolmogorov complexity of the true environment . For these surprising complex environments, is obviously large and hence the bound is weaker which automatically accounts for errors that will be made after the environment switches. A finite total number of errors only implies that the number of future errors eventually converges to zero. The purpose of the following future bound however is to use the information obtained so far in to give a tighter, more useful bound.
In the case of future errors, the bound is again in terms of the Kolmogorov complexity of the true environment but now it is conditioned on the past observation sequence
. Formally it can be shown [
39] that
This bound is highly intuitive. The dominant term,
, depends on the relationship between what has been seen so far and what will be seen in the future. As described previously, this Kolmogorov complexity measures the complexity of environment
μ in relation to side information
. Therefore if the principle of uniformity holds and the future does resemble the past, then this term is small. This means that once a sample has been seen which is large enough to be representative of the entire population or the future sequence, then the future number of prediction errors is expected to be relatively small. On the other hand if the future is going to be vastly different from the past then this history
is not much help at all for understanding
μ, so the future bound
will be almost as high as the initial total bound
. In other words, the bound measures the value of the history
for learning the future.
Consider for instance a sequence of identical images I of high complexity . Since the true environment μ simply repeats this image it also has complexity . After making even just one observation of I the dramatic difference between the total bound and the total future bound becomes apparent. The total bound on the number of errors is proportional to the complexity of the true environment , so all this tells us is that the total number of errors will be approximately one less than . But since this sequence is simply a repetition of the image I we expect a much smaller number of errors. The bound above tells us that the total number of future errors is bounded by after seeing I once. But the complexity of μ in relation to I is since μ only needs to copy and paste I repeatedly. Therefore the total number of future errors will be very small which agrees with intuition. This example illustrates the potential value of this future bound.
8.4. Universal is Better than Continuous
It has been argued that the universal class and prior are an excellent choice for completing the Bayesian framework as they lead to Solomonoff’s , which we have shown to be (Pareto) optimal and to perform excellently on any computable deterministic or stochastic environment μ. Although this assumption of computability is reasonable, the question of its performance in incomputable environments remains interesting. For example, we may want to know how it compares with other methods in predicting a biased coin being flipped where the bias θ is an incomputable number. Intuitively this should not be a major problem as the computable numbers are dense in the reals and therefore there are computable hypotheses that are arbitrarily close to θ.
It is indeed possible to formally prove that
M does as good as any Bayesian mixture
ξ over any model class
, continuous or discrete, and prior function
over this class. The reason for this is that although a specific environment
ν in
may be incomputable and its prior
may be zero, the prior function
and the overall mixture
ξ generally remain computable. This is precisely what occurs in Laplace’s rule for i.i.d. data. In this case the model class is
and the prior density
for any
θ. The majority of the values of
are incomputable since
is uncountable. Since
is a density it assigns a prior of zero to any particular value, but for any partial hypothesis
where
is incomputable,
is also incomputable. But the function
is itself computable, in fact very simple, and the Bayesian mixture
(for
s successes and
f failures in
x) is also computable and quite simple. This computability of
ξ implies the following general result for any, possibly incomputable, environment
μ:
The Kullback–Leibler divergence
itself upper bounds the various total losses defined in
Section 4. For here it suffices to know that small
implies small total error/loss. If
ξ is computable, which is usually the case even for continuous classes, then
is finite and often quite small. The importance of this result is that it implies that classical Bayesian bounds for
ξ based on continuous classes like the one in
Subsection 4.11 also hold for the universal predictor
M even for the incomputable
μ in continuous classes
. This means that
M performs not much worse than any Bayesian mixture
ξ (and often much better). Indeed, even more general, if there exists any computable predictor that converges to
μ in KL-divergence, then so does
M, whatever
μ. This means that if there is any computable predictor that performs well in some incomputable environment
μ, then
M will also perform well in this environment.
9. Approximations and Applications
Solomonoff’s universal probability M as well as Kolmogorov complexity K are not computable, hence need to be approximated in practice. But this does not diminish at all their usefulness as gold standards for measuring randomness and information, and for induction, prediction, and compression systems. Levin complexity is a down-scaled computable variant of K with nice theoretical properties, the context tree weighting (CTW) distribution may be regarded as a very efficient practical approximation of M, and the minimum encoding length principles (MDL&MML) are effective model selection principles based on Ockham’s razor quantifying complexity using practical compressors. K and M have also been used to well-define the clustering and the AI problem, and approximations thereof have been successfully applied to a plethora of complex real-world problems.
9.1. Golden Standard
“in spite of its incomputability, Algorithmic Probability can serve as a kind of `Gold standard’ for inductive systems”
—Ray Solomonoff, 1997
It is useful to keep this above attitude in mind when looking at how Solomonoff induction can be applied. This idea of a “gold standard” is certainly not new. There are various problems or scientific areas where an “optimal” solution or model is known but for practical purposes it must be approximated.
A simple example of this concept can be seen in the problem of playing optimal chess. It is known that a min-max tree search approach extended all the way to the end of a game will yield optimal play, but this is entirely infeasible due to the huge branching factor and extremely large depth of the tree. The magnitude of the tree required to solve chess is truly massive, with more possible chess games than there are atoms in the universe. Instead this approach is approximated using much smaller trees and heuristics for pruning the tree and evaluating board positions. These approximations can however perform very well in practice which was comprehensively demonstrated in 1997 when the chess computer Deep Blue finally defeated the reigning world Champion Gary Kasparov.
Even given the exponentially increasing processing power of computers there is no foreseeable future in which the computation of a complete chess min-max tree will be feasible. An infeasible problem is a problem that can not be practically computed and therefore must be approximated. An incomputable problem such as Solomonoff induction can also not be practically computed but can only be asymptotically computed given infinite resources. But when looking at practical applications we only consider feasible approximations and therefore it may be argued that there is little difference between an incomputable problem and an entirely infeasible problem. Rather it is important to find approximations that are useful, although this may often be more likely for problems that are only infeasible rather than incomputable.
Another example of a “golden standard” is quantum electrodynamics in relation to chemistry and physics. Quantum electrodynamics was called the “jewel of physics” by Richard Feynman because of its ability to make extremely accurate predictions of various phenomena. Theoretically this theory is able to accurately predict essentially any atomic interactions which of course extends to all chemical processes. However applying this theory to almost any non-trivial interactions requires extremely complex or infeasible calculations. Because of this, other methods are generally used which are, or can be considered, approximations of quantum electrodynamics, like the extremely successful Hartree–Fock approximation.
Even competitive Rubik’s cube solving may be seen as human approximation of a known, and computable, gold standard. It has been shown that a standard Rubik’s cube can be solved, from any position, in 20 moves. This is the theoretically best that can be achieved but any human attempt is still far from this. The level of planning and visualization necessary to compute this optimal solution is infeasible for a human but it does give a lower bound or “gold standard” on what is possible.
Even if a “gold standard” idea or theory cannot be implemented in practice, it is still valuable to the concerned field of study. By demonstrating a theoretically optimal solution to universal induction, Solomonoff is useful both as a guide for practical approximations and as a conceptual tool in understanding induction. By adding theoretically optimal decision making to this framework, the second author shows in [
17] that the resulting AIXI model can similarly be considered a “gold standard” for Artificial Intelligence.
Just as in the examples above, Solomonoff induction and Kolmogorov complexity can and have been successfully approximated.
9.2. Minimum Description Length Principle
The Minimum Description Length (MDL) principle is one such approximation of Solomonoff induction which is based on the idea that inductive inference can be achieved by finding the best compression of data since this requires learning and understanding the underlying structure of the data. Put simply it predicts data that minimizes the compression of this new data with the old data. MDL achieves computational feasibility by restricting the hypotheses, which are the methods of data compression, to probabilistic Shannon-Fano based encoding schemes [
40]. This principle is actually based on a similar earlier concept known as the minimal message length principle which considers a message to consist of the size of a model plus the size of the compressed data using this model [
33].
9.3. Resource Bounded Complexity and Prior
Levin Complexity is a direct variant of algorithmic complexity which is computable because it bounds the resources available to the execution. Specifically it uses a time-bounded version of Kolmogorov complexity defined as follows:
This avoids the problem of short programs
p that run indefinitely and hence may or may not produce
x. Eventually the time factor will invalidate them as candidates and hence they can be terminated [
27]. The speed prior
similarly approximates
by limiting the time available [
41].
Even off-the-shelf compressors such as Lempel-Ziv [
42] can be considered approximations of Kolmogorov complexity to varying degrees. The more advanced the techniques used to extract the structure from and hence compress a file, the better the approximation. In fact, one of the key insights by Solomonoff was that induction and compression are essentially equivalent problems.
The Kolmogorov complexity is an extremely broad concept which applies to any effectively describable object. In practice however we often only need to measure the complexity of an object relative to a specific class of objects, and this can make approximations much easier.
9.4. Context Tree Weighting
For example in the Context Tree Weighting (CTW) algorithm, described below, we want to find the complexity of a specific suffix tree measured against the class of all prediction suffix trees. Using a simple encoding scheme it is easy to create a set of binary prefix-free strings that are in one to one correspondence with the set of prediction suffix trees. These are therefore short unambiguous descriptions of each tree/environment and can be used to give an effective approximation of Kolmogorov complexity. If z is the prefix-free string that describes the prediction suffix tree p, the Kolmogorov complexity of p is approximated by . This approximation is also intuitive, since simpler trees have shorter descriptions and the corresponding prior when summed over all trees gives 1.
The context tree weighting algorithm, originally developed as a method for data compression [
43], can be used to approximate Solomonoff’s universal prior
. It is worth particular mention due to its elegant design and efficient performance. Universal induction is incomputable both because of the Kolmogorov complexity necessary to establish the priors and because of the infinite sum over Turing machines. It is often possible to establish an intuitively satisfying approximation of an environment’s complexity, as mentioned above with prediction suffix trees. However it is much more difficult to think of an efficient method of summing over a large, or infinite, class of environments. It is this property that makes the CTW algorithm noteworthy.
The CTW algorithm considers the class of all prediction suffix trees up to some fixed depth
d (it can also be implemented to use arbitrarily deep trees). The number of these grows double exponentially with the depth
d, so this quickly becomes a very large class. Remarkably the mixture model over this entire class, weighted according to the Kolmogorov complexity approximation above, turns out to be exactly equal to the probability given by a single structure called a context tree. This context tree can be implemented and updated very efficiently and therefore leads to a computationally feasible and effective approximation. Although this class is massively reduced from the universal class of all computable distributions, it is sufficiently rich to achieve excellent compression and has been shown to perform well in many interesting environments [
44].
9.5. Universal Similarity Measure
One interesting application of Kolmogorov complexity is in the constructions of a universal similarity measure. Intuitively two objects can be considered similar if it takes little effort to transform one into the other. This is precisely the concept captured using conditional Kolmogorov complexity since it measures the complexity of one string given another string. Formally, for objects
x and
y, the similarity metric is defined by symmetrizing and normalizing
as follows:
Since it takes no effort to change an object into itself it is clear that
and hence
. If there is no similarity between
x and
y then
and
and therefore
. Although the Kolmogorov complexity is incomputable, it is possible to achieve an effective approximation of this metric by approximating
K with a good compressor such as Lempel–Ziv, gzip, bzip, or CTW.
When comparing many objects, a similarity matrix is created by comparing each object to each other using the above metric. This matrix can then be used to construct trees based on the similarity of objects. This method has been used to achieve some astounding results [
45]. For example, it was used to accurately construct the exact evolutionary tree of 24 mammals based only on the structure of their DNA. It was also used to construct a tree of over 50 languages showing the common roots and evolution of these languages. Other successes include correctly categorizing music by their composers and files by their type [
46].
9.6. Universal Artificial Intelligence
Universal artificial intelligence involves the design of agents like AIXI that are able to learn and act rationally in arbitrary unknown environments. The problem of acting rationally in a known environment has been solved by sequential decision theory using the Bellman equations. Since the unknown environment can be approximated using Solomonoff induction, decision theory can be used to act optimally according to this approximation. The idea is that acting optimally according to an optimal approximation will yield an agent that will perform as well as possible in any environment with no prior knowledge.
This unification of universal induction and decision theory results in the AIXI agent [
17]. According to Legg and Hutter’s definition of intelligence, which they argue to be reasonable [
47], this AIXI agent is the most intelligent agent possible. Since this is an extension of Solomonoff induction it is clearly also incomputable, but again practical approximations exist and have produced promising results.
The MC-AIXI-CTW approximation builds on the context tree weighting algorithm described above by incorporating actions and rewards into the history and using an efficient Monte-Carlo tree search to make good decisions. Just as the context tree weighting algorithm is an efficient approximation of Solomonoff, MC-AIXI-CTW is an efficient approximation of AIXI [
44].
10. Discussion
Solomonoff [
7] created a completely general theory of inductive inference. Subsequent developments [
8] have shown that his system solves many of the philosophical and statistical problems that plague other approaches to induction. In the same/similar sense as classical logic solves the problem of how to reason deductively, Solomonoff solved the problem of how to reason inductively. No theory, be it universal induction or logic or else, is ever perfect, but lacking better alternatives, over time people often get used to a theory, and ultimately it becomes a de-facto standard. Classical logic is there already; Bayesian statistics and universal induction are slowly getting there. In this final section we briefly discuss the major pros and cons of Solomonoff induction before concluding.
10.1. Prior Knowledge
Philosophically speaking our predictions of the future are dependent on a lifetime of observations. In practice we need only consider relevant information to make useful prediction but this question of relevance is not always straightforward.
One of the problems with Solomonoff induction is that relevant background knowledge is not explicitly accounted for. There are two ways to modify Solomonoff induction to account for prior background knowledge y.
The first method is to judge the complexity of each environment ν in relation to this prior knowledge y. Formally this is done by providing y as extra input to the universal Turing machine when computing which leads to the conditional Kolmogorov complexity . One of the properties of the conditional Kolmogorov complexity is that it can be no bigger than the Kolmogorov complexity alone. This is because the extra input b can simply be ignored. This means that all environments, in particular the true environment, are weighted at least as high as they would be without the prior knowledge y. By biasing the prior towards environments that can be more easily expressed using our prior knowledge this method should intuitively never lead to worse convergence and often to faster convergence.
The second method is to prefix the observation sequence x, which we wish to predict, with the prior knowledge y. We are therefore predicting the continuation of the sequence . This method treats background knowledge as previous observations. In the case of an ideal agent that applies Solomonoff’s method as soon as it is initialized, or from “birth”, all previous knowledge is always contained in its history, so this method of prefixing x with y occurs implicitly.
In practice, the best method may depend on the type of background knowledge y that is available. If y is in the form of previous observations, perhaps taken from similar experiments or situations in the past, then it would be natural to prefix x with y. On the other hand, if y is a partial hypothesis which we know, or strongly suspect to be correct, it would be more appropriate to judge the complexity with the conditional Kolmogorov complexity given y. This can be thought of as looking at the complexity of different methods of completing the partial model we currently have. Although these different methods are conceptually useful due to different possible types of background knowledge, they are theoretically nearly equivalent. Intuitively this is because in both cases any information present in the background knowledge y is being used to simplify the model for x and it may not matter if this knowledge is provided with x or separately.
10.2. Dependence on Universal Turing Machine U
A common criticism of both Solomonoff’s universal predictor and the Kolmogorov complexity is the dependence on the choice of universal reference machine
U. As we discussed in
Section 5.9, the major problem is the difficulty of agreeing on a formal definition of a “natural” Turing machine. We argued that this is equivalent to agreeing on the definition of a natural encoding scheme which may seem simpler intuitively however the core problem remains. In any case, the choice of
U is only an issue for “short” sequences
x. This is because for short
x and any arbitrary finite continuation
y we can always choose
U that predicts
y to follow
x. However as the length of
x increases, the predicted continuation of
x will become independent of
U.
It is worth noting that this problem of arbitrary predictions for short sequences x is largely mitigated if we use the method of prefixing x with prior knowledge y. The more prior knowledge y that is encoded, the more effective this method becomes. Taken to the extreme we could let y represent all prior (scientific) knowledge, which is possibly all relevant knowledge. This means that for any x the string will be long and therefore prediction will be mostly unaffected by the choice of universal reference machine.
10.3. Advantages and Disadvantages
As we have seen, the universal Solomonoff approach has many favorable properties compared to previous methods of induction. In particular these include:
General total bounds for generic class, prior and loss function as well as instantaneous and future bounds for both the i.i.d. and universal cases.
The bound for continuous classes and the more general result that M works well even in non-computable environments.
Solomonoff satisfies both reparametrization and regrouping invariance.
Solomonoff solves many persistent philosophical problems such as the zero prior and confirmation problem for universal hypotheses. It also deals with the problem of old evidence and we argue that it should solve the black ravens paradox.
The issue of incorporating prior knowledge is also elegantly dealt with by providing two methods which theoretically allow any knowledge with any degree of relevance to be most effectively exploited.
These significant advantages do however come at a cost. Although it seems Solomonoff provides optimal prediction given no problem-specific knowledge, the persistent multiplicative or additive constants in most results mean this optimality may only occur asymptotically. For short sequences and specific problems, Solomonoff may not perform as well as other methods, but an automatic remedy is to take into account previous or common knowledge. Of course the most significant drawback to this approach is the incomputability of the universal predictors
M and
. Although approximations do exist, with some very interesting results, they are still either infeasible or fairly crude or limited approximations.
10.4. Conclusions
In this article we have argued that Solomonoff induction solves the problem of inductive inference. Not only does it perform well theoretically and solves many problems that have plagued other attempts, it also follows naturally from much of the significant work in induction that precedes it.
Initially we explained how the subjectivist interpretation of probability is appropriate for dealing with induction since induction concerns our beliefs about the unknown. Cox’s demonstration that the standard axioms of probability are a necessary consequence of any rational belief system provides strong theoretical justification for using the standard axioms while maintaining a subjectivist approach.
Bayes theorem is derived directly from these standard probability axioms and, when combined with the reasonable setup of holding some class of possible explanations, each with some prior plausibility, we arrive at the Bayesian framework. This framework provides a rational method of updating beliefs and in some sense it provides the optimal method of predicting future observations based on current beliefs and evidence. We argued that the concept of prediction is general enough to encompass all relevant problems of inductive inference and therefore this Bayesian framework is also optimal for inductive inference.
This framework requires that we have some pre-conceived beliefs about the possible causes for our observations. Ideally these beliefs are formed before any evidence has been observed so they must be based on an objective and universally acceptable principle. By combining the ideas of Occam and Epicurus we are at such a principle which is both intuitive and philosophically appealing and applies to the largest reasonable class of possible environments. A strict formalization of this principle is achieved through contributions of Turing and Kolmogorov.
Completing the Bayesian framework with this universal model class and prior produces Solomonoff induction. In a very loose sense this demonstrates that Solomonoff induction follows as a natural consequence of rationality. Although incomputable, this universal method for inductive inference can be used to guide practical implementations and also gives us new insights into the mechanics of our own thinking.
By refuting Maher’s invalid claim that probability alone can solve the problem of confirmation, we have shown that these failings of other systems of induction remain present, while Solomonoff deals with confirmation successfully by assigning non-zero priors to all computable hypotheses. We have also looked briefly at how Solomonoff induction deals with the black ravens paradox and argued that it should give the desired result.
We hope that this accessible overview of Solomonoff induction in contemporary and historical context will bring an appreciation and awareness of these ideas to a larger audience and facilitate progress in and applications of this exciting and important field.