Abstract
Statistical complexity measures (SCM) are the composition of two ingredients: (i) entropies and (ii) distances in probability-space. In consequence, SCMs provide a simultaneous quantification of the randomness and the correlational structures present in the system under study. We address in this review important topics underlying the SCM structure, viz., (a) a good choice of probability metric space and (b) how to assess the best distance-choice, which in this context is called a “disequilibrium” and is denoted with the letter . , indeed the crucial SCM ingredient, is cast in terms of an associated distance . Since out input data consists of time-series, we also discuss the best way of extracting from the time series a probability distribution P. As an illustration, we show just how these issues affect the description of the classical limit of quantum mechanics.
Keywords:
generalized statistical complexity; disequilibrium; information theory; selection of the probability distribution; semiclassical theories; quantum chaos PACS:
05.45.Tp (Time series analysis); 03.65.Sq (Semiclassical theories and applications); 05.45.Mt (Quantum chaos; semiclassical methods)
1. Statistical Complexity Measures
In this review we discuss the role that distances in probability space, as ingredients of statistical complexity measures, play in describing the dynamics of the quantum-classical (QC) transition. We choose an exceedingly well-known model, whose physics has received detailed attention over the years, as our test ground. The details of the QC-transition have been elucidated in a series of publications in which the pertinent equations of motion are solved [1,2,3,4]. Our statistical recapitulation covers references [5,6,7]. We review here these three works that allow one to ascertain the usefulness of statistical considerations in describing dynamic features. Why is this of importance? Because (i) usually, statistical approaches are easier to implement than solving equations of motion and (ii) in many cases, they offer the only way of dealing with otherwise intractable problems.
1.1. Meaning of the Concept
Complexity denotes a state of affairs that one can easily appreciate when confronted with it; however, in physics there is no universal agreement on a proper definition of complexity, although its quantitative characterization has received considerable attention. In the last two decades several complexity measures together with methodologies for their evaluation have been proposed, which capture various aspects of complex systems and are based on data compression algorithms, optimal predictability, recurrence plots, symbolic analysis, wavelet analysis, among others [8,9,10,11,12,13,14,15,16,17,18]. An important contribution in the context of defining complexity is due to P. Grassberger [19], being related to the pattern-generation by the dynamics of a system. The most complex situation is neither the one with highest Shannon information S (random structure) nor the one with lowest S (ordered structures). Thus, in the Grassberger view complexity is represented by a mixture of order and disorder, regularity and randomness (for a graphical example, see Figure 1 of [10]).
One can begin by excluding processes that are certainly not complex, such as those exhibiting periodic motion. Additionally, a purely random process cannot be considered complex either, notwithstanding its irregular and unpredictable character, because it does not contain any non-trivial, patterned structure. Complexity is often characterized by the paradoxical situation of a complicated dynamics generated from relatively simple systems. Obviously, if the system itself is already involved enough and is constituted by many different parts, it clearly may support a rather intricate dynamics, but perhaps without the emergence of typical characteristic patterns [20]. Therefore, a complex system does not necessarily generate a complex output. In the previous context, we understand “complexity” as a concept related to patterned structures hidden in the dynamics, emerging from a system which itself can be much simpler than the dynamics it generates [20]. “Statistical complexity” becomes then a kind of indicator for hidden “order”.
1.2. Information Measures
An information measure can primarily be viewed as a quantity that characterizes a given probability distribution. is regarded as the measure of the uncertainty associated to the physical processes described by the probability distribution , with N the number of possible states of the system under study. From now on we assume that the only restriction on the PDF representing the state of our system is (micro-canonical representation). If we are in a position to predict with certainty which of the N possible outcomes will actually take place. Our knowledge of the underlying process described by the probability distribution is in this instance maximal. On the other hand, it is our ignorance which is maximized if ; , being the uniform distribution. These two extreme circumstances of (i) maximum foreknowledge (“perfect order”) and (ii) maximum ignorance (or maximum “randomness”) can, in a sense, be regarded as “trivial” ones. We define for a given probability distribution P and its associate information measure , an amount of “disorder” in the fashion
We have thus .
Following the Shannon-Kinchin paradigm we define in terms of entropies. In particular, in the present work we restrict ourselves to the canonical formulation (that of Boltzmann-Gibbs) of statistical mechanics. However, extension to other entropic formulations, like Renyi’s and Tsallis’, can be made without undue effort (see i.e., 18,21]). Thus, for a discrete distribution, we define the disorder in the fashion
were represents Shannon’s logarithmic entropy, given by
and .
1.3. Distances and Statistical Complexity Measure
A definition of Statistical Complexity Measure (SCM) can not be made in terms of just “disorder” or “information”. A proper SCM needs to use some distance of the given P to the uniform distribution of the accessible states of the system [11,16,17]. This motivates introducing, as a special distance-form, the so-called “disequilibrium-distance” as
where is a normalization constant () with its value equal to the inverse of the maximum possible value of the distance . This maximum distance is obtained when one of the components of P, say , is equal to one and the remaining components are equal to zero. The disequilibrium-distance would reflect on the systems’ “architecture”, being different from zero if there exist “privileged”, or “more likely” states among the accessible ones.
Consequently, we adopt the following functional product form for the SCM introduced originally by López-Ruiz, Mancini and Calbet (LMC) [11]
This quantity, on the basis of our statistical description of the system, reflects, at a given “scale”, the delicate interplay extant between the amount of information stored in the system and its disequilibrium (the measure of probability hierarchies between the observed parts of its accessible states) [11]. In particular, as we will show in this work, complex dynamics, in which several regimes coexist, namely, chaos, stability islands and even curves that are neither chaotic nor periodic, can be characterized by this SCM.
As for the metrics and its induced distance entering ’s definition one faces a panoply of choices. These several distance-forms open several possibilities for the SCM. Recently, to avoid such multiplicity the entropic descriptor of complex behavior per cell (or state) using only entropy (), its maximal value () and minimal one () has been introduced [22]. This work is mainly focused on characterizing the multi-scale complexity of binary and grey level patterns. Such entropic descriptor can be also employed to reconstruct microstructure details [23].
For , with discrete probability distributions, we limit our considerations here to [18,21]:
- (a)
- Euclidean norm in [11]:This is the “natural” choice (the most simple one) for the distance . We haveThis is the disequilibrium form for the complexity measure proposed by López-Ruiz, Mancini and Calbet (LMC-complexity measure [11]). Such straightforward definition of distance has been criticized by Wootters in an illuminating communication [24] because, in using the Euclidean norm, one is ignoring the fact that we are dealing with a space of probability distributions and thus disregarding the stochastic nature of the distribution P.
- (b)
- Wootters’s distance [16,24]:The concept of “statistical distance” originates in a quantum mechanical context. One uses it primarily to distinguish among different preparations of a given quantum state, and, more generally, to ascertain to what an extent two such states differ from one another. The concomitant considerations being of an intrinsic statistical nature, the concept can be applied to “any” probabilistic space [24]. The main idea underlying this notion of distance is that of adequately taking into account statistical fluctuations inherent to any finite sample. As a result of the associated statistical errors, the observed frequencies of occurrence of the various possible outcomes typically differ somewhat from the actual probabilities, with the result that, in a given fixed number of trials, two preparations are indistinguishable if the difference between the actual probabilities is smaller than the size of a typical fluctuation [24].
Following Basseville [25], two divergence classes can be built up starting with functionals of the entropy. The first class includes divergences defined as relative entropies, while the second one deals with divergences defined as entropic differences. Several possibilities are open to us.
- (c)
- Kullbak-Leibler relative entropy [18,26]:The relative entropy of with respect to associated to Shannons measure is the relative Kullbak-Leibler Shannon entropy, that in the discrete case readsConsider now the probability distribution P and the uniform distribution . The distance between these two distributions, in Kullback-Leiber Shannon terms, will be
- (d)
- Jensen divergence [17,18]:In general, the entropic difference does not define an information gain (or divergence) because the difference is not necessarily positive definite. Something else is needed. An important example is provided by Jensen’s divergence, which is a symmetric version of the Kullback-Leibler relative entropy, which in terms of the Shannon entropy can be written as:The Jensen-Shannon divergence verifies the following propertiesMoreover, it square root satisfies the triangle inequalitywhich implies that the square root of the Jensen-Shannon divergence is a metric [27]. Note also that it is defined in terms of entropies and, in consequence, is an extensive quantity in the thermodynamical sense. Thus, the corresponding statistical complexity will be an intensive quantity as well.
On the basis of the LMC-functional product form we obtain a family of SCMs for each of four distinct disequilibriums just enumerated, namely,
The index tell us that the disequilibrium distance is to be evaluated with the appropriate distance measure (Euclidean, Wootters, Kullback-Leibler, and Jensen-Shannon, respectively).
It is interesting to note that for the SCM family becomes
Such is the generalized functional form advanced by Shiner, Davison, and Landsberg [13] for the SCM. One could raise the objection that this SCM is just a simple function of the entropy. As a consequence, it might not contain new information vis-a-vis the measure of order. Such an objection is discussed at length in [28,29,30].
We stress the fact that the remaining members of the family () are not trivial functions of the entropy because they depend on two different probabilities distributions, the one associated to the system under analysis, P, and the uniform distribution . Furthermore, it has been shown that for a given value, there exists a range of possible SCM values, from a minimum one up to a maximal value . Evaluation of yields, consequently, new information according to the peculiarities of the pertinent probability distribution. A general procedure to obtain the bounds and corresponding to the generalized -family is given in [31]. Thus, it is clear that important additional information related to the correlational structure between the components of the physical system is provided by evaluating the statistical complexity.
1.4. Time Evolution
In statistical mechanics one is often interested in isolated systems characterized by an initial, arbitrary, and discrete probability distribution. Evolution towards equilibrium is to be described, as the overriding goal. At equilibrium, we can think, without loss of generality, that this state is given by the uniform distribution . In order to study the time evolution of the SCM a diagram of versus time t can then be used. But, as we know, the second law of thermodynamics states that in isolated system entropy grows monotonically with time () [32]. This implies that can be regarded as an arrow of time, so that an equivalent way to study the time evolution of the SCM is to plot versus . In this way, the normalized entropy-axis substitutes for the time-axis. This kind of diagram has been used also to study changes in the dynamics of a system originated by modifications of some characteristic parameters (see, for instance, [11,18,21,33], and references therein).
1.5. Additional Issues
As we mentioned before, if we recover the statistical complexity measure definition given originally by López-Ruiz, Mancini and Calbet (LMC) [11]. It has been pointed out by Crutchfield and co-workers [12] that the LMC measure is marred by some troublesome characteristics that we list below:
- (1)
- it is neither an intensive nor an extensive quantity.
- (2)
- it vanishes exponentially in the thermodynamic limit for all one-dimensional, finite range systems.
The above authors forcefully argue that a reasonable SCM should
- (3)
- be able to distinguish among different degrees of periodicity;
- (4)
- vanish only for unity periodicity.
Finally, and with reference to the ability of the LMC measure to adequately capture essential dynamical aspects, some difficulties have also been encountered [34].
The product functional form for the generalized SCM makes it impossible to overcome the second deficiency mentioned above. In previous works we have shown that, after performing some suitable changes in the definition of the disequilibrium distance, by means of utilization of either Wootters distance [16] or Jensen’s divergence [17], one is in a position to obtain a generalized SCM that is:
- (i)
- able to grasp essential details of the dynamics (i.e., chaos, intermittency, etc.)
- (ii)
- capable of discerning between different degrees of periodicity, and
- (iii)
- an intensive quantity if Jensen’s divergence is used.
2. Methodologies for Selecting PDFs
An important point for the evaluation of the previous information quantifiers (entropy and generalized statistical complexity measures) is the proper determination of the underlying probability distribution function (PDF) P, associated to a given dynamical system or time series . This often neglected issue deserves serious consideration as the probability distribution P and the sample space Ω are inextricably linked.
Many schemes have been proposed for a proper selection of the probability space . We can mention, among others: (a) frequency count [35] (b) procedures based on amplitude statistics (histograms) [36], (c) binary symbolic dynamics [37], (d) Fourier analysis [38] and, (e) wavelet transform [39]. Their applicability depends on particular characteristics of the data such as stationarity, length of the time series, variation of the parameters, level of noise contamination, etc. In all these cases the global aspects of the dynamics can be somehow captured, but the different approaches are not equivalent in their ability to discern all the relevant physical details. One must also acknowledge the fact that the above techniques are introduced in a rather ad hoc fashion and are not directly derived from dynamical properties of the system under study. This can be adequately effected, for instance, by recourse to the Bandt-Pompe methodology [14].
In the present work we use two different approaches to capture different aspects of the dynamics associated to the classical limit of quantum mechanics (CLQM), which plays here the role of a testing model. The first of these is broadly used and computes P using a histogram of amplitudes. The second one is based on Bandt-Pompe symbolization dynamics. The main idea is to show the importance of inclusion of time causality in the corresponding PDF construction for an accurate description of the dynamics under study. Why choose the classical limit of quantum mechanics as an illustration of these considerations? Because we will in this respect employ a model whose physics is exceedingly well-known (see, for instance, [3,40,41], and references therein), so that methodological effects will become delineated with great clarity. A previous work of this kind was made using the logistic map as a testing device [21].
2.1. PDF Based on Histograms
In order to extract a PDF via amplitude statistics, the interval (with a and b being the minimum and maximum of the time series ) is first divided into a finite number of non-overlapping subintervals : and . One then employs the usual histogram method, based on counting the relative frequencies of the time series values within each subinterval.
It should be clear that the resulting PDF lacks any information regarding temporal ordering (temporal causality). The only pieces of information we have here are the values that allow one to assign inclusion within a given bin, ignoring their temporal location (this is, the subindex i). Note that N in Equations (3) to (16) is equal to . Let us also point out that it is relevant to consider a judiciously chosen optimal value for (see i.e., De Micco et al. [36]).
2.2. PDF Based on Bandt and Pompe’s Methodology
To use the Bandt and Pompe [14] methodology for evaluating the probability distribution P associated to the time series (dynamical system) under study, one starts by considering partitions of the pertinent D-dimensional space that will hopefully “reveal” relevant details of the ordinal structure of a given one-dimensional time series with embedding dimension and time delay τ. In the following we take [14]. We are interested in “ordinal patterns” of order D [14,42] generated by
which assigns to each time s the D-dimensional vector of values at times . Clearly, the greater the value, the more information on the past is incorporated into our vectors. By “ordinal pattern” related to the time we mean the permutation of defined by
In order to get a unique result we set if . This is justified if the values of have a continuous distribution so that equal values are very unusual.
Thus, for all the possible permutations π of order D, their associated relative frequencies can be naturally computed by the number of times this particular order sequence is found in the time series divided by the total number of sequences. The probability distribution is defined by
In this expression, the symbol ♯ stands for “number”.
The procedure can be better illustrated with a simple example; let us assume that we start with the time series , and we set the embedding dimension . In this case the state space is divided into partitions and 24 mutually exclusive permutation symbols are considered. The first 4-dimensional vector is . According to Equation (17) this vector corresponds with . Following Equation (18) we find that . Then, the ordinal pattern which allows us to fulfill Equation (18) will be . The second 4-dimensional vector is , and will be its associated permutation, and so on. For the computation of the Bandt and Pompe PDF we follow the very fast algorithm described by Keller and Sinn [42], in which the different ordinal patterns are generated in lexicographic ordering.
The Bandt-Pompe methodology is not restricted to time series representative of low dimensional dynamical systems but can be applied to any type of time series (regular, chaotic, noisy, or reality based), with a very weak stationary assumption (for , the probability for should not depend on t [14]). It also assumes that enough data are available for a correct embedding procedure. Of course, the embedding dimension D plays an important role in the evaluation of the appropriate probability distribution because D determines the number of accessible states . Also, it conditions the minimum acceptable length of the time series that one needs in order to extract reliable statistics.
The main difference between entropy and complexity measures evaluated with a PDF histogram or a PDF Bandt and Pompe is that, unlike those quantifiers based on a PDF histogram, those obtained à la Bandt and Pompe are invariant with respect to strictly monotonic distortions of the data. This point will be very important in the case of empiric natural time series (i.e., sedimentary data are related to rainfall by an unknown nonlinear function [43]). However, due to their invariance properties, quantifiers based on Bandt and Pompe’s perspective, when applied to any other data series that is strictly monotonic in the given data, will yield the same results. Therefore, in general, ordinal data processing tools based on ranked numbers would lead to results that could be more useful for data analysis than those obtained using tools based on metric properties.
3. The Classical Limit of Quantum Mechanics (a Special Semi-Classical Model)
Since the introduction of the decoherence concept in the early 1980s by, among others, Zeh, Zurek, and Habib [44,45,46], the emergence of the classical world from Quantum Mechanics has been a subject of much interest. It is clear that much quantum insight is to be gained from semiclassical perspectives. Several methodologies are available (WKB, Born-Oppenheimer approach, etc.). The models of Bonilla and Guinea [40], Cooper et al. [41], Kowalski et al. [3], consider two interacting systems: one of them classical, the other quantal. This makes sense whenever the quantum effects of one of the two systems are negligible in comparison to those of the other one. Examples include Bloch equations, two-level systems interacting with an electromagnetic field within a cavity, collective nuclear motion, etc. We deal with a special bipartite system that represents the zero-th mode contribution of a strong external field to the production of charged meson pairs [3,41], whose Hamiltonian reads
where (i) and are quantum operators, (ii) A and classical canonical conjugate variables and (iii) is an interaction term that introduces nonlinearity, being a frequency. The quantities and are masses corresponding to the quantum and classical systems, respectively. As shown in [3], in dealing with Equation (20) one faces an autonomous system of nonlinear coupled equations
Here . The system of Equations (21) follows immediately from Ehrenfest’s relations [1]. To study the classical limit we also need to consider the classical counterpart of the Hamiltonian Equation (20), i.e.,
where all the variables are classical. Recourse to Hamilton’s equations allows one to find the classical version of Equation (21). These equations are identical in form to Equation (21) after suitable replacement of quantum mean values by classical variables, i.e., , and . The classical limit is obtained by letting the “relative energy”
(), where E is the total energy of the system and I is an invariant of the motion described by the system of equations previously introduced (Equation (21)), related to the Uncertainty Principle
A classical computation of I yields . Thus, I vanishes when it is evaluated using the classical variables A and , for all t, i.e., , a fact that exhibits the self-consistency of our methodology. A measure of the degree of convergence between classical and quantum results in the limit of Equation (23) is given by the norm of the vector [1],
where the three components vector is the “quantum” part of the solution of the system defined by Equation (21) and its classical counterpart.
A detailed study of this model was performed in [3]. The main results of this reference, pertinent for our discussion, can be succinctly detailed as follows: in plotting diverse dynamical quantities as a function of (as it grows from unity to ∞), one finds an abrupt change in the system’s dynamics for a special value of , to be denoted by . From this value onwards, the pertinent dynamics starts converging to the classical one. It is thus possible to assert that provides us with an indicator of the presence of a quantum-classical “border”. The zone corresponds to the semi-quantal regime [3]. This regime, in turn, is characterized by two different sub-zones. One of them is almost purely quantal, in which the microscopic quantal oscillator is just slightly perturbed by the classical one, and the other section exhibits a transitional nature (semi-quantal). The border between these two sub-zones can be well characterized by a relative energy value . A significant feature of this point resides in the fact that, for , chaos is always found. The relative number of chaotic orbits (with respect to the total number of orbits) grows with and tends to unity for [3].
Thus, as grows from (the “pure quantum instance”) to (the classical situation), a significant series of morphology changes is detected, especially in the transition zone (). The concomitant orbits exhibit features that are not easily describable in terms of Equation (25), which is a global measure of the degree of convergence in amplitude (of the signal). What one needs instead is a statistical type of characterization, involving the notions of entropy and statistical complexity [5,6,7].
4. Results and Discussion
We present here our results that to a large extent yield information with respect to the use of either the Wooters’ or the Jensen-Shannon distance measures. Our data points are the solutions of (21), from which we extract the values of and the (classical) values of at the time t (for a fixed ). We have also performed these calculations extracting instead the quantities – together with –L, and obtained thereby entirely similar results to those reported below. We will deal with data points, for each orbit.
In obtaining our numerical results we chose for the system’s parameters. As initial conditions needed to tackle Equation (21) we took , i.e., we fixed E and then varied I so as to obtain our different -values. Additionally, we set , (both in the quantum and the classical instances). takes values in the interval , with .
Figure 1 displays the “signal amplitude vs. time” graphs, each corresponding to a fixed -value. On the vertical axis one plots . As grows from (the “pure quantum instance”) to (the classical situation), a significant series of morphology changes is detected. Indeed, one can speak of three types of graphs: (a) from till , regular oscillatory behavior. (b) for parameter values between and no dominant morphology is apparent, several regimens coexist. “Randomness” and disorder prevail, both in amplitude and in frequency. For , quasi-periodic motion starts to be detected for small times, characterized by a repetition of peaks and valleys that give the impression of “waves”. (c) for valleys become more pronounced, so that the number of “wave-peaks” diminish. When one reaches , just one peak becomes noticeable. At the bottom right we plot the classical signal vs. time. Of course, the classical signal derives from the classical Hamiltonian. It is important to note in Figure 1 that the special -value coincides with that particular value referred to above. Likewise, here the value corresponds to .
The dependence with the parameter of the normalized Shannon entropy and generalized statistical complexity quantifiers corresponding to data pertaining to the classical limit of quantum mechanics (CLQM) dynamics (Figure 1) were evaluated using both amplitude histograms and the Bandt-Pompe methodology described in the previous section. For the PDF histogram case, we map first the corresponding time series into the interval and we consider . In this form, we avoid the variation of bins-size due to different signal-amplitude ranges and all our numerical values become compatible. For the PDF Bandt and Pompe evaluation, a pattern length (embedding dimension) was selected. As we deal with vectors with components of at least data points for each orbit, the condition is clearly satisfied. We take the customary time delay [14]. For additional arguments and details in relation to the election of , consult [7].
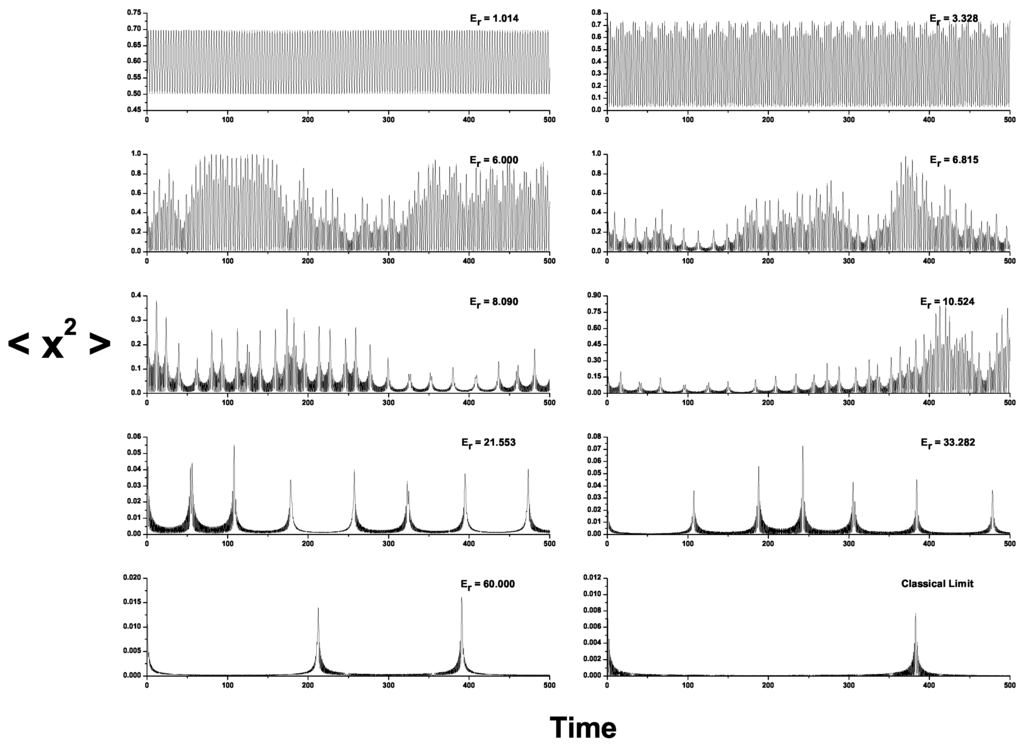
Figure 1.
Signal vs. time graphs. Subplots 1–9: solutions of the system (21) (semi-quantum signal), for representative fixed values of . Subplot 10: solution of the classical counterpart of the system (21) (classical, ). We took . Initial conditions: , and . The uppermost left plot corresponds to the “pure quantum” signal. At the bottom right we plot the classical signal vs. time. The remaining are intermediate situations. All quantities are dimensionless.
In Figure 2, Figure 3 and Figure 4 we depict both Entropy and Statistical Complexity vs. in a large variability range. Also in these figures we just consider that special range that allows for easy visualization of all the zones of our process, viz., quantal, transitional, and classic, as delimited by, respectively, and .
Because the dynamics is of a quasi-periodic character, we expect the entropies to be smaller in the quantum zone than in both the classical one (that exhibits chaotic dynamics) and the transition sector (complex dynamics, in which several regimes coexist, namely, chaos, stability islands and even curves that are neither chaotic nor periodic). It is thus clear that the entropy should be smaller in the transition region than in the classical one. Likewise, the statistical complexity should be maximal in the transition zone. We also expect that the two information quantifiers will converge towards classicality for large values (i.e., to the corresponding quantifiers values, calculated using data obtained from the classical versions of Equations (21)).
- In Figure 2a,b we plot the Normalized Shannon Entropy, , for PDF histogram and for PDF Bandt and Pompe. Notice in Figure 2a that both definitions tend to different final results for large values. These are the classical results, i.e., the corresponding entropic values calculated using data obtained from the classical versions of Equations (21). Also note in Figure 2b that the PDF histogram’s entropy does not clearly distinguish between transitional and classical sectors. The Bandt and Pompe entropy does distinguish the three process zones and correctly orders entropic sizes according the the physical criteria expounded above (Figure 2b), i.e., it can be said to appropriately represent our three regions.
- The LMC statistical complexity, (Figure 3b) does not distinguish between transitional and classical zones in its PDF histogram version, and neither is able to correctly represent the classical sector. Also, the LMC’s PDF Bandt and Pompe version fails to aptly describe the quantal region (see Figure 3b).
- The MPR statistical complexity with Wooters’ distance (Figure 4b) does distinguish amongst the three zones in its two PDF versions. For the PDF histogram, maximum complexity is attained at . Its quantal sector representation is marred by the fact that one detects complexity values within it larger than those encountered within the transition region (Figure 4b). For the PDF Bandt and Pompe version the associated representation is for all zones grosso modo correct. One would expect, however, that the classical zone’s complexity should not be so similar to that for the transitional one. Note that this classical zone’s complexity is slightly smaller than the maximal complexity attained at (Figure 4b).
- The MPR (Jensen-Shannon) statistical complexity (Figure 4c,d) is quite similar to its MPR (Wootters) counterpart (Figure 4a,b), and distinguishes quite well amongst the three typical regions for both PDF versions, although the quantal representation in the PDF histogram’s case fails, as was the case with the MPR (Wootters) counterpart (Figure 4b), a facet that is improved by the Bandt and Pompe PDF treatment. Consequently, the symbolic MPR (Jensen-Shannon) statistical complexity exhibits the best overall performance (Figure 4d).
The symbolic MPR (Jensen–Shannon) statistical complexity is maximal where it should be (see [47,48] and references therein), i.e., within the transition zone. Moreover, it exhibits similar small values in the quantum zone and in the classical one. More importantly, these values are clearly smaller than those pertaining to the transition zone. Of course, the complexity cannot vanish either in the quantum zone, because we deal there with frequency superposition (non-periodic dynamics), or in the classical one, due to the chaotic character of the associated motion (obviously, chaotic and random are not equivalent concepts in this respect). We thus find that the symbolic MPR (Jensen-Shannon distance) version optimizes the description of the quantum-classical transition corresponding to the semiclassical model of Section 3.
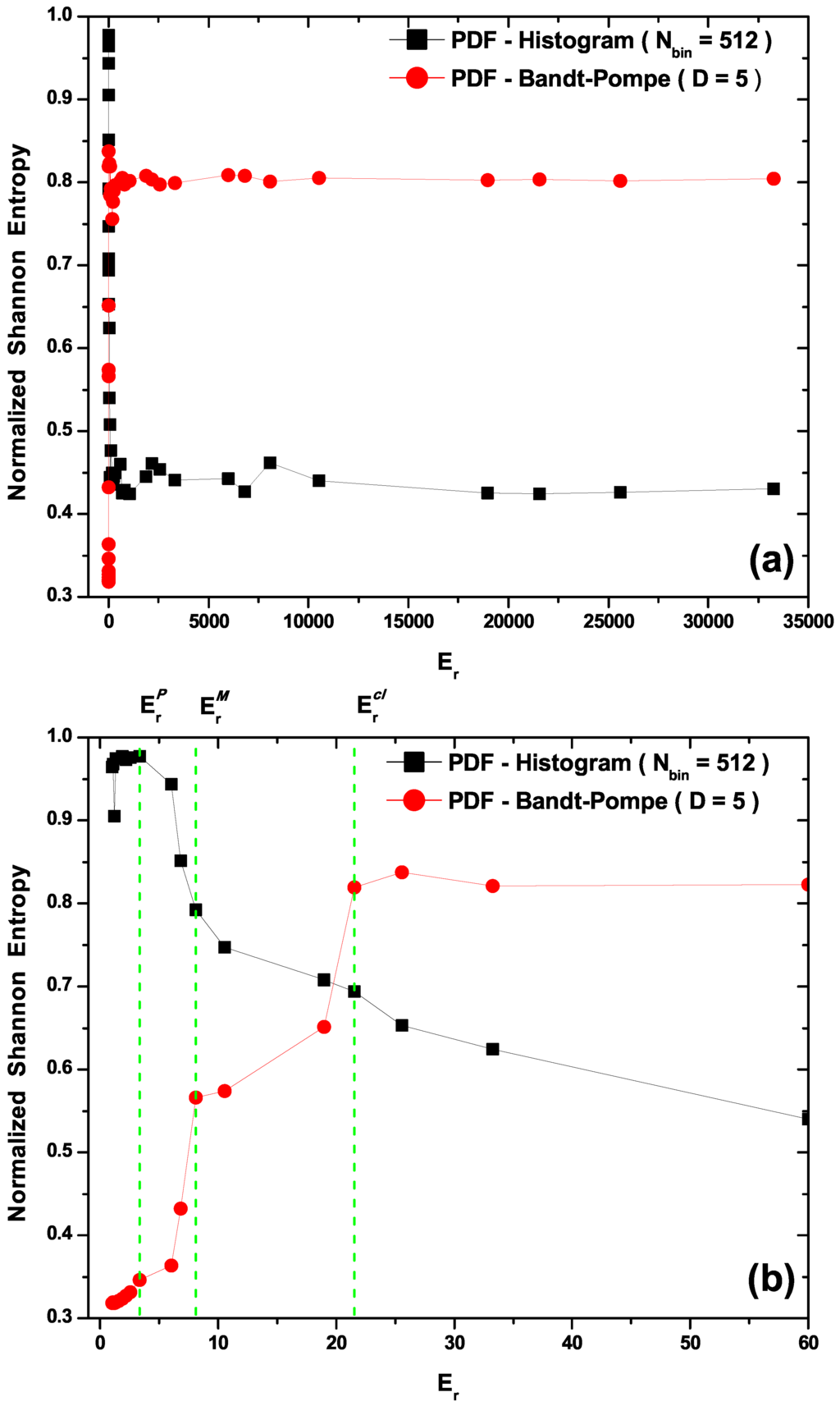
Figure 2.
Normalized Shannon entropies for two PDF types: “histogram” and Bandt and Pompe are plotted vs. . (a) convergence to classicality. (b) the PDF histogram’s entropy does not clearly distinguish between transition and classical zones while the Bandt and Pompe one does distinguish and appropriately represents our three regions.
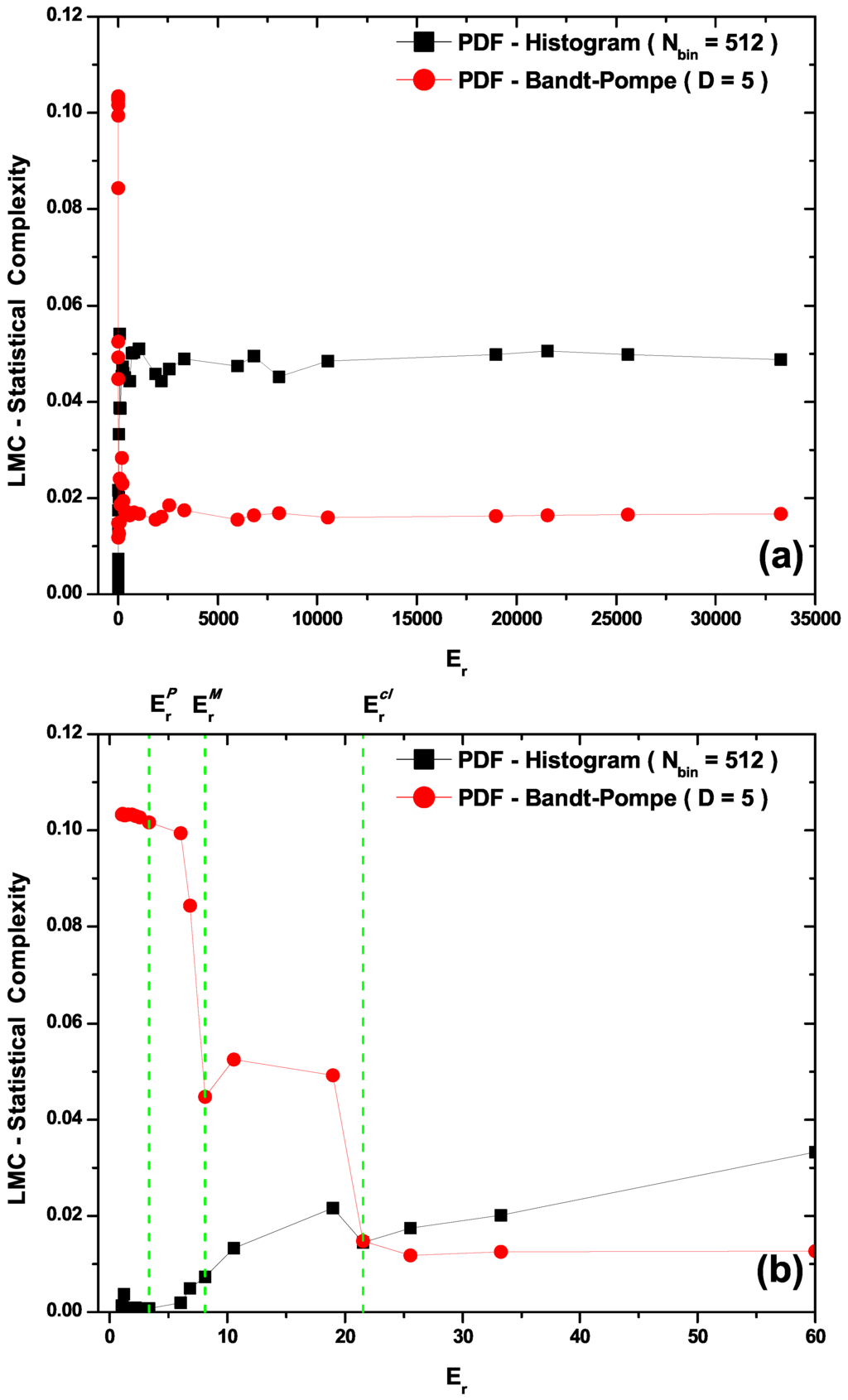
Figure 3.
LMC statistical complexity for histogram and Bandt-Pompe PDF’s vs. . The LMC statistical complexity neither distinguishes the transition from the classical zones in its histogram PDF version nor can correctly represent the classical sector (see (b)). Also, the LMC’s PDF Bandt and Pompe version fails to aptly describe the quantal region.
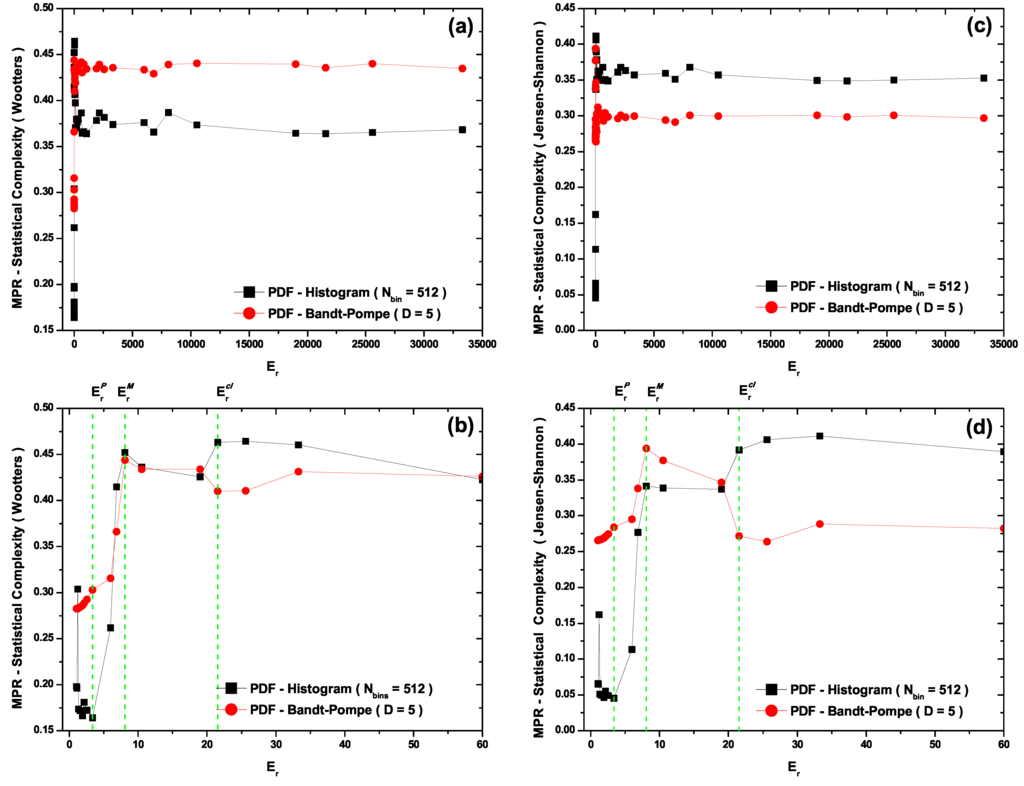
Figure 4.
(a)–(b) MPR statistical complexity (Wooters) vs. , where one distinguishes the three zones for the two PDF versions (see (b)). The PDF histogram, MPR statistical complexity fails to describe the quantal region, see (b). The PDF Bandt-Pompe treatment is, for all zones, grosso modo correct. (c)–(d) MPR (Jensen-Shannon) statistical complexity vs. . One distinguishes the three typical regions for both PDF versions. The quantal representation in the PDF histogram’s case fails as is the case of its MPR (Wootters) counterpart (see (d)).
Finally, we display in Figure 5 the -planes for both PDF evaluation (histogram and Bandt-Pompe), and for the three instances of statistical complexity definitions under consideration, viz., LMC, MPR (Wootters), and MPR (Jensen-Shannon). The two continuous curves represent, respectively, the maximum, , and minimum , statistical complexity values evaluated as explained in [31] for the corresponding N (number of degree of freedom).
In the PDF histogram we observe in Figure 5a–c that the entropy in the quantum zone is larger than in the classic one. Thus, for increasing values of the parameter , the curve in -plane responds differently to entropy growth. Such behavior is found in all three distinct SCM definition options and becomes thus a feature of the PDF histogram. Quantum and transition regions occupy the right hand side of the graphs. Note the location of the signal points , y with reference to the associated complexity plots. The small variation range of the LMC complexity (Figure 3) leaves the whole associated curve almost totally attached to the minimum complexity bound, which of course limits the possibility of visualizing behavior facets. This is not the situation for both the MPR Wooters and the MPR Jensen–Shannon (Figure 4), where things become easier to visualize, and thus distinguish between different physical zones delimited by . In the PDF Bandt and Pompe scenario, Figure 5d–f, the planar trajectory in is the “natural” one as entropy grows, and no location inversion of the signal points is to be detected, as was earlier the case.
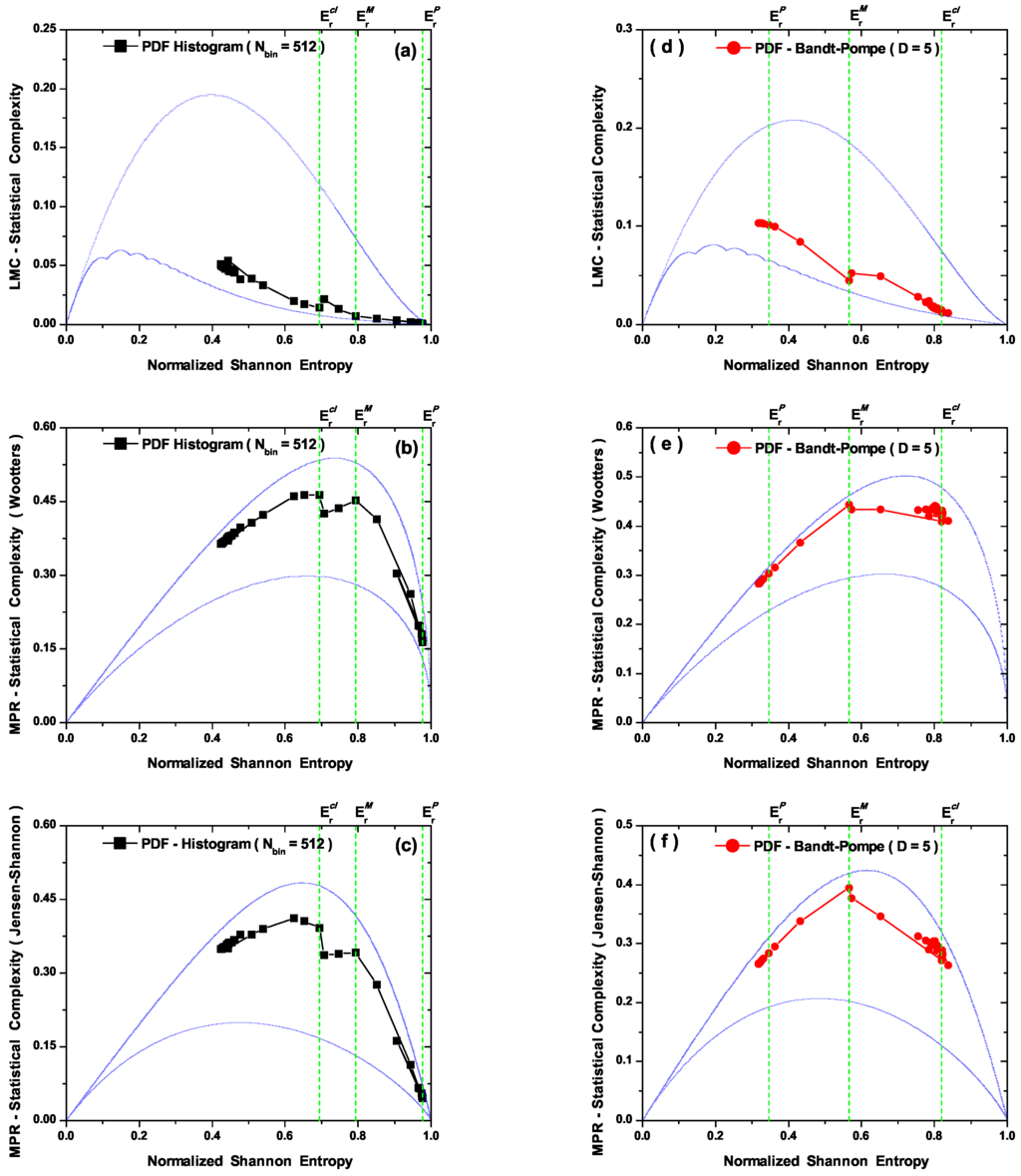
Figure 5.
Entropy-complexity plane using a PDF histogram (), for: (a) LMC statistical complexity, (b) MPR statistical complexity with Wootters distance, (c) MPR statistical complexity with Jensen-Shannon distance. Entropy-complexity plane in the case of the PDF Bandt and Pompe (), for: (d) LMC statistical complexity, (e) MPR statistical complexity with Wooters’ distance, (f) MPR statistical complexity with Jensen-Shannon distance. We also display the maximum and minimum possible values of the corresponding statistical complexity (continuous curves) and the signal points (dashed lines).
5. Conclusions
In this work we have analyzed the conditions that a statistical complexity measure must satisfy so as to appropriately characterize a time series by recourse to an example for which the underlying physics is exceedingly well-known. We are speaking of the classical-quantal frontier for a special semiclassical system (see Equation (20)) [3,41]. We have seen that critical factors of this characterization are:
- The selection of an appropriate disequilibrium distance form .
- The selection of an adequate probability distribution function (PDF).
The Bandt and Pompe’s PDF turns out to be the optimal option in selecting the probability distribution (See Figure 2 concerning the entropy). If determinism is an important feature to be taken into account, the Bandt and Pompe prescription has advantages over other choices. For the statistical complexity this choice is not sufficient by itself.
Acknowledgment
A.M. Kowalski is supported by CIC of Argentina. OAR acknowledges partial support from CONICET, Argentina, and CAPES, PVE fellowship, Brazil. M. Casas is funded by the Spain Ministry of Science and Innovation (Project FIS2008-00781) and by FEDER funds (EU).
References
- Kowalski, A.M.; Martín, M.T.; Nuñez, J.; Plastino, A.; Proto, A.N. Quantitative indicator for semiquantum chaos. Phys. Rev. A 1998, 58, 2596–2599. [Google Scholar] [CrossRef]
- Kowalski, A.M.; Martín, M.T.; Nuñez, J.; Plastino, A.; Proto, A.N. Semiquantum chaos and the uncertainty principle. Physica A 2000, 276, 95–108. [Google Scholar] [CrossRef]
- Kowalski, A.M.; Plastino, A.; Proto, A.N. Classical limits. Phys. Lett. A 2002, 297, 162–172. [Google Scholar] [CrossRef]
- Kowalski, A.M.; Martín, M.T.; Plastino, A.; Proto, A.N. Classical limit and chaotic regime in a semi-quantum hamiltonian. Int. J. Bifurcation Chaos 2003, 13, 2315–2325. [Google Scholar] [CrossRef]
- Kowalski, A.M.; Martín, M.T.; Plastino, A.; Proto, A.N.; Rosso, O.A. Wavelet statistical complexity analysis of classical limit. Phys. Lett. A 2003, 311, 180–191. [Google Scholar] [CrossRef]
- Kowalski, A.M.; Martín, M.T.; Plastino, A.; Rosso, O.A. Entropic non-triviality, the classical limit, and geometry-dynamics correlations. Int. J. Modern Phys. B 2005, 14, 2273–2285. [Google Scholar] [CrossRef]
- Kowalski, A.M.; Martín, M.T.; Plastino, A.; Rosso, O.A. Bandt-pompe approach to the classical-quantum transition. Physica D 2007, 233, 21–31. [Google Scholar] [CrossRef]
- Lempel, A.; Ziv, j. Complexity of finite sequences. IEEE Trans. Inf. Theory 1976, 22, 75–81. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Young, K. Inferring statistical complexity. Phys. Rev. Lett. 1989, 63, 105–108. [Google Scholar] [CrossRef] [PubMed]
- Wackerbauer, R.; Witt, R.A.; Atmanspacher, H.; Kurths, J.; Scheingraber, H. A comparative classification of complexity-measures. Chaos Solitons Fractals 1994, 4, 133–173. [Google Scholar] [CrossRef]
- López-Ruiz, L.; Mancini, H.; Calbet, X. A statistical measure of complexity. Phys. Lett. A 1995, 209, 321–326. [Google Scholar] [CrossRef]
- Feldman, D.P.; Crutchfield, J.P. Measures of statistical complexity: Why? Phys. Lett. A 1998, 238, 244–252. [Google Scholar] [CrossRef]
- Shiner, J.S.; Davison, M.; Landsberg, P.T. Simple measure for complexity. Phys. Rev. E 1999, 59, 1459–1464. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Marwan, N.; Wessel, N.; Meyerfeldt, U.; Schirdewan, A.; Kurths, J. Recurrence-plot based measures of complexity and their application to heart-rate-variability data. Phys. Rev. E 2002, 66, 026702. [Google Scholar] [CrossRef]
- Martín, M.T.; Plastino, A.; Rosso, O.A. Statistical complexity and disequilibrium. Phys. Lett. A 2003, 311, 126–132. [Google Scholar] [CrossRef]
- Lamberti, P.W.; Martín, M.T.; Plastino, A.; Rosso, O.A. Intensive entropic nontriviality measure. Physica A 2004, 334, 119–131. [Google Scholar] [CrossRef]
- Rosso, O.A.; Martín, M.T.; Figliola, A.; Keller, K.; Plastino, A. EEG analysis using wavelet-based information tools. J. Neurosci. Meth. 2006, 153, 163–182. [Google Scholar] [CrossRef] [PubMed]
- Grassberger, P. Toward a qualitative theory of self-generated complexity. Int. J. Theor. Phys. 1988, 25, 907–938. [Google Scholar] [CrossRef]
- Kantz, H.; Kurths, J.; Meyer-Kress, G. Nonlinear Analysis of Physiological Data; Springer: Berlin, Germany, 1998. [Google Scholar]
- Rosso, O.A.; De Micco, L.; Larrondo, H.A.; Martín, M.T.; Plastino, A. Generalized statistical complexity measure. Int. J. Bif. Chaos 2010, 20, 775–785. [Google Scholar] [CrossRef]
- Piasecki, R.; Plastino, A. Entropic descriptor of a complex behaviour. Physica A 2010, 389, 397–407. [Google Scholar] [CrossRef]
- Piasecki, R. Microstructure reconstruction using entropic descriptors. Proc. R. Soc. A 2011, 467, 806–820. [Google Scholar] [CrossRef]
- Wootters, K.W. Statistical distance and Hilbert space. Phys. Rev. D 1981, 23, 357–362. [Google Scholar] [CrossRef]
- Basseville, M. Information: Entropies, Divergences et Mayennes; Institut de Recherche en Informatique et Systèmes Aléatoires, Publication Interne 1020. Rennes Cedex: IRISA, 1996. [Google Scholar]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Briët, J.; Harremoës, P. Properties of classical and quantum Jensen-Shannon divergence. Phys. Rev. A 2009, 79, 052311. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Feldman, D.P.; Shalizi, C.R. Comment I on: simple measure of complexity. Phys. Rev. E 2000, 62, 2996–2997. [Google Scholar] [CrossRef]
- Binder, P.M.; Perry, N. Comment II on: Simple measure of complexity. Phys. Rev. E 2000, 62, 2998–2999. [Google Scholar] [CrossRef]
- Shiner, J.S.; Davison, M.; Landsberg, P.T. Replay to comments on: simple measure for complexity. Phys. Rev. E 2000, 62, 3000–3003. [Google Scholar] [CrossRef]
- Martín, M.T.; Plastino, A.; Rosso, O.A. Generalized statistical complexity measures: Geometrical and analytical properties. Physica A 2006, 369, 439–462. [Google Scholar] [CrossRef]
- Plastino, A.R.; Plastino, A. Symmetries of the Fokker-Plank equation and Fisher-Frieden arrow of time. Phys. Rev. E 1996, 54, 4423–4326. [Google Scholar] [CrossRef]
- Rosso, O.A.; Larrondo, H.A.; Martín, M.T.; Plastino, A.; Fuentes, M.A. Distinguishing noise from chaos. Phys. Rev. Lett. 2007, 99, 154102. [Google Scholar] [CrossRef] [PubMed]
- Anteneodo, C.; Plastino, A.R. Some features of the López-Ruiz-Mancini-Calbet (LMC) statistical measure of complexity. Phys. Lett. A 1996, 223, 348–354. [Google Scholar] [CrossRef]
- Rosso, O.A.; Craig, H.; Moscato, P. Shakespeare and other english renaissance authors as characterized by Information Theory complexity quantifiers. Physica A 2009, 388, 916–926. [Google Scholar] [CrossRef]
- De Micco, L.; González, C.M.; Larrondo, H.A.; Martín, M.T.; Plastino, A.; Rosso, O.A. Randomizing nonlinear maps via symbolic dynamics. Physica A 2008, 387, 3373–3383. [Google Scholar] [CrossRef]
- Mischaikow, K.; Mrozek, M.; Reiss, J.; Szymczak, A. Construction of symbolic dynamics from experimental time series. Phys. Rev. Lett. 1999, 82, 1114–1147. [Google Scholar] [CrossRef]
- Powell, G.E.; Percival, I. A spectral entropy method for distinguishing regular and irregular motion of hamiltonian systems. J. Phys. A: Math. Gen. 1979, 12, 2053–2071. [Google Scholar] [CrossRef]
- Rosso, O.A.; Blanco, S.; Jordanova, J.; Kolev, V.; Figliola, A.; Schürmann, M.; Başar, E. Wavelet entropy: a new tool for analysis of short duration brain electrical signals. J. Neurosc. Meth. 2001, 105, 65–75. [Google Scholar] [CrossRef]
- Bonilla, L.L.; Guinea, F. Collapse of the wave packet and chaos in a model with classical and quantum degrees of freedom. Phys. Rev. A 1992, 45, 7718–7728. [Google Scholar] [CrossRef] [PubMed]
- Cooper, F.; Dawson, J.; Habib, S.; Ryne, R.D. Chaos in time-dependent variational approximations to quantum dynamics. Phys. Rev. E 1998, 57, 1489–1498. [Google Scholar] [CrossRef]
- Keller, K.; Sinn, M. Ordinal analysis of time series. Physica A 2005, 356, 114–120. [Google Scholar] [CrossRef]
- Saco, P.M.; Carpi, L.C.; Figliola, A.; Serrano, E.; Rosso, O.A. Entropy analysis of the dynamics of el Niño/southern oscillation during the holocene. Physica A 2010, 389, 5022–5027. [Google Scholar] [CrossRef]
- Zeh, H.D. Why Bohms quantum theory? Found. Phys. Lett. 1999, 12, 197–200. [Google Scholar] [CrossRef]
- Zurek, W.H. Pointer basis of quantum apparatus: Into what mixture does the wave packet collapse? Phys. Rev. D 1981, 24, 1516–1525. [Google Scholar] [CrossRef]
- Zurek, W.H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 2003, 75, 715–775. [Google Scholar] [CrossRef]
- Rosso, O.A.; Martín, M.T.; Plastino, A. Evidence of self-organization in brain electrical activity using wavelet-based informational tools. Physica A 2005, 347, 444–464. [Google Scholar] [CrossRef]
- Plastino, A.; Martín, M.T.; Rosso, O.A. Generalized information measures and the analysis of brain electrical signals. In Nonextensive Entropy—Interdisciplinary Applications; Gell-Mann, M., Tsallis, C., Eds.; Oxford University Press: New York, USA, 2004; pp. 261–293. [Google Scholar]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).