Maximum Profit Configurations of Commercial Engines
Abstract
:1. Introduction
2. Model Description
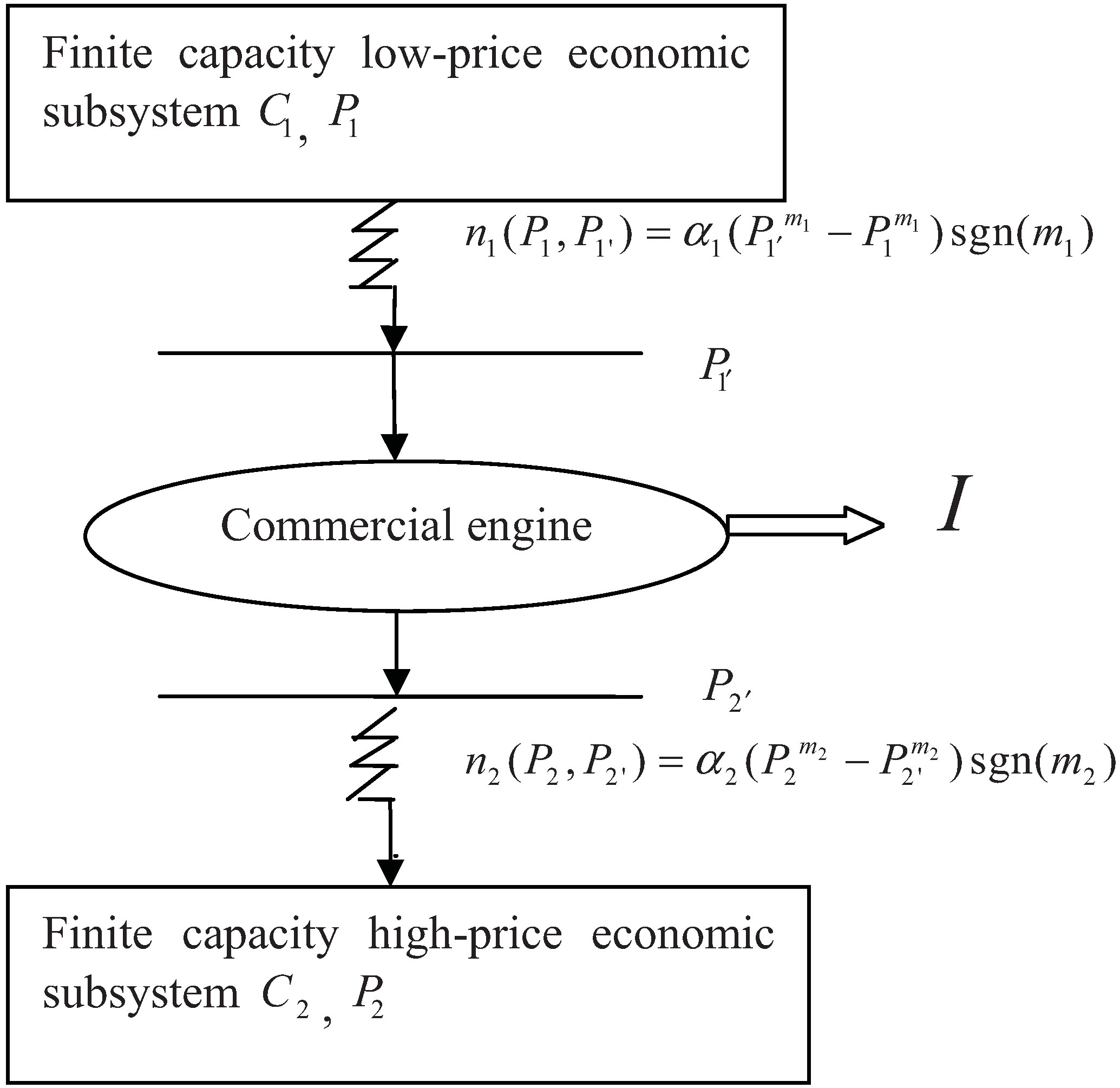
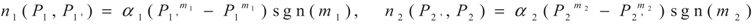
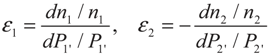
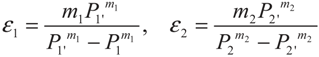
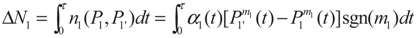
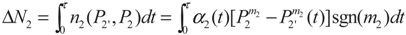
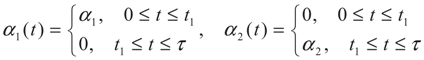
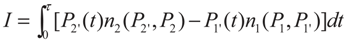
3. Optimization
3.1. Problem 1
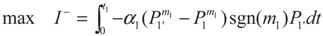
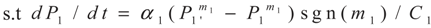
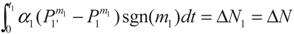
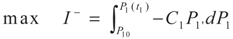
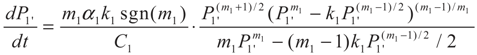
3.2. Problem 2
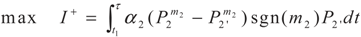
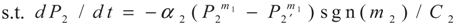
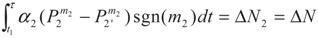
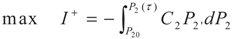
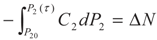
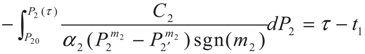
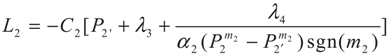
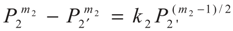
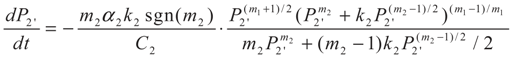
4. Special case with m1 = 1 and m2 = 1
4.1. Analytical Solutions
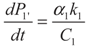 , P1′ − P1 = k1 and
, P1′ − P1 = k1 and 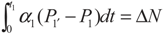 , respectively, in this case. Solving the system gives the paths of P1 and P1′, respectively:
, respectively, in this case. Solving the system gives the paths of P1 and P1′, respectively:
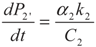 , P2′ − P2 = k2 and
, P2′ − P2 = k2 and 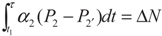 , respectively, in this case. Solving the system gives the paths of P2 and P2′, respectively:
, respectively, in this case. Solving the system gives the paths of P2 and P2′, respectively:
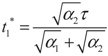
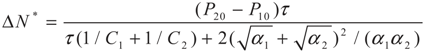
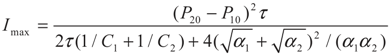
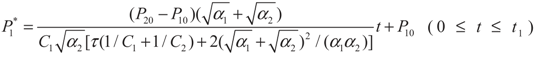
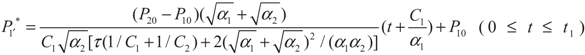
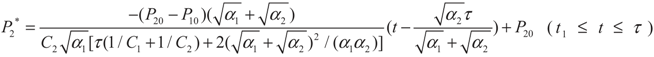
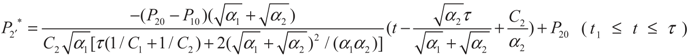
4.2. Results and Discussion
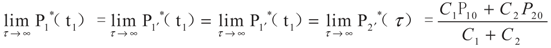
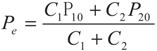
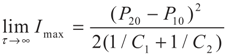
5. Special Case with m1 = − 1 and m2 = − 1
5.1. Analytical Solutions
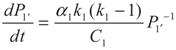 ,
, 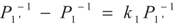 and
and 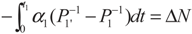 , respectively. Solving the system gives the paths of P1 and P1′, respectively:
, respectively. Solving the system gives the paths of P1 and P1′, respectively:
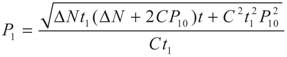
 ,
,  and
and  , respectively. Solving the system gives the paths of P2 and P2′, respectively:
, respectively. Solving the system gives the paths of P2 and P2′, respectively:

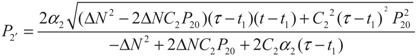
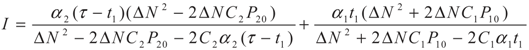
5.2. Results and Discussion
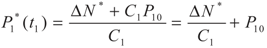
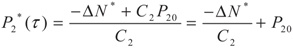
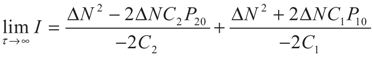
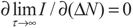 yields:
yields:
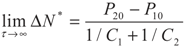
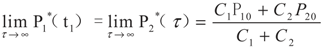
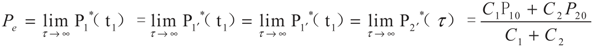
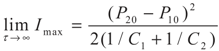
6. Conclusions
Acknowledgements
References
- Andresen, B.; Berry, R.S.; Ondrechen, M.J.; Salamon, P. Thermodynamics for processes in finite time. Acc. Chem. Res. 1984, 17, 266–271. [Google Scholar] [CrossRef]
- Sieniutycz, S.; Salamon, P. Advances in Thermodynamics. Volume 4: Finite Time Thermodynamics and Thermoeconomics; Taylor & Francis: New York, NY, USA, 1990. [Google Scholar]
- Bejan, A. Entropy generation minimization: The new thermodynamics of finite-size device and finite-time processes. J. Appl. Phys. 1996, 79, 1191–1218. [Google Scholar] [CrossRef]
- Berry, R.S.; Kazakov, V.A.; Sieniutycz, S.; Szwast, Z.; Tsirlin, A.M. Thermodynamic Optimization of Finite Time Processes; Wiley: Chichester, UK, 1999. [Google Scholar]
- Chen, L.; Wu, C.; Sun, F. Finite time thermodynamic optimization or entropy generation minimization of energy systems. J. Non-Equil. Thermodyn. 1999, 24, 327–359. [Google Scholar] [CrossRef]
- Mironova, V.A.; Amelkin, S.A.; Tsirlin, A.M. Mathematical Methods of Finite Time Thermodynamics; Khimia: Moscow, Russia, 2000. [Google Scholar]
- Tsirlin, A.M. Optimization Methods in Thermodynamics and Microeconomics; Nauka: Moscow, Russia, 2002. [Google Scholar]
- Hoffman, K.H.; Burzler, J.; Fischer, A.; Schaller, M.; Schubert, S. Optimal process pathes for endoreversible systems. J. Non-Equil. Thermodyn. 2003, 28, 233–268. [Google Scholar] [CrossRef]
- Sieniutycz, S. Thermodynamic limits on production or consumption of mechanical energy in practical and industry systems. Progr. Energ. Combust. Sci. 2003, 29, 193–246. [Google Scholar] [CrossRef]
- Tsirlin, A.M. Irreversible Estimates of Limiting Possibilities of Thermodynamic and Microeconomic Systems; Nauka: Moscow, Russia, 2003. [Google Scholar]
- Chen, L.; Sun, F. Advances in Finite Time Thermodynamics: Analysis and optimization; Nova Science Publishers: New York, NY, USA, 2004. [Google Scholar]
- Durmayaz, A.; Sogut, O.S.; Sahin, B.; Yavuz, H. Optimization of thermal systems based on finite-time thermodynamics and thermoeconomics. Progr.s Energ. Combust. Sci. 2004, 30, 175–217. [Google Scholar] [CrossRef]
- Chen, L. Finite Time Thermodynamic Analysis of Irreversible Progresses and Cycles; High Education Press: Beijing, China, 2005. [Google Scholar]
- Tsirlin, A.M. Optimal processes in open controllable macrosystems. Autom. Rem. Contr. 2006, 67, 132–147. [Google Scholar] [CrossRef]
- de Vos, A. Thermodynamics of Solar Energy Conversion; Wiley-VCH Verlag: Berlin, Germany, 2008. [Google Scholar]
- Sieniutycz, S.; Jezowski, J. Energy Optimization in Process Systems; Elsevier: Oxford, UK, 2009. [Google Scholar]
- Curzon, F.L.; Ahlborn, B. Efficiency of a Carnot engine at maximum power output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Cutowicz-Krusin, D.; Procaccia, J.; Ross, J. On the efficiency of rate process: Power and efficiency of heat engines. J. Chem. Phys. 1978, 69, 3898–3906. [Google Scholar] [CrossRef]
- Ondrechen, M.J.; Rubin, M.H.; Band, Y.B. The generalized Carnot cycles: A working fluid operating in finite time between heat sources and sinks. J. Chem. Phys. 1983, 78, 4721–4727. [Google Scholar] [CrossRef]
- Chen, L.; Zhou, S.; Sun, F.; Wu, C. Optimal configuration and performance of heat engines with heat leak and finite heat capacity. Open Syst. Inform. Dynam. 2002, 9, 85–96. [Google Scholar] [CrossRef]
- Linetskii, S.B.; Tsirlin, A.M. Evaluating thermodynamic efficiency and optimizing heat exchangers. Therm. Eng. 1988, 35, 593–597. [Google Scholar]
- Andresen, B.; Gordon, J.M. Optimal heating and cooling strategies for heat exchanger design. J. Appl. Phys. 1992, 71, 76–80. [Google Scholar] [CrossRef]
- Badescu, V. Optimal strategies for steady state heat exchanger operation. J. Phys. D: Appl. Phys. 2004, 37, 2298–2304. [Google Scholar] [CrossRef]
- Xia, S.; Chen, L.; Sun, F. Optimization for entransy dissipation minimization in heat exchanger. Chin. Sci. Bull. 2009, 54, 3587–3595. [Google Scholar] [CrossRef]
- de Vos, A. Efficiency of some heat engines at maximum power conditions. Am. J. Phys. 1985, 53, 570–573. [Google Scholar] [CrossRef]
- Chen, L.; Yan, Z. The effect of heat transfer law on the performance of a two-heat-source endoreversible cycle. J. Chem. Phys. 1989, 90, 3740–3743. [Google Scholar] [CrossRef]
- Chen, L.; Sun, F.; Wu, C. The influence of heat transfer law on the endoreversible Carnot refrigerator. J. Inst. Energ. 1996, 69, 96–100. [Google Scholar]
- Chen, L.; Sun, F.; Wu, C. Effect of heat transfer law on the performance of a generalized irreversible Carnot engine. J. Phys. D: Appl. Phys. 1999, 32, 99–105. [Google Scholar] [CrossRef]
- Huleihil, M.; Andresen, B. Convective heat transfer law for an endoreversible engine. J. Appl. Phys. 2006, 100, 014911. [Google Scholar] [CrossRef]
- Yan, Z.; Chen, J. Optimal performance of a generalized Carnot cycle for another linear heat transfer law. J. Chem. Phys. 1990, 92, 1994–1998. [Google Scholar] [CrossRef]
- Chen, L.; Sun, F.; Wu, C. Optimal configuration of a two-heat-reservoir heat- engine with heat leak and finite thermal capacity. Appl. Energ. 2006, 83, 71–81. [Google Scholar] [CrossRef]
- Xiong, G.; Chen, J.; Yan, Z. The effect of heat transfer law on the performance of a generalized Carnot cycle. J. Xiamen Univ. (Nature Science) 1989, 28, 489–494. [Google Scholar]
- Chen, L.; Zhu, X.; Sun, F.; Wu, C. Optimal configurations and performance for a generalized Carnot cycle assuming the heat transfer law Q ∝ (ΔT)m. Appl. Energ. 2004, 78, 305–313. [Google Scholar] [CrossRef]
- Chen, L.; Zhu, X.; Sun, F.; Wu, C. Effect of mixed heat resistance on the optimal configuration and performance of a heat-engine cycle. Appl. Energ. 2006, 83, 537–544. [Google Scholar] [CrossRef]
- Li, J.; Chen, L.; Sun, F. Optimal configuration for a finite high-temperature source heat engine cycle with complex heat transfer law. Sci. China Ser. G 2009, 52, 587–592. [Google Scholar] [CrossRef]
- Andresen, B.; Gordon, J.M. Optimal paths for minimizing entropy generation in a common class of finite time heating and cooling processes. Int. J. Heat Fluid Flow 1992, 13, 294–299. [Google Scholar] [CrossRef]
- Badescu, V. Optimal paths for minimizing lost available work during usual heat transfer processes. J. Non-Equil. Thermodyn. 2004, 29, 53–73. [Google Scholar] [CrossRef]
- Chen, L.; Xia, S.; Sun, F. Optimal paths for minimizing entropy generation during heat transfer processes with a generalized heat transfer law. J. Appl. Phys. 2009, 105, 044907. [Google Scholar] [CrossRef]
- Xia, S.; Chen, L.; Sun, F. Optimization for minimizing lost available work during heat transfer processes with complex heat transfer law. Braz. J. Phys. 2009, 39, 98–105. [Google Scholar] [CrossRef]
- Xia, S.; Chen, L.; Sun, F. Optimal paths for minimizing entransy dissipation during heat transfer processes with generalized radiative heat transfer law. Appl. Math. Model. 2010, 34, 2242–2255. [Google Scholar] [CrossRef]
- Rozonoer, L.I. A generalized thermodynamic approach to resource exchange and allocation. I. Autom. Rem. contr. 1973, 5, 781–795. [Google Scholar]
- Rozonoer, L.I. A generalized thermodynamic approach to resource exchange and allocation. II. Autom. Rem. Contr. 1973, 6, 915–927. [Google Scholar]
- Rozonoer, L.I. A generalized thermodynamic approach to resource exchange and allocation. III. Autom. Rem. Contr. 1973, 8, 1272–1290. [Google Scholar]
- Berry, R.S.; Andresen, B. Thermodynamics constraints in economic analysis. In Self-Organization and Dissipative Structures: Applications in Physical and Social Sciences; Schieve, W.C., Allen, P.M., Eds.; University of Texas Press: Ausin, TX, USA, 1982. [Google Scholar]
- Saslow, W.M. An economic analogy to thermodynamics. Am. J. Phys. 1999, 67, 1239–1247. [Google Scholar] [CrossRef]
- Salamon, P.; Komlos, J.; Andresen, B.; Nulton, J.D. A geometric view of welfare gains with non-instantaneous adjustment. Math. Soc. Sci. 1987, 13, 153–160. [Google Scholar] [CrossRef]
- Tsirlin, A.M. Optimal control of resource exchange in economic systems. Autom. Rem. Contr. 1995, 56, 401–408. [Google Scholar]
- De Vos, A. Endoreversible thermoeconomics. Energ. Convers. Manag. 1995, 36, 1–5. [Google Scholar] [CrossRef]
- De Vos, A. Endoreversible economics. Energ. Convers. Manag. 1997, 38, 311–317. [Google Scholar] [CrossRef]
- De Vos, A. Endoreversible thermodynamics versus economics. Energ. Convers. Manag. 1999, 40, 1009–1019. [Google Scholar] [CrossRef]
- Martinas, K. About irreversibility in economics. Open Syst. Inform. Dynam. 2000, 7, 349–364. [Google Scholar] [CrossRef]
- Tsirlin, A.M. Irreversible microeconomics: optimal processes and control. Autom. Rem. Contr. 2001, 62, 820–830. [Google Scholar] [CrossRef]
- Tsirlin, A.M.; Kazakov, V.; Kolinko, N.A. Irreversibility and limiting possibilities of macrocontrolled systems: I. Thermodynamics. Open Syst. Inform. Dynam. 2001, 8, 315–328. [Google Scholar] [CrossRef]
- Tsirlin, A.M.; Kazakov, V.; Kolinko, N.A. Irreversibility and limiting possibilities of macrocontrolled systems: II. Microeconomics. Open Syst. Inform. Dynam. 2001, 8, 329–347. [Google Scholar] [CrossRef]
- Tsirlin, A.M.; Kazakov, V.A. Optimal processes in irreversible thermodynamics and microeconomics. Interdiscipl. Description Complex Syst. 2004, 2, 29–42. [Google Scholar]
- Amelkin, S.A.; Martinas, K.; Tsirlin, A.M. Optimal control for irreversible processes in thermodynamics and microeconomics. Autom. Rem. Contr. 2002, 63, 519–539. [Google Scholar] [CrossRef]
- Amelkin, S.A. Limiting possibilities of resource exchange process in complex open microeconomic system. Interdiscipl. Description Complex Syst. 2004, 2, 43–52. [Google Scholar]
- Tsirlin, A.M.; Kazakov, V. Optimal processes in irreversible microeconomics. Interdiscipl. Description Complex Syst. 2006, 4, 102–123. [Google Scholar]
- Tsirlin, A.M. Problems and methods of averaged optimization. Proc. Steklov Inst. Math. 2008, 261, 270–286. [Google Scholar] [CrossRef]
- Gyftopoulos, E.P. Fundamentals of analysis of processes. Energ. Convers. Manag. 1997, 38, 1525–1533. [Google Scholar] [CrossRef]
- Sekulic, D. P. A fallacious argument in the finite time thermodynamics concept of endoreversibility. J. Appl. Phys. 1998, 83, 4561–4565. [Google Scholar] [CrossRef]
- Moran, M.J. Proceedings of the (ECOS’98) Efficiency, Cost, Optimization, Simulation and Environmental Aspects of Energy Systems and Processes, Nancy, France, 8–10 July 1998; Bejan, A., Feidt, M., Moran, M.J., Tsatsaronis, G., Eds.; Springer: Berlin, Germany, 1998; Volume II, pp. 1147–1150.
- Moran, M.J. On second-law analysis and the failed promise of finite-time thermodynamics. Energy 1998, 23, 517–519. [Google Scholar] [CrossRef]
- Gyftopoulos, E.P. Infinite time (reversible) versus finite time (irreversible) thermodynamics: A misconceived distinction. Energy 1999, 24, 1035–1039. [Google Scholar] [CrossRef]
- Salamon, P. Physics versus engineering of finite-time thermodynamic models and optimizations. In Thermodynamic Optimization of Complex Energy Systems, NATO Advanced Study Institute, Neptun, Romania, 13—24 July 1998; Bejan, A., Mamut, E., Eds.; Kluwer Academic Publishers: The Netherlands, 1999; pp. 421–424. [Google Scholar]
- Salamon, P. A Contrast between the physical and the engineering approaches to finite-time thermodynamic models and optimizations. In Recent Advances in Finite Time Thermodynamics; Wu, C., Chen, L., Chen, J., Eds.; Nova Science Publishers: New York, NY, USA, 1999; pp. 541–552. [Google Scholar]
- Chen, J.; Yan, Z.; Lin, G.; Andresen, B. On the Curzon-Ahlborn efficiency and its connection with the efficiencies of real heat engines. Energ. Convers. Manag. 2001, 42, 173–181. [Google Scholar] [CrossRef]
- Salamon, P.; Nulton, J.D.; Siragusa, G.; Andresen, T.R.; Limon, A. Principles of control thermodynamics. Energy 2001, 26, 307–319. [Google Scholar] [CrossRef]
- Salamon, P.; Hoffmann, K.H.; Schubert, S.; Berry, R.S.; Andresen, B. What conditions make minimum entropy production equivalent to maximum power production? J. Non-Equibri. Thermodyn. 2001, 26, 73–83. [Google Scholar] [CrossRef]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chen, Y. Maximum Profit Configurations of Commercial Engines. Entropy 2011, 13, 1137-1151. https://doi.org/10.3390/e13061137
Chen Y. Maximum Profit Configurations of Commercial Engines. Entropy. 2011; 13(6):1137-1151. https://doi.org/10.3390/e13061137
Chicago/Turabian StyleChen, Yiran. 2011. "Maximum Profit Configurations of Commercial Engines" Entropy 13, no. 6: 1137-1151. https://doi.org/10.3390/e13061137
APA StyleChen, Y. (2011). Maximum Profit Configurations of Commercial Engines. Entropy, 13(6), 1137-1151. https://doi.org/10.3390/e13061137



