Second Law Analysis of Viscoelastic Fluid over a Stretching Sheet Subject to a Transverse Magnetic Field with Heat and Mass Transfer

Abstract

This paper concerns the second law analysis of a viscoelastic fluid over a stretching sheet subject to a transverse magnetic field with heat and mass transfer. The velocity, temperature and concentration profiles are obtained analytically using Kummer’s functions. The effects of the magnetic and viscoelastic parameters on both the longitudianl and the transverse velocities are investigated. The influence of Prandt number, the magnetic parameter and the heat source/sink parameter on the temperature is analysed. The concentration and its variations with the Schmidt number and the magnetic parameter is presented as well. The velocity, the temperature and the concentration profiles are used to compute the entropy generation number. This number is graphed and studied as function of the magnetic parameter, the Prandtl number, The Schmidt number, the Reynolds number, the dimensionless group, the Hartmann number, the ratio of the dimensionless concentration difference to the dimensionless temperature difference and the constant parameter.

1. Introduction

The study of MHD flow of viscoelastic fluids over a continuously moving surface has a wide range of applications in technological and industrial manufacturing processes. This concerns the production of synthetic sheets, aerodynamic extrusion of plastic sheets, cooling of metallic plates, etc.

Crane [1] considered the laminar boundary layer flow of a Newtonian fluid caused by a flat elastic sheet whose velocity varies linearly with the distance from the fixed point of the sheet. Rajagopal et al. [2] and Chang [3] presented an analysis of flow of viscoelastic fluid over stretching sheets. The heat transfer cases of these studies have been considered by Dandapat and Gupta [4] and Vajravelu and Rollins [5], while flow of viscoelastic fluid over a stretching surface under the influence of uniform magnetic field has been investigated by Andersson [6].

Thereafter, a series of studies on heat transfer effects on viscoelastic fluid have been made by many authors under different physical situations [7,8,9,10,11,12,13]. Khan and Sanjayanand [14] have derived a similarity solution of a viscoelastic boundary layer flow and heat transfer over an exponential stretching surface.

Recently, Cortell [15] studied flow and heat transfer of a viscoelastic fluid over a stretching surface considering both constant sheet temperature and prescribed sheet temperature. Abel et al. [16] carried out a study of viscoelastic boundary layer flow and heat transfer over a stretching surface in the presence of non-uniform heat source and viscous dissipation considering prescribed surface temperature and prescribed surface heat flux.

Although the preceeding research works have covered a wide range of problems involving the flow and heat transfer of viscoelastic fluid over stretching surface they have been restricted, from z thermodynamic point of view, to only the first law analysis. The contemporary trend in the field of heat transfer and thermal design is the second law of thermodynamics analysis and its related concept of entropy generation minimization.

Entropy generation is closely associated with thermodynamic irreversibility, which is encountered in all heat transfer processes. Different sources such as heat transfer and viscous dissipation are responsible for generation of entropy [17,18]. The analysis of entropy generation rate in a circular duct with imposed heat flux at the wall and its extension to determine the optimum Reynolds number as function of the Prandtl number and the duty parameter were presented by Bejan [18,19]. Sahin [20] introduced the second law analysis to a viscous fluid in circular duct with isothermal boundary conditions.

In another paper, Sahin [21] presented the effect of variable viscosity on entropy generation rate for heated circular duct. A comparative study of entropy generation rate inside duct of different shapes and the determination of the optimum duct shape subjected to isothermal boundary condition were done by Sahin [22]. Narusawa [23] gave an analytical and numerical analysis of the second law for flow and heat transfer inside a rectangular duct.

In more recent papers, Mahmud and Fraser [24,25,26] applied the second law analysis to fundamental convective heat transfer problems and to non-Newtonian fluid flow through a channel made of two parallel plates. The study of entropy generation in a falling liquid film along an inclined heated plate was carried out by Saouli and Aïboud-Saouli [27]. As far as the effect of a magnetic field on the entropy generation is concerned, Mahmud et al. [28] studied the case of mixed convection in a channel. The effects of magnetic field and viscous dissipation on entropy generation in a falling film and channel were studied by Aïboud-saouli et al. [29,30].

The objective of this paper is the thermodynamic analysis of a viscoelastic magnetohydrodynamic flow over a stretching sheet with prescribed surface temperature in the presence of heat and mass transfer and a uniform transverse magnetic field.

Figure 1. Physical model for the flow.

Figure 1. Physical model for the flow.

2. Mathematical Formulation and Solution

In two-dimensional Cartesian coordinate system $\left(x,y\right)$ we consider magneto-convection, steady, laminar, electrically conductor, boundary layer flow of a second grade fluid caused by a stretching surface in the presence of a uniform transverse magnetic field. As shown in Figure 1, the $x$-axis is taken in the direction of the main flow along the plate and the $y$-axis is normal to the plate with velocity components $u,v$ in these directions.

Under the usual boundary layer approximations, the governing equations are:

Continuity Equation:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$

(1)

Momentum Equation:

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\nu \frac{{\partial }^{2}u}{\partial y^2}-k_0\left(u\frac{{\partial }^{3}u}{\partial x\partial y^2}+v\frac{{\partial }^{3}u}{\partial y^3}-\frac{\partial u}{\partial y}\frac{{\partial }^{2}u}{\partial x\partial y}+\frac{\partial u}{\partial x}\frac{{\partial }^{2}u}{\partial y^2}\right)-\frac{\sigma B_0^2}{\rho }u$$

(2)

Energy Equation:

By using the usual boundary layer approximations, the equation of energy with temperature dependent heat source/sink in the flow direction is given by:

$$\rho C_P\left(u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}\right)=k\frac{{\partial }^{2}T}{\partial y^2}+Q\left(T-T_{\infty }\right)$$

(3)

where Q is the rate of internal heat generation (positive) or absorption (negative).

Diffusion Equation:

$$u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=D\frac{{\partial }^{2}C}{\partial y^2}$$

(4)

The appropriate boundary conditions for velocity field are:

$$y=0,u=u_0=\lambda x,v=0$$

(5a)

$$y=\infty ,u=0,\frac{\partial u}{\partial y}=0$$

(5b)

The thermal conditions for the energy Equation 3 are:

$$y=0,T=T_0=A{\left(\frac{x}{l}\right)}^2+T_{\infty }$$

(6a)

$$y=\infty ,T=T_{\infty }$$

(6a)

For the diffusion Equation 4, the boundary conditions are:

$$y=0,C=C_0=A{\left(\frac{x}{l}\right)}^2+C_{\infty }$$

(7a)

$$y=\infty ,C=C_{\infty }$$

(7b)

Defining new variables

$$u=\lambda x{f}^{\prime }\left(\eta \right)...,v=-\sqrt{\nu \lambda }f\left(\eta \right)$$

(8)

where:

$$\eta =y\sqrt{\frac{\lambda }{\nu }}$$

(9)

and substituting into Equation 2 gives:

$${f^{\prime }}^2\left(\eta \right)-f\left(\eta \right)f^{″}\left(\eta \right)=f^{‴}\left(\eta \right)-k_1\left[2f^{\prime }\left(\eta \right)f^{‴}\left(\eta \right)-f\left(\eta \right)f^{IV}\left(\eta \right)-{f^{″}}^2\right]-Mn{f}^{\prime }\left(\eta \right)$$

(10)

where:

$$Mn=\frac{\sigma B_0^2}{\rho \lambda }\text{ and }{k}_1=\frac{k_0\lambda }{\nu }$$

(11)

The boundary conditions Equation 5a and Equation 5b become:

$$\eta =0,f=0,f^{\prime }=1$$

(12a)

$$\eta =\infty ,f^{\prime }=0,f^{″}=0$$

(12b)

The solution of Equation 10, satisfying the boundary conditions (Equation 12a) and (Equation 12b) is:

$$f^{\prime }\left(\eta \right)=e^{-\alpha \eta }(\alpha \succ 0)$$

(13)

$$\alpha =\sqrt{\frac{1+Mn}{1-k_1}}$$

(14)

This gives the velocity components:

$$u=\lambda x{e}^{-\alpha \eta }$$

(15)

$$v=\frac{-\sqrt{\nu \lambda }\left(1-e^{-\alpha \eta }\right)}{\alpha }$$

(16)

Introducing the dimensionless temperature as:

$$\Theta \left(\eta \right)=\frac{T-T_{\infty }}{T_0-T_{\infty }}$$

(17)

and using Equation 8 and Equation 9, then the energy equation (Equation 3) becomes:

$${\Theta }^{″}\left(\eta \right)+\frac{\mathit{Pr}}{\alpha }\left(1-e^{-\alpha \eta }\right){\Theta }^{\prime }\left(\eta \right)-\left(2\mathit{Pr}{e}^{-\alpha \eta }-\beta \right)\Theta \left(\eta \right)=0$$

(18)

where $Pr=\frac{\mu C_P}{k}$ and $\beta =\frac{Q\nu }{\rho C_P}$ are respectively the Prandtl number and the heat source/sink parameter.

The corresponding thermal boundary conditions are:

$$\eta =0,\Theta =1$$

(19a)

$$\eta =\infty ,\Theta =0$$

(19b)

The solution of Equation 18 is written as:

$$\Theta \left(\eta \right)=e^{-\alpha \left(a+b\right)\eta }\frac{M\left(a+b-2,2b+1,-\frac{\mathit{Pr}}{{\alpha }^2}{e}^{-\alpha \eta }\right)}{M\left(a+b-2,2b+1,-\frac{\mathit{Pr}}{{\alpha }^2}\right)}$$

(20)

where $a=\frac{\mathit{Pr}}{2{\alpha }^2}$ and $b=\frac{\sqrt{{\mathit{Pr}}^2-4{\alpha }^2\beta }}{2{\alpha }^2}$.

Here $M\left(q,r,z\right)$ is the Kummer’s function defined by the following equation:

$$M\left(q,r,z\right)={\displaystyle \sum _{n=0}^{n=\infty }\frac{{\left(q\right)}_n}{{\left(r\right)}_n}}\frac{z^n}{n!}$$

(21)

where ${\left(q\right)}_n$ and ${\left(r\right)}_n$ are the Pochhammer’s symbols, defined by:

$${\left(q\right)}_n=q\left(q+1\right)\left(q+2\right).......\left(q+n-1\right)$$

(22)

$${\left(r\right)}_n=r\left(r+1\right)\left(r+2\right).......\left(r+n-1\right)$$

(23)

Defining the dimensionless concentration by the following relationship:

$$\Phi \left(\eta \right)=\frac{C-C_{\infty }}{C_0-C_{\infty }}$$

(24)

The equation of diffusion becomes:

$${\Phi }^{″}\left(\eta \right)+\frac{Sc}{\alpha }\left(1-e^{-\alpha \eta }\right){\Phi }^{\prime }\left(\eta \right)-2Sc{e}^{-\alpha \eta }\Phi \left(\eta \right)=0$$

(25)

where $Sc=\frac{\nu }{D}$ is the Schmidt number.

The relevant boundary conditions for Equation 24 are:

$$\eta =0,\Phi =1$$

(26a)

$$\eta =\infty ,\Phi =0$$

(26b)

The solution of Equation 24 is then:

$$\Phi \left(\eta \right)=e^{-\frac{Sc}{\alpha }\eta }\frac{M\left(\frac{Sc}{{\alpha }^2}-2,\frac{Sc}{{\alpha }^2}+1,-\frac{Sc}{{\alpha }^2}{e}^{-\alpha \eta }\right)}{M\left(\frac{Sc}{{\alpha }^2}-2,\frac{Sc}{{\alpha }^2}+1,-\frac{Sc}{{\alpha }^2}\right)}$$

(27)

3. Second Law Analysis

According to Woods [31] and Megherbi et al. [32], the local volumetric rate of entropy generation in the presence of a magnetic field is given by:

$$S_G=\frac{k}{T_{\infty }^2}\left[{\left(\frac{\partial T}{\partial x}\right)}^2+{\left(\frac{\partial T}{\partial y}\right)}^2\right]+\frac{\mu }{T_{\infty }}{\left(\frac{\partial u}{\partial y}\right)}^2+\frac{\sigma B_0^2}{T_{\infty }}{u}^2+\frac{RD}{C_{\infty }}\left[{\left(\frac{\partial C}{\partial x}\right)}^2+{\left(\frac{\partial C}{\partial y}\right)}^2\right]$$

(28)

Equation 28 clearly shows contributions of four sources of entropy generation. The first term on the right-hand side of Equation 28 is the local entropy generation due to heat transfer across a finite temperature difference; the second term is the local entropy generation due to viscous dissipation, the third term is the local entropy generation due to the effect of the magnetic field, whereas the fourth term is the local entropy generation due to mass transfer across finite concentration difference. It is appropriate to define dimensionless number for entropy generation rate $N_S$. This number is defined by dividing the local volumetric entropy generation rate $S_G$ to a characteristic entropy generation rate $S_{G0}$. For prescribed boundary condition the characteristic entropy generation rate is:

$$S_{G0}=\frac{k{\left(\Delta T\right)}^2}{l^2{T}_{\infty }^2}$$

(29)

therefore, the entropy generation number is:

$$N_S=\frac{S_G}{S_{G0}}$$

(30)

Using the expressions of dimensionless velocity, temperature and concentration, the entropy generation number is given by:

$$\begin{array}{l}{N}_S=\frac{4}{X^2}{\Theta }^2\left(\eta \right)+{\mathit{Re}}_l{{\Theta }^{\prime }}^2\left(\eta \right)+{\mathit{Re}}_l\frac{Br}{\Omega }{f^{″}}^2\left(\eta \right)+H{a}^2\frac{Br}{\Omega }{f^{\prime }}^2\left(\eta \right)+\\ \\ \epsilon \frac{4}{X^2}\frac{{\Sigma }^2}{{\Omega }^2}{\Phi }^2\left(\eta \right)+\epsilon {\mathit{Re}}_L\frac{{\Sigma }^2}{{\Omega }^2}{{\Phi }^{\prime }}^2\left(\eta \right)\end{array}$$

(31)

where ${\mathit{Re}}_l$ , $Br$, $Ha$ are respectively the Reynolds number, the Brinkman number and the Hartman number. $\Omega$ and $\Sigma$ are respectively the dimensionless temperature difference and the dimensionless concentration difference. $\epsilon$ is a constant parameter. These parameters are given by the following relationships:

$${\mathit{Re}}_l=\frac{u_{l}l}{\nu },Br=\frac{\mu u_0^2}{k\Delta T},Ha=B_{0}l\sqrt{\frac{\sigma }{\mu }},\Omega =\frac{\Delta T}{T_{\infty }},\Sigma =\frac{\Delta C}{C_{\infty }},\epsilon =\frac{RD{C}_{\infty }}{k}$$

(32)

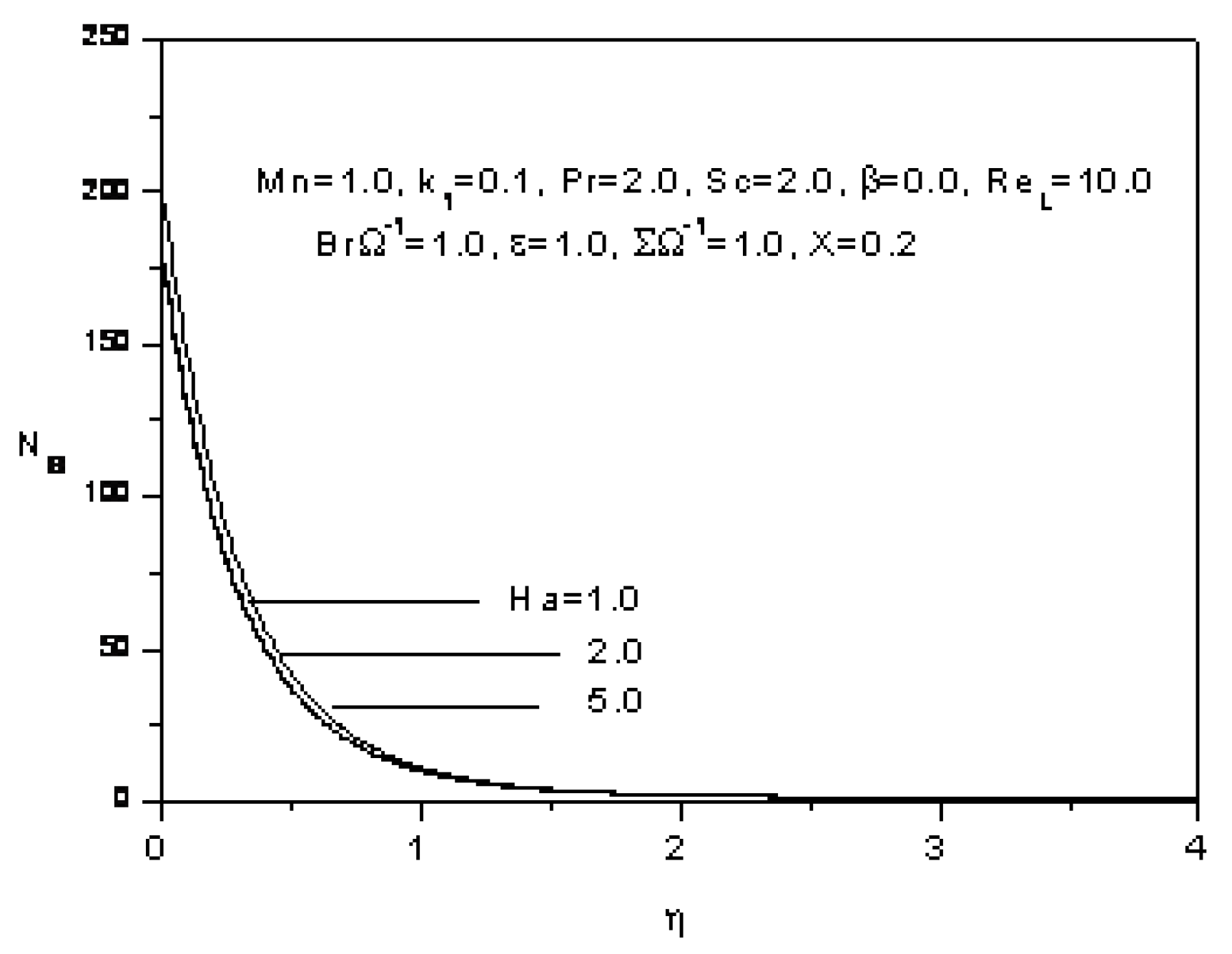
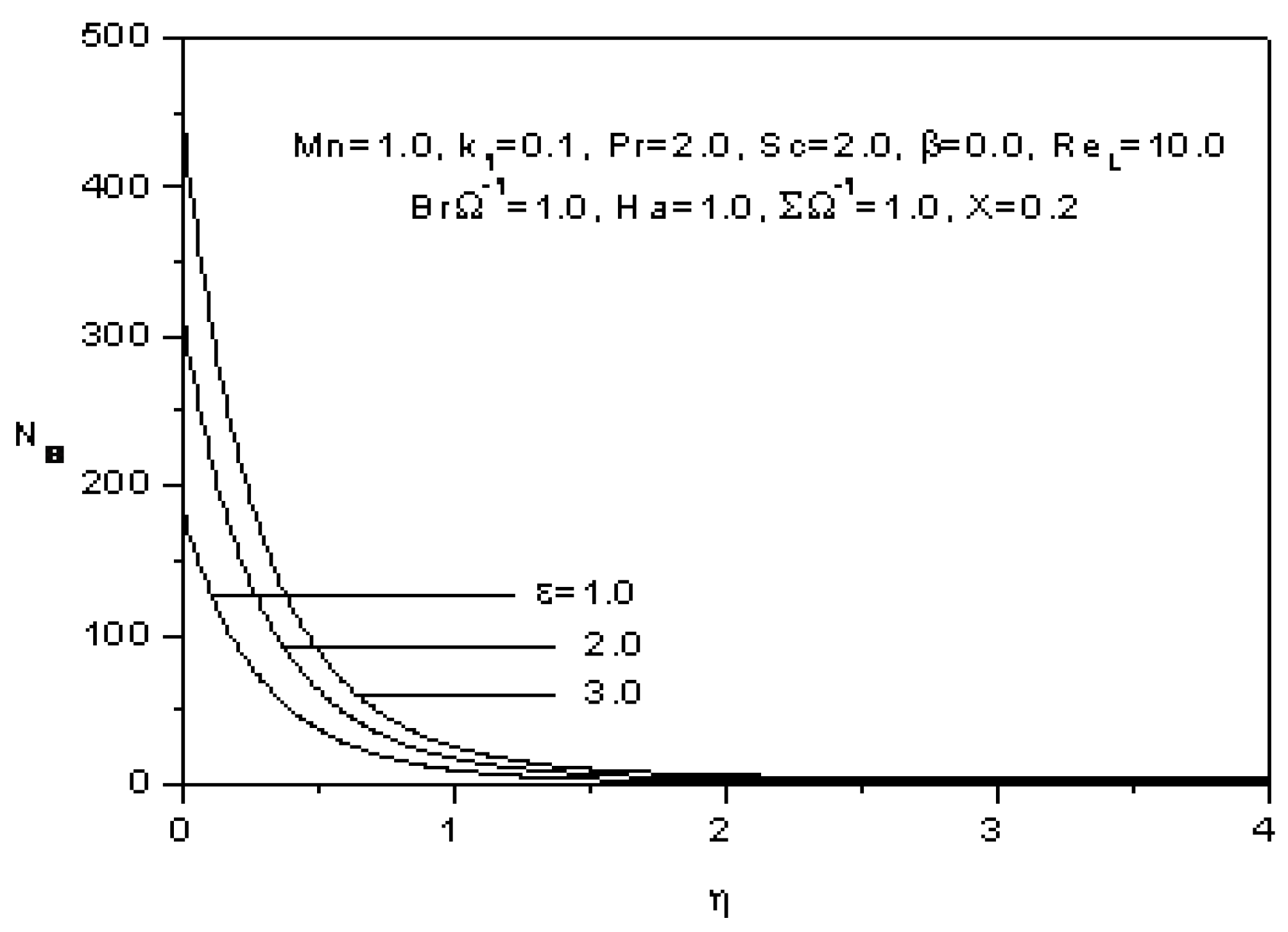
4. Results and Discussion

The flow, heat and mass transfers in a viscoelastic fluid under the influence of a transverse uniform magnetic field has been solved analytically using Kummer’s functions and analytic expressions of the velocity, temperature and concentration have been used to compute the entropy generation.

Figure 2 and Figure 3 show the variations of the longitudinal velocity f´(η) and the transverse velocity f(η) (Equation 8) as function of η for several values of magnetic parameter Mn. It can be observed that f´(η) decreases with η and f(η) increases with η asymptotically for Mn keeping constant. For a fixed position η, both f´(η) and f(η) decreases with Mn, thus the presence of the magnetic field decreases the momentum boundary layer thickness and increase the power needed to stretch the sheet.

Figure 2. Effect of the magnetic parameter on the longitudinal velocity.

Figure 2. Effect of the magnetic parameter on the longitudinal velocity.

Figure 3. Effect of the magnetic parameter on the transverse velocity.

Figure 3. Effect of the magnetic parameter on the transverse velocity.

The effects of the viscoelastic parameter $k_1$ on the longitudinal velocity $f^{\prime }\left(\eta \right)$ and the transverse velocity $f\left(\eta \right)$ are illustrated in Figure 4 and Figure 5. As it can be seen, for a fixed value of $\eta$, both $f^{\prime }\left(\eta \right)$ and $f\left(\eta \right)$ decrease as viscoelastic parameter rises. This can be explained by the fact that, as the viscoelastic parameter increases, the hydrodynamic boundary layer adheres strongly to the surface, which in turn retards the flow in the longitudinal and the transverse directions.

Figure 4. Effect of the viscoelastic parameter on the longitudial velocity.

Figure 4. Effect of the viscoelastic parameter on the longitudial velocity.

Figure 6 depicts the temperature profiles Θ(η) (Equation 19) as a function of η for different values of the Prandtl number Pr. As it can be noticed, decreases with η whatever is the value of the Prandtl number, For a fixed value of η, the temperature Θ(η) decreases with an increase in Prandtl number, which means that the hydrodynamic boundary layer is thicker than the thermal boundary layer.

Figure 5. Effect of the viscoelastic parameter on the transverse velocity.

Figure 5. Effect of the viscoelastic parameter on the transverse velocity.

Figure 6. Effect of the Prandtl number on the temperature.

Figure 6. Effect of the Prandtl number on the temperature.

The temperature profiles Θ(η) as a function of η for different values of the magnetic Mn are plotted in Figure 7. An increase in the magnetic parameter Mn results in an increase of the temperature; this is due to the fact that the thermal boundary layer increases with the magnetic parameter.

Figure 7. Effect of the magnetic parameter on the temperature.

Figure 7. Effect of the magnetic parameter on the temperature.

Figure 8 represents graphs of temperature profiles Θ(η) as function of η for various values of the heat source/sink parameter β. For fixed value of η, the temperature Θ(η) augments with the heat source/sink parameter β. This is due to the fact that the increase of the heat source/sink parameter means an increase of the heat generated inside the boundary layer leading to higher temperature profile.

Figure 8. Effect of the heat source/sink parameter on the temperature.

Figure 8. Effect of the heat source/sink parameter on the temperature.

Figure 9 depicts the concentration profiles Φ(η) (Equation 26) as function of η for different values of the Schmidt number Sc. We infer that concentration decreases with an increase in Schmidt number which means that the hydrodynamic boundary layer is thicker than the diffusion boundary layer.

Figure 9. Effect of the Schmidt number on the concentration.

Figure 9. Effect of the Schmidt number on the concentration.

The concentration profiles Φ(η) for different values of the magnetic Mn are plotted in Figure 10. As it can be noticed, an increase in the magnetic parameter results in an increase of the concentration, this is due to the fact that the concentration boundary layer increases with the magnetic parameter.

The influence of the magnetic parameter Mn on the entropy generation number N_s is shown on Figure 11. The entropy generation number N_s (Eqation 31) decreases with η for Mn keeping constant. For fixed value of η, the entropy generation number increases with the magnetic parameter, because the presence of the magnetic field creates more entropy in the fluid. Moreover, the entropy generation number is higher near the surface where both temperature and velocity are at their maximum values. This means that the surface acts as a strong source of irreversibility.

Figure 10. Effect of the magnetic parameter on the concentration.

Figure 10. Effect of the magnetic parameter on the concentration.

Figure 11. Effect of the magnetic parameter on the entropy generation number.

Figure 11. Effect of the magnetic parameter on the entropy generation number.

Figure 12 illustrates the effect of the Prandtl number Pr on the entropy generation number N_s (Equation 31). The entropy generation number is higher for higher Prandtl number near the surface, and then, the situation is inverted as η increases.

Figure 12. Effect of the Prandtl number on the entropy generation number.

Figure 12. Effect of the Prandtl number on the entropy generation number.

The effect of the Schmidt number Sc on the entropy generation number N_s (Equation 31) is illustrated in Figure 13. The entropy generation number is lower for higher Schmidt number near the surface, and then, the situation is inverted as η increases.

Figure 13. Effect of the Schmidt number on the entropy generation number.

Figure 13. Effect of the Schmidt number on the entropy generation number.

The influence of the Reynolds number Re_L on the entropy generation number N_s (second, third and sixth term of Equation 31) is plotted on Figure 14. For a given value of η, the entropy generation number increases as the Reynolds number increases. The augmentation of the Reynolds number increases the contribution of the entropy generation number due to fluid friction, heat and mass transfer in the boundary layer.

Figure 14. Effect of the Reynolds number on the entropy generation number.

Figure 14. Effect of the Reynolds number on the entropy generation number.

The effect of the dimensionless group parameter BrΩ^-1on the entropy generation number N_s (third and fourth term of Equation 31) is depicted in Figure 15. The dimensionless group determines the relative importance of viscous effect. For a given η, the entropy generation number is higher for higher dimensionless group. This is due to the fact that for higher dimensionless group, the entropy generation numbers due to the fluid friction and to the magnetic field increase.

Figure 15. Effect of the dimensionless group on the entropy generation number.

Figure 15. Effect of the dimensionless group on the entropy generation number.

The effect of the Hartmann number Ha on the entropy generation number N_s (fourth term of Equation 31) is plotted in Figure 16. For a given η, as the Hartmann number increases, the entropy generation number increases. The entropy generation number is proportional to the Hartmann number which proportional to the magnetic field. The presence of the magnetic field creates additional entropy.

The effect of the parameter ΣΩ^-1 which is the ratio of the dimensionless concentration difference to the dimensionless temperature difference, on the entropy generation number N_s (fifth and sixth term of Equation 31) is plotted in Figure 17. For a given η, as this parameter increases, the entropy generation number increases. This augmentation is due to the contribution of the mass transfer to the entropy generation number.

Figure 16. Effect of the Hartmann number on the entropy generation number.

Figure 16. Effect of the Hartmann number on the entropy generation number.

An augmentation of the constant parameter ε on the entropy generation number N_s (fifth and sixth term of Equation 31) is plotted in Figure 18. For a given η, as the constant parameter increases, the entropy generation number increases. This increase is the contribution of the mass transfer to the entropy generation number.

Figure 17. Effect of the ratio of the dimensionless concentration difference to the dimensionless temperature difference on the entropy generation number.

Figure 17. Effect of the ratio of the dimensionless concentration difference to the dimensionless temperature difference on the entropy generation number.

Figure 18. Effect of the constant parameter on the entropy generation number.

Figure 18. Effect of the constant parameter on the entropy generation number.

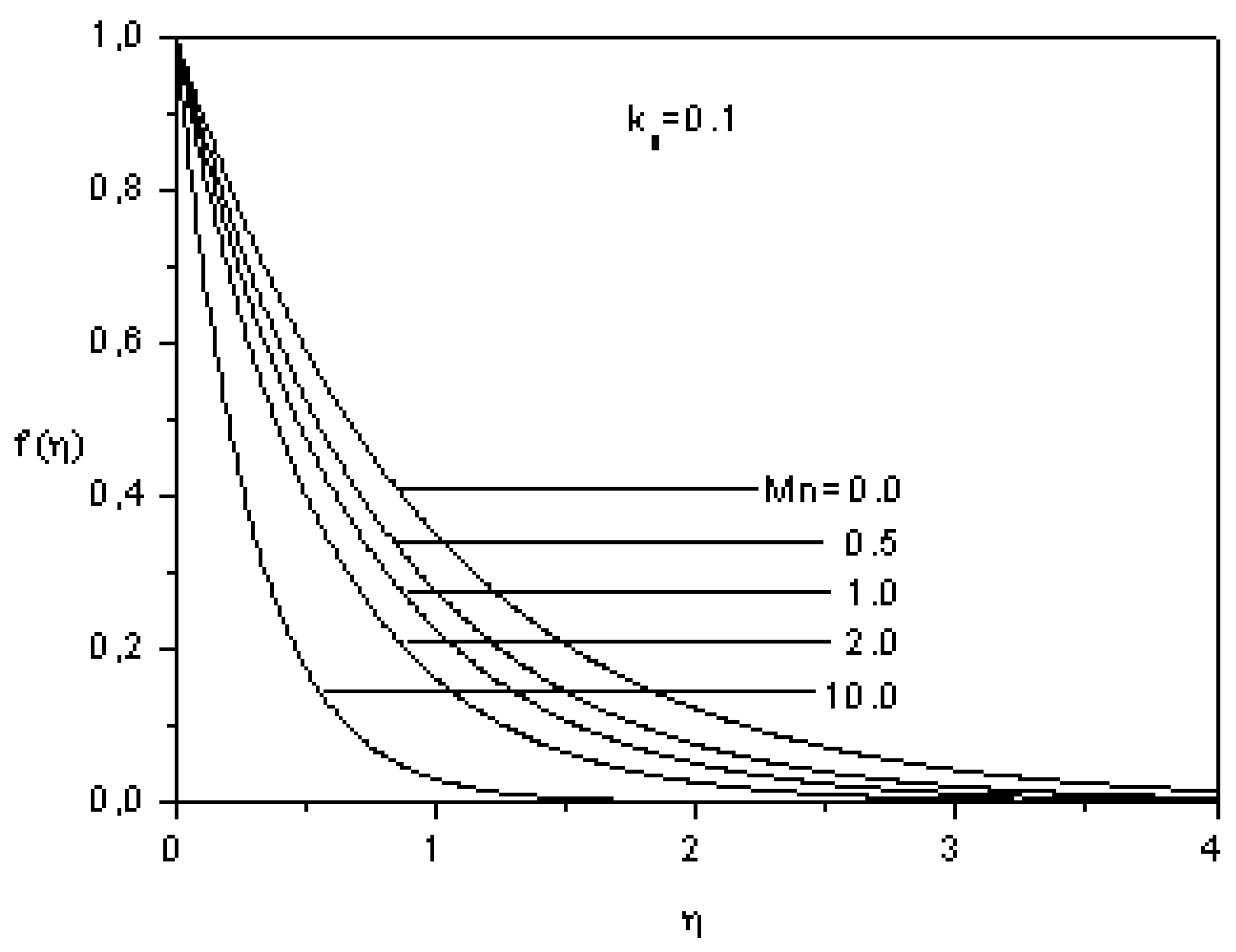
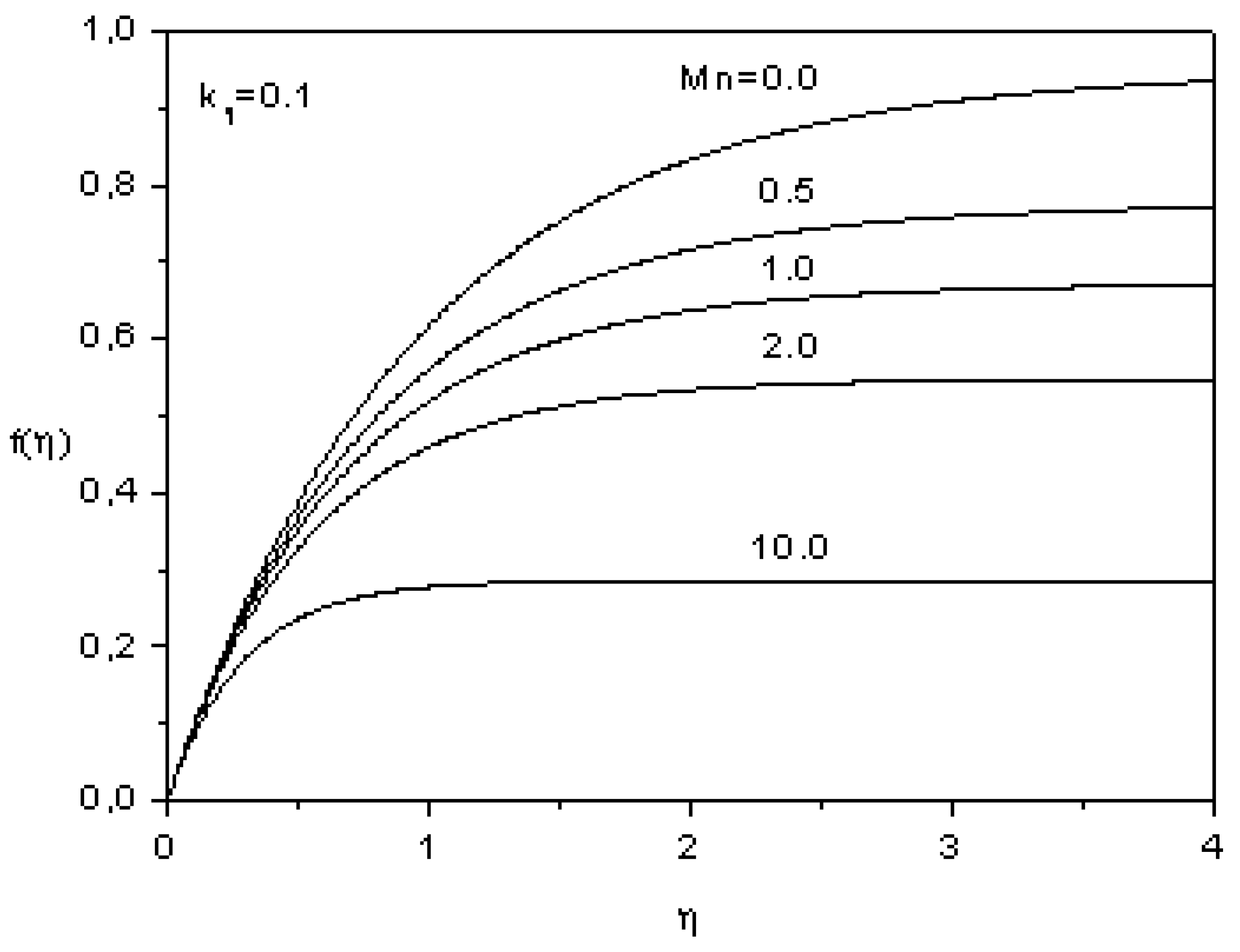
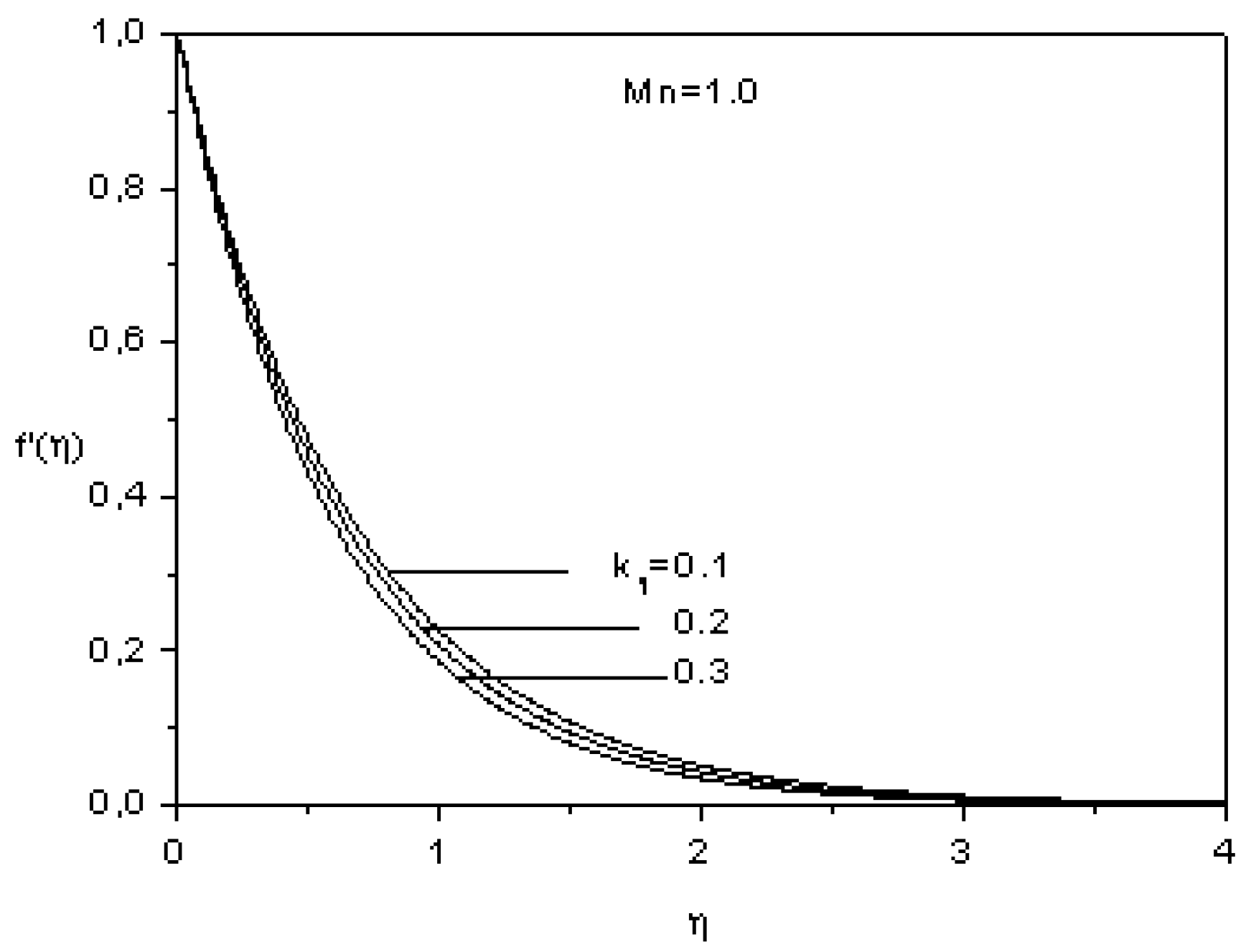
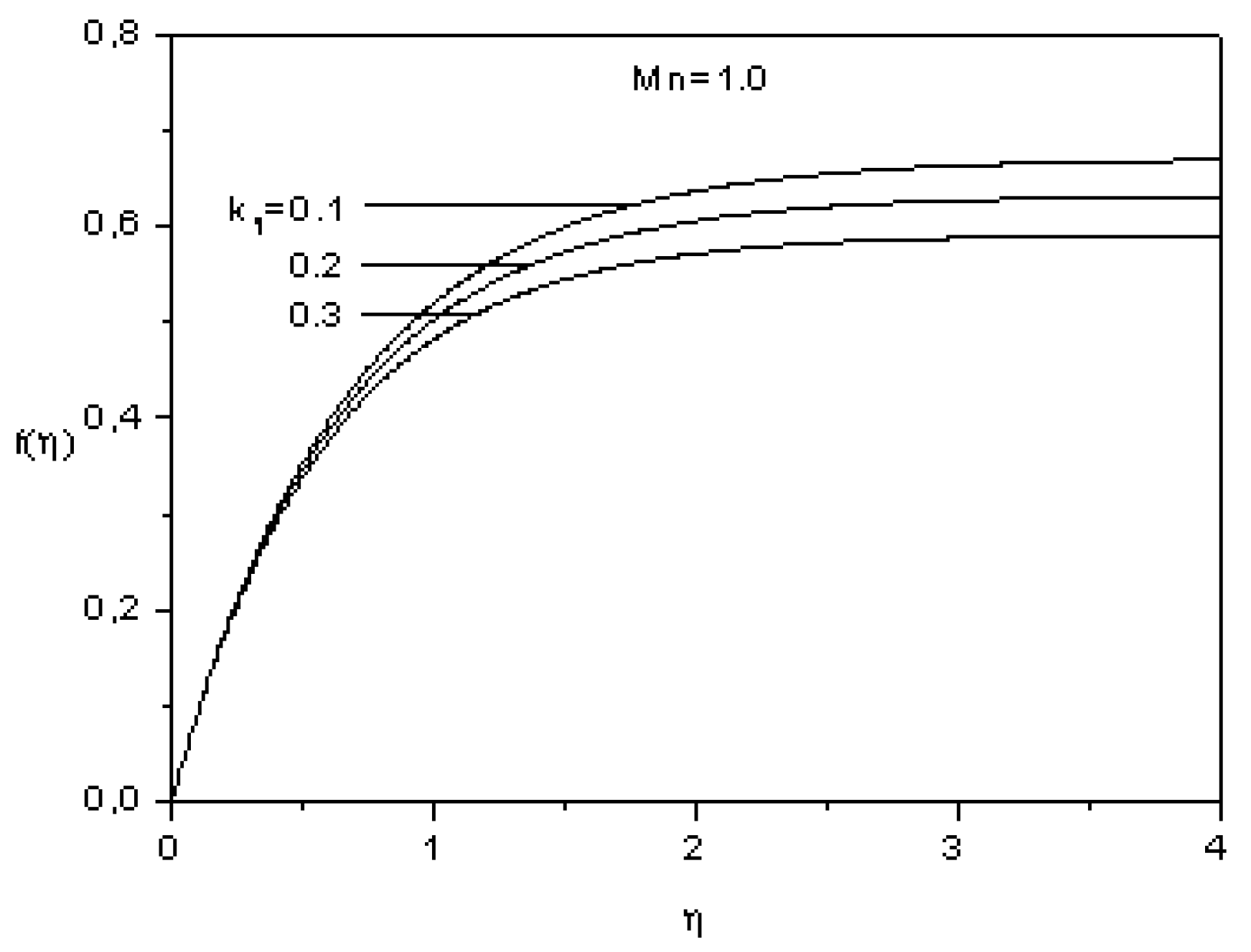
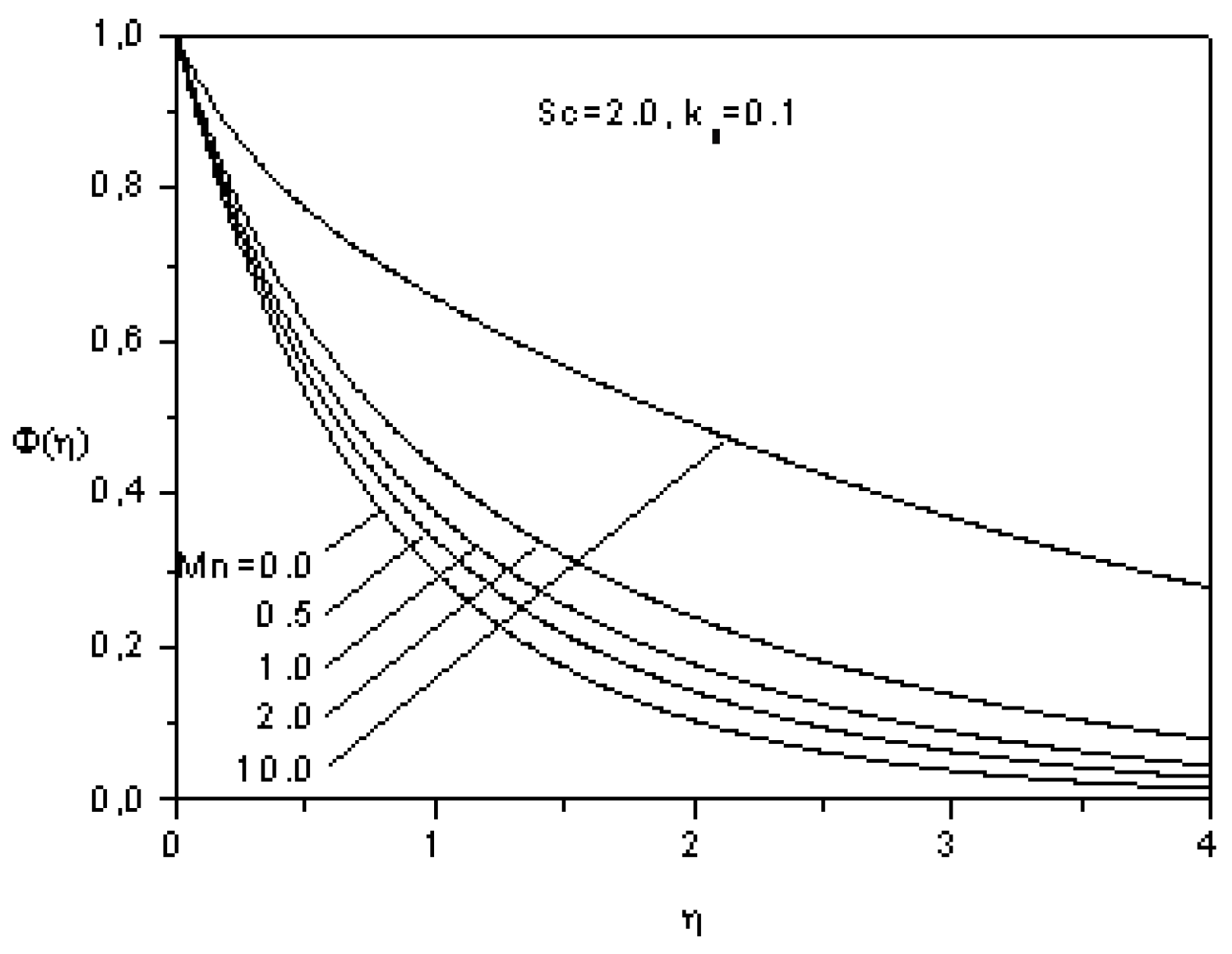
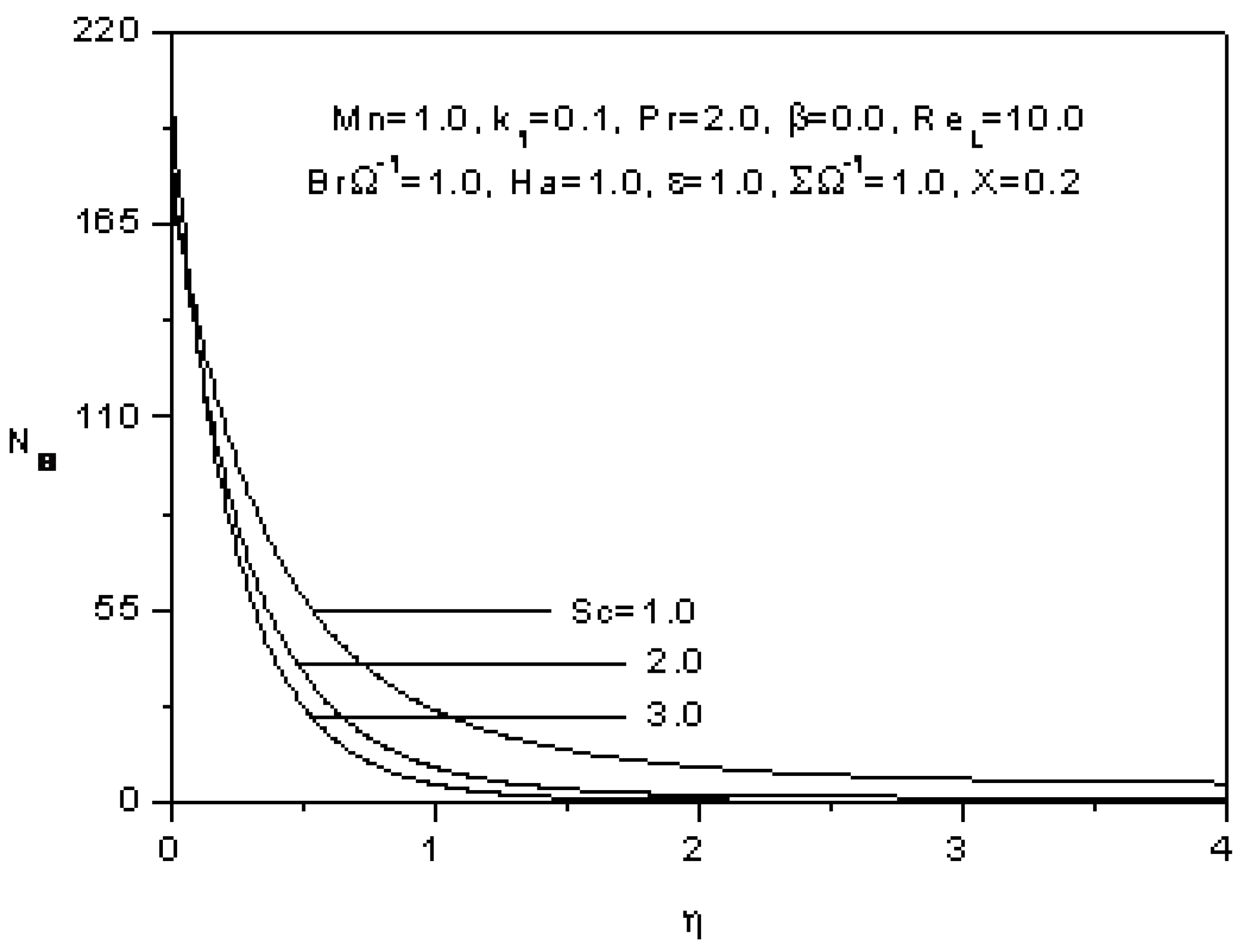
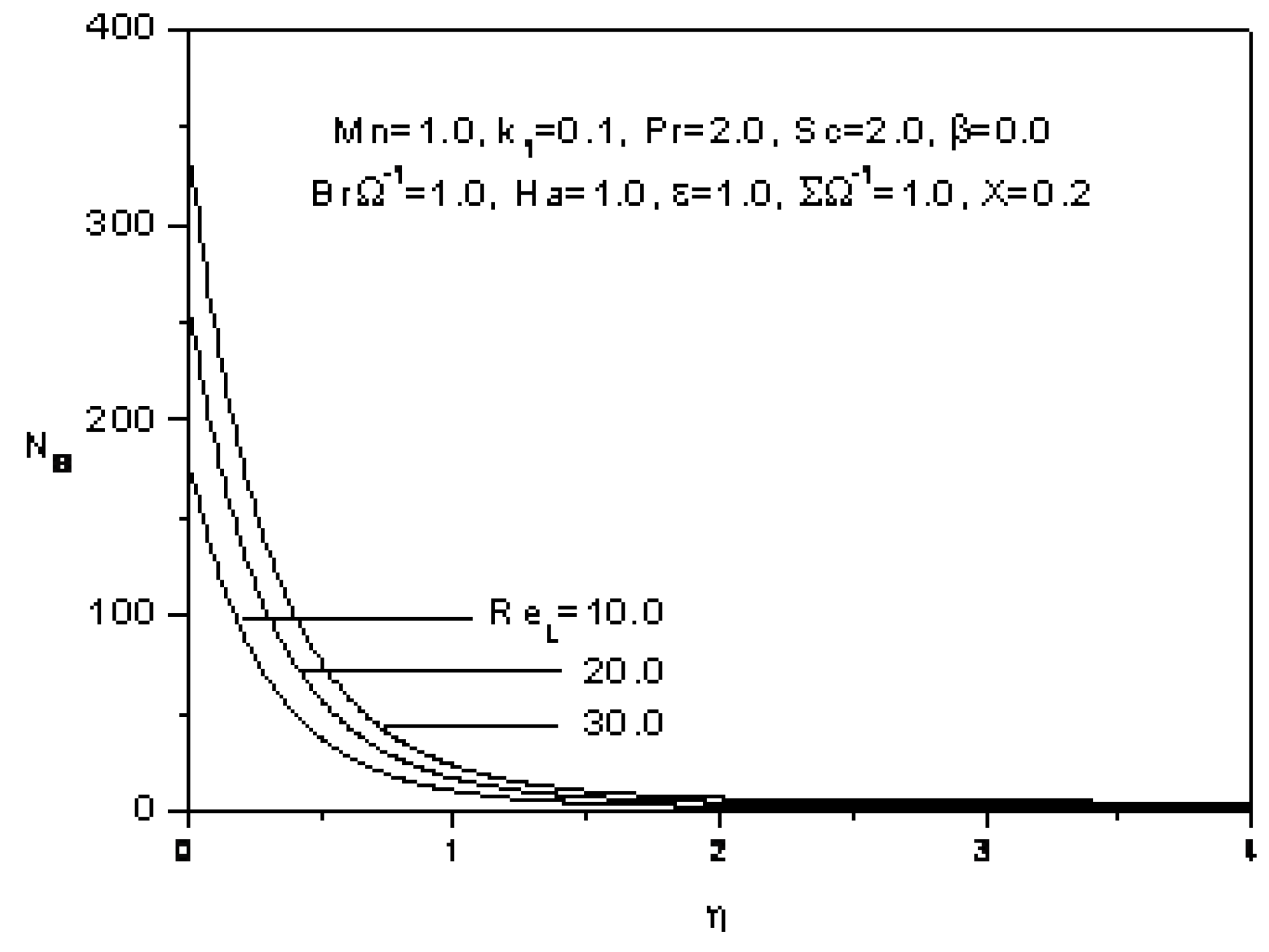
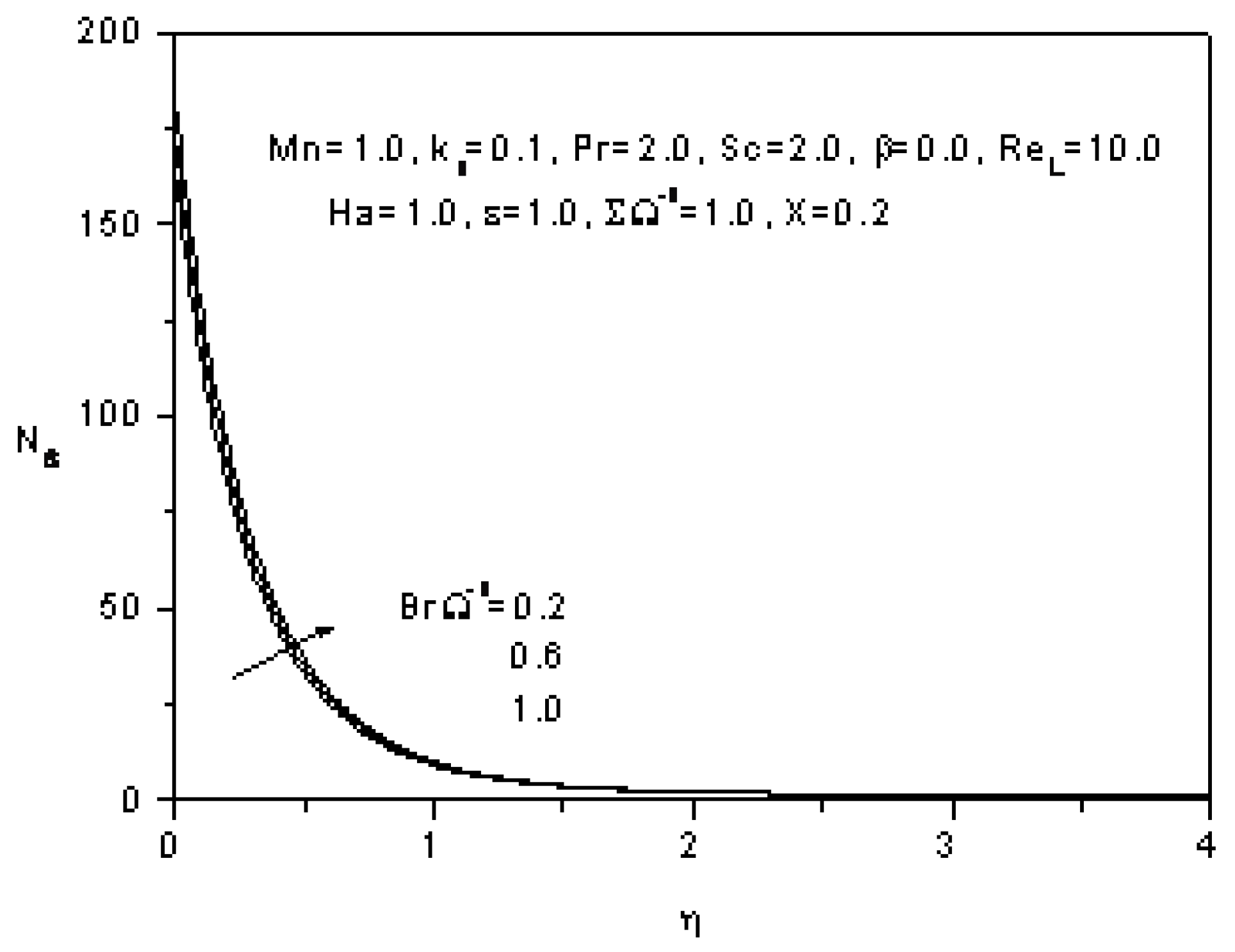
5. Conclusions

The velocity, temperature and concentration profiles are obtained analytically and used to compute the entropy generation number in a viscoelastic fluid over a stretching sheet subject to a transverse magnetic field with heat and mass transfer.

The effects of the magnetic parameter and the viscoelastic parameter on the longitudinal and transverse velocities are discussed. The influences of the Prandtl number, the magnetic parameter and the heat source/sink parameter on the temperature profiles are presented. The dependence of the concentration profiles on the Schmidt number and the magnetic parameter is also presented. As far as the entropy generation number is concerned, its dependence on the magnetic parameter, the Prandlt, the Schmidt number, the Reynolds number, the dimensionless group, the Hartmann number, the ratio of the dimensionless concentration difference to the dimensionless temperature difference and the constant parameter are illustrated and analyzed.

From the results the following conclusions could be drawn:

(a)

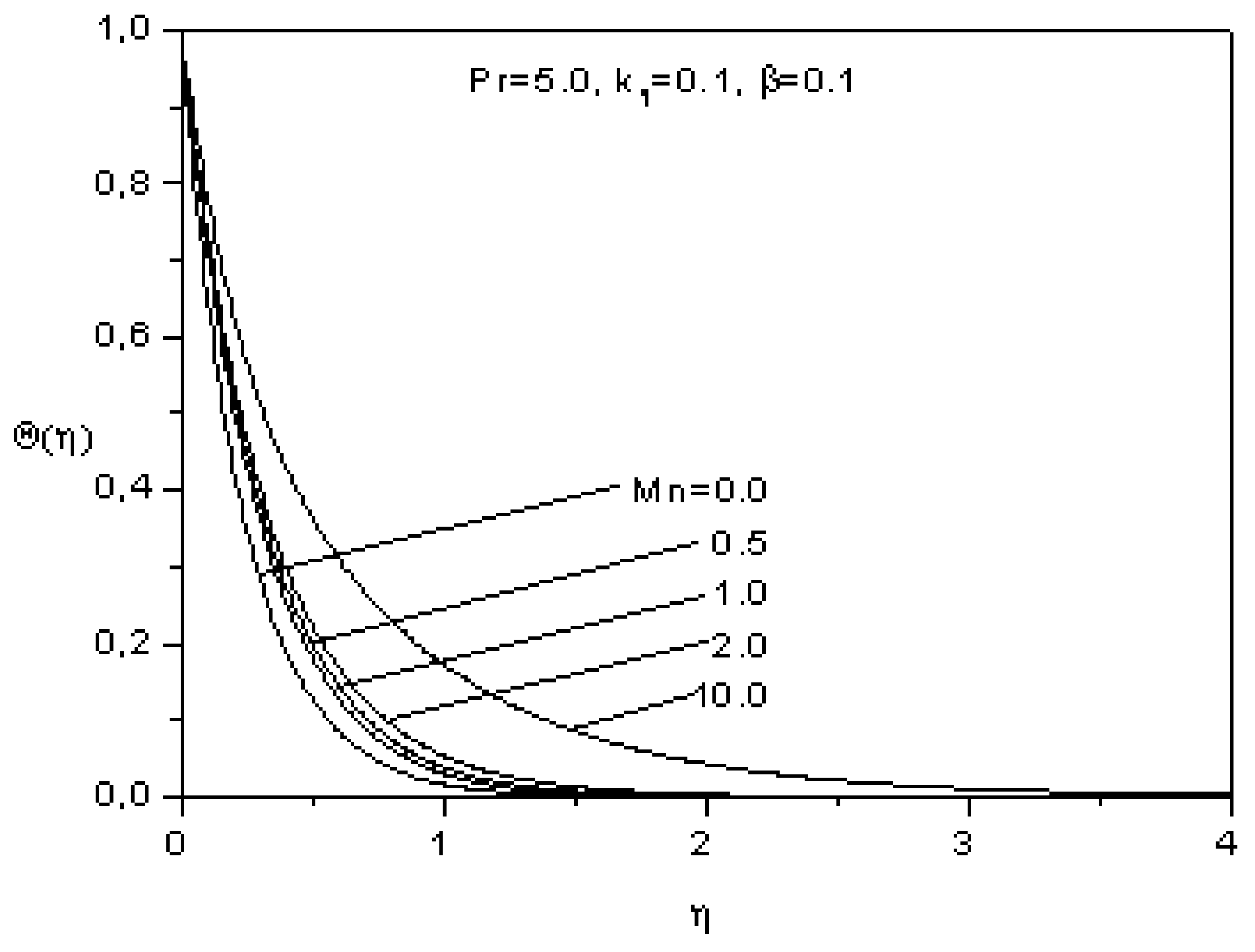
The longitudinal and the transverse velocities decrease as the magnetic parameter and the viscoelastic paramaeter increase.

(b)

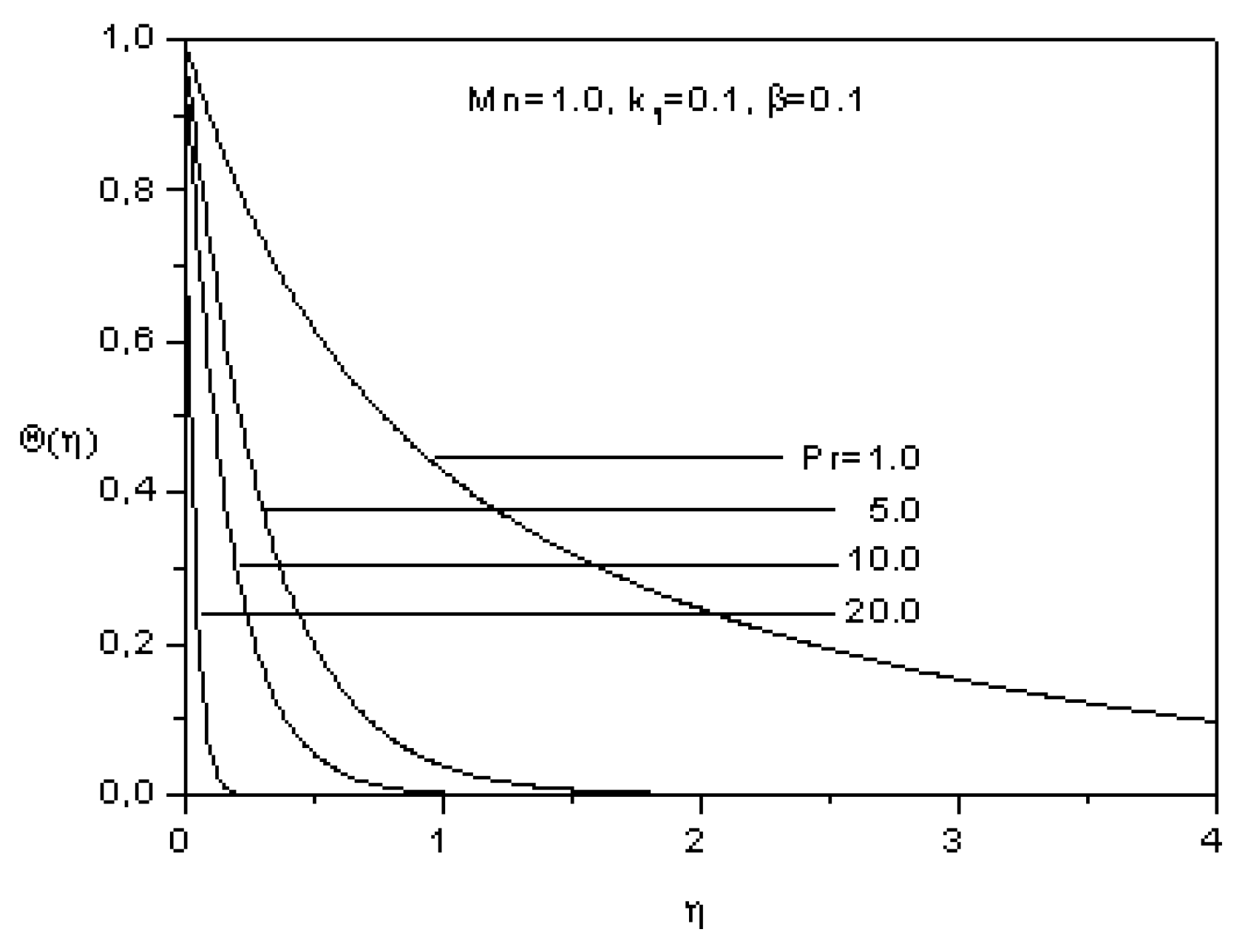
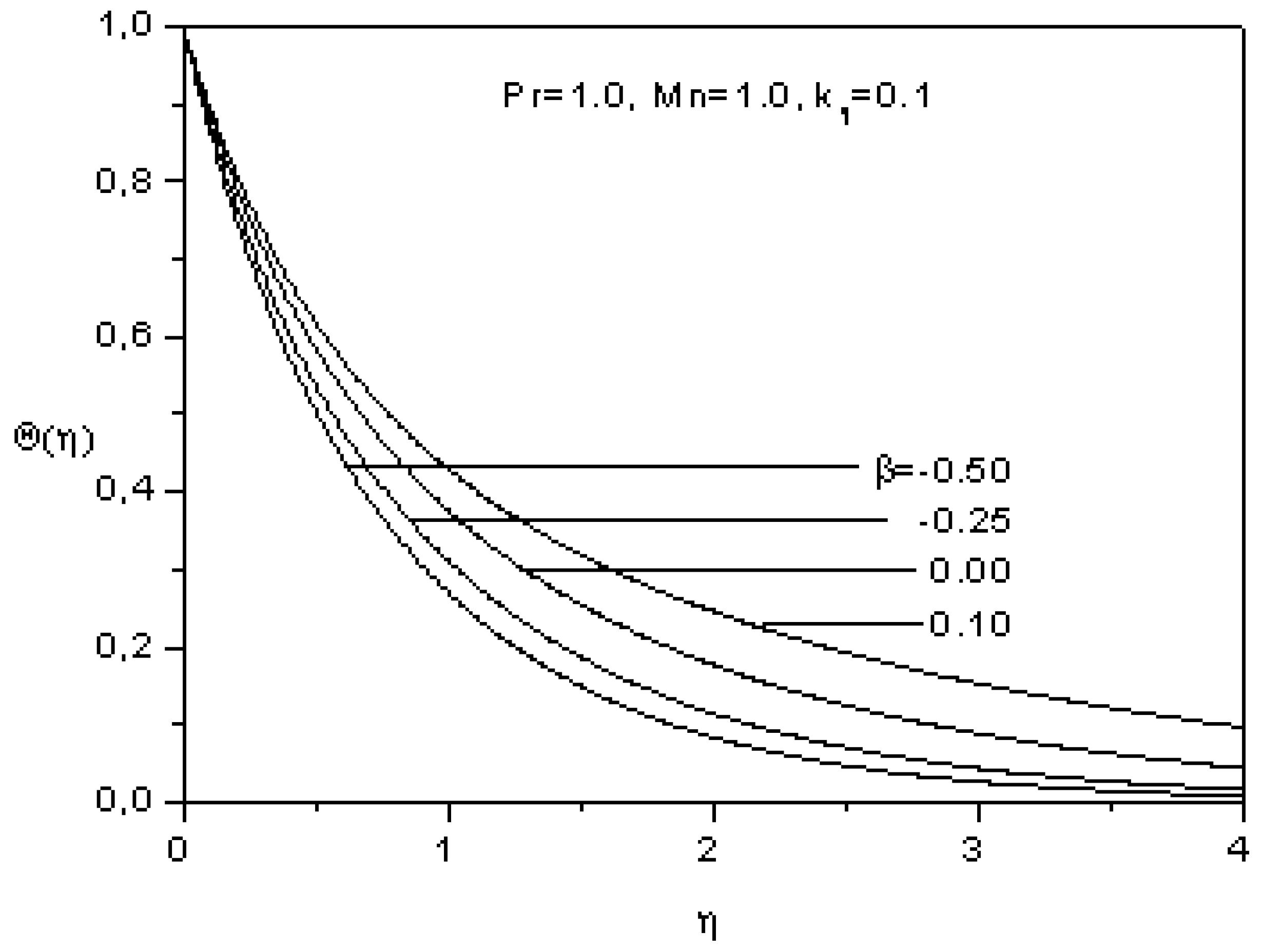
The temperature increases as the magnetic parameter and the heat source sink parameter increases, but it decreases as the Prandtl number increases.

(c)

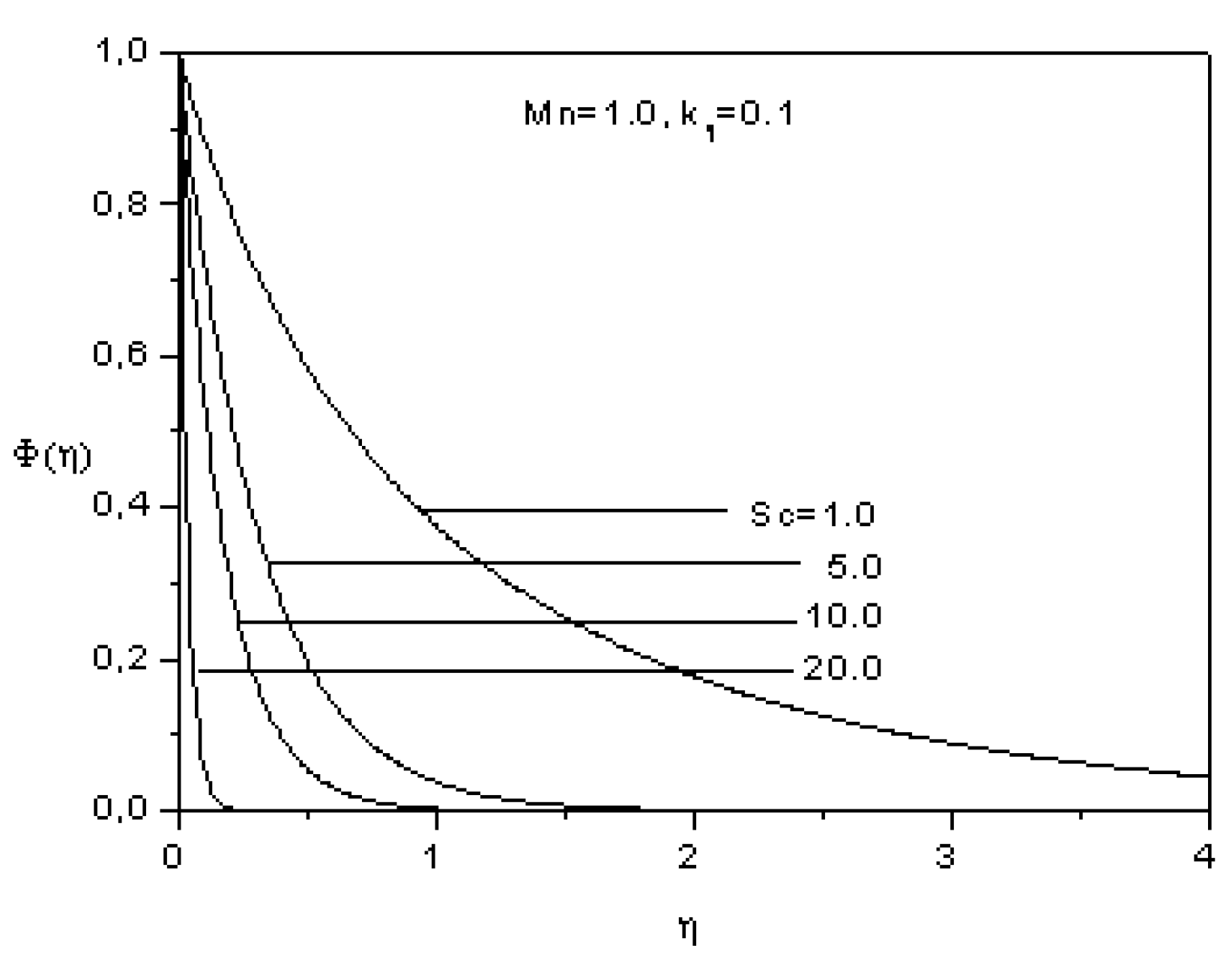
The concentration augmentes as the magnetic parameter increases, however it dimishes as the Schmidt number increases.

(d)

The entropy generation increases with the increase of the magnetic parameter, the Prandlt number, The Schmidt number, the Reynolds number, the dimensionless group, the Hartmann number and also with ratio of the dimensionless concentration difference to the dimensionless temperature difference and the constant parameter.

(e)

The surface acts as a strong source of irreversibility.