Abstract
Distinctly quantum friction effects of three types are surveyed: internal friction, measurement-induced friction, and quantum-fluctuation-induced friction. We demonstrate that external driving will lead to quantum internal friction, and critique the measurement-based interpretation of friction. We conclude that in general systems will experience internal and external quantum friction over and beyond the classical frictional contributions.
Friction is the price for moving too fast. An attempt to induce a rapid change in the state of a system would be accompanied by additional entropy generation and will be encumbered by energy costs. As an example of friction we can consider a body moving rapidly against a stationary background. Its kinetic energy is dissipated, generating heat and entropy in the environment. The amount of dissipation is proportional to the velocity. Another archtypical case of friction is a driven gas compression process. For a system that is thermally decoupled from its environment, rapid changes in the piston position that compresses the gas will result in internal heating of the gas and entropy generation. To restore the system to its slow quasi-static compression equivalent, heat has to be removed from the gas. This additional heat is equivalent to extra work against friction.
Friction is typically modeled by a phenomenological theory within classical mechanics. How does it extend to the quantum domain? Can a first principles model of friction be developed? There are ample examples of quantum frictional phenomena. These include friction observed in micro-mechanical systems at low temperatures [1], in superfluid theory [2], and even in quantum cosmology [3] and more. Are such quantum examples of friction essentially classical phenomena that endure into the quantum domain, or is there something distinctly quantum about (at least some kinds of) friction? In this review we will argue that the latter is the case—there are distinctly quantum types of friction. Even more so, quantum mechanics generally adds frictional affects above and beyond any classical ones, so that a quantum (and therefore fuller) description of the system will include more friction.
Several important changes occur in the transition into quantum mechanics. First, the physics of an isolated system is strictly reversible and unitary. We will argue below that internal friction still occurs but its analytical description requires a proper extension of the classical concepts of entropy and temperature. Furthermore, we will point to a new mechanism that creates distinctly quantum internal friction.
Secondly, the quantum description of the system plus its environment allows for entanglement correlations that have no classical analog. We will describe the quantum theory of open systems in some detail, and argue that in the quantum domain it is difficult to separate the system from its environment. This difficulty has led to misunderstandings and incorrect attempts to characterize friction.
Finally, quantum fluctuations and zero-point energy change the nature of the environment, which leads to additional frictional forces.
This paper will attempt to describe a broad conceptual framework that can be used to understand friction in both the classical and the quantum domains. We will argue that friction is manifested as two phenomena:
- External friction amounts to the dissipation of kinetic energy from a small “open system” to its environment, creating entropy and heat. The relevance of kinetic energy is related to the isotropy of the environment, and the asymmetry of a particular direction of (non-zero) velocity. Irreversibility and the generation of heat and entropy are related to the disparity in the size and time scales of the systems, leading to effective irreversible memoryless dynamics and a large entropy generation. Heuristically, external friction is the attempt by the environment to lower the system to a “symmetric” velocity of zero.
- Internal friction, which is the generation of excitations (which are then typically dissipated by external friction) due to the disparity between the internal time-scales of the system and the external driving time scale. Heuristically, internal friction is the resistance of the system to rapid change.
Both processes can have quantum contributions. Quantum fluctuations will generally function as an extra dissipative environment, while quantum non-commutativity will ensure that the system cannot perfectly follow external changes.
We do not intend a thorough review of all quantum friction phenomena. Instead, we will demonstrate our suggested framework through quintessential cases (an ideal gas piston for internal friction and Brownian motion for external friction), and present one further case (the dynamical Casimir effect) as an example of its broader applicability. In Section 1 we will consider internal friction and note the quantum considerations necessitating it and the quantum concepts necessary to observe it. In Section 2 we will discuss the theory of quantum open systems, and in Section 3 apply it to Brownian motion to explore the nature of external friction. We will consider the effects of quantum fluctuations in Section 4. Finally, we devote a fifth section to discuss the results.
Throughout our treatment we will consider quantum systems exclusively. We will refer to the classical limit when appropriate.
1. Internal Friction
Internal friction is induced in a system when its external constrains are changed rapidly. Consider a quantum system with a discrete energy spectrum (we will further assume non-degeneracy for simplicity). An ensemble will have some average energy (where is the probability to find the system in a certain energy eigenstate). A rapid change in external constraints corresponds to a change in some external semi-classical field in the system’s Hamiltonian. For the paradigmatic case of a gas in a piston the field will be related to the location of the potential barrier confining the gas particles. If the change to the external field is slow enough, the quantum adiabatic theorem assures us that there will be no change in the energy populations and therefore the change in the energy will be due only to the change in energy levels. The energy in such a “quasistatic” process changes minimally in this sense.
Now consider a faster change. The rapid change in energy levels can now lead to population changes, changing the energy beyond the “minimal” quasistatic change of the energy levels themselves. For simplicity, let us assume for now that we start from the ground state. Then we can only lose population density to higher states, so that we can only reach a higher (or equal) energy compared to the quasistatic change. Thus we receive a “resistance” to velocity: when we strive to drive the system quickly we need to invest more work.
This process, by itself, is reversible. Simply reversing the field-change protocol will yield back the original state and the original energy. The evolution is reversible because it is a unitary dynamics. However, consider appending a non-unitary step to the process. Now we leave the field at its final value for a time, while bringing the system into contact with a heat bath at its original temperature (zero temperature, in this example). This will induce irreversible thermalization and loss of information about the original state. Such thermalization will convert the extra energy required into extra heat in the environment.
This process can be generalized for a finite temperature. Allahverdyan and Nieuwenhuizen proved that, barring level-crossing, for a system initially at a thermal state the minimal work (energy) is reached by a quasistatic process [4,5]. The derivation is too long to be repeated here, but in general it hinges on realizing that the state’s eigenvalues do not change during unitary evolution, and that for a smooth enough field-change protocol the adiabatic theorem ensures absence of transitions between states. Having an initial thermal state is not required, but it is necessary to have an initial state with decreasing occupations in the energy eigenbasis. Most importantly, the requirement for no level crossing is satisfied for a single varying field parameter, a result known as the non-crossing rule [6,7]. No level crossing, in turn, allows us to estimate the time scale required for the quasistatic limit as related to the inverse of the minimum energy level gap [8,9,10,11]. We emphasize that if level-crossing does occur, Allahverdyan and Nieuwenhuizen show that the quasistatic protocol may not be the optimal one. A quasistatic timescale for the adiabatic theorem can still be defined in this case [12,13].
For a concrete example we turn to the paradigmatic case of ideal gas in a piston. For simplicity, we consider spinless particles in one dimension and furthermore replace the square-well confining potential with an harmonic well [14]. A change in piston size corresponds to changing the frequency of the harmonic potential. We are therefore dealing with an ensemble of time-dependent harmonic oscillators.
The harmonic oscillator has an adiabatic conserved quantity, (where is the oscillator’s Hamiltonian) [15]. This means that in the “quasistatic limit” of a slow change in frequency , this quantity will be conserved. A quasistatic change from and energy to will therefore lead to a final energy of . Since there is no heat exchange with any environment, it is only possible to interpret this energy change as work. This is the baseline quasistatic work that a faster change needs to be compared against.
Treating faster, finite-time, frequency change protocol requires more mathematical tools. We can begin by considering the system initially at zero temperature. Then, the energy for any later time will be given by [16]
where is a parameter introduced by Husimi [17] and is related to a quasistatic protocol: it is unity for a quasistatic change and increases the faster the change in frequency is [18]. This makes the effects of non-adiabacity readily apparent but we would like to deal with the more general initial thermal Gibbs state.
To properly consider an initial thermal state, we turn to the concept of a dynamical Lie algebra [19]. A dynamical Lie algebra is a Lie algebra generated by the Hamiltonian of the system. The idea is to look for a Lie algebra with elements so that any operator within the algebra will remain within the algebra under the dynamics generated by commutation with the Hamiltonian, . This is most easily assured by taking as all the operators within the Hamiltonian and then adding elements by commutation with the Hamiltonian until no new operators are generated. For the harmonic oscillator the Hamiltonian can be considered to be comprised of two time-independent operators with time-dependant parameters, , with and . The minimal completion of this algebra is then ; it can be verified that forms a closed S(1,1) Lie algebra under commutation. Alternative dynamical Lie algebras can be constructed by linear superpositions of these three operators. Using the creation and annihilation operators one such algebra is .
One advantage of using a dynamical Lie algebra is that it allows one to easily write down a state whose form is conserved by the dynamics. Consider the state
Although this operator does not lie within the dynamical Lie algebra, its form is conserved in the dynamics. This can be verified by expanding the exponentials and examining the commutations order by order [14]. Note that the thermal Gibbs state is obtained for ; this corresponds to a state with no coherences and no position-momentum correlations.
Another advantage of the dynamical Lie algebra is that it allows one to easily identify dynamical invariants of the motion. “Dynamical invariants” are quantities that remain constant, but are explicit functions of time-dependent parameters and of (implicitly time-dependent) expectation values; for the harmonic oscillator, the first such invariant was noted by Lewis [20]. Korsch and Koshual used dynamical algebras to derive the dynamical invariants which lie within the algebra [21,22] (i.e., invariants which are linear in the expectation values of the algebra’s operators), and Sarris and Proto demonstrated that for our state (Equation 2) it is possible to generalize further and derive dynamical invariants that are outside the algebra [23], consisting of higher powers of the the algebra’s expectation values (they actually consider maximum entropy states, , but a product form and exponential sum are interchangeable (see [24], corollary to theorem 2)). One such invariant in our case was found to be [25]
The normalization of the state (Equation 2) requires , so that , and the maximum occurs only in the thermal state ().
We now have the tools to return to analyzing the time-dependent harmonic oscillator under a finite change of frequency. We assume an initial thermal state so that and the state is diagonal in the energy eigenbasis. A quasistatic change from to will maintain the diagonal form, leading to another thermal state with and some energy , set by the constant . Now consider what would have happened if we would have changed the field quickly. In general we would not expect the final state to be thermal, so that and the invariance of (Equation 3) now implies a higher energy. Reaching a final thermal state may be possible, but would require a specially-chosen protocol and even then will only lead to the same final energy, not a lower one. We conclude that for any initial thermal state a non-quasistatic protocol will generally lead to higher energies (than the quasistatic baseline), . As noted above, appending a thermalization stage will convert this extra energy into excess heat.
We have demonstrated that driving the system at a finite rate will require excess energy to make the same change. But has it generated more entropy and increased the system’s temperature? To answer this we must first consider what entropy and temperature mean in the quantum domain. The entropy of quantum states is usually considered to be the von Neumann entropy, . This quantity can be shown to be invariant to unitary transformation (e.g., [26], Section 2.3), and in particular to the Hamiltonian dynamics at hand. For our system, the von Neumann entropy can be shown to depend only on the dynamical invariant [25]. This entropy does not increase during the creation of the “internal friction”—in this respect it appears that there is no friction!
The paradox can be resolved by realizing that the von Neumann entropy is an idealized entropy, representing the information missing after all possible measurements have been made. This is not a measure that is necessarily relevant. Since we are interested in the dissipation and dynamics of energy it makes sense to consider an entropy that is related to energy. And indeed, if we look at the Shannon energy entropy, (where is the probability of finding the system in the energy state), we find that a non-quasistatic change always increases it. The two entropies are equal only when the state is diagonal in the energy eigenbasis, i.e., when and the state is thermal. A finite rate of frequency change will generally lead to the development of coherences () and therefore to the deviation from the diagonal form in the energy eigenbase. Since the von Neumann entropy is always smaller than any other Shannon entropy [27,28], the Shannon energy entropy will be higher in these cases—internal friction indeed generates entropy.
What about increasing the system’s temperature? Note that when , β no longer serve as the (inverse) temperature. To understand what the temperature is, we have to go back to its thermodynamic definition as the ratio between energy and entropy change. The Shannon energy entropy of our system is the same as that of a thermal oscillator with the same energy [14],
This is a concave monotonically increasing function of energy. Since non-quasistatic dynamics leads to higher energies at the same frequencies, such dynamics will result in lower slopes. The inverse-slope will therefore be higher, and the inverse-slope is the temperature (see Figure 1). We arrive at higher temperatures under non-quasistatic dynamics.
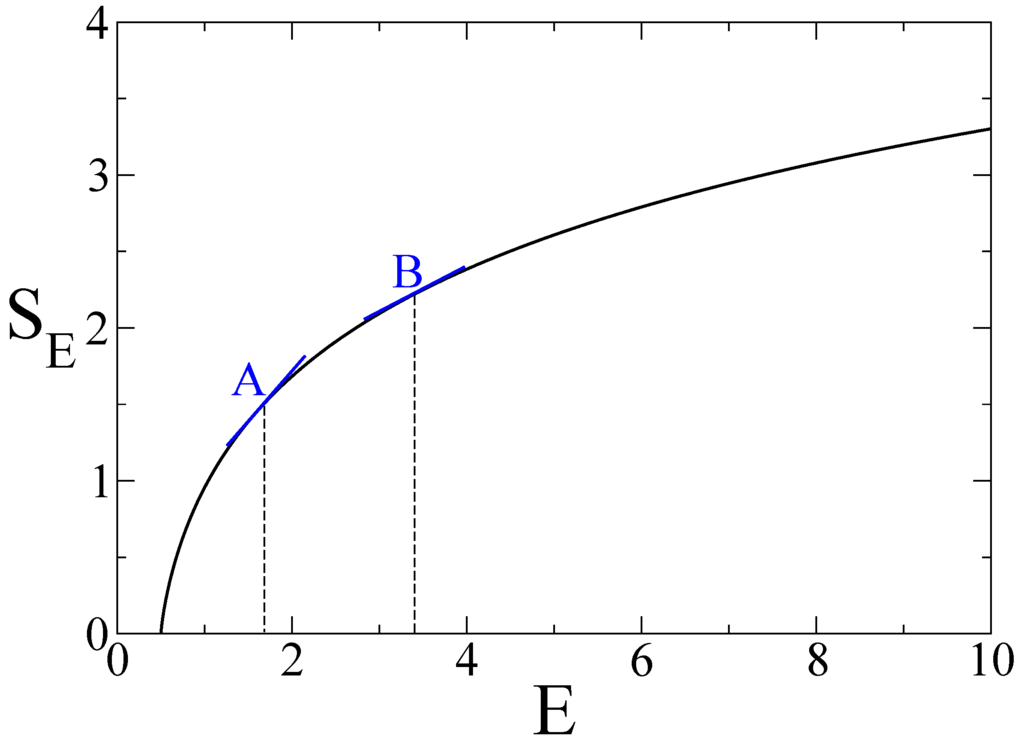
Figure 1.
The Shannon energy entropy for a fixed frequency , as a function of the energy E in units of . In a quasistatic process from some initial thermal state we will reach some final energy and therefore entropy at the final frequency, represented by point A. A faster process reaching the same final frequency will generally result in higher energy, represented by point B. The slope at point B is lower than in point A, and therefore the inverse slope will be higher. Using the thermodynamic identification , this figure shows that non-quasistatic dynamics will yield higher temperatures.
We received all the hallmarks of friction—excess work needed to enact the same change, entropy production, and temperature increase. The latter two, however, are only true from the appropriate (quantum) perspective. We note that these effects are purely due to the fact that the system could not adiabatically follow the change in frequency, which is in turn due to the fact that the system’s Hamiltonian does not commute at different times
which is a purely quantum feature. Quantum internal friction, therefore, stems from the non-Abelian nature of quantum algebra.
In our treatment we separated out the thermalization phase from the driving phase. In realistic cases, however, driven systems will be at least weakly coupled to thermal environments. The two processes will occur simultaneously, implying that any external driving will be converted through dissipation to some quantum friction (although this effect may be negligible).
Furthermore, residual interactions with the environment can also lead to dephasing noise. This will also be the effect of imperfect control over the external field. Since pure dephasing is identical to a weak measurement of the momentary energy, one would expect it to draw the state towards the momentary energy eigenbasis, thereby approximating the quasistatic process and thus acting as a “quantum lubricant” that reduces friction. This indeed happens in some cases [29]. However, in at least some cases pure dephasing of this sort can decrease efficiency [30]. The effect of dephasing noise in general is still not sufficiently understood, but it does not appear to eliminate quantum internal friction entirely even when it does function as a lubricant.
It should be noted that, formally, there are frequency-change protocols that avoid generating friction (in these solutions at some finite time ). Using such protocols, it is seemingly possible to drive the system at a finite rate and still avoid friction. However, although it appears that such processes can occur in arbitrarily short time [30,31,32], that requires an arbitrarily large available energy. This can be understood in light of the energy-time uncertainty relation: an infinitely fast process would require an infinite variance in energy. An instantaneous frictionless solution is therefore not viable and any finite-period solution will result in dissipative losses to the environment on its points where . In at least some cases, frictionless solutions also seem unstable under dephasing noise [30]. In the realistic case of weak coupling, then, some frictional loss is unavoidable (although it may be negligible in practice).
Our results are not limited to the harmonic oscillator - separate analysis reveals that it is valid for spin systems [30,33], and holds under continuous coupling to the bath for a three-level system [34]. Since the underlying features that give rise to the phenomena are the non-commutative nature of the Hamiltonian at different times and the irreversible nature of thermalization, there is good reason to believe that this kind of quantum friction would be endemic in all realistic systems.
A constraint on the universal applicability of our results is the assumption of a thermal environment. We have so far treated the thermalization and dephasing processes only roughly, so will now amend this lacuna by devoting the next section to examining more carefully how dissipation to the environment occurs.
2. Dissipation to the Environment
The description of interactions with the environment has been left intentionally vague in the above section, but since external friction involves dissipation into the environment we need to consider their interaction in some detail. One approach to think of the interaction of an (open) system with the environment is to formally consider both the system and the environment as a single closed “extended” quantum system, and then develop the dynamics of only the part involving the degrees of freedom of the open system, where signifies tracing over the environment’s degrees of freedom, and and are the extended and open system’s density operators (i.e., states), respectively.
Consider some extended system, with an Hamiltonian in the Hilbert space . The evolution of this system is given, with no approximation, by the Liouville-von Neumann equation
where the Liouville operator operates on the state to produce its dynamics.
Since we are interested only in the degrees of freedom of the open system, we can attempt to define a projection operator that projects any operator from the extended system’s Hilbert space to the “relevant” subspace of interest, namely the open system’s subspace . Since operates on the extended Hilbert space , however, it is formally necessary to consider the operator as projecting from and to the extended Hilbert space. It is typically taken as where is a time-independent thermal state of the environment.
Following Zwanzig [35], we now further define a complementary projection into the “irrelevant” part. By simply writing the Liouville-von Neumann equation in these terms, it is possible to formally solve it to obtain
with the memory kernel . This equation is known as the Nakajima-Zwanzig (NZ) equation [26]. Limiting the initial conditions to ones that are not altered by the projection, , removes the first term, leaving us with an exact closed equation for the dynamics of the relevant part. For the typical projector operator given above, this condition is fulfilled if the initial state is already separable . Formally, it is possible to present the NZ equation in time-convolutionless form,
where is a complicated operator that is local in time (for details and a more rigorous derivation of the NZ equation, see [26]; for an alternative derivation, see [36]).
Solving the dynamics of the relevant part therefore involves a memory kernel or local operator which is very complex and hard to apply. However, the local operator can become much simpler under reasonable physical assumptions. It is common to consider an environment that acts as a heat bath, dissipating the energy the system gives to it on time scales that are much faster than the system’s time scales . We therefore have a separation of time scales, where . Over time scales above , we would then expect the environment to “forget” its past interactions with the system, leading to a loss of the memory in the NZ equation for “coarse grained” evolution (averaging over times below the graining). The resulting local-time propagator is now a constant . It still generally depends on the initial state of the overall system, but if we assume that a single operator exists for a group of initial conditions (such as separable initial states), we can eliminate this dependence and obtain a Markovian dynamics
Since the propagator is independent of time and initial state, we can formally solve the dynamics and present the time evolution propagator as a dynamical semigroup, . Lindblad determined the most general structure of a “completely positive” quantum dynamical semigroup as [37]
where are the “generators” of the evolution, and we have dropped the subscript . “Complete positivity” here is intended to capture the fact that the evolution must be compatible with a greater unitary dynamics, and specifically conforms to maintaining the free evolution of a dummy system () that does not interact with the open system [37,38]. Amongst other properties, a completely positive map maintains the positivity of the density. Equation 10 defines the acclaimed Lindblad form, which appears to be applicable under reasonable physical assumptions yet provides a very concrete and (as we will see below) useful form.
Some cautionary words are in order. First, the Markovian approximation depended on a coarse-graining of the evolution in time, which makes it inapplicable to short time scales, where there is generally “slippage”. This was demonstrated by Gnutzmann and Haake [39]. Define the difference between the constant (Markovian) and local-in-time convolutionless propagator . We can now write the evolution equation as
Separating out the time-independent evolution, , one can formally solve the evolution of the effective density
where denotes the time ordered integral. The the last approximation is valid since the integrand approaches zero for times longer than the bath relaxation time . Equation 12 indicates that the evolution at long times is Markovian (), but if this long-time approximation is applied to the initial-time it yields a wrong “initial state” . Specifically, this effective density may be non-positive at short times. The requirements of complete positivity are therefore excessive, as they guarantee positivity even for arbitrarily short times. Real Markovian dynamics that develop at long times need not be completely positive (see [39] for a more thorough discussion).
Similarly, an upper bound on the appropriate time scale is set by quantum recurrence. Further caution is urged by Pechukas [38] (but see also [40]), who demonstrates that beyond the weak coupling limit complete positivity is not guaranteed, and that even within this limit it requires a separable initial state.
Despite these misgivings, it should be emphasized that completely positive master equations have been derived from microscopic models ([41,42,43,44] and more), under suitable assumptions. Equations of Lindblad form can be relevant and correct approximations and are often successfully applied to model thermalization and other processes. Indeed, sometimes several Lindblad forms are applicable for different conditions or from different perspectives.
In conclusion, the theory of quantum open systems allows us to explicitly see that the irreversibility induced by the environment is due to the fast time scale separation between the bath and open system, allowing the environment to quickly spread the effects of the interaction with the system over many degrees of freedom [45]. This creates irreversible dynamics at not-too-long times, which (under suitable assumptions) will be of the Markovian kind. In other words, energy dissipation can be identified with situations where the environment acts as an energy sink, for particular modes of energy, within the relevant time-scales.
For driven systems, the combination of energy excitation by the driving and their irreversible dissipation by the large environment creates friction.
3. Brownian Motion
Brownian motion includes the dumping of momentum, or velocity, dissipating the kinetic energy into the medium. But why does the dissipative environment lower the velocity, of all things? Consider a classical particle moving against some uniform background environment. Assuming that the environment around it is in thermal equilibrium we could imagine it getting hit by elastic collisions, so the dynamics would be a combination of a free evolution and elastic collisions. In the laboratory frame the momentum distribution of the environment is assumed to be isotropic, so that . A particle moving at velocity , however, will see an asymmetrical distribution in its co-moving frame, [46] (with obvious notation). Since the environment is thermal it will have higher densities at higher momenta and this asymmetry will translate into the damping of momentum. The existence of friction can therefore be attributed to symmetry breaking: a contrast between the isotropy of the interactions at the laboratory frame and the symmetry-breaking direction of the particle’s velocity. More abstractly, the environment acts to restore the symmetry of zero momentum, but is dissipative (irreversible) in the large-system approximation, wherein it retains its isotropy (an approximation that is broken by the quantum recurrence time).
Note that we would also expect thermal stochastic fluctuations which will lead to diffusion in momentum. Overall, for movement in a homogenous background one can expect a Fokker-Plank equation, with a friction (momentum damping) term and a (momentum) diffusion term [47].
This is a classical mechanism description of friction, and so we will not expand on it in this paper. However, it is worth bringing up that to the extent that complete positivity is assumed it has no quantum analog. Quantum mechanics requires interactions with the environment to include interactions with location as well as momentum, and connects them to diffusion in position as well as in momentum. We will devote the rest of this section to explaining why and when this is valid.
To expand on this idea, let us consider quantum Brownian motion specifically. In a seminal paper, Caldeira and Leggett considered a particle interacting with the environment solely through a pair-wise spatial interaction, (where the summation is over the environment’s particles, and x is the particle’s position). Under suitable assumptions (such as a large environment), they find in the semiclassical region a Fokker-Plank like equation [48]
However, this dynamics is not of Lindblad form [26], and is therefore not completely positive. Equation 13 can be “extended” to conform to Lindblad’s form by the addition of a spatial diffusion term, , which will complete the form if [26,49]. This reveals a quantum effect—friction, momentum diffusion and spatial diffusion are all connected, there cannot be one without the other. However, as an abstract requirement, its origin remains obscure.
The result can be understood in light of the so-called “unraveling” of the master equation. The Lindblad form (Equation 10) is mathematically equivalent to taking a stochastically-determined series of measurements on a pure state (defining a “quantum trajectory”), and then combining different trajectories statistically to recover the ensemble picture [26]. These measurements are precisely the Lindblad generators. The “extension” of the Fokker-Plank like equation is equivalent to working with a generator that is a linear superposition of position and momentum [26]. Working from a linear combination , Gao likewise obtains a Lindblad form solution [50]. Similarly, Vacchini provided an alternative microscopic derivation that preserves the Lindblad form and results in the generators (with and a thermal wavelength).
From this perspective, it seems necessary for the environment to measure, and hence interact with, both the momentum and the position of the particle. This approach was taken by Barnett and Cresser, who developed the Lindblad master equation associated with simulatenous measurement of both these observables [49]. Note that they maintain the classical assumption of elastic, momentum-exchange collisions. In the continuous measurement limit, they obtain a master equation of the Lindblad form. In a beautiful paper [51], Barnett et al. posit that measurement is therefore the underlying mechanism behind the phenomena of quantum friction—the open system is measured by the environment, which induces both friction and the two types of diffusion.
Such a conclusion is not tenable. The reason that friction is not related to measurement is simply that not all conditions giving rise to friction correspond to such a measurement by the environment. It is possible that a Markovian but not completely positive master equation can be derived for the behavior of the subsystem. As explained in Section 2 this will lead to seemingly-unphysical results at short times and indeed the Caldeira-Leggett equation can result in negative probabilities for short times [51,52,53]. But such short times should not be considered seriously, as they lie below the coarse-graining. The conclusion that friction and the two diffusions are connected therefore needs to be taken with a grain of salt—it is valid only when complete positivity is a good approximation, which need not generally be the case. The firm affirmation of their connection stated in the literature is not justified.
It is important to note the significance of this. Requiring completely positive (sub)dynamics led us to the conclusion that “in quantum theory we cannot have separate friction and diffusion terms” (Vacchini, [54]). Completely positive subdynamics is equivalent to measuring the system [55,56]. If Barnett et al. are wrong, this means that it is impossible to consider the open system as a separate system that is being continuously (and weakly) measured by the environment. Instead, quantum mechanics requires a more holistic treatment in which the dynamics of the observables in the open system subspace can be followed (a “subdynamics” exists), but the system can not be truly considered independently of the extended system. To paraphrase Vacchini, “in quantum theory we cannot have separate system and environment”.
4. Quantum Fluctuations
One of the features that set quantum mechanics apart from classical mechanics are the ever-present quantum fluctuations, in addition to and beyond any thermal fluctuations. One way to see this is from the perspective of a Feynman–Vernon path integral [57,58]. In this formalism a quantum particle is considered to take all paths between initial and final points, and the probability amplitudes are summed up with the weight , where S is the path’s action. The dominant contribution to this sum is from the classical action, , which is the minimum action. But there are sizeable contributions from all paths whose action is within ħ of the minimum, so that one is likely to observe results in this range. This results in quantum fluctuations whose scale is determined by ħ. Fluctuations are related to dissipation through the fluctuation dissipation theorem (most notably, [47]), so that quantum fluctuations would lead to quantum dissipation—quantum friction.
Quantum fluctuations are usually drowned by thermal fluctuations, but can still lead to measurable effects. Perhaps the most famous is the Casimir effect, i.e., an attraction between two conducting plates, that can be attributed to the influence of the plates on the fluctuations of the electromagnetic field between and around them [58]. If the plates are allowed to move, the zero-point fluctuations will also create a “dynamical Casimir effect” of a dissipative force [59,60,61,62]. The dissipative force can be obtained by a consideration of the vacuum modes [63], but up to a numerical factor the result can be obtained by a dimensional analysis. For a large and smooth enough body, we would expect the force to be proportional to the area of the body’s surface, A [64]. As noted before, the fluctuations (and therefore the dissipative force) should also be proportional to ħ. The dissipative force is also related to electromagnetic effects and therefore to the speed of light c, and to some derivative of the spatial location . Balancing the dimensions of the dissipation force leads to only one possible scaling [65],
What is the origin of this friction? In light of the above section, it can be appreciated that the situation is very much like Brownian motion, with the plate flowing through the viscous quantum vacuum foam [58,66,67]. The reason that the other plate is needed is to set a reference point, a “stationary” laboratory frame. Physically, the plate is affected by the image pictures induced on the other plates, that (because of causality) do not react instantaneously to the plate’s change of position and therefore act to slow it down [68]. Alternatively, one can see the entire system as a closed cavity that is driven externally, in which case one would expect to see internal friction for high rates of change. And indeed, the dynamical Casimir effect only occurs for high (relativistic) changes [69]. On this view, the internal friction is then dissipated by the luminosity and detection of the photons emerging from the cavity.
Another quantum aspect of this friction force is its relation to the non-commutativeness of the position and the momentum. Barton [64] considers very large uncertainties, of the order where T is a typical measurement time. He obtains that for a large body of linear dimension a, the regime is inconsistent. The Heisenberg uncertainty relations make it impossible to measure deviations in position or momentum in this limit. Only large bodies, whose size is too large for light to travel their length during the measurement, would suffer from the above dissipative force. Causality therefore indicates the source of the force as residing in the time-lapse between the object’s movement and the change of the electric field. This delay-based friction mechanism is purely classical, but its presence is required by the quantum uncertainty relations if the environment is to measure the system.
5. Discussion
We have discussed three examples of quantum friction. In the harmonic oscillator, we showed explicitly that driving the system created internal friction that was distinctly quantum in origin. The internal heating can be dissipated through an interaction with an environment, so that realistic systems, which are not ideally isolated, should suffer additional quantum friction when driven. The dissipative effect can be attributed to the dispersion of the interaction across many degrees of freedom, that creates effective irreversibility by separation of time scales; it should not be confused with the irreversibility of completely positive maps, that is related to quantum measurements. Quantum friction needs to be understood as a combination of both the excitations induced by external driving and the more general irreversible dynamics. Although we treated only the case of an harmonic oscillator this treatment can be generalized and has been applied to other systems.
We also considered systems that are already driven, assuming some velocity in the Brownian motion and dynamic Casimir effect. Brownian motion demonstrated that the cause of the dissipation of momentum was the symmetries of interactions with the environment, combined with the asymmetry of the system’s velocity. These are largely classical effects, although the underlying mechanics (and therefore some of the details) are quantum. The dynamic Casimir effect also demonstrated that quantum fluctuations can act as a dissipative environment, and that external driving can lead to internal friction in a cavity too.
We conclude that quantum effects can, and generically do, create friction in two ways. They can set up quantum environments that create a dissipative external friction like the fluctuations underlying the dynamic Casimir effect; and they create excitations that are then dissipated by such means, as in the case of the driven harmonic oscillator. Both these effects are generally omnipresent.
Quantum friction may be ubiquitous, but when is it non-negligible? Quantum fluctuations are relevant when the action is of the order of Planck’s constant. These will constitute external dissipation when there is an asymmetry such as a velocity in a particular direction, with the scale of the dissipative force depending on the precise dimensionality and scales of the problem (as in the Brownian motion example). The relevance of this external friction is therefore dependant on the precision of the measurement compared to the scale of this force.
Internal friction will develop when the field is changed rapidly, and therefore depends on the dimensionless factor (where is now some generic external field with units of rate). Since the direction of change need not matter, friction needs to be a second order phenomena in this parameter. The change in energy would as an upper estimate be proportional to some fraction of the initial energy, but also to the time . The time of the process, in turn, must be smaller than the inverse of the energy to maintain the quasistatic limit, setting the time scale to give . We should not expect to see relevant internal friction phenomena if our energy resolution is below this limit, but may encounter friction below it.
We note that the connection found in the literature between diffusion and friction for Brownian motion cannot be maintained beyond the conditions of complete positivity, indicating that quantum treatment requires a holistic approach.
Acknowledgments
I thank Ronnie Kosloff for discussions and advice. This work was supported by the Israel Science Foundation. The Fritz Haber Centre is supported by the Minerva Gesellschaft für die Forschung GmbH, München, Germany.
References
- Ahn, K.; Mohanty, P. Quantum friction of micromechanical resonators at low temperatures. Phys. Rev. Lett. 2003, 90, 85504. [Google Scholar] [CrossRef] [PubMed]
- Calogeracos, A.; Volovik, G. Rotational quantum friction in superfluids: Radiation from object rotating in superfluid vacuum. JETP Lett. 1999, 69, 281–287. [Google Scholar] [CrossRef]
- Bojowald, M.; Maartens, R.; Singh, P. Loop quantum gravity and the cyclic universe. Phys. Rev. D 2004, 70, 83517. [Google Scholar] [CrossRef]
- Allahverdyan, A.; Nieuwenhuizen, T. Adiabatic processes need not correspond to optimal work. Phys. E 2005, 29, 74–81. [Google Scholar] [CrossRef]
- Allahverdyan, A.; Nieuwenhuizen, T. Minimal work principle: Proof and counterexamples. Phys. Rev. E 2005, 71, 46107. [Google Scholar] [CrossRef] [PubMed]
- Longuet-Higgins, H. The intersection of potential energy surfaces in polyatomic molecules. Proc. Roy. Soc. London Ser. A 1975, 344, 147–156. [Google Scholar] [CrossRef]
- Mead, C. Thenoncrossingrule for electronic potential energy surfaces: The role of time-reversal invariance. J. Chem. Phys. 1979, 70, 2276. [Google Scholar] [CrossRef]
- Hwang, J.; Pechukas, P. The adiabatic theorem in the complex plane and the semiclassical calculation of nonadiabatic transition amplitudes. J. Chem. Phys. 1977, 67, 4640. [Google Scholar] [CrossRef]
- Demkov, Y.; Ostrovskii, V.; Solov’ev, E. Two-state approximation in the adiabatic and sudden-perturbation limits. Phys. Rev. A 1978, 18, 2089–2096. [Google Scholar] [CrossRef]
- Wilkinson, M.; Morgan, M. Nonadiabatic transitions in multilevel systems. Phys. Rev. A 2000, 61, 62104. [Google Scholar] [CrossRef]
- Sarandy, M.; Wu, L.; Lidar, D. Consistency of the adiabatic theorem. Quantum Inf. Proc. 2004, 3, 331–349. [Google Scholar] [CrossRef]
- Avron, J.; Elgart, A. Adiabatic theorem without a gap condition. Commun. math. phys. 1999, 203, 445–463. [Google Scholar] [CrossRef]
- Avron, J.; Elgart, A. Adiabatic theorem without a gap condition: Two-level system coupled to quantized radiation field. Phys. Rev. A 1998, 58, 4300–4306. [Google Scholar] [CrossRef]
- Rezek, Y.; Kosloff, R. Irreversible performance of a quantum harmonic heat engine. New J. Phys. 2006, 8, 83. [Google Scholar] [CrossRef]
- Kulsrud, R. Adiabatic invariant of the harmonic oscillator. Phys. Rev. 1957, 106, 205–207. [Google Scholar] [CrossRef]
- Galve, F.; Lutz, E. Nonequilibrium thermodynamic analysis of squeezing. Phys. Rev. A 2009, 79, 55804. [Google Scholar] [CrossRef]
- Husimi, K. Miscellanea in elementary quantum mechanics II. Prog. Theor. Phys. 1953, 9, 381–402. [Google Scholar] [CrossRef]
- Deffner, S.; Lutz, E. Nonequilibrium work distribution of a quantum harmonic oscillator. Phys. Rev. E 2008, 77, 21128. [Google Scholar] [CrossRef] [PubMed]
- Alhassid, Y.; Levine, R. Connection between the maximal entropy and the scattering theoretic analyses of collision processes. Phys. Rev. A 1978, 18, 89–116. [Google Scholar] [CrossRef]
- Lewis, H., Jr. Class of exact invariants for classical and quantum time-dependent harmonic oscillators. J. Math. Phys. 1968, 9, 1976. [Google Scholar] [CrossRef]
- Korsch, H. Dynamical invariants and time-dependent harmonic systems. Phys. Lett. A 1979, 74, 294–296. [Google Scholar] [CrossRef]
- Kaushal, R.; Korsch, H. Dynamical Noether invariants for time-dependent nonlinear systems. J. Math. Phys. 1981, 22, 1904. [Google Scholar] [CrossRef]
- Sarris, C.; Proto, A. Time-dependent invariants of motion for complete sets of non-commuting observables. Phys. A 2005, 348, 97–109. [Google Scholar] [CrossRef]
- Wei, J.; Norman, E. On global representations of the solutions of linear differential equations as a product of exponentials. Proc. Amer. Math. Soc. 1964, 15, 327–334. [Google Scholar] [CrossRef]
- Peter, S.; Heinz, H.; Yair, R. Maximum work in minimum time from a conservative quantum system. Phys. Chem. Chem. Phys. 2009, 11, 1027–1032. [Google Scholar]
- Breuer, H.; Petruccione, F. The theory of open quantum systems; Oxford University Press inc.: New York, NY, USA, 2002. [Google Scholar]
- Hughston, L.; Jozsa, R.; Wootters, W. A complete classification of quantum ensembles having a given density matrix. Phys. Lett. A 1993, 183, 14–18. [Google Scholar] [CrossRef]
- Wehrl, A. General properties of entropy. Rev. Mod. Phys. 1978, 50, 221–260. [Google Scholar] [CrossRef]
- Feldmann, T.; Kosloff, R. Quantum lubrication: Suppression of friction in a first-principles four-stroke heat engine. Phys. Rev. E 2006, 73, 25107. [Google Scholar] [CrossRef] [PubMed]
- Feldmann, T.; Kosloff, R. Minimal temperature of quantum refrigerators. Europhys. Lett. 2010, 89, 20004. [Google Scholar] [CrossRef]
- Muga, J.; Chen, X.; Ruschhaupt, A.; Guéry-Odelin, D. Frictionless dynamics of Bose–Einstein condensates under fast trap variations. J. Phys. B - At. Mol. Opt. Phys. 2009, 42, 241001. [Google Scholar] [CrossRef]
- Chen, X.; Ruschhaupt, A.; Schmidt, S.; del Campo, A.; Guery-Odelin, D.; Muga, J.G. Fast optimal frictionless atom cooling in harmonic traps: Shortcut to adiabaticity. Phys. Rev. Lett. 2010, 104. [Google Scholar] [CrossRef] [PubMed]
- Kosloff, R.; Feldmann, T. Discrete four-stroke quantum heat engine exploring the origin of friction. Phys. Revi. E 2002, 65, 55102. [Google Scholar] [CrossRef] [PubMed]
- Geva, E.; Kosloff, R. Three-level quantum amplifier as a heat engine: A study in finite-time thermodynamics. Phys. Rev. E 1994, 49, 3903–3918. [Google Scholar] [CrossRef]
- Zwanzig, R. Ensemble method in the theory of irreversibility. J. Chem. Phys. 1960, 33, 1338. [Google Scholar] [CrossRef]
- Chruscinski, D.; Kossakowski, A. Non-Markovian quantum dynamics: local versus non-local. arXiv . 2009, 0912.1259. [Google Scholar]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119–130. [Google Scholar] [CrossRef]
- Pechukas, P. Reduced dynamics need not be completely positive. Phys. Rev. Lett. 1994, 73, 1060–1062. [Google Scholar] [CrossRef] [PubMed]
- Gnutzmann, S.; Haake, F. Positivity violation and initial slips in open systems. Z. Phys. B Cond. Matt. 1996, 101, 263–273. [Google Scholar] [CrossRef]
- Alicki, R. Comment on reduced dynamics need not be completely positive. Phys. Rev. Lett. 1995, 75, 3020–3020. [Google Scholar] [CrossRef] [PubMed]
- Schaller, G.; Brandes, T. Preservation of positivity by dynamical coarse graining. Phys. Rev. A 2008, 78, 22106. [Google Scholar] [CrossRef]
- Fleming, C.; Cummings, N.; Anastopoulos, C.; Hu, B. The rotating-wave approximation: consistency and applicability from an open quantum system analysis. arXiv . 2010, 1003.1749. [Google Scholar] [CrossRef]
- Smirne, A.; Vacchini, B. Quantum master equation for collisional dynamics of massive particles with internal degrees of freedom. arXiv . 2010, 1003.0998. [Google Scholar] [CrossRef]
- Dominguez-Clarimon, A. A particle across a medium: How decoherence relates to the index of refraction. Ann. Phys. 2007, 322, 2085–2103. [Google Scholar] [CrossRef]
- Lindblad, G. Brownian motion of quantum harmonic oscillators: Existence of a subdynamics. J. Math. Phys. 1998, 39, 2763. [Google Scholar] [CrossRef]
- Diosi, L. Quantum master equation of a particle in a gas environment. Europhys. Lett. 1995, 30, 63–68. [Google Scholar] [CrossRef]
- Kubo, R. The fluctuation-dissipation theorem. Rep. Progr. Phys. 1966, 29, 255–284. [Google Scholar] [CrossRef]
- Caldeira, A.O.; Leggett, A.J. Path integral approach to quantum brownian motion. Phys. A 1983, 121, 587–616. [Google Scholar] [CrossRef]
- Barnett, S.; Cresser, J. Quantum theory of friction. Phys. Rev. A 2005, 72, 22107. [Google Scholar] [CrossRef]
- Gao, S. Dissipative quantum dynamics with a Lindblad functional. Phys. Rev. Lett. 1997, 79, 3101–3104. [Google Scholar] [CrossRef]
- Barnett, S.; Jeffers, J.; Cresser, J. From measurements to quantum friction. J. Phys. Cond. Matt. 2006, 18, S401–S410. [Google Scholar] [CrossRef] [PubMed]
- Talkner, P. Gauss Markov process of a quantum oscillator. Z. Phys. B Cond. Matt. 1981, 41, 365–374. [Google Scholar] [CrossRef]
- Tameshtit, A.; Sipe, J. Positive quantum brownian evolution. Phys. Rev. Lett. 1996, 77, 2600–2603. [Google Scholar] [CrossRef] [PubMed]
- Vacchini, B. Completely positive quantum dissipation. Phys. Rev. Lett. 2000, 84, 1374–1377. [Google Scholar] [CrossRef] [PubMed]
- Kraus, K. States, Effects and Operations: Fundamental Notions of Quantum Theory; Springer-Verlag: Berlin, Germany, 1983. [Google Scholar]
- Kraus, K. General state changes in quantum theory. Ann. Phys. 1971, 64, 311–335. [Google Scholar] [CrossRef]
- Feynman, R.; Hibbs, A. Quantum Mechanics and Path Integrals; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Kardar, M.; Golestanian, R. The friction of vacuum, and other fluctuation-induced forces. Rev. Mod. Phys. 1999, 71, 1233–1245. [Google Scholar] [CrossRef]
- Jaekel, M.; Reynaud, S. Motional Casimir force. J. Phys. I. (France) 1992, 2, 149. [Google Scholar] [CrossRef]
- Barton, G.; Eberlein, C. On quantum radiation from a moving body with finite refractive index. Ann. Phys. 1993, 227, 222–274. [Google Scholar] [CrossRef]
- Machado, L.; Maia Neto, P. Inertial forces in the Casimir effect with two moving plates. Phys. Rev. D 2002, 65, 125005. [Google Scholar] [CrossRef]
- Dodonov, V.; Dodonov, A. Quantum harmonic oscillator and nonstationary Casimir effect. J. Russ. Laser Res. 2005, 26, 445–483. [Google Scholar] [CrossRef]
- Dodonov, V.; Klimov, A.; Man’ko, V. Nonstationary Casimir effect and oscillator energy level shift. Phy. Lett. A 1989, 142, 511–513. [Google Scholar] [CrossRef]
- Barton, G. On the fluctuations of the Casimir forces. II. The stress-correlation function. J. Phys. A: Math. Gen. 1991, 24, 5533–5551. [Google Scholar] [CrossRef]
- Maia Neto, P.; Reynaud, S. Dissipative force on a sphere moving in vacuum. Phys. Rev. A 1993, 47, 1639–1646. [Google Scholar] [CrossRef] [PubMed]
- Pendry, J. Shearing the vacuum-quantum friction. J. Phys. Cond. Matt. 1997, 9, 10301–10320. [Google Scholar] [CrossRef]
- Davies, P. Quantum vacuum friction. J. Opt. B Quantum Semicl. Opt. 2005, 7, S40–S46. [Google Scholar] [CrossRef]
- Pendry, J. Quantum friction–fact or fiction? New J. Phys. 2010, 12, 033028. [Google Scholar] [CrossRef]
- Dodonov, V. Current status of the Dynamical Casimir Effect. arXiv . 2010, 1004.3301. [Google Scholar] [CrossRef]
© 2010 by the author; licensee MDPI, Basel, Switzerland. This article is an Open Access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).