1. Introduction
The American anthropologist Marvin Harris viewed social life as a response to the practical problems of human existence [
1]. He proposed that habits, traditions and taboos are means of survival for a society [
2,
3]. This materialistic tenet sees external factors, including environmental, technological and economic aspects, as primary in causing culture when that is defined exclusively as overt, observable behavior. This was a challenge to ‘idealism’ which privileged inner factors such as psychological phenomena in generating any culture that includes also covert mental processes and immaterial symbolic terms [
4]. The materialist rationalization of collective human behavior was deemed at the time of its proposal to be a bold hypothesis [
5], but today it is seen as merely obvious that human subsistence depends on group activities to acquire and distribute numerous environmental assets. Moreover, the materialist claim that cultural succession reflects society’s evolution in its changing environment was initially thought to undervalue the intricacy and diversity in social behavior [
6], but today’s complex changes in lifestyles are considered merely as modern societies’ motivated responses to technological, economic and ecological transformations [
7]. The most general assertion of cultural materialism is that cultural changes couple with changes in a society’s energy consumption [
8]. The unmistakable link between the way of life and the consumption of energy is of a particular significance. This has been noticed not only by Harris, and the relationship has been quantified by others in numerous contexts [
9,
10,
11,
12,
13]. It is revealing that cultural trajectories intermingle with the conquest, consumption and collapse of resources that can be valued in terms of energy. The profound connection between a society’s energy consumption and its culture suggests that social systems, just as ecosystems [
14] and economies [
15,
16], manifest a particular universal principle—the 2
nd Law of Thermodynamics [
17,
18,
19]. The role of culture in sustaining society’s energy consumption has been recently pointed out also by Jared Diamond, when inspecting past processes [
20,
21]. Despite this accumulating understanding, it appears to us that the deep physical foundation of social systems has actually remained obscure.
The reduction of social behavior to physical determinism is aversive to many, and for good reasons. However, the theory of statistical physics for open systems, when properly formulated, provides quite the opposite portrayal, of the indeterminism in complex systems [
22]. Despite using exclusively concepts of physics, the theory gives a holistic account of inanimate and animate systems as well as of their inherently non-deterministic motions [
23,
24], and these characterize social systems as well. The theory asserts that the trajectories of evolving systems are impossible to predict in detail,
i.e., are non-deterministic, but the inexorable quest to diminish energy gradients in the least time impinges on all activities at all levels of hierarchical nature [
25,
26,
27]. Therefore societies, just as individuals, change by adopting mechanisms as well as generating new and abandoning old ones to facilitate energy consumption from their respective surroundings [
12]. Despite the trajectories of social changes being intractable [
28,
29,
30] the associated flows of energy always direct along paths of least action [
31]. Consequently social systems, just as organisms, ecosystems and economies, evolve along sigmoid time-courses that cumulate from skewed distributions and manifest as power-laws [
32,
33,
34]. Despite these universal characteristics being found also in social systems, the physical portrayal of collective human behavior may nonetheless be disturbing to some, seeming to narrow the agency of free will. This consciousness-associated attribute is often assigned exclusively to humans as if it were their finest distinctive character. However discomforting it may be, thermodynamics clarifies that our actions are ultimately limited by our means, not by our will. To be responsible is first to be realistic.
The objective of this study is to clarify a view of what societies are in the most fundamental and general sense, and why they emerge, flourish and eventually expire. The supreme natural law provides a general rationale to understand in a general way the diversity of social structures and for various cultural activities, but it does not specifically pinpoint single causes for particular habits and it does not predict particular social changes. On the contrary this study shows that the universal law itself, when formulated mathematically, can be analyzed to show why deterministic and reductionist assessments are not possible. Nonetheless, societies do not evolve at random, but tend to adopt practices and activities that are in accord with the thermodynamic principle to consume free energy in the least time. Moreover, the physical portrayal of a society helps to understand some of the most central concepts of culture, such as identity and class. All in all, this study provides with examples the physical basis for the materialistic thinking that characterizes several American anthropologists [
1,
12,
13,
35,
36,
37,
38].
Our inquiry is based on an evolutionary theory even as Harris drew from the general epistemological principles of science, but our view is unrelated to sociobiology and biological reductionism. For example, the materialist tenet does not associate fitness merely with differential proliferation, and it does not give a special role in social behavior to the propagation of genes. Instead evolution, when formulated as a physical process, describes a system at any level in the hierarchy of nature as being in motion, with whatever means it has, to diminish energy differences within it and relative to its surroundings in the least time. Undoubtedly genotypes, just as other representations of information [
39,
40], such as codes, norms and laws of a society, do associate with highly effective, orchestrated energy transduction, but here a genotype is understood as an effective mechanism among many others, but not privileged as it is in the modern evolutionary synthesis [
41,
42]. As well, the human mind, albeit recognized as highly effective in commanding behavior, is not given the pivotal position it has in cultural structuralism [
43]. In contrast, thermodynamics values everything in terms of energy just as Harris valued material relations as vital means of subsistence, but declared his distance from the determinism of dialectical materialism. For example, cultural materialism does not see social upheavals to arise from a social class structure, and it does not associate the accumulation of capital as a single source of tension. The thermodynamic account regards social reforms as natural processes that aim to diminish energy differences within the system in the least time. Importantly, this leveling off free energy does not imply destruction of the class structure, which itself is considered to be a natural consequence of the quest for the most effective dispersal of energy. According to the physical viewpoint, adopting Harris’ perspective [
8], there is nothing hypothetical or mysterious about a society and its culture. When everything is viewed as embodied in energy, everything becomes in principle observable as well, because all observations involve flows of energy. We emphasize the ‘in principle’ here. In practice is quite another thing, especially as we note that prediction of energy flow pathways is next to impossible in any natural system. The resulting understanding is neither simplistic nor static. In contrast, the formalism could potentially give an extremely detailed account of society’s constituents and processes, as well as its interactions with its surroundings. Yet the naturalistic theory offers salient insight into the complexity by way of a simple if subtle principle. The emergence, evolution and extinction of societies are natural processes, in many ways mechanistically complex and intricate, but in principal simple and austere. It is this universal principle, not particular practices that we wish to clarify here in context of social systems. To recognize that the 2
nd Law of Thermodynamics underlies the reasoning of Harris and others does not diminish the value of social studies but adds to them by deepening our understanding by using a profound principle.
2. Society as an Energy Transduction System
The 2
nd Law of Thermodynamics is conceptually a minimal but all-embracing concept. When formulated as an equation of motion it indicates that energy differences of any kind tend to diminish in least time. It is a simple matter to rank chemical constituents of a reaction mixture in energetic terms because the directions of the reactions independent of particular kinetic mechanisms reveal the energy differences among the compounds. To rank more complex entities, such as species in an ecological food web, is however—in principle—no different. As long as there is some interaction mechanism(s), direct or indirect, the energy density differences between any two entities would be apparent from the flows of energy that manifest themselves directly as economic transactions and information exchange, or indirectly as various ways of utilizing the common environment. The diverse means of internal interactions within a social system and its transactions with its surrounding environment, including other social systems, collectively subsume culture. Thus culture has the same significance for a society as behavior has for an individual. In essence culture is the society’s way of making its living [
44]. Just as an individual behaves by operating cellular, organ and motor functions to access and consume free energy, so does a society function by using its infrastructure in diverse actions to extract and distribute energy. Just as we can regard animate reflexes, instincts and conditioning as mechanisms for using the underlying biological machinery in a coordinated manner, so also can habits, practices, traditions, taboos and values be viewed as motivated social stances and responses enlisted to operate its infrastructure in an orchestrated manner. Moreover, just as behavioral changes signal changes within an individual, so cultural changes reflect changes within a society. In terms of physics, a society is an energy transduction system that houses numerous bound forms of energy. These repositories of energy couple to each other and to their surroundings by flows of energy. These characteristic interactions can be viewed as aspects of culture. However as will become evident below, the repositories of energy and the flows of energy are inseparable from each other. After all, the bound and free forms of energy convert to each other. In other words, a society’s evolution is influenced by its culture and vice versa.
Our strictly material and operational standpoint, may nonetheless strike some as deficient. For example, are not habits, traditions, taboos and values immaterial? We follow Harris in arguing that no manifestation of culture, just as no piece of information, can exist without some physical form of embodiment [
12,
40]. This assertion, though, may appear to some as insignificant. For example, are not the small energetic costs of some material manifestations of values, e.g., flags to show patriotism, sometimes inconsequential? We keep to Harris in emphasizing that this very observation targets a key idea of cultural materialism [
8,
3]. Namely, minimal-cost functions and representations would be, physically speaking, realizations of the principle of least action. That principle, equivalent to the 2
nd law [
31], guides a social system toward cultural means that attempt to acquire and consume free energy most effectively. Harris exemplifies the principle by maintaining, for example, that food taboos and religious practices, as voluntary routine actions, tend to be more cost-effective means for a society to ensure its cohesive energy transduction activities than to spend greater resources in enforcing particular codes of conducts, for example, by using police force or security services [
45]. The simple rationale for the principal guidelines of complex behavior provided by cultural materialism may appear to some to be too simple. Thus, a particular taboo may not seem to be a means of adaptation to surrounding conditions when it is viewed detached from the socio-environmental context,
i.e., etically in anthropological terms, by observers from a different culture. In cultural materialism the term emic refers to the participant’s perspective, whereas etic refers to the observer’s view [
46]. Social obligations imposed on an individual, e.g., via religion, should be evaluated against associated benefits provided by the social contract. Society obliges its members, e.g., via taxation, to provide it with the means for survival, with the balance sheet subject to continual internal debate.
This scale-independent description of nature from atoms to societies using a universal law may appear to some to be a wrong-headed attempt to reduce societies to atoms. On the contrary, the statistical physics of open systems merely asserts the generality that an influx of energy from the environment, together with modifiable systemic configurations, is the vital ingredient for the emergence of new mechanisms of any kind. Just as atoms in energy-dense surroundings bond to molecules by mutual interactions that absorb quanta from surrounding sources, so do communities integrate to societies by mutual efforts that incorporate energy from surrounding supplies. The emergent properties cannot be deduced from the prior systemic constituents alone since available external energy is also involved in the transition to a new state with new characteristics [
48]. In contrast, an isoenergic system remains stationary without emergent properties. It moves along closed orbits determined by the symmetry of the system [
49], and is amply described by the traditional Hamiltonian mechanics. Moreover, just as a biological system invests in improving its metabolic mechanisms and behavioral routines to access and conduct free energy, so does a society spend on developing its infrastructure and cultural procedures to acquire and consume free energy. Changes in surroundings impose forces,
i.e., energy gradients, on the system, and conversely, to satisfy the conservation of energy, the society influences its surrounding environment by outgoing flows through the common interface. Furthermore, changes in the large scale environment, e.g., climate, compel societies to make cultural changes to adapt their consumption of free energy. Likewise, compelling changes in circumstances prompt individuals to change behavior. Just as a species with particular phenotypic properties will go extinct if it fails to adapt its biological machinery to continue its consumption of free energy from changed surroundings, so will a society with specific cultural characteristics perish if it fails to transform its infrastructure in order to continue tapping into surrounding supplies [
21]. The natural imperative to attain the free energy minimum governed by the surroundings is exemplified in the same way at the molecular scale where complex molecules form via endergonic reactions in energy-dense surroundings and disintegrate via exoergic reactions in energy-deficient surroundings. The particular reactions, just as biological adaptations and social changes, are ultimately driven by the energy difference in respect to the surroundings. Admittedly, when examining some scenarios from the past, it seems at first sight astonishing why some societies failed to transform seemingly detrimental cultural traits into more beneficial practices. The physical formalism can provide insight into such peculiarities by representing the driving and opposing forces of social change in a single basic currency. The resulting skeletal simplification can clarify the balance of fundamental tendencies in a way that may more readily explain events than would a detailed examination of the more elaborate ethnographic surface.
3. Physical Formalism of Energy Conduction
The physical portrayal of a society as an energy transduction system and its culture as a means of conduction allows us to view society and its culture in a profound way. The formal representation serves to secure that energy is conserved in all processes. The central concept is an energy density
ϕj = exp(
Gj/
kBT), where
Gj denotes the energy level populated by a kind of entity, indexed with
j, in relation to the average energy per entity,
kBT, in the system of interacting entities where
kB is the Boltzmann constant [
49]. For a simple chemical reaction mixture it is not difficult to determine
Gj for various compounds as well as
kBT from measured concentrations, whereas it may be in practice impossible to value precisely a specific component in a social system. However, even when the particular values are not known, it does not prevent us from using the natural principle to describe the overall evolutionary behavior and dynamics of a society, just as of any other system. The directions of natural processes themselves, independent from particular kinetic mechanisms, reveal the relative values of systemic constituents.
The self-similar formalism does not take a society or any other entity as granted, but acknowledges that its existence at any moment is a result of earlier evolutionary processes. For example, a molecule is a result of chemical syntheses, just as is an individual organism. In the same way a mature ecosystem is a result of myriad of processes, as also a developed society. Thus the probability
Pj of an entity
j to exist depends on its ingredients, namely on the constituent densities,
ϕk, and energy, Δ
Qjk, from the surroundings that couples to the
jk-assembly process. We follow Boltzmann [
50] when assigning
Pj [
22,
23]
to a pool of indistinguishable
j-entities in numbers
Nj. The formula is self-similar so that each
j-entity is a product Π
Nk of embedded
k-entities, each distinct type available in numbers
Nk. The degeneracy,
gjk, numbers those
k-entity copies that remain indistinguishable (symmetric, exchangeable) within the
j-entity. The energy difference between the
j- and
k-entity is Δ
Gjk =
Gj –
Gk. The energy influx from the surroundings to the system is denoted by Δ
Qjk. It couples to the
jk-transformation orthogonal to Δ
Gjk, hence indicated by
i. The two orthogonal forms of energy are customarily referred to as scalar and vector potentials. For example, when an electron is falling down along scalar potential gradient, it radiates perpendicularly to its path,
i.e., generates a vector potential gradient known as Poynting vector. It is worth emphasizing that a steady state requires a continual stream of quanta from the surroundings. A society is in its entirety a flow-through system. It is constantly regenerating its infrastructure and culture to tap and distribute the vital influx just as other animates depend on the energy influx to replenish their mechanisms and carry on their characteristic behavior. A society’s infrastructure, as noted by Harris, is the principal interface between culture and the surrounding natural world [
8].
The probability measure
Pj relates, in energetic terms, a
j-entity to other entities in its surroundings. For example, a sugar molecule is an entity among entities that form an organism, and likewise a bacterium is an entity in an ecosystem, and a disposal package is an entity in an economic system, just as a habit-of-saying-hello is an entity in a social system (
Figure 1). When for an organism the energetic costs to synthesize a particular
j-molecule are minimal in relation to the energetic gains brought into the system by the
j-molecule, the corresponding
Pj is high. Then the
j-molecule would be found in abundant numbers,
Nj, in that organism. Likewise, when the energetic costs of a particular
j-habit are minimal in relation to the energetic gains brought to the community by practicing the
j-habit, that habit is frequently practiced. For example, uttering hello is an inexpensive habit to reinforce social bonding. Hence the corresponding probability of its occurrence is high. Likewise, symbols are abundant when they serve as inexpensive representatives of common values that direct coherent actions. For example, social cohesion against intruders is cheap to signal by wearing badges and livery. From our perspective, however, high cost events/items are not shunned, but embraced in the various acts of striving. This points up the fact that low cost items are common, thereby being frequent sinks for energy dissipation rather than rarer high cost sinks.
However, even when resources are abundant, they are finite. According to the Darwinian notion, entities compete over common ingredients, and the evolutionary process will naturally select the fittest [
51]. During the struggle for existence minor differences or even sporadic events, known as random variation, will lead to distinctions within a species, and can differentiate survivors from losers. As well, according to the natural law, competition over common consumables between the distinct species will generally govern their populations’ presences [
52]. According to the physical tenet, the entities (e.g., individuals of a population or populations of species), are subject to energy gradients, and the ensuing flows of energy will naturally select those transduction mechanisms that will level off the differences in least time. Notably, the natural imperative does not imply competition or co-operation as such, but it favors whatever means there are to diminish energy density differences as soon as possible. The maximal rate of consumption of free energy does not equate with mere dissipation (squandering), but depending on circumstances, supplies are invested in means to access even more free energy. For example, in a society greetings can be pictured as cost-effective means of social bonding that in turn facilitates cohesive actions to consume free energy from surrounding sources beyond those accessible by individual efforts. Likewise, watchwords are cost-effective means of authentication for rival groups rather than starting a detailed questioning of motives during an encounter. Cultural characteristics that require minimal physical representations, such as symbols or verbalizations of values are highly cost-effective means for a social system to direct its members’ actions in a coordinated manner. Standardization of habits such as greetings and codes, and a common language, are viewed by us as means to facilitate the energy transductions of a society. In the same way the chirality consensus of amino acids and a common genetic code facilitate energy transductions within an ecosystem [
53].
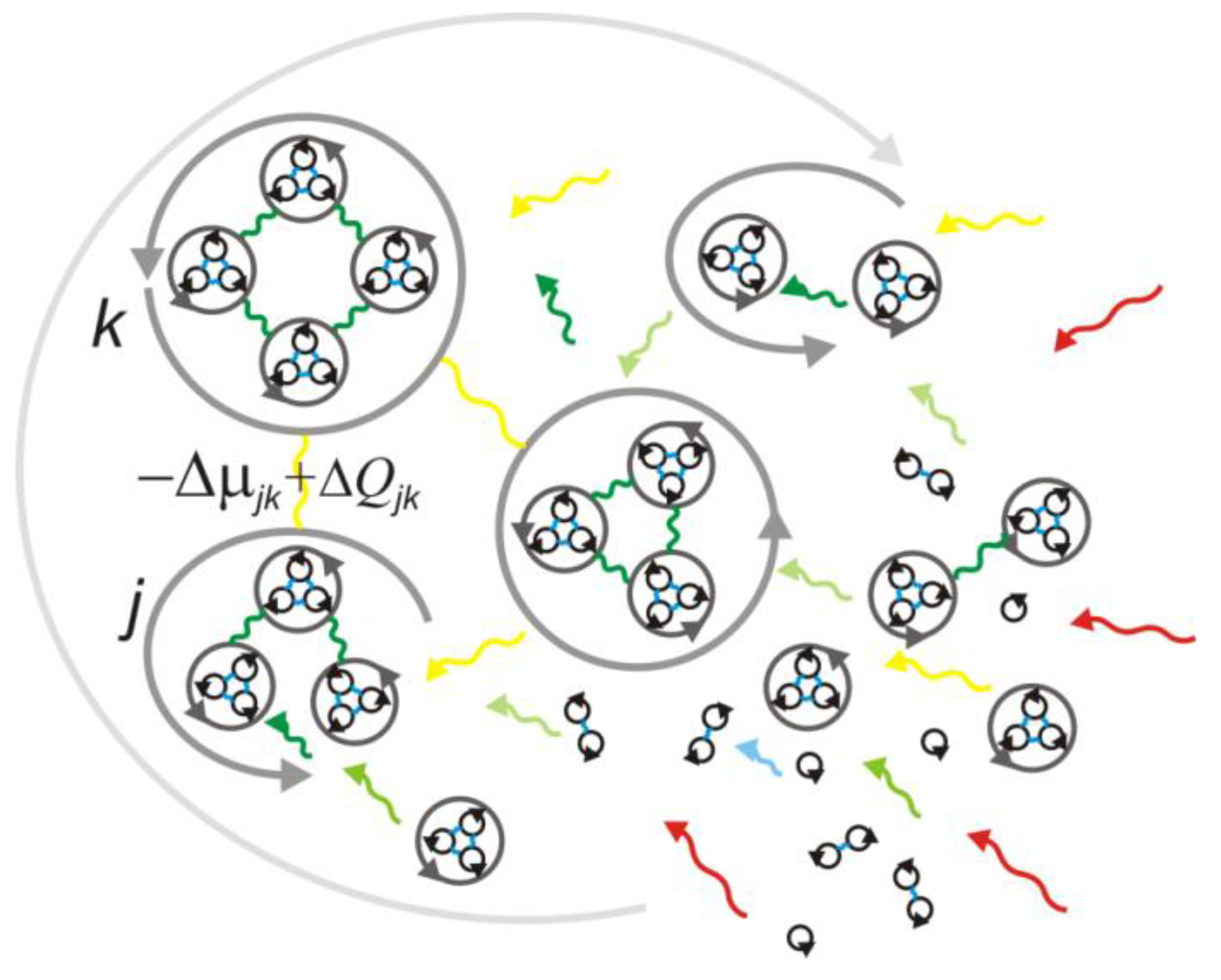
Figure 1.
This self-similar diagram depicts energy transduction systems in a nested hierarchy of systems within systems. Each system (loop) is immersed in a surrounding system (larger loop). Interactions (color-coded wavy arrows) hold the system’s constituents together. A stationary system that is not subject to forces moves along closed trajectories. The mutual density differences, Δμjk, and those relative to the surroundings, ΔQjk, drive the j and k systems (open loops) in evolution along open, inherently unpredictable trajectories toward more probable states. Social systems are here regarded as energy transduction systems within systems that couple to each other and to their respective surroundings via cultural interactions that diminish differences in energy.
Figure 1.
This self-similar diagram depicts energy transduction systems in a nested hierarchy of systems within systems. Each system (loop) is immersed in a surrounding system (larger loop). Interactions (color-coded wavy arrows) hold the system’s constituents together. A stationary system that is not subject to forces moves along closed trajectories. The mutual density differences, Δμjk, and those relative to the surroundings, ΔQjk, drive the j and k systems (open loops) in evolution along open, inherently unpredictable trajectories toward more probable states. Social systems are here regarded as energy transduction systems within systems that couple to each other and to their respective surroundings via cultural interactions that diminish differences in energy.
The energetic status measure
P for the entire system is obtained as a product over all
Pj [
22,
23]:
where each entity is in turn indexed with
j so that all levels and all
jk-transformations are counted. The
P status will change when the system changes its state due to an energy influx or efflux. In contrast,
P is constant for a stationary system. Since populations are non-negative, so is
P. The status measure is conditional since as it depends on the energetic conditions within the system and in its surroundings. Moreover
P cannot be normalized to unity because the energy content of an evolving system is not a constant. Entropy
S =
kBln
P is an additive statistical measure for the energetic status of the system. When the average energy per entity
kBT is a sufficient statistic [
54], Stirling’s approximation ln
Nj! ≈
Nj(ln
Nj – 1) holds and yields:
where the potential difference is Δ
μjk =
kBT(Σln
ϕk –ln
ϕj) [
55]. This definition of entropy via bound Σ
kBTNj and free energy, Σ
Nj(–Δ
μjk +
iΔ
Qjk), differs, e.g., from
S = –
kBΣ
Pjln
Pj that is limited to closed systems without evolutionary forces. Importantly entropy, when defined in energetic terms (Equation 3.3), is consistent with thermodynamics. All natural processes direct toward the free energy minimum state which is equivalent to the entropy maximum. Moreover, the concept of order relates to coherent motions and disorder to incoherent motions, not directly to entropy [
23].
The formalisms of statistical physics clarify that identities are established during interactions. For example, the identity of a cell is established by way of cell-cell interactions. When interactions are dissipative,
i.e. Δ
Qjk ≠ 0, then the
j- and
k-entities are found distinct from each other. Conversely, Δ
Qjj = 0 means that the
j-entities, as found by the particular method of examination are indistinguishable members of the
j-class. More powerful methods may resolve finer details, perhaps ultimately to the precision of a quantum of action. The identity of an individual develops and matures in dissipative interactions that supply ingredients (
Figure 1). The identity of a system is here a composition of its integral and interacting subsystems. For example, the identity of a national team is a composition of its interacting members. The identity of a society manifests itself in diverse and numerous dissipative interactions. It is a result of its history,
i.e., a series of prior dissipative processes. The flow of time experienced by a system is here identified with the flow of energy from the surroundings (or
vice versa), whereas a stationary system is conserved in energy [
23] so that generations would follow generations while nothing really changes.
Identical entities belong to the same class. The class might break down to distinct subclasses upon closer examination,
i.e., when subsystem-specific forces are applied. For example, cellular components are distinguished from each other in a laboratory by applying a density gradient using a centrifuge just as team members are distinguished from each other using score charts that have been compiled from goal recordings. Moreover, a particular action taken by a subsystem (e.g., a team member) is deemed selfish or altruistic depending on an observer’s subjective expectation on the member’s degree of integration in the organization. According to the statistical theory there is no objective viewpoint because all observations are flows of energy between subjects. The subjectivity, however, does not necessarily lead to advocating cultural relativism, since all parties in the present perspective have the same profound objective [
40]. The thermodynamic principle to consume free energy in the least time is the same for all parties, but differing conditions and behavioral mechanisms lead to different responses and evaluations of meanings.
The statistical theory clarifies that within a class,
i.e., among energetically indistinguishable entities there is no free energy to draw from. Thus, differences between distinct subsystems that manifest, e.g., as a division of work, allow an integrated system to outperform independent subsystems in energy transduction. For example, modern societies maintain technologies such as those needed in oil exploration by numerous group activities, not merely those of immediate use in the field but including even education, health care and legislation. The quest to diminish energy difference is the natural driving force to cultivate identities, e.g., by strengthening specific practices and by defining borders to distinguish systems within systems. A subsystem attempts to improve its energy transduction by building an independent and distinguishable identity. For example, cells differentiate during development, just as members of a community tend to specialize in performing distinct professions to gain more from the joint surroundings by co-operation. Conversely, when resources narrow, an integrated system may consume its integral entity by labeling it for exclusion. For example, a eukaryote cell under starvation will engulf some of its cytoplasm by coating it for combustion in autophagocytosis [
56]. Likewise, a society under a crisis may identify some its constituent populations, restricting their activities and eventually working against their survival. Energy differences that are encountered in interactions between a social system and its surrounding systems are perceived by the society to be potentially dangerous because the corresponding forces will perturb the society’s identity and trigger cultural changes. For example, a society that is colonizing a new habitant faces a clash,
i.e., substantial forces and struggles to adapt its culture to surrounding resources as well as to shape its surroundings to suit better to the society’s traditional way of making living [
21]. Eventually, when the forces have vanished, the system has arrived in a stationary state for the moment, where it is fully integrated in its surroundings via sustainable activities.
These few examples illustrate that a cause of a particular action, just as causes of a set of actions, are not here understood by studying the mechanisms themselves, i.e., the culture, but by focusing on conditions that impose forces on the system and drive its motions, as well as acknowledging the society’s past history which has resulted in its accumulating culture. Different conditions give rise to cultural diversity just as different conditions give rise to biodiversity. Importantly, cultural diversity in our perspective would not itself motivate relativistic valuations. Despite diversity in the outcomes, the principle is the same: to diminish energy differences in the least time, which we take to be the general expression for natural selection, as will be motivated below. Thermodynamics makes no distinction between inanimate and animate systems but considers all processes to be ‘natural’. The consumption of free energy in least time is regarded as a natural bias in evaluations. Since entropy is a systemic status measure, all assessments are subjective. For the same reason no value-neutral statements can be made because all observations would be biased by flows of energy.
4. Society in Evolution
The statistical physics of open systems is not limited to the usual account of stationary systems but can also be used to picture a society as an energy transduction system that evolves by consuming free energy,
Ajk = Δ
μjk –
iΔ
Qjk in population changes,
dNj/
dt, of diverse
j-entities. The progress toward more probable states is measured by
P that increases with time according to the evolutionary equation of motion [
22,
23]:
where
L is the generator of any process that consumes free energy. Evidently there are many ways, denoted by the
jk-indexing, for a system to consume various components of free energy,
Ajk, however, the statistical principle claims that the system aims at maximizing the total probability in least time. Therefore a dissipative system’s evolution will naturally select the paths,
i.e., the ways of functioning where
dP/
dt increases most rapidly. The form of
L (Equation 4.1) reveals that the flows, which manifest themselves as population changes
dNj/
dt, are inseparable from the forces,
Ajk when there are three or more degrees of freedom. This consequence is familiar from the three-body problem [
57]. Curiously, these paths of least action cannot be determined by integration to a closed form of the seemingly simple equation of motion. And so the fundamental reason for the inherent unpredictability of social changes can be taken to be the fact that the energy of an evolving system is not constant. A net influx of energy supports growth and a net efflux drives decline. Mathematically speaking, there are no constants of motion. Hence eigenvalues of a characteristic equation cannot be obtained. The inherent inability to predict evolution in detail, found from analysis of the mathematical form, illuminates in a deep way the unpredictability of social changes. Any state along an open evolutionary path depends on its past trajectory,
i.e., its history, because the driving forces and flows are inseparably linked. This is the characteristic of chaos, because even a small or stochastic change at an early stage may affect substantially the future status. Therefore it is not immaterial for the future of a society how it consumes its current repositories of free energy. It may invest in operations that will open paths for further productive activities or it may squander resources in futile activities. So the element of free will is present, but the physical portrayal maps it onto the ever changing currently available free energy.
Analyses of many past scenarios reveal that even when evolutionary tendencies have been sensed in a society, it has nevertheless been difficult to forecast precisely how and when they will transpire. This is apparent from recent economic turmoil. A good part of the unpredictability results from mechanistic changes that will speed up energy transformations by increasing some rates of conduction, as well as by initiating various convective episodes. Autocatalytic effects are apparent in economic systems [
58]. The rate of change of a population:
is proportional to the free energy by a coefficient
σjk. It is worth emphasizing that this form differs from the law of mass action where the rate is assumed to be proportional to populations. Consequently the kinetics and thermodynamics are erroneously viewed as unrelated to each other. According to the hierarchical theory the mechanisms of energy transduction are systems themselves. Therefore a particular mechanism may also evolve when the system evolves so that
σjk does not remain constant during evolution. In particular when a flow opens for the first time, a pioneering mechanism may soon be replaced by more effective means of conduction or convection to consume free energy more rapidly. Autocatalytic processes are not limited to biological systems but are familiar from economic evolution where profit is invested to increase production further [
16]. Likewise, a social change might speed up when initial cultural changes are superseded by more profound changes that allow even faster reforms. Eventually, when the free energy declines due to its consumption, an evolutionary course will stall. Therefore social changes, like other natural processes, would be expected to ignite by punctuation and proceed toward a stasis [
59] such as that which our own economy may face when we have passed peak fossil energy derivation. The overall cumulative course is convex up to the climax and subsequently concave. The resulting sigmoid curve on a log-log plot follows mostly a power-law pattern. The unimodal distribution of a population of entities as a function of energy and its cumulative curve as a function of time are self-similar. For example, when a non-renewable energy resource is consumed, a sigmoid population growth is followed by a sigmoid decline. The two subsequent sections together resolve as a unimodal pattern as a function of time. Often these natural processes, including bifurcations and chaotic behavior [
60], are modeled by iterative maps [
61] without ascribing them to being effects of the 2
nd Law of Thermodynamics in the form of the equation of motion. However, the approximate analytic forms easily give the false impression that surrounding energy capacity would be constant [
62] and that chaotic trajectories could be thought of as deterministic.
It is a common practice to rewrite the equation of evolution (Equation 4.1) using the definition of entropy
S =
kBln
P as
dS/
dt =
kBL, and further on by multiplying with
T as the equation for the flows of energy,
i.e., the equation of power [
22,
23]:
A society, according to the physical portrayal, tends to consume various sources of free energy
Ajk via diverse
jk-transformations with the maximal power to arrive in least time at the maximum-entropy partition of classes housing various entities
Nj. Physically speaking the class structure is a partition of energy among the system’s entities. In the spontaneous physical quest for the free energy minimum state, class structure as a functional mechanism emerges during the evolutionary processes for increased energy transformation. The corresponding class structure of an ecosystem is referred to as the food chain [
14]. Its emergence there is a natural process [
63]. The structuring of social interactions is apparently a highly cost-effective means to orchestrate the energy transduction by the division of labor. Just as the trophic level structure stratifies during ecological succession, the class structure develops during cultural succession when societies grow larger and emerge with more and more energy-intense functions [
64,
65]. For example, the accumulation of capital at the top of the hierarchy allows investments in effective transduction machinery whereas more distributed assets disperse among less effective mechanisms.
It is worth emphasizing that energy flows to the system from its surroundings bring about changes, not only in the society, but also in the surroundings. In other words, when energy differences across the society-environment interface are diminishing, both the entropy of the system and its surroundings are increasing because entropy is a function of both bound and free energy (Equation 3.3). Since the system and its surroundings share the same flows of energy across their mutual interface, it would violate the conservation of energy that the entropy of a system would decrease at the expense of entropy increase in its surroundings, which is a common misunderstanding of non-equilibrium thermodynamics. Any surroundings is a fund within a yet wider surroundings, so that heat energy will disperse throughout.
5. The Steady-State Society
Fervent extraction of free energy from non-renewable repositories is rapidly transforming contemporary societies. Intuition about such irreversible motion down along the energy gradient has been reflected in our Western notion of time as being directional. However, many other communities perceived time as cyclic. Generations followed generations just as years passed one after the other without overall changes. For us such a stationary-state society would be an oddity, yet it could be worthy of analysis because it may well be the best future option eventually for us too. An ever-increasing economic growth is not possible, especially when consuming ever-declining resources. At best a steady state might be attained by tapping into resources that are renewed by consuming gigantic reservoirs of free energy such as that available from insolation.
The steady-state condition
dP/
dt = 0 determines the maximum-entropy partition of entities [
22,
66]:
independently from kinetics,
i.e., from
σjk. The skewed distribution is the maximum entropy partition of mechanisms that together consume diverse sources of free energy in the least time. The distribution’s low end is populated by ineffective but energetically inexpensive mechanisms whereas the high end houses highly effective but energetically expensive mechanisms. The free energy minimum state is stable according to Lyapunov criteria [
67,
68]: any perturbation
δNj away from the optimum
Njss will lead to a diminished status measure,
S(
δNj) < 0, and induce a returning force
Ajk to drive the flow
dNj/
dt back toward
Njss so that
dS(
δNj)/
dt > 0 [
69]. In other words, when a society fails repeatedly to find new opportunities either intentionally or accidently, it could function conservatively to maintain itself at an optimum where actions follow closed orbits. Nevertheless a social system, just as an ecosystem, may oscillate about the optimum without net loss or gain of energy [
70]. The oscillations are rarely symmetric about the past and future [
71] because the energy landscape of a complex system is seldom of a high symmetry. The history of a conserved system tends to repeat itself.
Cultural characteristics reflect a society’s survival history. In a new environment a founder effect may retain its past habits for a while, but eventually, in the quest for the maximum entropy partition, its practices, habits and values will adapt to surrounding imperatives. Physically speaking, it takes time,
i.e. flows of energy, to disassemble and reassemble infrastructure and interactions as well as social bonding that constitute the society’s inertia. Systems that have access to large resources are able to accumulate large capacity on the one hand to impose, and on the other hand to resist, changes in their surroundings. Such dominant courses are well documented in the histories of cultures that have enjoyed the resources of the large Eurasian continent [
20]. This species-area relationship is also familiar from ecology [
14,
72]. The energy in the system is reflected in heat capacity
TdS/
dT (
cf. Equation 3.3). It is not easily removed or transformed to another type of social bonding, even under circumstances that clearly disfavor traditional traits. Over a period time the society’s capacity may be sufficient to limit flows by restricting interactions, but ultimately the requirements of its superior surroundings leave no option but to adapt, or perish. Ecological imperatives will require a society to change, and social pressure placed by a community on an individual would be qualitatively no different at that level.
6. Discussion
The naturalistic view of culture as a society’s means to survive is instructive. The holistic tenet integrates a social system seamlessly to its biotic and abiotic surroundings as well as to its subordinate systems. Thus we find that cultural diversity is in principle no different from biodiversity when viewed physically. Diversity allows consumption of the free energies contained in diverse sources. Effective species devour and require intense resources whereas less effective species survive with modest supplies. The various realms of Nature – physical, biological,
etc. are related to each other as classes and subclasses [
26], and so by taking a physical perspective, we delete details of the higher levels without disturbing the fundamental relations established in the most generally present realm, the physical, which subsumes the others. The physical portrayal of a society as an energy transduction system allows us to apply the most central concepts and universal principles, as well as to use mathematical formalisms to analyze basic aspects of social behavior and rationalize many cultural characteristics. The results obtained are insightful, but perhaps also perplexing. Customarily, a theory of physics is expected to provide predictions, but the statistical physics of open systems reveals that detailed trajectories of social changes cannot be forecasted because neither energy nor energy flow pathways are conserved within an evolving system. Moreover, the thermodynamic equation of motion for open systems reveals that the history of a society is unique when the forces (
i.e., the free energies) that propel evolution from one state to another, more probable, one, are not independent of the flows of energy that transform the society. In other words the mathematical analysis yields the basic observation that the future evolution of a society depends inherently on the past path,
i.e., history. While the key result of inherent intractability itself is no surprise in context of social systems, the 2
nd law maintains that the flows of energy tend to channel along cultural conduits that provide paths of least action. This imperative couples the energy consumption of a society with aspects of its cultural characteristics. This prime incentive can be easily recognized in economic activities but it also illuminates curious cultural characteristics, e.g., taboos and symbols, as well as manners and values, as highly effective means to maintain energy transduction. This conclusion as such may not be surprising, but is based here on physical first principles.
To describe a society and its culture via concepts of physics may seem at first sight to be utterly unsatisfactory, as if it were neglecting our dearest human characteristics: consciousness and free will. However, the self-similar formalism regards each individual as an agentive system of its own interacting with his / her surrounding systems by way of choosing and modulating flows of energy. Integration over counteractive fluxes is perceived at times as troubled decision making. Today’s modern societies are equipped with highly effective means to acquire information from surrounding systems and from their integral systems. The resulting environmental awareness and social cohesion contribute, although not always along parallel lines, in directing the consumption of free energy along paths that are expected to provide yet more free energy. And so modern societies too, when deciding their future courses, struggle forward among conflicting forces. The statistical physics of open systems does not deny our freedom to choose the future paths, but makes it indisputable that the set of choices depends on past history and is limited by current resources. A potentially testable hypothesis is opened up as well – that organizations and individuals will tend statistically, when given alternative choices, to choose actions that will require the largest energy flows. Moreover, our choices are critical since they will not only open some paths but inevitably close others forever.
The onetime rebuttal of the central claims of cultural materialism can today be regarded simply as an attempt to retain a prior
status quo in the field of anthropology. But perhaps some of that refusal may also be interpreted as a challenge to provide a fundamental basis that would truly justify the revolutionary reasoning espoused by cultural materialism. Undoubtedly the profound principle promoted here comes in a form that is strange for some. Our presentation of holistic and scale-independent thinking may appear intangible to someone uninitiated in the self-similar formalism. However, the more familiar skewed distributions and sigmoid cumulative curves characterizing aspects of social systems, as well as their unpredictable, and at times chaotic behavior, are unmistakable signatures that the 2
nd Law of Thermodynamics has its ‘say’ in social systems too. Moreover, due to the common but unfortunate misconception that increasing entropy production would parallel decreasing order, the 2
nd Law is one-sidedly viewed to command destructive processes. However, when surroundings are rich in energy, the natural law describes the emergence of constructive and organized functions that are the very mechanisms needed to channel the flow of energy from surrounding supplies to the developing system. Several anthropological theories have sought a universal principle to rationalize complex patterns of cultural diversity [
73]. Indeed one may recognize elements in several that are in agreement with the physical portrayal of social systems, but cultural materialism best captures the essence of this physical principle. Moreover this doctrine has been refined largely to a consistent description of societies as systems within their surrounding systems [
74,
75].
It is of course pertinent to ask what is really new in this study since the universal imperatives to maximize entropy production and to minimize free energy have been advocated early on [
76], and frequently thereafter, yet might be found somehow insufficient or inconsistent to describe the emergence and evolution of living systems. The explanation is subtle but significant. First, when the formula of entropy is derived from the statistical physics of open systems, it is understood that the increase of entropy results from the decrease of free energy. In other words the two imperatives are in principle equivalent, as they should be according to the basic maxim of thermodynamics. Moreover, the increase of entropy does not associate in a simple way with the decrease of order. When the surroundings supply energy such as solar insolation, orderly structures emerge and evolve to capture and consume more free energy. Life is not an oddity but a natural outcome of the 2
nd Law of Thermodynamics [
11]. Secondly, the objective of energy transduction is not efficiency of use [
77] but the maximal consumption of free energy, which in turn is not simply maximal dissipation because in order to maintain the maximum entropy production state some free energy must be consumed in regenerating the dissipative machinery. Thirdly, the statistical physics of open systems is hierarchical in it its formalism, so that each system is within a surrounding system. Consequently, the flows of energy through all mutual interfaces must be counted. Then it becomes clear that when the energy difference across the system-environment interface diminishes, both the entropies within the system and its surrounding system increase, rather than that the entropy for either one could possibly decrease, because such a process would violate both conservation and continuity. Moreover, the holistic description makes it clear that no system and no process can be fully understood without considering its surroundings.
Finally it is intriguing to view science as social activity too [
78]. Specialization to disciplines has brought great benefits in energy transduction, but this process has required the disciplines to establish their vital identities, e.g., by forming schools, speaking segregating languages and conducting practices commissioned by interested parties. Undoubtedly, the few concepts of physics that are needed to outline energy transduction do not map one-to-one to those established in social studies, and therefore, for example, leave room to question: What did Harris really mean? We give our answer herein. For this holistic tenet to gain ground and to provide ensuing benefits, cultural naturalism will need to be absorbed via a cross-disciplinary integration that would be most rewarding when founded on the most central concepts and universal principles.