Multi-Criteria Evaluation of Energy Systems with Sustainability Considerations
Abstract
:1. Introduction
2. From Sustainability Indicators to Composite Sustainability Index
2.1. Selection and Grouping of Indicators
- Technical indicators (energetic efficiency, exergetic efficiency, power density, fuel consumption, reliability, availability, etc.)
- Environmental indicators (quantities of emitted pollutants, effect on health, effect on flora and fauna, etc.)
- Economic indicators (life cycle cost, internal rate of return, payback period, etc.)
- Social indicators (job creation, general welfare, etc.).
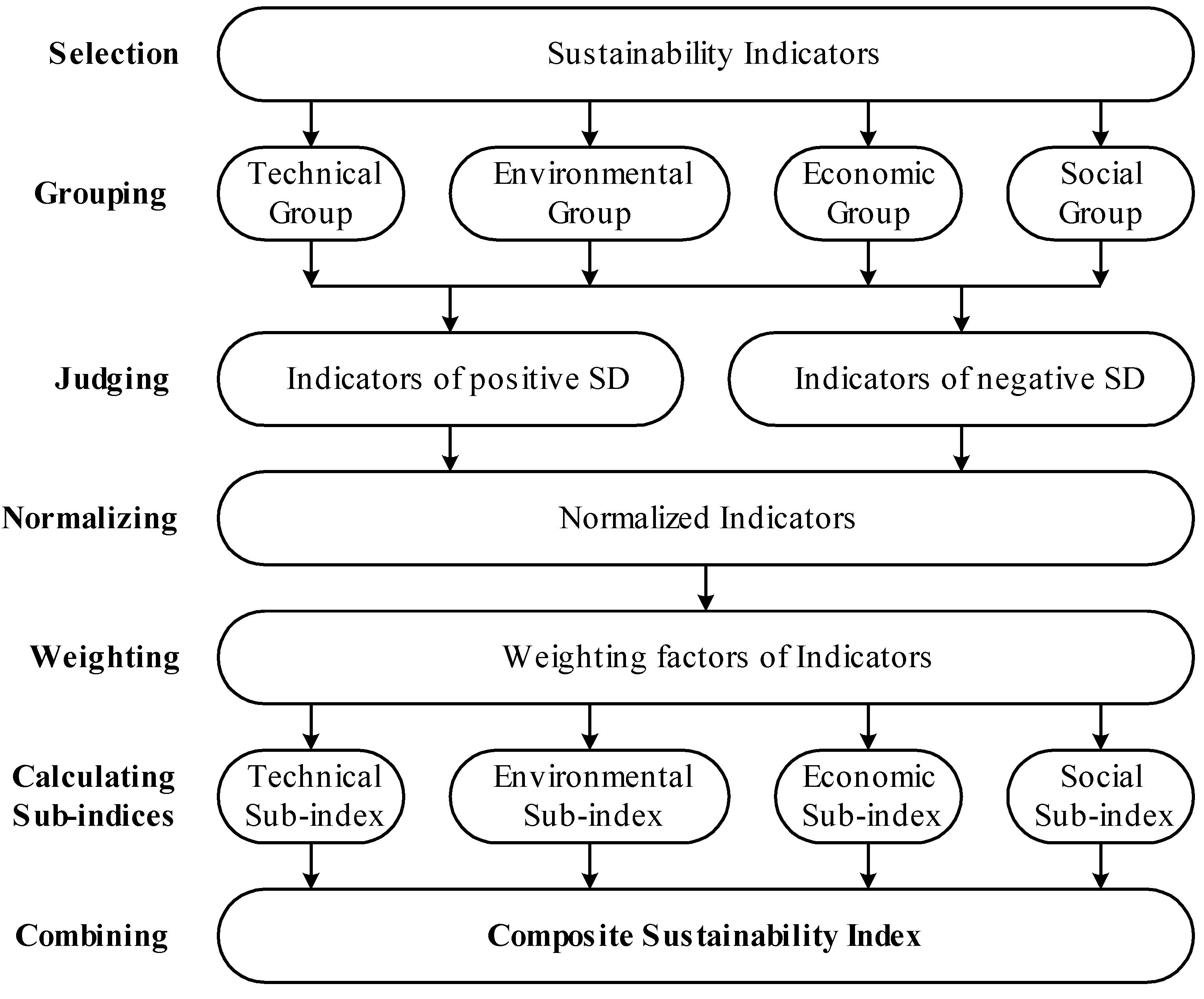
2.2. Judging the Indicators
2.3. Normalizing the Indicators
2.4. Weighting the Indicators and Calculating the Sub-Indices
2.5. The Composite Sustainability Index
3. Case Study: Assessment of Alternative Energy Systems Related to An Industrial Unit
3.1. Selection of Indicators
| i | Symbol | Units | Description |
|---|---|---|---|
| 1 | – | Energetic electric efficiency | |
| 2 | – | Energetic total efficiency | |
| 3 | – | Exergetic electric efficiency | |
| 4 | – | Exergetic total efficiency | |
| 5 | kg/a | Annual emission of NOx | |
| 6 | kg/a | Annual emission of CO | |
| 7 | kg/a | Annual emission of UHC (unburned hydrocarbons) | |
| 8 | kg/a | Annual emission of PM10 (particular mater of a diameter up to 10 μm) | |
| 9 | kg/a | Annual emission of CO2 | |
| 10 | kg/a | Annual emission of SOx | |
| 11 | NPC | € | Net Present Cost (conventional analysis) |
| 12 | NPCenv | € | Net Present Cost including environmental externalities |
3.2. Energy Needs of the Industrial Unit and Alternative Energy Systems
| Electric power: | kW |
| Mass flow rate of saturated steam: | kg/s |
| Steam pressure: | bar |
| Feed water properties: | bar, T = 25 °C |
| Annual operation: | h (11 months/a × 680 h/month) |
- System A:
- Electricity from the local network and steam from a boiler operating with natural gas and located in the industrial unit.
- System B:
- System C:
- Cogeneration system with dual fuel reciprocating internal combustion engine.
| Lower heating value of natural gas: | kJ/Nm3 |
| Temperature of the environment: | T0 = 25 °C (298.15 K) |
| Exergy to energy ratio of natural gas: | |
| Technical life of the system: | years |
| Salvage value at the end of N years: | |
| Cost of natural gas: | €/Nm3 |
| Market interest rate: | i = 0.10 |
| General inflation rate: | f = 0.03 |
| Fuel inflation rate: | ff = 0.04 |
| Annual insurance rate: | of investment |
| Pollutant | Specific emissions (g/kWh) | External environmental cost (€/kg) | |||
|---|---|---|---|---|---|
| Electric network | Boiler | Gas turbine | Dual Fuel Engine | ||
| NOx | 0.5 | 0.3466 | 1.4225 | 2 | 3.4384 |
| CO | 0.3 | 0.0266 | 0.0864 | 5 | 1.1600 |
| UHC | 0 | 0 | 0.0665 | 3 | 0.1608 |
| PM10 | 0.04 | 0.0177 | 0.04653 | 0.0299 | 15.1114 |
| CO2 | 531.68 | 224.488 | 537.198 | 429 | 0.0190 |
| SOx | 0 | 0 | 0 | 0.067 | 1.0000 |
3.3. Additional Information about System A
| Technical Data | |
|---|---|
| Efficiency of the electricity generation and supply by the local network: | |
| Contribution of fuels to the electricity production (small contribution from other sources is neglected) Lignite: Natural gas: Petroleum products: | 61.6% 21.4% 17.0% |
| Exergy to energy ratio of fuels used for electricity generation by the network (weighted average): | |
| Efficiency of the boiler: | |
| Economic Data | |
| Installed cost of boiler: | € |
| Construction period of boiler: | 1 year |
| Electricity tariff system. Power charge: | XZ = 2.1581 €/kW/month |
| Energy charge: | €/kWh |
| Operation and maintenance cost of boiler (excluding fuel): | €/MWhth |
- Total energetic efficienc:
- Exergetic efficiency of the electricity network:
- Volumetric flow rate of fuel consumed by the boiler:
- Exergy flow rate of fuel consumed by the boile
- Total exergetic efficiency of System A:
3.4. Additional Information about System B
| Technical Data | |
|---|---|
| Electric energetic efficiency: | |
| Thermal energetic efficiency: | |
| Total energetic efficiency: | |
| Electric exergetic efficiency: | |
| Thermal exergetic efficiency: | |
| Total exergetic efficiency: | |
| Economic Data | |
| Installed cost of the system: | € |
| Construction period: | 2 years |
| Operation and maintenance cost (excluding fuel): | €/MWhe |
3.5. Additional Information about System C
| Technical Data | |
|---|---|
| Thermal power of the dual fuel engine: | kWth |
| Thermal power of the boiler (): | kWth |
| Electric energetic efficiency of the engine: | |
| Thermal energetic efficiency of the engine: | |
| Total energetic efficiency of the engine: | |
| Efficiency of the boiler: | |
| Lower heating value of Diesel oil: | kJ/kg |
| Exergy to energy ratio of Diesel oil: | |
| Density of Diesel oil: | kg/lt |
| Economic Data | |
| Installed cost of the cogeneration system: | € |
| Installed cost of the boiler: | € |
| Construction period: | 2 years |
| Cost of Diesel oil: | €/lt |
| Operation and maintenance cost of the cogeneration system: | €/MWhe |
| Operation and maintenance cost of the boiler: | €/MWhth |
- Volumetric flow rate of natural gas consumed by the dual fuel engine:
- Mass flow rate of Diesel oil consumed by the dual fuel engine:
- Total energetic efficiency of System C:
- Exergy flow rate of fuels in the dual fuel engine
- Exergy flow rate of steam produced by the cogeneration system
- Exergy flow rate of steam produced by the boiler
- Volumetric flow rate of fuel consumed by the boiler:
- Exergy flow rate of fuel consumed by the boile
- Total exergetic efficiency of System C:
4. Results and Discussion
4.1. Calculation of Indicators, Sub-Indices and the Composite Sustainability Index
| i | Symbol | Units | System A | System B | System C |
|---|---|---|---|---|---|
| 1 | – | 0.38 | 0.3761 | 0.47 | |
| 2 | – | 0.56 | 0.8483 | 0.86 | |
| 3 | – | 0.36 | 0.36 | 0.451 | |
| 4 | – | 0.337 | 0.513 | 0.522 | |
| 5 | kg/a | 209,856.8 | 319,209 | 483,574.1 | |
| 6 | kg/a | 74,814.7 | 19,388 | 1,124,668.8 | |
| 7 | kg/a | 0 | 14,923 | 673,199 | |
| 8 | kg/a | 13,963 | 10,441 | 8,485.8 | |
| 9 | kg/a | 182,559,976.6 | 120,547,231 | 118,790,310 | |
| 10 | kg/a | 0 | 0 | 15,035 | |
| 11 | NPC | € | 319,384,905.1 | 181,429,678 | 232,009,565.8 |
| 12 | NPCenv | € | 357,593,745 | 211,828,489.5 | 278,628,728.5 |
| i | Symbol | Units | Lower threshold | Upper threshold |
|---|---|---|---|---|
| 1 | – | 0 | 0.80 | |
| 2 | – | 0 | 1 | |
| 3 | – | 0 | 1 | |
| 4 | – | 0 | 1 | |
| 5 | kg/a | 209,856.8 | 483,574.1 | |
| 6 | kg/a | 19,388 | 1,124,668.8 | |
| 7 | kg/a | 0 | 673,199 | |
| 8 | kg/a | 8,485.8 | 13,963 | |
| 9 | kg/a | 118,790,310 | 182,559,976.6 | |
| 10 | kg/a | 0 | 15,035 | |
| 11 | NPC | € | 181,429,678 | 319,384,905.1 |
| 12 | NPCenv | € | 211,828,489.5 | 357,593,745 |
| No. | Indicator | Physical Symbol | System A | System B | System C |
|---|---|---|---|---|---|
| 1 | 0.475 | 0.4701 | 0.5875 | ||
| 2 | 0.56 | 0.8483 | 0.86 | ||
| 3 | 0.36 | 0.36 | 0.451 | ||
| 4 | 0.337 | 0.513 | 0.522 | ||
| 5 | 1 | 0.6005 | 0 | ||
| 6 | 0.9498 | 1 | 0 | ||
| 7 | 1 | 0.9778 | 0 | ||
| 8 | 0 | 0.6430 | 1 | ||
| 9 | 0 | 0.9724 | 1 | ||
| 10 | 1 | 1 | 0 | ||
| 11 | NPC | 0 | 1 | 0.6327 | |
| 12 | NPCenv | 0 | 1 | 0.5417 | |
| – | 0.474 | 0.782 | 0.466 |
| Index | System A | System B | System C |
|---|---|---|---|
| 0.433 | 0.548 | 0.605 | |
| 0.658 | 0.866 | 0.333 | |
| 0 | 1 | 0.587 | |
| 0.364 | 0.805 | 0.508 |
4.2. Graphical Presentation of the Results
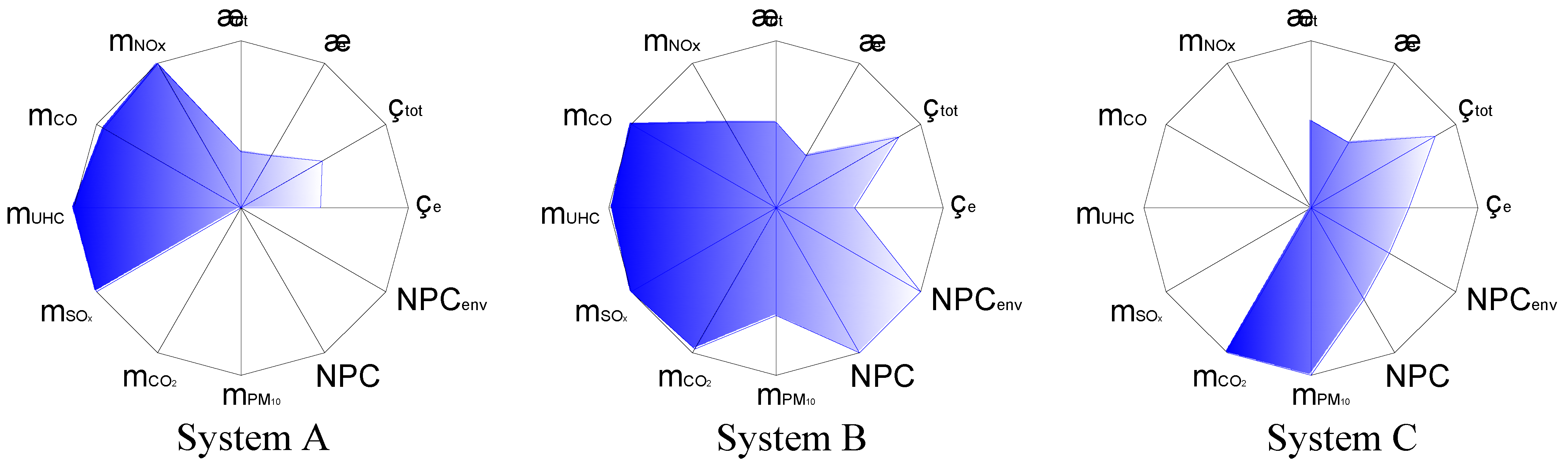
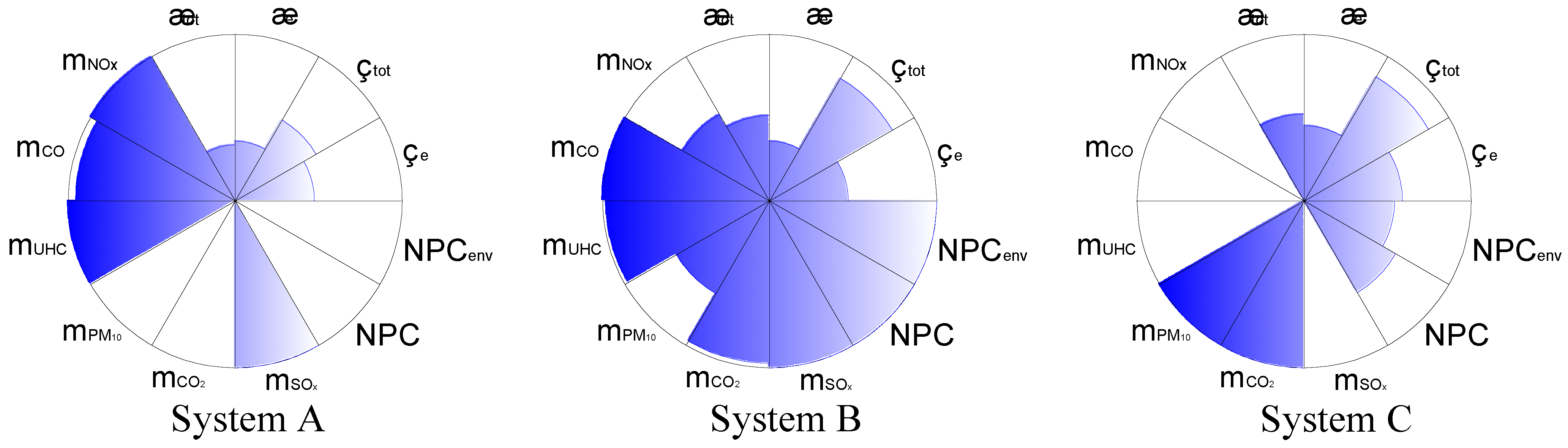
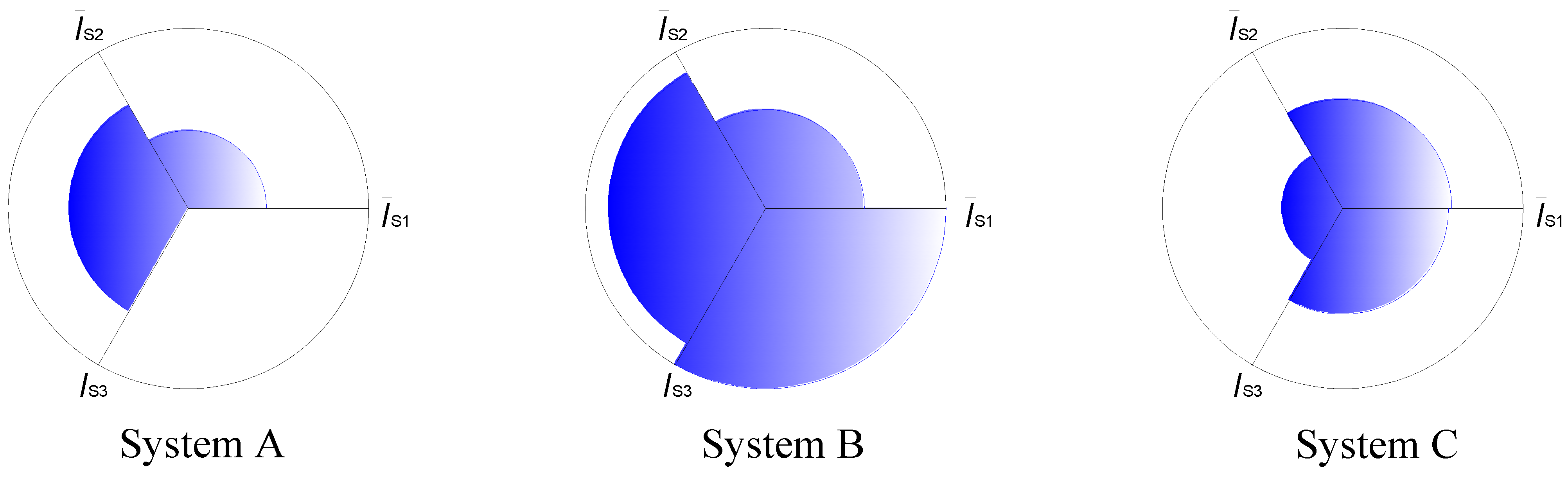
4.3. Comments on the Results
4. Conclusions and Recommendations
References
- WCED. Our Common Future. In Report of the UN World Commission on Environment and Development, Gro Harlem Brundtland, Chair; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Lior, N. About sustainability metrics for energy development. In Proceedings of the 6th Biennial International Workshop “Advances in Energy Studies”, Graz, Austria, 29 June–2 July 2008; pp. 390–401.
- Keramioti, D.E. Performance Evaluation Of Energy Systems With Sustainability Considerations. Diploma Thesis, National Technical University of Athens, School of Naval Architecture and Marine Engineering, Athens, Greece, October 2009. [Google Scholar]
- Afgan, N.H.; Carvalho, M.G. Sustainable Assessment Method for Energy Systems: Indicators, Criteria and Decision Making Procedure; Kluwer Academic Publishers: Boston, MA, USA, 2000. [Google Scholar]
- Tonon, S.; Brown, M.T.; Luchi, F.; Mirandola, A.; Stoppato, A.; Ulgiati, S. An integrated assessment of energy conversion processes by means of thermodynamic, economic and environmental parameters. Energy 2006, 31, 149–163. [Google Scholar] [CrossRef]
- Krajnc, D; Glavič, P. How to compare companies on relevant dimensions of sustainability. Ecol. Econ. 2005, 55, 551–563. [Google Scholar] [CrossRef]
- Afgan, N.H.; Carvalho, M.G. Sustainability assessment of hydrogen energy systems. Int. J. Hydrogen Energy 2004, 29, 1327–1342. [Google Scholar] [CrossRef]
- Valero, A.; Lozano, M.A.; Serra, L; Tsatsaronis, G.; Pisa, J; Frangopoulos, C; von Spakovsky, M.R. CGAM Problem: Definition and conventional solution. Energy 1994, 19, 279–286. [Google Scholar] [CrossRef]
- Frangopoulos, C.A. Application of the Thermoeconomic Functional Approach to the CGAM Problem. Energy 1994, 19, 323–342. [Google Scholar] [CrossRef]
- COGEN Europe. EDUCOGEN—The European Educational Tool on Cogeneration, 2nd Edition. ed; The European Association for the Promotion of Cogeneration: Brussels, Belgium, 2001; Available online: http://www.cogen.org/projects/educogen.htm/.
- Dorai, V.S.; Frangopoulos, C.A. Estimation of Environmental Externalities and their Effect on the Optimization of a Cogeneration system. In 21st International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems, ECOS 2008, Kraków, Poland, 24–27 June 2008; pp. 1419–1428.
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Frangopoulos, C.A.; Keramioti, D.E. Multi-Criteria Evaluation of Energy Systems with Sustainability Considerations. Entropy 2010, 12, 1006-1020. https://doi.org/10.3390/e12051006
Frangopoulos CA, Keramioti DE. Multi-Criteria Evaluation of Energy Systems with Sustainability Considerations. Entropy. 2010; 12(5):1006-1020. https://doi.org/10.3390/e12051006
Chicago/Turabian StyleFrangopoulos, Christos A., and Despoina E. Keramioti. 2010. "Multi-Criteria Evaluation of Energy Systems with Sustainability Considerations" Entropy 12, no. 5: 1006-1020. https://doi.org/10.3390/e12051006
APA StyleFrangopoulos, C. A., & Keramioti, D. E. (2010). Multi-Criteria Evaluation of Energy Systems with Sustainability Considerations. Entropy, 12(5), 1006-1020. https://doi.org/10.3390/e12051006




