Improvement of Energy Conversion/Utilization by Exergy Analysis: Selected Cases for Non-Reactive and Reactive Systems
Abstract
:1. Introduction
2. Non-Reactive Energy Systems
2.1. Case 1—332 MWe Steam Power Plant (Energy Conversion; Design/Optimization)
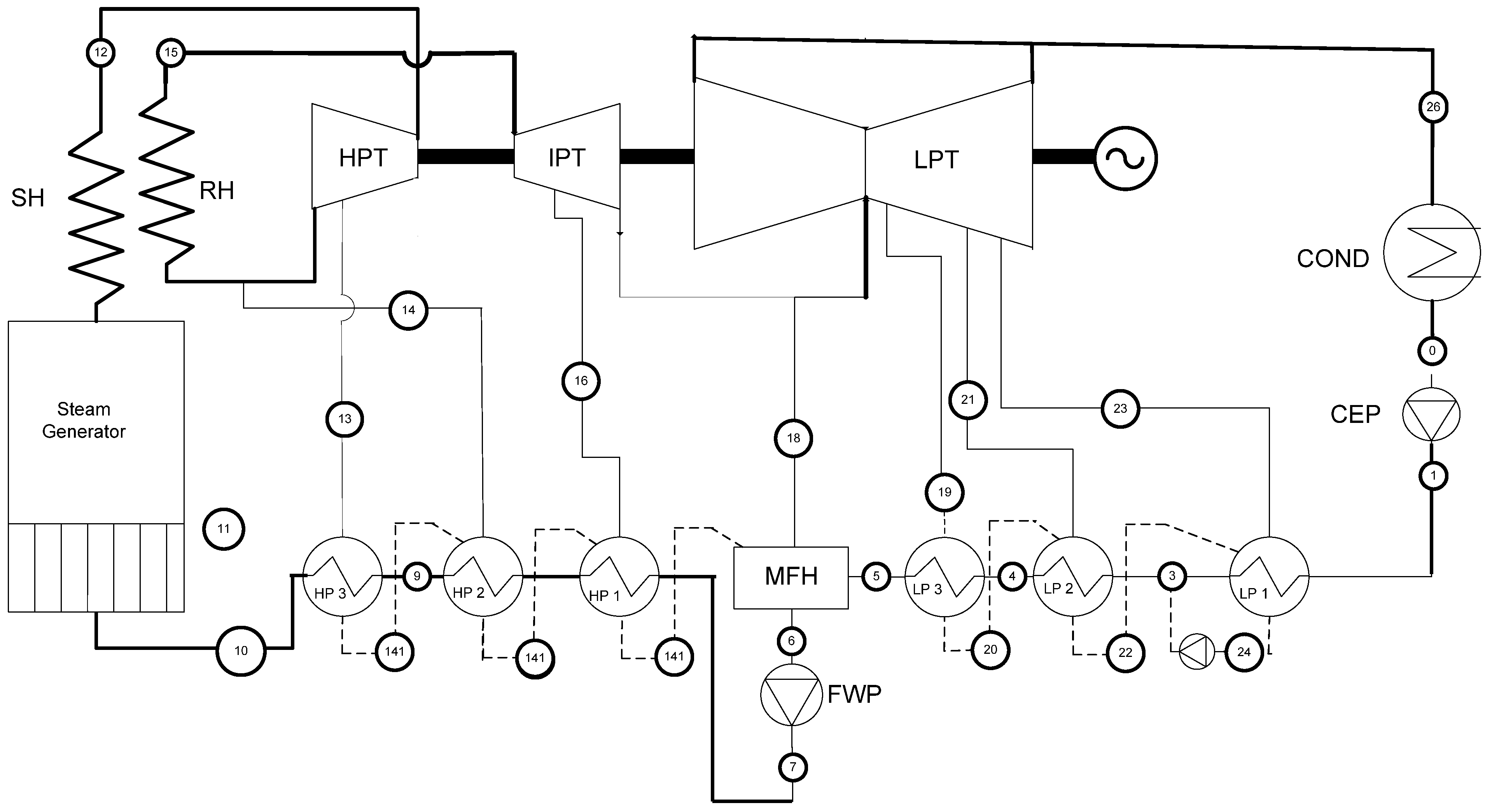
2.2. Case 2—Solar Thermal Steam Power Plant (Energy Conversion; Standard/Optimum Control)
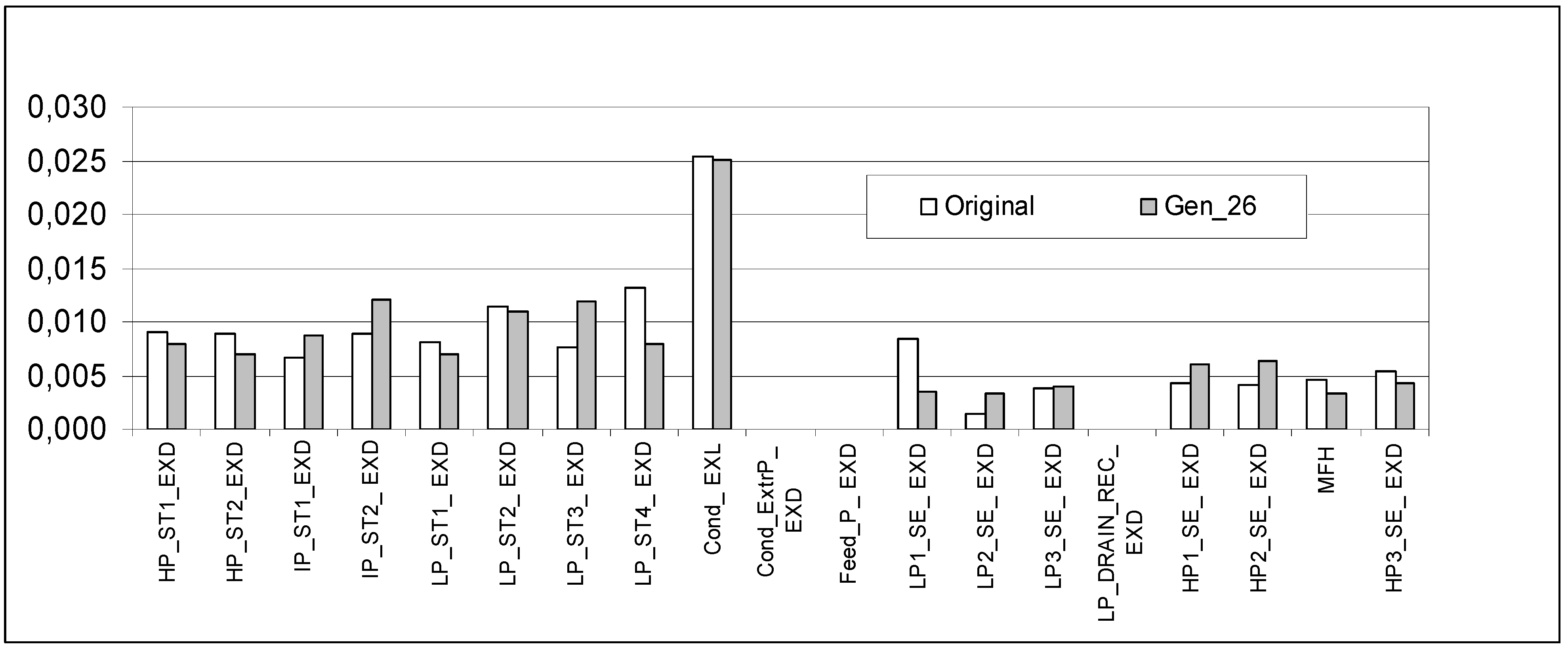
| Variable | Base Case | Optimized |
|---|---|---|
| ηHPT | 0,88 | 0,88 |
| ηIPT | 0,89 | 0,89 |
| ηLPT | 0,90 | 0,90 |
| TSH = TRH °C | 538 | 538 |
| pCond bar | 0,05 | 0,05 |
| pSH bar | 170 | 170 |
| p13 bar | 78,3 | 88,03 |
| p14 bar | 37,75 | 49,91 |
| p16 bar | 16,94 | 19,02 |
| p18 bar | 7,24 | 6,454 |
| p19 bar | 2,6 | 2,661 |
| p21 bar | 0,76 | 0,7295 |
| p23 bar | 0,29 | 0,1481 |
| η | 0,4687 | 0,4710 |
| ηx | 0,869 | 0,871 |
| Generation | 1 | 26 |
- -
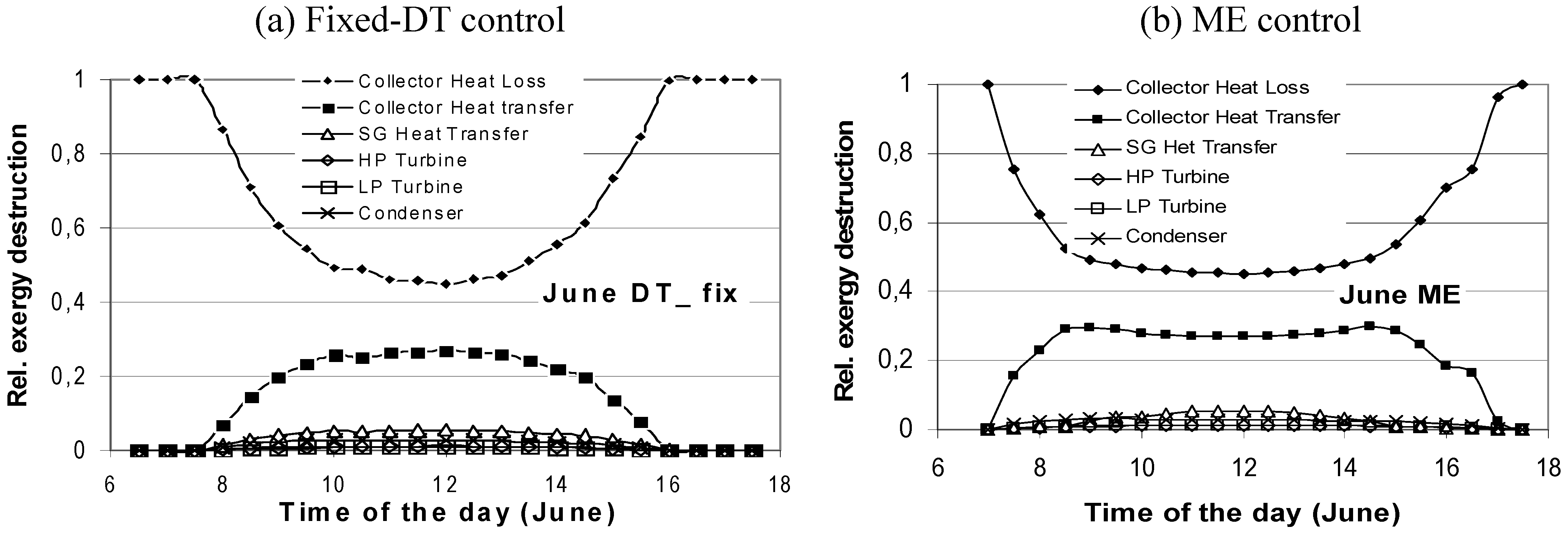
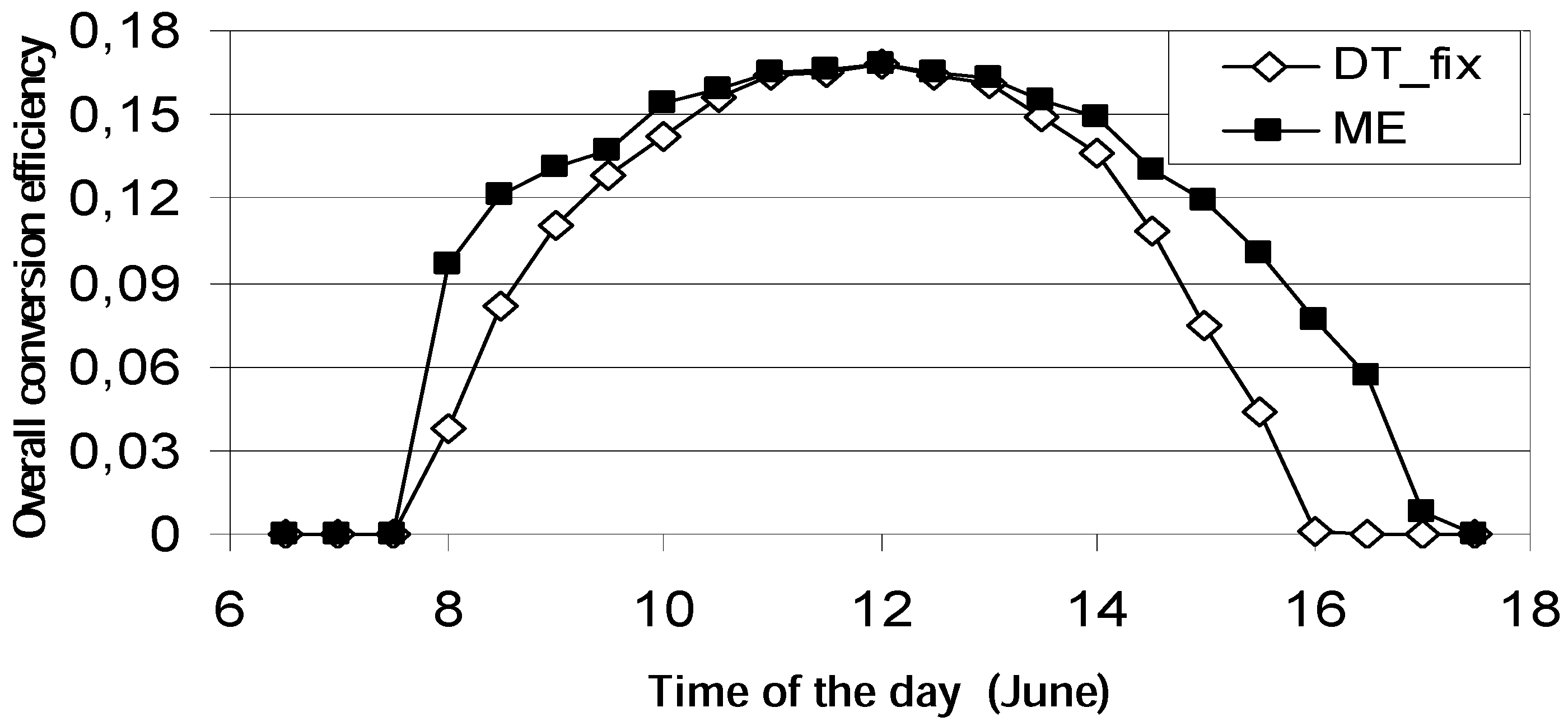
- In order to have low thermal losses and transfer most of the heat to the fluid, the solar collector should be operated at a high thermal efficiency, with a low average absorber temperature (Tfo + Tfi)/2. The collector transfers large quantities of heat to the fluid, but it is low-quality heat.
- -
- If the average absorber temperature is raised, the collector transfers less heat to the fluid (but with a higher quality); the heat loss to the environment is increased. If I is low or Tfo is raised too much, the collector reaches shut-off conditions (no useful energy output, zero efficiency)
- -
- Between these two conditions (which depend on Ta and I, as well as on Tfo), a condition of maximum exergy output (referring to the collector) must exist.
- -
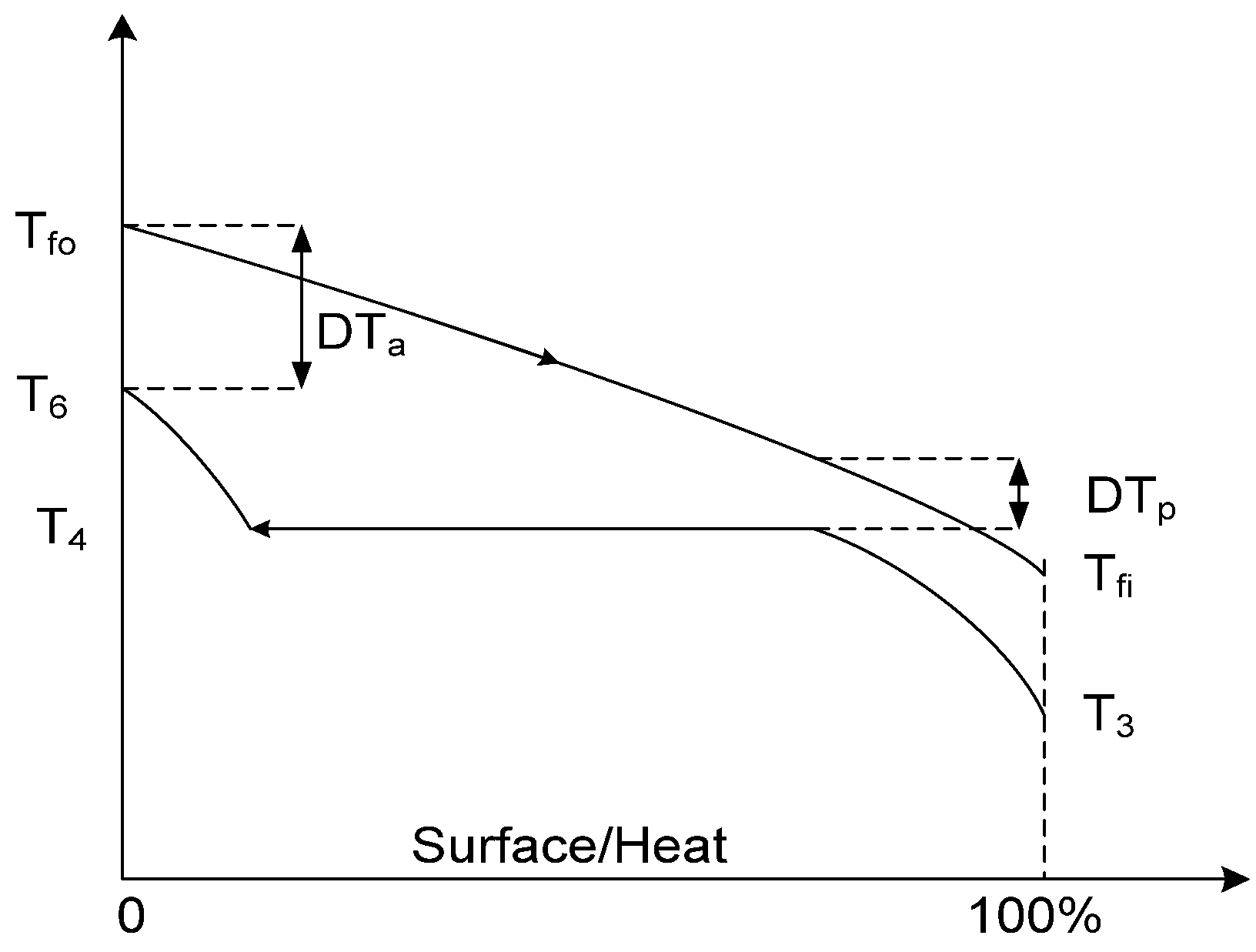
- The pinch temperature difference in the steam generator.
- -
- The operating pressure of the MFH, which in turn determines the saturated liquid conditions at its outlet.

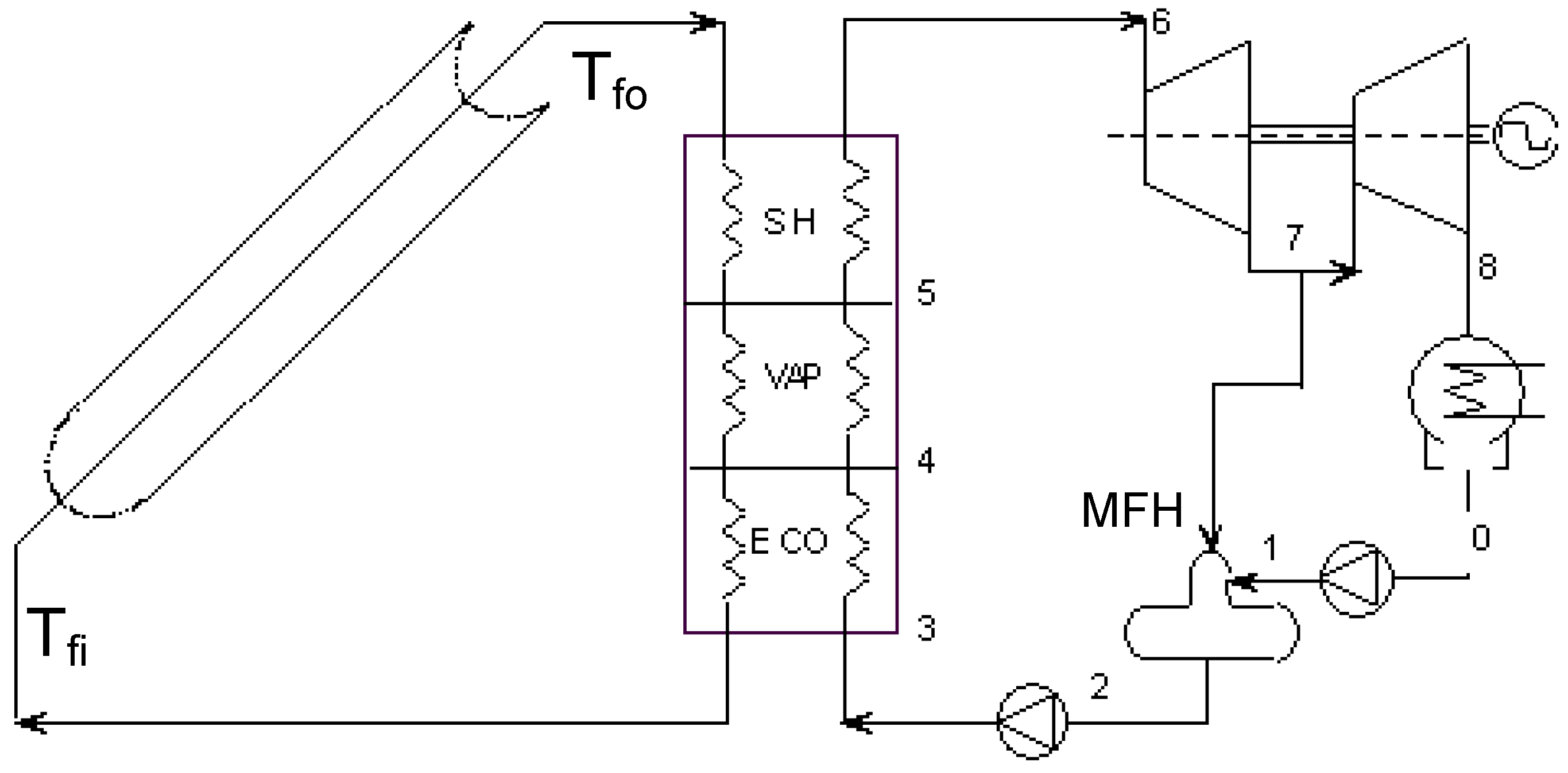
2.3. Case 3—Solar Collector Design (Thermal Utilization/Heat Transfer; Design)
Exergy analysis of solar collectors—calculation model
- To determine the quality of collected heat, on the basis of its temperature, in order to somehow merge the two main performance parameters of solar collectors: efficiency and temperature rise of the fluid;
- To assess the main sources of collector exergy destructions and losses and their amount, which is closely related to temperature levels of the fluid and of the environment (the latter is the reference restricted dead state);
- To keep the exergy consumption of the pump (mechanical work) in consideration when the collector thermal performance is determined. This can be of great help in collector design because it could suggest, for example, to limit some design parameters (diameters of tube, roughness, piping layout, etc.) that lead to high values of pressure losses, and consequently, to high energy consumption of the pump.
- Exergy from the sun with sun temperature defined as the 75% of the sun considered as a black body, in agreement with [20]: , Ta is the environmental reference temperature. I is the overall radiation (beam + diffused) per unit surface and AC is the collector surface area.
- Work Exergy from the circulating pump (Wpump):
- a)
- Exergy loss due to incomplete absorption of the incident radiation coming from sun (a fraction is reflected by the cover—in case of glazed collectors—and the transmitted fraction is not completely absorbed by the plate). Thus, the loss is given by the difference between incident and actually absorbed radiation (S):
- b)
- Exergy loss due to heat dispersed to the environment:
- c)
- Exergy destruction due to the temperature difference between the sun and the absorber plate:
- d)
- Exergy destruction due to the temperature difference between the absorber plate and the fluid:where Tml is the log-mean inlet—outlet fluid temperature difference:
- e)
- Exergy destruction due to pump work, whose only purpose is to ensure fluid motion against the piping head losses, with no additional useful effect:
- f)
- The collector friction loss is the sum of distributed and lumped losses; these last are due to curves, corners, etc. and are globally evaluated as . The coefficient 2 accounts for a T connection (or a 90° curve) at inlet and one at outlet. Thus, the complete expression of the friction loss—which must be compensated by direct pump work, equivalent to exergy; with a compensation for pump efficiency—is given by:ηpump (here assumed 0.6) is the overall pump efficiency (including fluid dynamics and electrical engine efficiency).
Exergy efficiency curves of solar collectors
- 1)
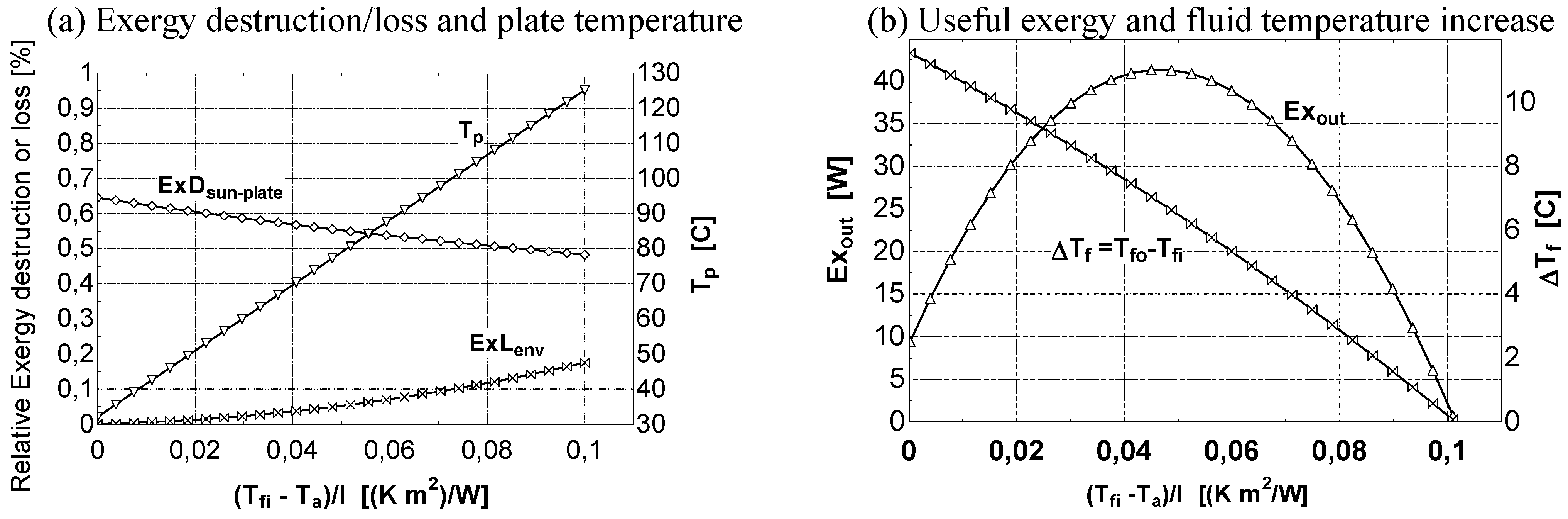
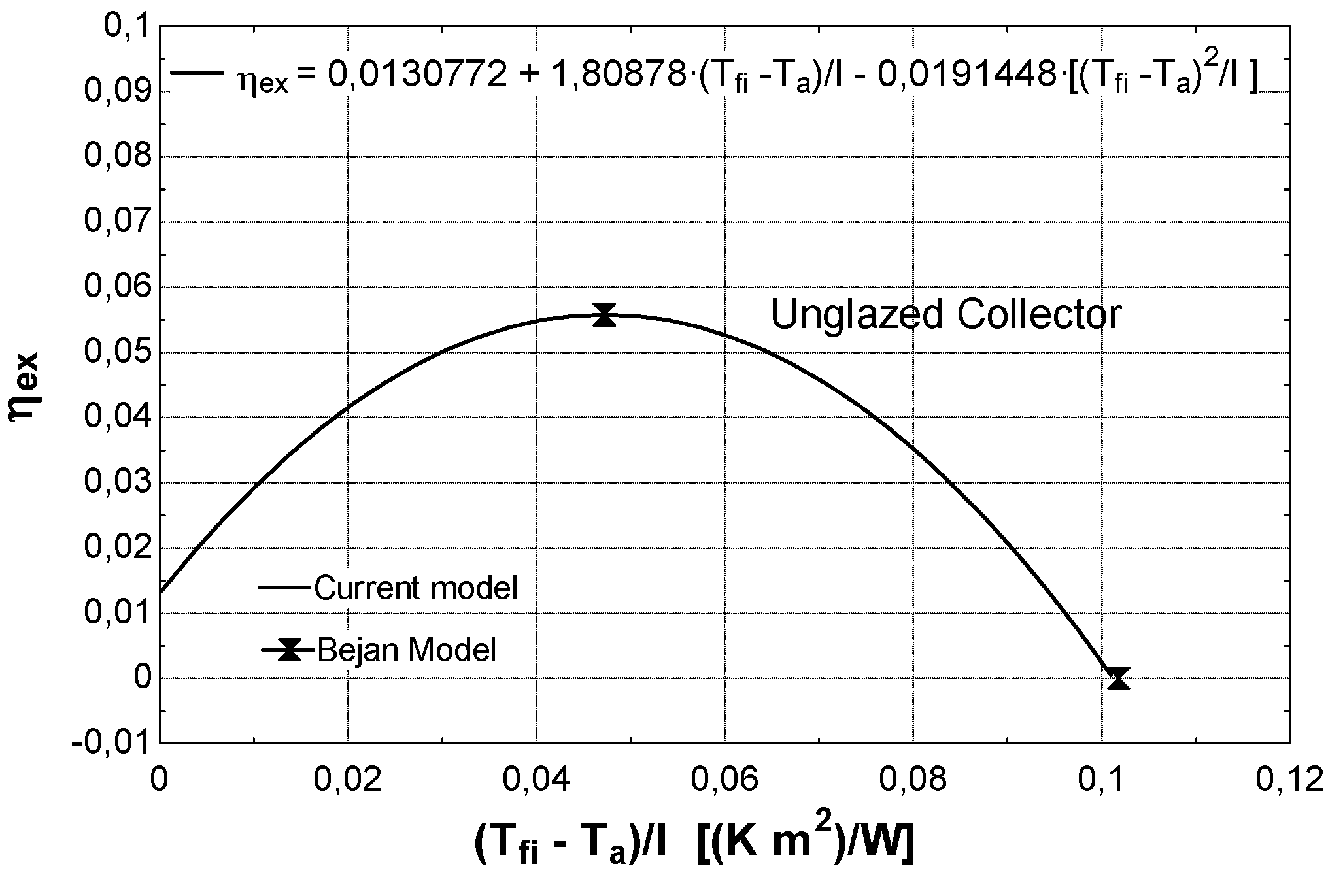
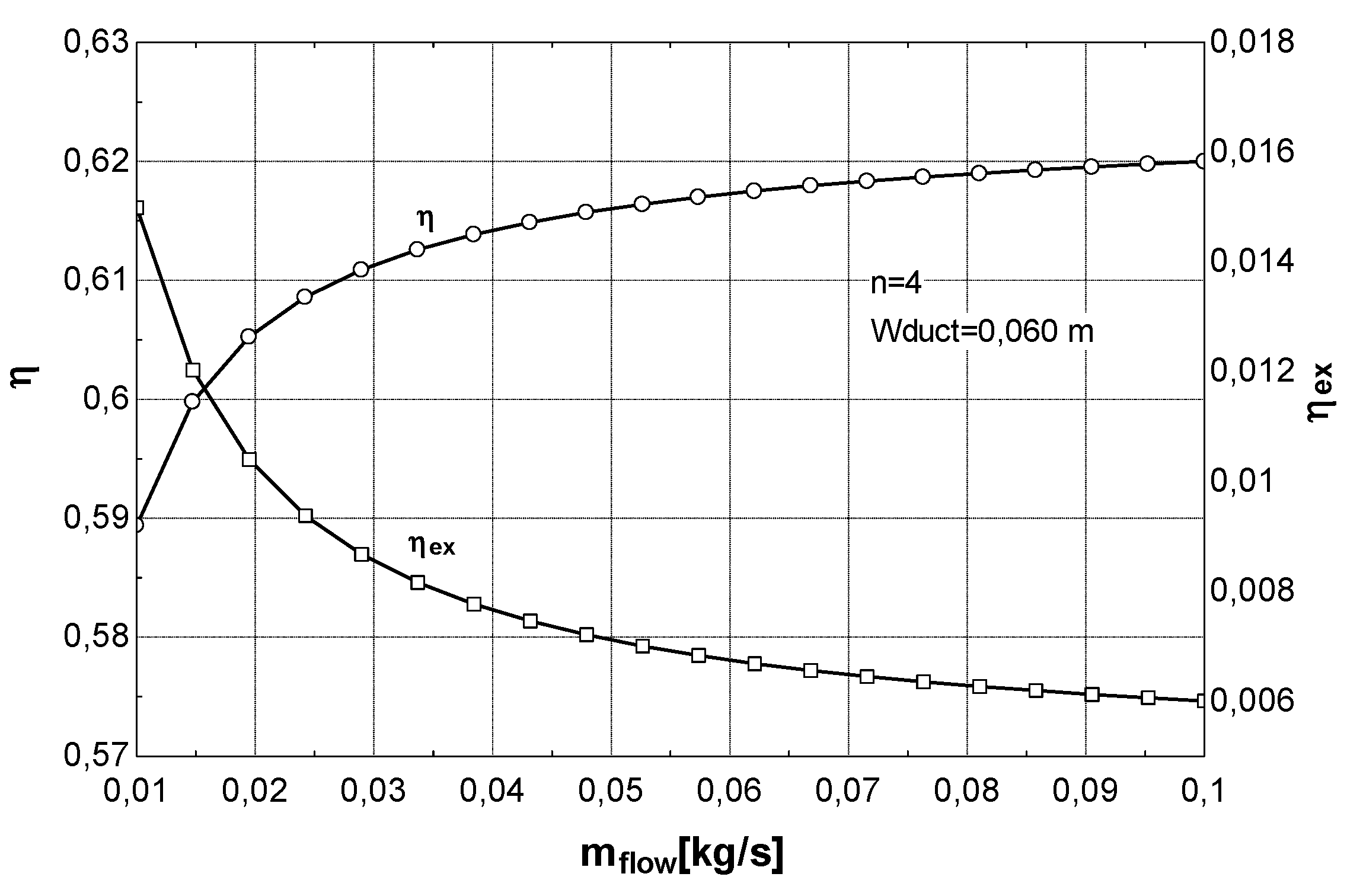
- at low values of the fluid inlet temperature Tfi, the thermal efficiency reaches its maximum value (Figure 8b). On the contrary, exergy efficiency (Figure 8a) is low because the fluid and plate temperatures (very close each other) are small. A consistent fraction of the original sun radiation exergy is destroyed because of heat degradation the absorber plate temperature level, while the loss to the environment is marginal (Figure 9a).
- 2)
- 3)
- at intermediate values of temperature Tfi, the collector exergy efficiency shows an optimizing value (Figure 8a); this happens both for the un-glazed and glazed cases, corresponding to about 60–70 °C for the first one and 70–80 °C for the second one.
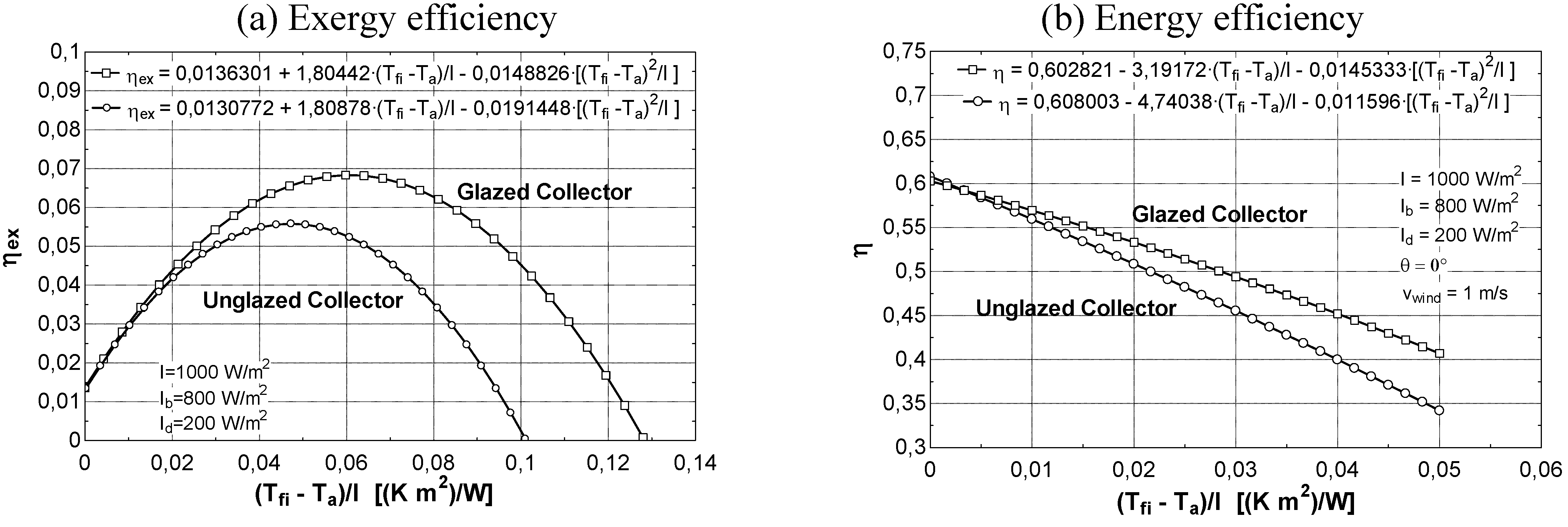
- 1)
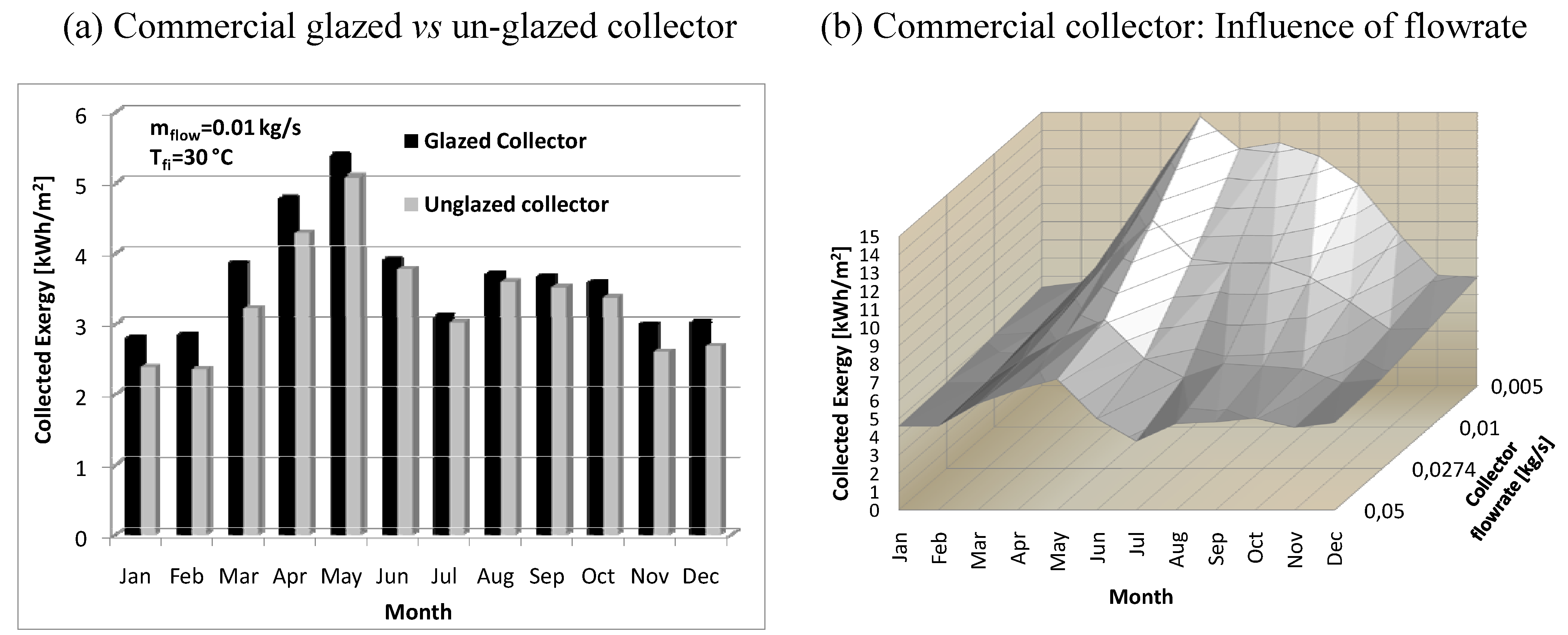
- in winter the fluid temperature rise across the collector is modest, consequently the exergy collected is reduced.
- 2)
- in summer, in spite of larger temperature rise, the higher environmental temperature (representing the reference state) is responsible for reduced exergy performance.
3. Reactive Systems
3.1. Case 4—Fuel Cell/Gas Turbine Integration—Reforming of Methanol
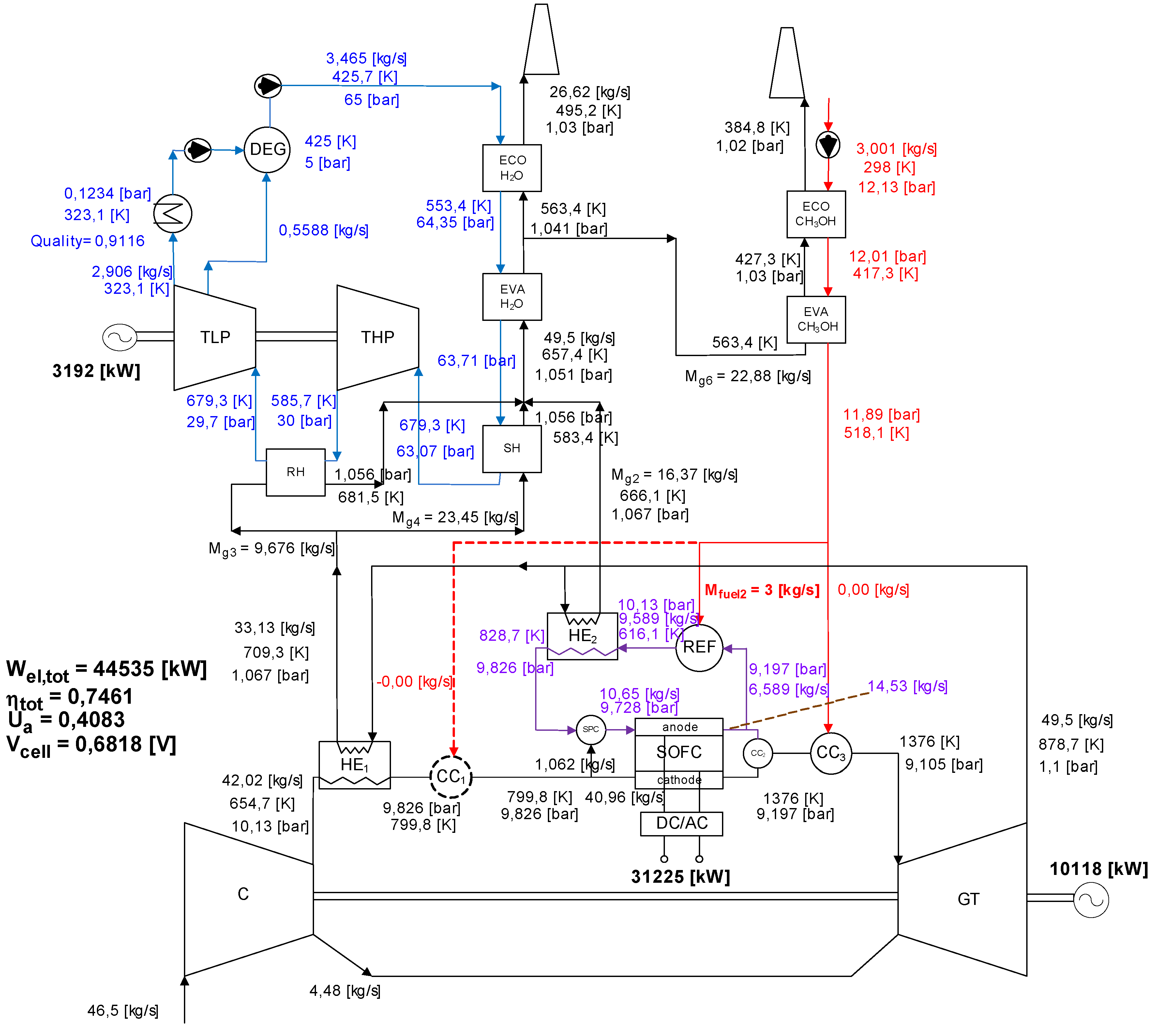
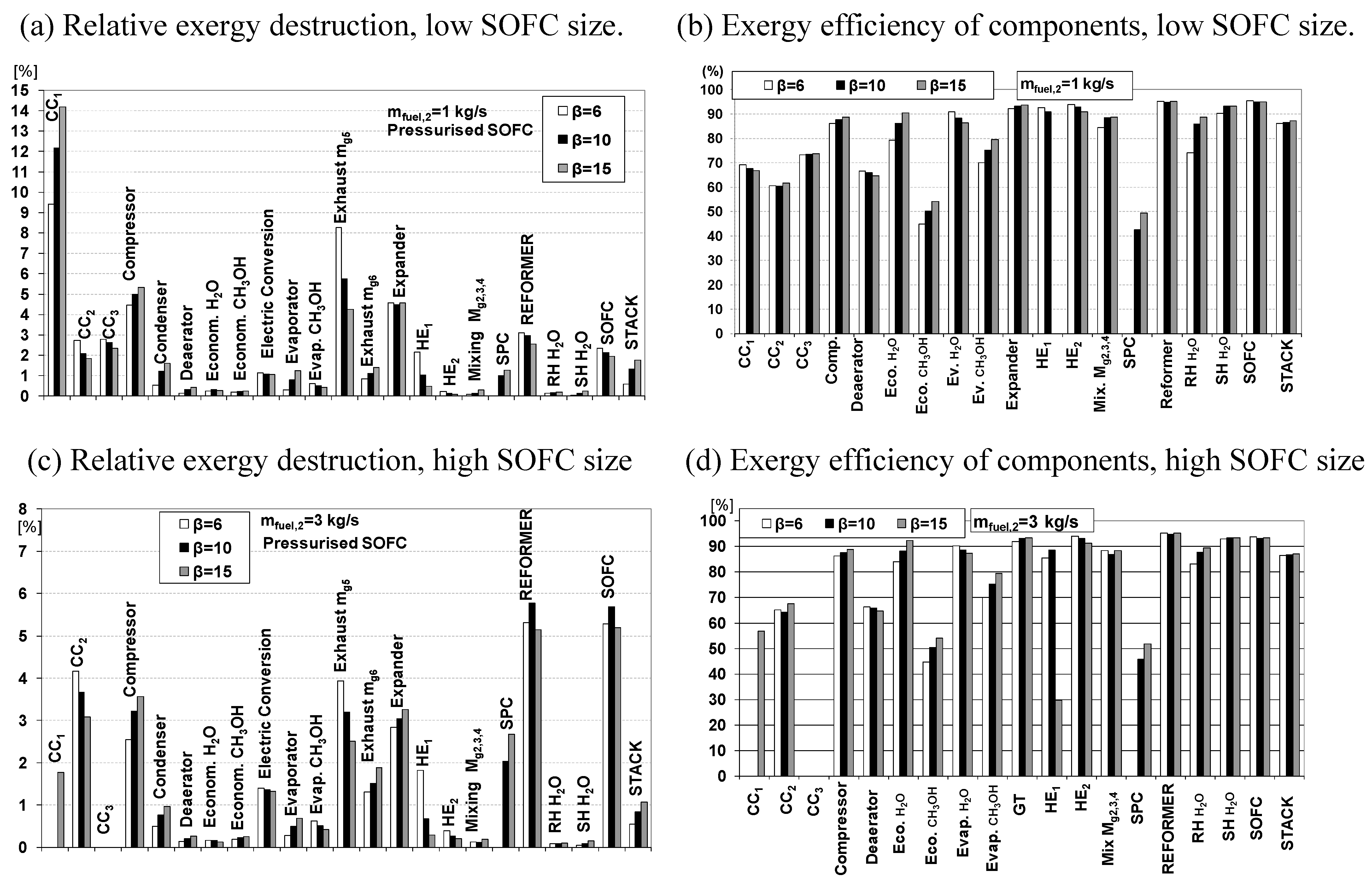
3.2. Exergy Analysis of SOFC-GTCC-A (Pressurized SOFC).
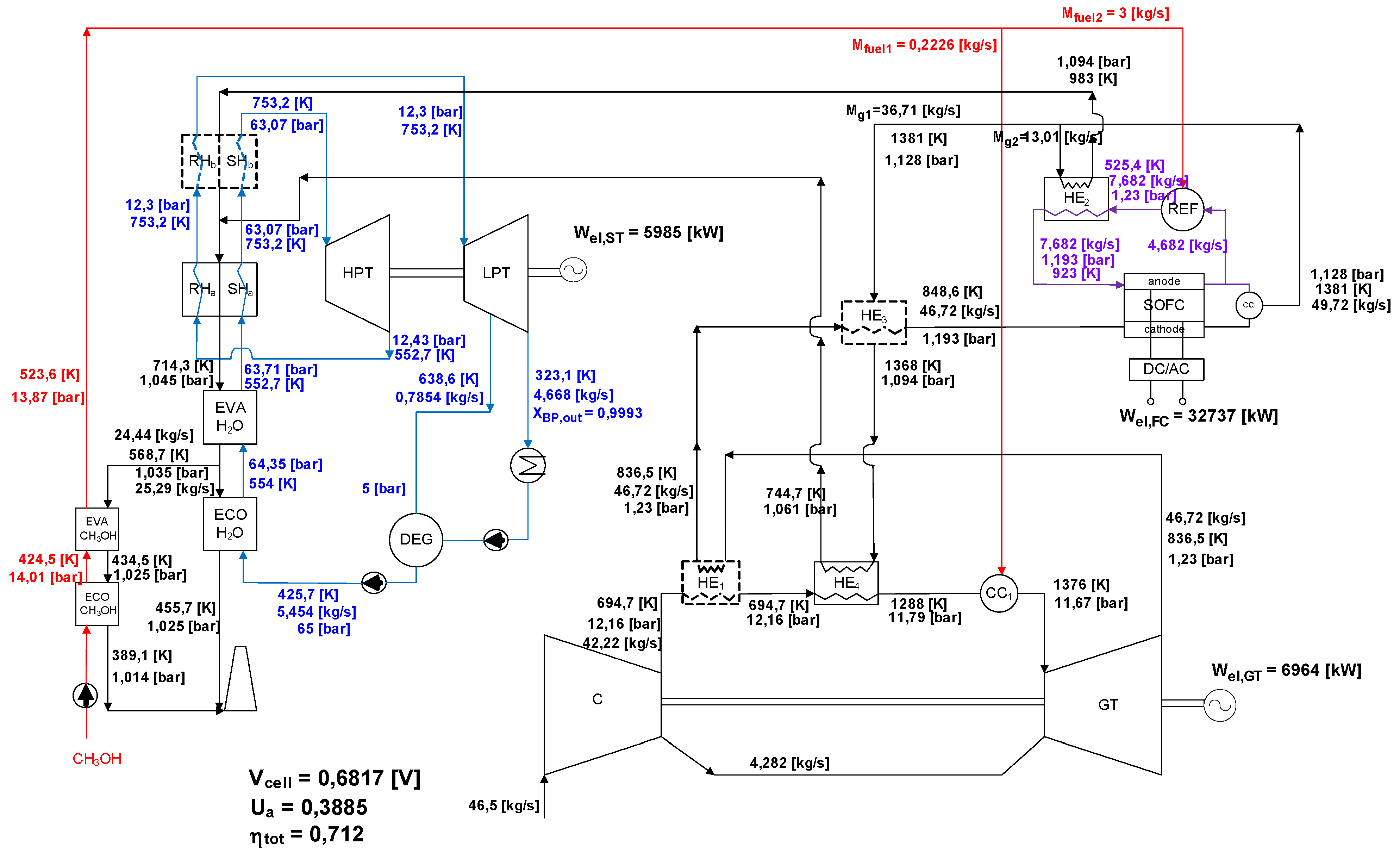
3.3. Exergy Analysis of SOFC-GTCC-B (Atmospheric SOFC)
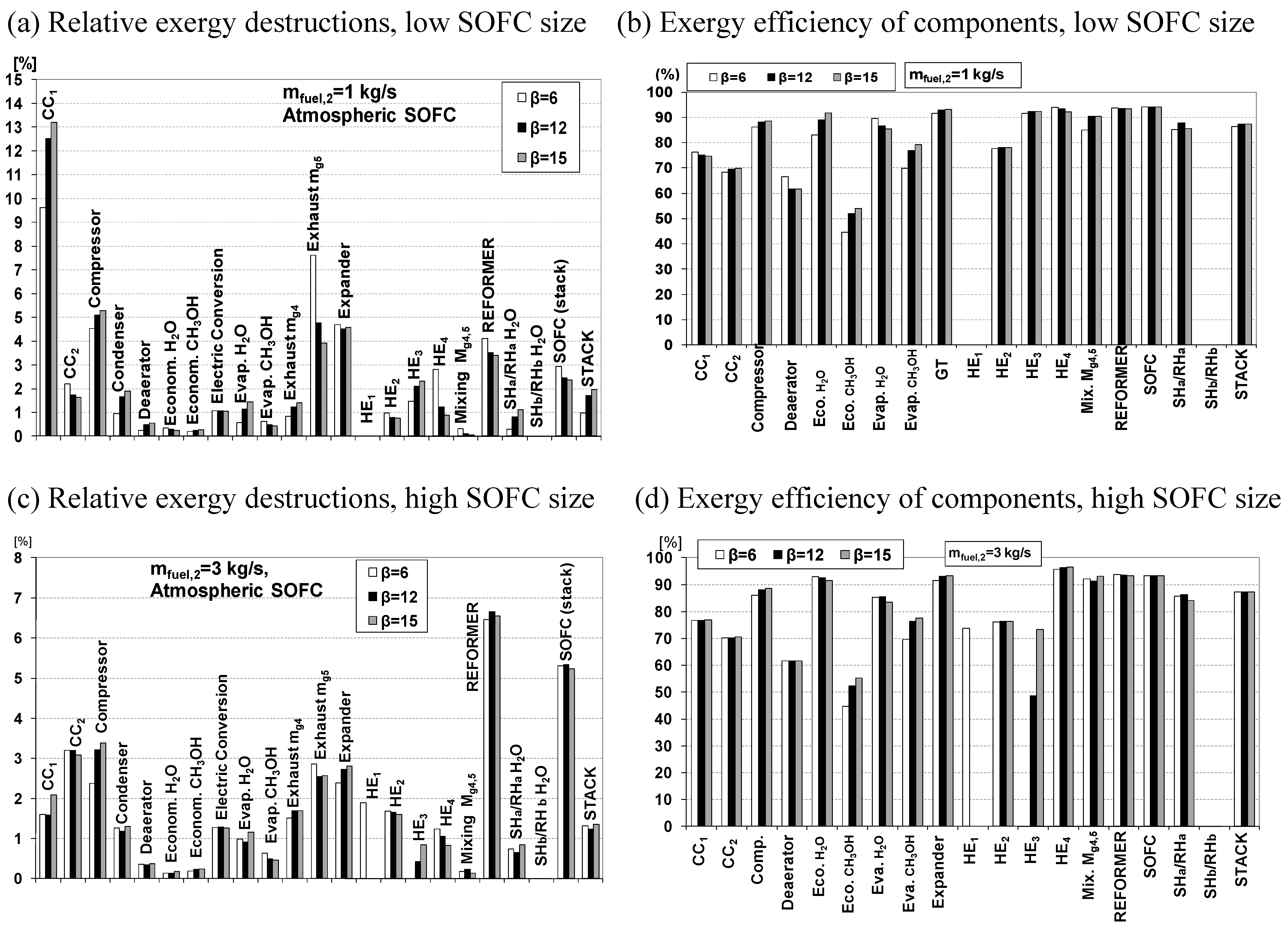
4. Conclusions
Nomenclature
| ηex,dir | Direct expression of collector exergy efficiency |
| ηex,ind | Indirect expression of collector exergy efficiency |
| ρflow | Flow density [kg/m3] |
| ∆ppcc | circuit lumped head losses [bar] |
| ∆ptot | Overall circuit head losses [bar] |
| ηpump | Efficiency of circulating pump |
| θ | collector tilt angle [°] |
| Ac | Collector surface area [m2] |
Exergy destruction due to the absorber plate – fluid temperature difference [W] | |
Exergy destruction due to the pump work [W] | |
Exergy destruction due to the sun – absorber plate temperature difference [W] | |
Overall exergy input to solar collector [W] | |
Circulation pump exergy inlet [W] | |
Exergy from the sun [W] | |
Exergy loss due to incomplete absorption of the incident radiation [W] | |
Exergy loss due to heat lost to the environment [W] | |
Overall exergy losses and destructions [W] | |
useful exergy extracted from the collector [W] | |
| I | Overall incident solar radiation per square meter [W/m2] |
| Ib | Beam incident solar radiation per square meter [W/m2] |
| Id | Diffused incident solar radiation per square meter [W/m2] |
| mflow | Water mass flowrate [kg/s] |
| Qu | Useful heat extracted by the working fluid [W] |
| S | Solar radiation actually absorbed by the collector [W/m2] |
| Ta | Environmental temperature [C] |
| Tfi | collector inlet temperature [C] |
| Tfo | collector outlet temperature [C] |
| Tml | Log-mean inlet—outlet fluid temperature difference [K] |
| Tp | Collector plate temperature [C] |
| Tsun | Sun temperature [K] |
| Utot | Overall plate—environment heat transfer coefficient |
| vflow | Flow velocity [m/s] |
| vwind | Wind velocity [m/s] |
| Wpump | Pump work [W] |
References
- Bejan, A.; Tsatsaronis, G.; Moran, M. Thermal Design and Optimization; Wiley Interscience: New York, NY, USA, 1996. [Google Scholar]
- Kotas, T.J. The Exergy Method of Thermal Plant Analysis; Krieger: New York, NY, USA, 1995. [Google Scholar]
- Szargut, J.; Morris, D.R.; Stewart, F.R. Exergy Analysis of Thermal, Chemical and Metallurgical Processes; Hemisphere: New York, NY, USA, 1988. [Google Scholar]
- Moran, M. Availability Analysis: A Guide to Efficient Energy Usage; Prentice-Hall: Upper Saddle River, NJ, USA, 1982. [Google Scholar]
- Ahern, J.E. The Exergy Method of Energy System Analysis; Wiley: New York, NY, USA, 1980. [Google Scholar]
- Kotas, T.J. The Exergy Method of Thermal Plant Analysis, Reprint ed.; Krieger: Malabar, FL, USA, 1995. [Google Scholar]
- F-Chart Software. Available online: http://www.fchart.com/ees/ees.shtml (accessed on December 31, 2009).
- Odeh, S.D. Unified model of solar thermal electric generation systems. Renewable Energy 2003, 28, 755–767. [Google Scholar] [CrossRef]
- Mills, D. Advances in solar thermal electricity technology. Sol. Energy 2004, 76, 19–31. [Google Scholar] [CrossRef]
- Camacho, E.; Berenguel, M.; Rubio, F.R. Advanced Control of Solar Plants; Springer-Verlag: London, UK, 1997. [Google Scholar]
- Duffie, J.A.; Beckman, W.A. Solar Energy Thermal Processes; Wiley: New York, NY, USA, 1984. [Google Scholar]
- Therminol. Heat Transfer Fluids by Solutia. Available online: http://www.therminol.com (accessed on 31 December, 2009).
- Manfrida, G.; Kawambwa, S. A two-phase solar collector powering a rankine organic cycle. In Presented at World Renewable Energy Congress, Reading, UK, September 1990.
- ARCHIMEDE—ENEA Grande Progetto Solare Termodinamico. Available online: http://www.enea.it/com/solar/index.html (accessed on 31 December, 2009).
- Valenzuela, M.; Zarza, E.; Berenguel, M.; Camacho, E.F. Control concepts for direct steam generation in parabolic troughs. Sol. Energy 2005, 78, 301–311. [Google Scholar] [CrossRef]
- Manfrida, G. The choice of the optimal working point for solar collectors. Sol. Energy 1985, 34, 6. [Google Scholar] [CrossRef]
- Manfrida, G.; Kawambwa, S. Exergy control for a flat-plate collector/Rankine cycle solar power system. J. Sol. Energy Eng. 1991, 113, 89–93. [Google Scholar] [CrossRef]
- Schuster, A.; Karellas, S; Kakaras, E.; Spliethoff, H. Energetic and economic investigation of Organic Rankine Cycle applications. Appl. Therm. Eng. 2009, 29, 8–9, 1809–1817. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Through Heat and Fluid Flow; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Farahat, S.; Sarhaddi, F.; Ajam, F. Exergetic optimization of flat plate solar collector. Renewable Energy 2008, 34, 1169–1174. [Google Scholar] [CrossRef]
- Baldini, A.; Manfrida, G.; Tempesti, D. Model of a solar collector/storage system for industrial thermal applications. In ECOS Conference, Krakow, Poland, June 2008.
- Fiaschi, D.; Manfrida, G.; Anselmi, S. Performance analysis and comparison of hybrid SOFC-GT cycles fuelled with methanol. In ASME paper IGTI Turbo GT2008-51367, Berlin, Germany, June 2008.
© 2010 by the authors. Licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Fiaschi, D.; Manfrida, G. Improvement of Energy Conversion/Utilization by Exergy Analysis: Selected Cases for Non-Reactive and Reactive Systems. Entropy 2010, 12, 243-261. https://doi.org/10.3390/e12020243
Fiaschi D, Manfrida G. Improvement of Energy Conversion/Utilization by Exergy Analysis: Selected Cases for Non-Reactive and Reactive Systems. Entropy. 2010; 12(2):243-261. https://doi.org/10.3390/e12020243
Chicago/Turabian StyleFiaschi, Daniele, and Giampaolo Manfrida. 2010. "Improvement of Energy Conversion/Utilization by Exergy Analysis: Selected Cases for Non-Reactive and Reactive Systems" Entropy 12, no. 2: 243-261. https://doi.org/10.3390/e12020243
APA StyleFiaschi, D., & Manfrida, G. (2010). Improvement of Energy Conversion/Utilization by Exergy Analysis: Selected Cases for Non-Reactive and Reactive Systems. Entropy, 12(2), 243-261. https://doi.org/10.3390/e12020243





