Abstract
In the biosemiotic literature there is a tension between the naturalistic reference to biological processes and the category of ‘meaning’ which is central in the concept of semiosis. A crucial term bridging the two dimensions is ‘information’. I argue that the tension can be resolved if we reconsider the relation between information and entropy and downgrade the conceptual centrality of Shannon information in the standard approach to entropy and information. Entropy comes into full play if semiosis is seen as a physical process involving causal interactions between physical systems with functions. Functions emerge from evolutionary processes, as conceived in recent philosophical contributions to teleosemantics. In this context, causal interactions can be interpreted in a dual mode, namely as standard causation and as an observation. Thus, a function appears to be the interpretant in the Peircian triadic notion of the sign. Recognizing this duality, the Gibbs/Jaynes notion of entropy is added to the picture, which shares an essential conceptual feature with the notion of function: Both concepts are part of a physicalist ontology, but are observer relative at the same time. Thus, it is possible to give an account of semiosis within the entropy framework without limiting the notion of entropy to the Shannon measure, but taking full account of the thermodynamic definition. A central feature of this approach is the conceptual linkage between the evolution of functions and maximum entropy production. I show how we can conceive of the semiosphere as a fundamental physical phenomenon. Following an early contribution by Hayek, in conclusion I argue that the category of ‘meaning’ supervenes on nested functions in semiosis, and has a function itself, namely to enable functional self-reference, which otherwise mainfests functional break-down because of standard set-theoretic paradoxes.
Even at the purely phenomenological level, entropy is an anthropomorphic concept.E.T. Jaynes
1. Introduction
1.1. Signs are physical!
The tension between the thermodynamic account of entropy and the information-theoretic account has been the cause of numerous debates and misunderstandings. This tension overlaps with the great diversity and resulting opaqueness of the uses of the term ‘information’ across and even within the different sciences, which is often caused by the interpretive dualism between the Shannon approach to information and the semantic approach. Since the Shannon approach is formally homologous to entropy, the conceptual relation between entropy and semantic information has received less attention [1]. There is even the opposite conclusion that in the analysis of meaning, Shannon information and hence, entropy, is irrelevant [2]. The topic is of special interest for disciplines such as biosemiotics, in which the relation between semantic functions and biological, that is, physical processes, is scrutinized. So it seems worthwhile to consider the relation between the fundamental process of semiosis (commonly understood as production of meaning through the emergence and transformation of signs) and the concept of entropy in thermodynamics. Such an approach differs from the strand of literature which analyzes the thermodynamics of information processing, in the sense of its entropic costs [3], because I focus on the emergence and evolution of information (and not on processing given information). As I will demonstrate, entropy obtains a central position in the entire theoretical construct if we realize that semiosis is also a physical process, in the sense that the production and consumption of signs relates with energetic flows through populations of sign users, and that, for this reason, semiosis is part and parcel of the general process of evolution under physical constraints [4]. More than that, all signs are themselves states of matterenergy. That is, I maintain the famous statement: information is physical [5,6,7], but at the same time I argue that the homology between entropy and Shannon information is insufficient to understand the relation between semiosis and entropy.
To get this point clear, I need to do an exercise in ontology, in the sense of a science based ontology à la Bunge [8]. I take the famous Schrödinger [9] proposition as a starting point, namely defining life as a process that feeds on energy throughputs and continuously reproduces states of low entropy by exporting high entropy into the environment. I argue that something is missing in this picture, which is the role of information to realize that transformation, hereby following Corning [10], amongst others [11,12]. If we take information as physical, we end up with a triadic structure, instead of the simple system-environment dualism. This is analogous to the Peircian transition from a dualistic sign-object relation to the triadic sign (vehicle)-object-interpretant relation [13]. Making this comparison, it springs to the eye that the interpretant is crucial. I present a physical, or, more general, naturalistic account of the interpretant, which follows some ideas already ventilated in the biosemiotics literature, e.g., [14,15]. This I achieve by equating the interpretant with a function. I argue that physical systems with functions differ fundamentally from physical systems without functions, and that this allows to relate the Peircian notion of a sign with the notion of entropy, because the production and consumption of signs is a physical causal process that essentially involves energy flows and changes in entropy. From this follows a radical step in the interpretation of entropy: I translate the Jaynes’ [16] ‘anthropomorphic’ concept of entropy, hence an observer relative magnitude in the sense of Searle’s [17], into a function relative magnitude. This feeds back onto the interpretation of semiosis: I equate the Peircian interpretant with an evolved function, and the relation between sign vehicle and object as Peircian abduction, now formally specified as Jaynes’ inference, thus naturalizing semiosis. This builds the conceptual integration of semiosis and entropy, transcending the Shannon approach. The path to this view has been already laid by Salthe [18], who presented the idea that, in principle, the notion of the observer can be extended beyond human systems to achieve a generalization of Peircian semiosis. If we naturalize Peircian semiosis, the important consequence is that ‘information’ does no longer stand aside the physical processes, as in many conceptualizations, but inheres the structure of signs as physical phenomena.
In doing this, I rely on recent developments in analytical philosophy, especially teleosemantics [19]. Teleosemantics shows how meaning is embedded into functions that emerge evolutionarily. This embeddedness can be understood as a reduction or a relation of supervenience, depending on the particular stance adopted. My argument presents a special solution in showing that meaning emerges from a subset of physical systems with functions, which are self-referential ones, both in the sense of mutually interlocking functions and infinitively nested functions. So, finally, I reconsider the problem of qualia. Many authors have argued that qualia demonstrate the limitations of a purely physical approach to semiosis, in the sense of a wedge driven between physical and mental phenomena. However, if at the same time the concept of semiosis is extend to biology at least, this position comes close to attributing some mental capacities to things, comparable to earlier approaches to vitalism, panpychism and others [20] (certainly one needs to add that this position would correspond to the original Peirce, who maintained a psycho-physical monism which is clearly non-materialist [113]). I offer an alternative view on qualia showing that they are the reflection of paradoxes in self-referential systems which remain physical in ontological terms. This argument has been presented for the first time by Hayek in a much-neglected work [22].
The entire argument is highly abstract. However, it is directly relevant for applying semiotic concepts on human social and economic systems. Therefore, my reconsideration of the role of entropy in the cybersemiotic framework also helps to continue with the Georgescu-Roegen [23] tradition in economics, thereby overcoming its later narrowing down to purely environmental concerns in ecological economics. A sound conceptualization of entropy and information can provide a restatement of the role of entropy in economics, thus contributing to a small, yet vigorous strand in this literature [24,25,26,27].
1.2. Summary of the argument
The paper proceeds as follows. In Section 2, I begin with a brief discussion of the difficulties inhering the notion of ‘biological information,’ which result from a confusion about the flow of causality with the flow of information. These difficulties presage the transition to a Peircian view. Having elucidated the problems with Shannon information in this context, I continue with a discussion of the Jaynes concept of inference, which explicitely recognizes the central role of the observer (the experimenter) in the definition of entropy. This opens the view on the distinction between observer independent and observer relative entropy. In Section 3, I develop these initial thoughts systematically. I start with introducing the notion of ‘function,’ for which the the distinction between observer relativity and observer independence is also crucial. These two features of function alternate, depending on the level of the embedding system that is considered. Thus, I can also further clarify the meaning of these distinctions in the context of Jaynes’ notion of entropy, which corresponds to an earlier distinction by Salthe between internalist and externalist views. It is then straightforward to equate the concept of an observer relative entropy by that of a function relative entropy.
The next step I take is to put the concept of function into an evolutionary context, which means to add the notion of selection, and then to enlarge the notion of causality by the concept of an energy throughput that is necessary to maintain proper functioning. Basically, this means that I apply the general framework of evolutionary epistemology to both functions and observation, thus unifying the two concepts. Accordingly, I argue that the Jaynes concept of inference, hence the Maximum Entropy Principle, can be interpreted ontologically as describing the relation between evolving functions and object systems. In this relation, the function is gradually adapted to the macrolevel constraints on the microlevel states of the object system. In an evolutionary context, this implies that, given these constraints, that the observed system is in an maximum entropy production state. These steps of a naturalization of the Jaynes notion of inference are completed by considering the case when the object system is a function, too. The important conclusion from this is that evolving functions do not represent states of lower entropy, but are actually physical mechanisms of increasing entropy, that is, functional evolution directly corresponds to the Second Law. The physical correlate of this, in the theory of life, is the central role of Lotka’s principle, i.e., the maximization of energy flux in living systems. Thus, evolution can be conceived as a process of increasing observer independent and observer relative entropies, driven by functional differentiation, which reflects the increasing complexity of constraints on object systems. These constraints define the gap between the two entropies, following seminal conceptualizations by Layzer, Brooks and Wiley, and Salthe.
In Section 4 I use this conceptual apparatus to achieve the major goal of this paper, namely, the naturalization of Peircian semiosis. This is straightforward, as I can equate the object with the object system, the sign with the functional effect, and the interpretant with the embedding function. This relation is dynamic, as the interpretant evolves. Hence, Peirce’s notion of abduction easily fits to the Jaynes scheme of inference. I show how the problem of genetic information, by which I introduced the discussion of this paper, can be solved in this reconstruction of the Peircian triangle. The next step in completing the naturalization of semiotics is to define the energetics of signs. One possible approach is Chaisson’s measure of free energy rate density of physical objects, which allows to conceive of the semiosphere as a physical phenomenon. I conclude the section with a sketch of the semiotic version of the anthropic principle, following an argument on evolution that has been presented by Deutsch. This allows for a new view on the Peircian notion of ‘Firstness’.
The paper concludes with a brief consideration of qualia. Following a proposal by Hayek, I argue that qualia are a function that enables self-referential physical systems with functions to solve the paradoxes of self-referentiality, which is favoured by natural selection. This implies that qualia have no separate ontological status as a ‘mental’ category but can be given a systematic place in a naturalistic approach to semiosis.
2. Causality, Information and Entropy
It is a well-acknowledged fact that Shannon’s notion of ‘information’ focuses on the quantitative aspects of data communication and explicitly leaves semantics aside [28]. Following the information revolution instigated by him and others, however, the use of the term ‘information’ across all sciences has obscured this distinction, and, in fact, very often ‘information’ is used in an entirely different sense than in Shannon’s original use. This also impedes a proper understanding of the role of entropy in semiosis, which is the central concern of this paper. In simple terms, focusing on the formal convergence between Shannon entropy and Boltzmann entropy would limit the possible relevance of the thermodynamic notion of entropy to the processes of data processing in the technical sense, which has resulted in a large literature on the energetic costs of computing and on reversible computing [6,20,21,22,23,24,25,26,27,28,29]. This technical notion can be expanded into a universal physical notion, if physical processes themselves are seen as computations [2,31,32,33]. However, this reduction of information on data processing, even on the most elementary level of quantum states [34], cannot establish any relation between entropy and semantic information, i.e., continues to cut off the meaning of the data from the notion of information, even though a complete definition of information will always include meaning into its scope [35]. From this perspective, reservations about Shannon information and its use across the sciences seem justified, which converges with views in the broader biosemiotics literature [36]. But this also defines the challenge: How to establish a conceptual link between semiosis and entropy?
2.1. The missing link between causality and information
The problem is immediately evident if we consider the term ‘biological information’, or, more specifically even, ‘genetic information’ [37,38]. It has become almost a commonplace that biological information is said to be ‘stored’ in the genome. What people have in mind is that all phenotypical properties are somehow projected into this storage of information, if only in the sense of the control information that guides ontogeny (the ‘recipe’ interpretation of the genome). The recent debate over systemic approaches to the genome has shown that this view is very misleading. In the Shannon sense, the information stored in the genome is just that: the relation between the realized sequences of nucleic acid bases and the state space of possible sequences. Evidently, this is not the same as storing an image of the phenotype or even a blueprint or something else. There is no ‘information’ about the phenotype in the genotype at all. If we thought of the relation between genotype and phenotype as a Shannon communication process, the simple fact is that the state spaces of information processed by the sender and the receiver are totally different, which is true even for the very first stages of protein production. This is the ultimate reason why the very notion of the ‘gene’ has proven so intractable in biology, after for decades following the discovery of the DNA researchers had been convinced to be able to dig into the storage of ‘biological information,’ whereas today the sheer complexity of gene interactions, vast regions of junk DNA or the existence of functional hierarchies in the genome render this vision obsolete [39].
That is, if we use the term biological information, in fact, we already talk about the semantics exclusively [40]. This is what the systemic view in biology emphasizes, converging with the biosemiotics approach [106]: The genome needs to be interpreted by a complex system of cells undergoing reproduction, so that, if at all, the unit that carries biological information, is at least the cell, if not far beyond [42,43]. What we call biological information is constructed in the process of development. This directly also affects the Shannon interpretation of this information: As a pure measure of the quantity of information, because of the entirely different state spaces in different stages of ontogeny, the quantity of information in the phenotype is vastly larger than the quantity of information in the genotype. This quantity also changes in the life cycle of an organism [18]. The linkage between the two is created by a physical process, which is development. Development is a causal process linking genotype and phenotype.
Why does it happen that the confusion about the term biological information is so widespread, even inducing foundational debates in the biological and social sciences about genetic reductionism and related issues? The reason lies in the confusion between the causal process and the information flow. Once the causal sequences in ontogeny had been discovered, and so the causal priority of the processes related to the chromosomes had been realized, it was a quick step to infer the informational sequence from the causal sequence. Ontogeny as a causal process seemed to suggest that the flow of information goes into the same direction, again, in the Shannon sense, hence equating the causality with a flow of messages.
This confusion between causal and informational processes is flawed. There is no direct relation whatsoever between causality and information transmitted. This is straightforward to realize if we compare a scenario of multiple possible causes of an event with a scenario of multiple events related to a single cause. In both cases, there is even deterministic causation. Yet, observing the event transmits entirely different amounts of information, in the Shannon sense. This clarification, due to Dretske [44], should be accompanied by a second point made by Dretske, namely that meaning is entirely unrelated to information. This should be obvious from our use of everyday language: We can use lexically identical sentences to transfer vastly different information, depending on context.
To hammer down this point conclusively, the lack of congruence between causality and information even affects foundational issues in quantum physics: In an experiment with a photon source and a beam splitter, tilted at 45° to the beam, a detector behind the beam will register photons with a probability of one half. However, an observer who observes the detector will not conclude that the photon was emitted with a probability of one half by the source, but with certainty, which, however contradicts the reverse application of the quantum rules, which would, again, result into one-half probability [45]. This is the most straightforward demonstration why quantum uncertainty does not directly affect the so-called ‘classical world’: It does not necessarily translate into information uncertainty, depending on the way how different systems, involving an relation of observation, are coupled. The deepest reason for this is that causality and information flow in opposite directions.
This preliminary discussion has shown that widespread notions of how information is seen to be stored in some source and then transmitted to a sender may be absolutely appropriate if the pure process of communication is considered, as Shannon originally did, but are misplaced for the very notion of information proper. Information rests in the coupling of at least two systems, which is a precondition for communication. Against the background of the discussion of the biological example, the notion of information that is the broadest one matching this idea is that of ‘environmental information’ [28,44], which is an observer-independent notion in the first place: Two systems a and b are causally coupled in a way so that, if system a is in state F, system b is in state G, which implies that state G carries information about state F. This notion of information is independent from the existence of a sender and a receiver, yet, the actualization of the information depends on a third system that is coupled with those two systems, and which infers F from G, which is a movement in the reverse direction than the causality. Normally, this is where the observer comes into play again, who interprets the causal coupling in terms of an inference. So we can reach the important conclusion that the most general notion of information already points towards the more complete picture of semiosis. This is what I wish to explore in more detail.
2.2. Inference and the Jaynes notion of entropy
The previous discussion is immediately relevant for the relation between information and entropy. It is the purely formal congruence between the Shannon and the Boltzmann definitions of entropy which had suggested the equation between the two. However, as the underlying formula only relates to a single system, and does nor refer to a coupling of systems, already for that reason, and not for the more complex issue of semantics, this conceptual equation must be wrong. Interestingly, the most general definition of information that is implied by the notion of environmental information refers to a concept that has also a central place in the physical debate over the concept of entropy. This is the notion of inference. Environmental information is information that can be activated by an inference that relates to the underlying causal process [44]. So, in the example of the genotype/phenotype distinction, it is the phenotype that carries information about the genotype, because we could imagine to infer certain properties of the genotype from the phenotype, given our observation about the underlying causality. This statement reveals why the notion of the genotype carrying information about the phenotype is wrong, and this precisely with the context of the Neo-Darwinian paradigm including the Weisman doctrine: The genotype does not carry information about the phenotype just because there is no reverse causality from phenotype to genotype. If we start out from the genotype, and try to reconstruct the information that is supposed to flow to the phenotype, we face the problem of the arbitrary assignment between source and channel in information theory, i.e., the so-called ‘parity thesis’ [38]: Thus, we can see the environment as a channel through which the (hypothesized) information of the genotype as a source flows, or we can see the genotype as the channel through which the (hypothesized) information carried by the environment flows. This reflects the fact that information only resides in the entire causal chain, and that only the phenotype can be regarded as a sign that points towards that information. This is where inference comes into play.
The role of inference in the observer relative notion of information allows to rethink the analogy between Shannon information and entropy. This is because in the physics discussion of entropy, inference also plays a central role. Following Gibbs, Jaynes [46] had shown that entropy always refers to a state of ignorance about a physical system. However, his approach is entirely different from the Shannon approach, which only superficially corresponds to the Boltzmann notion. Jaynes argued that entropy is a measure of the degree of uncertainty related to the number of possible microstates that corresponds to an observable macrostate. This uncertainty can be interpreted in two senses. One is the sense that an observer is ignorant about the realized microstate, given the knowledge about the macrostate. The other is the degree of control that an experimenter has about the microstate if he is only able to manipulate the macrostate. That is, the Gibbs/Jaynes version puts the relation between micro- and macrostate into the center, whereas the Boltzmann/Shannon version only concentrates on the microstates, relegating the macrostates to the purely epiphenomenal realm. Consequently, there is a fundamental difference between the two approaches, if we consider entropy as a measurable quantity. In the Gibbs/Jaynes version, the measure of the entropy of a physical system depends on the degrees of freedom of the macrostate. These degrees of freedom, however, are not a physical given, but they depend on the experimental setting chosen by the observer. Hence, entropy appears to be an observer relative term also on the macro level. In the Boltzmann/Shannon version, observer relativity only inheres the definition of the state space, implicitely. In a reductionist statistical mechanics setting, this state space would appear to be observer independent because it it can be reduced to the 6N dimensions of particles; in the Shannon setting, the state space becomes a contingent reference frame between sender and receiver. Thus, only the Gibbs/Jaynes notion establishes a direct linkage between this fundamental definition of the state space and entropy as a macro phenomenon, hence in the sense of phenomenological thermodynamics [47].
From this brief discussion we can deduce an interesting question. How far can we relate the inferential relation that underlies the notion of environmental information with the inferential relation that underlies Jaynes’ conception of entropy? On first sight, this is straightforward. We just think of a physical system which can be described in two different ways, namely as ‘system a’ and ‘system b’ (see Figure 1). System a is described in terms of the microstates of statistical mechanics, hence manifesting microstates F1,…,n; system b is described according to a chosen system of degrees of freedom of the macrostate, hence having macrostates G1,…,m. The two systems are ontologically identical, but there is a large number of ways how the states Gm can be causally reduced to states Fn. One has to be careful here with using the notion of causality. Most physicists would tend to deny that phenomenological properties are caused by the microstates, thus thinking in fully reductionist terms, which was also the Boltzmann perspective, thinking in terms of mechanics and atomism (for a dissenting view in physics, see [48]). From the philosophical perspective [49], however, causation, beyond the many details and controversies of the pertinent debates, just refers to a particular relation between two events, such as, in our case, certain microstates and a measurement on the macrolevel that establishes correlated macro-properties. Especially, and fitting into the Jaynes picture, causality has been related with agentive manipulability, which corresponds to the experimental setting normally imagined by physicists [50]. From that perspective, we can say that heating a liquid causes an increase of the kinetic energy of the molecules, which in turn causes an increase of the temperature.
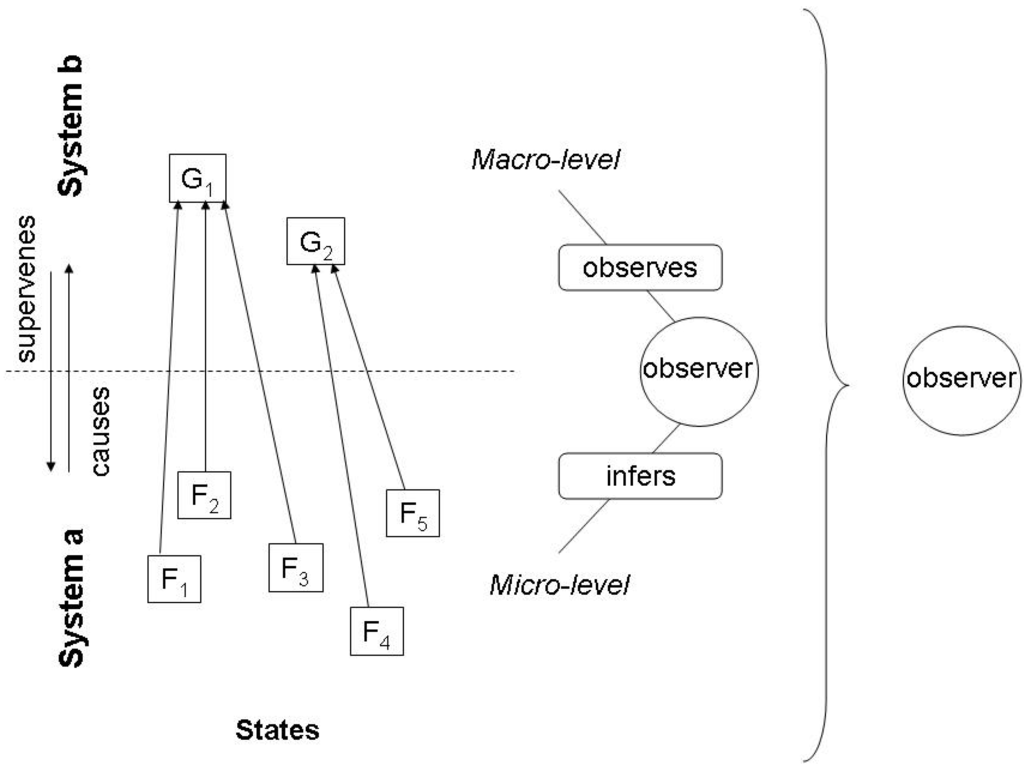
Figure 1.
Observer and system in the Jaynes approach to entropy.
The information that G carries about F depends on the specific causality that underlies that relation, and this in turn varies with the state space of G, not F. This corresponds to Jaynes’ notion of entropy: The less certain the information G carries about F, the higher the degree of entropy in the corresponding micro-system. To be exact, Jaynes argues that for this reason the entropy of the system a is not a physical given, but obtains different magnitudes relative to the specific process of inference. But we can also say that this endogeneity, i.e., observer relativity of the entropy of system a means that the coupled systems can have different entropies, depending on the nature of the underlying causal process of coupling (Jaynes gives the example of a crystal, which can be put into different experimental settings, one with choosing temperature, pressure and volume as macrostates, another with temperature, strain and electric polarization etc.).
The complexity that goes with this reconstruction springs to the eye if we consider the aforementioned critique that properties Gm are not caused by properties Fn but are mere conceptual correlates on the macro-level of causal processes that exclusively work on the micro-level. This corresponds to the Weismann doctrine with reference to the phenotype: The phenotype is merely a correlate of the genotype, there is no reverse causality, and therefore the phenotype is ephemeral to the evolutionary dynamics. Indeed, the formal structure of molecular Darwinism is just a case of applied statistical mechanics. Yet, the biological criticism of the notion of biological information, as commonly reduced to the genotype, exactly fits into the Jaynes notion of entropy. This cannot be invalidated by the lack of reverse causation. Just the other way round: because there is unidirectional causality, or unidirectional determination of the correlation, information only inheres the inferential relation between G and F, as between the phenotype and the genotype. This means that the causal relation between system a and system b cannot be denied just by ontologically conflating the two as identical. From the philosophical standpoint, systems b and a stand in a relation of supervenience to each other, similar to the relation between mind and neuronal system, for example [51]. This means, the notion of multiple realizability holds for system b with relation to system a: All states of system b correspond to states of system a, but there are many states of system a that relate with the same state of system b; at the same time, if two states of system b differ, the underlying states of system a also differ.
From this follows, that information can only be determined exactly if the relation of observation that underlies the inference from system b to system a is embedded into another observation of higher order. In this case, observer relative entropy translates into observer independent entropy, because the actual determination of the degrees of freedom of system b is a given, from the viewpoint of the higher-order observer, who, for example, wishes to explain the behavior of the experimenter that results from the observation of certain measurements in the experiment.
To summarize, it seems promising to inquire further into the potential of the Jaynes approach to entropy for the analysis of information and semiosis, because for Jaynes, the relation of observation is central for the definition of entropy, and correspondingly, the process of inference. To my knowledge, the existing interpretations of the Jaynes approach all have ‘the physicist’ in mind, when they talk about the observer. Yet, this is by no means a necessary presumption: ‘The physicist’ is a physical process, too, hence only a special case of a much broader class of physical processes.
3. Functions, Evolution and Entropy
I now propose a radical shift of perspective: I generalize over the notion of the observer. In discussions about entropy, reference is mostly made to a human-like observer. This blocks the view on certain foundational aspects, as it happened with the decades long debate over the Maxwell’s demon paradox, where much progress could be chieved in thinking of the ‘demon’ as a physical mechanism [3]. In a naturalistic framework, the human observer is just a a physical system that interacts with the observed physical system, and observation is a physical interaction, too. Actually, the solution to Maxwell’s paradox has built on the recognition of this fact. However, the paradox has only played a significant role in the clarification of the Second Law, but is not involved in the further clarification of the notion of entropy. This is an unexploited theoretical opportunity, because we can think of giving a naturalistic interpretation to the observer relativity of the Gibbs/Jaynes entropy, in the sense that it is necessarily related to a physical relation of observation between physical systems. That would result into the endogenization of observer relative entropy into the physical system constituted by the observer system and the object system. Only for this joint system, hypothetically, an observer independent entropy could be formulated.
3.1. Functions and the subjective/objective distinction
We can distinguish between two forms of causal interaction, and I further specify the physical system that corresponds to the observer system O. This specification states that the system O contains a function. This is the most abstract expression of the intuitive fact that observations go back on a purpose, either intentional, as in the case of the human experimenter, or as a part of a cybernetic feedback mechanism, as in the case of a bacterium. Functions involve observations in the sense that they are selective, that is, a function is triggered by a certain property of the object system with which the relation of observation is constituted. The notion of a function is a most general one that applies for both biological systems and artificial ones [52], therefore includes, in particular, the physical interactions taking place in the context of human experiments.
A function is a special kind of causal process that can be described as having the following general structure [53]:
The function of X is Z means:
- (a)
- X is there because it does Z, and
- (b)
- Z is a consequence (or result) of X’s being there.
For example, the sun emits light which causes the existence of life on earth, but the sun does not have this function. The heart pumps blood, and because it does so, it exists. So the latter physical process has a function. It is important to notice that on this level of generality, functions do not only relate to technological functions (based on design) or physiological functions (a result of evolution), but also to all imaginable kinds of interlocking and embedding functions in larger systems. Thus, in the general conceptual frame, one cannot state in empirically meaningful senses that the prey exists because it feeds a predator, but one can say that the prey exists because it is a part of a larger ecological system, of which both prey and predator are a part. As it is shown in Figure 2a, we can therefore relate Z to another effect Z’, which is part of a larger system into which the relation (a) is embedded.
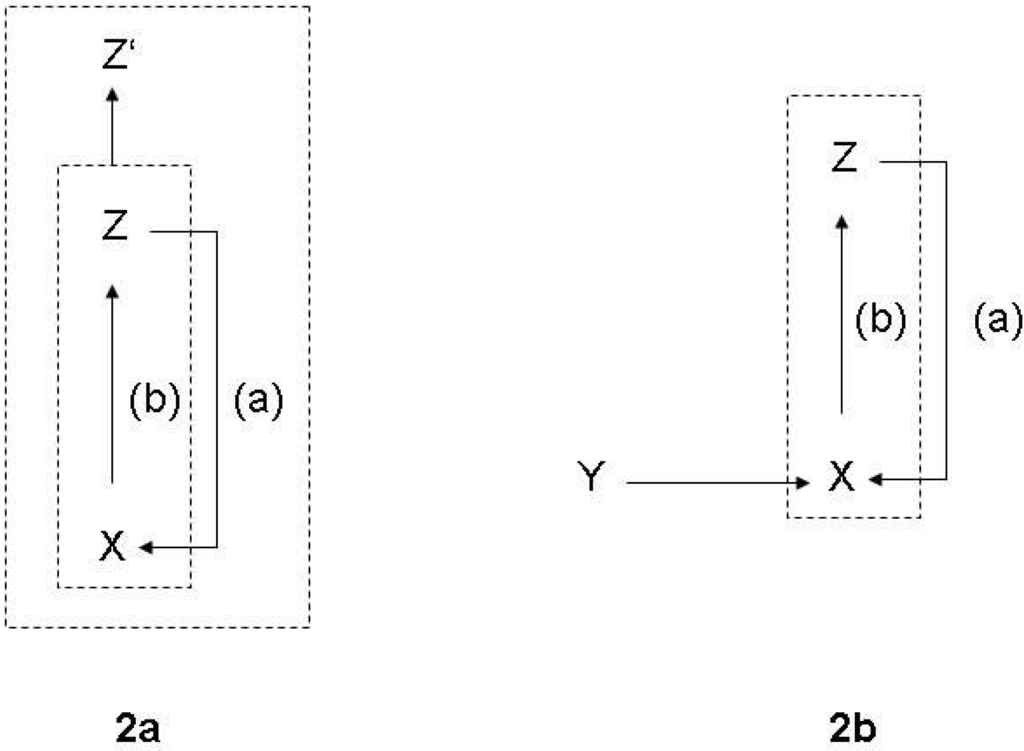
Figure 2.
(a): Elementary form of a function; (b): Autocatalysis.
The most simple function, corresponding to the definition given above, is a symmetric autocatalytic reaction cycle in chemistry [54] (Figure 2b). In this case, (b) describes the original chemical reaction linking up two cycle intermediates X and Z, and (a) describes the autocatalytic effect of the product. Y refers to the raw material of the reaction. Correspondingly, the ontologically primordial example of an embedded function is a an enzyme [15,58]. The enzyme has the function to increase the chemical production in a cell. This function is derived from the function of the product in the cell, from which the causal feedback to enzyme production is generated in the entire systemic interdependencies. The selectivity of enzymes is also the primordial example for a physical relation of observation.
The extensive philosophical discussion of functions has shown that this term manifests similar ontological and epistemological issues as the term entropy, which suggests that the two concepts belong to a related philosophical terrain. This is because a function, taken as a fact, can be epistemologically subjective and objective, as well as ontologically subjective and objective, depending on the fundamental philosophical stance taken [56]. There are opinions that functions are always assigned by human observers, and also other opinions which treat functions as objective physical phenomena. Hence, as with entropy, the notion vacillates between being observer relative or observer independent.
One possibility to classify functions is offered in Table 1. Following Searle [57], I distinguish between two kinds of judgment about facts, which can be epistemically subjective, thus depending on points of views of the person who makes and hears the judgment, or epistemically objective, thus depending on some independent criteria of truth. Additionally, I distinguish between two kinds of entities, which are the ontologically subjective ones, whose mode of existence depends on mental states, and ontologically objective ones, which are independent from mental states. In this two-dimensional box, one standard assignment looks like the following (differing, however, from Searle’s original position):
- Technological functions are epistemologically objective because statements on them relate to physical laws, but they are ontologically subjective because they relate to human design;
- Biological functions are epistemologically objective because statements on them are science-based, and they are ontologically objective, because they are the result of natural selection;
- Mental functions are ontologically objective because they relate to neuronal states, which are observer independent, but they are epistemologically subjective because we can only refer to them from the viewpoint of the person who experiences them (such as pain);
- Semantic functions are ontologically subjective because they relate to individual mental states, and they are epistemologically subjective, because they relate to individual intentionality.

Table 1.
Types of functions.
| Judgement | Epistemically subjective | Epistemically objective | |
|---|---|---|---|
| Entity | |||
| Ontologically subjective | Semantic function | Technological function | |
| Ontologically objective | Mental function | Biological function | |
This helps to further clarify the Jaynes statement that entropy is an “anthropomorphic concept.” On first sight, this means that entropy is a notion that is epistemologically objective, because it relates to physical laws, but ontologically subjective, because it relates with particular experimental settings which fix the degrees of freedom of the observed macrostate; the settings themselves reflect mental states of the experimenter. However, in the philosophical debate over functions the assignment of technological and biological functions has been questioned [52]. This is because it depends on the level of system which is under consideration. For example, we can certainly describe a part of an engine independent from the original design merely in terms of its endogenous functioning in the engine, hence assigning it to the ‘ontologically objective’ box. The deeper reason for this is that we analyze a two-level system, where the engine has a function that directly relates to human design, but a part of the engine contributes to that function, based on mere design necessities which follow physical laws. A similar reconsideration is possible if we adopt the perspective developed in Figure 1, which results into a mutual embedding of functions, treated as observers there. If we keep the technological function in the original box, a higher level observer may relate to the design process directly. This design process can be seen either as a mental function or a semantic function, depending on the particular methodological perspective taken. However, in both cases one can proceed along similar lines as when shifting the technological function to the ‘ontologically objective’ box: If we integrate the technological function and the design function qua mental function into one higher-level system, we could argue, for instance, that the technological function is a part of a mental function. This discussion directly applies for the Jaynes notion of entropy: Its assignment depends on whether we include the observer system O into the analysis or not.
Regarding this integrated view on a higher-level observer, there are two choices. This is evident from the ongoing controversy over evolutionary approaches to technology [58,59]. One position posits that the design notion distorts the facts about the population-level evolution of designs, thus attributing too strong a role to individuals. The other follows early approaches in evolutionary epistemology and reconstructs the design process as an evolutionary process in the human brain [60,61,62]. In both cases, the role of independent mental states in determining technological functions would be reduced, if not nullified altogether.
These different possibilities are directly relevant for the interpretation of the Jaynes conception of entropy. If we interpret the observer in Figure 1 as a neuronal system that is a component in an evolutionary process, concepts such as entropy would not relate to mental states, but to physical processes that establish a causal connection between a physical system A and an observer system O. In this case, the notion of the entropy of an integrated system <A,O> becomes meaningful, along the lines of the solutions to the Maxwell’s demon paradox: On the most abstract level, the observer and the object system are just two physical systems which stay in a causal relation to each other. Hence, we end up with a further clarification of the final conclusion of Section 2.1: Gibbs/Jaynes entropy can be interpreted
- Either as an epistemologically objective, but ontologically subjective notion, as long we consider the standard use in physics, which relates object systems with mental states of observers who conduct experiments,
- Or as an equally epistemologically objective and ontologically objective notion, if we consider the integrated system of observer and object system, and conceive of the former as a physical system, which implies that not only the experiment as such, but also the design of the experiment is a physical process.
Thus, by means of these distinctions we reach an important clarification and extension of the Jaynes proposition (Figure 3):
There are two different notions of entropy. Observer relative EntropyOR is ontologically subjective and can only be determined with reference to mental states of human observers, for example, the physicist conducting an experiment. Observer independent EntropyOI relates to coupled physical systems of observers and object systems.
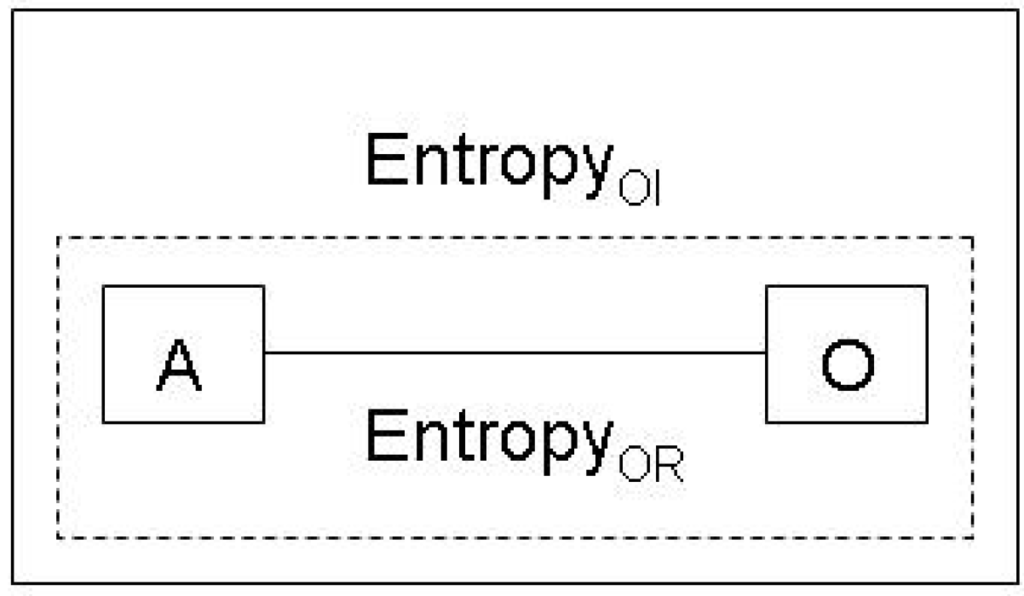
Figure 3.
Observer relative and observer independent entropy.
Obviously, this approach raises the question of the next-higher level observer. In Jaynes original approach, there is only entropyOR. So, entropyOI would obtain the role of an unattainable Ding an sich, since any approach to grasp it involves the establishment of an observer’s position in a potentially infinite sequence of nested observations. Subsequently, I wish to show that the distinction relates with the distinction between micro- and macrostates, and finally I come back on the tricky issue of levels of observers in the final section. This follows a line of thinking developed by Salthe [18], who distinguishes between the internalist and the externalist perspective. Correspondingly, Salthe argues that the total information capacity, hence entropy in the Boltzmann and Shannon sense, of a system can be decomposed into the capacity of a supersystem and the subsystems. Then, if we consider the internal position of the observer within the system, the observer is a subsystem that also has a particular information capacity which is a part of the total information capacity. This observer cannot, in principle, take a position outside the supersystem in order to measure its total information capacity. The only way is to estimate the information capacity by the observation of another subsystem. In doing so, the observer adapts structurally, hence also changing its information capacity. Thus, total information capacity from the internalist perspective is the sum of the observer’s and the observed subsystem’s information capacity, which, however, does not imply that the total information capacity is directly measured by the observer inside the system. This argument states the distinction between entropyOR and entropyOI, without referring to the Jaynes conception. An important consequence would be that the two entropies are not simply two different views on the same physical magnitude, but will always differ, as entropyOR does not include the observer, unless the latter establishes a self-referential relation.
Let us now explore the consequences of introducing the notion of function into our analysis of the Jaynes appproach to entropy, which is straightforward because observations are just special kinds of functions.
3.2. Evolving functions and maximum entropy production
Subsequently, I follow those strands in the literature which propose an evolutionary generalization of the concept of function. This states that all functions are the outcome of evolutionary processes, which, at the same time, determines the generic criterion for proper functioning, that is, reproducibility of the functions [63]. In a nutshell, all functions are evolved functions, and the continuing existence of a function lies in the fact that the function reproduces through time, independent from the specific mechanism of reproduction. Thus, a machine function is being reproduced if there is an energy throughput and a regular maintainance, or an ecological function is reproduced by stabilizing natural selection, given an energy throughput. This perspective is straightforward to accept for biological functions, it seems. As for technological functions, I just follow the previously mentioned evolutionary approaches which eschew the centrality of the design notion. As for mental functions, I accept the different versions of neuronal network selectionism in the brain sciences. So, in principle, a unified evolutionary approach to functions is possible. In this approach, the previous version of the Jynes proposition would have to be translated into:
There are two different notions of entropy. Observer relative EntropyOR is ontologically subjective and can only be determined with reference to a function. Observer independent EntropyOI relates to coupled physical systems of functions and object systems.
If two physical systems are causally connected in a way that the proper functioning of system O is the result, we have a substantial modification of the standard conception of causality [46]. This is because the effect of system A on O is mediated by all other factors that determine the proper functioning of O. In both artefacts and living systems, the most general condition for proper functioning is energy throughput. If we remain on a purely ontological level, following Bunge’s [8] exposition, energy is an additive property of all things which measures their degree of changeability relative to a reference frame. Accordingly, a causal relation is a sequence of events through time in which energy is transferred from x to x’. In a slightly more specific way, all causal relations involve the transformation of free energy into bound energy, and, following the Second Law, the production of entropy. Therefore, interactions involving physical systems with functions differ fundamentally from other forms of causality, as they both manifest a causal relation between system A and system O, hence an energetic transformation, and a simultaneous energy throughput in system O which is necessary for the function to be realized. We can also state the the energy throughput is necessary for the reproduction of the function. So, Figure 2a can be modified and extended into Figure 4.
It is important to notice that, if we regard as the observer system O the entire structure of embedded functions, the causal impact of A on O only happens on the level of the single function. So, for example, a causal impact is the kinetic impact of a substrate on the active site of an enzyme. The enzyme reaction occurs in the heat bath of the cell, so involves an energy throughput. The function of the fundamental enzyme reaction is embedded into a hierarchy of functions in the cell.
So far, the argument of functions seems to come close to the famous Schrödinger definition of life, because it is tempting to see the function as a biological function which, according to Schrödinger’s view, feeds on energy and produces both negentropy as internal order and exports entropy in the environment. However, although this is an inspiring idea, it does not grasp the essential point. This is the role of functions in the physical process. In the notion of function, it is also easy to accomodate the alternative argument related to non-equilibrium systems in which energy dissipation results into the formation of structure, which corresponds to a Second Law trajectory, thus seems to contradict the Schrödinger definition. The notion of function includes both possibilities, because it does not have any implications about the way how the underlying physical patterns emerged.
In order to further clarify the physical role of functions, I propose to explore an evolutionary approach to the Jaynes conception of entropy. This means, I present a naturalization of the concept of inference which follows the lines of evolutionary epistemology [65,66]. In such kind of approach, the experimenter in Jaynes original setting is seen as an evolving system O which produces inferences about the behavior of system A, which translate into further causal interactions between system A and O, that in turn impact on the reproducibility of system O. This process takes place against the background of a population of observer systems O1,…,n, the reproduction of which is maintained by energy throughputs which are constrained so that selection among observer systems takes place, depending on the degree how far the observations approximate the true physical functioning of system A. In other words, I assume that observations have a fitness value.
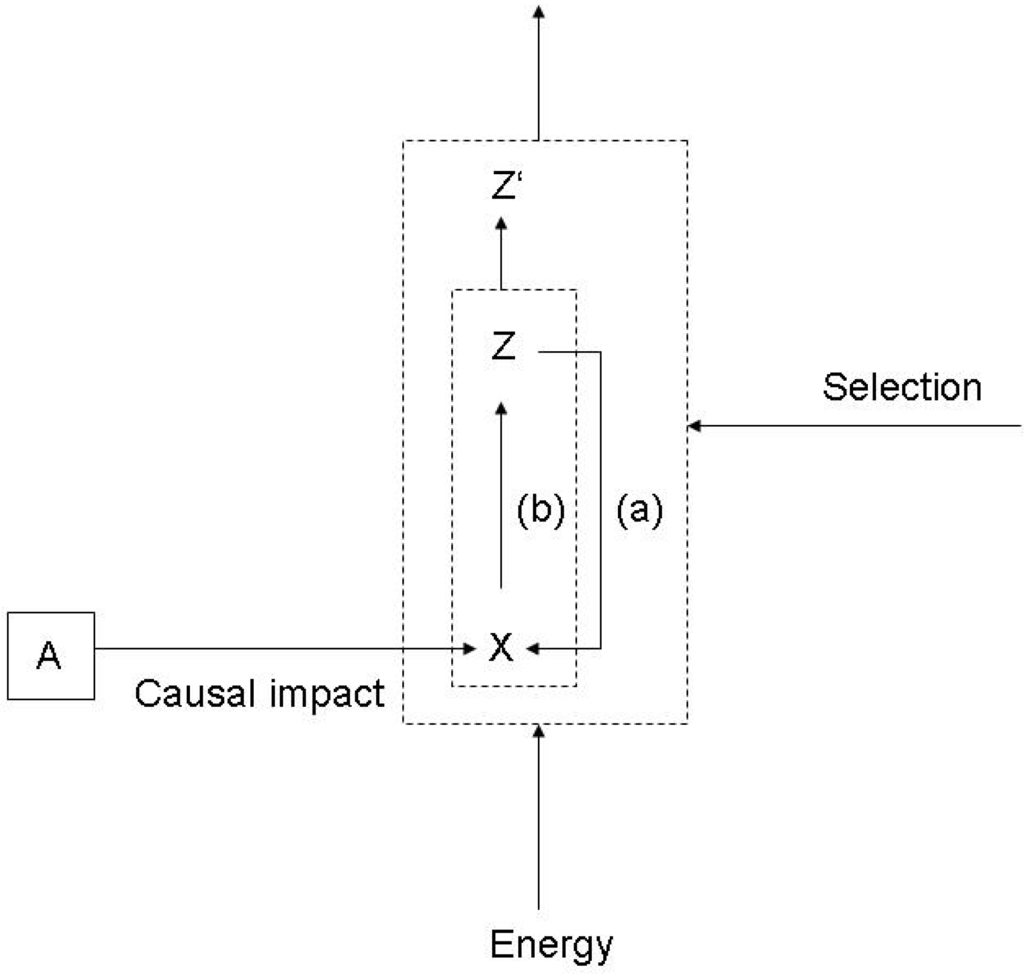
Figure 4.
Function and causality.
Along the lines of the Jaynes approach, the degrees of freedom of the system A can only be specified with relation to the function of the system O. A function can be fulfilled or can fail. In case of failure, system O collapses or loses out in competition with the other systems. Therefore, the question is whether the degrees of freedom that are specified with relation to a function result into a pattern of causal interaction between system A and O in which proper functioning of O is possible, given the selective pressures. A function is a mechanism that relates an observation to a process, in the sense that the function defines certain states of the object system which relate to states of the system with the function. These states can be grained to vastly differing degrees, depending on the functioning, and depending on the energetic costs of the observation. So, in any kind of function a distinction between micro- and macrostates is involved, with the macrostates being those directly relevant for the function: This results in functional selectivity.
From this follows, that the entropy measure implied by the Gibbs/Jaynes approach is not arbitrary if the two systems interact with a function involved. The function implies a certain set of constraints on the macrostates of system A, and it is the possible tension between functional relevance and irrelevance that determines the evolution of constraints, in a similar way as the experimenter produces physical models in order to explain her observations, and continuously improves the estimates. If we envisage a selection of functions, the crucial question is whether unobserved microstates are relevant for the functioning, such that the causal interaction results into a less than proper functioning of system O. If the functioning does not distinguish between microstates, even though they affect the functioning causally, the system would have to change the number and kind of degrees of freedom in the macrostate which are implied by the function. In the evolutionary setting, this does not happen because of a new design created by an experimenter, but by variation and selective retention in the population of observer systems.
So we end up with a further modification of the basic structure of a function in a physical context (Figure 5). Physically, the causal impact of system A on O happens between the microstates of A and X, such as the kinetic or quantum level interactions between substrate molecules and enzymes. The relation of observation supervenes on the microlevels in the sense that the molecular shape of the active site of the enzyme (which is an emergent property of the quantum level [67,68]) fits into the molecular shape of the substrate. The relation between the two levels becomes physically explicit in the induced fit process in which the two sides adapt to each other. As for the function, a similar consideration holds. The causation (b) is between the microstates of X and Z, but the relation (a) operates on the macro-level, which is implied by the proper function with relation to Z’, i.e., the embedding system. For proper functioning, certain variations on the micro-level of X do not matter, even though they operate in the causality between X and Z. For example, the products of the enzymatic reaction may manifest slight variations in some respects resulting from the chemical process (e.g., the product may be deviating from a pure substance), but for the functioning only the pure substance features are relevant. So, in this example it is possible to reconstruct the notion of ‘molecular structure’ as the set of constraints, so that it is the very fact of chemical reactivity which establishes the differentiation between the macro- and the microlevel (i.e., molecular structure and quantum level processes): The notion of a chemical substance refers to the patterns of reactivity, which obtains the status of a proper functioning, e.g., when conducting a test [69,70].
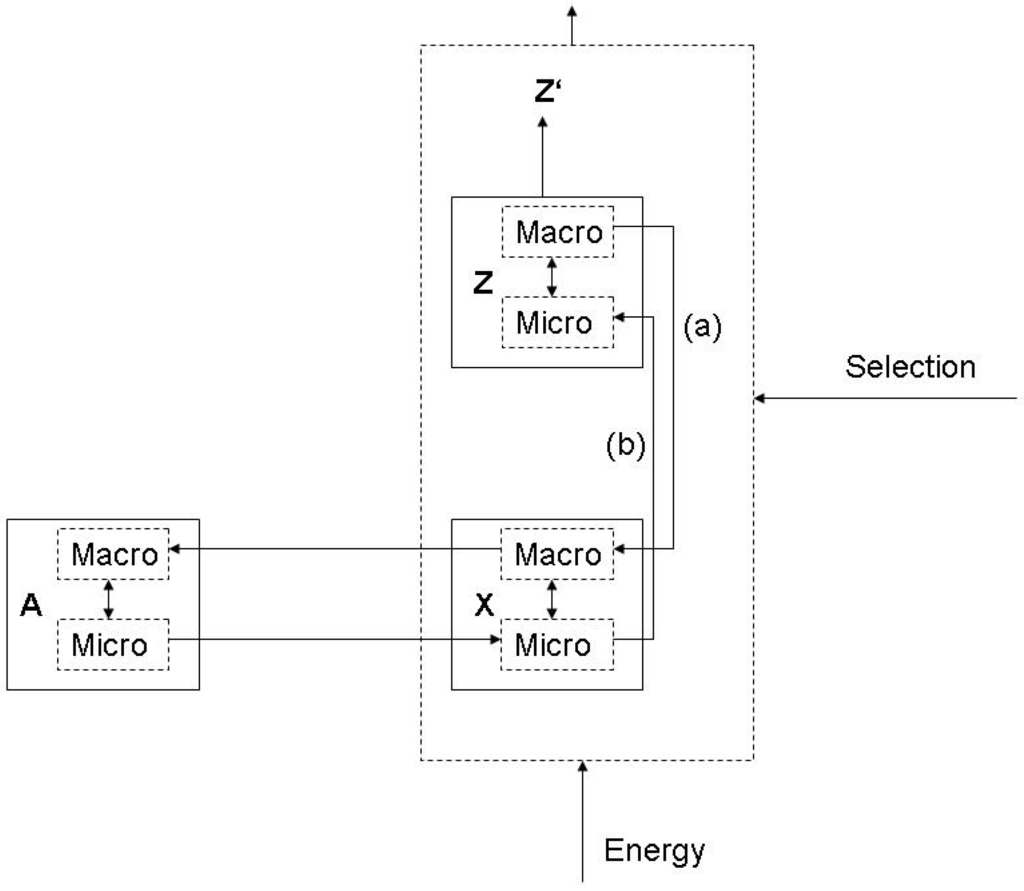
Figure 5.
Functional selectivity and the Micro/Macro distinction.
In this evolutionary setting, the central question is whether we can interpret the Maximum Entropy correction process in the Jaynes model of inference as an evolutionary optimization. I posit that a function operates properly if the macrostates that underly its functioning correspond to a maximum entropyOR state of the microstates. This is just an evolutionary extension of the Jaynes approach to maximum entropy in statistics [46]: If the least-biased assignment of probabilities does not apply, this is an indication that the constraints have not been properly defined, and hence need readjustment. So, one can view the series of statistical tests in which degrees of freedom are changed by the tester according to the criterion whether MaxEnt applies as steps in an evolutionary sequence of selections. Hence, the MaxEnt principle is also a principle of learning. In other words, if the initial observation results into observations which fail to confirm the MaxEnt distribution, this is a cause for a realignment of the constraints on the macrostates. Following Dewar [71], we can apply this on the relation between physical theories and the MaxEnt principle (Figure 6): The physical theory posits a set of macroscopic constraints of an object system, and the MaxEnt principle serves to generate predictions about the macro-behavior of the system, such that a failure of those predictions implies the need to change the physical theory. From the viewpont of evolutionary epistemology, and therefore equating the physical theory as a function in the sense of a physical state of the observer system, we can therefore also argue, that in a process of natural selection, the MaxEnt principle will also underlie the convergence of functional macrostates with macrostates of object systems. Proper functioning requires that all other possible causal interactions between the object system and the function are irrelevant to the fulfilment to the function, such that any information about a deviation from equal probability of all states is also irrelevant. For this conceptual transfer of the of the MaxEnt principle from theory evolution to physical evolution it is sufficient to refer to a general principle of computational efficiency, in the sense that the MaxEnt principle allows for a minimization of effort (time, energy, resources) invested into the processing of epistemically or functionally relevant information.
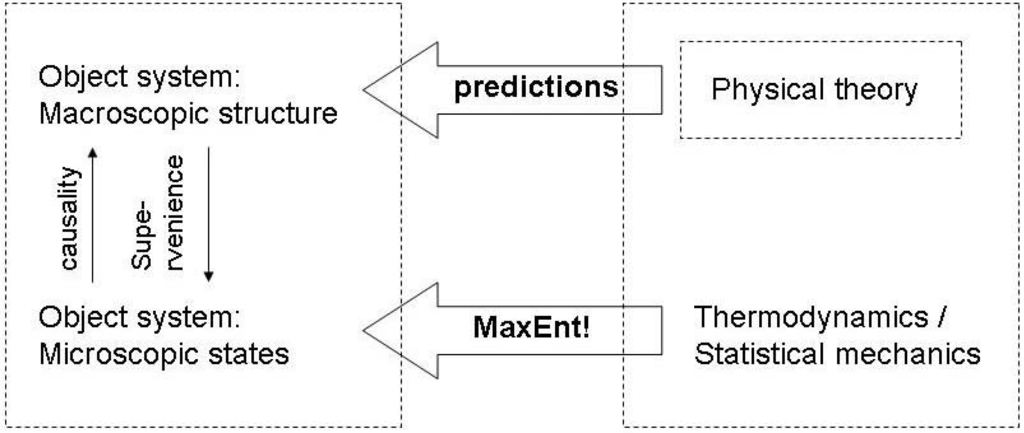
Figure 6.
MaxEnt as inference.
I summarize:
The Jaynes approach to entropy as an inference procedure corresponds to an evolutionary sequence of adaptations of macro level constraints in the observing system O to the macro level constraints in the observed system A, such that all micro states of the observed system are assigned to the maximum entropyOR state. This process is driven by natural selection, such that deviations from the state of equiprobability trigger further adaptations of the observer system, if they prove to be causally relevant for its proper functioning. Hence, evolutionary change follows the MaxEnt principle.
This argument links the reproducibility of the function with the reproducibility of the macrostates of system A, in the sense of that predictions which correspond to the MaxEnt principle will be confirmed in the course of time. In other words, if the MaxEnt principle is the best way how to predict macrostates which relate with a large number of causally productive microstates, or, as in Dewar’s [72] reformulation, microscopic paths that result into the same particular macrostate, then the principle of natural selection of functions implies that they will approximate the MaxEnt principle in a sequence of observations across a population of functions, i.e., observer systems.
By this argument we have stated that evolving functions as observations will maximize entropyOR in the process of adapting their structure according to the macrostates of the system A with which they causally interact. This is a statement about the informational content of the evolving structures, in the classical Shannon sense. The question is whether this purely informational view also corresponds to a physical reality, in the sense of whether the implied MaxEnt principle also corresponds to maximum entropy production. In fact, this correspondence between the MaxEnt principle and the MEP hypothesis has been stated recently for many non-equilibrium systems, as an alternative to the older dissipative systems hypothesis [73]. Interestingly, this approach also includes basic feedback mechanisms which correspond to the general notion of a function that I have outlined previously: That is, a MEP steady state can be described as a trade-off between a thermodynamic force and a thermodynamic flux, in which changes of the flux cause changes in the force, which generate subsequent changes of the flux that lead back to the steady state [74]. Beyond the specific thermodynamic assumptions, the correspondence thesis can be supported by a purely ontological argument on the structure of the evolutionary system that I have just described. If the MaxEnt principle correctly grasps the evolutionary dynamics of evolving functions, then it must also present an approximately true picture of the underlying physical reality of the system A. That means, if the notion of observation is naturalized, then the epistemic aspect of the maximum entropy principle corresponds to the ontological aspect of maximum entropy production, in the sense that with properly identified macro-constraints, the observed system will also be in a state of maximum entropy production (this may correspond to Virgo’s [75] proposal that the MEP principle relates with the problem of how to define the relevant system boundary). This argument stand aside the thermodynamic analysis of non-equilibrium systems that shows that those systems will maximize entropy, given a local variable with a local balance of flux and local sources [72,76].
Clearly, this assertion is actually a statement of the relation between entropyOR and entropyOI, as maximum entropy production is a process that is observer independent. Yet, at the same time the determination of this entropy can only happen in a relation between observer and observed system. So, the evolutionary correspondence between the MaxEnt principle and the Maximum Entropy Production provides the foundation for the assumption that the two entropies converge.
This second step in the evolutionary interpretation of Jaynes’ notion of entropy results into the hypothesis:
In physical systems with evolving functions, the structural features of the functions which establish an observational relation between them and object systems will result into a causal interaction between functions and systems in which those structures correspond to a set of constraints on the macro-level of the object systems which maximize entropyOI in the object system. This entails a correspondence between the MaxEnt principle and MaxEnt production.
Now, we can further develop on this insight by modifying the assumption about system A: We consider the case that system A is a function, too. In other words, we deal with the case of mutual observation. In this case, the structural features of function O become the constraints that are the object of the observation by system A’. Again, if we add the evolutionary context, hence envisaging a population of systems A’1,…,n, then we can reproduce the entire argument that I have presented above. Evidently, this interlocking of evolving functions implies a problem. This is analogous to the determination of equilibria in games where agents have to adapt their mutual expectations. If the observer system changes its structure because of an adaptation to the then existing structure of system A’, system A’ will adapt its structure to this new structure, because this is driven by the ongoing process of selection. A mutual fit of structures corresponds to the notion of Nash equilibrium in games in the sense that both systems will keep a certain structure in which the mutual predictions of their macrostates will be correct, that is, self-reinforcing through time. In game theory, this is a state of pure mental coordination. In the naturalistic interpretation of the observation relation, we can say that this is a structural equilibrium that, according to the MaxEnt process, results into maximum entropy production of both systems, hence also of the coupled system. So we can posit another hypothesis:
In physical systems with coupled evolving functions, the functions will mutually adapt their structures such that the implied constraints of the respective object system maximize entropyOI production; from this follows, that the integrated system also maximizes entropyOI production. Maximum entropy production defines the point of optimal mutual adaptation, hence an equilibrium. In this state, entropyOR and entropyOI converge because the mutual adaptation of constraints removes the contingency involved in observer relative entropy.
This hypothesis is very significant, as it shows that the Schrödinger approach needs to be corrected and amended, for very fundamental ontological reasons. Systems with functions evolve structural constraints precisely by means of maximizing entropy production. For this, we do not need the more special approach of dissipative systems, because the ontological argument counts for both equilibrium and non-equilibrium states. Reconsidering the fundamental point, it boils down to this: In the Schrödinger view, it is the structure of the functions which is regarded to be a state of lower entropy. In my view, it is precisely the evolution of the structure that results into maximum entropy production. The emphasis is on ‘maximum’ here, because entropy production as such happens under any circumstances involving energy flows. Therefore, in most general terms, and contrary to Schrödinger, the evolution of biological functions corresponds to the Second Law, and by no means contradicts it. However, there are also reasons to assume that the MaxEnt state is also the state of minimum entropy of the system that produces entropy [74,77]. To this we can add the additional insight, that in evolutionarily coupled functions the contingency of the relation between entropyOR and entropyOI is reduced, as a result of the mutual coupling. Again, this statement leaves open the question of hierarchical embeddedness into higher-level relations of observation. Interestingly, this observation corresponds to a speculation by Deutsch [78] who argued that only evolution by means of natural selection can reach states in which certain structures are stable across different parallel universes, if seen according to the Everett interpretation of quantum theory. I will come back on this idea later.
3.3. Endogenous entropy and evolution
Before I continue to develop on the more general philosophical argument, I present the most significant example for coupled functions, which is the emergence of life, understood as a fundamental chemical process. One of the pertinent theories that corresponds directly to the general framework developed in this paper is the ETIF theory (Emergence of templated information and functionality) [79]. The basic unit are TSD reactions (template and sequence directed). The central building block of this theory are two coupled reaction cycles, both occuring in a heat bath with the necessary chemical components (Figure 7). One cycle is the translation cycle in which peptide synthesis takes place from amino acids and proto tRNA and proto mRNA, the other is the replication cycle, in which RNA is produced via template RNA. The connection between the cycles is constituted by the catalytic function of peptides resulting from the translation cycle on the replication cycle. In this system, we have one autocatalytic cycle, the translation cycle, which therefore contains the most elementary type of function. At the same time, there is a more complex feed-back loop via the catalysis of the RNA replication. This elementary feedback loop can evolve into more complex structures and manifests increasing selectivity of the chemical reactions, resulting into an increasing capacity to distinguish between different chemical species.
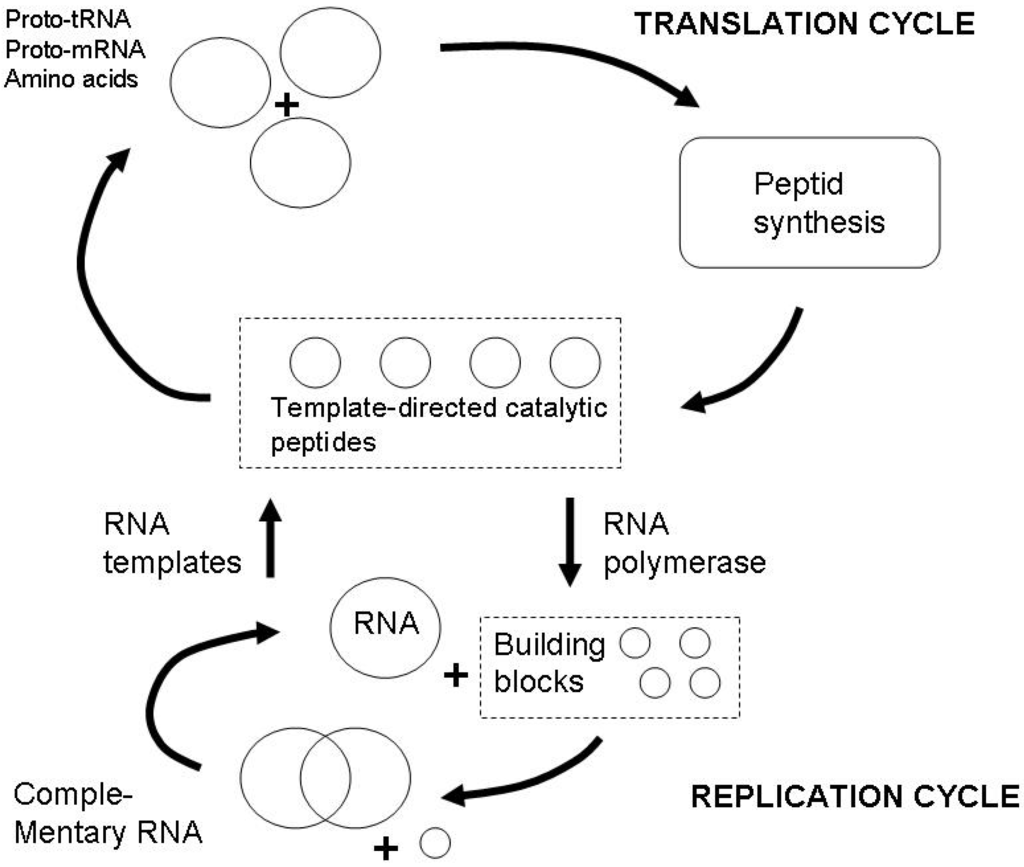
Figure 7.
Emergence of templated information and functionality, after Lahav et al. [55].
From the viewpoint of the previously presented argument, the increasing selectivity of the evolving networks of chemical reactions corresponds to the Second Law, but simultanously reduces the contingency of entropyOR on the level of the single functions, in the sense of the contingency of the constraints operating in the MaxEnt process. This reduction of contingency is what we perceive as increasing “order,” but it does not imply that the Second Law does not hold.
There are two aspects of origin of life theories that need further scrutiny in our context. The ETIF model is one specific version of the general chemoton model which works without enzymes [54]. In this model, an autocatalytic reaction cycle corresponds to the metabolic subsystem of an elementary living system, which interacts with a cycle of template replication. This cycle produces a byproduct which reacts with another byproduct of the metabolic subsystem to form a membranogenic molecule. The latter process creates the possibility of a physical separation of different chemotons, which is the precondition for evolutionary selection of different functions. Clearly, the chemoton is a system of coupled functions in the sense of Section 3.2.
Now, compartmentation is crucial for two reasons (as an important aside, this provides the ultimate explanation of the central role of the notion of membranes in biosemiotics [80]). The first is that compartmentation happens as a result of the Second Law, and not against it. In this, compartmentation is similar to the lumping together of matter which results from the entropic transformation of gravitational energy. Similarly, the formation of fluid vesicels and, especially on particular sites such as rocks supports compartmentation, simply because they represent states of higher entropy. However, compartmentation triggers a fundamental change of the evolutionary process, because it causes the emergence of group selection [81,82]. Group selection offers the evolutionary explanation of the nesting of functions. It is important to notice that group selection is a necessary statistical outcome in systems with elementary heredity, mutation and replication.
The reason for this is easy to grasp when one considers the fact that in a selective environment, the production of a byproduct (or the catalytic use of the original product) that catalyzes another reaction is costly in terms of the reproduction of the base reaction [54]. In this sense, cross-catalyzation cannot be an evolutionary stable equilibrium because the mass of molecules that do not cross-catalyze will grow stronger as the former. On the other hand, a cycle will always grow stronger compared to other cycles if cross-catalysis happens. The only way how this can be stabilized through time is by compartmentation. That is, if cycles with different degrees of ‘molecular altruism’ separate, the cycle with higher catalytic potential can reproduce better than other cycles. Absent compartmentation, this ‘altruistic’ molecule would be driven out by parasites. ‘Altruism’ in this context just designates the emergence of a new function, matching our elementary model of function. That is, once a chemical web including autocatalytic and replicative cycles manifests compartmentation, there is a possibility that a Z’ can emerge, i.e., a higher-level function to which the lower-level function is directed.
This argument further supports the general view that evolution does not contradict the Second Law, because the emergence of more complex functions is a necessary result of the underlying physical processes, in this case even of a very simple mechanical fact, that is, compartmentation. However, this conclusion depends on how we conceive of the process of selection. In our scenario discussed so far, the central feature is that even on the primordial level of molecular evolution, chemical reactions compete for the acquisition of substrate and the utilization of thermodynamic potentials.
The second aspect of life is the throughput of energy that relates to the most universal selective constraint on the fundamental chemical processes. Evolution is a physical process in the sense that the ultimate currency for selection is the relative capacity for processing energy, relative to a reference frame, which is endogenous in the sense of being co-determined by the existence of other living systems which compete for the same energy sources.
This observation allows to relate the argument so far with Lotka’s principle of maximum energy flows in evolution, which is, of course, a corresponding principle to the principle of Maximum Entropy Production [74,83]. Lotka’s principle has been invoked in many contexts, fitting to my general argument. There are also different levels of empirical specification, reaching from Lotka’s most general argument to biological systems and to human technological systems [84,85,86,87,88]. This broad scope shows that it is related with the general notion of function as developed in this paper. Therefore, we can state another formulation of Lotka’s principle:
Systems with coupled evolving function will evolve along a trajectory in which states with increasing energetic throughputs will be achieved in temporal sequence. These states correspond to states of MEP, in which entropyOI and entropyOR converge, relative to the set of coupled functions.
There are different specific mechanism that produce this result. The most general one is the principle of maximum power in the sense that living systems will evolve into states which manifest a growing capacity to do useful work, such as larger size, greater reach, higher speed etc. [87]. There are more specific mechanisms, such as the Red Queen principle that applies to interlocking functionings of the predator-prey type [89]. The Red Queen principle triggers the maximization of power as a result of an arms race. As we shall see in the next section, the most important mechanism is signal selection [90]. Signal selection builds in the so-called handicap principle [91,92]: Natural selection favours the mutual coordination of living systems via signals that are costly, because only costly signals transmit truthful information. Signal selection therefore drives the evolution of seemingly non-functional diversity, such as colours or additions to body structure.
Lotka’s principle is a description of the general trajectory taken by systems with evolving functions. However, the relation to entropy is not a simple one. This is immediately obvious if we go back to the Jaynes approach, where the measure of entropy which links the micro- and the macrolevel is specific to the particular observation, hence function. This means, in a sequence of coupled systems O1↔A’1, ….., On↔A’n, the corresponding measures of entropy S1,…,Sn are incommensurable, because they define different entropiesOR. So we have two different propositions that we need to reconcile. One is that in an evolutionary systems, with reference to a given state space, hence set of functions and their structural characteristics, the mutual adaptation of functions results into the maximization of entropyOR. At the same time, the entire sequence of evolving functions follows Lotka’s principle, and hence maximizes entropy with reference to the environment, which is entropyOI. Yet, the state-specific entropies and the general entropy are not commensurable, even though on a foundational level, the Second Law holds under every circumstances, and refers to maximum entropyOI production..
This problem can only be solved if we consider the role of functions again. Coming back to our original discussion of the notion of information, we can say that the MaxEnt process with reference to given functions results into a state-specific information capacity in the original Shannon sense. This information capacity does not change endogenously, but by the emergence of another function which has certain structural features that identify a bias in the distribution of microstates that was not identified in the previous function. In other words, the MaxEnt principle, viewed from the evolutionary perspective, ultimately only applies when the functional structure fully corresponds to the constraints that actually hold in the object system. Now, in a system with coupled functions this is not a given, but every change of a function opens up new evolutionary possibilities for another, observing function. That means, the evolution of functions implies a continuous increase of the information capacity of the encompassing system of all evolving functions. The central point is that the information that is carried by a function is not ‘stored’ in any meaningful sense in that function, but relates with another function that is causally connected with that function. So, a function evolves following the MaxEnt principle, and at the same time becomes information relative to another function.
In other words, it is wrong to state that a function carries information with reference to the state space that reflects its specific constraints. It can only carry information relative to other functions that are coupled with it. The best illustration for this distinction is the fact that genomes carry a lot of ‘junk’ DNA. Interestingly, there is even no relation between genome size and complexity and the level of complexity of the phenotype. This observation clearly shows that there is no direct correspondence between the role of the genome in causing development and its role of carrying information. The information resides in the system into which the genome as a set of functions is embedded. For this system, only parts of the genome carry information, here understood as having a higher level function. From this follows, that the increasing divergence between the functional and the non-functional DNA in genomes just reflects the MaxEnt process over time: All functions evolve into a state in which there is a maximum amount of diversity which is non-functional. In plain, this is why simple organisms can have larger genomes than humans: All depends on whether the system can make use of the genome, which otherwise just accumulates diversity.
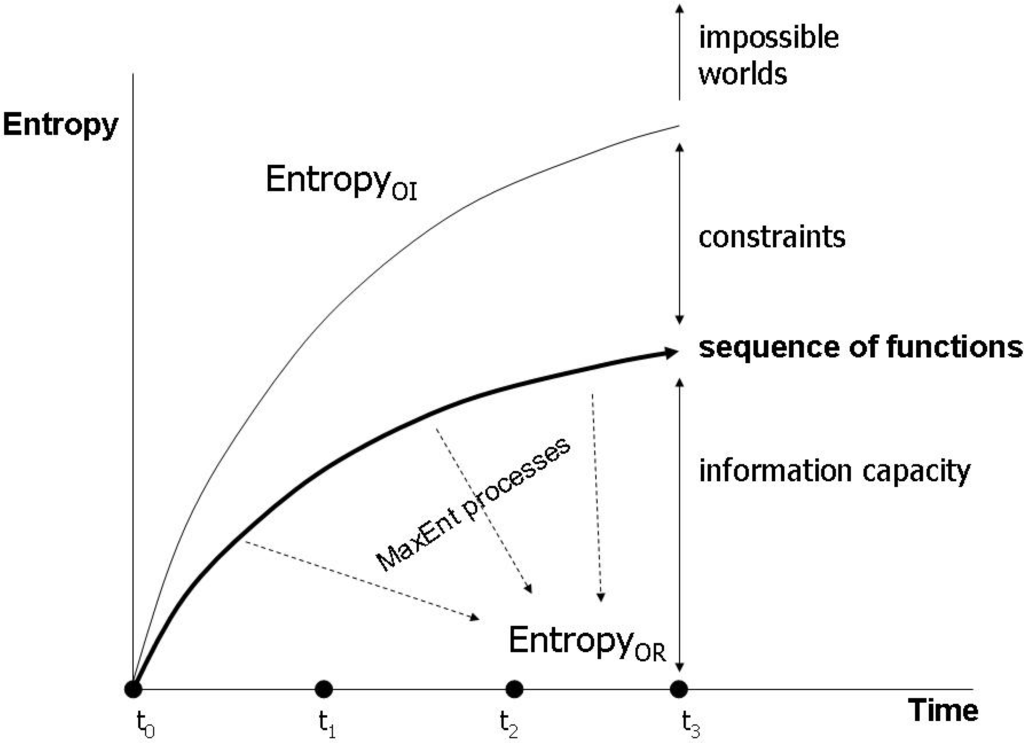
Figure 8.
Evolution of entropies.
This particular relation between functional evolution and information capacity has been stated by Brooks and Wiley [93] (building on earlier work by Layzer [94] and has been further developed by Salthe [18], whose distinction between externalist and internalist notions of entropy corresponds to my distinction between entropyOI and entropyOR, as we have already seen. So we can adapt a diagram that has been recurrently used in the literature (Figure 8). The important insight is that the evolution of functions implies a series of MaxEnt processes with reference to entropyOR. EntropyOI increases simultanously because the entire process is driven by energy throughputs and follows Lotka’s principle. This means that an increasing amount of energy is dissipated into bound energy, so that entropyOI in the general thermodynamic sense increases.
The important additional insight that we can gain from this graphical exposition is that we recognize the role of functions explicitely. Instead of envisaging the role of an observer who measures the entropy of a system and processes information, we see a sequence of evolving functions, which are coupled and nested in an increasingly complex way, such that the entire embedding system evolves into states with an increasing number and scope of constraints [74,76]. There is no way to get out of this process and adopt the perspective of an entirely exogenous observer (actually, Maxwell’s demon). Instead, we realize that evolving functions imply an endogenous state space, and therefore create new information capacity that materialized if new coupled functions evolve. The entire process operates according to the Jaynes MaxEnt principle, which, in the evolutionary context, also implies that the MEP hypothesis holds. The MEP hypothesis refers to the evolution of the outer curve in the diagram, hence entropyOI.
We have now sketched the necessary theoretical framework to discuss the relation between entropy and semiosis in a fresh way. It is already obvious that Shannon information only plays a marginal, because merely descriptive role here, in certain contexts. Instead, we concentrate on the thermodynamic notion of entropy and the Gibbs/Jaynes view on the relation between macro- and microlevel. We only need to do a simple step: Semiosis is a function.
4. Entropy and Semiosis: Naturalizing Peirce
In order to complete the conceptual transition from function to semiosis it is useful to consider the most simple function again (Figure 2a). All functions involve a mechanism of discriminating between causal impacts that support the function and that do not: Functions are selective. This is also the basis for the notion of a proper functioning which is evident if we think of a failed functioning as a failure to identify a certain property of physical system A by system O, which is essential for the function. In teleosemantics, this is the problem of misrepresentation, which is understood as a failure to function properly. This is possible even on the molecular level: For some reason, an enzyme might fail to establish the proper relation between substrate and active site, that is, might misidentify a molecule. As this will relate to a particular part of the substrate molecule, we can say that this part is a sign of the substrate. In most general terms, we can state (in modification of Matthen [95], and using the previous notation):
A function F attributes the feature a to an object system A if the attribution causes a proper functioning in terms of the causal consequence Z with relation to A. Proper functioning relates to the embedding function Z’, which is the result of a process of natural selection.
Of course, this formulation just repeats the gist of the previous analysis, but with an important conceptual twist, namely using the term ‘feature a’. Evidently, this feature a is a ‘sign’ in the most elementary Peircian sense, or, more exactly, ‘sign vehicle’. In the teleosemantic nomenklature, this is the “representation”, especially as “mental representation”, and the point about the statement is that therefore the representation does not have a meaning, but a function. The term “sign” seems to be a better choice, as it does not imply the many problematic connotations of the term “representation” right from the beginning. Thus, a particular molecular shape does not “represent” the substrate, because there is no mental intermediate involved. But it can be called a “sign” of the substrate in the sense that all other properties of the substrate are not directly relevant for triggering the proper functioning of the enzyme.
4.1. Reconstructing semiosis as proper functioning
This transition to semiosis is more salient if we switch our attention to more complex, yet still primordial forms of life. Ben Jacob and colleagues have argued that the Schrödinger definition of life does not apply for bacteria because it misses the fundamental role of emergent internal information that feeds on latent information in the environment [11,96]. This analysis corresponds to my argument of the evolution of functions. The central empirical observation on bacteria is the selectivity of functions that channel their search and consumption of food resources in their environment. For example, bacteria have evolved functions which enable them to analyze the composition of different sugars in their environment, so that they can identify the most preferred source when investing time and energy into the feeding process (this happens via the combination of different repressor and activator genes in their genome network). Further, these and other processes are supported by group-level effects within colonies of bacteria, for example, in reaching a form of collective coordination in the transition to sporulation. Such phenomena correspond to the previously analyzed case of group selection of functions. The main effect of this is to enable bacteria to process more complex contextual information in the environment, which goes beyond their capacities in terms of the individual genetic mechanisms. In all these processes, it has become fairly common to talk about “language”, e.g., “chemical language.” The term ‘language,’ however, suggests many features that those simple forms of functional coordination do not possess, such as a syntax. Therefore, the use of ‘sign’ in the biosemiotic sense seems to be more appropriate [97].
This brief glance at bacteria shows that the central category in the teleosemantic analysis is the role of the features that are extracted in the interaction between the function and an object system. In the previous sections, I have called this an ‘observation.’ Functional evolution ends up in an increasing degree of structuration. If we put the two perspectives of this section, as illuminated so far, and the previous sections together, this results into the conclusion that the notion of the sign is related to the notion of constraints. That is, the sign in the teleosemantic sense is a feature that reflects the constraints of an object system, relative to the proper functioning of the function, in way such that a state of maximum entropy for all other, functionally irrelevant properties of the object system is attained.
These initial thoughts can be put into the more systematic framework of the Peircian analysis of signs. The dualism of causality in case of functions reflects the fact that functions can be also analyzed as a fundamental process in semiosis [104]. I use a common diagram to illustrate Peirce’s notion of a sign (Figure 9) [2,36]). Peirce distinguishes between the object, the sign (sign vehicle, earlier ‘representamen’) and the interpretant. This triadic structure is generally seen as his seminal idea, because it goes beyond the simple idea of a dyadic relation between sign and object [98]. Sign and object are essentially related with the interpretant. It is then straightforward to establish an equivalence with the components of functions, in a double sense. Firstly, the triadic structure reflects the different structure of causality in relating a cause=object to an effect=sign via a function=interpretant. Secondly, we can use the same triadic structure to analyze the function: The object corresponds to the object system A, the sign corresponds to the effect Z in the function, and the interpretant is the embedding function with Z’. The X is the pivot in the sense of being the physical link between the two causalities, one the direct physical impact from A to X, and the other the functional causality involving X and Z, that is, the two relations a) and b), according to Figure 2a). In this exposition, it is of utmost importance to recognize that the sign is nothing external to the function, but is actually part of the function, and that its nature as a sign depends on the embedding function. This is the exact statement of the notion of observer relativity in the semiotic context.
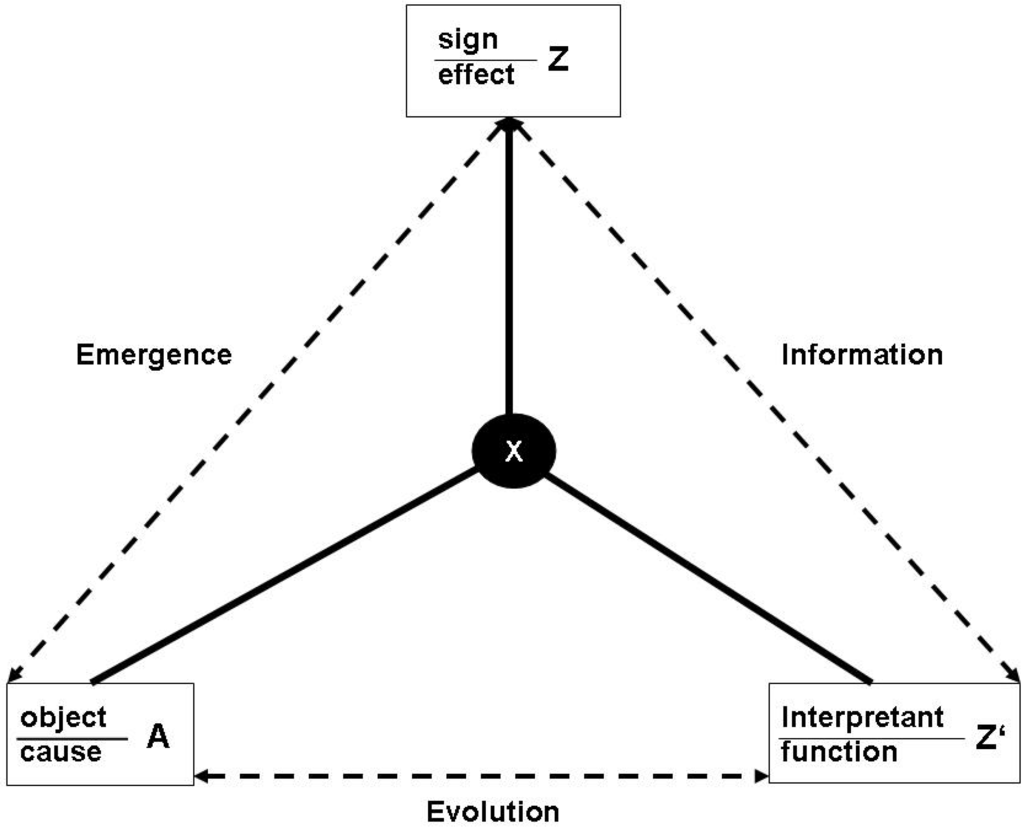
Figure 9.
Function and semiosis.
The sign obtains a central position in the entire structure because objects can never be observables directly, but only via certain aspects. These aspects are the signs. I do not delve into the more complex taxonomy of signs here that Peirce developed through his lifetime, especially in his correspondences [99]. If we relate this idea to the general structure of functions, we can realize the mappings that are shown in Figure 9. The central point is that semiosis can be seen as a function in the sense that the fundamental causal relation between an object system A and X in the function is insignificant, unless it is coupled with the Z that results from proper functioning with relation to Z’ (for a related analysis of cognitive neuroethology in teleosemantics, see Neander [100]). Therefore, it is the Z that is the sign in the Peircian sense. We can also refer to the micro-macro distinction here, because the Z is a sign for the reason that it only reflects certain properties of the object, and not the object in its entirety. In this sense, we can understand the properties that correlate with Z as an observer relative phenomenon as emergent properties of the object. The sign relates with the constraints of the state space of the object, in the sense that those constraints are essential to define the object relative to an observer, i.e., a functioning, with all other causal relations between object A and X becoming irrelevant [98].
This reflects the result of the MaxEnt process as described in the previous section, and in the original Peirce approach, this correspondence can be seen against the background of what Peirce called ‘tychism’, i.e., his ontological view that all reality is stochastic, such that exact laws are not possible, but only emerging regularities in an evolutionary process [21]. In analyzing the MaxEnt process, we started out from the Jaynes notion of inference, which hence allows to include another Peircian concept here, namely the notion of abduction. In Peirce’s logical system, abduction is the process of the generation of hypotheses in facing a fundamentally stochastic world, which are then exposed to selection by empirical testing (thus, essentially corresponding to Popper’s [65] version of evolutionary epistemology). In our context, abduction corresponds to a sequence of Jaynesian inferences in the sense that, relative to an interpretant, a sign is seen as an indicator of underlying constraints of the object. The inferred constraints become subject to further interactions between object and interpretant, which can result into a further modification of the sign. Thus, abduction naturalized refers to the evolutionary sequence of signs and interpretants, converging to an underlying set of physical constraints on the object. From this follows, that the evolution of interpretants correlates essentially with the emergence of properties on the side of the object. This process, in Peircian terms, is grasped by the distinction between ‘immediate object’ and ‘dynamical object,’ i.e., the object in ontological terms evolves via the emergence of properties that operate as signs in evolving functionings. This process implies also an accumulation of information, in sense of semantic information, beyond mere Shannon information. This evolving information corresponds to the emergence of the ‘dynamical object’ from the ‘immediate object.’ In Peircian terms, the epistemic process of evolving information is seen as ‘abduction,’ which I could reconstruct as a sequence of Jaynesian inferences that inhere the evolution of the functions.
This analysis provides the foundation for the assumption that signs are not simply arbitrary, but objects impose constraints on signs and vice versa. If it seems that a sign is arbitrary, such as an arbitrary proper name, it is overlooked that the use of the sign depends on rules that ultimately relate to constraints of the object. Even an arbitrary proper name, if it has the function of identifying a person, has to allow for the proper functioning. Proper functioning implies that the name refers to certain criteria how to apply the name on whom, and why. These identification procedures are functional, in turn (see Millikan [101,102]). So, any kind of sign establishes a relation between certain constraints of the state space of the object and the sign.
If we ask for the interpretant, we cannot say that the elementary function as such is the interpretant, but only the function into which the elementary function is embedded. In other words, a function establishes the relation between sign and object, and only the embeddedness of the function into other functions completes the Peircian triangle, i.e., the Z’ in my description of the function. From this follows that the underlying causal relation can be interpreted in many different ways. Especially, we can speak of an evolution of interpretants, which corresponds to the notion of abduction. As we have seen, this has been emphasized by Peirce in thinking of a dynamic process of semiosis, in which the object is increasingly differentiated via more and more complex signs. This process can now be seen as an evolving nesting of functions Z’, Z’’,…. So, we have a more precise idea of how signs can evolve dynamically. For example, a simple enzymatic reaction, an elementary function, can obtain more and more complex roles by becoming embedded into increasingly complex systems of interpretants in a hierarchically structured biological organism.
In the Peircian triangle it is also evident that the sign does not carry information but that the information is created by the relation with the interpretant. This is the part of the argument which allows to draw the separating line to Shannon information. It is impossible to relate the use of the sign as such to a space of states of signs, similar to a message in a space of possible messages. This is because the process of semiosis, seen in physical terms, involves the MaxEnt process in the evolution of the functions, i.e., the interpretants, which is a process that leads to more and more complex internal contexts of the primordial object-sign relation. This results into a sequence of entropiesOR. That is, we do not need to refer to the category of meaning in order to show that there is an observer relative role of information. Meaning is dissolved into the hierarchy of functionings. In other words, if we ask for a meaning, we just ask for a higher-level function. So, on the one hand we are able to interpret a particular entropyOR in the sequence of functions in the Shannon sense, and we would even be able to think of the sequence of entropiesOR as sequences of Shannon information. But this would only be a static snapshot of the essential dynamic process, and would fail to grasp the increase of complexity that inheres the evolution of functions Z’, Z’’,….It is then straightforward to see that the embeddedness of functions is equivalent to changing role of signs and interpretants through evolution, that is, an interpretant becomes a sign in the higher level function, which in turn corresponds to a further step in the growing complexity of the dynamical object. I visualize this connectedness of semiotic relations as a chain of Peircian triangles in Figure 10 (compare a related approach in [36]). From this it is evident that the immediate object remains the anchor of the entire process, and that the dynamical object corresponds to the evolving structure.
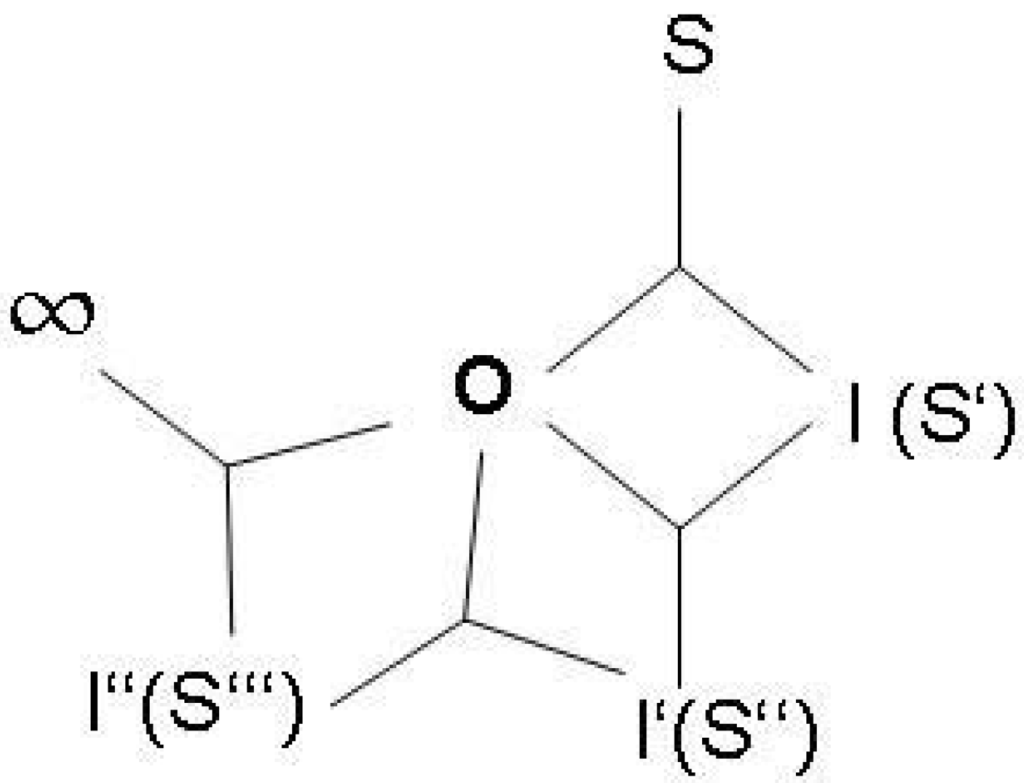
Figure 10.
Embeddedness of functions viewed as an infinite semiotic chain.
It may be useful to consider an illustration of the new Peircian triangle that goes back to our initial discussion of genetic information (Figure 11). In the Peircian triangle, the genome obtains the role of the object, and the gene expressions such as proteins that emerge in the process of development are the signs. The intermediate chemical reactions are in the center and correspond to the X. Then it is immediately obvious that information does not reside in the genome, but in the relation between the sign, i.e., the proteins, and the embedding function, which I have, for simplicity, named as the cell. The genome does not carry information, in this view.
It is important to notice that my version of the Peircian triangle, as applied on the genome, differs substantially from common approaches in the biosemiotics literature, following the early attempts by Emmeche and Hoffmeyer [97]. In these approaches, the genome is treated as a sign, and the proteins are treated as the object [36]. It seems that this still carries over the old informational misunderstanding about genes, which is otherwise discussed critically in that literature. Treating the genome as a sign would still assign a pivotal role to it in the information process. Against the background of my analysis, the only reasonable hypothesis appears to be that the hierarchically ordered organism, a system of nested functions, focuses on the genome as the object. This also allows for conceptual coherence, as we can equate the three sides of the triangle in Figure 9 with corresponding notions in biology: emergence of properties corresponds to development, the increasing complexity of living systems to evolution, and the relation between emerging properties qua signs to the increasingly complex living systems corresponds to information. In this process, the ‘naked’ genome is the immediate object, and the sequence of stages in ontogeny corresponds to different states of the dynamical object.
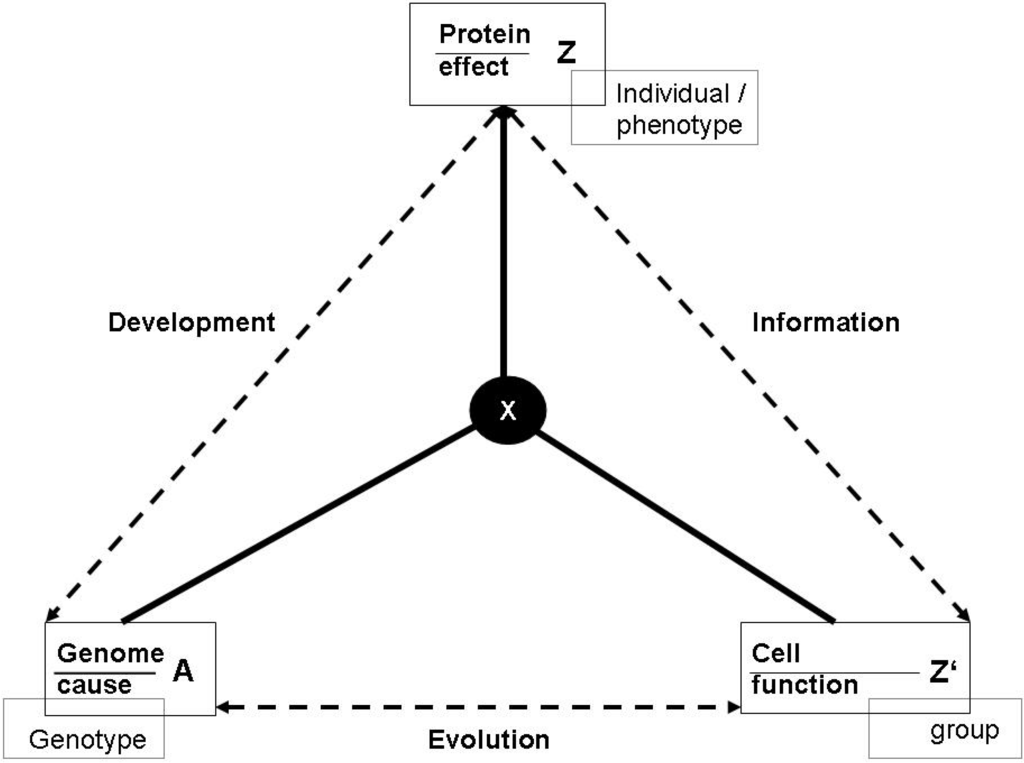
Figure 11.
Function and semiosis in the genotype/phenotype relation.
This approach yields many interesting insights: I have added three other boxes, namely the genotype and the phenotype, understood here as human individual. The information that the phenotype gives about the genotype can only reside in an embedding function, which means, in the environment. The latter is, as a most important example, constituted by human groups. Thus, it is the group in which those features of the individual are identified that may be causally related with the object, the genotype. Development is a process where certain causal interactions between object and sign are being functionally specified, enhanced and even created: Without development, no significance of the so-called information stored in the genome [42,43]. This is precisely the reason why in a purely Shannon interpretation of this relation the parity thesis holds, that is, the information that is said to be expressed in the phenotype can be both seen as being carried in the genotype or the environment. This oscillation can be resolved in the Peircian triangle.
Then it is also straightforward to understand why similar genetic material can have very different effects in different organisms, while at the same time many effects maintain a particular identity, and why there is no clear relation between genome complexity and the complexity of the organism. This is because of different functional contexts which have evolved through time. In a nutshell, the most significant difference between a genome of a mouse and the genome of a human is just that: The human genome is part of a human organism, and the mouse’s genome is part of a mouse organism. It is the difference in the interpretant that matters in semiosis, not the difference in the object, i.e., the genome. However, at the same time we have to recognize that, following Figure 11, in the semiotic chain the genome continues to play a role of the anchor. Only in this sense we can speak of a central role of the gene in evolution.
The radical conclusion of my arguments is that semiosis does not require the concept of meaning. This is, in a nutshell, what a naturalization of Peircian semiosis means. In the reconstructed Peircian triangle, there is also no place for meaning in the standard sense. The interpretant is a functioning that connects two levels of functions. In other words, if we believe to see a ‘meaning,’ we have not yet realized the embedding function.
Now, if we recognize that all functions are interconnected in some way, unless a total ontological separation occurs, we can state the general principle of a semiosphere. The notion of semiosphere has been used by Lotman [103] in a purely mentalist sense, related to literature, the arts and language. Hoffmeyer [104] has extended it into a category of living systems in general, i.e., posits an equation between biosphere and semiosphere. I can now offer a naturalistic interpretation, which would imply that the semiosphere is the physical set of functionally interconnected signs. For practical matters, and inverting a discussion by Lotman himself, the semiosphere is just identical with the biosphere in the sense of another Russian scholar, Vernadsky (see the historical account by Smil [105]). Clearly, the biosphere is the set of all functions of living systems, reaching from the LUCA (last universal common ancestor), hence the most simple form of biological function, to the present, and it is therefore a case of infinite semiosis in the sense of Figure 10. Adopting this perspective, the semiosphere and the biosphere are just two sides of one coin, which is a common physical reality. This implies that our previous analysis of the role of energy flows in functions also applies for the semiosphere. This is the final step in naturalizing Peircian semiosis.
4.2. Energetics of the semiosphere
We can now re-enter the role of energy to the picture (compare [4,106]). To be more specific, the information relation between the sign and the interpretant corresponds to what Corning [10] has dubbed the ‘control information’. Similar ideas have been proposed also in other contexts, as in the previously mentioned ETIF theory of the origin of life [79]. However, semiotic analysis shows that the use of the term ‘information’ is misleading here. What is central is the notion of the sign as such. The sign obtains a central role in the entire process of evolving entropies, if we consider the energetic side. This is because the sign relates to the constraints of the object system, so that depending on the nature of this relation, certain energetic flows happen in a particular way. That is, only the sign is specific to the physical processes, whereas there is no particular physical realization of the so-called “control information”: It is literally smeared across the networks of functionings involving Z’, Z’’, …, so that, in the end, the physical complement of control information would be the entire system as such. Although this is true in a certain sense, it does not help to identify the more specific role of the sign in semiosis. This is easy to understand if we consider a technological function: If we want to steer a car, but we only have a device that shows us whether we drive slow or fast, we cannot use the car in the same way as if we have a more sensitive speedometer. This is independent from the fact that our brain certainly is able to operate the car more exactly. So, proper functioning essentially depends on the physical nature of the signs.
There are two direct relations between signs and energy. One is that the sign, as an effect of a function, directly operates as the causal trigger of energy transforming processes. For example, the sign can be part of a chemical reaction which catalyzes other reactions in a hypercycle. As such, the sign is the physical entity that makes a reduction of energy possible. In this sense, the sign is directed at an exogenous process involving energies. The other is the fact that the sign itself is physical and hence, corresponds to an matterenergy state. That is, functions have two sides of a coin: One is to change the size and direction of energy flows in a system, the other is to use energy by themselves. Both aspects are by no means directly related to each other. That is, there is no necessary relation between the size of energy flows related with the function and those related with its effect on the larger system. This is precisely the characteristic of control information in the Corning sense.
In this context, the general theory of evolution has a substantial extension which has been achieved by Zahavi and Zahavi [90]. This is the so-called ‘handicap principle’ which obtains a central position also in a naturalized semiotics. If we consider coupled systems in an evolutionary context, there is no prima facie reason why the information processed in the systems should be truthful. As in the case of cross-catalysis, all functional couplings can involve interactions which favour only one side. In a biological context, for example, if a prey can cheat a predator, it will survive to the detriment of the predator. The handicap principle states that evolutionary systems will evolve signalling systems in which signals transfer truthful signals because they are costly in energetic terms. This is also a theorem well-known from economics, e.g., labour markets. The argument rests upon the idea that, for example, a prey that would signal strength, can only send a signal that is truthful in the sense of the proper functioning of the predator, if the predator can interpret this unambigously. This is the case if the signal is costly, because only a costly signal can be afforded by a strong and healthy prey. So, the costly signal is an evolutionarily optimal solution to the problem of coordination between prey and predator. As I have already stated previously, the theory of signal selection implies that in the semiosis of living systems, there is an inherent tendency to increase energy throughputs, as a most universal indicator of costs, and this is because the information processed is approximating the true states in coupled functions. This argument is a substantial modification to Corning’s notion of control information, which just focuses on the energetic efficiency. In the theory of signal selection, energy throughput becomes a sign itself.
As I have argued previously, signal selection can be seen as a correlate to Lotka’s principle. We can even hypothesize a direct relation between signal selection, the Red Queen principle, and Lotka’s principle:
Evolution with signal selection implies that there will be mutual leveraging of information transmitting signals, such that relative advantages tend to converge (Red Queen principle), with increasing levels of energy thoughput. (Lotka’s principle).
There is one possibility to directly relate Lotka’s principle with the energetics of signs. This is Chaisson’s [107,108] measure of free energy rate intensity Φm (measured in erg s-1g-1), whch is an intensive measure of complexity which includes the efficiency of a system in processing energy flows. Empirically, Chaisson hypothesizes about a general regularity of increasing Φm during the evolution of the world, which also applies to systems and subsystems. For example, protocells have a lower Φm than plants, or the human brain has a much higher energy rate intensity than the human body etc. Also, the miniaturization of technological functions involves an increasing free energy rate intensity.
Interestingly, Chaisson builds this approach on certain cosmological assumptions about the relation between maximum entropy and realized entropy, which goes back on the argument put forward by Layzer [94], that was also applied by the work of Brooks and Wiley [93] and Salthe [18], underlying my Figure 8. Therefore, without being able to go into more details here, we can think of directly applying Chaisson’s measure on signs as physical objects. That means, we can treat the signs as the physical complements of functions, insofar as all signs are structures of matterenergy. In this perspective, we can put forward the hypothesis that the evolution of the semiosphere follows a line of increasing free energy rate density as an expression of the fundamental processes of maximum entropy production that we have scrutinized in the previous sections. In other words, the increasing free energy rate density is just the evolving physical state of the world that results from maximum entropy production, thus corresponding to the Second Law. In Chaisson’s view, this principle unifies the spheres of physics, biology and human sciences (Figure 12).
This allows for an extension of Figure 8 into Figure 13. As Chaisson has argued, the general process of entropy increase correlates with the increasing population of the world with things that have a higher free energy rate density. This describes the evolution of the semiosphere, in the sense above. From this follows that we can give an additional interpretation of the lines in the diagram of Figure 8. The two areas below and above are the objects and the signs. The evolving interpretants as functions separate the semiosphere and the world of objects in the sense that both the objects and the signs are ontologically related to them. As an illustration, the evolving functions in terms of chemical reactions have resulted into an increasingly complex world of chemical objects. A chemical object is defined by the way how it reacts with other chemical objects. Therefore, it is the evolving set of functions qua reactions that defines the chemical world, which is, at the same time, observer relative, i.e., reaction specific. Below the line, we have the world of chemical objects in terms of their individuality, i.e., all existing realizations and mixtures of different chemical objects, such as in a puddle, and in real substances as opposed to pure substances. This is tantamount to the growth of entropyOR. On the other hand, the evolving functions result into a growing set of chemical signs, now understood as the corresponding pure substances that make up a reaction. This is the ultimate reason why the notion of substance is so central to chemistry [69,70]. With the notion of the substance, a set of constraints on physical processes in the world is identified, which evolve through time, in the course of the emergence of new kinds of substances and reactions, including synthetic chemistry. Again, we can put this into the Peircian triangle, with the quantum level view on the molecule being the object, the molecular shape as the sign, and the reactions as the interpretant.
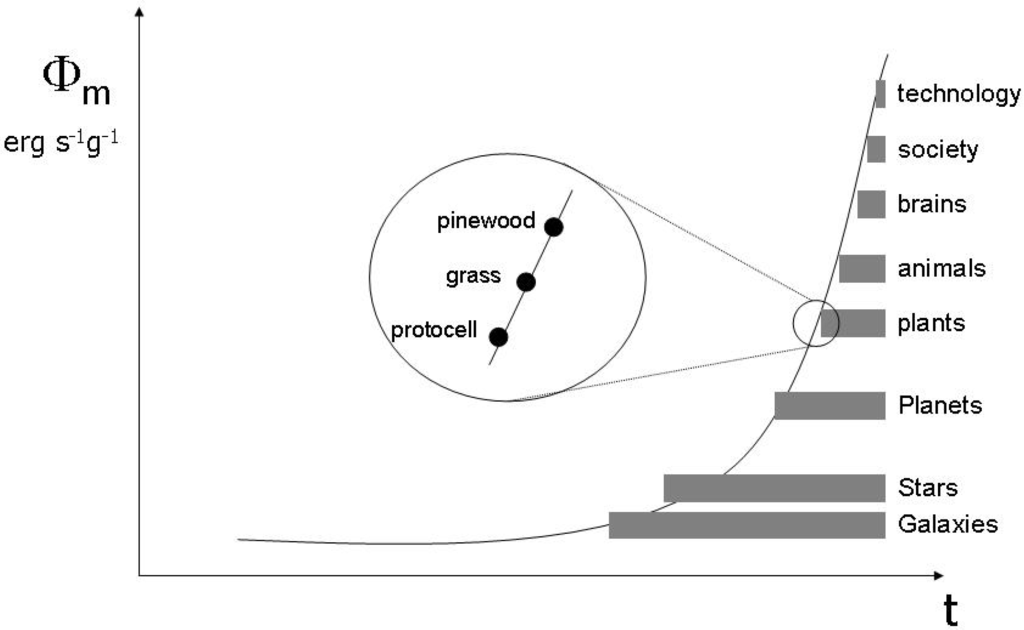
Figure 12.
Evolution of free energy rate intensity (exemplary, after Chaisson [81]).
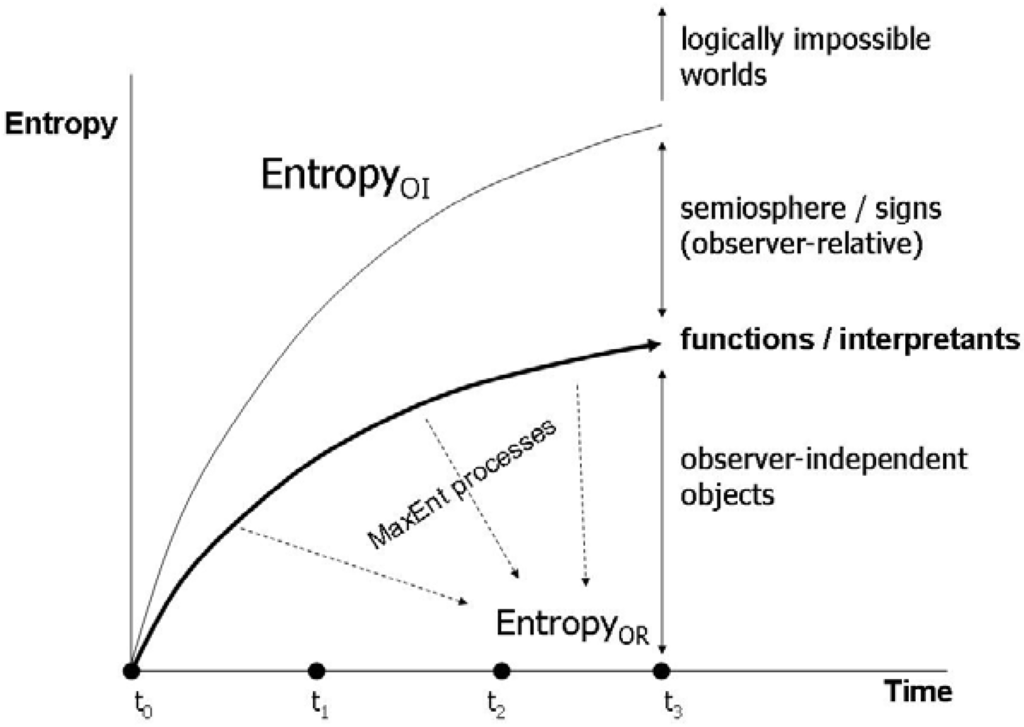
Figure 13.
Semiosphere and entropies.
As this example demonstrates, semiosis is indeed a universal feature of the physical world, which might even extend beyond the biological realm. This is a topic that I cannot further pursue here, but inheres the Chaisson approach that I already used in the previous argument. However, one particular aspect of semiosis deserves attention, that is, the relation between the semiosphere and the physical reality.
4.3. A semiotic reformulation of the anthropic principle
I will end this section with a speculation. Deutsch [78] argues that life is a physical phenomenon of a special sort since the process of selection causes the emergence of structures which converge across parallel universes, in the Everett interpretation of quantum theory, which he regards to be the only empirically valid one. His point is that selection operates in a way so that random variations are channeled towards adaptive states of higher fitness. That is, in a multiverse with varying environmental conditions and varying patterns of mutation of a genotye, as long as the variation is within a certain range, the adaptively optimal structures will be the same across different parallel universes. So, Deutsch argues that over a certain set of parallel universes, we might observe a huge variety of physical realizations of stars, geological formations and other structures of matterenergy, but at the same time a convergence of forms of life where it occurs, such as adaptive genotypes.
This argument can now be extended to the semiosphere in general. If semiosis is an evolutionary process, the semiosphere is a strong link across parallel universes. This is because semiosis is physically based on functions, and, following Deutsch, we can assume that functions converge across parallel universes because of the evolutionary forces of variation, selection and retention. As semiosis is a truly universal phenomenon, encompassing functions of many different kinds, especially mental, technological, biological and semantic, we can therefore conclude, extending on Deutsch, that the semiosphere is a phenomenon of fundamental physical significance. Interestingly, this corresponds to the Peircian view of assigning the status of ‘Firstness’ to the signs, and seeing the objects as ‘Secondness’. That would correspond to the view that the semiosphere is the fundamental anchor for unifying reality across parallel universes, manifesting an infinite diversity of objects otherwise. If the laws of physics are the foundations of the unity of the multiverse, we can now state that the semiosphere provides the basis for the physically contingent, but physically universal convergence of certain structures, i.e., the signs. The two physical phenomena are related through the fundamental laws of thermodynamics, as we have seen. This implies that thermodynamics is as foundational as quantum theory, as it is the only theory that can explain why the range of randomness in the multiverse is restricted, that is to say, why the multiverse may have an encompassing structure that goes beyond the laws of fundamental physics.
A quick thought shows that this reasoning applies on all kinds of functions: For example, basic patterns of the genetic material may converge, as structures of bacterial communication, or cultural artefacts of human societies, insofar as the follow an evolutionary trajectory, patterned by the Darwinian principles of variation, selection and retention. That is, we can describe the fundamental ontology as being divided into a set of different zones (Figure 14): The logically impossible; the physically possible, but not realized; the multiverse consisting of parallel universes in the quantum view; and the semiosphere which links the parallel universes.
However, as we have seen, a central process characteristics of semiosis is the concurrence of the MaxEnt principle with the principle of MEP, the result of which is the convergence of signs with the constraints of the object systems with which functions causally interact. From this follows, that the convergence of the semiosphere also must imply a convergence of object systems across the multiverse. This is an idea that has been ventilated recently in Elitzur’s [12] definition of life (for a corresponding view in biosemiotics, see [36]). Elitzur argues that the information dynamics, in conjunction with the thermodynamics, leads to the emergence of living structures whose forms are increasingly independent from the specific realizations of matterenergy. Forms, in his view, reflect the basic invariant spatio-temporal regularities in physical reality. We can translate this into the view that the semiosphere is the physical realization of this set of emerging forms (which corresponds to the original Peircian notion of ‘habits’ in the world, understood as emerging physical regularities).
Figure 14.
Basic ontology and the semiosphere.
This perspective allows for a fresh view on one of the most disputed hypotheses in recent physical speculative cosmological thinking, which is the anthropic principle. In one of its original versions, the anthropic principle states that the physical laws in the universe must have taken the form to make life possible, because firstly, this is what we state empirically today, i.e., life exists, and secondly, because there is a number of lawlike physical magnitudes, in particular constants, which are highly improbable and cannot be deduced from universal physical laws. Thus, the value of the constants is explained as resulting from the requirement to make life possible. As it is easy to recognize, the anthropic principle is a statement about a function in the sense of this paper: The physical laws (X) have the emergence of life as a consequence (Z), and this is why they have the shape that they have. In recent restatements of the anthropic principle, this has been made more tractable, for example, by string theorists when they argue that there is a multiplicity of universes having different physical constants, such that life just happens to be in that universe where the constant fits [109]. This is, basically, an evolutionary argument without relying on selection (so, just thinking of a huge expanding set of possibilities). There are also more strictly evolutionary renderings of the anthropic principle, such as in the theory of natural selection of universes, which eschew the implicit anthropomorphism [110,111].
With regard to the Deutsch argument, and my reconstruction of the role of the semiosphere, it is possible to refute one argument against the anthropic principle that has been put forward by Penrose precisely with reference to the Everett view [45]. Penrose uses Schrödinger’s cat as an example. Basically, the argument about the fit between life and different possible universes can also be recast in the parallel universe framework favoured by Deutsch. Penrose thinks that this is not feasible because, as in the example of Schrödinger’s cat, the Everett view would imply that there is a set of possible states which includes entangled states of the object and the observer, such as combining the states of ‘dead cat’ with ‘pervceiving life cat’ etc, which cannot happen because they are contradictory. This would imply that the anthropic principle, which highlights the central role of the observer, cannot help to fix this problem, as long as it is cast in the framework of quantum theory exclusively.
However, if we approach this question from the viewpoint developed in this paper, and arguing along the Deutsch lines, then we would now state critically that Penrose, in describing physical states as propositions, introduces a purely mental observer which has no physical meaning. Instead, we would look at the evolution of the underlying functions, and hence the semiosis that makes the process of observation possible. In this view, and corresponding to the general teleosemantic approach, relations of observation are part and parcel of an evolutionary process in which proper functionings emerge. The requirement of proper functioning, however, imposes a constraint on physically possible entanglements of states, which would then ne identified with certain propositions by an external observer (such as Penrose). So, the combination of a dead cat with the state of the observer who sees a live cat is not evolutionarily stable, if the cat, in the past of human phylogeny, was a dangerous animal. This is precisely what Deutsch has in mind when he says that evolution causes structural convergence across parallel universes. In other words, the evolution of the multiverse and the evolution of the semiosphere/biosphere are physically interconnected in a foundational sense.
So, I end up with proposing an alternative to the anthropic principle, the semiotic principle. Physical reality inheres both the constraints of the physical laws and the constraints of the evolving semiosphere, which in turn converges with physical constraints, following the processes of maximum entropy production. Interestingly, this might converge with the views of one of the leading protagonists of evolutionary epistemology, whom Deutsch also quotes approvingly, namely Karl Popper [65,112]. Popper has posited the theory of ‘three worlds’, with world 3 being the products of the human mind. We can make better sense of this now in doing away with the human mind as the ultimate reference, and interpreting ‘world 3’ as the semiosphere. The semiosphere, however, is not a world apart, but part and parcel of the unified physical world.
5. The Final Brick: Meaning and Paradox
I have tried to show that we can understand Peircian semiosis in purely physical terms. In the literature, there are two different views on this possibility. One view states that this naturalization finally has to fail because it cannot deal with the notion of ‘consciousness’, with which the notions of ‘intentionality’ and ‘meaning’ are essentially related [2]. In the literature on Peirce, this is also reflected in the diversity, if not opacity of the different interpretations given to the fundamental concepts of ‘Firstness’, ‘Secondness’ and ‘Thirdness’ [21]. One school of thought argues, and certainly also finds strong confirmation with Peirce himself, that ‘Firstness’ corresponds to the notion of internal mental states. This is the reason why biosemiotics frequently tends to argue in an anthropomorphic fashion, even though, at the same time, a naturalistic framework is adhered to in principle [14]. At the same time, as I have indicated previously, there are also other statements by Peirce in which the sign is assigned to the category of Firstness. Indeed, qualia, internal mental states, are a major issue in the philosophy of mind, as intentional states are as well. How can we resolve this tension?
This is a very difficult issue, and I only want to present a largely forgotten argument that has been developed by Hayek more than fifty years ago [22], leaving a more detailed discussion for another paper (compare [113]). This argument states, in my parlance, that systems with nested and networked functions will always develop “meaning” as a category of functioning to refer to themselves, because self-reference entails fundamental logical paradoxes. Hayek applied this argument on the brain as a neuronal system; it can be translated on other systems in a homologous way (compare e.g., Ben Jacob [96] on self referential genomes).
I can be quick here, because I assume that most readers of this article are familiar with the larger background. What is distinctive with Hayek’s view is that he presents a fully-fledged physicalist view of the human brain and relates this with a perspective on logical paradoxes which comes close to the Gödel theorems (which Hayek himself only has realized much later [114]), thus adopting a view which today is maintained, for example, in the universal theory of cellular automata and computation [115]). Hayek argues that the brain can be seen as a purely physical network of neurons and their interactions. Such kind of a network, according to Hayek, can never give a full acount of its own operations in physical terms, because that would require to build a copy of itself with larger complexity than its own, which is a contradiction in terms. Hayek states that the notion of ‘mind’ just refers to the total ensemble of the neuronal network, which, so to speak, cannot be viewed upon from the outside. This notion is a functional substitute for the impossible construction of a workable internal copy of itself. The argument also applies for the description of other neuronal systems, as long as this also would have to include the model that the other system employs of the observing system (compare [116]): So, in order to predict the behavior of another system, the system needs to rely on a concept of ‘mind’ that substitutes for a full model, which would fall into the trap of paradoxes of self-referentiality (interestingly, ‘mentalizing’ is an empirical fact about the cognitive growth of human infants, and presumably the self-perception of ‘mind’ results from an internalization of projections of intentionality onto others, see [117,118,119]).
However, according to Hayek, this implies that also all constituent neuronal processes will be interpreted as being ‘mental’ phenomena, because the full significance, even though being a purely functional one, of the single process rests on its embeddedness in the entire system. In other words, the explanatory gap on the level of the entire system affects all explanations on the lower levels. From this follows that any kind of neuronal system, when referring to itself, will always introduce the ‘mental’ as a category that closes this gap. In other words, the ‘mental’ has a particular function in resolving a certain task in a neuronal system, namely the function of self-reference. That is, the naturalization of the ‘mental’ as qualia eventually relates back to the notion of evolution: A neuronal system that is not able to handle the paradoxes of self-referentiality would be weeded out by natural selection in the competition with systems that evolve the category of the ‘mental,’ for instance, for the simple reason that the latter can respond faster, as they do not get stuck in infinite regresses and other consequences of set-theoretic paradoxes of self-referentiality. So, in this view, the ‘mind’ is nothing but a special function.
Hayek’s argument seems to be directly relevant for our approach to semiotics. Hayek posits a strictly physicalist ontology, and in fact he describes a most general system of nested functions in the brain. Yet, he recognizes a place for the category of ‘meaning.’ This, however, is clearly limited to a particular kind of explanations, namely explanations that are self-referential. There is a clear connection with the many arguments in the literature on the Gödel theorem which state that, if applied on fundamental issues of mind and intelligence, Gödel has shown that there is a place for intuition and autonomous human thought and creativity [120,121]. Yet, I would now add that this has no ontological implications, in the sense of introducing a separate category of ‘mind’.
In the context of the naturalization of semiosis we can take the notion seriously that the mental has a function. We only need to accept the view that qualia are in fact signs, which emerge in the communication between brains about their self-referential states. The problem with relating the signs to the objects results from the fact that in the case of self-referentiality, abduction faces fundamental logical limits that have been shown up by the Gödel theorem and related theorems. So, if at all, qualia are an epistemological problem, but not an ontological one. Qualia cannot put into doubt the coherence of the naturalistic approach to semiotics.
6. Conclusions
In this paper I have embarked on the construction of a naturalistic approach to semiosis that essentially builds on the notion of entropy as one central concept. This perspective is as close to the original Peirce, as it also departs substantially. The point of convergence lies in the attempt to take the fundamental fact of randomness of the world seriously, which corresponds to Peirce’s so-called ‘Tychism’, the point of dissent lies in avoiding the anthropomorphic implications of the notion of semiosis, which would result into an ontological hypostasis of the category of the ‘mental’.
There are two core ideas which clear the ground for this exercise. One is to regard functions as a special kind of physical causation, which connects with the general evolutionary paradigm, which is also central in Peirce’s thinking. The evolutionary, that is, selectionist argument is not necessary to explain functions as such, but to explain the emergence of nested functions. The latter is crucial to get a full view on semiosis in a naturalistic perspective. The other idea is to establish a conceptual link between Jaynes’ notion of entropy and functions in terms of observations. There is an important bridge between the two concepts, which is the notion of observer relativity. This notion plays the role of a conceptual catharsis with reference to any possible tendency to anthropomorphism. This is not only useful to clarify semiosis, but also some aspects of the concept of entropy.
One main result of this conceptual blending is that I can present a naturalistic interpretation of Jaynes inferential concept of entropy. If I substitute the ‘anthropomorphic’ observer by a sequence of evolving functions, basically following generalizations of evolutionary epistemology, I can draw the conclusion that functional evolution will end in a relation between function and object system in which the function reflects the constraints of the object system on the macrolevel, corresponding to a state of maximum entropy on the microlevel. Further, in the naturalistic framework, this interpretation of Jaynes inference implies that the object system also manifests maximum entropy production. From this follows, that the evolution of functions obeys to the Second Law.
Once this framework is established, it is relatively straightforward to complete the naturalization of semiosis, if one recognizes the equation between function and interpretant. I have discussed extensions that follow from that, in particular the notion of the semiosphere. The naturalization of semiosis allows to establish conceptual linkages with other recent approaches to entropy and evolution, such as Chaisson’s approach.
I think that this approach can be very useful to substantiate applications of the notion of entropy cross-disciplinary. A most promising field is economics, where so far the concept of entropy is mostly related to the analysis of energy flows and environmental issues, following Georgescu-Roegen [23], who, incidentally, had serious conceptual difficulties with Boltzmann entropy, which we can avoid in my approach. Critics mostly concentrate on the resulting high level of abstraction, rendering the notion almost meaningless in the empirical sense, and the perceived irrelevance for analyzing fundamental economic processes such as innovation which build on human creativity, seen as a mental phenomenon (see e.g., [122]). The notion of the semiosphere can help to build a new bridge between physics and economics, as it concentrates on the evolution of human artefacts in the context of economic systems, which function as signs that coordinate economic interactions (for a related approach, still without the Peircian perspective, see my [123]). The analysis of technological artefacts is a research tradition that is lost in economics today (for earlier approaches, see [124]), and only very recently rediscovered (e.g., [125]). A naturalized Peircian semiotics can offer a synthesis.
Acknowledgements
Thanks to Nicole Lünsdorf, who directed my attention to the Jaynes notion of entropy, and thanks to John Hartley, who introduced me to Lotman’s work. The entire project was incited by reading Søren Brier’s book on Cybersemiotics. Thanks are due to him and his critical remarks that helped me to sharpen my argument.
References and Notes
- Volkenstein, M.V. Entropy and Information; Birkhäuser: Basel, Boston, Berlin, 2009. [Google Scholar]
- Brier, S. Cybersemiotics. Why Information Is Not Enough! University of Toronto Press: London, UK, 2008. [Google Scholar]
- Maroney, O. Information processing and thermodynamic entropy. The Stanford Encyclopedia of Philosophy; Fall 2009 ed.. Edward, N., Ed.; The Metaphysics Research Lab Center for the Study of Language and Information Stanford University. http://plato.stanford.edu/archives/fall2009/entries/information-entropy/ (accessed on 3 January 2010).
- Taborsky, E. The complex information process. Entropy 2000, 2, 81–97. [Google Scholar] [CrossRef]
- Landauer, R. Irreversibility and heat generation in the computing process (reprint). IBM J. Res. Develop. 1961/2000, 4, 261–269. [Google Scholar]
- von Baeyer, H.C. Information. The New Language of Science; Harvard University Press: Cambridge, MA and London, USA and UK, 2003. [Google Scholar]
- Aunger, R. The Electric Meme. A New Theory of How We Think; Free Press: New York, NY, USA, 2002. [Google Scholar]
- Bunge, M. Ontology I: The furniture of the world. In Treatise on Basic Philosophy; Reidel: Dordrecht, Netherland, 1977; Volume 3. [Google Scholar]
- Schrödinger, E. What Is Life? The Physical Aspect of the Living Cell; Cambridge University Press: Cambridge, UK, 1944. [Google Scholar]
- Corning, P.A. Holistic Darwinism. Synergy, Cybernetics, and the Bioeconomics of Evolution; Chicago University Press: London, UK, 2005. [Google Scholar]
- Ben Jacob, E.; Shapira, Y.; Tauber, A.I. Seeking the foundations of cognition in bacteria: from schrödinger’s negative entropy to latent information. Physica A 2006, 359, 495–524. [Google Scholar] [CrossRef]
- Elitzur, A.C. When form outlasts its medium: a definition of life integrating platonism and thermodynamics. In Life as We Know It; Seckbach, J., Ed.; Kluwer Academic Publishers: Dordrecht, Netherland, 2005; pp. 607–620. [Google Scholar]
- Peirce, C.S. The Essential Peirce. Selected Philosophical Writings; Houser, N., Kloesel, C., Eds.; Indiana University Press: Bloomington, IN, USA, 1992; Volume 1. [Google Scholar]
- Vehkavaara, T. Why and how to naturalize semiotic concepts for biosemiotics. Sign Syst. Stud. 2002, 30, 293–313. [Google Scholar]
- Emmeche, C. The chicken and the orphan egg: on the function of meaning and the meaning of function. Sign Syst. Stud. 2002, 30, 15–32. [Google Scholar]
- Jaynes, E.T. Gibbs vs. Boltzmann Entropies. Amer. J. Phys. 1965, 33, 391–398. [Google Scholar] [CrossRef]
- Searle, J.R. The Construction of Social Reality; Free Press: New York, NY, USA, 1995. [Google Scholar]
- Salthe, S.N. Development and Evolution. Complexity and Change in Biology; MIT Press: Cambridge MA and London, USA and UK, 1993. [Google Scholar]
- Macdonald, G.; Papineau, D. (Eds.) Teleosemantics. New Philosophical Essays; Oxford University Press: Oxford, New York, NY, USA, 2006.
- Seager, W.; Sean, A.-H. Panpsychism. The Stanford Encyclopedia of Philosophy; Edward, N.Z., Ed.; The Metaphysics Research Lab Center for the Study of Language and Information Stanford University, 2007. http://plato.stanford.edu/archives/spr2007/entries/panpsychism/ (accessed on 12 August, 2008).
- Burch, R.; Charles, S. Peirce. The Stanford Encyclopedia of Philosophy; Spring 2010 ed.. Edward, N.Z., Ed.; The Metaphysics Research Lab Center for the Study of Language and Information Stanford University, 2010. http://plato.stanford.edu/archives/spr2010/entries/peirce/ (accessed on 5 January, 2010).
- von Hayek, F.A. The Sensory Order. An Inquiry into the Foundations of Theoretical Psychology; University of Chicago Press: Chicago, IL, USA, 1952. [Google Scholar]
- Georgescu-Roegen, N. The Entropy Law and the Economic Process; Harvard University Press: Cambridge, MA, USA, 1971. [Google Scholar]
- Ayres, R.U. Information, Entropy, and Progress. A New Evolutionary Paradigm; AIP Press: New York, NY, USA, 1994. [Google Scholar]
- Ayres, R.U.; Warr, B. Accounting for growth: the role of physical work. Struct. Change Econ. Dyn. 2005, 16, 181–209. [Google Scholar] [CrossRef]
- Ruth, M. Insights from thermodynamics for the analysis of economic processes. In Non-equilibrium Thermodynamics and the Production of Entropy. Life, Earth, and Beyond; Kleidon, A., Lorenz, R., Eds.; Springer: Heidelberg, Germany, 2005; pp. 243–254. [Google Scholar]
- Annila, A.; Salthe, S. Economies evolve by energy dispersal. Entropy 2009, 11, 606–633. [Google Scholar] [CrossRef]
- Floridi, L. Semantic Conceptions of information. The Stanford Encyclopedia of Philosoph; Spring 2007 ed.. Edward, N.Z., Ed.; The Metaphysics Research Lab Center for the Study of Language and Information Stanford University, 2007. http://plato.stanford.edu/archives/spr2007/ entries/information-semantic/ (accessed on1 March, 2009).
- Bub, J. Maxwell’s demon and the thermodynamics of computation. arXiv:quant-ph/0203017, 2002. [Google Scholar] [CrossRef]
- Bennett, C.H. Notes on landauer’s principle, reversible computation, and maxwell’s demon. arXiv:physics/0210005, 2003. [Google Scholar] [CrossRef]
- Lloyd, S. Ultimate physical limits to computation. arXiv:quant-ph/9908043, 2000. [Google Scholar]
- Lloyd, S. Computational capacity of the universe. arXiv:quant-ph/0110141, 2001. [Google Scholar] [CrossRef]
- Lloyd, S. Progamming the Universe. A Quantum Computer Scientist Takes on the Cosmos; Knopf: New York, NY, USA, 2006. [Google Scholar]
- Zeilinger, A. A foundational principle for quantum mechanics. Found. Phys. 1999, 29, 631–643. [Google Scholar] [CrossRef]
- Floridi, L. Information. In The Blackwell Guide to the Philosophy of Computing and Information; Floridi, L., Ed.; Blackwell: Oxford, UK, 2003; pp. 40–61. [Google Scholar]
- El-Hani, C.N.; Queiroz, J.; Emmeche, C. A semiotic analysis of the genetic information system. Semiotica 2006, 160, 1–68. [Google Scholar] [CrossRef]
- Smith, J.M. The concept of information in biology. Phil. Sci. 2000, 67, 177–194. [Google Scholar] [CrossRef]
- Griffiths, P.E. Genetic information: A metaphor in search of a theory. Phil. Sci. 2001, 68, 394–412. [Google Scholar] [CrossRef]
- Rheinberger, H.-J.; Staffan, M.-W. Gene. The Stanford Encyclopedia of Philosophy; Fall 2007 ed.. Edward, N.Z., Ed.; The Metaphysics Research Lab Center for the Study of Language and Information Stanford University. http://plato.stanford.edu/archives/fall2007/entries/gene/ (accessed on 3 June, 2008).
- Küppers, B.-O. Der Ursprung biologischer Information. Zur Naturphilosophie der Lebensentstehun; Piper: München, Zürich, 1986. [Google Scholar]
- Hoffmeyer, J. The biology of signification. Perspect Biol.Med. 2000, 43, 252–268. [Google Scholar] [CrossRef] [PubMed]
- Oyama, S. Evolution’s Eye. A Systems View of the Biology-Culture Divide; Duke University Press: Durham NC and London, USA and UK, 2000. [Google Scholar]
- Oyama, S. The Ontogeny of Information. Developmental Systems and Evolution; Duke University Press: Durham NC and London, USA and UK, 2001. [Google Scholar]
- Dretske, F. Knowledge and the Flow of Information, Reprint ed.; CSLI Publications: Stanford, CA, USA, 1981/1999. [Google Scholar]
- Penrose, R. The Road to Reality. A Complete Guide to the Laws of the Universe; Knopf: New York, NY, USA, 2006. [Google Scholar]
- Jaynes, E.T. The second law as physical fact and as human inference. http://bayes.wustl.edu/etj/articles/second.law.pdf/ (accessed 12 November 2009).
- Gull, S.F. Some misconceptions about entropy. http://www.ucl.ac.uk/~ucesjph/reality/ entropy/text.html/ (accessed on 3 December, 2009).
- Laughlin, R.B. A Different Universe. Reinventing Physics From the Bottom Down; Basic Books: New York, NY, USA, 2005. [Google Scholar]
- Schaffer, J. The metaphysics of causation. The Stanford Encyclopedia of Philosophy; Winter 2007 ed.. Edward, N.Z., Ed.; The Metaphysics Research Lab Center for the Study of Language and Information Stanford University. http://plato.stanford.edu/archives/win2007/entries/causation-metaphysics/ (accessed on 3 March, 2008).
- Woodward, J. Making Things Happen. A Theory of Causal Explanation; Oxford Uiniversity Press: Oxford, UK, 2003. [Google Scholar]
- McLaughlin, B.; Bennett, K. Supervenience. The Stanford Encyclopedia of Philosophy; Fall 2006 ed.. Edward, N.Z., Ed.; The Metaphysics Research Lab Center for the Study of Language and Information Stanford University. http://plato.stanford.edu/archives/fall2006/entries/supervenience/ (accessed on 3 April, 2007).
- Perlman, M. Changing the mission of theories of teleology: dos and don’ts for thinking about function. In Functions in Biological and Artifical Worlds; Krohs, U., Kroes, P., Eds.; MIT Press: Cambridge, MA, 2009; pp. 17–35. [Google Scholar]
- Wright, L. Functions. Philos. Rev. 1973, 82, 139–168. [Google Scholar] [CrossRef]
- Smith, J.M.; Szathmáry, E. The Major Transitions in Evolution; Freeman: New York, NY, USA, 1995. [Google Scholar]
- Stein, R. Towards a process philosophy of chemistry. HYLE–Int. J. Philos. Chem. 2004, 10, 5–22. [Google Scholar]
- Vermaas, P.E. On unification: taking technological functions as objective (and biological functions as subjective). In Functions in Biological and Artifical Worlds; Krohs, U., Kroes, P., Eds.; MIT Press: Cambridge, MA, USA, 2009; pp. 69–87. [Google Scholar]
- Searle, J.R. The Construction of Social Reality; Free Press: New York, NY, USA, 1995. [Google Scholar]
- Ziman, J. (Ed.) Technological Innovation as an Evolutionary Process; Cambridge University Press: Cambridge, MA, USA, 2000.
- Lewens, T. Innovation and population. In Functions in Biological and Artifical Worlds; Krohs, Ul., Kroes, P., Eds.; MIT Press: Cambridge, MA, USA, 2009; pp. 243–257. [Google Scholar]
- Campbell, D.T. Blind variation and selective retention in creative thought as in other knowledge processes. In Evolutionary Epistemology, Rationality, and the Sociology of Knowledge; Radnitzky, G., Bartley, W.W., III, Eds.; Open Court: La Salle, France, 1987/1960; pp. 91–114. [Google Scholar]
- Edelman, G.M. Neural Darwinism. The Theory of Neuronal Group Selection; Basic Books: New York, NY, USA, 1987. [Google Scholar]
- Edelman, Gerald M. Second Nature. Brain Science and Human Knowledge; Yale University Press: New Haven and London, 2006. [Google Scholar]
- Macdonald, G.; Papineau, D. Introduction: Prospects and Problems for teleosemantics. In Teleosemantics. New Philosophical Essays; Macdonald, G., Papineau, D, Eds.; Oxford University Press: New York, NY, USA, 2006; pp. 1–22. [Google Scholar]
- Ellis, G.F. On the nature of causation in complex systems. 2008. http://www.mth.uct.ac.za/~ellis/Top-down%20Ellis.pdf/ (accessed on 24 January, 2010).
- Popper, K.R. Objective Knowledge. An Evolutionary Approach; Oxford: Clarendon, UK, 1972. [Google Scholar]
- Bradie, M.; Harms, W. Evolutionary Epistemology. The Stanford Encyclopedia of Philosophy; Fall 2006 ed.. Edward, N.Z., Ed.; The Metaphysics Research Lab Center for the Study of Language and Information Stanford University, 2006. http://plato.stanford.edu/archives/fall2006/entries/epistemology-evolutionary/ (accessed on 24 July, 2008).
- Hendry, R.F. Is There Downward Causation in Chemistry? In Philosophy of Chemistry. Synthesis of a New Discipline; Baird, D., Scerri, E., McIntyre, L., Eds.; Springer: Dordrecht, Netherlands, 2006; pp. 173–190. [Google Scholar]
- Del Re, G. Ontological status of molecular structure. HYLE–Int. J. Philos. Chem. 1998, 4, 81–103. [Google Scholar]
- van Brakel, J. The nature of chemical substances. In Of Minds and Molecules. New Philosophical Perspectives on Chemistry; Bhushan, N., Rosenfeld, S., Eds.; Oxford University Press: New York, NY, USA, 2000; pp. 162–18. [Google Scholar]
- Schummer, J. The chemical core of chemistry I: a conceptual approach. HYLE–Int. J. Philos. Chem. 1998, 4, 129–162. [Google Scholar]
- Dewar, R.C. Maximum entropy production as an inference algorithm that rranslates physical assumptions into macroscopic predictions: don’ shoot the messenger. Entropy 2009, 11, 931–944. [Google Scholar] [CrossRef]
- Dewar, R.C. Maximum-entropy production and non-equilibrium statistical mechanics. In Non-equilibrium Thermodynamics and the Production of Entropy. Life, Earth, and Beyond; Kleidon, A., Lorenz, R., Eds.; Springer: Heidelberg, Germany, 2005; pp. 41–55. [Google Scholar]
- Kleidon, A.; Lorenz, R. (Eds.) Non-equilibrium Thermodynamics and the Production of Entropy. Life, Earth, and Beyond; Springer: Heidelberg, Germany, 2005.
- Kleidon, A. Non-equilibrium thermodynamics and maximum entropy production in the earth system: applications and implications. Naturwissenschaften 2009, 96, 653–677. [Google Scholar] [CrossRef] [PubMed]
- Virgo, N. From maximum entropy to maximum entropy production: a new approach. Entropy 2010, 12, 107–126. [Google Scholar] [CrossRef]
- Kleidon, A. Non-equilibrium thermodynamics, maximum entropy production and earth-system evolution. Philos. Trans. R. Sco. London A 2010, 368, 181–196. [Google Scholar] [CrossRef] [PubMed]
- Paltridge, G.W. A story and a recommendation about the principle of maximum entropy production. Entropy 2009, 11, 945–948. [Google Scholar] [CrossRef]
- Deutsch, D. The Fabric of Reality; Penguin: London, UK, 1997. [Google Scholar]
- Lahav, N.; Nir, S.; Elitzur, A.C. The emergence of life on earth. Progr. Biophys. Mol. Biol. 2001, 75, 75–120. [Google Scholar] [CrossRef]
- Hoffmeyer, J. Genes, development and semiosis. In Genes in Development. Re-reading the Molecular Paradigm; Neumann-Held, E., Rehmann-Sutter, C., Eds.; Duke University Press: London, UK, 2006; pp. 152–174. [Google Scholar]
- Sober, E.; Wilson, D.S. Unto Others. The Evolution and Psychology of Un-selfish Behavior; Harvard University Press: London, UK, 1998. [Google Scholar]
- Price, R.G. The Nature of Selection. J. Theor. Biol. 1995, 175, 389–396. [Google Scholar] [CrossRef] [PubMed]
- Kleidon, A.; Ralph, L. Entropy production in earth system processes. In Non-equilibrium Thermodynamics and the Production of Entropy. Life, Earth, and Beyond; Kleidon, A., Lorenz, R., Eds.; Springer: Heidelberg, Germany, 2005; pp. 1–20. [Google Scholar]
- Lotka, A. Contribution to the energetics of evolution. Proc. Natl. Acad. Sci. USA 1922, 8, 147–151. [Google Scholar] [CrossRef] [PubMed]
- Lotka, A. Natural selection as a physical principle. Proc. Natl. Acad. Sci. USA 1922, 8, 151–154. [Google Scholar] [CrossRef] [PubMed]
- Lotka, A. The law of evolution as a maximal principle. Human Biology 1945, 17, 167–194. [Google Scholar]
- Vermeij, G.J. Nature: An Economic History; Princeton University Press: Princeton, NJ, USA, 2004. [Google Scholar]
- Odum, H.T. Environment, Power, and Society for the Twenty-First Century. The Hierarchy of Energy; Columbia University Press: New York, NY, USA, 2007. [Google Scholar]
- Robson, A.J. Complex evolutionary systems and the red queen. Econ. J. 2005, 115, F211–F224. [Google Scholar] [CrossRef]
- Zahavi, A.; Zahavi, A. . The Handicap Principle. A Missing Piece of Darwin’s Puzzle; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Dawkins, R. The Selfish Gene. New edition; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Grafen, A. Biological signals as handicaps. J. Theor. Biol. 1990, 144, 517–546. [Google Scholar] [CrossRef]
- Brooks, D.R.; Wiley, E.O. Evolution as Entropy. Toward a Unified Theory of Biology; Chicago University Press: Chicago, IL, USA, 1988. [Google Scholar]
- Layzer, D. Growth of order in the universe. In Entropy, Information, and Evolution. New Perspectives on Physical and Biological Evolution; Weber, B.H., Depew, D.J., Smith, J.D., Eds.; MIT Press: Cambridge, MA, USA, 1988; pp. 23–40. [Google Scholar]
- Matthen, M. Teleosemantics and the consumer. In Teleosemantics. New Philosophical Essays; Macdonald, G., Papineau, D., Eds.; Oxford University Press: Oxford, UK, 2006; pp. 146–166. [Google Scholar]
- Ben Jacob, E. Bacterial wisdom, gödel’s theorem and creative genomic webs. Physica. A 1998, 248, 57–76. [Google Scholar] [CrossRef]
- Emmeche, C.; Hoffmeyer, J. From language to nature–the semiotic metaphor in biology. Semiotica 1991, 84, 1–42. [Google Scholar] [CrossRef]
- Atkin, A. Peirce's theory of signs. The Stanford Encyclopedia of Philosophy; Spring 2009 ed.. Edward, N.Z., Ed.; The Metaphysics Research Lab Center for the Study of Language and Information Stanford University. http://plato.stanford.edu/archives/spr2009/entries/peirce-semiotics/ (accessed on 3 January, 2010).
- Peirce, C.S. The Essential Peirce. Selected Philosophical Writings; Houser, N., Kloesel, C., Eds.; Indiana University Press: Bloomington, IN, USA, 1998; Volume 2. [Google Scholar]
- Neander, K. Content for cognitive science. In Teleosemantics. New Philosophical Essays; Macdonald, G., Papineau, D., Eds.; Oxford University Press: New York, NY, USA, 2006; pp. 167–194. [Google Scholar]
- Millikan, R. Biosemantics. J. Philos. 1989, 86, 281–297. [Google Scholar] [CrossRef]
- Millikan, R. Language: A Biological Model; Clarendon: Oxford, UK, 2005. [Google Scholar]
- Lotman, J. On the semiosphere. Sign Syst. Stud. 2005, 33, 205–229. [Google Scholar] [CrossRef]
- Hoffmeyer, J. Signs of Meaning in the Universe; Indiana University Press: Bloomington, IN, USA, 1999. [Google Scholar]
- Smil, V. Energy in Nature and Society. General Energetics of Complex Systems; MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Andrade, E. A Semiotic framework for evolutionary and developmental biology. Biosystems 2007, 90, 389–404. [Google Scholar] [CrossRef] [PubMed]
- Chaisson, E.J. Cosmic Evolution. The Rise of Complexity in Nature; Harvard University Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Chaisson, E.J. Non-equilibrium thermodynamics in an energy-rich universe. In Non-equilibrium Thermodynamics and the Production of Entropy. Life, Earth, and Beyond; Kleidon, A., Lorenz, R, Eds.; Springer: Heidelberg, Germany, 2005; pp. 21–31. [Google Scholar]
- Susskind, L. The Cosmic Landscape. String Theory and the Illusion of Intelligent Design; Little, Brown and Company: New York, NY, USA, 2006. [Google Scholar]
- Smolin, L. The Life of The Cosmos; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Smolin, L. Scientific alternatives to the anthropic principle. 2007; Cornell University Library; arXiv:hep-th/0407213. [Google Scholar]
- Popper, K.R. Realism and the Aim of Science; Hutchinson: London, UK, 1983. [Google Scholar]
- Herrmann-Pillath, C. The brain, its sensory order and the evolutionary concept of mind. on hayek's contribution to evolutionary epistemology. J. Soc. Biol. Struct. 1992, 15, 145–187. [Google Scholar]
- von Hayek, F.A. Studies in Philosophy, Politics, and Economics; Routledge & Kegan Paul: London, UK, 1967. [Google Scholar]
- Wolfram, S. A New Kind of Science; Wolfram Media: Champaign, IL, USA, 2002. [Google Scholar]
- Wolpert, D. Computational capabilities of physical systems. Phys. Rev. E. 2001, 65, 016128. [Google Scholar] [CrossRef]
- Tomasello, M.; Carpenter, M.; Call, J.; Behne, T.; Moll, H. Understanding and sharing intentions: the origin of cultural cognition. Behav. Brain Sci. 2005, 28, 675–735. [Google Scholar] [CrossRef] [PubMed]
- Frith, C.D.; Singer, T. The role of social cognition in decision making. Philos. Trans. R. Sco. London B 2008, 363, 3975–3886. [Google Scholar] [CrossRef] [PubMed]
- Frith, U.; Frith, C.D. Development and neurophysiology of mentalizing. Philos. Trans. R. Sco. London B 2003, 358, 459–473. [Google Scholar] [CrossRef] [PubMed]
- Penrose, R. The Emperor’s New Mind. Concerning Computers, Minds, and the Laws of Physics; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Lucas, J.R. Minds, machines, and Gödel. Philosophy 1961, XXXVI, 112–127. [Google Scholar] [CrossRef]
- Buenstorf, G. The Economics of Energy and the Production Process. An Evolutionary Approach; Edward Elgar: Cheltenham, UK, 2004. [Google Scholar]
- Herrmann-Pillath, C. The Economics of Identity and Creativity. A Cultural Science Approach; University of Queensland Press: Brisbane, Australia, 2010. [Google Scholar]
- Ayres, C.E. The Theory of Economic Progress; University of North Carolina Press: Chapel Hill, NC, USA, 1944. [Google Scholar]
- Pinch, T.; Swedberg, R. (Eds.) Living in a Material World. Economic Sociology Meets Science and Technology Studies; MIT Press: Cambridge, MA, USA, 2008.
© 2010 by the author; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).