Autonomously Moving Colloidal Objects that Resemble Living Matter
Abstract
:1. Introduction
2. Emergent Behavior and Autonomous Motion
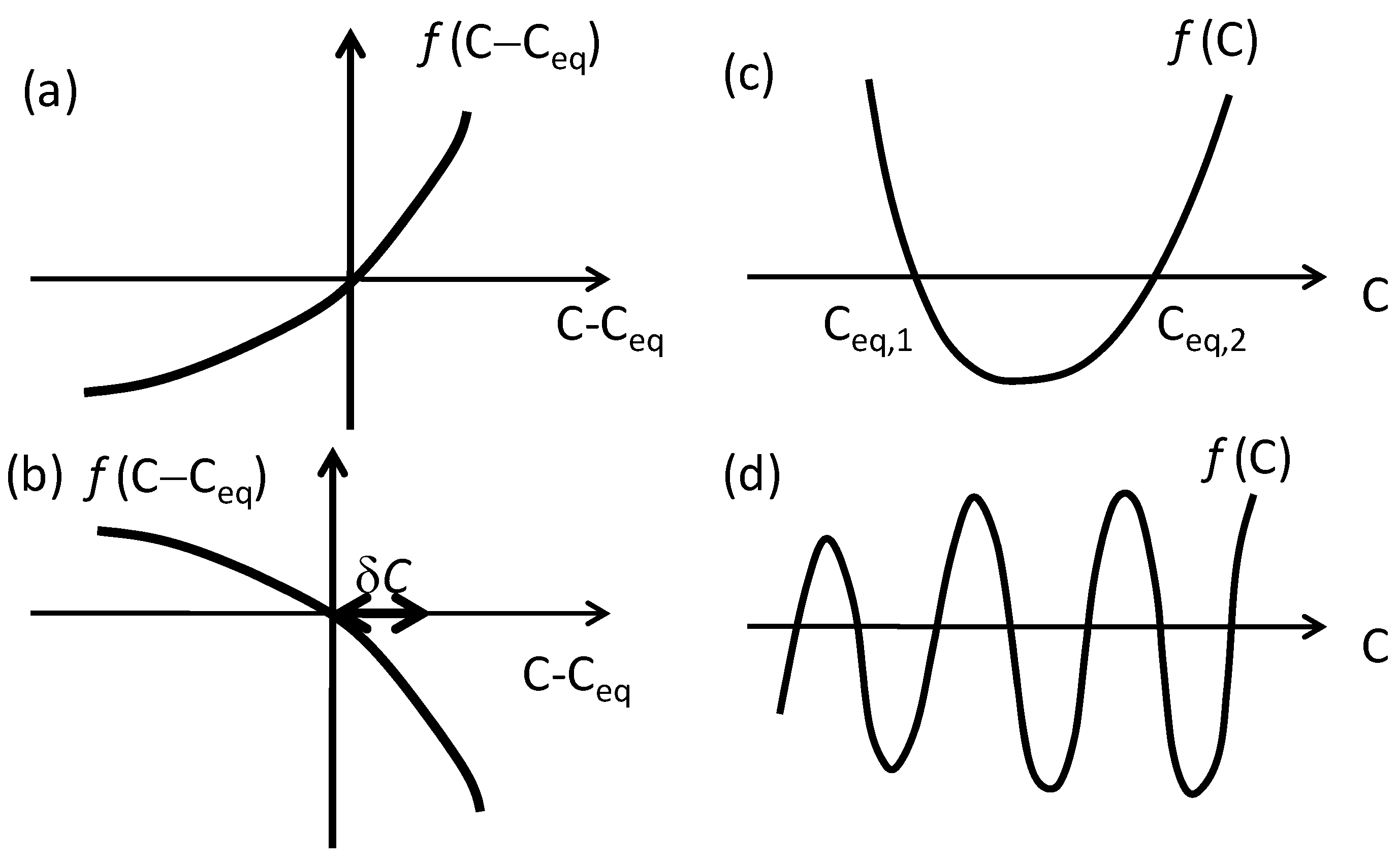
3. Autonomously Moving Droplet
3.1. Reactive Droplet on Solid Substrate

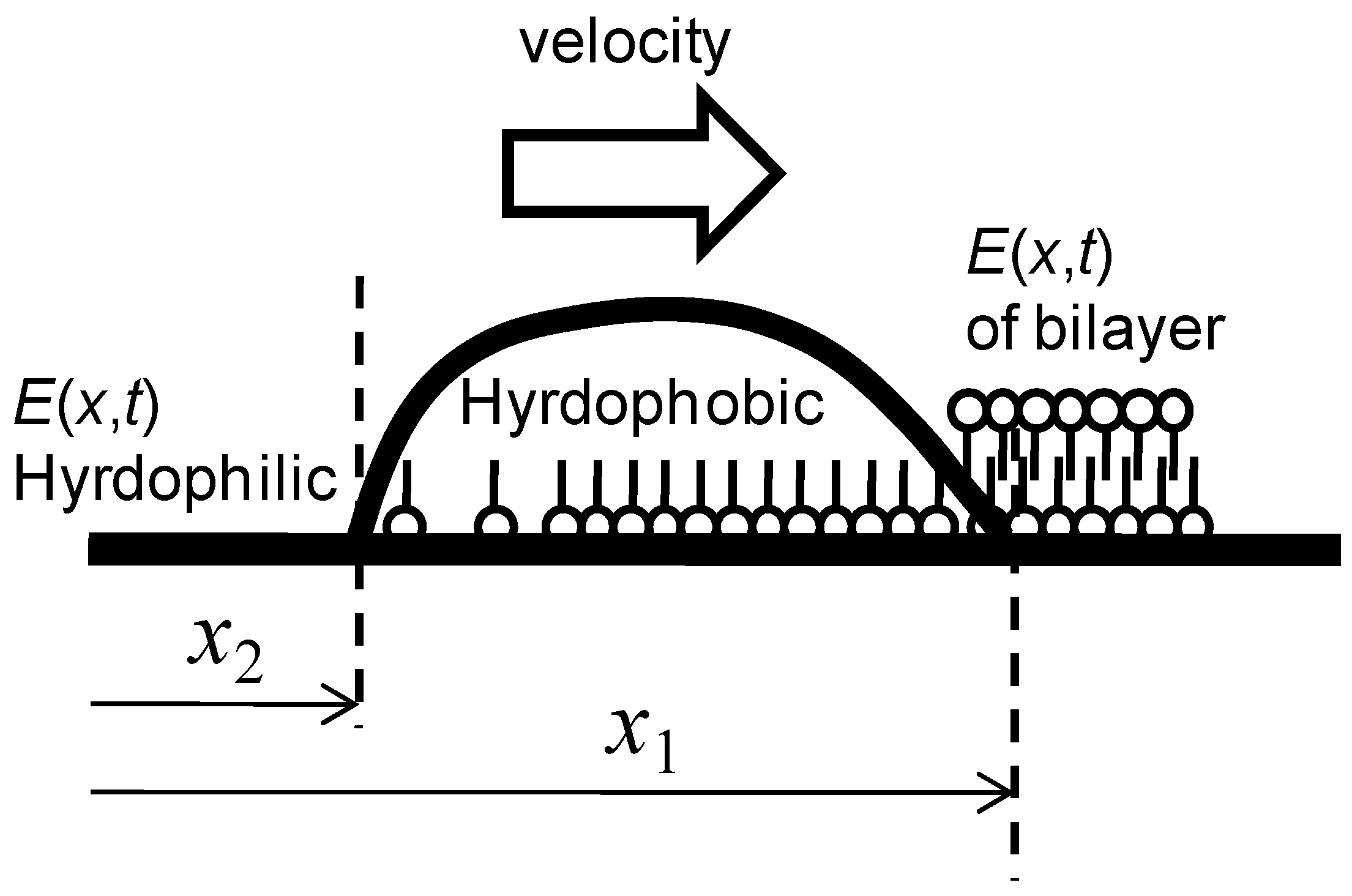
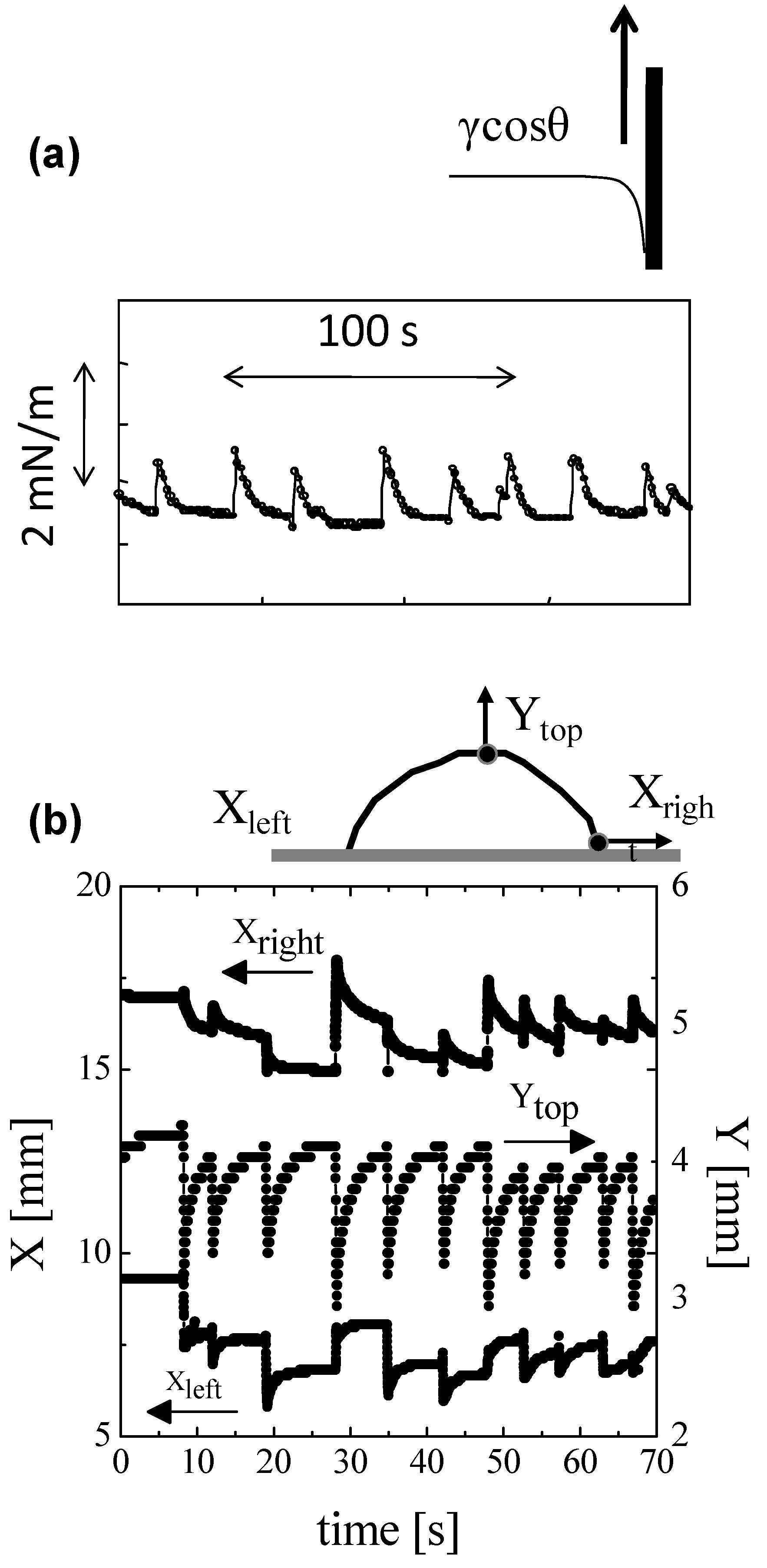
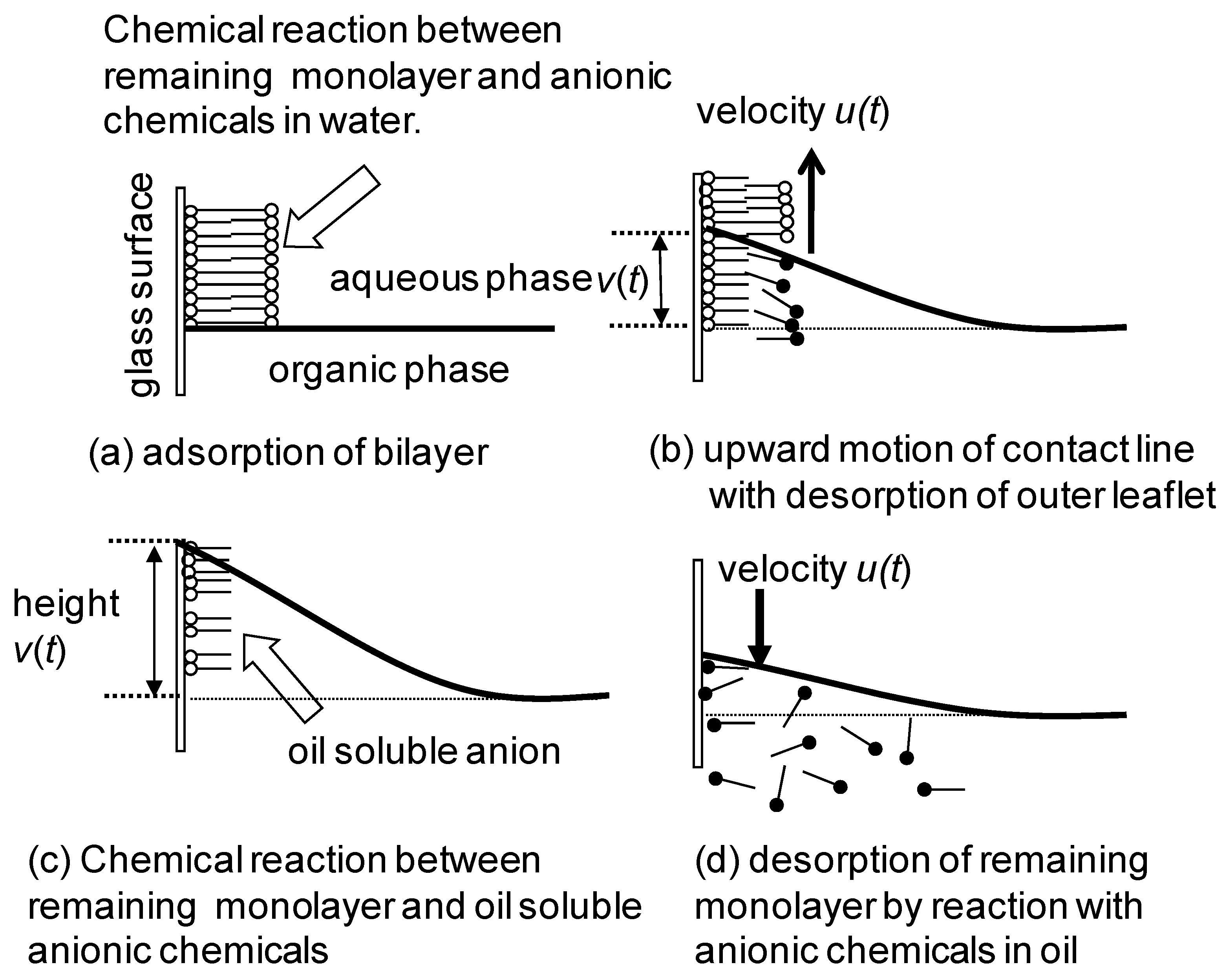
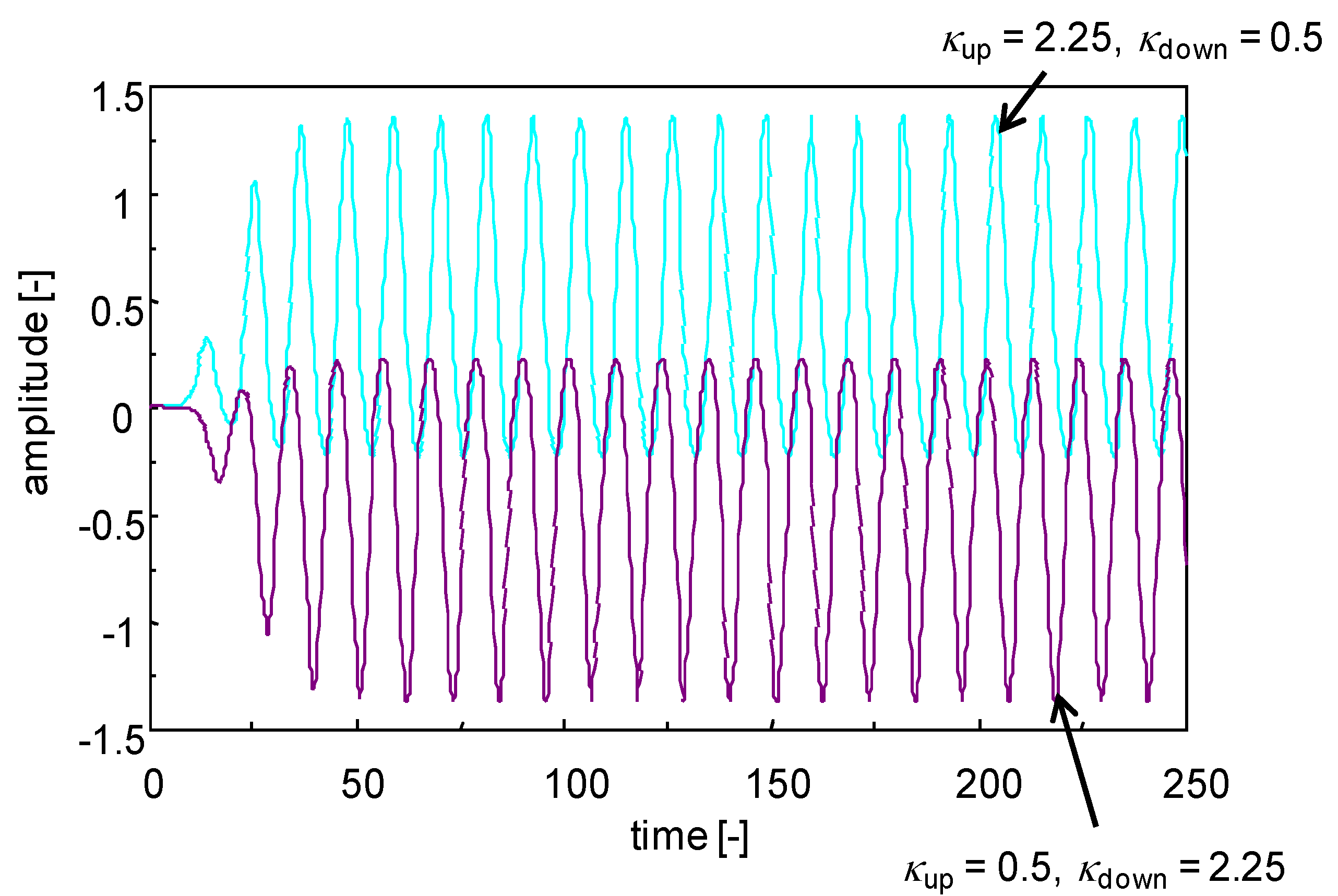
3.2. Droplet Motion without Solid Substrate
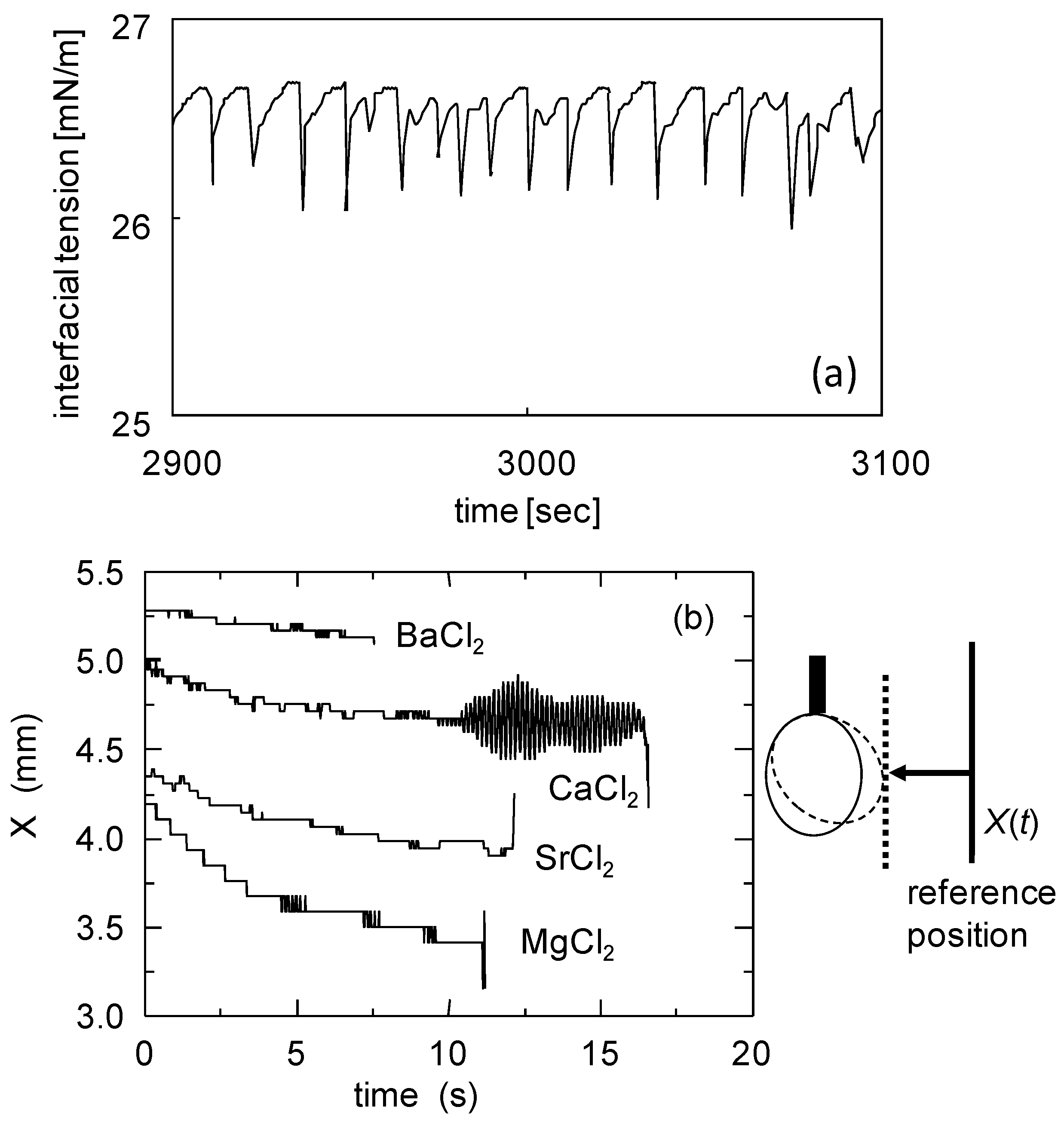
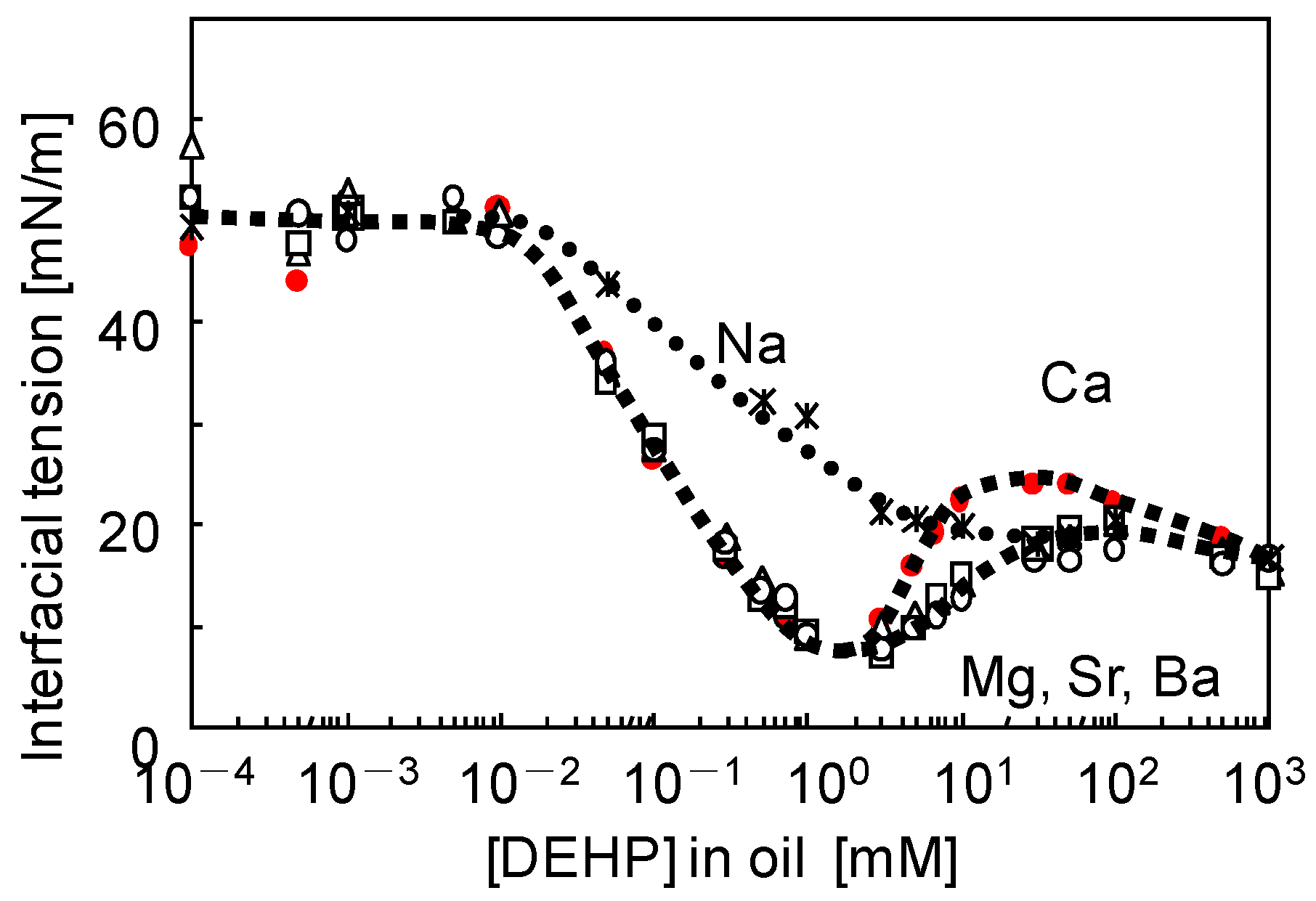
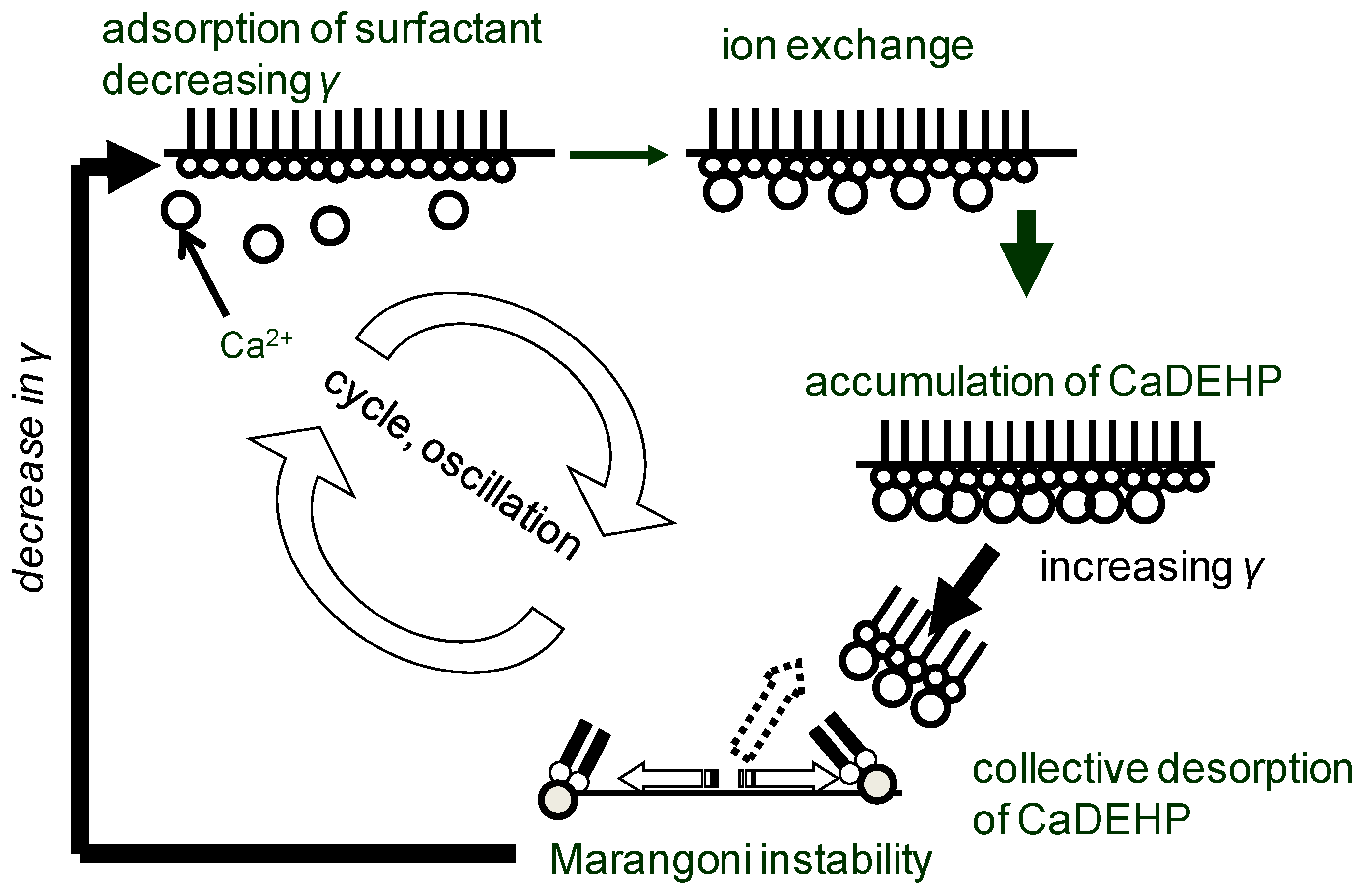
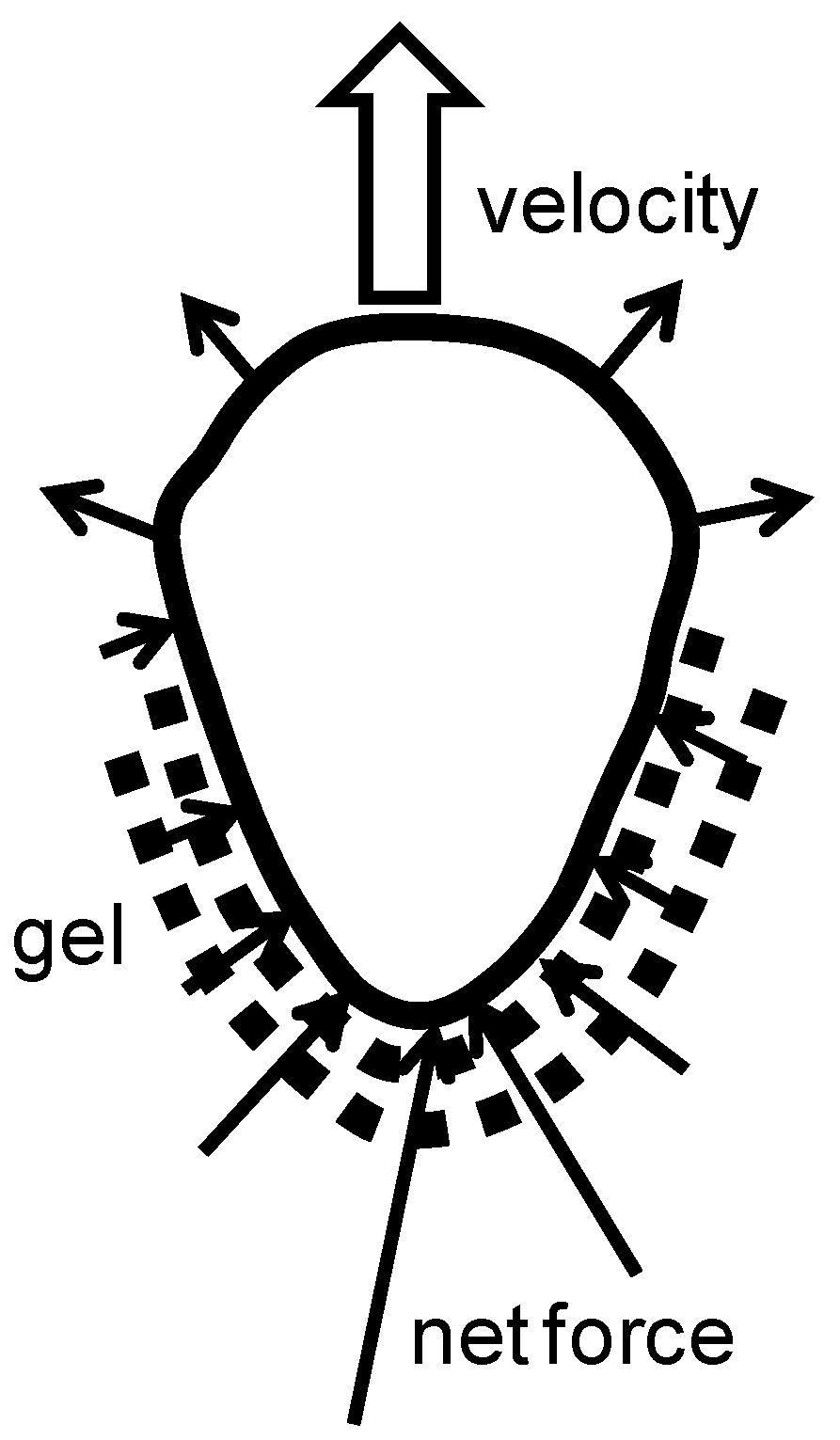
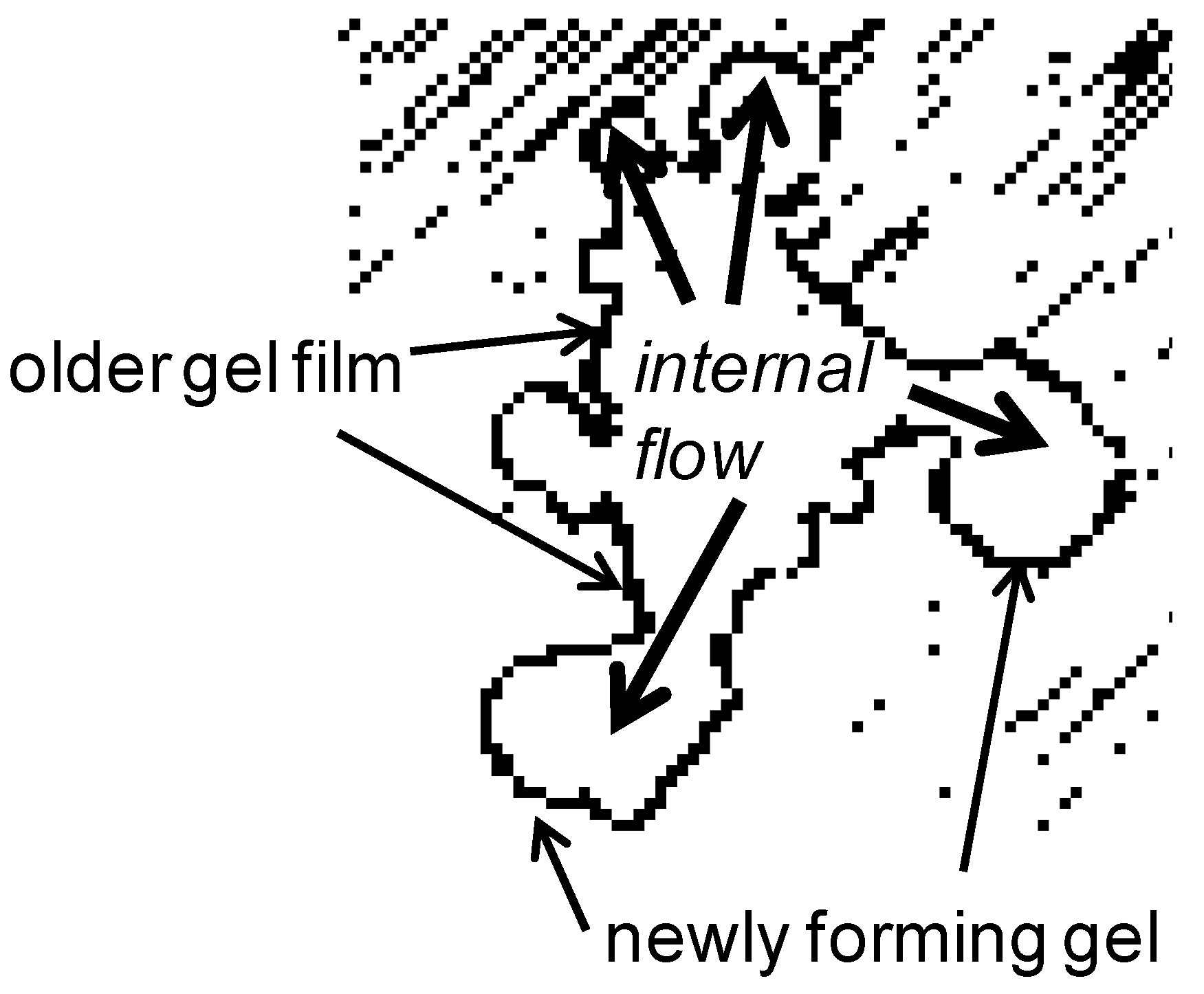
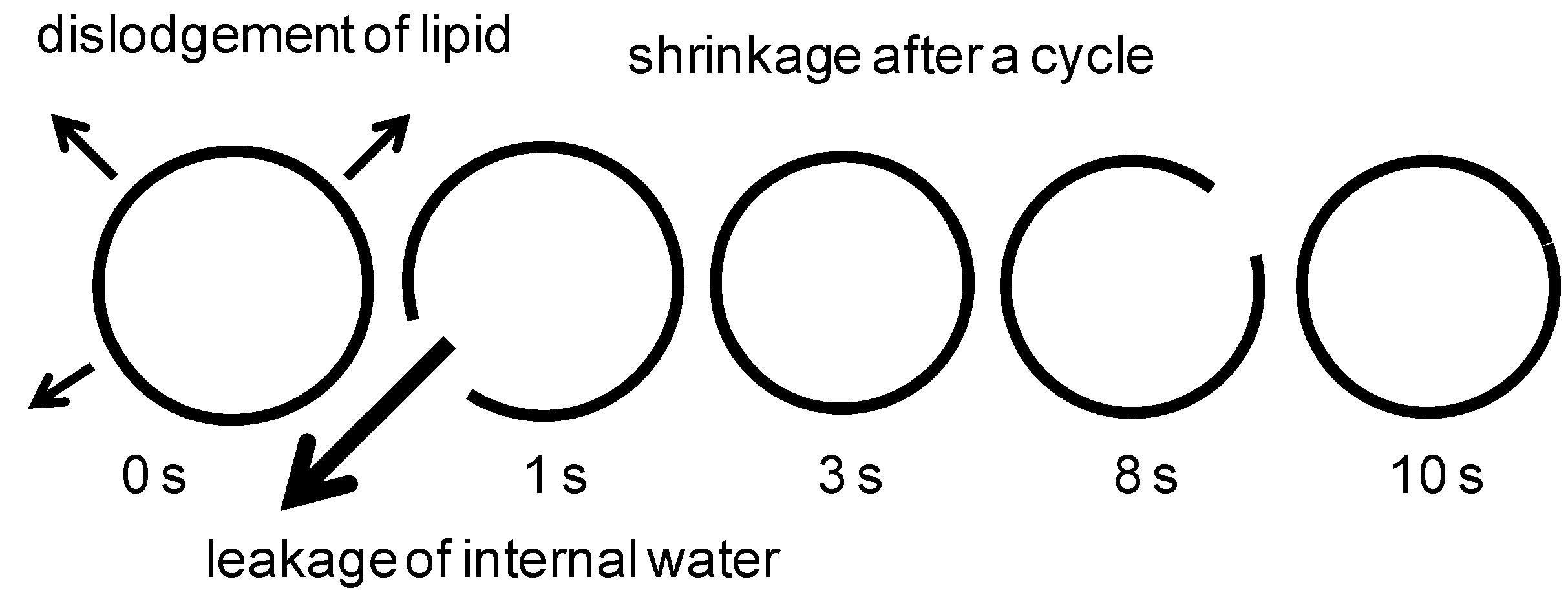
4. Autonomously Moving Vesicles

5. Autonomously Moving Particles
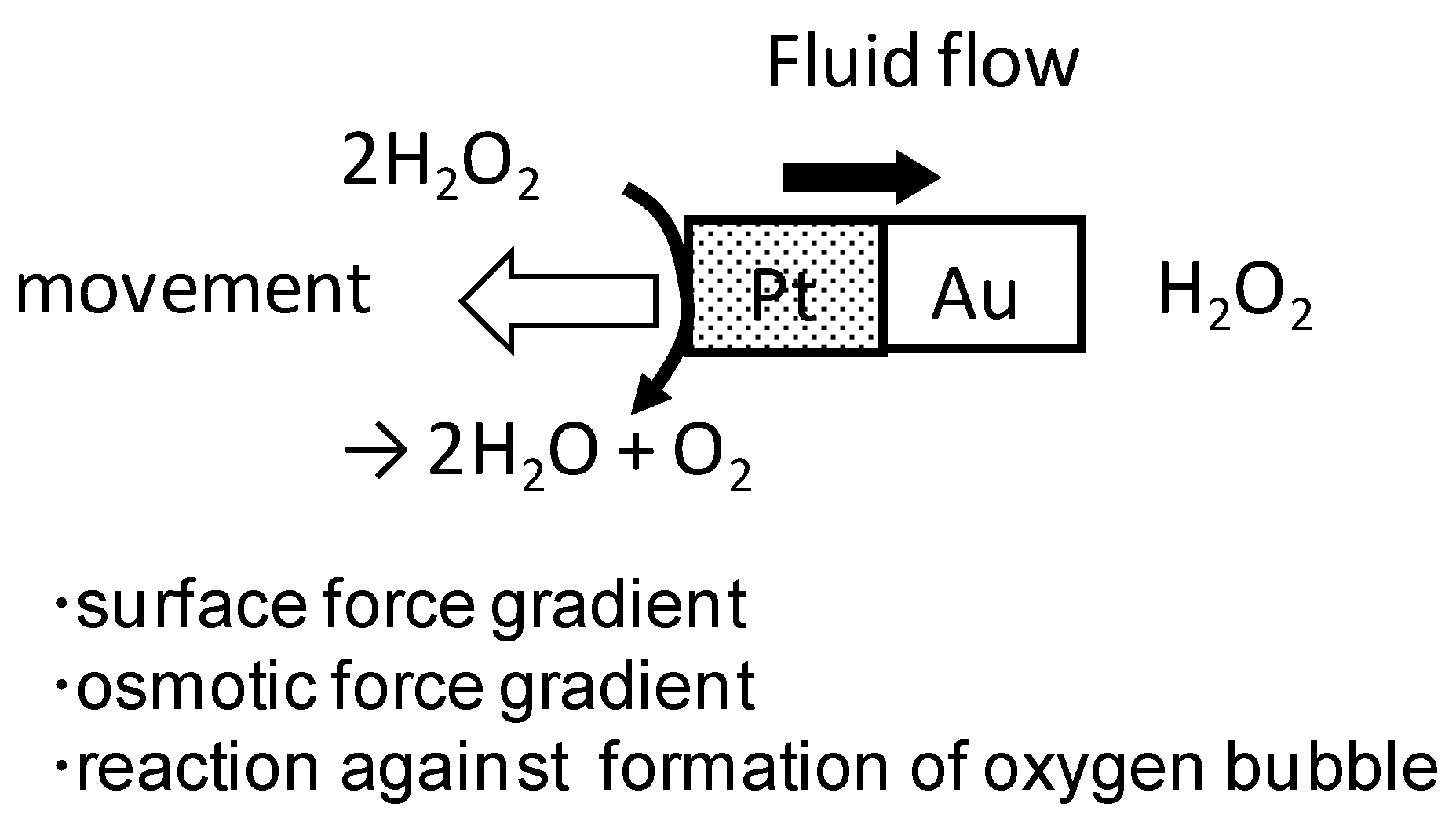
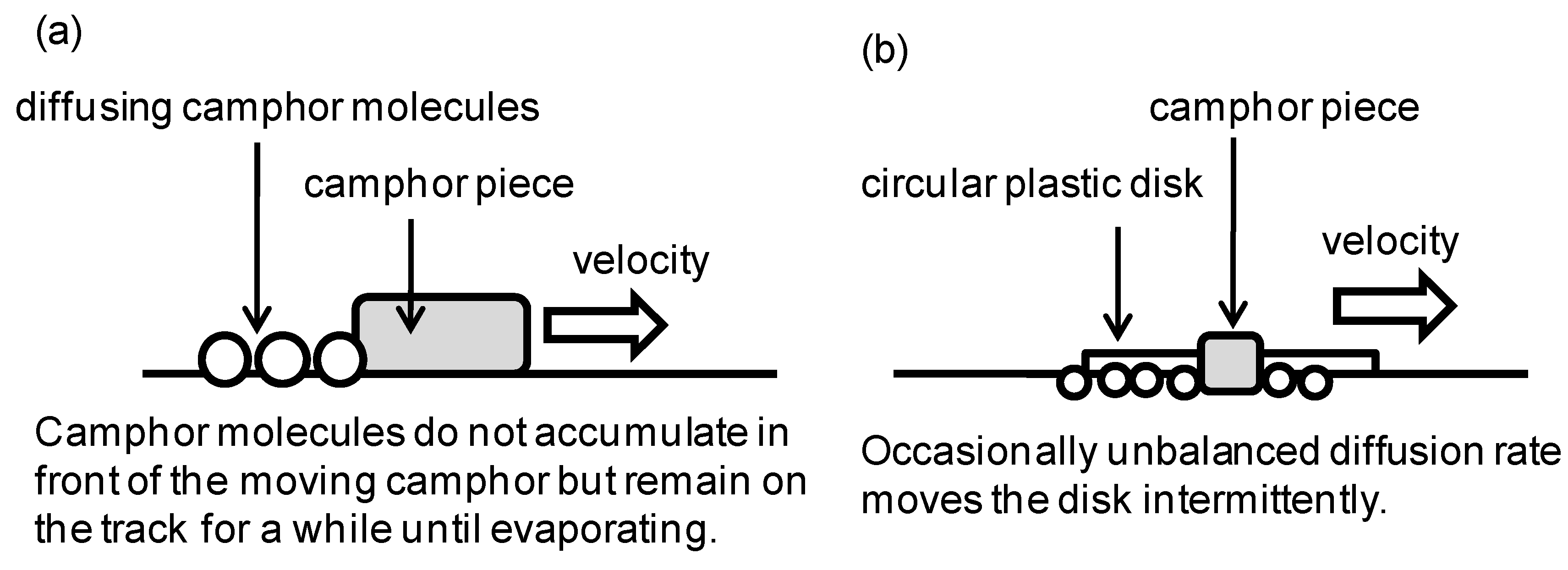
| Colloidal Object | Mechanism of Motion | References |
|---|---|---|
| droplet | surface energy gradient | [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,30,32,33,34,35,36,37,38,39,40,41,42,43,44,45] |
| elastic stress | [56,57] | |
| vesicle | surface energy gradient | [53] |
| elastic stress/membrane tension | [54,55,58] | |
| particle | surface energy gradient | [65,66,73,74,75,76] |
| diffusiophoresis, osmotic force | [62,63,64,67,68,69,70,71,72] |
6. Summary
References
- Lodish, H.; Berk, A.; Matsudaira, P.; Kaiser, C.A.; Krieger, M.; Scott, M.P.; Zipursky, S.L.; Darnell, J. Molecular Cell Biology, 5th ed.; W. H. Freeman and Company: New York, NY, USA, 2004. [Google Scholar]
- Sterling, C.V.; Scriven, L.E. Interfacial turbulence: Hydrodynamic instability and the marangoni effect. AIChE 1959, 5, 514–523. [Google Scholar] [CrossRef]
- Pearson, J.R.A. On convection cells induced by surface tension. J. Fluid Mech. 1958, 4, 489–500. [Google Scholar] [CrossRef]
- Brian, P.L.T.; Smith, K.A. Influence of Gibbs adsorption on oscillatory Marangoni instability. AIChE 1972, 18, 231–233. [Google Scholar] [CrossRef]
- Hilborn, R.C. Chaos and Nonlinear Dynamics an Introduction for Scientists and Engineers, 2nd ed.; Oxford University Press Inc.: New York, NY, USA, 2000. [Google Scholar]
- Colinet, P.; Legros, J.C.; Verlarde, M.G. Nonlinear Dynamics of Surface-Tension-Driven Instabilities; Wiley-VCH Verlag: Berlin, Germany, 2001. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; John Wiley & Sons, Inc.: New York, NY, USA, 1960. [Google Scholar]
- Zhabotinskii, A.M. Periodic course of oxidation of malonic acid in solution (investigation of the kinetics of the reaction of Belousov). Biophysics 1964, 9, 329–335. [Google Scholar]
- Field, R.J.; Noyes, R.M. Oscillations in chemical systems. IV. Limit cycle behavior in a model of a real chemical reaction. J. Chem. Phys. 1974, 60, 1877–1884. [Google Scholar] [CrossRef]
- Tyson, J.J.; Fife, P.C. Target patterns in a realistic model of the Belouzov-Zhabotinskii reaction. J. Chem. Phys. 1980, 73, 2224–2237. [Google Scholar] [CrossRef]
- Chaudhury, M.K.; Whitesides, G.M. How to make water run uphill. Science 1992, 256, 1539–1541. [Google Scholar] [CrossRef] [PubMed]
- Santos, F.D.D.; Ondarcuhu, T. Free-running droplets. Phys. Rev. Lett. 1995, 75, 2972–2975. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.W.; Laibinis, P.E. Directed movement of liquids on patterned surfaces using noncovalent molecular adsorption. J. Am. Chem. Soc. 2000, 122, 5395–5396. [Google Scholar] [CrossRef]
- Ichimura, K.; Oh, S.K.; Makagawa, M. Light-driven motion of liquids on a photoresponsive surface. Science 2000, 288, 1624–1626. [Google Scholar] [CrossRef] [PubMed]
- Wasan, D.T.; Nikolov, A.D.; Brenner, H. Droplets speeding on surfaces. Science 2001, 291, 605–606. [Google Scholar] [CrossRef] [PubMed]
- Daniel, S.; Chaudhury, M.K.; Chen, J.C. Fast drop movements resulting from the phase change on a gradient surface. Science 2001, 291, 633–636. [Google Scholar] [CrossRef] [PubMed]
- Bain, C.D. Motion of liquids on surfaces. ChemPhysChem 2001, 2, 580–582. [Google Scholar] [CrossRef]
- de Gennes, P.G. The dynamics of reactive wetting on solid surfaces. Physica A 1998, 249, 196–205. [Google Scholar] [CrossRef]
- Nakache, E; Dupeyrat, M.; Vignes-Adler, M. The contribution of chemistry to new Marangoni mass‑transfer instabilities at the oil/water interface. Faraday Discuss. Chem. Soc. 1984, 77, 189–196. [Google Scholar]
- Nakache, E.; Dupeyrat, M. Chemical reactions and oscillating potential difference variations at an oil-water interface. Bioelectrochemistry 1982, 9, 583–590. [Google Scholar] [CrossRef]
- Kai, S.; Muller, S.C.; Mori, T.; Miki, M. Chemically driven nonlinear waves and oscillations at an oil-water interface. Physica D 1991, 50, 412–428. [Google Scholar] [CrossRef]
- Yoshikawa, K.; Magome, M. Chemomechanical Transduction in an oil-water system. Regulation of the macroscopic mechanical motion. Bull. Chem. Soc. Jpn. 1993, 66, 3352–3357. [Google Scholar] [CrossRef]
- Miura, T. Private Communications in Doshisha University, Department of Chemical Engineering & Materials Science, Doshisha University: Kyotanabe, Kyoto, Japan, 2009.
- Shioi, A.; Katano, K.; Onodera, Y. Effect of solid walls on spontaneous wave formation at water/oil interfaces. J. Coll. Int. Sci. 2003, 266, 415–421. [Google Scholar] [CrossRef]
- Atkin, R.; Craig, V.S.J.; Wanless, E.J.; Biggs, S. Mechanism of cationic surfactant adsorption at the solid-aqueous interface. Adv. Colloid Interface Sci. 2003, 103, 219–304. [Google Scholar] [CrossRef]
- Kuragane, S.; Fujii, T.; Ban, T.; Shioi, A. Spontaneous wave driven by chemical autophobing with oscillatory dynamics at glass/oil/water interfaces. Colloid. Surface. A 2007, 311, 16–25. [Google Scholar] [CrossRef]
- Kitahata, K.; Yoshikawa, K. Chemo-mechanical energy transduction through interfacial instability. Physica D 2005, 205, 283–291. [Google Scholar] [CrossRef]
- Sumino, Y.; Magome, N.; Hamada, T.; Yoshikawa, K. Self-running droplet: Emergence of regular motion from nonequilibrium noise. Phys. Rev. Lett. 2005, 94, 068301. [Google Scholar] [CrossRef] [PubMed]
- Sumino, Y.; Kitahata, H.; Yoshikawa, K.; Nagayama, M.; Nomura, S.M.; Magome, N.; Mori, Y. Chemosensitive running droplet. Phys. Rev. E 2005, 1672, 041603. [Google Scholar] [CrossRef]
- Ban, T.; Suzuki, S.; Abe, S.; Shioi, A. Anionic control of autonomous motion of oil/water interface with cationic surfactant. Chem. Lett. 2007, 36, 1040–1041. [Google Scholar] [CrossRef]
- Ban, T.; Shioi, A. Autonomous motion of liquids interface controlled by chemical reaction. In Chemical Reaction on Surfaces; Duncan, J.I., Klein, A.B., Eds.; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2008; pp. 155–194. [Google Scholar]
- Shioi, A.; Ban, T.; Suzuki, S. Noise-induced kinetic model for autonomous motion of contact line in oil/water system with chemical reaction. Phy. Rev. E 2008, 77, 036208. [Google Scholar] [CrossRef]
- Morimune, Y.; Sugiyama, T.; Ban, T.; Shioi, A. Traveling wave patterns reproduced by a simple model for oil/water interface–Transducer of chemical potential into work–. Int. J. Soc. Mat. Eng. Resources 2010, 17, 115–119. [Google Scholar] [CrossRef]
- Shioi, A.; Ban, T.; Suzuki, S. Model of traveling wave formed by noise-induced autonomous motion of contact line with oil/water interface. Chem. Phys. Lett. 2008, 467, 210–215. [Google Scholar] [CrossRef]
- Lewis, J.B.; Pratt, H.R.C. Oscillating droplets. Nature 1953, 171, 1155–1156. [Google Scholar] [CrossRef]
- Ban, T.; Hatada, Y.; Takahashi, K. Spontaneous motion of a droplet evolved by resonant oscillation of a vortex pair. Phys. Rev. E 2009, 79, 031602. [Google Scholar] [CrossRef]
- Shioi, A.; Sugiura, Y.; Nagaoka, R. Oscillation of interfacial tension at liquid/liquid interface composed of di(2-ethylhexyl) phosphoric acid and calcium chloride. Langmuir 2001, 17, 4189–4195. [Google Scholar] [CrossRef]
- Shioi, A.; Kumagai, H.; Sugiua, S.; Kitayama, Y. Oscillation of interfacial tension and spontaneous interfacial flow at water/oil interface composed of di(2-ethylhexyl) phosphoric acid. Langmuir 2002, 18, 5516–5522. [Google Scholar] [CrossRef]
- Shioi, A.; Yamada, K.; Shiota, R.; Hase, F.; Ban, T. Chemically driven tension fluctuation and motion of interface with divalent cation and di(2-ethylhexyl)phosphoric acid. Bull. Chem. Soc. Jpn. 2006, 79, 1696–1703. [Google Scholar] [CrossRef]
- Ban, T.; Kurisaka, K.; Fujii, T.; Shioi, A. Ionic control of droplet motion. Chem. Lett. 2006, 35, 1134–1135. [Google Scholar] [CrossRef]
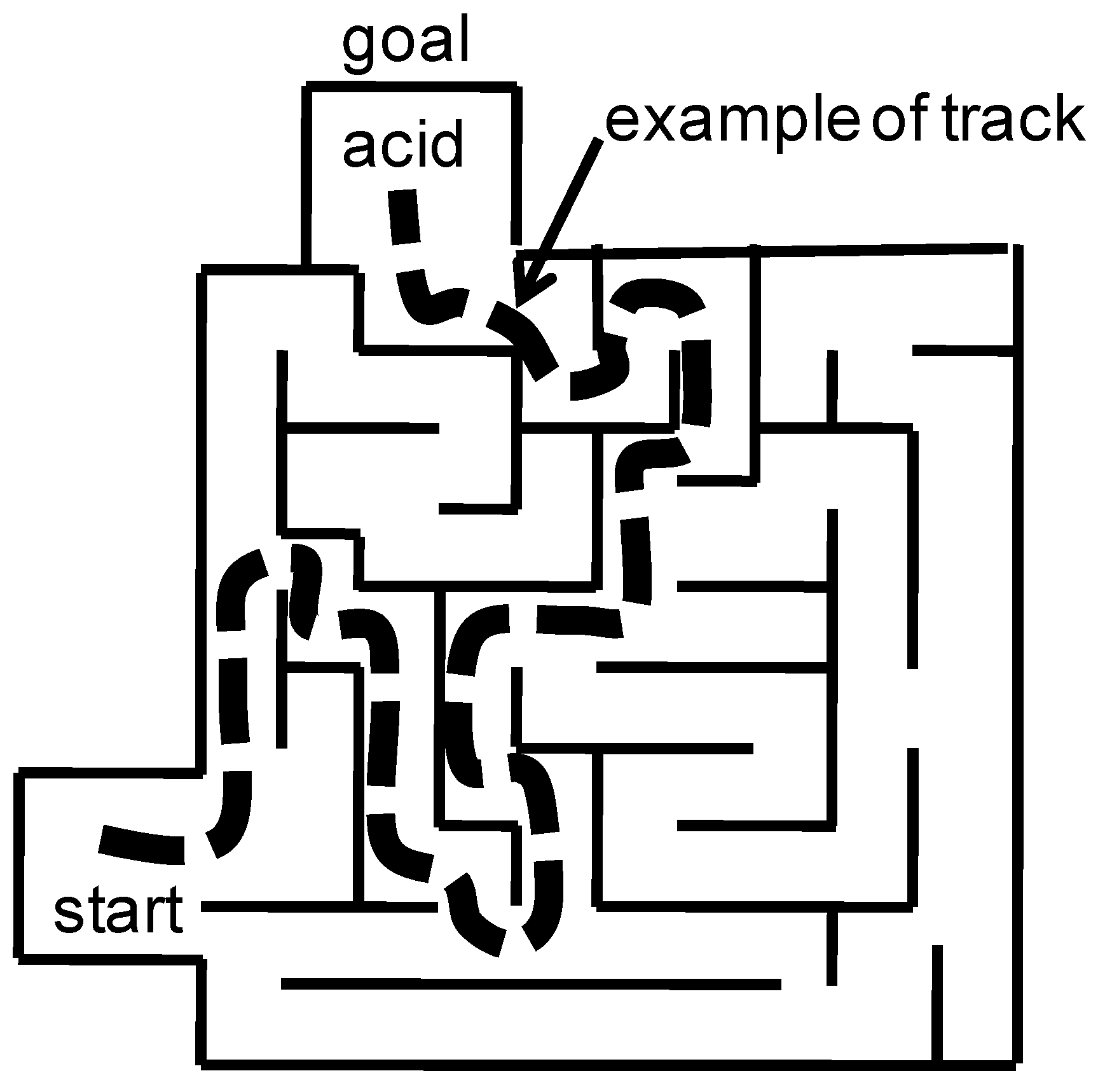
- Lagzi, I.; Soh, S.; Wesson, P.J.; Browne, K.P.; Grzybowski, B.A. Maze solving by chemotactic droplets. J. Am. Chem. Soc. 2010, 132, 1198–1199. [Google Scholar] [CrossRef] [PubMed]
- Nakagaki, T.; Yamada, H.; Toth, A. Path finding by tube morphogenesis in an amoeboid organism. Biophys. Chem. 2001, 92, 47–52. [Google Scholar] [CrossRef]
- Tero, A; Kobayashia, R.; Nakagaki, T. Physarum solver: A biologically inspired method of road‑network navigation. Physica A 2006, 363, 115–119. [Google Scholar]
- Toyota, T.; Maru, N.; Hanczyc, M.M.; Ikegami, T.; Sugawara, T. Self-propelled oil droplets consuming “fuel” surfactant. J. Am. Chem. Soc. 2009, 131, 5012–5013. [Google Scholar] [CrossRef] [PubMed]
- Hanczyc, M.M.; Toyota, T.; Ikegami, T.; Packard, N.; Sugawara, T. Fatty acid chemistry at the oil‑water interface: Self-propelled oil droplets. J. Am. Chem. Soc. 2007, 129, 9386–9391. [Google Scholar] [CrossRef] [PubMed]
- Peskin, C.S.; Odell, G.M.; Oster, G.F. Cellular motions and thermal fluctuations: The Brownian ratchet. Biophys. J. 1993, 65, 316–324. [Google Scholar] [CrossRef]
- Mogilner, A.; Oster, G. Cell motility driven by actin polymerization. Biophys. J. 1996, 71, 3030–3045. [Google Scholar] [CrossRef]
- Gerbal, F.; Chaikin, P.; Rabin, Y.; Prost, J. An elastic analysis of Listeria monocytogenes propulsion. Biophys. J. 2000, 79, 2259–2275. [Google Scholar] [CrossRef]
- Mogilner, A.; Oster, G. Force generation by actin polymerization II: The elastic ratchet and tethered filaments. Biophys. J. 2003, 84, 1591–1605. [Google Scholar] [CrossRef]
- Nomura, F.; Nagata, M.; Inaba, T.; Hiramatsu, H.; Hotani, H.; Takiguchi, K. Capabilities of liposomes for topological transformation. Proc. Nat. Acad. Sci. 2001, 98, 2340–2345. [Google Scholar] [CrossRef] [PubMed]
- Umeda, T.; Nomura, F.; Inaba, T.; Takiguchi, K.; Hotani, H. Stepwise shrinkage of liposomes driven by thermal fluctuations of the membranes. ChemPhysChem 2005, 6, 1047–1050. [Google Scholar] [CrossRef] [PubMed]
- Hamada, T.; Hirabayashi, Y.; Ohta, T.; Takagi, M. Rhythmic pore dynamics in a shrinking lipid vesicle. Phys. Rev. E 2009, 80, 051921. [Google Scholar] [CrossRef]
- Solon, J.; Streicher, P.; Richter, R.; Brochard-Wyart, F.; Bassereau, P. Vesicles surfing on a lipid bilayer: Self-induced haptotactic motion. Proc. Nat. Acad. Sci. 2006, 103, 12382–12387. [Google Scholar] [CrossRef] [PubMed]
- Giardini, P.A.; Fletcher, D.A.; Theriot, J.A. Compression forces generated by actin comet tails on lipid vesicles. Proc. Nat. Acad. Sci. 2003, 100, 6493–6498. [Google Scholar] [CrossRef] [PubMed]
- Upadhyaya, A.; Chabot, J.R.; Andreeva, A.; Samadani, A.; Oudenaarden, A. Probing polymerization forces by using actin-propelled lipid vesicles. Proc. Nat. Acad. Sci. 2003, 100, 4521–4526. [Google Scholar] [CrossRef] [PubMed]
- Boukellal, H.; Campás, O.; Joanny, J.-F.; Prost, J.; Sykes, C. Soft Listeria: Actin-based propulsion of liquid drops. Phys. Rev. E 2004, 69, 061906. [Google Scholar] [CrossRef]
- Sumino, Y.; Kitahata, H.; Seto, H.; Yoshikawa, K. Blebbing dynamics in an oil-water-surfactant system through the generation and destruction of a gel-like structure. Phys. Rev. E 2007, 76, 055202. [Google Scholar] [CrossRef]
- Miura, T.; Oosawa, H.; Sakai, M.; Syundo, Y.; Ban, T.; Shioi, A. Autonomous motion of vesicles via ion exchange. Langmuir 2010, 26, 1610–1618. [Google Scholar] [CrossRef] [PubMed]
- Seifert, U. Configurations of fluid membranes and vesicles. Adv. Phys. 1997, 46, 13–137. [Google Scholar] [CrossRef]
- Kaga, M.; Ohta, T. Shrinkage dynamics of a vesicle in surfactant solutions. Eur. Phys. J. E 2006, 21, 91–98. [Google Scholar] [CrossRef] [PubMed]
- Kaga, M.; Ohta, T. Shrinkage dynamics of a vesicle induced by chemical reactions. J. Phys. Soc. Jpn. 2007, 76, 094003. [Google Scholar] [CrossRef]
- Anderson, J.L. Colloid transport by interfacial forces. Ann. Rev. Fluid Mech. 1989, 21, 61–99. [Google Scholar] [CrossRef]
- Anderson, J.L.; Lowell, M.E.; Prive, D.C. Motion of a particle generated by chemical gradient Part 1. Non-electrolytes. J. Fluid Mech. 1982, 117, 107–121. [Google Scholar] [CrossRef]
- Prieve, D.C.; Anderson, J.L.; Ebel, J.P.; Lowell, M.E. Motion of a particle generated by chemical gradient. Part 2. Electrolytes. J. Fluid Mech. 1984, 148, 247–269. [Google Scholar] [CrossRef]
- Paxton, W.F.; Kevin, K.C.; Kistler, C.; Christine, C.; Olmeda, C.; Sen, A.; Angelo, S.K.; Angelo, Y.; Mallouk, T.E.; Lammert, P.E.; Crespi, V.H. Catalytic nanomotors: Autonomous movement of striped nanorods. J. Am. Chem. Soc. 2004, 126, 13424–13431. [Google Scholar] [CrossRef] [PubMed]
- Paxton, W.F.; Baker, P.T.; Kline, T.R.; Wang, Y.; Mallouk, T.E.; Sen, A. Catalytically induced electrokinetics for motors and micropumps. J. Am. Chem. Soc. 2006, 128, 14881–14888. [Google Scholar] [CrossRef] [PubMed]
- Golestanian, R.; Liverpool, T.B.; Ajdari, A. Propulsion of a molecular machine by asymmetric distribution of reaction products. Phys. Rev. Lett. 2005, 94, 220801. [Google Scholar] [CrossRef] [PubMed]
- Kung, H.H.; Kung, M.C. Catalytic nanomotors-promising leads for new catalytic applications. Appl. Catal. A Gen. 2006, 309, 159–161. [Google Scholar] [CrossRef]
- Tao, Y.G.; Kapral, R. Design of chemically propelled nanodimer motors. J. Chem. Phys. 2008, 128, 164518. [Google Scholar] [CrossRef] [PubMed]
- Cordova-Figueroa, U.M.; Brady, J.F. Osmotic propulsion: The osmotic motor. Phys. Rev. Lett. 2008, 100, 158303. [Google Scholar] [CrossRef] [PubMed]
- Tao, Y.G.; Kapral, R. Dynamics of chemically powered nanodimer motors subject to an external force. J. Chem. Phys. 2009, 131, 024113. [Google Scholar] [CrossRef] [PubMed]
- Bertin, E.; Droz, M.; Gregoire, G. Hydrodynamic equations for self-propelled particles: Microscopic derivation and stability analysis. J. Phys. A Math. Theor. 2009, 42, 445001. [Google Scholar] [CrossRef]
- Nakata, S.; Doi, Y.; Kitahata, H. Synchronized sailing of two camphor boats in polygonal chambers. J. Phys. Chem. B 2005, 109, 1798–1802. [Google Scholar] [CrossRef] [PubMed]
- Nakata, S.; Kawagishi, N.; Murakami, M.; Suematsu, N.J.; Nakamura, M. Intermittent motion of a camphor float depending on the nature of the float surface on water. Colloid. Surface. A 2009, 349, 74–77. [Google Scholar] [CrossRef]
- Suematsu, N.J.; Ikura, Y.; Nagayama, M.; Kitahata, H.; Kawagishi, N.; Murakami, M.; Nakata, S. Mode-switching of the self-motion of a camphor boat depending on the diffusion distance of camphor molecules. J. Phys. Chem. C 2010, 114, 9876–9882. [Google Scholar] [CrossRef]
- Nakata, S.; Murakami, M. Self-motion of a camphor disk on an aqueous phase depending on the alkyl chain length of sulfate surfactants. Langmuir 2010, 26, 2414–2417. [Google Scholar] [CrossRef] [PubMed]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Shioi, A.; Ban, T.; Morimune, Y. Autonomously Moving Colloidal Objects that Resemble Living Matter. Entropy 2010, 12, 2308-2332. https://doi.org/10.3390/e12112308
Shioi A, Ban T, Morimune Y. Autonomously Moving Colloidal Objects that Resemble Living Matter. Entropy. 2010; 12(11):2308-2332. https://doi.org/10.3390/e12112308
Chicago/Turabian StyleShioi, Akihisa, Takahiko Ban, and Youichi Morimune. 2010. "Autonomously Moving Colloidal Objects that Resemble Living Matter" Entropy 12, no. 11: 2308-2332. https://doi.org/10.3390/e12112308
APA StyleShioi, A., Ban, T., & Morimune, Y. (2010). Autonomously Moving Colloidal Objects that Resemble Living Matter. Entropy, 12(11), 2308-2332. https://doi.org/10.3390/e12112308




