1. Introduction
Actions integrate momenta along paths of an energy landscape [
1,
2,
3]. According to the principle of least action flows of energy delineate on least-time trajectories. These geodesics can be determined when the energy landscape remains invariant under the influence of action whereas this task turns out to be intractable when the flows themselves drive the landscape in evolution. Physics, however, is able to tackle even such problematic processes with its most general concepts.
Nature can be pictured in its entirety and every detail as an energy landscape that consists of diverse densities of energy. When energy flows from a spatial density to another, the landscape will change so that continuity and conservation of energy are satisfied. Specifically, when the flows of energy circulate on closed, bound orbits, the local landscape will retain its symmetry over the conserved motional period [
4]. In general, when flows spiral along open, unbound paths, the landscape will evolve irreversibly by breaking its steady-state symmetry to another in non-conserved transformations. The laws of motion can be expressed concisely as actions in classical electromagnetism [
5], general relativity [
6] and quantum electrodynamics [
7] but it is perhaps less appreciated that also the 2nd law of thermodynamics [
8] can be formulated accordingly to describe evolutionary processes.
Customarily the 2nd law is written as a differential equation, but the universal law can also be written in integral form. Then the natural law is known as the principle of least action where the integrand is kinetic energy 2
K [
1] that equals temperature
T multiplied by entropy
S. This identity allows us to recognize that when the system evolves along the least-action path from one state to another by consuming free energy at the maximal rate, entropy will be increasing in least time. In other words, the principle of increasing entropy given as a differential equation of motion and the principle of least action given as an integral equation of motion are equivalent imperatives [
9]. The natural law for the maximal energy dispersal accounts for diverse irreversible processes that consume differences in energy density,
i.e., free energy [
10,
11,
12]. Eventually, when all forms of free energy have been used, the system’s open evolutionary path closes to the optimum orbit of a conserved stationary state. Then the energy landscape is even and can be characterized by a group of symmetry. Thus, the evolutionary equation derived from the statistical physics of open systems [
13,
14] offers insights as well to the motions of Hamiltonian systems where energy is conserved over the period of integration. The objective of this study is to show how some familiar forms of physics unite when nature is described in a comprehensive and self-similar manner as actions within surrounding actions.
2. The Natural Law of Maximal Energy Dispersal
The classical notion of the 2nd law of thermodynamics [
8] simply says that differences in energy will level off so that the free energy minimum state will be attained. Consumption of free energy powers evolution from one state to another. Motions as flows of energy channel preferentially along the steepest descent in time (∂
t = ∂/∂
t) which is equivalent to the steepest directional (
i.e., velocity
v) gradient (
D =
v·∇). Along these paths the flows of energy are most voluminous and the free-energy minimum state will be attained in least time. In other words, the natural process directs itself along the resultant of forces. The statistical measure for the natural process is entropy
S =
kBln
P which is the logarithmic probability and hence an additive measure [
15]. Since the most voluminous flows of energy will direct along the steepest directional descents, entropy will not only be increasing but it will be increasing in least time. This universal imperative is recognized in the maximum entropy production principle [
16,
17]. The maximal consumption of free energy implies also the maximum power principle [
18]. Since the natural process follows the least-time path, it can be also formulated by the principle of least action.
The principle of increasing entropy as the evolutionary equation of motion is obtained from the statistical physics of open systems [
13,
14]:
where the rate of entropy change is proportional by Boltzmann’s factor
kB to the process generator
L =
TđtQ in accordance with classical thermodynamics [
8]. The probability in motion
dtP =
LP (Equation 1) is expressed using energy densities [
19] so that each energy density
ϕj, present in indistinguishable numbers
Nj of
j-entities, is assigned with
ϕj =
Njexp(
Gj/
kBT) where
Gj is relative to the average energy
kBT of the system per entity. According to the scale-free formalism [
20,
21] each
j-entity itself is regarded as a system of diverse
k-entities. Thus each population
Nk is associated with
ϕk =
Nkexp(
Gk/
kBT). These are bound forms of energy. When energy flows from one bound form to another, energy is in a free form.
The entire system is composed of diverse systems within systems [
22] (
Figure 1). It is summarized by the total probability [
13,
14]:
defined in a recursive manner so that each
j-entity, in indistinguishable numbers
Nj, is a product Π
Nk of embedded
k-entities, each distinct type available in numbers
Nk. The energy difference between entities
j and
k is Δ
Gjk =
Gj −
Gk or
gjkΔ
Gjk =
Gj −
gjkGk when the
j-entity is formed from indistinguishable (symmetrical)
k-entities in degenerate numbers
gjk. The change in vector potential,
i.e., radiation Δ
Qjk couples to the
jk-transformation orthogonal, as indicated by
i, to the scalar potential difference. The notation emphasizes, for example, that when an electron falls along the electric potential gradient, it will radiate light orthogonally to its path. Likewise, electromagnetic radiation as a transverse wave will induce a varying voltage in an antenna perpendicular to the direction of propagation. The notation that explicitly distinguishes scalar and vector potentials, is of no apparent value in equilibrium thermodynamics since in the thermodynamic steady state there is no net flux of energy between the system and its surroundings. Moreover, since the statistical mechanics of closed systems aims only to reveal the stationary-state partition, there is no need to include explicitly the vector potential because at the equilibrium the net flux vanishes. However, here when describing evolutionary processes as evolving landscapes, it is useful to make the explicit distinction between bound and free forms of energy.
The probability in Equation 2 is a physical quantity, as usual in statistical mechanics. When it is multiplied by
kB:
the aforementioned additive statistical measure, entropy
S for the entire system is obtained [
23]. The free energy
Ajk = Δ
μjk −
iΔ
Qjk, also known as affinity [
24], is the motive force that directs the transforming flow
dtNj from
Nk to
Nj by its scalar (chemical) potential Δ
μjk =
μj − Σ
μk =
kBT(ln
ϕj − Σln
ϕk) and vector Δ
Qjk potential differences. The adopted approximation ln
Nj! ≈
Njln
Nj −
Nj implies that ln
Pj is a sufficient statistic [
25] for
kBT when the
j-system is allowed absorb or emit quanta without a marked change in its average energy content,
i.e.,
Ajk/
kBT << 1. In its diverse populations
Nj and in the free energy terms
Ajk the system holds capacity
C =
TdS/
dT to resist the changes in its average energy imposed by its surroundings at a different temperature.
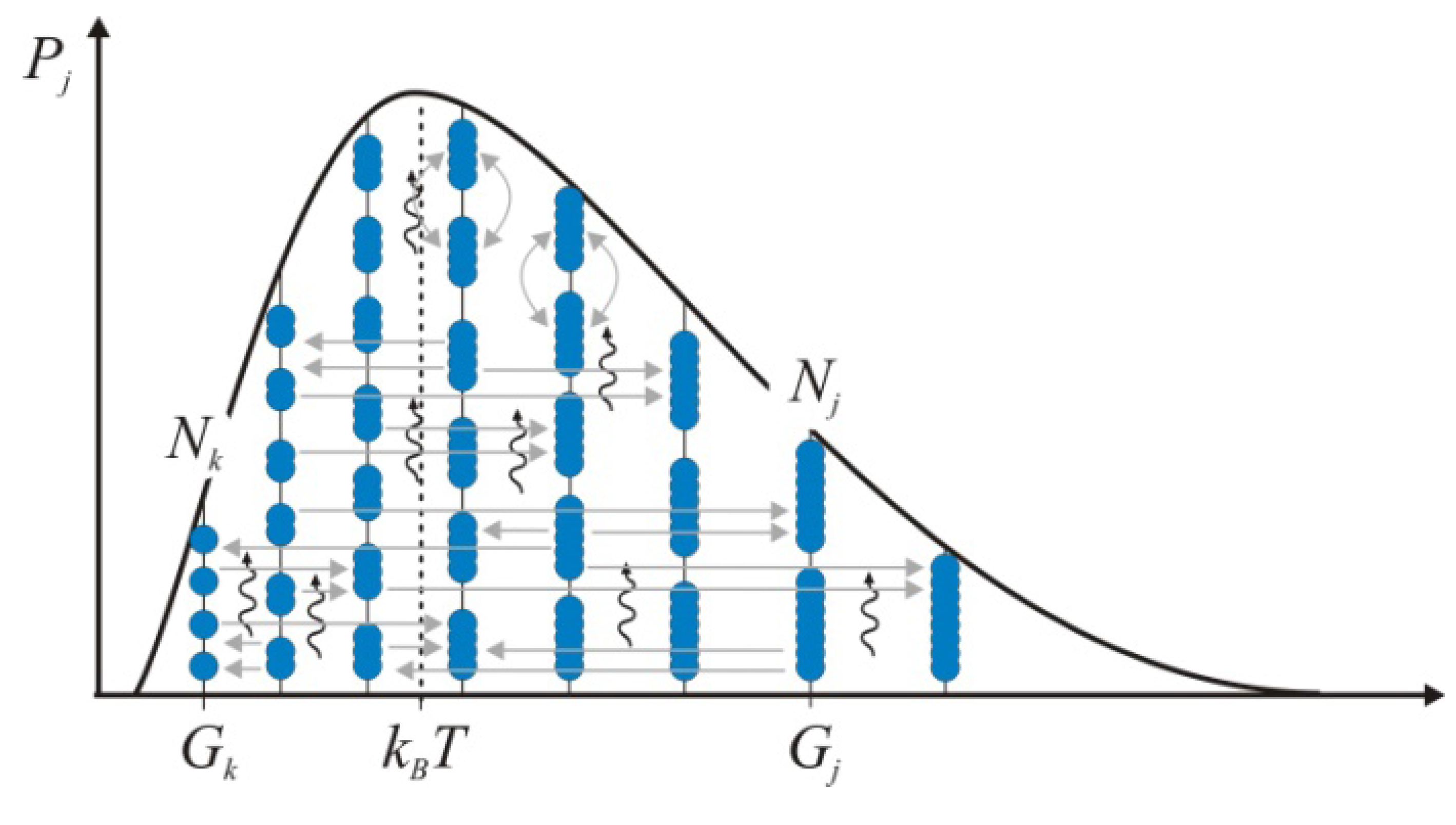
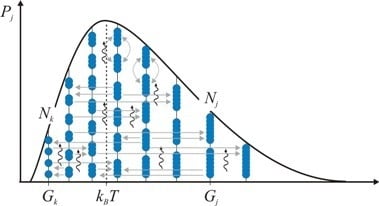
Figure 1.
A self-similar energy level diagram describes the nested hierarchy of nature where each j-system (a composite solid in blue color) is regarded as a system within systems that are all being ultimately composed of multiple elementary constituents (blue solids). All systems evolve via step-by-step jk-transformations toward more probable states by consuming mutual energy density differences contained in chemical potentials Δμjk (horizontal arrows) and those in vector potentials ΔQjk (vertical wavy arrows) relative to the surroundings. During this natural process, the entities will distribute on the energy levels so that the free energy is consumed in least time. Therefore at any given time the probability distribution Pj closely outlines the maximum entropy partition of a statistical system. Exchange of entities at the same level (bow arrows) does not introduce a change in energy. Thus these reversible processes do not affect the average energy kBT.
Figure 1.
A self-similar energy level diagram describes the nested hierarchy of nature where each j-system (a composite solid in blue color) is regarded as a system within systems that are all being ultimately composed of multiple elementary constituents (blue solids). All systems evolve via step-by-step jk-transformations toward more probable states by consuming mutual energy density differences contained in chemical potentials Δμjk (horizontal arrows) and those in vector potentials ΔQjk (vertical wavy arrows) relative to the surroundings. During this natural process, the entities will distribute on the energy levels so that the free energy is consumed in least time. Therefore at any given time the probability distribution Pj closely outlines the maximum entropy partition of a statistical system. Exchange of entities at the same level (bow arrows) does not introduce a change in energy. Thus these reversible processes do not affect the average energy kBT.
When a system is small, it does not have much capacity to resist changes that are imposed by the energy difference relative to its surroundings. Therefore such a system will undergo a dramatic change of state,
i.e., it will evolve abruptly. During these critical events [
26], e.g., when a new
j-species emerges or an old one goes extinct,
Pj will change at once, e.g., from fifty-fifty indeterminism to full certainty. Moreover, when interactions are insufficient to establish common
kBT over a given period
τ of time, the entities fail to form a system but remain as constituents that surround statistical systems at a lower level of hierarchy where interactions are more frequent and intense [
27,
28,
29].
According to the natural law, given as an equation of evolution (Equation 1), a system which is higher in energy density than its surroundings, will evolve from its current state to a more probable one by displacing quanta to the sparse surroundings. Conversely, a system having lower energy density than its respective surroundings will evolve by acquiring quanta from the dense surroundings. Any two states are distinguishable from each other only when the
jk-transforming flow is dissipative Δ
Qjk ≠ 0 [
14,
30]. In view of that a net non-dissipative system is stationary. The maximum entropy state is stable so that an internal perturbation
δNj away from the steady-state population
Njss will induce returning forces and opposing flows,
i.e.,
dS(
δNj) < 0 and
dtS(
δNj) > 0 [
31]. In contrast any change in surroundings will compel the system to move toward a new steady state. In other words the equilibrium will shift to counteract the imposed change so that a new equilibrium will be established [
32].
The evolutionary equation of motion (Equation 1) is obtained from Equation 3 by differentiating (∂
Pj/∂
Nj)(
dNj/
dt) [
13,
14]:
when the time step Δ
t is denoted as continuous
dt. The notion of continuous motion is in accordance with entropy being a sufficient statistic for
kBT. It means that the steps of evolution are small in energy compared to the total energy of the system. However, the actual
jk-transformations do advance in quantized steps of Δ
Qjk during Δ
t since each state associates with a group of symmetry [
4] and a breaking one symmetry to another is a discontinuous event.
3. The Evolving Energy Landscape
The equation of motion for the evolving energy landscape is attained by multiplying Equation 4 with
kBT to give continuity for the flows of energy [
14,
30]:
which result from changes in the scalar and vector potentials. Using the definitions
μj =
∂NjUjk and
dtNj =
vj∂xNj and
vj =
dtxj the three-term formula is transcribed to a convenient continuum approximation:
where the changes in kinetic energy 2
K and scalar
U and vector
Q potentials are given in the Cartesian base of space
j,
k = {
x,
y,
z} and time
t. The flow equation simply says that when the irrotational potential energy
Ujk = −
xjmjkak is consumed during
dt, the power
∂tQjk =
vj∂tmjkvk =
vj∂tEjkvk/
c2 is dissipated and the balance is maintained by the change in the kinetic energy 2
Kjk =
vjmjkvk (
Figure 2). This conversion of energy from one form to another has been conjectured already a long time ago [
33,
34]. Of course the change in mass (
dm) is often very small, but conceptually important because it accompanies a change of state. For example, in a chemical reaction the change of mass per molecule is only a very small fraction of the mass of electron, nevertheless to recognize
dm is essential because it signifies the transition from one state to another.
When the system is in a steady state, the divergence-free part of the force, i.e., the net dissipation vanishes. Then the energy content of the stationary landscape spanned by the j- and k-entities is denoted by the invariant inertia xjmjkxk and by the invariant mass mjk. According to m = E/c2 the mass defines the jk-system’s energy content in terms of a radiation equivalent which can be dissipated, i.e., absorbed into the surrounding energy density, the free space known as the vacuum. It makes sense to give the energy content in terms of photon equivalents because heat, i.e., electromagnetic radiation is the lowest form of energy. The systemic energy is related to its surrounding radiation by the index njk = c2/vjvk (isotropic vj = vk). For example, energy in radiation, when it is spatially confined to a standing wave, can be given in terms of a mass equivalent. Thus the conservation of energy is respected in the transformation between the bound and free forms of energy.
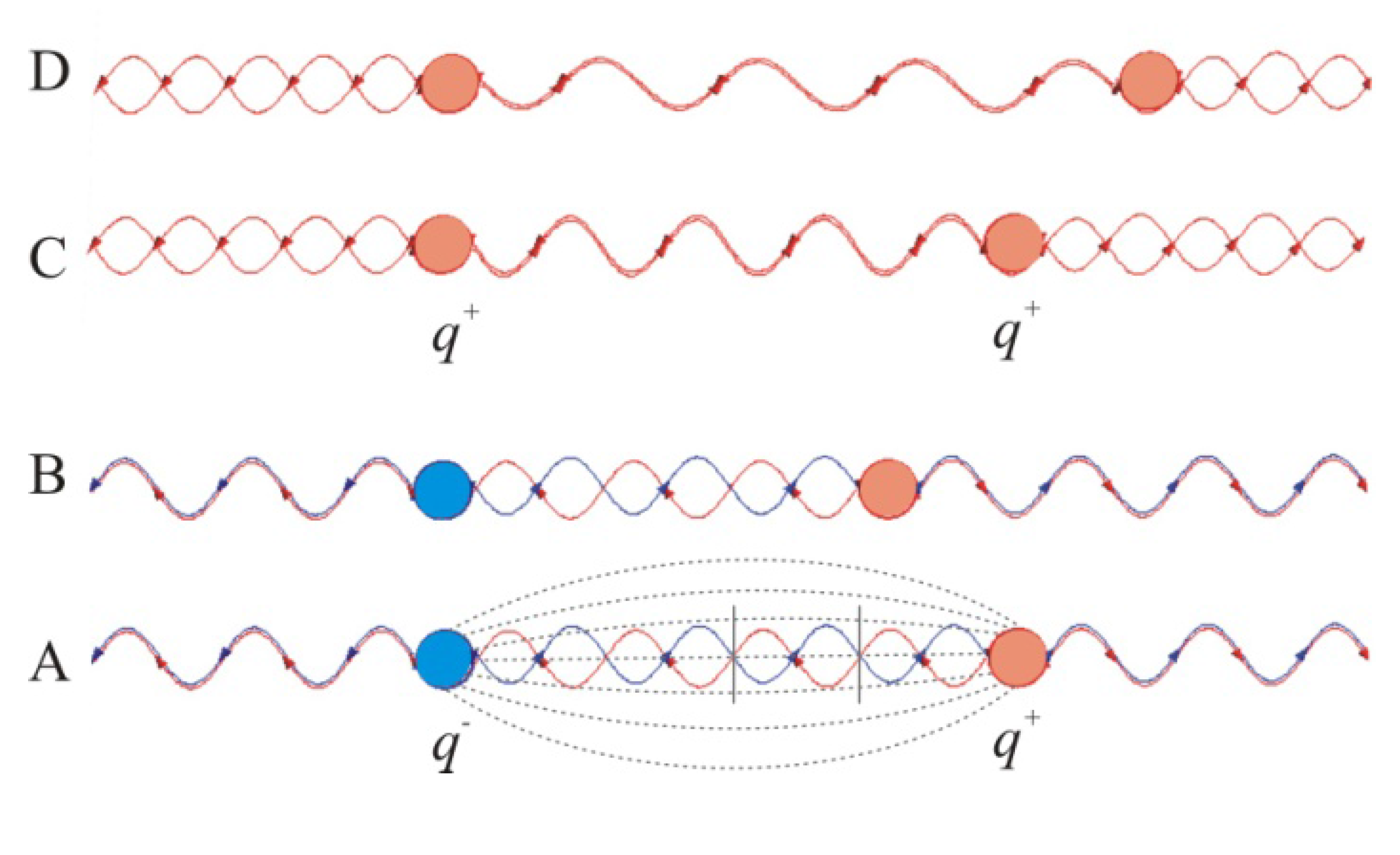
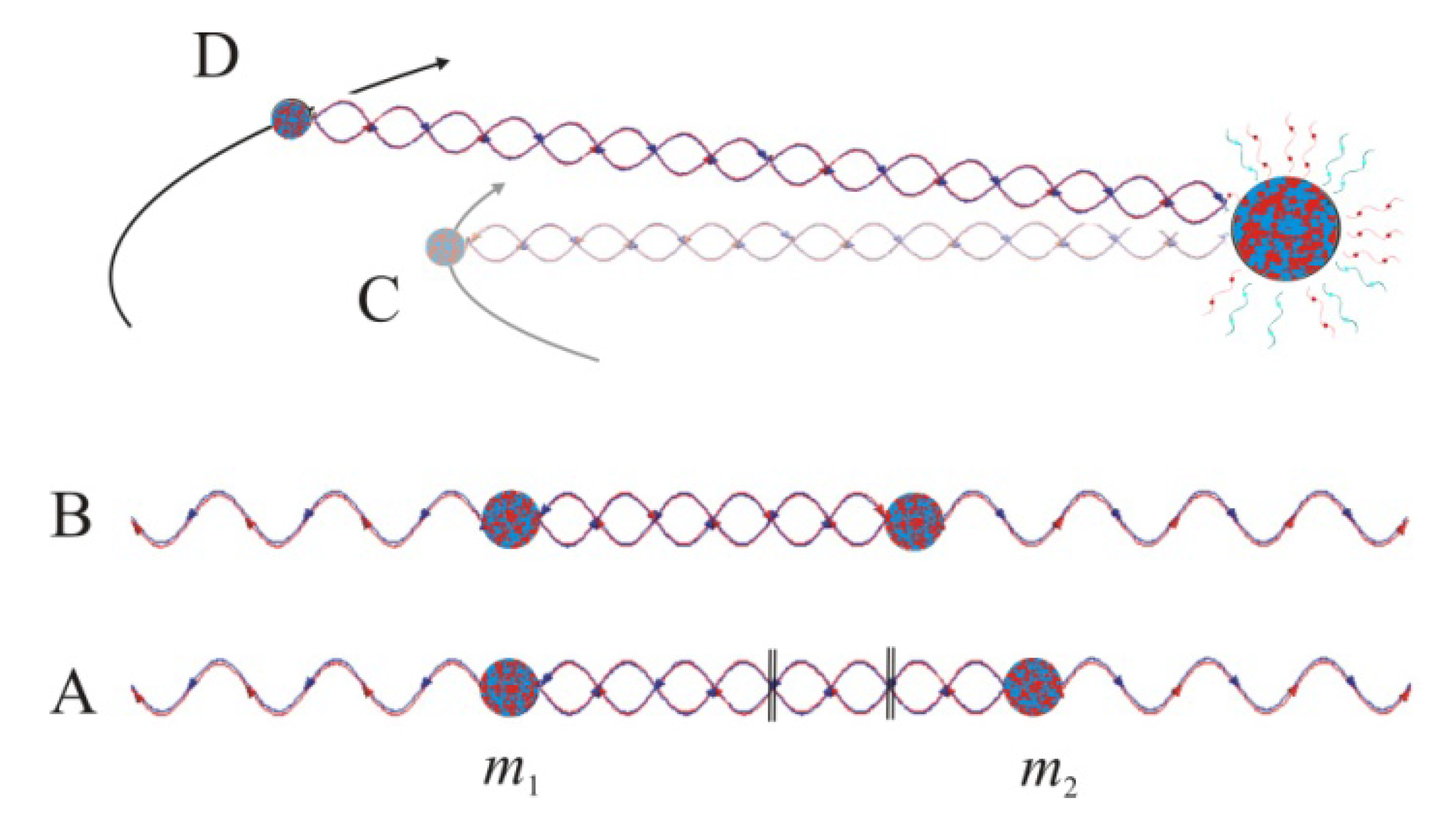
Figure 2.
A step of evolution is a transformation from a closed action coordinated at xk to another bound state at xj so that the change in kinetic energy dt2K balances the changes in the scalar vx∂xU and vector potentials ∂tQ. The dissipation to the surroundings results from the concomitant change in mass Δm = ΔE/c2. In the stationary state, net fluxes vanish so that the closed least-action trajectory dt2K = 0 can be integrated over the motional period τ to yield the steady-state balance 2K + U = 0.
Figure 2.
A step of evolution is a transformation from a closed action coordinated at xk to another bound state at xj so that the change in kinetic energy dt2K balances the changes in the scalar vx∂xU and vector potentials ∂tQ. The dissipation to the surroundings results from the concomitant change in mass Δm = ΔE/c2. In the stationary state, net fluxes vanish so that the closed least-action trajectory dt2K = 0 can be integrated over the motional period τ to yield the steady-state balance 2K + U = 0.
The notion of an energy landscape in motion becomes more vivid when the dissipative flow from the density at
xk toward the density at
xj during
t is described to channel along an arc
sjk. The affine connection along a continuous curve
x =
x(
t) between the two spatial density loci spans a length
s = ∫(
F·
v)
½dt = ∫(
dt2
K)
½dt [
35]. When the landscape is stationary, the curve is integrable. In contrast when the landscape is evolving, the flows of energy are non-integrable because their paths keep changing as the landscape is changing due to the flows themselves. At branching points where paths diverge, differentials
đt are inexact. A small flow will not perturb much a statistical system and its trajectories can be estimated rather well. However, even a small flow of energy will be sufficient to move a microscopic system substantially. Eventually the step of change from an initial state may be so dramatic that the system at a final state is beyond recognition.
The concise notation for the many motions of the differentiable landscape (Equation 6) is developed further by denoting the spatial
∂x and temporal
∂t gradients as a 4-vector [
36,
37]:
when
∂μ acts on the scalar
U and vector
Q potentials which, in turn, are given as the free energy 4-vector potential in the one-form space-time basis:
the curvature in the two-form
F =
dA is obtained. It is represented by the covariant antisymmetric rank 2 tensor:
where the translational and rotational changes in momentum are
dtp =
F = −∇
U +
∂tQ/
c and
R = ∇ ×
Q. When the components of scalar
ϕ =
U/
q and vector
A = −
Q/
qc potentials are divided by charge
q,
Fμν is the electromagnetic force. The change
dtp,
i.e.,
F relates to the change in the angular momentum
dtL,
i.e., torque
τ =
r ×
F normalized by radius of curvature
r (
Figure 2). The continuity is preserved by the invariants
FμνFμν = 2(
F2 −
R2) and ∗
FμνFμν = 4
F ·
R and ∗
Fμν∗
Fμν = 2(
F2 +
R2).
Specifically, at the stationary state the exterior derivate of the system’s curvature yields the conserved currents by d*F = J so that the conserved energy density, i.e., the invariant mass, orbits with phase velocity dtφ = ω exactly once in a period τ = ω−1 on the closed least-action path according to p × ω = −∇U. In the thermodynamic steady state there is no net emission from the system or net absorption to the surroundings over the motional period. Then the exterior algebra of the system’s dual dF = 0 says that the surrounding is a flat landscape with respect to the system and thus exerts no forces. In other words, the system’s average energy density kBT exactly matches that of the surroundings. In the stationary state there is no net force and light propagates straight.
The surrounding vacuum cannot evolve a step further down because the electromagnetic radiation with its symmetry group U(1), the most elementary one, cannot be broken down any further. Since this form of action is already an open path, it cannot be opened any more to release photons. This is to say that the photons have no mass. Photons are the massless gauge bosons of quantum electrodynamics that communicate exchanges of energy in interactions that conserve the stationary state. These reversible flows are the familiar conserved currents along tractable trajectories that are straight geodesics of even landscapes [
4]. Since the closed actions have fixed energies, they comply with the ordering relations. Therefore the steady states are countable, and any-one closed ring as a subset of affine space is an algebraic variety [
38,
39].
In general, the evolving energy landscape, represented by the curvature 2-form F = dA of some principal high-symmetry bundle, is leveling off via symmetry-breaking transformations from one state to another more probable one. Bound forms of energy, i.e., fermions open up to output free forms of energy, i.e., bosons that dissipate to the surroundings. Since the system and its surroundings share a common interface for the flows of energy, the entropy of both the system and its surroundings will increase when mutual energy density differences decrease. The conservation of energy including both the system and its dual is respected by the differential geometry. The star operator transforms an oriented inner product density contained in an element of space, e.g., given in the Cartesian base, *(dx ∧ dy ∧ dz) = dt to radiated energy density that is carried away by an element of time.
It is worth noting that continuous transformations of the Lorentz group SO(3,1) with metric signature (+,+,+,−) [
40] are conserved,
i.e., not evolutionary processes. When no symmetry is broken, no quantum is dissipated and no change of state has happened. The sesquilinear inner product defines the stationary-state unitary space with the Euclidean norm. The space is invariant under multiplication by the complex numbers of a unit norm. In these special cases, the equation of motion describes merely a phase precession at constant energy. Since energy is constant, there is a norm and the equation for the phase precession can be solved by a unitary transformation that will remove explicit time dependence from all variables. In contrast the equation of evolution cannot be solved when a natural process has two or more alternatives paths from one state to alternative states. The difficulty in computing a non-computable [
41,
42] is familiar from the three-body problem [
43]. Admittedly the non-Abelian gauge theory [
44] accounts for directional transitions but when the integrand of action is forced to remain invariant, no net evolution will take place. Then the directional transformations formalize merely the to-and-fro flows of energy. Therefore no continuous group of transformations will account for the natural processes since in these irreversible processes from one state to another, symmetry is broken.
During evolution the landscape’s curvature due to the differences in energy levels will decrease when the spatial potentials
μj = ∂
NjUjk and
μk = ∂
NkUjk adjust to accommodate or discard the vector potential that couples the system to its surroundings via the
jk-transformations. The diminishing curvature of a differentiable landscape,
i.e., the force can be represented by a vector field gradient. The non-vanishing Lie’s derivative [
45] means that the change
v =
dtx in the coordinate and the change
F =
dtp in the momentum, are not collinear due to the net energy flux ∂
tQ over
dt to the system from the surroundings or
vice versa. Therefore operators in [
,
] = −
iħ do not commute by the minimum amount of action in a change of state. This uncertainty of at least one quantum in determining the state of the system is inherent in any measurement because the detection requires that at least one quantum is either emitted from the system to the detector or
vice versa but that very quantum will change the state of the system. Consequently the systems that are undergoing changes of state contain open actions. These evolving systems cannot be ranked with respect to each other because their energy is changing.
The evolving energy landscape is represented by:
where the 4-vector velocity
vμ = (−
c,
vx,
vy,
vz). The flow tensor contracts to the 0-form
dt2
K = Σ
dt2
Kμν = −
v · ∇
U +
∂tQ +
v ×
R where the change in the kinetic energy balances the changes in the scalar potential due to matter flows as well as the changes in the vector potential due to radiation fluxes. When the system communicates with its surroundings exclusively via radiation, Equation 10 is familiar from the theory of electromagnetism [
46] where the radiation
Q at the speed of light
c dissipates orthogonal to the source moving down along –∇
U at velocity
v (
Figure 2) [
14]. Conversely, when the system is stationary
∂tQ +
v ×
R = 0, its stable orbits are governed by
∂t2
K +
v · ∇
U = 0 which is integrable to the steady-state balance 2
K +
U = 0 or differentiable to the equation for standing waves.
The energy flow from the density
ϕj, which defines its spatial locus
xj, to
ϕk, which in turn defines
xk, is identified as the flow of time [
14]. Thus the notion of time presupposes the notion of space [
47]. The motion down along the spatial gradient is irreversible when emitted quanta escape forever and reversible when quanta are reabsorbed. Emission will change the coordinate of the source relative to the sink, and absorption will change the coordinate of sink relative to the source (or
vice versa). Conversely, when the system is stationary, so are its surroundings. It is familiar from unitary transformations that the steady phase velocity
dtφ =
ω does not suffice to distinguish the systemic motions from the surrounding motions.
4. The Preon Action
Evolution from one stationary-state symmetry to another implies that actions are quantized because the stationary states’ conserved currents are on closed orbits, and all bound curves are modular. The divisible circular group means a periodic orbit, and a rational winding number is equivalent to a mode-locked motion. Physically speaking, the state is stable when the corresponding action is modular,
i.e., quantized over the closed least-action path. The curve with zeros (nodes) is familiar from the Bohr’s model of an atom where angular momentum
L =
px = 2
Kτ =
nħ equals the elementary action
ħ in
n multiples. The kinetic energy 2
K within the period
τ is distributed on the closed orbit in modules enumerated by the principal quantum number
n. Thus a step of evolution from one stationary state to another is mathematically speaking a step in the modulus of the cyclic group. When the sum of points on the ring changes, also its divisor will change. This is explicit in Equation 5 and implicit in Equation 6 where the dissipation-driven evolutionary step of
Nj will in fact cause the action to step in momentum
p and in length
x =
vt from one closed orbit to another. The constant of action
ħ, as the absolutely least action, can be considered as a physical entity (
Figure 3). The most elementary fermion is the energy density of the bound geodesic given by the geometric product
L =
px [
48] which has a specific handedness, usually referred to as spin ±½.
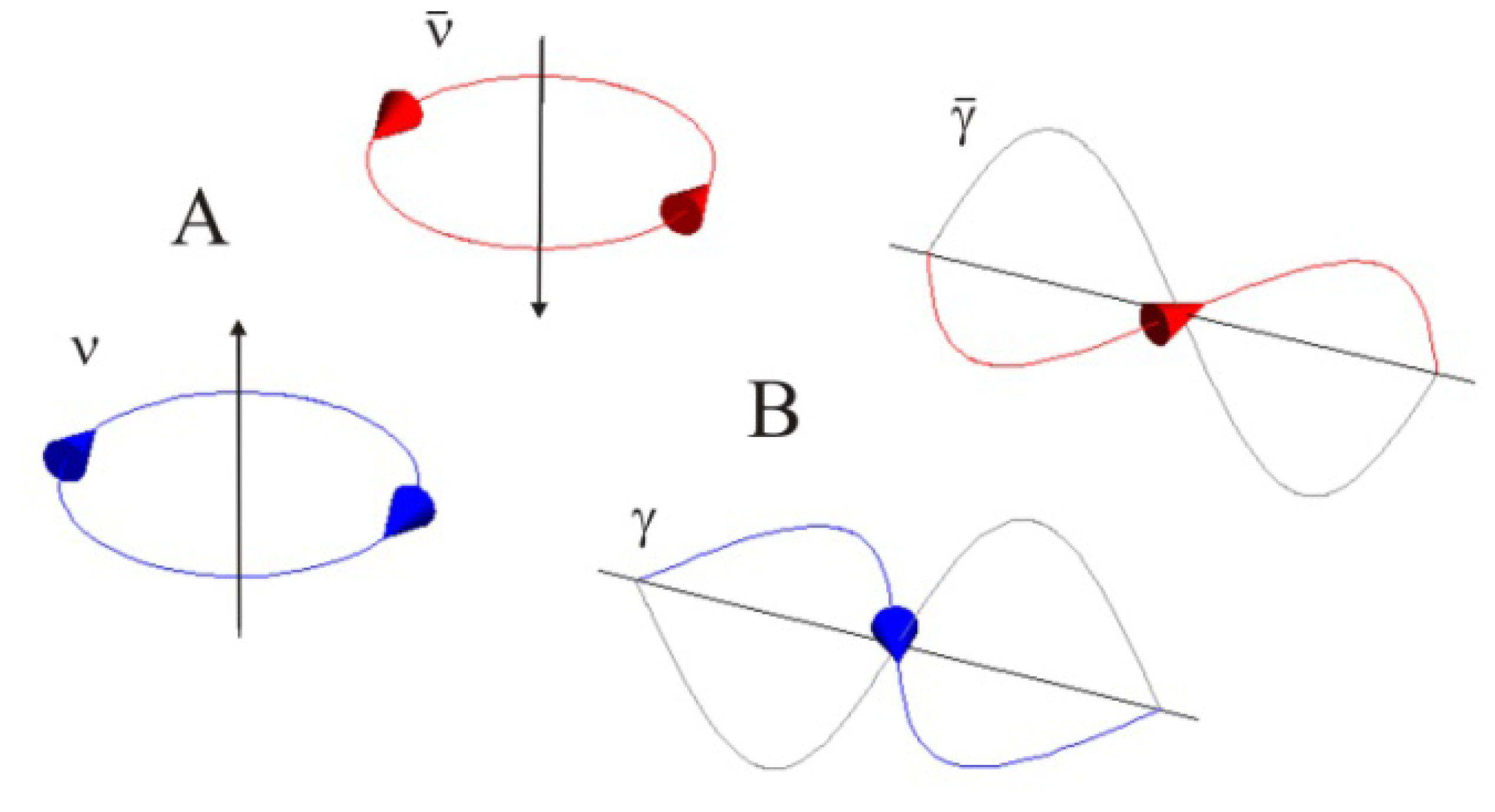
Figure 3.
(A) The basic element of space is the most elementary fermion, the neutrino. The confined circulation of energy exists in two chiral forms ν and ν* corresponding to the opposite senses of circulation. The vertical bars denote the respective scalar potentials −U = 2K and U = −2K. (B) The basic element of time is the most elementary boson, the photon. The open flow of energy exists in two forms γ and γ* of opposite polarizations that correspond to the opposite (color-coded) phases iQ and −iQ (the figures were drawn with Mathematica 7 that was appended with CurvesGraphics6 written by G. Gorni.)
Figure 3.
(A) The basic element of space is the most elementary fermion, the neutrino. The confined circulation of energy exists in two chiral forms ν and ν* corresponding to the opposite senses of circulation. The vertical bars denote the respective scalar potentials −U = 2K and U = −2K. (B) The basic element of time is the most elementary boson, the photon. The open flow of energy exists in two forms γ and γ* of opposite polarizations that correspond to the opposite (color-coded) phases iQ and −iQ (the figures were drawn with Mathematica 7 that was appended with CurvesGraphics6 written by G. Gorni.)
This oriented element of space is equal to the absolutely least angular momentum
L associated with the kinetic energy within the orbital period 2
Kτ =
ħ. Thus
ħ can be regarded as the fundamental element of space. The most elementary boson carries the energy along the open directed geodesic
pvt which has a specific handedness, usually referred to as polarization ±1. This oriented element of time is equal to the absolutely least action 2
Kt =
h that contains the energy carried within the wave’s period. This open action that equals Planck’s constant can be regarded as the fundamental element of time. It takes two of these actions to reverse the polarization from +1 to −1. The first will interfere destructively (head-on) with the original handedness and the other will create the mirror hand. In the following we will refer to the fundamental oriented element of time as the photon γ and its opposite sense of polarization as the antiphoton γ
∗. Thus the photon is considered as its own antiparticle. Accordingly, we will refer to the fundamental oriented element of space as the neutrino ν and its opposite sense of circulation as the antineutrino ν
∗. According to the physical portrayal of nature, the constant of action is the most elementary action which is abbreviated here as the preon [
49].
5. Multiple Actions
The principle of least action regards all entities of space and time,
i.e., diverse fermions and bosons [
50] as being ultimately composed of the preon actions. Since the action is a directed path, each fermion and each boson is distinguishable from its own antiparticle which is the reversed action. An electron e
− is described as a least action path where preons coil to a closed torus having the electron neutrino ν
e chirality (
Figure 4). Electron’s steady-state characteristics are obtained from
dtL = 0. This resolves to a constant 2
K = ∫
ρv·
Edt = ∫
ρE·
dx =
e2/4π
εx where the density
ρ distributes on the torus’ path length
x so that the conserved quantity, known as the elementary charge
e =
ρx, sums from the current in the field
E according to Gauss’s law. The invariant fine structure identifies by integration to the normalized constant
L/
ħ = ∫2
Κdt/
ħ =
e2(
μ/
ε)
½/2
h =
α where the squared impedance
Z2 =
μ/
ε = (
cε)
−2, in turn, characterizes the stationary-state density that satisfies the invariant condition ∂
tϕ +
c2∇·
A = 0 [
51]. Moreover, the circulation gives rise to the magnetic moment
μe = ∫
r×
ρvdx =
er×
p/
me =
eL/
me. Its anomaly
α/2π [
52],
i.e., the excess of
μe over
μB =
eħ/
me results from the helical pitch. The rise of coiling contributes to
μe =
eIω/
me =
ex2/
t along the torus path length
x beyond the plain multiples of
ħ (as if the path were without pitch) where inertia
I =
mex2 and
L =
Iω (
Figure 4).
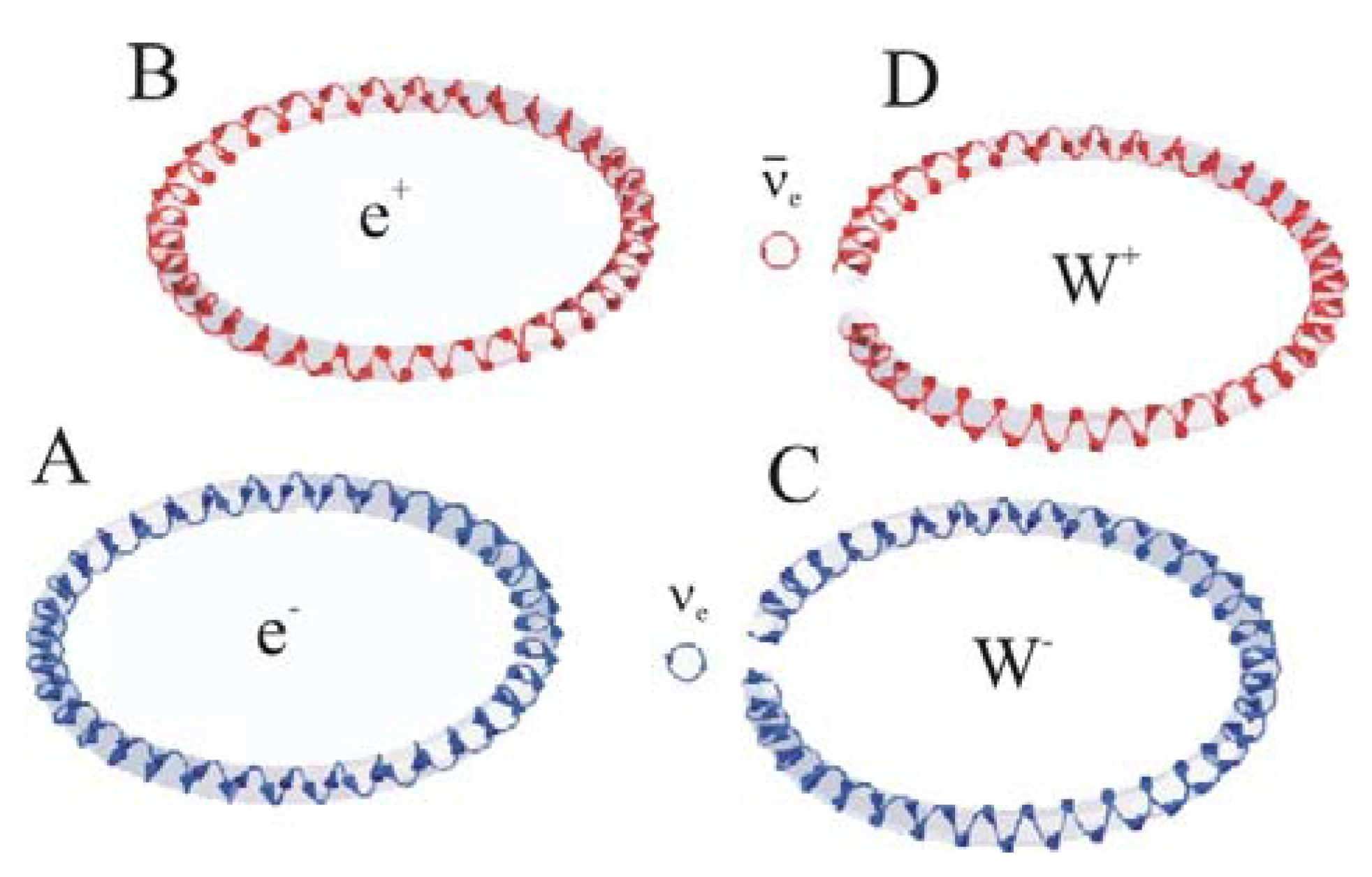
As well, the positron e
+ is a torus but with antineutrino ν
e∗ handedness. In energy-sparse surroundings e
+ and e
- interfere almost completely destructively. Only the helical-pitch modulation does not cancel. Thus, the annihilation bursts out anti-parallel rays of photons γ and γ
∗ so that each is equivalent to the comparatively low mass
me = 511 keV/
c2 that is characteristic of the elementary charge (
Figure 4). In topological terms, the low mass means that the winding number of the elementary charge about the torroid’s center is low. When dissipation is normalized by the quantum of action, the characteristic trembling frequency
ω = 2
mec2/
ħ [
53], is obtained.
The W− boson that mediates the weak force is regarded as an open-ended helix of νe-chirality. The helical line is of high energy and thus in energy-sparse surroundings it is not the least-action path but decays as W− → e− + νe*. The pitch-accumulated lag-phase φ = 2π is absorbed at the torus closure by the antineutrino. Since the torus itself is a loop, the elementary charge is conserved in the decay process. Likewise, the W+ boson is an open-ended helix of νe*-chirality that processes as W+ → e+ + νe. The neutral Z0 boson is also an open-ended path where a γ-linker joins two helices one having νe and the other νe∗-chirality. Energy-sparse surroundings drive the decay Z0 → e+ + e−. The weak bosons display extraordinary high masses in comparison to their closed form fermion-antifermion counterparts, because these open paths have comparatively little topological self-screening via intrinsic phase cancellation, i.e., their winding numbers are high.
Figure 4.
(A) Electron e− is a closed least-action torus which is composed of multiple preon actions having neutrino sense of chirality. The helical pitch is seen from the roll of the arrow heads. The lag-phase due to each winding totals φ = 2π around the torus. (The pitch is exaggerated for clarity). (B) Conversely, positron e+ is a closed torus of multiple preons having antineutrino sense of chirality. (C) When the surrounding energy density is high, e− will convert by breaking its closed chiral symmetry to the open W− boson and electron neutrino νe. (D) Conversely, e+ will convert to W+ boson and electron antineutrino νe*. The actions having opposite sense of circulations will annihilate so that streams of γ and γ* stem only from the lag-phase modulation which accrued along the opposite helical pitches.
Figure 4.
(A) Electron e− is a closed least-action torus which is composed of multiple preon actions having neutrino sense of chirality. The helical pitch is seen from the roll of the arrow heads. The lag-phase due to each winding totals φ = 2π around the torus. (The pitch is exaggerated for clarity). (B) Conversely, positron e+ is a closed torus of multiple preons having antineutrino sense of chirality. (C) When the surrounding energy density is high, e− will convert by breaking its closed chiral symmetry to the open W− boson and electron neutrino νe. (D) Conversely, e+ will convert to W+ boson and electron antineutrino νe*. The actions having opposite sense of circulations will annihilate so that streams of γ and γ* stem only from the lag-phase modulation which accrued along the opposite helical pitches.
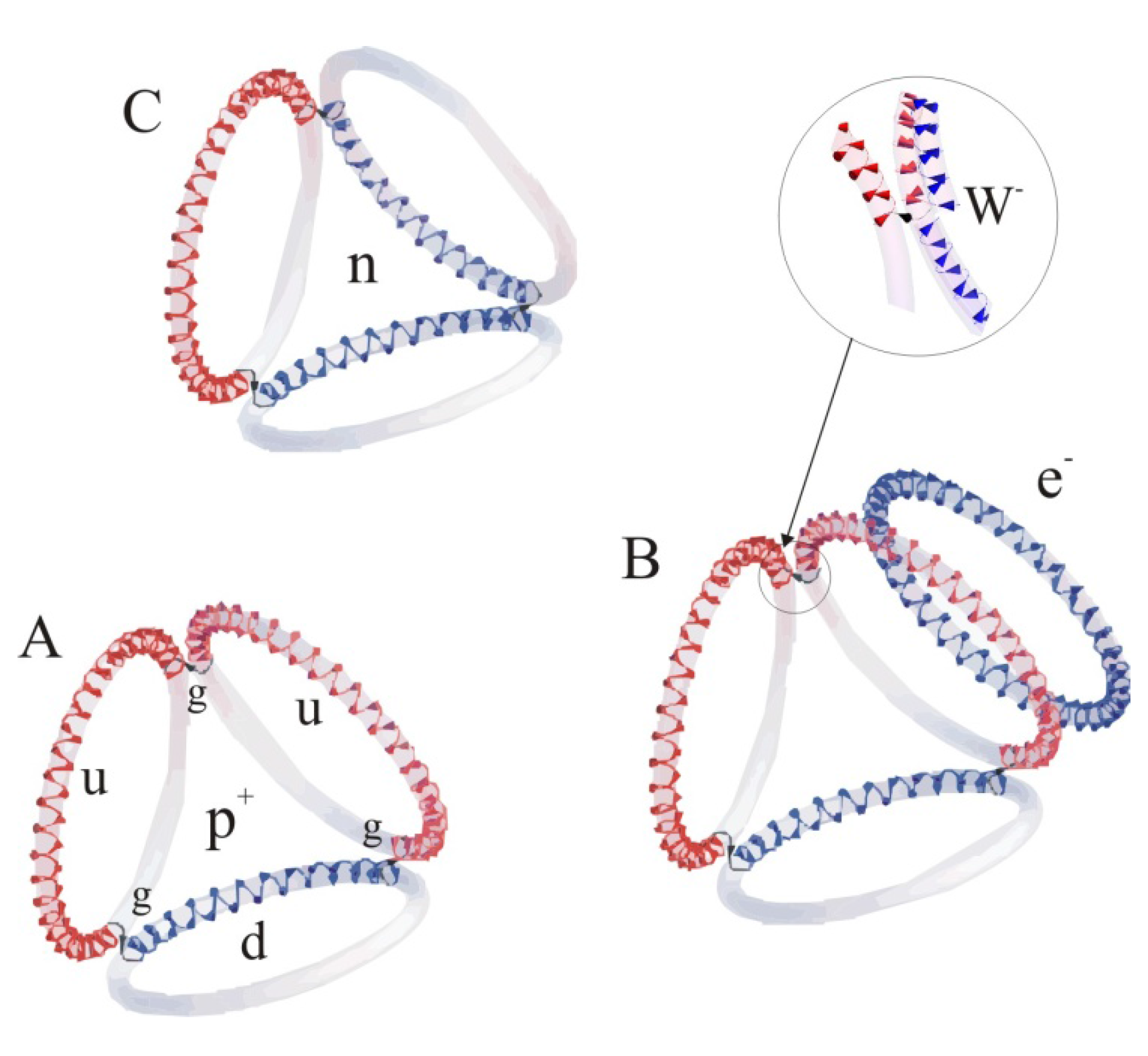
In an atomic nucleus, proton p
+ is portrayed as a least-action path where two
2/
3-helices of ν
e∗-chirality, known as up-quarks u, and one
1/
3-helix of ν
e-chiralily,
i.e., down-quark d, join via three γ-linkers, known as gluons g. Along each u the helical path accumulates
φ =
4π/
3 and likewise d accrues
φ =
2π/
3 so that a gluon, as an open preon, links any two quarks at the angles that the faces of an equilateral tetrahedron make with each other (
Figure 5). The front-end ⊙ of one u links via g to the back-end ⊗ of the other u, and then further ⊙-u links via g to ⊗-d and finally ⊙-d links via g to ⊗-u to close the path. In the tripod constellation each quark as a directional element of the closed path is distinguishable from any another which is the essence of quantum chromodynamics.
Proton p
+ transforms to neutron n via electron capture where e
− breaks, when attracted to u, to W
− which makes a snug fit at u so that a partial annihilation will commence and yield d (
Figure 5). Likewise, when n is free,
i.e., in energy-sparse surroundings, the reverse process begins when W
+ is attracted to make a snug fit at d and the partial W
+d-annihilation will yield u. The provided “wire frame models” are illustrative but perhaps puzzling since p
+ by the perimeter is longer than n, yet the mass of the neutron is slightly bigger than that of a proton. However as clarified earlier above, the mass is a measure of energy in terms of net dissipation. The topological self-screening of u in p
+ and d in n are nearly the same. The small difference is accrued from the incomplete cancellation of opposite phases of pitch. The significant difference in proton and neutron magnetic moments, in turn, is understood to stem from the substantial differences in the oriented areas that are closed by the respective currents. The wire frames (
Figure 5) allow an easy imagination of various natural process such as a pion decay π
+: ud
* → W
+ → e
+ + ν
e*, where the ud
*-ring opens so that d
* (oppositely wound d) will resettle via the high-mass intermediate W
+ integrally to the low-mass e
+-torus.
Figure 5.
(A) Proton p+ is a closed circulation where each up-quark u (red) is 2/3 of torus of νe*-chirality and the down-quark d (blue) is 1/3 of torus of νe-chirality. The lag-phase φ = 4π/3 accrued along each u and φ = 2π/3 along d due to the helical pitch, define the relative angles of quarks, i.e., symmetry of the closure linked by gluons g (black arrows). (B) Electron capture p+ + e− + νe* → n is intermediated by W- which as an open action will initiate a partial annihilation at an exposed end of u (blow-up) that will yield d. (C) The resulting neutron n is a three-gluon-linked closed action udd.
Figure 5.
(A) Proton p+ is a closed circulation where each up-quark u (red) is 2/3 of torus of νe*-chirality and the down-quark d (blue) is 1/3 of torus of νe-chirality. The lag-phase φ = 4π/3 accrued along each u and φ = 2π/3 along d due to the helical pitch, define the relative angles of quarks, i.e., symmetry of the closure linked by gluons g (black arrows). (B) Electron capture p+ + e− + νe* → n is intermediated by W- which as an open action will initiate a partial annihilation at an exposed end of u (blow-up) that will yield d. (C) The resulting neutron n is a three-gluon-linked closed action udd.
On the other hand the proton decay as a putative process p
+ → e
+ + π
0 [
54] is seen in terms of actions so that the X-boson (balanced by e
+ + d
*) would be attracted to p
+ to make a snug fit along u-⊗-g-⊙-u. However, such an annihilation process is unlikely to take place in low-density surroundings (Equation 1) because it would yield disjoint d and d
* which are high-energy by-products. The process does not yield the anticipated pion π
0 which would indeed have only moderate mass since in the meson, the circulations of linked quark and antiquark pair cancel apart from the lag-phase accrued along their opposite pitches. Thus, the violation of color confinement would require extraordinarily high-energy surroundings to provide the asymptotic freedom [
55] for quark-gluon plasma, or the violation of baryon number conservation would require a blazing transformation [
56,
57].
Heavier fermions are viewed as excited strings of the aforementioned ground-state actions. An excitation lifts the elementary closed symmetry SU(2) so that an action at a higher harmonic (bending) mode has more to dissipate and thus manifests itself as a heavier particle that tends to decay back to ground state. Altogether the collective modulations of the preon multiples are known in the Standard Model as flavors of leptons, quarks and mesons.
6. Fundamental Forces
According to the principle of least action a difference of energy of any kind is a force that will be leveled off in the least time. Consequently no interaction is fundamentally any different from any other, when everything is viewed as being ultimately composed of multiple preon actions. Energy dispersal only manifests itself differently at different densities of energy. High-density actions are highly curved paths. A strong force is required to open these closed actions, i.e., to turn a fermion to a boson. In this sense for every fermion there is a corresponding boson which is the notion of supersymmetry. At high nuclear densities quarks integrate seamlessly via gluons to a closed path. Internal reflections at density boundaries, familiar from optics, presumably confined as well the very high density of the nascent Universe. Likewise, a weak force is sufficient to open lepton curvatures to weak bosons and photons.
The Coulomb interaction, in turn, manifests itself between actions whose circulations generate charges. In the thermodynamic steady state the bosons form standing waves between the oppositely charged fermions. For example, at intermediate densities a bound action known as the hydrogen atom results from exchange of γ and γ
* between p
+ and e
− (
Figure 6).
Figure 6.
(A) Electromagnetic interaction arises from the density difference between charged fermions and their surroundings. (B) Sparse surroundings cause attraction by accepting full wavelength modules |∞| of photons from the bound actions that pair opposite charges q− and q+. For clarity only the action along the shortest electromagnetic field line (dashed) is decorated with density modules. Beyond the bound pair of charges energy density propagates at the speed c2 = 1/μoεo. The energy density remains finite also long the dipole axis where the anti-phase waves do not couple to the antenna. (C) Like charges generate alike-polarized, open actions that cannot pair to form a bound action. (D) Therefore in sparse surroundings repulsion remains the mechanism to dilute the density between q+ and q+.
Figure 6.
(A) Electromagnetic interaction arises from the density difference between charged fermions and their surroundings. (B) Sparse surroundings cause attraction by accepting full wavelength modules |∞| of photons from the bound actions that pair opposite charges q− and q+. For clarity only the action along the shortest electromagnetic field line (dashed) is decorated with density modules. Beyond the bound pair of charges energy density propagates at the speed c2 = 1/μoεo. The energy density remains finite also long the dipole axis where the anti-phase waves do not couple to the antenna. (C) Like charges generate alike-polarized, open actions that cannot pair to form a bound action. (D) Therefore in sparse surroundings repulsion remains the mechanism to dilute the density between q+ and q+.
When the surrounding density increases, photons from the surroundings will integrate in the modular paths along the field lines so that these will extend up to an excited state. Conversely, when the surrounding density settles down again, the sparse surroundings will accept the discarded full-wavelength modules of photons as the system returns to the ground state. In contrast, like charges, which generate fields of like polarization, cannot support standing waves between them to form a stable state. In the sparse surroundings the density between them will dilute by repulsion.
Moreover, it is important to realize that the density due to the four-potential (Equation 8) exists beyond net neutral bodies although the resultant electromagnetic field of anti-phase waves,
i.e., the force experienced by charges, vanishes. Interference effects of the non-vanishing density manifest themselves in double-slit experiments [
14].
The gravitational interaction, just as other interactions, can be understood to result from density differences. Two net neutral bodies are attracted when their sparse surroundings, characterized by
μoεo =
c−2 and
μo/
εo = Z
2, accept actions that are released in transitions from one standing-wave orbit to another (
Figure 7).
Figure 7.
(A) Gravitational interaction arises from the energy density difference between net neutral bodies and their surroundings. (B) Sparse surroundings attract by accepting doubly paired density modules ||∞|| of gravitons from the bound actions that pair the bodies along gravitational lines. (C) Irradiative combustion of high-density actions is a powerful mechanism to diminish the density difference between a body and its surroundings. (D) The burning star gives away density, hence the conservation of energy (Equation 6) requires for a planet to advance its perimeter from one modular orbit to another.
Figure 7.
(A) Gravitational interaction arises from the energy density difference between net neutral bodies and their surroundings. (B) Sparse surroundings attract by accepting doubly paired density modules ||∞|| of gravitons from the bound actions that pair the bodies along gravitational lines. (C) Irradiative combustion of high-density actions is a powerful mechanism to diminish the density difference between a body and its surroundings. (D) The burning star gives away density, hence the conservation of energy (Equation 6) requires for a planet to advance its perimeter from one modular orbit to another.
The gravitational force is the difference in density between two celestial bodies and their surrounding density just as it is the difference between the density in a microscopy cavity and its surrounding density. A cavity, tiny or enormous, cannot accommodate all the standing modes propagating in the universal surroundings [
58]. The fundamental modulus of a standing gravitational wave is a pair of bosons with opposite phases. The expression of a standing wave as a sum of oppositely propagating waves subject to boundary conditions [
59] is familiar from the derivation of Planck’s law of radiation [
60]. Since a modulus of density wave between net neutral bodies is without longitudinal vector character, a traceless symmetric rank-2 tensor (
cf. electromagnetic wave) describes transverse modes of this particle, known as the graviton. It takes four elementary actions to reverse the polarization of graviton from +2 to −2. Two preons will interfere destructively with the pair with original handedness and the other two will create the mirror-handed pair.
The familiar form of the conserved potential
U for two net neutral bodies displaced by
r12 is obtained, as before, from the steady-state condition,
i.e., the least-action which is equivalent to the steady-state balance 2
K +
U = 0 as follows:
where the angular momentum
L =
Iω depends on inertia
I = Σ
miriri = Σ
mimjrij2/Σ
mi = Σ
mimjrij2/
M and period
τ2 = 1/
ω2 =
t2r3/
R3. The inertia, when normalized by the total mass
M of the Universe, can be seen as an expression of the principle 2π
Gρt2 = 1 where the mass density
ρ is within the radius
R =
ct [
61], so that any given density is coupled to every other density. The numerous (decay) paths to disperse energy span the affine energy landscape, the universal buoyancy where the density flows level off any density difference in the least time. Thus the cosmological principle,
i.e., homogeneity at the largest scale can be seen as a consequence of a natural selection for the maximal dispersal.
According to the 2nd law of thermodynamics a system may emit quanta when its surroundings are lower in energy density. The ultimate sink is the universal surrounding free space. Today, at
t = 13.7 billion years, the very low average mass density
ρ ≈ 9.9 ° 10
−27 kg/m
3 [
62,
63] corresponds to a tiny curvature over a titanic radius
R =
ct [
64,
65,
66] and sets the gravitational constant
G = 1/2π
ρt2 to its current value. The minute but non-negligible acceleration
at =
GM/
R2 = 1/
εoμoR =
c2/
R =
c/
t =
cH drives the on-going expansion at the rate
H [
67,
68] that is changing as
dtH = −
H2 = −2π
ρG. On the basis of
ρ or equivalently of
H the dilution factor
n =
L/
ħ is on the order of 10
120. This factor is the well-known discrepancy between reality and the calculated vacuum energy density (as if no expansion had taken place). At any given time the total mass of the Universe in its dissipative equivalent
Mc2 =
MatR =
R∂
rU = −
U matches the scalar potential. This innate equivalence is known also as the zero-energy principle [
6]. The balance is also reflected in the quantization of the electromagnetic spectrum. The cosmic microwave background radiation profiles according to the Planck’s law a discrete quasi-stationary entropy partition of fermions (
Figure 1). The unfolding Universe is stepping from one mode to lower and lower harmonics [
69] along its least action path toward the perfect,
i.e., torsion-free flatness
dtL = τ = 0. The acceleration, which is proportional to the winding number
θ ∝
R−2 of those folded actions, will be gradually limiting toward zero. When all densities have vanished, no differences,
i.e., forces will exist either.
The Universe has today evolved to span numerous levels of hierarchy but there is no fundamental distinction between the diverse forms of energy, e.g., light, quarks, atoms, molecules, beings, planets, solar systems and galaxies, since they all are ultimately composed of preons. The vast variation in energy densities is reflected in the relative strengths of interactions that extend over some 38 orders of magnitude but there is no profound distinction between strong, weak, electromagnetic and gravitational interactions. All forces as density differences between the preons in diverse fermionic varieties are communicated by the preons in various bosonic forms. At any level of nature’s hierarchy, e.g., from neutrino via electron to an atom, a closed least action affords at most three dimensions of space which are usually interpreted as the degrees of freedom. One axis is orthogonal to the plane of the other two where the least action curve exists and closes to a cycle. Indeed it makes sense to see space at higher and higher magnifications as being folded to densely curved actions, but not to imagine the degrees of freedom as an abstract concept without physical correspondence. In turn, an open action associates with the degree of freedom that span the dimension interpreted as time. When the system evolves from one spatial state to another, open actions carry the flow of energy that is experienced as the flow of time. Its direction is due to diminishing density differences. At a thermodynamic steady state in- and outgoing bosons are equally abundant. When the two populations of polarizations form a standing wave, motions are fully reversible. There is no time-dependence but then time is a bidirectional parameter with two degrees of freedom. Indeed it makes sense to see time when broken down to finer and finer steps, as a quantized energy transduction process but not to regard irreversibility and reversibility as abstract notions without physical correspondence.
7. The Mass Gap
Evolution is basically an energy dispersal process that advances from one state to another by spontaneous symmetry breaking. Although it is obvious, it is important to note that any transformation from a closed orbit to an open curve is discontinuous. In other words, the action is either closed or open but not anything in between since no change of symmetry is indivisible. Eventually, when evolution arrives at the state of next most elementary symmetry, the closed preon opens up and drains altogether as an open preon (
Figure 8).
The winding number of the most elementary non-commutative ring is ±1 whereas for an open wave it is zero. Thus the closed preon associated with the SU(2) symmetry has the least mass mν > 0, i.e., the conserved quantity whereas the open preon associated with U(1) is without mass mγ = 0. The most elementary symmetry cannot be broken any further. For that reason there is no primitive root of unity, i.e., a standing-wave solution corresponding to a mass. It follows that there is a mass gap which is a finite difference in energy between the lowest bound state and the free, open state.
It is common to denote by a vacuum vector Ω the eigenstate of Hamiltonian
H with zero energy
HΩ = 0, but this notion is abstract without physical correspondence. When there is no energy density, there is no state either. The surrounding free space of the Universe is not empty but the energy density known as the vacuum amplitude, in some theories referred to as the Higgs field, is in balance with its fermion systems (
Figure 1). This balance between radiation and matter is apparent from the cosmic microwave spectrum that matches the black-body spectrum. The conservation of energy requires that at any given step during the universal energy dispersal process, the change in kinetic energy density, deemed as continuous in
dt(
ρv2) = −
v∇·
u −
εοc2∇·(
E×B), balances the change in the scalar potential density
u due to the average density
ρ of matter with the change in the electromagnetic radiation density. The vector
μο−1E°B [
46] embodies energy of free space which is unique up to a phase and invariant under the Poincaré group in accordance with Maxwell equation
dF = 0 in the absence of charges and currents.
The Lie derivative is conveniently continuous in evaluating the change of one vector field (∂tQ/c) along the flow of another vector field (v·∇U). The smooth, differentiable manifold, such as the gauge group U(1)×SU(2)×SU(3) of the Standard Model, is admittedly suitable for mathematical manipulation, but it would be appropriate only for a stationary system because it fails to describe the discontinuous event of breaking symmetry.
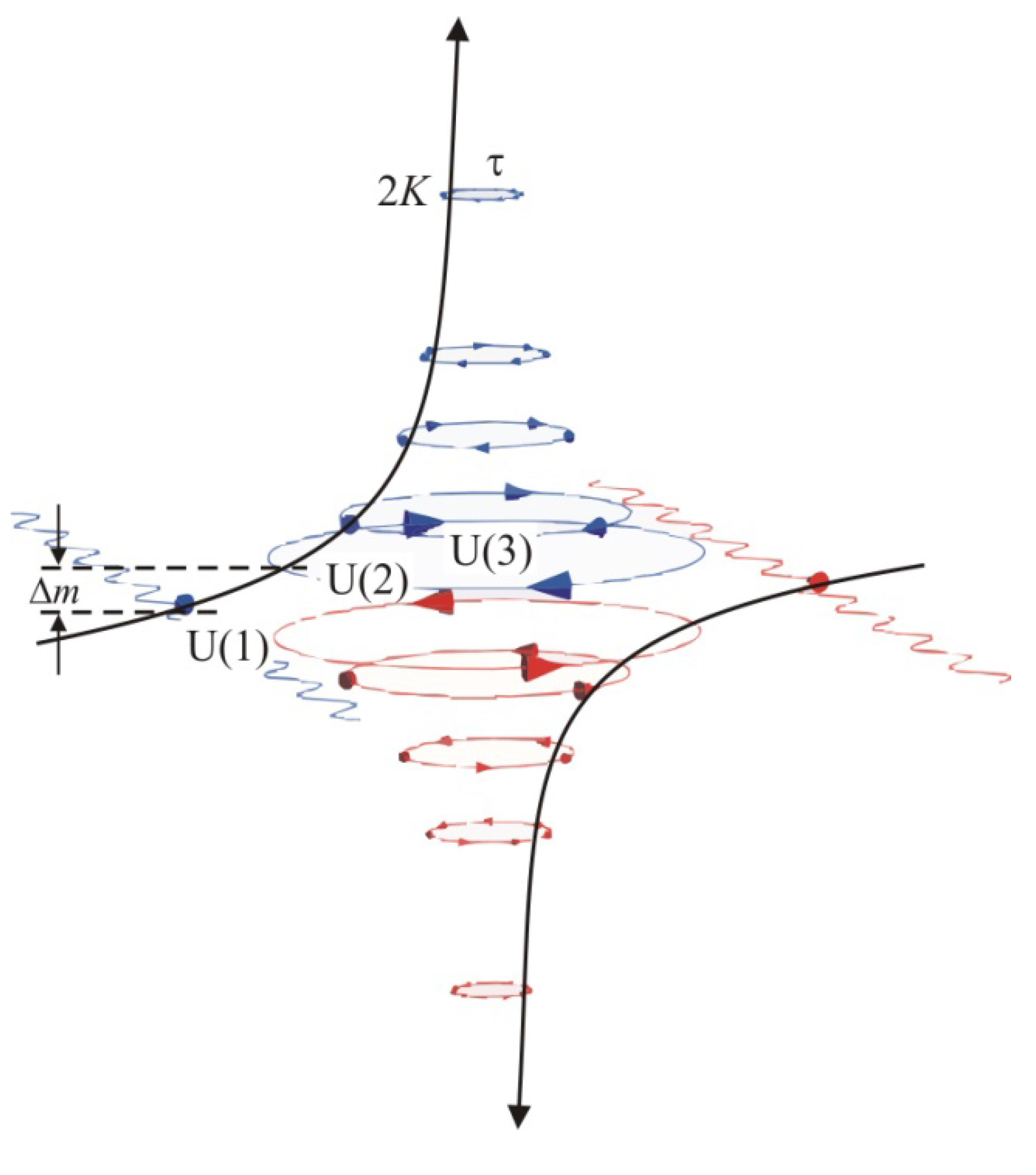
Figure 8.
Level diagram depicts an array of actions (colored) that are classified according to unitary groups of symmetry. Each stationary action equals the kinetic energy 2K integrated over the period τ along a directed path. It associates via Noether’s theorem with a conserved quantity m. A mass gap Δm ≠ 0 exists between the closed action of the most elementary fermions, the neutrinos defined by the next lowest symmetry group U(2) and the open action of the propagating photons defined by the most elementary group U(1). The radiated energy ΔΕ = Δmc2 in the transformation from U(2) down to U(1) amounts from the photons that disperse in the surrounding free space. The energy density of the free space is non-zero as is apparent from the finite speed of light. Only one of the two chiral forms of U(2) fermions can be detected via emissive transformations to U(1) whereas a detection by absorption would transform the U(2) particle to another one of a higher symmetry group.
Figure 8.
Level diagram depicts an array of actions (colored) that are classified according to unitary groups of symmetry. Each stationary action equals the kinetic energy 2K integrated over the period τ along a directed path. It associates via Noether’s theorem with a conserved quantity m. A mass gap Δm ≠ 0 exists between the closed action of the most elementary fermions, the neutrinos defined by the next lowest symmetry group U(2) and the open action of the propagating photons defined by the most elementary group U(1). The radiated energy ΔΕ = Δmc2 in the transformation from U(2) down to U(1) amounts from the photons that disperse in the surrounding free space. The energy density of the free space is non-zero as is apparent from the finite speed of light. Only one of the two chiral forms of U(2) fermions can be detected via emissive transformations to U(1) whereas a detection by absorption would transform the U(2) particle to another one of a higher symmetry group.
The step from one stationary-state symmetry to another takes at least one quantum of action from the system to its surroundings. When the quantized action is understood as the basic constituent of nature, no renormalization is required to escape from singularities that trouble theories which are based on the energy concept [
70]. Thus, it is not productive to maintain that the Lagrangian would be invariant and that evolution would be a continuous group of transformations. Accordingly, it is inconsistent to insist on the existence of a theory which would both comply with a gauge group via renormalization, and also display a mass gap [
71].
Theorem: For any-one compact simple gauge group G, there exists no quantum Yang-Mills theory on R4 that has a mass gap.
Proof: The Yang-Mills Lagrangian:
where the two-form
F denotes curvature via a gauge-covariant extension of the exterior derivative from the one-form
A of the G gauge connection and
g2 is the determinant of the metric tensor of the spacetime. It follows that G governs the symmetry of the action, which is the integral of
L. Since the quadratic form that is constructed from
F and its Hodge dual *
F on the Lie algebra of G on
R4 is invariant, so also
L is invariant and so is its integral action invariant. The invariant action relates via the Noether’s theorem to a quantity
m whose value is conserved. It then follows that a difference between any two values
mG and
mH of a conserved quantity cannot be compared within any-one theory based only on a single gauge group. Specifically, in a Yang–Mills theory that is based exclusively on one gauge group G describes only a single, invariant state. When the theory is based on U(1), it describes the vacuum state (the free space). When the theory is based on another Lie group, it describes another state. The difference Δ
m =
mH −
mG ≠ 0 in the conserved quantity between U(1) and the next lowest symmetry group is referred to as the mass gap. However, the gap is not defined,
i.e., it does not exist within any given theory based exclusively on a single gauge group.
Corollary: For any-two distinct gauge groups G and H, there exists a theory on R4 that has a mass gap.
Proof: Each gauge group relates the symmetry of action as the invariant integral of Lagrangian on R4 via the Noether’s theorem to a quantity m whose value is conserved. Conversely, the two distinct gauge groups relate two distinct symmetries of invariant actions to two different values mG and mH of the conserved quantity. Thus there exists a difference Δm = mH − mG ≠ 0 in the conserved quantity, i.e., the mass gap, between the vacuum state energy EG governed by the most elementary G = U(1) symmetry group and the lowest excited state energy EH governed by the next most elementary symmetry group H.
The resolution of the Yang-Mills existence and the mass gap, while trivial in its proof, is revealing. The focus is not on energy but on action which is quantized for each state according to the corresponding gauge symmetry (
Figure 8). Therefore, no matter how small the energy
E of an excited state will become over an increasing time
t, the product
Et =
nħ remains invariant holding at least one (
n = 1) multiple of the quantized action. Likewise, no matter how far the range
x of a field will be extending with diminishing momentum
p, their product
px remains invariant so that associated observables remain countable. In other words, a theory based on action is self-similar but does not require renormalization since it is not troubled by infinities and singularities related to energy and time as well as to momentum and length. Yet, it may appear for some to be unconvincing to claim, as above, that SU(2) which is by determinant isomorphic to U(1), does have a distinct property,
i.e., mass. However, a unitary group U(
n) is non-Abelian for
n > 1 whereas U(1) is Abelian. The sense of circulation distinguishes the closed action from a point, and also from its open form because when the chiral, closed action is mapped on the polarized open action, the two open termini are distinct from the integrally closed and connected path. To bridge a topological inequivalence requires a dissipative transformation process. The mass gap is between the photon and the neutrino. Moreover, the Euler-Lagrange integral of a bound trajectory is well-defined,
i.e.,countable whereas Maupertuis’ action as an open path is ambiguous,
i.e.,uncountable. The ambiguity is reflected in the assignment of a value to the free energy of the vacuum. Instead the surrounding vacuum characteristics
c2 = 1/
εoμo are defined via the closure according to the Stokes theorem.
8. Algebraic and Non-algebraic Varieties
In the universal energy landscape a system as a variety composed of varieties is in relation to all other varieties via flows of energy. The energetic status of a system can be quantified by probability:
where actions are quantized
L = 2
Kt =
kBTt =
nħ (see Equation 2). The stationary state (
dtP = 0) measure ln
P = Σ
Nj is a sum over all closed graphs, as is familiar from index theory [
72] and from the linked cluster theorem for reversible,
i.e., non-propagating processes [
73].
It is in the objective of physics to predict by way of calculation. However, as has been emphasized all along, natural processes are in general non-computable. Computation is ultimately ranking, and intuitively it is impossible to rank a quantity such as an eigenvalue that is changing during the computation. Since an evolutionary step means a change in the modulus of an action, a descending sequence eventually attains the preon ring (infima) in some finite surroundings. Conversely, an ascending sequence attains some maximum number of modules (suprema) at a congruence which corresponds to the thermodynamic steady state in some finite surroundings. The ordering ensures that any bounded space is compact. The stationary state’s to-and-fro flows of energy are the affine connections that establish the ordering relations between conserved actions. These equivalence relations identify the countable subspaces, known as algebraic varieties, from which new spaces can in turn be constructed algebraically. The stationary state varieties form an orbit space. Specifically any two varieties are equivalent if and only if they are on the same orbit. Conversely, the finiteness properties ensure that when the orbit space, an n-dimensional oriented and closed manifold M, is divided in two, the system’s group of k varieties and to the surrounding’s group of n-k varieties are duals Hk(M) > Hn−k(M). The Poincaré duality theorem states that for M the kth cohomology group of M is isomorphic to the (n − k)th homology group of M, for all integers k.
The correspondence between the system and its surroundings is stated by the Hodge conjecture so that de Rham cohomology classes are algebraic,
i.e., they are sums of Poincaré duals of the homology classes of subvarieties. The conjecture says in terms of physics that the stationary systems can be algebraically constructed from subsystems that are duals of the stationary surroundings’ subsystems. Since at the conserved stationary state there are no open actions, all Hodge classes are generated by the Hodge classes of divisors where a divisor on an algebraic curve is a formal sum of its closed points on the basis of the Lefschetz theorem on (1,1)-classes. All closed curves with zeros (nodes) are modular in accordance with all rational elliptic curves being modular [
74]. Since an algebraic variety is the set of solutions of a system of polynomial equations (elliptic curves), an algebraic number field has a norm and at least one zero. It can be considered as a geometric object of the affine manifold [
75]. Since every non-constant single-variable polynomial with complex coefficients has at least one complex root, the field of complex numbers is algebraically closed. Moreover, Hilbert’s Nullstellensatz relates ideals of polynomial rings to subsets of affine space.
The stationary energy landscape with its closed, oriented and unitary structure is a Kähler manifold M that can be decomposed to its cohomology with complex coefficients, corresponding to the scalar and vector potentials, so that Hn(M, X) = ⊕ Hp,q(M) where p + q = n and Hp,q(M) is the subgroup of cohomology classes that are represented by harmonic forms of type (p, q). It is instructive to consider the (twice) differentiable and connected M, because an n-form ω, i.e., the Lagrangian, can be paired by integration, i.e., via the action ∫ω = 〈ω, [M]〉 with the homology class [M], i.e., the fundamental class whose the top relative homology group is infinite cyclic Hn(M, Z) > Z. The action ∫ω over M depends only on the cohomology class of ω. The physical insight to the mathematical problem of non-countability is consistent with the fact that the Hodge conjecture holds for sufficiently general and simple Abelian varieties such as for products of elliptic curves. Moreover, the stationary least action is consistent with the combination of two theorems of Lefschetz that prove the Hodge conjecture true when the manifold has dimension at most three which is required for the stability of the free-energy minimum varieties.
Although the Hodge conjecture complies with conservation and continuity, it is ambiguous in how the duality came about. It is in essence asking an evolutionary question, which cohomology classes in Hk,k(M) form from the complex subvarieties? Of course, it has been found mathematically that there are also non-algebraic varieties. For example, when the variety has complex multiplication by an imaginary quadratic field, then the Hodge class is not generated by products of divisor classes. These troublesome varieties correspond to the open actions. They are without norm, hence non-modular and indivisible. The n-form ω of a non-modular curve over a finite field is non-intergrable because it is without bounds. Although the natural processes terminate at the irreducible open preon, the path is open because one photon after another leaves the system. The manifold keeps contracting, mathematically without a bound, but physically the landscape ceases to exist when the last fermion opens up and transforms to boson that leaves forever. Also singularities associated with the squared operators, e.g., the square of an exterior derivate, are troublesome abstractions. At a singular point the algebraic variety is not flat which means it is non-stationary and uncountable. Thus the proof of the conjecture that Hodge cycles are rational linear combinations of algebraic cycles, hinges on excluding non-integrable classes, i.e., those without divisors. This depends on the definition of manifold.
Conjecture: Let M be a projective complex manifold. Then every Hodge class on M is a linear combination with rational coefficients of the cohomology classes of complex subvarieties of M.
Proof: A divisor on an algebraic curve is a formal sum of its closed points. It follows that if
M holds any Hodge class that cannot be generated by the Hodge classes of divisors, then the conjecture must be false. The definition of a projective complex manifold as a submanifold of a complex projective space determined by the zeros of a set of homogeneous polynomials, excludes any indivisible polynomial without roots [
76]. Since transition functions between coordinate charts are by definition holomorphic functions, also singular points are excluded from
M. The coordinate chart is a map
ϕ:
U →
V from an open set in
M to an open set in
Rn of the dimension of
M is one-to-one. The homeomorphism excludes any open curve,
i.e., any polynomial without at least one root. Thus it follows that Hodge cycles are rational linear combinations of algebraic cycles on a projective complex manifold. Since the projective complex manifold has no class without a divisor, the conjecture is true.
9. Discussion
The value of a natural principle is in comprehending complex as well as simple phenomena in the same basic terms. The principle of least action came first into sight by Fermat, when addressing the particular least-time propagation of light and later by Maupertuis when rationalizing the general least-time flows of any form of energy. However, Euler and especially Lagrange found mathematical reasons to narrow the general formulation to computable cases, i.e., to bound and stationary systems. Ever since physics has mostly trotted along reductionist and deterministic tracks nevertheless, there is nothing in the character of physics that would exclude to pursue holistic and non-deterministic prospects.
Physics, just as any other discipline, is beguiled by ambiguity in its central concepts, most notably space and time. According to the principle of least action space at any level of natural hierarchy is embodied in closed, stationary actions that evolve by the act of time which, in turn, is embodied in quanta of open actions. Density differences diminish when dense systems are discarding quanta to their sparse surroundings and as well when sparse systems are acquiring quanta from their dense surroundings. Curiously though, when there are alternative paths for the flows, the natural processes are non-deterministic because the flows by the very fact of flowing affect the driving density differences. This non-computable character of nature may not please our desire to predict but we had better acknowledge it and get acquainted with its basis. Also we need to recognize that an observation is a causal connection via energy transduction process from an object to an observer where indeterminism in outcomes arises from the relative phases of transmitter and receiver motions [
14,
30,
77].
The worldview provided by the least-time principle recognizes no fundamental distinction between fundamental particles and fundamental forces but regards all structures and processes as having emerged, proliferated and eventually been extinguished in leveling off density differences. According to the 2nd law of thermodynamics the flows of energy will search and naturally select [
78] mechanisms inanimate and animate so that flows will level off energy differences in the least time [
79,
80,
81,
82]. In other words, evolution keeps redirecting its course along the resultant of forces. Although it is natural to search for symmetry, as it relates to a free-energy minimum state, the mathematical beauty as such cannot tell us how it came about and how it will break down. Closed currents as manifestations of symmetry and topological invariance give rise to conserved quantities, most notably to mass which is ultimately valued in open-action equivalents that are accommodated in the thinning of surrounding space—the physical vacuum [
83].
The principle of least action accounts for everything by counting preons. This holistic picture of nature is not new [
84,
85,
86] nonetheless the tenet may appear to some as naive, but in return it provides insight to parameters and processes also beyond those analyzed here. Plethora of particles and diaspora of fundamental forces are seen as merely manifestations of energy dispersal not as ultimate causes or consequences. The on-going universal unfolding of strings of actions accelerates with the increasing radius of curvature, just as earlier, when primordial high densities, presumably similar those in present flavors of elementary particles, began to thin out from resonant confinements closed by internal reflections. The chirality consensus in actions that settled in at baryogenesis is seen as to have been an effective means to disperse energy just as the chirality standard of natural amino acids that established itself at prebiotic genesis as an effective means to facilitate energy dispersal [
87,
88]. Diversity in nature is astounding but not arbitrary. We recognize rules and regularities. Scale-independent power-laws, log-normal distributions and tree-like structures that branch out in logistic manner as well as spirals that wind out in logarithmic manner are found in diverse disciplines. The universal spatial patterns as well as ubiquitous time courses of sigmoid growth, bifurcations and chaos are ascribed to the decrease of free energy in the least time [
89]. Moreover, the physical portrayal of nature by diverse actions in multiples of
ħ is tangible in illustrating mathematical problems related to intractability [
41,
90,
91], emergence, change in modularity [
92,
93,
94,
95], symmetry breaking and division in duals which all are troubled by the problem of the uncountable.
Varied writings of Pierre Louis Moreau de Maupertuis reveal that he was outwardly stimulated in applying the principle of least action to decipher puzzles and phenomena in diverse disciplines [
96]. Although Maupertuis’ formulation failed to meet the integrability condition that was insisted upon by his rigorous contemporaries and has been required ever since on diverse occasions, it took time to understand the underlying reason that distinguishes reversible from irreversible and tractability from intractability and that discerns space from time. Undoubtedly the revision of M[aupertuis’]-theory presented here does not cohere with current classiness but calls for revival of intuition in the quest of unity.