Dispersal (Entropy) and Recognition (Information) as Foundations of Emergence and Dissolvence

1. Introduction

The objective of this essay is to reflect on possible relationships between entropy and emergence. A qualitative, relational approach is followed. The argument is schematized in Figure 1, to be understood as a roadmap with arrows as our guiding threads. We begin by highlighting that entropy has a richer semantic content than the concept of disorder it is a measure of and is frequently reduced to. Entropy indeed includes the concept of dissipation, the latter being understood as implying both decay and dispersal. We believe, and will endeavor to show, that dispersal is indeed relevant to our enquiry.

Figure 1. A schematic representation of informational processes involved in the formation and self-organization of complex systems. This Figure must be seen as a roadmap whose arrows represent the relations to be discussed herein. Entropy as dispersal increases the range of possible encounters between agents. Their recognition necessitates information exchange leading to coherent behavior. This is equivalent to stating that the agents experience top-down constraints, a phenomenon also known as dissolvence or submergence which decreases their behavior and property space and increases the information content of the complex system. A better recognized property of complex systems is their dissipative nature, another major factor contributing to their homeostasis and adaptability.

Figure 1. A schematic representation of informational processes involved in the formation and self-organization of complex systems. This Figure must be seen as a roadmap whose arrows represent the relations to be discussed herein. Entropy as dispersal increases the range of possible encounters between agents. Their recognition necessitates information exchange leading to coherent behavior. This is equivalent to stating that the agents experience top-down constraints, a phenomenon also known as dissolvence or submergence which decreases their behavior and property space and increases the information content of the complex system. A better recognized property of complex systems is their dissipative nature, another major factor contributing to their homeostasis and adaptability.

Emergence is a property of complex systems such as atoms, organisms, ecosystems or galaxies. It arises from the collective, coordinated behavior of many entities, be they identical or (more often than not) different. But for a collective behavior to arise, the agents to be coordinated must recognize each other, usually their neighbors. In other words, agents must interact by information exchange. Recognition is how information is understood here, and as stated it is partly a short-range process, particularly at a (bio) molecular level where electrostatic interaction fields are operative.

What needs to be acknowledged, and will be argued here, is that the scope and variety of recognition processes between agents is increased when preceded by their dispersal. The latter indeed multiplies the number of encounters among agents (and their variety in case of many different types of agents), thus creating a richer potential for recognition. As observed for example in many fields of experimental sciences, the movement of molecules in reactors and cells, or the dispersal of plants and animals beyond their niche, creates opportunities for new encounters and new complex systems to emerge.

Another process relevant to emergence is dissolvence, also known as submergence (see Section 5). Indeed, agents integrated into a higher-level whole experience top-down constraints which restrict their property and behavior spaces. As such, dissolvence participates in the information-entropy interplay involved in the creation and decay of higher-level entities.

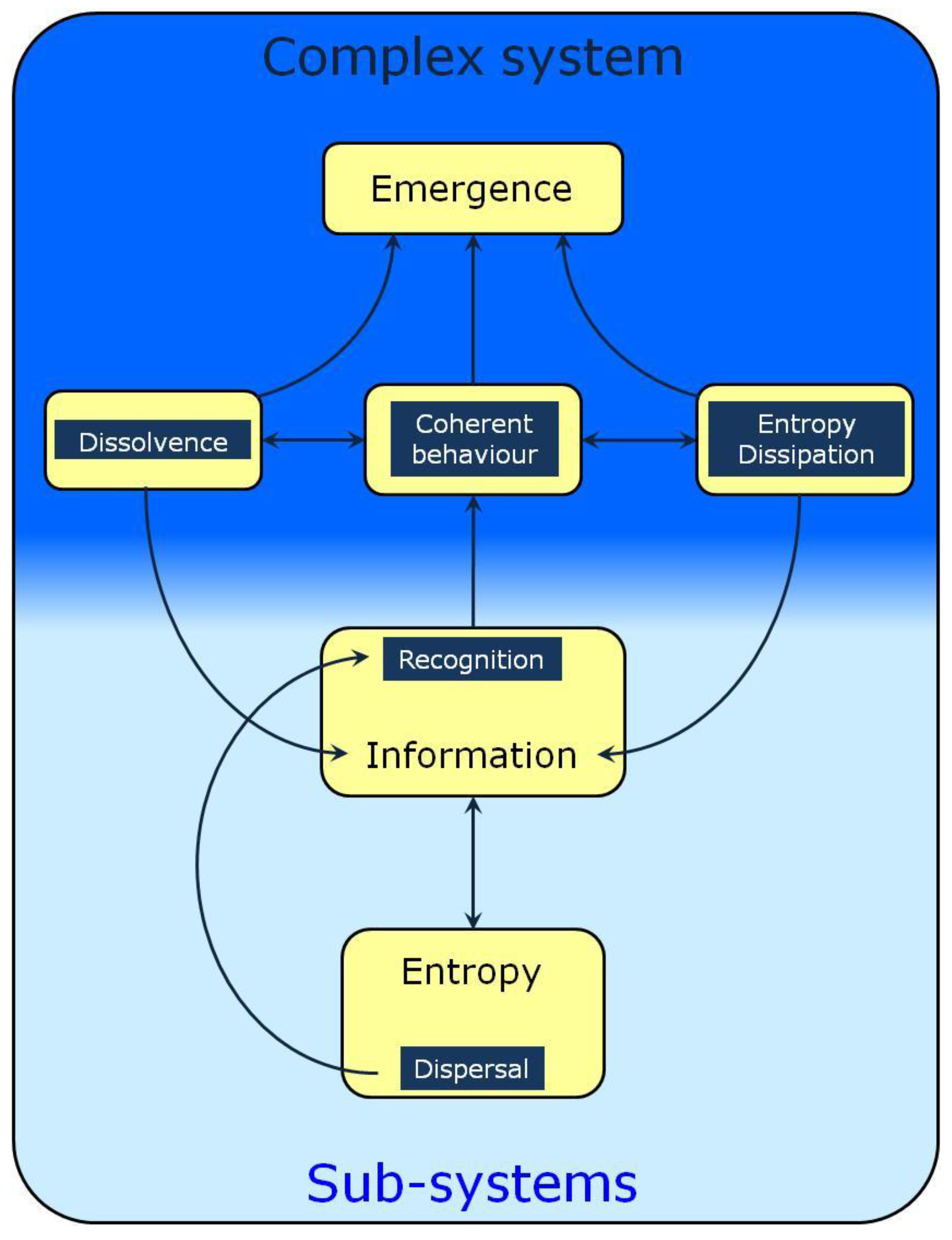
2. Entropy and Dispersal

Much variety exists in the literature, even in so-called “popular science” books written by distinguished scientists [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16], on how entropy is conceptualized and described. From an extrinsic perspective, entropy is a measure of an observer’s ignorance of the state of a system. This definition relates directly to information, and we shall return to it.

In a thermodynamic sense, entropy is of course a measure of the quality of energy, more precisely of the extent to which heat in a system is not available for conversion into mechanical work [1,9]. It is also, in a statistical sense, a measure of the amount of disorder in a system, and as such is proportional to the number of distinct states a system can occupy, and to an observer’s ignorance of the actual state of a system.

This has led a number of researchers to adopt a more dynamical perspective by interpreting entropy as being related not only to the number of states a ensemble of agents can occupy, but also to the phase space a system can explore, [2,4,8,11,13]. Entropy is thus understood as relating to physical migration of agents (e.g., molecules) and as reflecting the capacity of a system to fluctuate within its phase space—in other words to explore it. This allows entropy to be defined in terms of a probability distribution such as a histogram, with divergence between two distributions assessed by the Kullback-Leibler distance [17,18].

In the context of dynamical interpretation, we consider as particularly pregnant and inspiring Stuart Kauffman’s reference to the “adjacent possible” [6,7], which sets limits to the accessible space and simultaneously recalls Antoine Danchin’s view of entropy as a measure of exploration [4].

Here, we use the term dispersal to convey this dynamical interpretation of entropy [14], although the word “dissipation” has also been used [2]. By dispersal, we mean the exploration of territories of possibilities, and the opening of new territories when heat is supplied to a system and increases its fluctuations.

3. Recognition and Information

Materials systems at all levels of organization are able to emit “signals” understood as vectors of information “encoded” by the emitter and to be “decoded” by the receiver [4,19,20,21,22]. At the chemical level for example, molecules are surrounded by molecular fields such as electrostatic and hydrophobic potentials [23,24]. They can thus interact with other chemical systems (ions, molecules, macromolecules, molecular assemblies) able to decode (interpret) these signals and react accordingly by experiencing attraction (or repulsion, also a form of recognition). In other words, information is transmitted when signals are interpreted and given meaning [25]. A “meaningful” signal is thus understood here as a signal recognized as such by the recipient and able to modify its information content and its behavior. And information exchange between two systems implies their mutual recognition [2], namely the communication of relationships [21]. The reader interested in a quantitative treatment of the topic is referred to a recent and extensive review on the information-theoretical approach [26].

Be it at the level of particles, atoms, molecules and macromolecules, cells and tissues, organisms and communities, recognition is the process underlying assembly and organization to create a higher-level system. Such a higher-level system must be more than the sum of its parts, as it consists in its parts plus their interactions [3]. These interactions are constrained in that they must be compatible with the relational and kinetic properties of the agents, an obvious point made explicit in some relevant writings [19,27,28].

4. Collective Behavior, Open Systems and Emergence

Collective behavior is a common phenomenon in nature, as observed for example with lattices of magnetic atoms (Ising models), bacteria growth, slime moulds, beehives, flocks of birds, or crowd behavior [29]. Such coherent, coordinated behavior arises from local interactions between agents, resulting from their mutual recognition. Specifically, vicinal recognition produces short-range order domains. However, these alone are not sufficient for a cohesive system to arise and behave as a whole. Long-range correlations characteristic of “small-world networks” [29,30] are indispensable and are believed to appear progressively during the built-up of a complex system. Thus, the formation of complex systems is initiated by the self-assembly of their components. The term autopoiesis has been proposed [31] to characterize the self-production and self-organization of complex systems. In more metaphorical language, complex systems are said to bootstrap themselves into existence and become autonomous; they “pull themselves up by their own bootstraps” and become distinct from their environment [31,32].

Quite naturally, a higher-order system shows properties and behavior patterns that do not exist in its components. Such qualitatively new properties are termed emergent rather than resultant when they are not possessed by any of the components [20]. The process itself is known as emergence [13,28,32,33].

Such a look at emergence would not be complete without giving due consideration to the critical role played by its boundary conditions on any system, that is to say the conditions imposed on the system by its environment [7,10,13]. These conditions are pre-existing and permanent, and their influence contributes to the organization of the system [34,35].

Another significant property of such systems is their open nature, which allows them to dissipate entropy into their environment, thereby maintaining or increasing their information content [13,33]. This interaction is strongly dependent on boundary conditions, again emphasizing that any attempt to define complex systems in isolation from their context is bound to remain unsatisfactory, a conclusion beautifully illustrated by Dawkins’ breakthrough concept of the “extended phenotype” [36].

Other characteristics of complex living systems include self-replication, homeostasis (self-regulation resulting from feedback), and adaptability [2,11]. This latter property describes their capacity to switch between different modes of behavior as their context changes [11]. At this point, Murray Gell-Mann’s pregnant sentence comes to mind, that “Basically, information is concerned with a selection from alternatives” [5]. In other words, the more information a complex system can contain, the more adaptable it may be.

Defining complexity “[...] as the logarithm of the number of possible states of the system: K = log N, where K is the complexity and N the number of possible, distinguishable states” [3] is simultaneously correct and misleadingly narrow. It is made clearer by its implication, borrowed from information theory, that “the more complex a system, the more information it is capable of carrying”. Taking a simple example from biochemistry, the conformational and property space of even a short peptide is considerably greater than that of its constituting amino acids [37]. But what this description of complexity misses are the structural and dynamic dimensions of complex systems. These indeed are characterized by an internal and hierarchical structure that must be both resilient to perturbations yet flexible and adaptable.

As an aside, the formal similarity of the above equation with Boltzmann’s might, wrongly of course, be taken to suggest that the more complex a system, the greater an observer’s ignorance of it. This illustrates the pitfalls of out-of-context definitions—even if mathematical in form.

It also results from the above definition of complexity that the process of autopoiesis must necessarily be an information-producing one. We discuss below a component of autopoiesis where increase in information is demonstrable.

5. Dissolvence

A process generally labeled as “top-down constraints” is mentioned in a number of writings, e.g., [2,28,31] and is described as “submergence” by Mahner and Bunge [20]. This is the process we have called “dissolvence” and which has been presented in detail in this Journal [38] and elsewhere [15,39].

As discussed above, the formation of complex systems is accompanied by the emergence of properties that are non-existent in the components. But what of the properties and behavior of such components interacting to form a system of a higher level of complexity? A variety of examples, from molecules to organisms and beyond, can be marshalled to show that simpler systems merging to form a higher-order system experience constraints with a partial loss of choice, options and independence. In other words, emergence in a complex system implies reduction in the number of probable states of its components; an associated process is entrainment, a synchrony imposed on the components [28]. Such processes of top-down constraints result from both the system (directly) and from its environment (indirectly), a reminder of the boundary conditions discussed above [34,35].

Dissolvence is seen for example in atoms when they merge to form molecules, in bio-molecules when they form macromolecules such as proteins, and in macromolecules when they form aggregates such as molecular machines or membranes. At higher biological levels, dissolvence occurs for example in components of cells (e.g., organelles), tissues (cells), organs (tissues), organisms (organs) and societies (individuals). As noted by Maturana and Varela [31], a continuum of degrees of autonomy exists at the components of a complex system, from a minimal degree in tissues in an organism, to the relatively large autonomy of individuals in human societies.

But what about the entropy-information variations resulting from dissolvence? This is a question that can be investigated at the level of components due to their probabilistic behavior [11]. In a series of computational simulations using molecular mechanics [40,41], top-down constraints experienced by the side-chains of residues in proteins compared to free amino acids were explored. The results revealed increased conformational constraints on the side-chains of residues compared to the same amino acids in monomeric (free) form. A Shannon entropy (SE) analysis of the conformational behavior of the side-chains showed in most cases a progressive and marked decrease in the SE of the χ₁ and χ₂ dihedral angles. This is equivalent to stating that conformational constraints on the side-chain of residues increase their information content and, hence, recognition specificity compared to free amino acids. In other words, the vastly increased capacity for recognition of a protein relative to its free monomers is embedded not only in the tertiary structure of the backbone, but also in the conformational behavior of its side-chains. The postulated implication is that both backbone and side-chains, by virtue of being conformationally constrained, contribute to the protein’s recognition specificity towards ligands and other macromolecules, a well-documented phenomenon in medicinal chemistry and biochemistry [42].

6. Conclusions

This Commentary in general, and its Figure in particular, aim at offering a schematic if partial overview of processes involved in the emergence, survival and further evolution of complex systems. Entropy and information are at the heart of these processes, being the two faces of the same coin. Antique mythology was familar with the concept of unseparable opposites, witness the two-faced Janus, god of gates, doors, doorways, beginnings and endings [43]. It is perhaps in this sense that we are to understand such an apparent oxymoron as “Under certain conditions, entropy itself becomes the progenitor of order” [44].