Fisher Information and Semiclassical Treatments

Abstract

We review here the difference between quantum statistical treatments and semiclassical ones, using as the main concomitant tool a semiclassical, shift-invariant Fisher information measure built up with Husimi distributions. Its semiclassical character notwithstanding, this measure also contains abundant information of a purely quantal nature. Such a tool allows us to refine the celebrated Lieb bound for Wehrl entropies and to discover thermodynamic-like relations that involve the degree of delocalization. Fisher-related thermal uncertainty relations are developed and the degree of purity of canonical distributions, regarded as mixed states, is connected to this Fisher measure as well.

1. Introduction

A quarter of century before Shannon, R.A. Fisher advanced a method to measure the information content of continuous (rather than digital) inputs using not the binary computer codes but the statistical distribution of classical probability theory [1]. Already in 1980 Wootters pointed out that Fisher’s information measure (FIM) and quantum mechanics share a common formalism and both relate probabilities to the squares of continuous functions [2].

The present review draws materials from much interesting work that is reported recently and devoted to the physical applications of Fisher’s information measure (see, for instance, [1,3,4,5,6]). Frieden and Soffer [3] have shown that Fisher’s information measure provides one with a powerful variational principle—the extreme physical information—that yields most of the canonical Lagrangians of theoretical physics [1,3]. Additionally, FIM has been shown to provide an interesting characterization of the “arrow of time”, alternative to the one associated with Boltzmann’s entropy [7,8]. Thus, unravelling the multiple FIM facets and their links to physics should be of general interest. The Legendre transform structure of thermodynamics can be replicated as well, without any change, if one replaces the Boltzmann–Gibbs–Shannon entropy S by Fisher’s information measure I. In particular, I possesses the all important concavity property [5], and use of the Fisher’s measure allows for the development of a thermodynamics that seems to be able to treat equilibrium and non-equilibrium situations in a manner entirely similar to the conventional one [5]. Here, the focus of our attention will be, following [9], the thermal description of harmonic oscillator (HO).

The semiclassical approximation (SC) has had a long and distinguished history and remains today a very important weapon in the physics armory. It is indeed indispensable in many areas of scientific endeavor. Also, it facilitates, in many circumstances, an intuitive understanding of the underlying physics that may remain hidden in extensive numerical solutions of Schrödinger’s equation. Although the SC-approach is as old as quantum mechanics itself, it remains active, as reported, for example, in [10] and [11].

Our emphasis in this review will be placed on the study of the differences between (i) statistical treatments of a purely quantal nature, on the one hand, and (ii) semiclassical ones, on the other. We will show that these differences can be neatly expressed entirely in terms of a special version, to be called $I_{\tau }$, of Fisher’s information measure: the so-called shift-invariant Fisher one [1], associated to phase space. Additionally $I_{\tau }$ is a functional of a semiclassical distribution function, namely, the Husimi function $\mu (x,p)$. The phase space measure $I_{\tau }$ will be shown to help to (1) refine the so-called Lieb-bound [12] and (2) connect this refinement with the delocalization in phase space. The latter can, of course, be visualized as information loss. $I_{\tau }$ will also be related to an interesting semiclassical measure that was early introduced to characterize the same phenomenon: the Wehrl entropy W [12],

$$W=-k_B{\langle ln\mu \rangle }_{\mu }$$

(1)

for which Lieb established the above cited lower bound $W\ge 1$, which is a manifestation of the uncertainty principle [13]. $k_B$ is the Boltzmann’s constant. Henceforth we will set $k_B=1$, for the sake of simplicity.

For the convenience of the reader, in the following section we describe some fundamental aspects of the HO canonical-ensemble description from a coherent states’ viewpoint [9], the Husimi probability distribution function, and the Wehrl information measure.

2. Background Notions

2.1. HO’s coherent states

In [9] the authors discuss quantum-mechanical phase space distributions expressed in terms of the celebrated coherent states $|z\rangle$ of the harmonic oscillator, eigenstates of the annihilation operator $\widehat{a}$ [14,15], i.e.,

$$\widehat{a}|z\rangle =z|z\rangle$$

(2)

with z a complex combination of the phase space coordinates x, p

$$z=\frac{x}{2{\sigma }_x}+\mathrm{i}\frac{p}{2{\sigma }_p}$$

(3)

where ${\sigma }_x={(\hslash /2m\omega )}^{1/2}$, ${\sigma }_p={(\hslash m\omega /2)}^{1/2}$, and ${\sigma }_x{\sigma }_p=\hslash /2$.

Coherent states span Hilbert’s space, constitute an over-complete basis and obey resolution of unity [15]

$$\int \frac{{\mathrm{d}}^{2}z}{\pi }|z\rangle \langle z|=\int \frac{\mathrm{d}x\mathrm{d}p}{2\pi \hslash }|x,p\rangle \langle x,p|=1$$

(4)

where the differential element of area in the $z-$plane is ${\mathrm{d}}^{2}z=\mathrm{d}x\mathrm{d}p/2\pi \hslash$ and the integration is carried out over the whole complex plane.

The coherent state $|z\rangle$ can be expanded in terms of the states of the HO as follows

$$|z\rangle =\sum _{n=0}^{\infty }{\left|\langle z|n\rangle \right|}^2|n\rangle$$

(5)

where $|n\rangle$ are eigenstates of the HO Hamiltonian whose form is $\widehat{H}=\hslash \omega [{\widehat{a}}^{†}\widehat{a}+1/2]$ and we have

$${\left|\langle z|n\rangle \right|}^2=\frac{{\left|z\right|}^{2n}}{n!}{e}^{-{\left|z\right|}^2}$$

(6)

2.2. HO-expressions

We write down now, for future reference, well-known quantal HO-expressions for, respectively, the partition function Z, the entropy S, the mean energy U, the mean excitation energy E, the free energy $F=U-TS$, and the specific heat C [16]

$$\begin{array}{ccc}\hfill Z& =& \frac{e^{-\beta \hslash \omega /2}}{1-e^{-\beta \hslash \omega }}\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill S& =& \beta \frac{\hslash \omega }{e^{\beta \hslash \omega }-1}-ln(1-e^{-\beta \hslash \omega })\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill U& =& \frac{\hslash \omega }{2}+E\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill E& =& \frac{\hslash \omega }{e^{\beta \hslash \omega }-1}\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill F& =& \frac{\hslash \omega }{2}+Tln(1-e^{-\beta \hslash \omega })\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill C& =& {\left(\frac{\beta \hslash \omega }{e^{\beta \hslash \omega }-1}\right)}^2{e}^{\beta \hslash \omega }\hfill \end{array}$$

(12)

2.3. Husimi probability distribution

In the wake of a discussion advanced in [17], we will be mainly concerned with building “Husimi–Fisher” bridges. It is well-known that the oldest and most elaborate phase space (PS) formulation of quantum mechanics is that of Wigner [18,19]. To every quantum state a PS function (the Wigner one) can be assigned. This PS function can, regrettably enough, assume negative values so that a probabilistic interpretation becomes questionable. Such limitation was overcome, among others, by Husimi [20]. In terms of the concomitant Husimi probability distributions, quantum mechanics can be completely reformulated [21,22,23,24]. This phase space distribution has the form of

$$\mu (x,p)\equiv \mu (z)=\langle z\left|\widehat{\rho }\right|z\rangle$$

(13)

where $\widehat{\rho }$ is the density operator of the system and $|z\rangle$ are the coherent states (see, for instance, [25] and references therein). The function $\mu (x,p)$ is normalized in the fashion

$$\int \frac{\mathrm{d}x\mathrm{d}p}{2\pi \hslash }\mu (x,p)=1$$

(14)

For a thermal equilibrium case $\widehat{\rho }=Z^{-1}{e}^{-\beta \widehat{H}}$, $Z=\mathrm{Tr}(e^{-\beta \widehat{H}})$ is the partition function, $\beta =1/T$, with T being the temperature. Specializing things for the HO of frequency ω, with eigenstates $|n\rangle$ associated to the eigenenergies $E_n=\hslash \omega \left(n+1/2\right)$, one has

$$\langle z|\widehat{\rho }|z\rangle =\frac{1}{Z}\sum _n{e}^{-\beta \widehat{H}}{\left|\langle z|n\rangle \right|}^2$$

(15)

with ${\left|\langle z|n\rangle \right|}^2$ given by Equation (6), and the normalized Husimi probability distribution is

$$\mu (z)=(1-e^{-\beta \hslash \omega })e^{-(1-e^{-\beta \hslash \omega }){\left|z\right|}^2}$$

(16)

2.4. Wehrl entropy

The Wehrl entropy is defined as [12]

$$W=-\int \frac{\mathrm{d}x\mathrm{d}p}{2\pi \hslash }\mu (x,p)ln\mu (x,p)$$

(17)

where $\mu (x,p)$ is the “classical” distribution function (13) associated to the density operator $\widehat{\rho }$ of the system. The uncertainty principle manifests itself through the inequality $W\ge 1$, which was first conjectured by Wehrl [12] and later proved by Lieb [13]. Equality holds if $\widehat{\rho }$ is a coherent state. After integration over all phase space, turns out to be [9]

$$W=1-ln(1-e^{-\beta \hslash \omega })$$

(18)

3. Fisher’s Information Measure

Let us consider a system that is specified by a physical parameter θ, while x is a real stochastic variable and $f_{\theta }(\mathbf{x})$, which in turn depends on the parameter θ, is the probability density for $\mathbf{x}$. An observer makes a measurement of $\mathbf{x}$ and estimates θ from this measurement, represented by $\tilde{\theta }=\tilde{\theta }(\mathbf{x})$. One wonders how well θ can be determined. Estimation theory [26] asserts that the best possible estimator $\tilde{\theta }(\mathbf{x})$, after a very large number of $\mathbf{x}$-samples is examined, suffers a mean-square error $e^2$ from θ that obeys a relationship involving Fisher’s I, namely, $I{e}^2=1$, where the Fisher information measure I is of the form

$$I(\theta )=\int \mathrm{d}\mathbf{x}{f}_{\theta }(\mathbf{x}){\left\{\frac{\partial ln{f}_{\theta }(\mathbf{x})}{\partial \theta }\right\}}^2$$

(19)

This “best” estimator is called the efficient estimator. Any other estimator must have a larger mean-square error. The only proviso to the above result is that all estimators be unbiased, i.e., satisfy $\langle \tilde{\theta }(\mathbf{x})\rangle =\theta$. Thus, Fisher’s information measure has a lower bound, in the sense that, no matter what parameter of the system we choose to measure, I has to be larger or equal than the inverse of the mean-square error associated with the concomitant experiment. This result, $I{e}^2\ge 1,$ is referred to as the Cramer–Rao bound [1,27]. A particular I-case is of great importance: that of translation families [1,4], i.e., distribution functions (DF) whose form does not change under θ-displacements. These DF are shift-invariant (à la Mach, no absolute origin for θ), and for them Fisher’s information measure adopts the somewhat simpler appearance [1]

$$I=\int \mathrm{d}\mathbf{x}f(\mathbf{x}){\left\{\frac{\partial lnf(\mathbf{x})}{\partial \mathbf{x}}\right\}}^2$$

(20)

Fisher’s measure is additive [1]: If $x\mathrm{and}p$ are independent, variables, $I(x+p)=I(x)+I(p)$. Notice that, for $\tau \equiv (x,p)$ (a point in phase-space), we face a shift-invariance situation. Since in defining z in terms of the variables x and p, these are scaled by their respective variances, the Fisher measure associated to the probability distribution $\mu (x,p)$ will be of the form [4]

$$I_{\tau }=\int \frac{\mathrm{d}x\mathrm{d}p}{2\pi \hslash }\mu (x,p)\mathcal{A}$$

(21)

with

$$\mathcal{A}={\sigma }_x^2{\left[\frac{\partial ln\mu (x,p)}{\partial x}\right]}^2+{\sigma }_p^2{\left[\frac{\partial ln\mu (x,p)}{\partial p}\right]}^2$$

(22)

Given the μ-expression (16), $I_{\tau }$ becomes

$$I_{\tau }=1-e^{-\beta \hslash \omega }$$

(23)

which, immediately yields

$$I_{\tau }{e}_{\left|z\right|}^2(\beta ,\omega )=1;(\mathrm{CR}\mathrm{bound}\mathrm{reached})$$

(24)

We realize at this point that the Fisher measure built up with Husimi distributions is to be best employed to estimate “phase space position” $\left|z\right|$. Further, efficient estimation is possible for all temperatures, a rather significant result. Comparison with Equation (18) allows one now to write

$$W=1-ln(I_{\tau })\Rightarrow W+ln(I_{\tau })=1$$

(25)

Since both W and $I_{\tau }$ are positive-definite quantities, (25) tells us that they are complementary informational quantities, thus if one of them gains, the other loses. Following Anderson et al. [9] let us now analyze the high and low temperatures limits. Given the form (23), when the temperature goes to zero $(\beta \to \infty )$, $I_{\tau }\approx 1$, its maximum possible value, since we know that the ground state will be the only one to be populated. If, on the other hand, the temperature tends to infinity $(\beta \to 0)$, then $I_{\tau }\approx \beta \hslash \omega$ and tends to zero, because we know beforehand that, in the limit, all energy levels will be populated in uniform. The uniform distribution is that of maximum ignorance [28,29,30,31]. The range of $I_{\tau }$ is $0\le I_{\tau }\le 1$, that of W is $1\le W\le \infty$, as we can see in Figure 1. Using $I_{\tau }$ together with Equation (7) we notice that

$$I_{\tau }=\frac{e^{-\beta \hslash \omega /2}}{Z}$$

(26)

so that it coincides with the canonical ensemble probability for finding the system in its ground state.

Figure 1. Fisher ($I_{\tau }$) and Wehrl (W) information measures vs. T (in $\hslash \omega$ units) for HO-Husimi distribution.

Figure 1. Fisher ($I_{\tau }$) and Wehrl (W) information measures vs. T (in $\hslash \omega$ units) for HO-Husimi distribution.

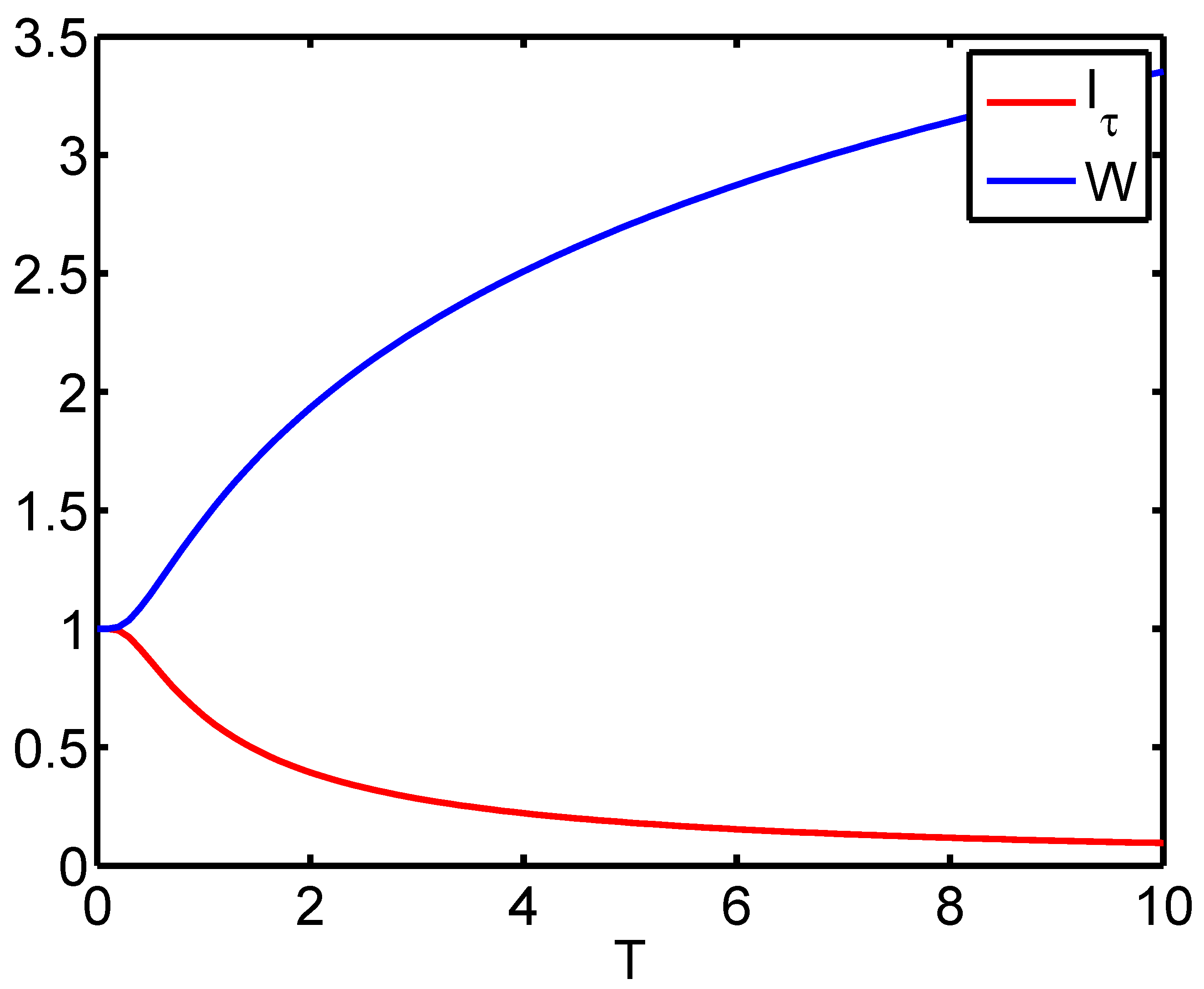
4. Fisher, Thermodynamics’ Third Law, and Thermodynamic Quantities

Consider now the general definition (19) of Fisher’s information measure in terms of the DF $\mu (x,p)$

$$I_{\beta }=\int \frac{\mathrm{d}x\mathrm{d}p}{2\pi \hslash }\mu (x,p){\left(\frac{\partial ln\mu (x,p)}{\partial \beta }\right)}^2$$

(27)

with $\theta \equiv \beta$ is the parameter to be estimated. Since

$$\frac{\partial ln\mu (x,p)}{\partial \beta }=\frac{\hslash \omega }{e^{\beta \hslash \omega }-1}[1-(1-e^{-\beta \hslash \omega }){\left|z\right|}^2]$$

(28)

one readily ascertains that (i) the μ-mean value of (28) vanishes and (ii)

$$I_{\beta }={\left(\frac{\hslash \omega }{e^{\beta \hslash \omega }-1}\right)}^2\left(T=[0,\infty ]\to I_{\beta }=[0,\infty ]\right)$$

(29)

which, in view of (12), entails

$$I_{\beta }=\frac{e^{-\beta \hslash \omega }}{{\beta }^2}C$$

(30)

Reflection upon the $I_{\beta }$-range (29) might led one to conclude that it constitutes a Fisher manifestation of thermodynamics’ third law. Not only Shannon’s measure but also Fisher’s (for the HO, at least) vanishes at zero temperature. Replacing now (23) and (29) into the entropy expression (8) we immediately arrive at the relation

$$S=\beta \sqrt{I_{\beta }}-ln{I}_{\tau }$$

(31)

The HO entropy can be expressed as the sum of two terms: one associated with the Fisher information $I_{\beta }$ and the other with the Fisher information for translation families $I_{\tau }$ corresponding to the phase space variables $(x,p)$. Using Equation (7) we also have

$$ln{I}_{\tau }=-\beta \frac{\hslash \omega }{2}-lnZ=-(\beta E_{gs}+lnZ)$$

(32)

with $E_{gs}$ denoting the ground state energy. Thus,

$$S=\beta \left(\frac{\hslash \omega }{2}+\sqrt{I_{\beta }}\right)+lnZ$$

(33)

which is to be compared to the well known canonical ensemble general expression connecting S and the mean energy U [16]

$$S=lnZ+\beta U$$

(34)

we see that $I_{\beta }$ is related to the excited spectrum contribution to U while $I_{\tau }$ is to be linked to the partition function. We will look now for a new connection between Fisher’s measures $I_{\tau }$ and $I_{\beta }$. From (29) it is possible to rewrite $I_{\beta }$ in the form

$$I_{\beta }\equiv {\left(\frac{\hslash \omega e^{-\beta \hslash \omega }}{1-e^{-\beta \hslash \omega }}\right)}^2$$

(35)

and therefore

$$I_{\tau }\sqrt{I_{\beta }}=\hslash \omega e^{-\beta \hslash \omega }=-\frac{\partial }{\partial \beta }(e^{-\beta \hslash \omega })$$

(36)

i.e., the product on the left hand side is the β-derivative of the Boltzmann factor (constant energy-wise) at the inverse temperature β. In other words, $I_{\tau }\sqrt{I_{\beta }}$ measures the β-gradient of the Boltzmann factor.

Equation (23) implies, via Equations (7) to (12), that the quantal HO expressions for the most important thermodynamic quantities can be expressed in terms of the semiclassical measure $I_{\tau }$. For this end we define the semiclassical free energy

$$F_{sc}=Tln{I}_{\tau }$$

(37)

which is the semiclassical contribution to the HO free-energy $F=\hslash \omega /2+F_{sc}$. Therefore, the thermodynamic quantities can be expressed as follows

$$\begin{array}{ccc}\hfill Z& =& \frac{e^{-\beta \hslash \omega /2}}{I_{\tau }}\hfill \end{array}$$

(38)

$$\begin{array}{ccc}\hfill E& =& \hslash \omega \frac{1-I_{\tau }}{I_{\tau }}\hfill \end{array}$$

(39)

$$\begin{array}{ccc}\hfill S& =& \beta \hslash \omega \frac{1-I_{\tau }}{I_{\tau }}-\frac{F_{sc}}{T}\hfill \end{array}$$

(40)

$$\begin{array}{ccc}\hfill C& =& {(\beta \hslash \omega )}^2\frac{1-I_{\tau }}{I_{\tau }^2}\hfill \end{array}$$

(41)

which shows that the semiclassical, Husimi-based $I_{\tau }-$information measure does contain purely quantum statistical information. Furthermore, since from Helmholtz’ free energy F, we can derive all of the HO quantal thermodynamics [16], we see that the the HO-quantum thermostatistics is, as far as information is considered, entirely of semiclassical nature, as it is completely expressed in terms of a semiclassical measure. We emphasize thus the fact that the semiclassical quantity $I_{\tau }$ contains all the relevant HO-statistical quantum information.

5. HO-Semiclassical Fisher’s Measure

5.1. MaxEnt approach

All the previous results are exact. No reference whatsoever needs to be made to Jaynes’ Maximum Entropy Principle (MaxEnt) [31] up to this point. We wish now to consider a MaxEnt viewpoint. It is shown in [14] that the HO-energy can be cast as the sum of the ground-state energy $\hslash \omega /2$ plus the expectation value of the HO-Hamiltonian with respect to the coherent state $|z\rangle$, which is the sum of the ground-state energy plus a semiclassical excitation energy $\mathcal{E}$. One has for the semiclassical excitation HO-energy $e(z)$ at z [14]

$$\begin{array}{c}e(z)=\langle z\left|\mathcal{H}\right|z\rangle -\hslash \omega /2={\hslash \omega \left|z\right|}^2,i.e.,\\ {\mathcal{E}}_{\nu }={\hslash \omega \langle \left|z\right|}^2{\rangle }_{\nu }\end{array}$$

(42)

where the last expectation value is computed using the distribution $\nu (z)$. This semiclassical excitation energy ${\mathcal{E}}_{\mu }$ is given, for a Husimi distribution μ, by [25]

$${\mathcal{E}}_{\mu }={\langle e(z)\rangle }_{\mu }=\frac{\hslash \omega }{I_{\tau }}$$

(43)

Note now that, from Equation (16), we can conveniently recast the HO-expression for μ into the Gaussian fashion

$$\mu (z)=I_{\tau }{e}^{-I_{\tau }{\left|z\right|}^2}$$

(44)

peaked at the origin. The probability density μ of Equation (44) is clearly of the maximum entropy [31].

As a consequence, it proves convenient, at this stage, to view $I_{\tau }$ in the following light. The semiclassical form of the entropy S has exhaustively been studied by Wehrl. It is the (cf. 1) Shannon’s information measure evaluated with Husimi distributions [12]. Assume we know a priori the value ${\mathcal{E}}_{\nu }={\hslash \omega \langle \left|z\right|}^2{\rangle }_{\nu }$. We wish to determine the distribution $\nu (z)$ that maximizes the Wehrl entropy under this ${\mathcal{E}}_{\nu }-$value constraint. Accordingly, the MaxEnt distribution will be [31]

$$\nu (z)=e^{-{\lambda }_o}{e}^{-\eta E(z)}$$

(45)

with ${\lambda }_o$ the normalization Lagrange multiplier and η the one associated to ${\mathcal{E}}_{\nu }$. According to MaxEnt tenets we have [31]

$${\lambda }_o={\lambda }_o(\eta )=ln\int \frac{{\mathrm{d}}^{2}z}{\pi }{e}^{-{\eta \hslash \omega \left|z\right|}^2}=-ln(\eta \hslash \omega )$$

(46)

Now, the $\eta -$multiplier is determined by the relation [31]

$$-{\mathcal{E}}_{\nu }=\frac{\partial {\lambda }_o}{\partial \eta }=-\frac{1}{\eta }$$

(47)

If we choose the Fisher-Husimi constraint given by Equation (43), this results in $\eta =I_{\tau }/\hslash \omega$ and from Equation (46) we get ${\lambda }_o=-ln{I}_{\tau }$, i.e., $e^{-{\lambda }_o}=I_{\tau }$, and we consequently arrive to the desired outcome

$$\nu (z)=I_{\tau }{e}^{-I_{\tau }{\left|z\right|}^2}\equiv \mu (z)$$

(48)

We have thus shown that the HO-Husimi distributions are MaxEnt-ones with the semiclassical excitation energy (43) as a constraint. It is clear from Equation (48) that $I_{\tau }$ plays there the role of an “inverse temperature”.

The preceding argument suggests that we are tacitly envisioning the existence of a quantity $T_W$ (the inverse of η) associated to the Wehrl measure that we here extend to extreme. This Wehrl temperature $T_W$ governs the width of our Gaussian Husimi distribution. On account of

$$\mu (z)=I_{\tau }{e}^{-(I_{\tau }/\hslash \omega )\hslash \omega {\left|z\right|}^2}=I_{\tau }{e}^{-{\mathcal{E}}_{\mu }/T_W}$$

(49)

which entails

$$T_W=\frac{\hslash \omega }{I_{\tau }}$$

(50)

and it is easy to see from the range of $I_{\tau }$ that the range of values of $T_W$ is then $\hslash \omega \le T_W\le \infty$. Due to the semiclassical nature of both W and μ, $T_W$ has a lower bound greater than zero.

5.2. Delocalization

The two quantities W and $I_{\tau }$ have been shown to be related, for the HO, according to Equation (25). Since the Wehrl temperature $T_W$ yields the width of our Gaussian Husimi distribution, we can conceive of introducing a “delocalization factor” D

$$D=\frac{T_W}{\hslash \omega }$$

(51)

The above definition leads to the relation

$$W=1+ln{T}_W-ln\hslash \omega =1+lnD$$

(52)

As stressed above, W has been constructed as a delocalization measure [12]. The preceding considerations clearly motivate one to regard the Fisher measure built up with Husimi distributions as a “localization estimator" in phase space. The HO-Gaussian expression for μ (44) illuminates the fact that the Fisher measure controls both the height and the spread (which is $\sim {\left[2I_{\tau }\right]}^{-1}$). Obviously, spread is here a “phase-space delocalization indicator”. This fact is reflected by the quantity D introduced above.

Thus, an original physical interpretation of Fisher’s measure emerges: localization control. The inverse of the Fisher measure, D, turns out to be a delocalization-indicator. Differentiating Fisher’s measure (23) with respect T, notice also that

$$\frac{\mathrm{d}{I}_{\tau }}{\mathrm{d}T}=-\frac{\hslash \omega }{T^2}{e}^{-\beta \hslash \omega }$$

(53)

so that Fisher’s information decreases exponentially as the temperature grows. Our Gaussian distribution loses phase-space “localization” as energy and/or temperature are injected into our system, as reflected via $T_W$ or D. Notice that (52) complements the Lieb bound $W\ge 1$. It tells us by just how much W exceeds unity. We see that it does it by virtue of delocalization effects. Moreover, this fact can be expressed using the shift-invariant Fisher measure. We will now show that D is proportional to the system’s energy fluctuations.

5.3. Second moment of the Husimi distribution

The second moment of the Husimi distribution $\mu (z)$ is an important measure to ascertain the “degree of complexity” of a quantum state (see below). It is a measure of the delocalization-degree of the Husimi distribution in phase space (see Reference [32] for details and discussions). It is defined as

$$M_2=\int \frac{{\mathrm{d}}^{2}z}{\pi }{\mu }^2(z)$$

(54)

that, after explicit evaluation of $M_2$ from Equation (44) reads

$$M_2=\frac{I_{\tau }}{2}$$

(55)

Using now (52) we conclude that

$$M_2(D)=\frac{1}{2D}$$

(56)

Thus, our energy-fluctuations turn out to be

$${\Delta }_{\mu }e=\frac{\hslash \omega }{I_{\tau }}=\hslash \omega D$$

(57)

with ${({\Delta }_{\mu }e)}^2={({\mathcal{E}}^2)}_{\mu }-{\mathcal{E}}_{\mu }^2$. As a consequence, we get

$$D=\frac{{\Delta }_{\mu }e}{\hslash \omega }$$

(58)

An important result is thus obtained: the delocalization factor D represents energy-fluctuations expressed in $\hslash \omega -$terms. Delocalization is clearly seen to be the counterpart of energy fluctuations.

6. Thermodynamics-Like Relations

Let us now go back to Equation (37) and revisit the entropic expression. It is immediately realized that we can recast the entropy S in terms of the quantal mean excitation energy E and the delocalization factor D as

$$\frac{E}{T}=S-lnD$$

(59)

i.e., if one injects into the system some excitation energy E, expressed in “natural” T units, it is apportioned partly as heat dissipation via S and partly via delocalization. More precisely, the part of this energy not dissipated is that employed to delocalize the system in phase space. Now, since $W=1-ln{I}_{\tau }=1+lnD$, the above equation can be recast in alternative forms, as

$$S=\frac{E}{T}+lnD=\frac{E}{T}-ln{I}_{\tau };\mathrm{or}$$

(60)

$$W=1+S-\frac{E}{T}$$

(61)

implying

$$W-S\mapsto 0\mathrm{for}T\mapsto \infty$$

(62)

which is a physically sensible result and

$$W-S\mapsto 1\mathrm{for}T\mapsto 0$$

(63)

as it should, since $S=0$ at $T=0$ (third law of thermodynamics), while W attains there its Lieb’s lower bound of unity.

One finds in Equation (60) some degree of resemblance to thermodynamics’s first law. To reassure ourselves on this respect, we slightly changed our underlying canonical probabilities μ, multiplying it by a factor $\delta \mathcal{F}=\mathrm{random}\mathrm{number}/100$. Specifically, we generated random numbers according to the normal distribution and divided them by 100 to obtain the above factors $\delta \mathcal{F}$. This process leads to new “perturbed” probabilities $P=\mu +\delta \mu$, conveniently normalized. With them we evaluate the concomitant changes $\mathrm{d}S$, $\mathrm{d}E$ (we do this 50 times, with different random numbers in each instance). We were then able to numerically verify that the difference $\mathrm{d}S-\beta \mathrm{d}E\sim 0$. The concomitant results are plotted in Figure 2) Since, as stated, numerically $\mathrm{d}S=(1/T)\mathrm{d}E$, this entails, from Equation (60), $\mathrm{d}{I}_{\tau }/I_{\tau }\simeq 0$. The physical connotations are as follows: if the only modification effected is that of a change $\delta \mu$ [16] in the canonical distribution μ, this implies that the system undergoes a heat transfer process [16] for which thermodynamics’ first law implies $\mathrm{d}U=T\mathrm{d}S$. This is numerically confirmed in the plots of Figure 2. The null contribution of $ln{I}_{\tau }$ to this process suggests that delocalization (not a thermodynamic effect, but a dynamic one) can be regarded as behaving (thermodynamically) like a kind of “work”.

Figure 2. Numerical computation results for the HO: changes $\mathrm{d}U$ and $\mathrm{d}{I}_{\tau }$ vs. $\mathrm{d}S$ that ensue after randomly generating variations $\delta p_i$ in the underlying microscopic canonical probabilities $p_i$.

Figure 2. Numerical computation results for the HO: changes $\mathrm{d}U$ and $\mathrm{d}{I}_{\tau }$ vs. $\mathrm{d}S$ that ensue after randomly generating variations $\delta p_i$ in the underlying microscopic canonical probabilities $p_i$.

Now, since (a) $I_{\tau }=1-e^{-\beta \hslash \omega },$ and (b) the mean energy of excitation is $E=\hslash \omega /(exp(\beta \hslash \omega )-1)$, one also finds, for the quantum-semiclassical difference (QsCD) $S-W$ the result

$$\begin{array}{cc}& W-S=1-\frac{I_{\tau }-1}{I_{\tau }}ln(1-I_{\tau })=F_1(I_{\tau })\end{array}$$

(64)

Moreover, since $0\le F_1(I_{\tau })\le 1$, we see that, always, $W\ge S$, as expected, since the semiclassical treatment contains less information than the quantal one. Note that the QsCD can be expressed exclusively in Fisher’s information terms. This is, the quantum-semiclassical entropic difference $S-W$ may be given in $I_{\tau }-$terms only. Figure (3) depicts S, $\beta E$, and $lnD$ vs. the dimensionless quantity $t=T/\hslash \omega$. Accordingly, entropy is apportioned in such a way that

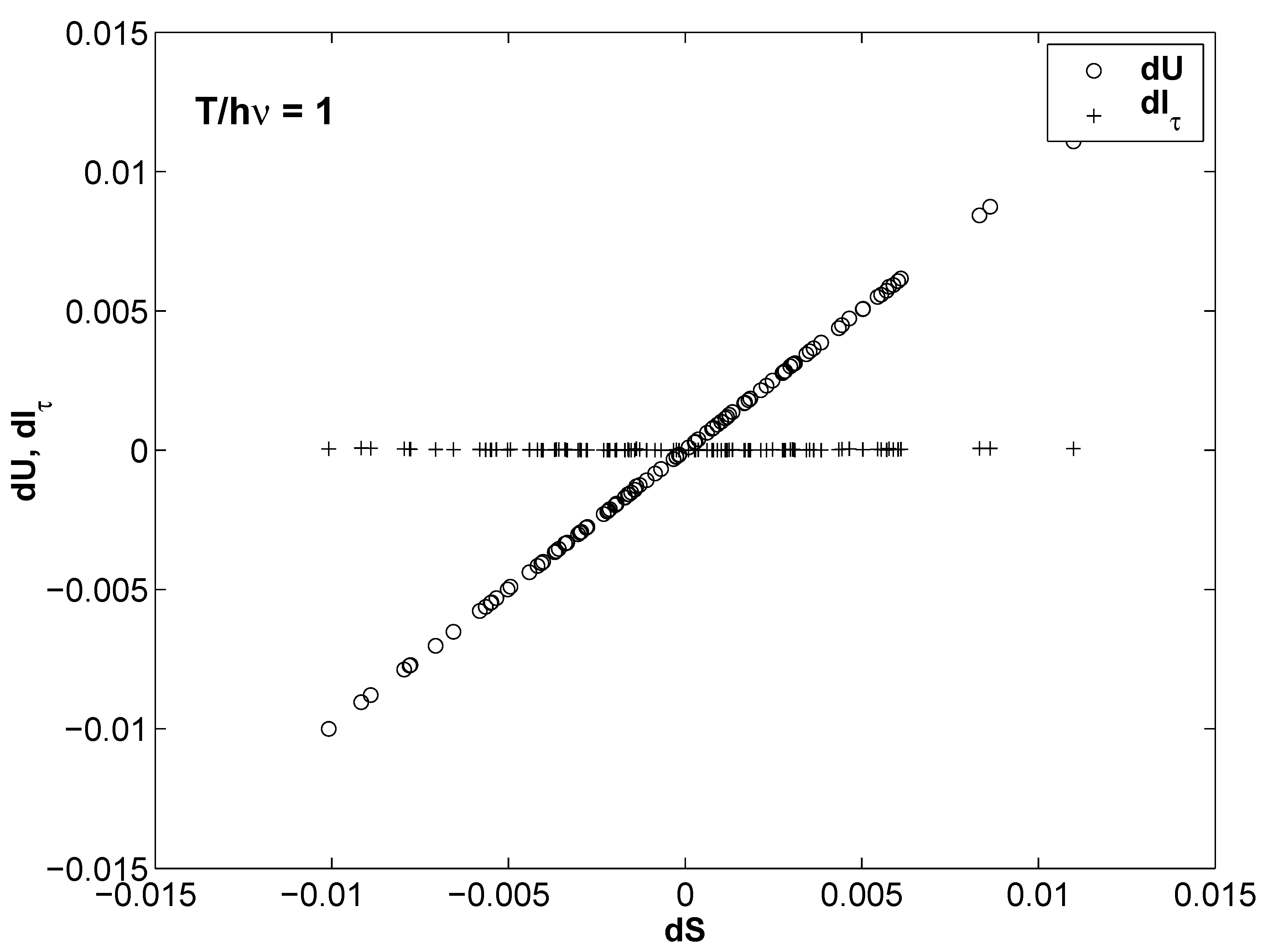
• part of it originates from excitation energy and
• the remaining is accounted for by phase space delocalization.

A bit of algebra allows one now to express the rate of entropic change per unit temperature increase as

$$\frac{\mathrm{d}S}{\mathrm{d}T}=\beta \frac{\mathrm{d}E}{\mathrm{d}T}=\beta C=\hslash \omega \frac{1}{T}\frac{\mathrm{d}D}{\mathrm{d}T},$$

(65)

entailing

$$C=\hslash \omega \frac{\mathrm{d}D}{\mathrm{d}T}$$

(66)

Figure 3. S, $lnD$, and $\beta E$ as a function of $t=T/\hslash \omega$.

Figure 3. S, $lnD$, and $\beta E$ as a function of $t=T/\hslash \omega$.

In the case of the one dimensional HO we see that the specific heat measures delocalization change per unit temperature increase. Also, $\mathrm{d}E/\mathrm{d}T\propto \mathrm{d}D/\mathrm{d}T$, providing us with a very simple relationship between mean excitation energy changes and delocalization ones.

$$\frac{\mathrm{d}E}{\mathrm{d}D}=\hslash \omega$$

(67)

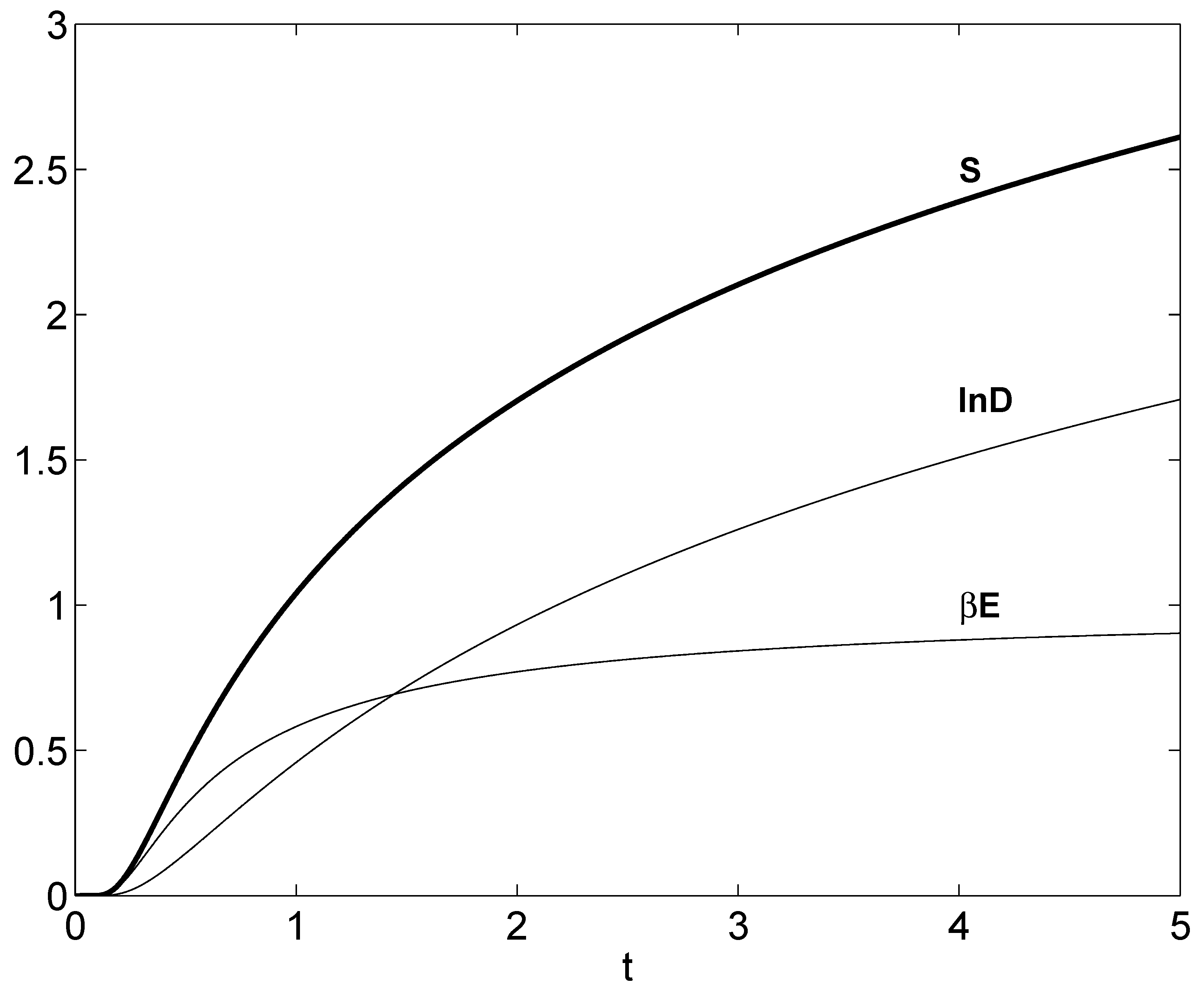
7. On Thermal Uncertainties

Additional considerations are in order with regards to thermal uncertainties, that express the effect of temperature on Heisenberg’s celebrated relations (see, for instance [6,33,34,35]). We use now a result obtained in [9] (Equation (3.12)), where the authors cast Wehrl’s information measure in terms of the coordinates’ variances ${\Delta }_{\mu }x$ and ${\Delta }_{\mu }p$, obtaining

$$W=ln\left\{\frac{e}{\hslash }{\Delta }_{\mu }x{\Delta }_{\mu }p\right\}$$

(68)

In the present context, the relation $W=1-ln{I}_{\tau }$ allows us to conclude that [17]

$$I_{\tau }{\Delta }_{\mu }x{\Delta }_{\mu }p=\hslash$$

(69)

which can be regarded as a “Fisher uncertainty principle” and adds still another meaning to $I_{\tau }$: since, necessarily, ${\Delta }_{\mu }x{\Delta }_{\mu }p\ge \hslash /2$, it is clear that $I_{\tau }/2$ is the “correcting factor” that permits one to reach the uncertainty’s lower bound $\hslash /2$, a rather interesting result.

Phase space “localization” is possible, with Husimi distributions, only up to ℏ [14]. This is to be compared to the uncertainties evaluated in a purely quantal fashion, without using Husimi distributions, and in particular with a previous result in [17]. With the virial theorem [16] one can easily ascertain in [17] that

$$\Delta x\Delta p=\frac{\hslash }{2}\frac{e^{\beta \hslash \omega }+1}{e^{\beta \hslash \omega }-1}$$

(70)

together with (69) yields

$${\Delta }_{\mu }x{\Delta }_{\mu }p=\frac{2\Delta x\Delta p}{1+e^{-\beta \hslash \omega }}$$

(71)

Thus We see that, as $\beta \to \infty$, ${\Delta }_{\mu }\equiv {\Delta }_{\mu }x{\Delta }_{\mu }p$ is twice the minimum quantum value for $\Delta x\Delta p$, and ${\Delta }_{\mu }\to \hslash$, the “minimal” phase-space cell. The quantum and semiclassical results do coincide at very high temperature though. Indeed, one readily verifies [17] that Heisenberg’s uncertainty relation, as a function of both frequency and temperature, is governed by a thermal “uncertainty function” F that acquires the aspect

$$F(\beta ,\omega )=\Delta x\Delta p=\frac{1}{2}\left[{\Delta }_{\mu }+\frac{E}{\omega }\right]$$

(72)

Coming back to results derivable within the present context, we realize here that F can be recast as

$$F(\beta ,\omega )=\frac{1}{2}\left[\hslash D+\frac{E}{\omega }\right]$$

(73)

so that, for T varying in $[0,\infty ]$, the range of possible $\Delta x\Delta p$-values is $[\hslash /2,\infty ].$ Equation (73) is a “Heisenberg–Fisher” thermal uncertainty relation (for a discussion of this concept see, for instance, [6,33,34]).

$F(\beta ,\omega )$ grows with both E and D. The usual result $\hslash /2$ is attained for minimum D and zero excitation energy. As for $\mathrm{d}F/\mathrm{d}T$, one is able to set $F\equiv F(E,D)$, since $2\mathrm{d}F=\hslash \mathrm{d}D+{\omega }^{-1}\mathrm{d}E$. Remarkably enough, the two contributions to $\mathrm{d}F/\mathrm{d}T$ are easily seen to be equal and $dF/dT\to (1/\omega )\mathrm{for}T\to \infty$. One can also write

$${\left(\frac{\partial F}{\partial D}\right)}_E=\frac{\hslash }{2};{\left(\frac{\partial F}{\partial E}\right)}_D=\frac{1}{2\omega }$$

(74)

providing us with a thermodynamic “costume” for the uncertainty function F that sheds some new light onto the meaning of both ℏ and ω. In particular, we see that $\hslash /2$ is the derivative of the uncertainty function F with respect to the delocalization factor D. Increases $\mathrm{d}F$ of the thermal uncertainty function F are of two types

• from the excitation energy, that supplies a $C/\omega$ contribution and
• from the delocalization factor D.

8. Degrees of Purity Relations

8.1. Semiclassical purity

The quantal concept of degree of purity of a general density operator $\widehat{\rho }$ is expressed via $\mathrm{Tr}{\widehat{\rho }}^2$ [36,37]. Its inverse, the so-called participation ratio

$$R=\frac{1}{\mathrm{Tr}{\widehat{\rho }}^2}$$

(75)

is particularly convenient for calculations [38]. It varies from unity for pure states to N for totally mixed states [38]. It may be interpreted as the effective number of pure states that enter a quantum mixture. Here we will consider the “degree of purity” $d_{\mu }$ of a semiclassical distribution, given by

$$d_{\mu }=\int \frac{{\mathrm{d}}^{2}z}{\pi }{\mu }^2(z)\le 1$$

(76)

Clearly, $d_{\mu }$ coincides with the second moment of the Husimi distribution (44) given by Equation (54), i.e.,

$$d_{\mu }=M_2=\frac{I_{\tau }}{2}$$

(77)

Using now (52) we relate the semiclassical degree of purity to the delocalization factor and to the Wehrl temperature $T_W$

$$d_{\mu }=\frac{1}{2D}=\frac{T_W}{2\hslash \omega }$$

(78)

and also to our semiclassical energy-fluctuations (57)

$$d_{\mu }=\frac{\hslash \omega }{2{\Delta }_{\mu }e}$$

(79)

Since $\hslash \omega \le T_W\le \infty$, the “best” purity attainable at the semiclassical level equals one-half.

8.2. Quantal purity

For the quantum mixed HO-state $\widehat{\rho }=e^{-\beta \mathcal{H}}/Z$, where $\mathcal{H}$ is the Hamiltonian of the harmonic oscillator and the partition function Z is given by Equation (7) [16], we have a degree of purity $d_{\widehat{\rho }}$ given by (see the detailed study by Dodonov [35])

$$d_{\widehat{\rho }}=\frac{e^{-\beta \hslash \omega }}{Z^2}\sum _{n=0}^{\infty }{e}^{-2\beta \hslash \omega n}$$

(80)

leading to

$$d_{\widehat{\rho }}=tanh(\beta \hslash \omega /2)$$

(81)

where $0\le d_{\widehat{\rho }}\le 1$. Thus, Heisenberg’ uncertainty relation can be cast in the fashion

$$\Delta x\Delta p=\frac{\hslash }{2}coth(\beta \hslash \omega /2)$$

(82)

where $\Delta x$ and $\Delta p$ are the quantum variances for the canonically conjugated observables x and p [35]

$$\Delta x\Delta p=\frac{\hslash }{2}\frac{1}{d_{\widehat{\rho }}}$$

(83)

which is to be compared to the semiclassical result that was derived above (cf. 71).

We relate now the degree of purity of our thermal state with various physical quantities both in its quantal and semiclassical versions. Using Equations (71) and (77) we get

$$d_{\mu }=\frac{I_{\tau }}{2}=(1-d_{\mu })d_{\widehat{\rho }}$$

(84)

which leads to

$$\begin{array}{ccc}\hfill d_{\widehat{\rho }}& =& \frac{d_{\mu }}{1-d_{\mu }}=\frac{I_{\tau }}{2-I_{\tau }}\hfill \end{array}$$

$$\begin{array}{ccc}\hfill d_{\mu }& =& \frac{d_{\widehat{\rho }}}{1+d_{\widehat{\rho }}}\hfill \end{array}$$

(85)

such as clearly shows that (i) $d_{\mu }\le d_{\widehat{\rho }}$, and (ii) for a pure state, again, its semiclassical counterpart has a degree of purity equal $1/2$.

Additionally, on account of Equation (69), on the one hand, and since the semiclassical degree of purity reads $d_{\mu }=I_{\tau }/2$, on the other one, we are led to an uncertainty relation for mixed states in terms of $d_{\mu }$, namely,

$${\Delta }_{\mu }x{\Delta }_{\mu }p=\frac{\hslash }{2}\frac{1}{d_{\mu }}$$

(86)

that tells us just how uncertainty grows as participation ratio $R=1/d_{\mu }$ augments. Equation (86) is of semiclassical origin, which makes it a bit different from the one that results form a purely quantal treatment (see [35], Equation (4)). Moreover, notice how information concerning the purely quantal notion of purity $d_{\widehat{\rho }}$ is already contained in the semiclassical measure $I_{\tau }$.

Figure 4. Semiclassical purity ${\mathrm{d}}_{\mu }$ vs. $T/h\nu$.

Figure 4. Semiclassical purity ${\mathrm{d}}_{\mu }$ vs. $T/h\nu$.

We appreciate the fact that R increases as delocalization grows, a quite sensible result. Figure (4) depicts $d_{\mu }(T)$, a monotonously decreasing function, which tells us that degree of purity of a mixed state acts here as a thermometer, and allows then to assign a $T-$value to any of our mixed states.

Also, using once again the result $d_{\mu }=I_{\tau }/2$ together with the uncertainties just derived we see that $\beta \hslash \omega =-ln(1-I_{\tau })$. Thus, we can rewrite Equation (64) in the following form

$$W-S=1+\beta \hslash \omega \frac{2d_{\mu }-1}{2d_{\mu }}=1+\beta \hslash \omega \frac{d_{\widehat{\rho }}-1}{2d_{\widehat{\rho }}}$$

(87)

which casts the difference between the quantal and semiclassical entropies in terms of the degrees of purity. From Equation (87) we can also give the quantal mean excitation energy E in terms of $d_{\mu }$ using (38)

$$E=\frac{\hslash \omega }{2}\frac{1-2d_{\mu }}{d_{\mu }}=\frac{\hslash \omega }{2}\frac{1-d_{\widehat{\rho }}}{d_{\widehat{\rho }}}$$

(88)

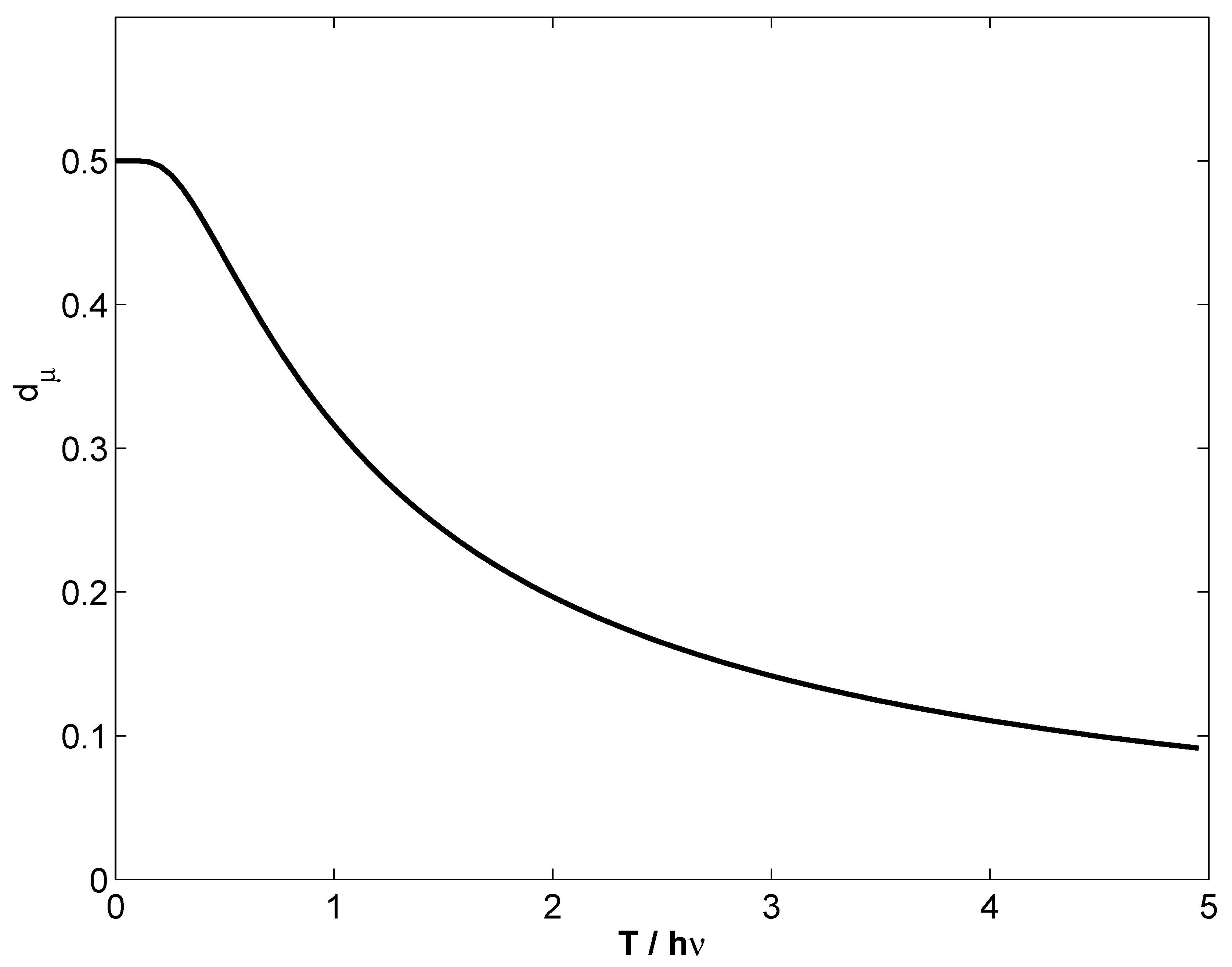
9. Conclusions

We have explored in this review connections between canonical ensemble quantities and two Fisher information measures, associated to the estimation of phase-space location ($I_{\tau }$) and temperature ($I_{\beta }$). Our most important result is, perhaps, to have shown that there exists a “Fisher-associated” third law of thermodynamics (at least for the HO). From a pure information-theoretic viewpoint, we have, obtained significant results, namely,

• a connection between Wehrl’s entropy and $I_{\tau }$ (cf. Equation (25)),
• an interpretation of $I_{\tau }$ as the HO’s ground state occupation probability (cf. Equation (26)),
• an interpretation of $I_{\beta }$ proportional to the HO’s specific heat (cf. Equation (30)),
• the possibility of expressing the HO’s entropy as a sum of two terms, one for each of the above FIM realizations (cf. Equation (31)),
• a new form of Heisenberg’s uncertainty relations in Fisher terms (cf. Equation (73)),
• that efficient $\left|z\right|$-estimation can be achieved with $I_{\tau }$ at all temperatures, as the minimum Cramer–Rao value is always reached (cf. Equation (24)).

Our statistical semiclassical treatment yielded, we believe, some new interesting physics that we proceed to summarize. We have, for the HO,

• established that the semiclassical Fisher measure $I_{\tau }$ contains all relevant statistical quantum information,
• shown that the Husimi distributions are MaxEnt ones, with the semiclassical excitation energy $\mathcal{E}$ as the only constraint,
• complemented the Lieb bound on the Wehrl entropy using $I_{\tau }$,
• observed in detailed fashion how delocalization becomes the counterpart of energy fluctuations,
• written down the difference $W-S$ between the semiclassical and quantal entropy also in $I_{\tau }-$terms,
• provided a relation between energy excitation and degree of delocalization,
• shown that the derivative of twice the uncertainty function $F(\beta \omega )=\Delta x\Delta p$ with respect to $I_{\tau }^{-1}$ is the Planck constant ℏ,
• established a semiclassical uncertainty relation in terms of the semiclassical purity $d_{\mu }$, and
• expressed both $d_{\mu }$ and the quantal degree of purity in terms of $I_{\tau }$.

These results are, of course, restricted to the harmonic oscillator. However, this is such an important system that HO insights usually have a wide impact, as the HO constitutes much more than a mere example. Nowadays it is of particular interest for the dynamics of bosonic or fermionic atoms contained in magnetic traps [39,40,41] as well as for any system that exhibits an equidistant level spacing in the vicinity of the ground state, like nuclei or Luttinger liquids. The treatment of Hamiltonians including anharmonic terms is the next logical step. We are currently undertaking such a task. To this end analytical considerations do not suffice, and numerical methods are required. The ensuing results will be published elsewhere.