3. Multi-Agent Systems and Equiprobability: General Derivation of the Asymptotic Distribution
In this section, we address the same problem above presented but in a general way. Let
b be a positive real constant (cases
have been indicated in the former section). If we have a set of positive variables
verifying the constraint
with an adequate mechanism assuring the equiprobability of all the possible states
into the volume given by expression (12), will we have for the generic variable
x the distribution
when we average over the ensemble in the limit
, with
, and constant
ϵ?. Now it is shown that the answer is affirmative. Similarly, we claim that if the weak inequality (12) is transformed in equality the result will be the same, as it has been proved for the cases
in References [
10,
11].
From the cases
, (see Equations (
3) and (
9)), we can extrapolate the general formula that will give us the statistical behavior
of the generic variable
x, when the system runs equiprobably into the volume defined by a constraint of type (12). The probability
of finding an agent with generic coordinate
x is proportional to the volume
formed by all the points into the
-dimensional symmetrical body limited by the constraint
. Thus, the
N-dimensional volume can be written as
Taking into account the normalization condition
, the expression for
is obtained:
The
N-dimensional volume,
, of a
b-symmetrical body with side of length
ρ is proportional to the term
and to a coefficient
that depends on
N:
The parameter
b indicates the original Equation (
12) that defines the boundaries of the volume
. Thus, for instance, from Equation (
2), we have
.
Coming back to Equation (
15), we can manipulate
to obtain (the index
b is omitted in the formula of
):
If we suppose
, then
ϵ represents the mean value of
in the collectivity, that is,
. If
N tends toward infinity, it results:
Thus,
Substituting this last expression in formula (
15), the exact form for
is found in the thermodynamic limit (
):
with
given by
Hence, the conjecture (13) is proved.
Doing a thermodinamical simile, we can calculate the dependence of
ϵ on the temperature by differentiating the entropy with respect to the energy. The entropy can be written as
, where
is given by Equation (
20) and
k is the Boltzmann constant. If we recall that
, we obtain
where it has been used that
The calculation of the temperature
T gives
Thus
, a result that recovers the theorem of equipartition of energy for the quadratic case
. The distribution for all
b is finally obtained:
4. Gamma Distributions, Economic Gas Models and Geometry: A Speculation
If we perform the change of variables
in the normalization condition of
,
, where
is expressed in (20), we find that
If we introduce the new variable
, the distribution
as function of
z reads:
Let us observe that the Gamma function appears in the normalization condition,
This implies that
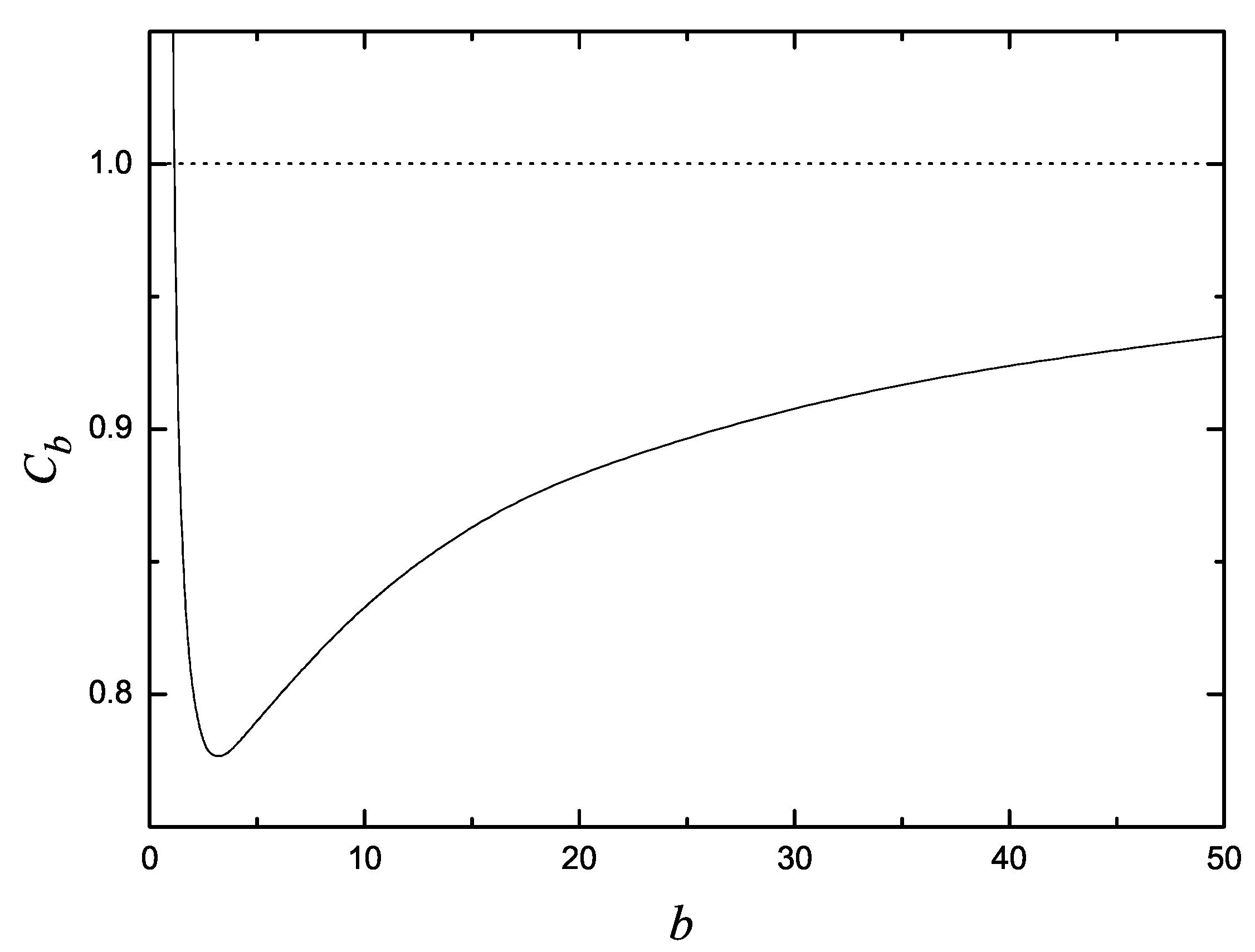
By using Mathematica the positive constant
is plotted versus
b in
Figure 1. We see that
, and that
. The minimum of
is reached for
, taking the value
. Still further, we can calculate from Equation (
28) the asymptotic dependence of
on b:
where
γ is the Euler constant,
. The asymptotic function (29) is obtained after substituting in (28) the value of
by
, and performing the Stirling approximation on this last expression, knowing that
. The function (30) is found after looking for the first Taylor expansion terms of the Gamma function around the origin
. They can be derived from the Euler’s reflection formula,
. We obtain
. From here, recalling that
, we get
, when
. Although this last term of the Taylor expansion,
, is negligible we maintain it in expression (30). The only minimum of
is reached for the solution
of the equation
, where
is the digamma function (see
Figure 1).
Let us now recall two interesting statistical economic models that display a statistical behavior given by distributions of the form (26), that is, the standard Gamma distributions with shape parameter
,
Figure 1.
Normalization constant
versus
b, calculated from Equation (
28). The asymptotic behavior is:
, and
. This last asymptote is represented by the dotted line. The minimum of
is reached for
, taking the value
.
Figure 1.
Normalization constant
versus
b, calculated from Equation (
28). The asymptotic behavior is:
, and
. This last asymptote is represented by the dotted line. The minimum of
is reached for
, taking the value
.
ECONOMIC MODEL A: The first one is the saving propensity model introduced by Chakraborti and Chakrabarti [
4]. In this model a set of
N economic agents, having each agent
i (with
) an amount of money,
, exchanges it under random binary
interactions,
, by the following the exchange rule:
with
, and
ϵ a random number in the interval
. The parameter
λ, with
, is fixed, and represents the fraction of money saved before carrying out the transaction. Let us observe that money is conserved,
i.e.,
, hence in this model the economy is closed. Defining the parameter
as
and scaling the wealth of the agents as
, with
representing the average money over the ensemble of agents, it is found that the asymptotic wealth distribution in this system obeys the standard Gamma distribution [
5]
The case
, which means a null saving propensity,
, recovers the model of Dragulescu and Yakovenko [
3] in which the Gibbs distribution is observed. If we compare Equations (
35) and (
31), a close relationship between this economic model and the geometrical problem solved in the former section can be established. It is enough to make
to have two equivalent systems. This means that, from Equation (
36), we can calculate
b from the saving parameter
λ with the formula
As
λ takes its values in the interval
, then the parameter
b also runs in the same interval
. On the other hand, recalling that
, we can get the equivalent variable
x from Equation (
37),
where
ϵ is a free parameter that determines the mean value of
in the equivalent geometrical system. Formula (
39) means to perform the change of variables
, with
, for all the particles/agents of the ensemble. Then, we conjecture that the economic system represented by the generic pair
, when it is transformed in the geometrical system given by the generic pair
, as indicated by the rules (38) and (39), runs in an equiprobable form on the surface defined by the relationship (12), where the inequality has been transformed in equality. This last detail is due to the fact the economic system is closed, and then it conserves the total money, whose equivalent quantity in the geometrical problem is
E. If the economic system were open, with an upper limit in the wealth, then the transformed system would evolve in an equiprobable way over the volume defined by the inequality (12), although its statistical behavior would continue to be the same as it has been proved for the cases
in [
10,
11].
ECONOMIC MODEL B: The second one is a model introduced in [
6]. In this model a set of
N economic agents, having each agent
i (with
) an amount of money,
, exchanges it under random binary
interactions,
, by the following the exchange rule:
where
with
ϵ a continuous uniform random number in the interval
. When this variable is transformed in a Bernouilli variable,
i.e., a discrete uniform random variable taking on the values 0 or 1, we have the model studied by Angle [
7], that gives very different asymptotic results. The exchange parameter,
ω, represents the maximum fraction of wealth lost by one of the two interacting agents (
). Whether the agent who is going to loose part of the money is the
i-th or the
j-th agent, depends nonlinearly on
, and this is decided by the random dichotomous function
:
(with additional probability
) and
(with additional probability
). Hence, when
, the value
produces a wealth transfer from agent
i to agent
j with probability
, and when
, the value
produces a wealth transfer from agent
j to agent
i with probability
. Defining in this case the parameter
as
and scaling the wealth of the agents as
, with
representing the average money over the ensemble of agents, it is found that the asymptotic wealth distribution in this system obeys the standard Gamma distribution [
6]
The case
, which means an exchange parameter
, recovers the model of Dragulescu and Yakovenko [
3] in which the Gibbs distribution is observed. If we compare Equations (
44) and (
31), a close relationship between this economic model and the geometrical problem solved in the last section can be established. It is enough to make
to have two equivalent systems. This means that, from Equation (
45), we can calculate
b from the exchange parameter
ω with the formula
As
ω takes its values in the interval
, then the parameter
b runs in the interval
. It is curious to observe that in this model the interval
maps on
, a fact that does not occur in MODEL A. On the other hand, recalling that
, we can get the equivalent variable
x from Equation (
46),
where
ϵ is a free parameter that determines the mean value of
in the equivalent geometrical system. Formula (
48) means to perform the change of variables
, with
, for all the particles/agents of the ensemble. Then, we conjecture that the economic system represented by the generic pair
, when it is transformed in the geometrical system given by the generic pair
, as indicated by the rules (47) and (48), runs in an equiprobable form on the surface defined by the relationship (12), where the inequality has been transformed in equality. As explained above, this last detail is due to the fact the economic system is closed, and then it conserves the total money, whose equivalent quantity in the geometrical problem is
E. If the economic system were open, with an upper limit in the wealth, then the transformed system would evolve in an equiprobable way over the volume defined by the inequality (12), although its statistical behavior would continue to be the same as it has been proved for the cases
in References [
10,
11].
5. Other Geometrical Questions
We shall proceed now to derive an asymptotic formula (
) for the volume of the
N-dimensional symmetrical body enclosed by the surface
The linear dimension
ρ of this volume,
i.e., the length of one of its sides verifies
. As argued in Equation (
16), the
N-dimensional volume,
, is proportional to the term
and to a coefficient
that depends on
N. Thus,
where the characteristic
b indicates the particular boundary given by Equation (
49).
For instance, from Equation (
2), we can write in a formal way:
From Equation (
8), if we take the diameter,
, as the linear dimension of the
N-sphere, we obtain:
These expressions (51) and (52) suggest a possible general formula for the factor
, let us say
where
a is a
b-dependent constant to be determined. For example,
for
and
for
.
In order to find the dependence of
a on the parameter
b, the regime
is supposed. Applying Stirling approximation for the factorial
in the denominator of expression (53), and inserting it in expression (21), it is straightforward to find out the relationship:
From here and formula (
28), we get:
that recovers the exact results for
. The behavior of
a is monotonous decreasing when
b is varied from
, where
a diverges as
, up to the limit
, where
a decays asymptotically toward the value
.
Hence, the formula for
is obtained:
It would be also possible to multiply this last expression (56) by a general polynomial
in the variable
N, and all the derivation done from Equation (
53) would continue to be correct. We omit this possibility in our calculations. For a fixed
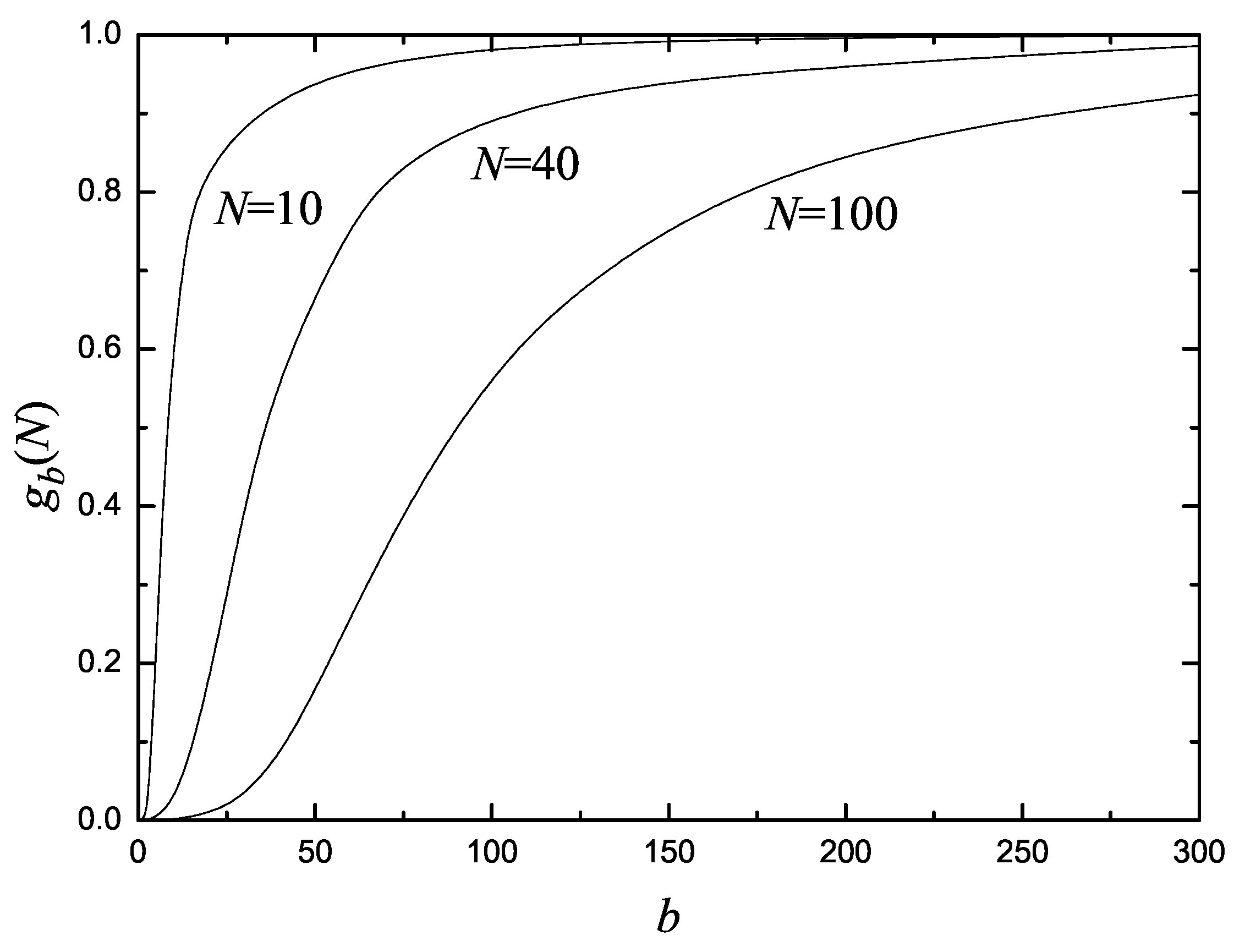
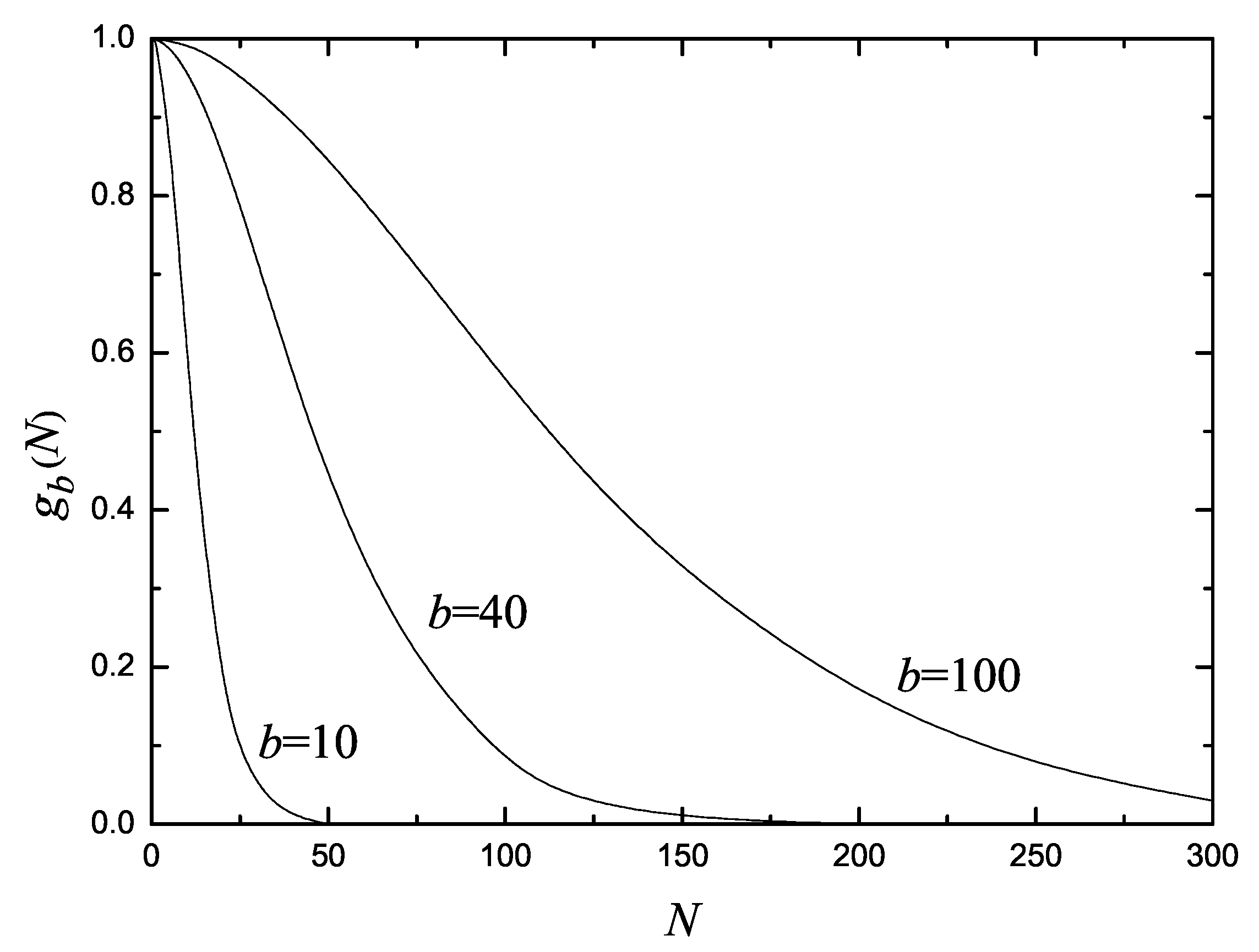
N, we have that
increases monotonously from
, for
, up to
, in the limit
(see
Figure 2). For a fixed
b, we have that
decreases monotonously from
, for
, up to
, in the limit
(see
Figure 3).
Figure 2.
The factor
versus
b for
, calculated from Equation (
56). Observe that
for
, and
.
Figure 2.
The factor
versus
b for
, calculated from Equation (
56). Observe that
for
, and
.
Figure 3.
The factor
versus
N for
, calculated from Equation (
56). Observe that
for
, and
.
Figure 3.
The factor
versus
N for
, calculated from Equation (
56). Observe that
for
, and
.
The final result for the volume of an
N-dimensional symmetrical body of characteristic
b given by the boundary (49) reads:
with
.