Dispersal (Entropy) and Recognition (Information) as Foundations of Emergence and Dissolvence
Abstract
:1. Introduction
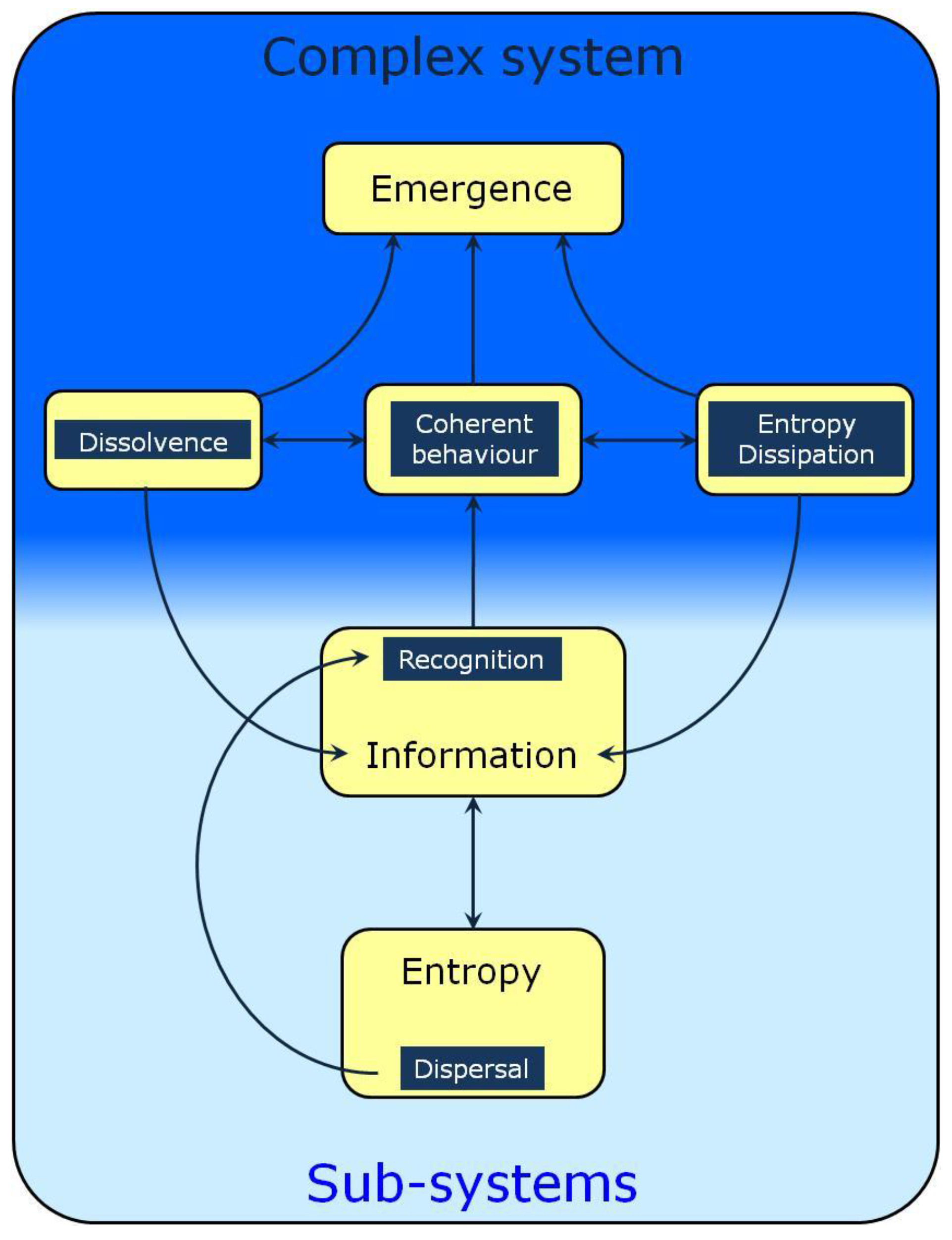
2. Entropy and Dispersal
3. Recognition and Information
4. Collective Behavior, Open Systems and Emergence
5. Dissolvence
6. Conclusions
References and Notes
- Atkins, P. Four Laws that Drive the Universe; Oxford University Press: Oxford, UK, 2007; pp. 49-50, 66-68, 103. [Google Scholar] [Green Version]
- Conrad, M. Adaptability—The Significance of Variability from Molecule to Ecosystem; Plenum Press: New York, NY, USA, 1983; pp. 11-20, 31-49. [Google Scholar] [Green Version]
- Cramer, F. Chaos and Order—The Complex Structure of Living Systems; VCH: Weinheim, Germany, 1993; pp. 12-16, 210-211. [Google Scholar] [Green Version]
- Danchin, A. The Delphic Boat—What Genomes Tell Us; Harvard University Press: Cambridge, MA, USA, 2002; pp. 156, 188-198, 205-206. [Google Scholar] [Green Version]
- Gell-Mann, M. The Quark and the Jaguar—Adventures in the Simple and the Complex; Abacus: London, UK, 1995; pp. 37-38, 223, 244-246. [Google Scholar] [Green Version]
- Kauffman, S. At Home in the Universe—The Search for Laws of Complexity; Penguin Books: London, UK, 1996; pp. 9, 184-188. [Google Scholar] [Green Version]
- Kauffman, S.A. Investigations; Oxford University Press: Oxford, UK, 2000; pp. 22, 48, 60. [Google Scholar] [Green Version]
- Kirschner, M.W.; Gerhart, J.C. The Plausibility of Life; Yale University Press: New Haven, CT, USA, 2005; p. 145. [Google Scholar] [Green Version]
- Laidler, K.J. Energy and the Unexpected; Oxford University Press: Oxford, UK, 2002; pp. 34–71. [Google Scholar] [Green Version]
- Morowitz, H.J. The Emergence of Everything—How the World Became Complex; Oxford University Press: New York, NY, USA, 2002; pp. 11, 176-177. [Google Scholar] [Green Version]
- Nicolis, G.; Prigogine, I. Exploring Complexity; Freeman: New York, NY, USA, 1989; pp. 148-153, 217-242. [Google Scholar] [Green Version]
- Ruelle, D. Chance and Chaos; Penguin Books: London, UK, 1993; pp. 103–108. [Google Scholar] [Green Version]
- Prigogine, I.; Stengers, I. Order out of Chaos; Fontana Paperbacks: London, UK, 1985; pp. 103-129, 171-176, 285-290. [Google Scholar] [Green Version]
- Brissaud, J.B. The meaning of entropy. Entropy 2005, 7, 68–96. [Google Scholar] [CrossRef]
- Kier, L.B. Science and Complexity for Life Science Students; Kendall/Hunt: Dubuque, IA, USA, 2007. [Google Scholar] [Green Version]
- Lockwood, M. The Labyrinth of Time; Oxford University Press: Oxford, UK, 2005; pp. 178-186, 221-232, 257-281. [Google Scholar] [Green Version]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Kullback, S. Information Theory and Statistics; Wiley: New York, NY, USA, 1959. [Google Scholar] [Green Version]
- Shannon, C. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379-423, 623-656. [Google Scholar] [CrossRef]
- Mahner, M.; Bunge, M. Foundations of Biophilosophy; Springer: Berlin, Germany, 1997; pp. 15-17, 24-34, 139-169, 280-284. [Google Scholar] [Green Version]
- von Baeyer, H.C. Information. The New language of Science; Weidenfeld & Nicolson: London, UK, 2003; pp. 4, 18-34. [Google Scholar] [Green Version]
- Loewenstein, W.R. The Touchstone of Life; Penguin Books: London, UK, 2000; pp. 6-20, 55-61, 121-124. [Google Scholar] [Green Version]
- Carrupt, P.A.; El Tayar, N.; Karlén, A.; Testa, B. Value and limits of molecular electrostatic potentials for characterizing drug-biosystem interactions. Meth. Enzymol. 1991, 203, 638–677. [Google Scholar] [PubMed]
- Carrupt, P.A.; Testa, B.; Gaillard, P. Computational approaches to lipophilicity: Methods and applications. Revs. Comput. Chem. 1997, 11, 241–315. [Google Scholar]
- Menant, C. Information and meaning. Entropy 2003, 5, 193–204. [Google Scholar] [CrossRef]
- Propopenko, M.; Boschetti, F.; Eyan, A.J. An information-theoretic primer on complexity, self-organization, and emergence. Complexity 2009, 15, 11–28. [Google Scholar] [CrossRef]
- Goodwin, B. How the Leopard Changed its Spots; Orion Books: London, UK, 1995; pp. 40–55. [Google Scholar] [Green Version]
- Holland, J.H. Emergence. From Chaos to Order; Perseus Books: Reading, MA, USA, 1999; pp. 1-10, 101-109, 225-231. [Google Scholar] [Green Version]
- Ball, P. Critical Mass; Randon House: London, UK, 2005; pp. 107-115, 135-140, 145-192, 443-466. [Google Scholar] [Green Version]
- Barabási, A.L. Linked; Penguin Books: London, UK, 2003. [Google Scholar] [Green Version]
- Maturana, H.R.; Varela, F.J. The Tree of Knowledge; Shambhala: Boston, MA, USA, 1998; pp. 33-52, 198-199. [Google Scholar] [Green Version]
- Johnson, S. Emergence. The Connected Lives of Ants, Brains, Cities,and Software; Scribner: New York, NY, USA, 2001; pp. 73-90, 112-121, 139-162. [Google Scholar] [Green Version]
- Pagels, H.R. The Dreams of Reason; Bantam Book: New York, NY, USA, 1989; pp. 54-70, 205-240. [Google Scholar] [Green Version]
- Salthe, S.N. Evolving Hierarchical Sytems: Their Structure and Representation; Columbia University Press: New York, NY, USA, 1985. [Google Scholar] [Green Version]
- Salthe, S.N. Summary of the principles of hierarchy theory. Gen. Syst. Bull. 2002, 31, 13–17. [Google Scholar]
- Dawkins, R. The Extended Phenotype, revised ed.; Oxford University Press: Oxford, UK, 1999. [Google Scholar] [Green Version]
- Testa, B.; Raynaud, I.; Kier, L.B. What differenciates free amino acids and amino acyl residues? An exploration of conformational and lipophilicity spaces. Helv. Chim. Acta 1999, 82, 657–665. [Google Scholar] [CrossRef]
- Testa, B.; Kier, L.B. Emergence and dissolvence in the self-organization of complex systems. Entropy 2000, 2, 1–25. [Google Scholar] [CrossRef]
- Testa, B.; Kier, L.B.; Carrupt, P.A. A systems approach to molecular structure, intermolecular recognition, and emergence-dissolvence in medicinal research. Med. Res. Rev. 1997, 17, 303–326. [Google Scholar] [CrossRef]
- Bojarski, A.J.; Nowak, M.; Testa, B. Conformational constraints on side chains in protein residues increase their information content. Cell. Molec. Life Sci. 2003, 60, 2526–2531. [Google Scholar] [CrossRef] [PubMed]
- Bojarski, A.J.; Nowak, M.; Testa, B. Conformational fluctuations versus constraints in amino acid side chains: The evolution of information content from free amino acids to proteins. Chem. Biodivers. 2006, 3, 245–273. [Google Scholar] [CrossRef] [PubMed]
- Testa, B.; Kier, L.B.; Bojarski, A.J. Molecules and meaning: How do molecules become biochemical signals? S.E.E.D J. 2002, 2, 84–101. [Google Scholar]
- Janus. Wikipedia entry. Available online: http://en.wikipedia.org/wiki/Janus (accessed November 30, 2009). [Green Version]
- Toffler, A. Foreword to [13], pp xi-xxvi.
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Testa, B. Dispersal (Entropy) and Recognition (Information) as Foundations of Emergence and Dissolvence. Entropy 2009, 11, 993-1000. https://doi.org/10.3390/e11040993
Testa B. Dispersal (Entropy) and Recognition (Information) as Foundations of Emergence and Dissolvence. Entropy. 2009; 11(4):993-1000. https://doi.org/10.3390/e11040993
Chicago/Turabian StyleTesta, Bernard. 2009. "Dispersal (Entropy) and Recognition (Information) as Foundations of Emergence and Dissolvence" Entropy 11, no. 4: 993-1000. https://doi.org/10.3390/e11040993
APA StyleTesta, B. (2009). Dispersal (Entropy) and Recognition (Information) as Foundations of Emergence and Dissolvence. Entropy, 11(4), 993-1000. https://doi.org/10.3390/e11040993



